Convergence and Rate Analysis of Neural Networks for Sparse Approximation

Abstract

We present an analysis of the Locally Competitive Algotihm (LCA), which is a Hopfield-style neural network that efficiently solves sparse approximation problems (e.g., approximating a vector from a dictionary using just a few nonzero coefficients). This class of problems plays a significant role in both theories of neural coding and applications in signal processing. However, the LCA lacks analysis of its convergence properties, and previous results on neural networks for nonsmooth optimization do not apply to the specifics of the LCA architecture. We show that the LCA has desirable convergence properties, such as stability and global convergence to the optimum of the objective function when it is unique. Under some mild conditions, the support of the solution is also proven to be reached in finite time. Furthermore, some restrictions on the problem specifics allow us to characterize the convergence rate of the system by showing that the LCA converges exponentially fast with an analytically bounded convergence rate. We support our analysis with several illustrative simulations.

I. Introduction

Sparse approximation has generated substantial interest in a wide range of research communities over the last two decades, including signal processing, machine learning, statistics, and computational neuroscience (see [2], [3] and references therein).¹ Specifically, sparse approximation involves solving an optimization problem to represent a signal using just a few atoms from some specified (possibly overcomplete) dictionary. In addition to describing compelling models of neural coding for sensory information [4], [5], this approach has led to state-of-the-art results in many types of inverse problems. One example of a regime that has leveraged this type of signal model is the theory of compressed sensing (CS) [6], [7]. In this domain, highly undersampled signals are recovered by solving a sparse approximation problem, thereby shifting the burden of data acquisition from the front-end sensor to a computationally intensive back end.

Because of the increasing interest in the sparse approximation paradigm, significant effort has been made to design efficient algorithms for solving (or approximately solving) least squares optimization problems that are regularized with a sparsity-inducing penalty (e.g., [8]–[10]). However, all of these algorithms are developed to run on digital computers in discrete time, which are both implausible for neural systems and suffer from several drawbacks as engineering approaches. In particular, the computational time required by these algorithms presents a barrier to real-time signal processing applications with high-dimensional signals at significant data rates. Specifically, digital algorithms tend to have storage requirements and convergence times that scale unfavorably with the dimensionality of the signals being approximated. Additionally, the power consumption of digital solutions can be prohibitive for many applications. Given these considerations, a fast and low-power method for solving sparse approximation problems in a parallel architecture would be valuable both for engineering systems and viable models of neural coding.

Analog neural networks have long been proposed for solving optimization problems [11], with an early example being Hopfield's pioneering results [12] using networks to solve linear optimization problems. Analog neural networks offer several potential advantages over comparable digital algorithms, including their ability to be implemented in analog architectures that are highly parallel, fast, and power-efficient. Recent advances in very-large-scale integration (VLSI) reconfigurable analog chips [13] make the design of such systems more feasible and affordable than has often been true in the past. A recent neural network architecture, called a Locally Competitive Algorithm (LCA) [14], has been proposed to solve the types of nonsmooth optimization problems that come up in sparse approximation. These Hopfield-style networks appear to efficiently solve a whole family of sparse approximation problems by incorporating ideal thresholding nonlinearities in the network dynamics. The results in [14] provide encouraging evidence that biological systems and engineering applications can use neural networks to solve these important sparse approximation problems.

However, despite encouraging evidence of its performance, the LCA lacks strong convergence guarantees and estimates of the convergence rate. Furthermore, the specifics of the LCA architecture violate many of the assumptions used in previous analysis, making the extensive literature on neural network convergence inapplicable for this system. For example, in previous work the activation function is often assumed to be linear [15], piecewise linear [16], or nonlinear but increasing and bounded [17]–[20]. In contrast, the LCA activation function is nonlinear and unbounded. Other analyses assume an interconnection matrix which is positive definite [16], [21], [22] or nonsingular [23], [24], while the LCA interconnection matrix may have negative eigenvalues as well as a nontrivial nullspace (because of the approximation dictionary being overcomplete). Other analyses consider a nonsmooth objective function with constraints which shows convergence only when the constraints are nonzero and convex [25], [26]. Finally, other relevant analyses assume that the objective function is convex [27] or piecewise linear [28], while the work in [29] focuses on the controllability of the network path.

The main contributions of this paper are to present a formal analysis of the LCA network architecture and its convergence properties, despite: 1) an activation function that is nonsmooth and not necessarily bounded or increasing and 2) a potentially singular interconnection matrix. Section III contains our first main result, which states that the fixed points of the LCA network correspond to critical points of the objective function. In the special case, where the objective is convex, this set coincides with the global minima of the objective. In addition, we show that the network is globally stable and that the outputs are quasi-convergent, in the sense that they get infinitely close to a set of fixed points. Finally, in the case where the objective function has isolated minima, we show that the LCA converges to the solution of the sparse approximation problem for any initial point (i.e., a much stronger condition than just the nonincreasing property of the energy function that was shown in previous work [14]). This section also shows that the LCA is well behaved in that it converges in a finite number of switches (i.e., nodes crossing above or below threshold). Section IV expands on these general results to show that, under additional mild conditions on the problem specifics, the LCA actually converges exponentially fast to the solution. Furthermore, we give an analytic expression for this convergence rate that depends on the properties of the detailed approximation problem. Finally, Section V presents simulation results showing the correspondence of our analytic results with empirical observations of the network behavior.

II. Background

Before presenting our main results, in this section we briefly give a precise statement of the sparse approximation problems of interest, a description of the LCA architecture, and some preliminary observations on the LCA network dynamics that will be useful in the subsequent analysis.

A. Sparse Approximation

As mentioned above, sparse approximation is an optimization program that seeks to find the approximation coefficients of a signal on a prescribed dictionary, using as few nonzero elements as possible. To fix notation, we denote the input signal by $y\in {\mathbb{R}}^M$, the unit-norm dictionary elements by the columns of the M × N matrix coefficients Φ = [Φ₁, . . . , Φ_N], and the by $a\in {\mathbb{R}}^N$. Generally, $M\ll N$ (i.e., the approximation dictionary is overcomplete), and the problem of recovering a from y is underdetermined. While similar in spirit to the well-known winner-take-all problem [30], sparse approximation problems are generally formulated as the solution to an optimization program because this approach can often yield strong performance guarantees in specific applications (e.g., recovery in a CS problem). In the most generic form, the objective function is the sum of a quadratic data fidelity term (i.e., mean squared error) and a regularization term that uses a sparsity-inducing cost function C(·)

$$\underset{a}{\text{min}}V\left(a\left(t\right)\right)=\frac{1}{2}{\Vert y-\Phi a\Vert }_2^2+\lambda \sum _{n=1}^{N}C\left(a_n\right)$$ (1)

where the parameter λ is a tradeoff between the two terms in the objective function. The “ideal” sparse approximation problem has a cost function that simply counts the number of nonzero elements, resulting in a nonconvex objective function that has many local minima [31].

One of the most widely used programs from this family is known as Basis Pursuit DeNoising (BPDN) [32], which is given by the objective function

$$\underset{a}{\text{min}}\frac{1}{2}{\Vert y-\Phi a\Vert }_2^2+\lambda {\Vert a\Vert }_1.$$ (2)

In BPDN, the ${\ell }_1\text{-norm}$ $({\Vert a\Vert }_1={\sum }_n\mid a_n\mid )$ is used as a convex surrogate the idealized counting norm. This program has gained in popularity as researchers have shown that, in many cases of interest, substituting the ${\ell }_1$ norm yields the same solution as using an idealized (and generally intractable) counting norm [33]. However, BPDN illustrates the canonical challenge of sparse approximation problems. Despite being convex, the BPDN objective function contains a nonsmooth nonlinearity which makes it considerably more difficult than a classic least-squares problem.

In the context of computational neuroscience, sparse approximation has been proposed as a neural coding scheme for sensory information. In one interpretation, programs such as BPDN can be viewed as Bayesian inference in a linear generative model with Gaussian noise and a prior with high kurtosis to encourage sparsity (e.g., the Laplacian prior in the case of BPDN) [5]. Given the prevalence of probabilistic inference as a successful description of human perception [34] and the theoretical benefits of sparse representations [3], it has long been conjectured that sensory systems may encode stimuli via sparse approximation. In fact, in classic results, sparse approximation applied to the statistics of natural stimuli in an unsupervised learning experiment has been shown to be sufficient to qualitatively and quantitatively explain the receptive field properties of simple cells in the primary visual cortex [4], [35] as well as the auditory nerve fibers [36]. Only recently have there been proposals of efficient neural networks that could efficiently solve the necessary optimization problems to implement this type of encoding [14], [35], [37], [38].

B. LCA Structure

Our primary interest will be the LCA [14], which is an analog continuous-time dynamical system that is a type of Hopfield-style network. In particular, each node in the LCA network is characterized by the evolution of a set of internal state variables, u_n(t) for n = 1, . . . , N, and uses a nonlinear activation function T_λ(·) to produce output variables a_n(t) for n = 1, . . . , N. The activation function is typically a nonsmooth nonlinear function (such as a thresholding function) to induce sparsity in the outputs. The dynamics of the internal state variables are governed by a set of coupled nonlinear ordinary differential equations (ODEs)

$$\begin{array}{cc}\hfill \tau \stackrel{.}{u}\left(t\right)& =-u\left(t\right)-({\Phi }^T\Phi -I)a\left(t\right)+{\Phi }^{T}y\hfill \\ \hfill a\left(t\right)& =T_{\lambda }\left(u\left(t\right)\right).\hfill \end{array}$$ (3)

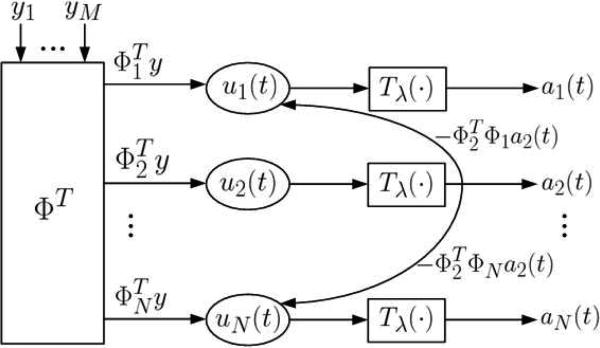
In this network, each node is associated with a single dictionary element Φ_n, n = 1, . . . , N, and the node outputs will be shown to be the solution to the optimization problem of interest. The architecture of a typical LCA is shown in Fig. 1.

Fig. 1.

Block diagram of the LCA [14], which is a Hopfield-style network architecture for solving sparse approximation problems.

The inputs to the LCA network are feedforward connections computing the vector of driving synaptic inputs Φ^T y, reflecting how well the signal y matches each dictionary element. The network also has recurrent inhibitory or excitatory connections between the nodes, modulated by weights corresponding to the interconnection matrix G = Φ^TΦ – I (i.e., a modified Grammian matrix for the dictionary). The more overlap there is between a pair of nodes (characterized by the inner product between their dictionary elements), the stronger will be the potential inhibition between those nodes. While the modulating weight is symmetric between any pair of nodes, the total inhibition is not, because it is also modulated by the activity of each individual node. Moreover, the matrix G potentially has both negative and positive eigenvalues, as well as a nontrivial nullspace. This inhibition structure ensures that nodes that carry the same information will not become active at the same time, thus meeting the goals of sparse approximation. The time constant τ is dependent on the physical properties of the solver implementing the ODEs. For our purposes, we will often assume τ = 1 without loss of generality.

It was shown in [14] that the objective function in (1) is nonincreasing along the LCA trajectory with the following relationship ($\forall a_n\in \mathbb{R}$ such that a_n ≠ 0) between the cost penalty term C(·) and the activation function T_λ(·)

$$\lambda \frac{dC\left(a_n\right)}{d{a}_n}=u_n-a_n=u_n-T_{\lambda }\left(u_n\right).$$ (4)

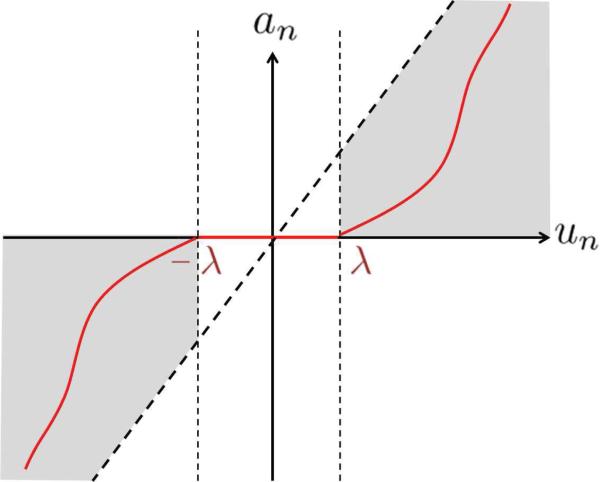
In the case of BPDN, the cost penalty is simply C(x)= |x| and the activation function obtained from (4) is the soft-thresholding function (Fig. 2) defined by

$$a_n\left(t\right)=T_{\lambda }\left(u_n\left(t\right)\right)=\{\begin{array}{cc}0,\hfill & \mid u_n\left(t\right)\mid \le \lambda \hfill \\ u_n\left(t\right)-\lambda \text{sign}\left(u_n\left(t\right)\right),\hfill & \mid u_n\left(t\right)\mid >\lambda .\hfill \end{array}\phantom{\}}$$

This function often arises in connection to algorithms for minimizing the absolute value of the coefficients (see [39]). Generalizing from the soft threshold, we focus on “thresholding” activation functions T_λ(·) of the form

$$a_n\left(t\right)=T_{\lambda }\left(u_n\left(t\right)\right)=\{\begin{array}{cc}0,\hfill & \mid u_n\left(t\right)\mid \le \lambda \hfill \\ f\left(u_n\left(t\right)\right),\hfill & \mid u_n\left(t\right)\mid >\lambda \hfill \end{array}\phantom{\}}$$ (5)

where the function f(·) is real-valued defined and continuous on the domain $\mathcal{D}=(-\infty ,-\lambda ]\cup [\lambda ,+\infty )$, differentiable on the interior if $\mathcal{D}$, and satisfying the conditions

$$f(-u_n)=-f\left(u_n\right)\forall u_n\in \mathcal{D}\text{and}f\left(\lambda \right)=0$$ (6a)

$$f^{\prime }\left(u_n\right)>0\forall u_n\in \mathcal{D}$$ (6b)

$$f\left(u_n\right)\le u_n\forall u_n\in \mathcal{D}\mathrm{s}.\mathrm{t}.u_n\ge 0.$$ (6c)

Fig. 2.

Soft-thresholding activation function. When this is used for the thresholding function T_λ(·), the LCA solves the popular BPDN optimization problem used in many sparse approximation applications.

Remark 1: Equation (6a) ensures that T_λ(·) is continuous on all $\mathbb{R}$ and, consequently, that u(t) and a(t) are continuous with respect to time. This ensures that the cost function C(·) is differentiable everywhere except at the origin. Equation (6b) makes f(·) a bijection on $\mathcal{D}$. Finally, (6a) and (6c) ensure, by a simple computation, that C(·) is positive and nondecreasing with the absolute value of the coefficient. Notice that the ${\ell }_1\text{-minimization}$ objective function satisfies the three criteria in (6), in addition to being convex (which is not required, but guarantees that the system will find a global minima). In Fig. 3, we plot a more generic stylized activation function that satisfies the conditions (6).

Fig. 3.

Generic activation function satisfying conditions (6). The area in gray represents where the activation function must lie in order to satisfy conditions (6b) and (6c).

As shown in Fig. 3, the activation function (5) is composed of two operating regions. The first region corresponds to the case where the internal state u_n is below the threshold λ, in which case the output a_n is zero. We call the nodes in this region inactive nodes. The second region corresponds to the case where the internal state u_n is above threshold, in which case (6b) guarantees that the output a_n is strictly increasing with u_n. We call the nodes that are above threshold active nodes, and we denote by Γ the active set (i.e., the set of indices corresponding to those nodes, Γ = {n ∈ [1, N] : |u_n(t)| > λ}). On the contrary, we denote the set of indices corresponding to nodes that are below threshold by Γ^c and call them the inactive set. While these two sets do change with time as the network evolves, for the sake of readability we omit the dependence on time in the notation.

Owing to the nonsmooth nature of the objective (1), we require the generalized notion of a subgradient (see [40] for more details). Note that V (a) is differentiable everywhere except at points a that contain zeros, due to the nondifferentiability of C(·) at the origin noted above for the cases of interest in sparse approximation. The subgradient ∂V (·) extends the classic notion of a gradient ∇V(·) at those points of discontinuity. The properties in (6) allow us to use the following simple definition:

$$\partial V\left(a\right)=co\left\{\underset{i\to \infty }{\text{lim}}\nabla V\left(a_i\right):a_i\to a,a_i\notin \mathcal{S},a_i\notin {\Omega }_V\right\}$$

where co is the convex hull, Ω_V is the set of points where V fails to be differentiable, and $\mathcal{S}$ is any set of Lebesgue measure 0 in ${\mathbb{R}}^N$. In other words, it is the smallest convex set containing the gradients of the function as we approach the discontinuity from any direction. Note that, when a is not a point of discontinuity, this simply reduces to ∇V(a).

C. LCA Node Dynamics

Because nodes can cross threshold and go from the inactive set to the active set (and vice versa), the LCA can be thought of as a switched system [41] where the ODEs change at each switching time (i.e., when a node crosses above or below threshold). In between two switching times, the active set Γ and inactive set Γ^c are fixed. Therefore, the dynamics on the two sets can be considered separately to facilitate analysis. In the following, ${\Phi }_{\mathcal{T}}$ is the matrix composed of the columns of Φ indexed by the set $\mathcal{T}$. Similarly, $u_{\mathcal{T}}$ and $a_{\mathcal{T}}$ refer to the elements in the original vectors indexed by $\mathcal{T}$. We also denote by ${\left\{t_k\right\}}_{\{k\in \mathbb{N}\}}$ the sequence of times for which the system switches from the set of active nodes Γ_k–1 to Γ_k. The notation T_λ(u(t)) refers to the vector [T_λ(u₁(t)), . . . , T_λ(u_N(t))]^T, and we denote by F′(t) the associated Jacobian matrix with respect to the internal state variables u. Because the activation function has the form in (5), the matrix F′(t) is diagonal with diagonal elements equal to zero for indices in the inactive set Γ^c and equal to f′(u_n) for indices n in the active set Γ.

Using the chain rule and (5), we can calculate the derivative with respect to time of the outputs on the active set Γ as

$${\stackrel{.}{a}}_{\Gamma }\left(t\right)=F_{\Gamma }^{\prime }\left(t\right){\stackrel{.}{u}}_{\Gamma }\left(t\right)=\text{diag}{\left(f^{\prime }\left(u_n\left(t\right)\right)\right)}_{\{n\in \Gamma \}}{\stackrel{.}{u}}_{\Gamma }\left(t\right).$$ (7)

As a consequence, the ODE (3) can be rewritten for nodes in the active set as follows:

$${\stackrel{.}{a}}_{\Gamma }\left(t\right)=F_{\Gamma }^{\prime }\left(t\right)\left[-u_{\Gamma }\left(t\right)+a_{\Gamma }\left(t\right)-{\Phi }_{\Gamma }^T{\Phi }_{\Gamma }{a}_{\Gamma }\left(t\right)+{\Phi }_{\Gamma }^{T}y\right].$$ (8)

The active nodes follow this ODE until the next switch occurs, changing the sets of active and inactive nodes. Similarly, we can rewrite the set of differential equations acting on the inactive nodes. Since the output of the activation function for nodes in Γ^c is zero, the ODE (3) on the inactive set becomes

$${\stackrel{.}{u}}_{{\Gamma }^c}\left(t\right)=-u_{{\Gamma }^c}\left(t\right)-{\Phi }_{{\Gamma }^c}^T{\Phi }_{\Gamma }{a}_{\Gamma }\left(t\right)+{\Phi }_{{\Gamma }^c}^{T}y.$$ (9)

Separating the system dynamics into two separate characterizations for the active nodes Γ and inactive nodes Γ^c yields two sets of differential equations that are partially decoupled, and this will be crucial for our subsequent analysis. This partial decoupling is possible because only the active nodes in the system produce inhibitory signals, coupling their dynamics to the dynamics of each node in the inactive set via the interconnection matrix. However, because inactive nodes do not inhibit active nodes, the dynamics on the active set are independent of the inactive set.

III. Convergence Results

In [14], the authors show that the LCA network trajectory is nonincreasing on the energy surface corresponding to the desired objective function. While this is a necessary behavior for a network that solves an optimization problem, it is not sufficient to actually show that the network converges to a fixed point (or set of points), let alone reaches a minimum of that desired objective function. Both of these are important guarantees to make before relying on this system as a viable model of neural processing or as an implementation in engineering applications.

In Section III-A, we analyze the general convergence properties of the LCA. In particular, in this section the interconnection matrix Φ^TΦ – I may have many negative or zero eigenvalues, which complicates the analysis. The main results of this first section show that the fixed points of the LCA correspond to critical points of the objective (1) and the outputs of the network converge from any initial state to the set of fixed points. In the case of isolated critical points of (1), we show that the LCA is globally convergent in the sense that starting from any initial state, the system converges to a fixed point. Elaborating on these results, Section III-B shows that the LCA (even under very general assumptions) is very well behaved, converging in a finite number of switches (i.e., nodes crossing above or below threshold) and therefore recovering the solution support (i.e., the set of nonzero elements) in finite time. Owing to the difficulties described above, our approach relies on classic results from nonsmooth analysis, such as subgradients and a generalized chain rule (see Appendix A).

A. Global Asymptotic Convergence

To begin, we recall some useful definitions of stability and concepts from Lyapunov theory (see [42] for more background). There exist several notions of stability associated with dynamical systems that describe the evolution of the nodes or their outputs both locally and globally. For a neural network described by a differential equation of the form

$$\stackrel{.}{x}=G\left(x\right),x\in {\mathbb{R}}^N$$ (10)

with outputs z = T_λ(x) defind as in (5), we say that a constant vector $x^{\ast }\in {\mathbb{R}}^N$ is a fixed point of (10) if and only if

$$G\left(x^{\ast }\right)=0.$$ (11)

On the other hand, the outputs of a system reach a critical point a^c of the objective function V(·) when they satisfy the inclusion

$$0\in \partial V\left(a^c\right).$$ (12)

Note that, if V(·) is convex, then the critical points correspond exactly to the global minima of V. We say that (10) is (Lyapunov) stable at x* if, for each ε > 0, there exists R > 0 such that for all x₀ with ∥x₀ – x*∥ < R, and all the solutions x(·) with initial state x₀

$$\Vert x\left(t\right)-x^{\ast }\Vert <∊\forall t>0.$$ (13)

This is clearly a local notion of stability, guaranteeing that, once the trajectory is close to a fixed point, it remains nearby. But this type of stability is insufficient to guarantee global convergence, which means that trajectories approach a fixed point as time goes to infinity. The following notion of stability is slightly stronger, guaranteeing that trajectories approach at least a set of fixed points regardless of the initial state.

Definition 1: We say that the outputs of (10) are globally quasi-convergent if there exists a set $\mathcal{E}=\{z^{\ast }\in {\mathbb{R}}^N:{\stackrel{.}{z}}^{\ast }=0\}$ such that for all $x_0\in {\mathbb{R}}^N$, the outputs z(·) = T_λ (x(·)) with initial state x₀ satisfy $\underset{t\to +\infty }{\text{lim}}z\left(t\right)\in \mathcal{E}$.

Finally, the strongest and most desirable form of convergence which guarantees that the nodes converge to a single fixed point is stated in the next definition.

Definition 2: We say that (10) is globally convergent, or equivalently globally asymptotically stable, if there exists a fixed point x* at which the system is stable, and if for all initial states $x_0\in {\mathbb{R}}^N$ the solutions x(·) satisfy $\underset{t\to +\infty }{\text{lim}}x\left(t\right)=x^{\ast }$.

Typically, global convergence is established through the use of a so-called Lyapunov function V. The notation V̇ refers to the derivative with respect to time, i.e., dV/dt.

Definition 3: A function $V:{\mathbb{R}}^N\mapsto \mathbb{R}$ is a weak Lyapunov function on ${\mathbb{R}}^N$ if:

1. V(x) > 0 $\forall x\ne 0$;

2. V is continuous on ${\mathbb{R}}^N$;

3. V̇(x) ≤ 0 $\forall x\in {\mathbb{R}}^N$;

4. V is radially unbounded

   $$\underset{\Vert x\Vert \to +\infty }{\text{lim}}V\left(x\right)=+\infty .$$

Similarly, a function is called a strict Lyapunov function if it meets the above conditions, with the exception of having a strict inequality in condition 3) (i.e., V̇(x) < 0, $\forall x\in {\mathbb{R}}^N$).

Remark 2: When it is possible to find a weak Lyapunov function for a given dynamical system, the first theorem of Lyapunov [42] guarantees that any fixed point of the system is stable in the sense of (13). However, to show global convergence of a system, the second theorem of Lyapunov requires a strict Lyapunov function.

One can check that the objective function in (1) is a weak Lyapunov function for (3), thus guaranteeing that the LCA is Lyapunov stable (which improves on the stability result obtained in [14]). However, it is not a strict Lyapunov function. Indeed, (1) only depends on the active nodes, meaning that it could stop decreasing while subthreshold nodes are still evolving. Continued evolution of the inactive nodes could cause a node in Γ^c to become active, thereby causing the objective function to start decreasing again. As a consequence, condition 3) in Definition 3 is not satisfied with strict inequality, and the standard approach of using the objective function as a Lyapunov function is not sufficient to show global convergence of the LCA. To show global convergence of the system to a fixed point, it is necessary to account for the dynamics on both active and inactive nodes.

Our main convergence theorem guarantees the global quasi-convergence of the LCA toward a set of critical points of the objective function. In the case of isolated critical points, this implies global convergence.

Theorem 1: The LCA system defined in (3), with an activation function of the form (5) satisfying conditions (6):

1. has fixed points that are critical points of the objective function defined in (1);

2. has globally quasi-convergent outputs;

3. is globally convergent, provided that the critical points of (1) are isolated.

Note that part 2 of the above theorem only relates to the output variables, while part 3 is a much stronger condition on the entire dynamical system (including subthreshold states). In the highly relevant case of convex objective functions with unique minima (e.g., BPDN), part 3 of the above theorem applies directly and we have the strongest possible notion of convergence. In fact, for most dictionaries Φ (e.g., random Gaussian), the minimum of the ${\ell }_1\text{-minimization}$ objective function (2) is unique [43]. Recent results on subgradient dynamical systems [26], [44] lead us to believe that part 3 could still hold in the case where the fixed points of the system are not isolated and there exists a subspace of solutions to (1), but this conjecture is beyond the scope of this paper. Section V-A illustrates the convergence behavior of the LCA in simulation. The proof of this theorem is in Appendix A, and relies on generalized notions of a subgradient due to the nonsmooth nature of the objective.

B. Convergence in a Finite Number of Switches

In the theorem below, we strengthen the previous result to establish that, under some mild conditions, the support of the final solution is reached with a finite number of switches. To prove this result, it is sufficient to assume that no node in the solution lies exactly on the threshold λ. This assumption precludes unwanted infinite oscillation behavior on the boundaries, known as Zeno behavior. In other words, we assume that there exists a margin (r > 0) above and below the threshold which contains no node in u*. One would expect this condition to hold with near-certainty for any signal that was not pathologically constructed.

Theorem 2: If (3) converges to a fixed point u* such that there exists r > 0

$$\begin{array}{c}\hfill \forall n\in {\Gamma }_{\ast },\hfill \\ \hfill \forall n\in {\Gamma }_{\ast }^c,\hfill \end{array}\mid \begin{array}{c}\hfill u_n^{\ast }\hfill \\ \hfill u_n^{\ast }\hfill \end{array}\mid \begin{array}{c}\hfill \ge \lambda +r\hfill \\ \hfill \le \lambda -r\hfill \end{array}$$

then the system converges after a finite number of switches. This implies that the neural network recovers the support of the solution a* in finite time. Section V-A explores the number of switches during the convergence of the LCA in simulation.

Proof: Let Γ_* be the set of active nodes in u*. By contradiction, assume that the sequence of switching times ${\left\{t_k\right\}}_{k\in \mathbb{N}}$ is infinite. Since the LCA converges to u*, we have

$$u\left(t_k\right)\underset{k\to +\infty }{\to }{u}^{\ast }.$$

As a consequence, for r > 0, there exists $K\in \mathbb{N}$ such that $\forall k\ge K,{\Vert u\left(t_k\right)-u^{\ast }\Vert }_2<r$. To begin, we show that for all k ≥ K, the state variables u(t_k) are in the subsystem Γ_*. For all k ≥ K, we have two cases.

1. Nodes that are above threshold in u* are above threshold in u(t_k). Indeed, $\forall n\in {\Gamma }_{\ast }$, we have

   $$\begin{array}{cc}\hfill r>\mid u_n\left(t_k\right)-u_n^{\ast }\mid & \ge \mid u_n^{\ast }\mid -\mid u_n\left(t_k\right)\mid \ge \lambda +r-\mid u_n\left(t_k\right)\mid \hfill \\ \hfill & \Rightarrow \mid u_n\left(t_k\right)\mid >\lambda .\hfill \end{array}$$

   Moreover, nodes are active with the correct sign; otherwise, we would have

   $$\begin{array}{cc}\hfill r>\mid u_n\left(t_k\right)-u_n^{\ast }\mid & =\mid u_n\left(t_k\right)\mid +\mid u_n^{\ast }\mid >\lambda +\lambda +r\hfill \\ \hfill & \Rightarrow 0>\lambda \hfill \end{array}$$

   which is a contradiction.
2. Nodes that are below threshold in u* are below threshold in u(t_k). Indeed, $\forall n\in {\Gamma }_{\ast }^c$, we have

   $$\begin{array}{cc}\hfill \mid u_n\left(t_k\right)\mid -\lambda & \le \mid u_n\left(t_k\right)\mid -\mid u_n^{\ast }\mid -r\le \mid u_n\left(t_k\right)-u_n^{\ast }\mid -r<0\hfill \\ \hfill & \Rightarrow \mid u_n\left(t_k\right)\mid <\lambda .\hfill \end{array}$$

As a consequence, for all k ≥ K, Γ_k = Γ_*. However, Γ_k and Γ_k+1 must be different to define the switching time t_k+1 and we reach a contradiction. This proves that after a finite number of switches K, there cannot be any switching out of subsystem Γ_*.

IV. Exponential Convergence Rate

With Theorem 1 showing that the LCA is globally convergent, the most pressing issue remaining is to determine the convergence rate of the network. Such a bound will be especially important for implementations, which must guarantee solution times. In this section, we show that, under some additional conditions on the problem's specifics [given in (16)], the LCA network converges exponentially fast to a unique fixed point u*. We also give an analytic characterization of the convergence speed.²

To begin this section, we recall the definition of exponential convergence.

Definition 4: The dynamical system in (10) is exponentially convergent to the solution x* if there exists a constant c > 0 such that for any initial point x(0), there exists a constant κ₀ > 0 [which may depend on x(0)] for which the trajectory x(t) of the system satisfies

$$\Vert x\left(t\right)-x^{\ast }\Vert \le {\kappa }_0{e}^{-ct}\forall t\ge 0.$$

The constant c is referred to as convergence speed of the system.

In order to state the main theorem of this section, we define the two following quantities. The first constant is denoted by α and provides a bound on the derivative of f(·) in (5)

$$\forall t\ge 0,\forall n=1,\dots ,N\mid f^{\prime }\left(u_n\left(t\right)\right)\mid \le \alpha .$$ (14)

Note that the constant α is always well defined since the trajectories u_n(t) are bounded and the function f(·) is continuous. The second constant, denoted by δ, is the smallest positive constant such that for any active set Γ visited by the algorithm and any vector x in ${\mathbb{R}}^N$ with active set $\tilde{\Gamma }=\Gamma \cup {\Gamma }_{\ast }$, where Γ_* is the active set of the solution to (1); we have

$$(1-\delta ){\Vert x\Vert }_2^2\le {\Vert \Phi x\Vert }_2^2\le (1+\delta ){\Vert x\Vert }_2^2.$$ (15)

The constant δ depends on the singular values of the matrix ${\Phi }_{\tilde{\Gamma }}$ and on the sequence of active sets visited by the system. It may not be well defined for any matrix Φ or any input y. However, in many interesting cases in CS, the constant δ is close to 0 and the dictionary elements are almost orthogonal for any small enough active set [45]. The following theorem shows that this constant directly relates to the convergence speed of the neural network.

Theorem 3: Under conditions (6) on the activation function in (5), and provided that the constants α and δ, defined in (14) and (15), respectively, satisfy

$$\delta <\text{min}\left(1,\frac{1}{{(2\alpha -1)}^2}\right)$$ (16)

the LCA system defined in (3) is globally exponentially convergent to a unique equilibrium, with convergence speed (1 – δ)/2τ.

If condition (16) is satisfied, the expression given for the convergence speed is positive and thus meaningful. It depends on the eigenvalues of the matrix ${\Phi }_{\Gamma }^T{\Phi }_{\Gamma }$, which vary with the active set Γ. A careful analysis of the sequence of active sets visited by the network is required to obtain a good estimate of δ. Since such a study is application dependent, we do not address this question here. Note that in the very interesting case of the soft-threshold function, α = 1 and so condition (16) reduces to δ < 1. The time constant τ of the physical solver implementing the LCA neural network appears in the expression of the speed of convergence. Lowering this time constant means the system will converge faster. Analog systems can have smaller time constants than their digital counterparts, which scale better with the problem size. Section V-B explores the convergence rate bounds for the LCA in simulation.

To establish the expression of the convergence speed, we use the following Lure-Postnikov-type Lyapunov function:

$$E\left(t\right)=\frac{1}{2}{\Vert \tilde{u}\left(t\right)\Vert }_2^2+\sum _{n=1}^N{\int }_0^{{\tilde{u}}_n\left(t\right)}{g}_n\left(s\right)ds$$ (17)

where we again redefine the output and state variables in terms of the distance from any arbitrary fixed point u* as

$$\begin{array}{cc}\hfill {\tilde{u}}_n\left(t\right)& =u_n\left(t\right)-u_n^{\ast }\hfill \\ \hfill {\tilde{a}}_n\left(t\right)& =a_n\left(t\right)-a_n^{\ast }=T_{\lambda }({\tilde{u}}_n\left(t\right)+u_n^{\ast })-T_{\lambda }\left(u_n^{\ast }\right)\hfill \end{array}$$ (18)

and the function $g_n\left(s\right)=T_{\lambda }(s+u_n^{\ast })-T_{\lambda }\left(u_n^{\ast }\right)$, which captures how a perturbation of the internal state affects the output. Because the second term in (17) is nonnegative, we have trivially that this energy function bounds the mean-squared error of the current state values to their steady-state values, i.e., (1/2) ${\Vert \tilde{u}\left(t\right)\Vert }_2^2\le E\left(t\right)$. The theorem will prove that u* is unique. The properties presented in the following Lemma (see Appendix B for proof) are useful to prove the main result of this section.

Lemma 1: Assume that the activation function (5) satisfies the conditions (6). Then, the set of variables $\tilde{u}$ and $\tilde{a}$ defined in (18) satisfy the following properties:

1. $\text{sign}\left({\tilde{a}}_n\right)=\text{sign}\left({\tilde{u}}_n\right)$;

2. $\mid {\tilde{a}}_n\mid \le \alpha \mid {\tilde{u}}_n\mid$

3. ${\tilde{a}}_{\mathcal{T}}^T{\tilde{a}}_{\mathcal{T}}\le \alpha {\tilde{u}}_{\mathcal{T}}^T{\tilde{a}}_{\mathcal{T}}\le {\alpha }^2{\tilde{u}}_{\mathcal{T}}^T{\tilde{u}}_{\mathcal{T}}$ for any $\mathcal{T}$ (in particular for $\mathcal{T}=\tilde{\Gamma }$);

4. ${\sum }_{n=1}^N{\int }_0^{{\tilde{u}}_n\left(t\right)}{g}_n\left(s\right)ds\le {\tilde{u}}^T\tilde{a}$.

Armed with this lemma, we can now give the proof of the main theorem.

Proof of Theorem 3: We begin by noting that since u* and a* are the internal state variables and the outputs at a fixed point of (3); we can rewrite the dynamics in terms of the new variables

$$\tau \dot{\tilde{u}}\left(t\right)=-\tilde{u}\left(t\right)-\left({\Phi }^T\Phi -I\right)\tilde{a}\left(t\right).$$ (19)

Using the chain rule, we find the expression for the derivative with respect to time of the energy function (17) as

$$\tau \stackrel{.}{E}\left(t\right)=\tau \frac{dE{\left(\tilde{u}\left(t\right)\right)}^T}{d\tilde{u}\left(t\right)}\frac{d\tilde{u}\left(t\right)}{dt}={\left(\tilde{u}\left(t\right)+\tilde{a}\left(t\right)\right)}^T\tau \dot{\tilde{u}}\left(t\right)t.$$

Using (19), this becomes

$$\tau \stackrel{.}{E}\left(t\right)=-{\left(\tilde{u}\left(t\right)+\tilde{a}\left(t\right)\right)}^T\left(\tilde{u}\left(t\right)+\left({\Phi }^T\Phi -I\right)\tilde{a}\left(t\right)\right).$$

Using the properties in Lemma 1 leads to the desired expression (and removing the term t to increase readability)

$$\begin{array}{cc}\hfill \tau \stackrel{.}{E}\left(t\right)& =-{\left(\tilde{u}+\tilde{a}\right)}^T\left(\tilde{u}+\left({\Phi }^T\Phi -I\right)\tilde{a}\right)\hfill \\ \hfill & ={(\tilde{u}+\tilde{a})}^T\left(-\tilde{u}+\tilde{a}-{\Phi }^T\Phi \tilde{a}\right)\hfill \\ \hfill & =-{\tilde{u}}^T\tilde{u}+{\tilde{a}}^T\tilde{a}-{\tilde{a}}^T{\Phi }^T\Phi \tilde{a}-{\tilde{u}}^T{\Phi }^T\Phi \tilde{a}.\hfill \end{array}$$

Adding and subtracting the term $(1∕2)\tilde{u}{\Phi }^T\Phi \tilde{u}$ results in

$$\begin{array}{cc}\hfill \tau \stackrel{.}{E}\left(t\right)& =-{\tilde{u}}^T\tilde{u}+{\tilde{a}}^T\tilde{a}-{\tilde{a}}^T{\Phi }^T\Phi \tilde{a}+\frac{1}{2}{(\tilde{u}-\tilde{a})}^T{\Phi }^T\Phi (\tilde{u}-\tilde{a})-\frac{1}{2}\tilde{u}{\Phi }^T\Phi \tilde{u}-\frac{1}{2}{\tilde{a}}^T{\Phi }^T\Phi \tilde{a}\hfill \\ \hfill & =-{\tilde{u}}^T\tilde{u}+{\tilde{a}}^T\tilde{a}-\frac{3}{2}{\Vert \Phi \tilde{a}\Vert }_2^2+\frac{1}{2}{\Vert \Phi (\tilde{u}-\tilde{a})\Vert }_2^2-\frac{1}{2}{\Vert \Phi \tilde{u}\Vert }_2^2.\hfill \end{array}$$

We separate the vectors into their components onto the active set $\tilde{\Gamma }=\Gamma \cup {\Gamma }^{\ast }$ of $\tilde{a}$ and its complement ${\tilde{\Gamma }}^c$ as

$$\begin{array}{cc}\hfill \frac{1}{2}{\Vert \Phi (\tilde{u}-\tilde{a})\Vert }_2^2-\frac{1}{2}{\Vert \Phi \tilde{u}\Vert }_2^2& =\frac{1}{2}{\Vert {\Phi }_{\tilde{\Gamma }}\left({\tilde{u}}_{\tilde{\Gamma }}-{\tilde{a}}_{\tilde{\Gamma }}\right)\Vert }_2^2+\frac{1}{2}{\Vert {\Phi }_{{\tilde{\Gamma }}^c}{\tilde{u}}_{{\tilde{\Gamma }}^c}\Vert }_2^2-\frac{1}{2}{\Vert \Phi \tilde{u}\Vert }_2^2\hfill \\ \hfill & =\frac{1}{2}{\Vert {\Phi }_{\tilde{\Gamma }}\left({\tilde{u}}_{\tilde{\Gamma }}-\tilde{a}\right)\Vert }_2^2-\frac{1}{2}{\Vert {\Phi }_{\tilde{\Gamma }}{\tilde{u}}_{\tilde{\Gamma }}\Vert }_2^2.\hfill \end{array}$$

We can now use the definition of δ in (15)

$$\begin{array}{cc}\hfill \tau \stackrel{.}{E}\left(t\right)& \le -{\tilde{u}}^T\tilde{u}+{\tilde{a}}^T\tilde{a}-\frac{3}{2}(1-\delta ){\Vert \tilde{a}\Vert }_2^2+\frac{1}{2}(1+\delta ){\Vert {\tilde{u}}_{\tilde{\Gamma }}-\tilde{a}\Vert }_2^2-\frac{1}{2}(1-\delta ){\Vert {\tilde{u}}_{\tilde{\Gamma }}\Vert }_2^2\hfill \\ \hfill & =-\frac{1}{2}(1-\delta ){\tilde{u}}^T\tilde{u}-(1-\delta ){\tilde{u}}^T\tilde{a}-\frac{1}{2}(1-\delta ){\tilde{u}}_{\tilde{\Gamma }}^T{\tilde{u}}_{\tilde{\Gamma }}-2\delta {\tilde{u}}_{\tilde{\Gamma }}^T\tilde{a}+2\delta {\tilde{a}}^T\tilde{a}-\frac{1}{2}(1+\delta ){\Vert {\tilde{u}}_{{\tilde{\Gamma }}^c}\Vert }_2^2\hfill \\ \hfill & \le -\frac{1}{2}(1-\delta ){\tilde{u}}^T\tilde{u}-(1-\delta ){\tilde{u}}^T\tilde{a}-\frac{1}{2}(1-\delta ){\tilde{u}}_{\tilde{\Gamma }}^T{\tilde{u}}_{\tilde{\Gamma }}-2\delta {\tilde{u}}_{\tilde{\Gamma }}^T\tilde{a}+2\delta {\tilde{a}}^T\tilde{a}.\hfill \end{array}$$

Now, using property 3) of Lemma 1, the expression becomes

$$\begin{array}{cc}\hfill \tau \stackrel{.}{E}\left(t\right)& \le -\frac{1}{2}(1-\delta ){\Vert \tilde{u}\Vert }_2^2-(1-\delta ){\tilde{u}}^T\tilde{a}+\left[-\frac{1}{2\alpha }(1-\delta )-2\delta +2\delta \alpha \right]{\tilde{u}}_{\tilde{\Gamma }}^T\tilde{a}\hfill \\ \hfill & =-\frac{1}{2}(1-\delta ){\Vert \tilde{u}\Vert }_2^2-(1-\delta ){\tilde{u}}^T\tilde{a}-\frac{1}{2\alpha }\left[1-\delta {(2\alpha -1)}^2\right]{\tilde{u}}_{\tilde{\Gamma }}^T\tilde{a}.\hfill \end{array}$$

From (16), we know that 1 – δ(2α – 1)² ≥ 0, and so

$$\tau \stackrel{.}{E}\left(t\right)\le -\frac{1}{2}(1-\delta ){\Vert \tilde{u}\Vert }_2^2-(1-\delta ){\tilde{u}}^T\tilde{a}.$$

Finally, using property 4) of Lemma 1 and the fact that δ ≤ 1, we arrive at

$$\begin{array}{cc}\hfill \tau \stackrel{.}{E}\left(t\right)& \le -\frac{1}{2}(1-\delta ){\Vert \tilde{u}\Vert }_2^2-(1-\delta )\sum _{n=1}^N{\int }_0^{{\tilde{u}}_n\left(t\right)}{g}_n\left(s\right)ds\hfill \\ \hfill & =-(1-\delta )E\left(t\right).\hfill \end{array}$$

Knowing already that E(t) is an upper bound on the quantity of interest, we can integrate both sides of the above inequality (i.e., apply Gronwall's inequality) to get a bound on E(t)

$$\frac{1}{2}{\Vert u\left(t\right)-u^{\ast }\Vert }_2^2\le E\left(t\right)\le e^{-(1-\delta )t∕\tau }E\left(0\right)$$ (20)

proving that the LCA is exponentially convergent to a unique fixed point u*. Taking the square root, this expression also shows that the convergence speed in the exponential is (1 – δ)/(2τ), as stated in the theorem.

V. Simulations

In this section, we illustrate the previous theoretical results in simulation. Each plot is based on the following canonical sparse approximation problem. We generate a “true” sparse vector $a_0\in {\mathbb{R}}^N$, with N = 512 and s = 5 nonzero entries. We select the locations of the nonzeros uniformly at random and draw their amplitudes from a normal Gaussian distribution (then normalizing to have unit norm). We choose a dictionary Φ as a union of the canonical basis and a sinusoidal basis having dimensions M × N with M = 256. The vector of measurements is $y=\Phi a_0+\eta \in {\mathbb{R}}^M$, where η is Gaussian random noise with standard deviation 0.0062. We use an LCA with a soft-threshold activation function, with the threshold set to λ = 0.025 and u(0) = 0. We simulate the LCA dynamical equations (3) through a discrete approximation in Matlab with a step size of 0.001 and a solver time constant chosen to be equal to τ = 0.01.

A. Convergence Results

From Theorem 1, the LCA should converge and recover the solution to the sparse approximation problem (1), which has a unique minimizer. Since the signal a₀ to recover is sparse, the outputs of the neural network are expected to converge to a solution close to the initial signal a₀. Fig. 4 shows the evolution of a few nodes u_n(t) selected at random. We see that both active and inactive nodes converge relatively quickly. Fig. 5 shows the fixed point reached by the LCA system and compares it to the initial signal a₀ and to the solution obtained using a standard digital solver for the same optimization program [8]. The solution reached by the network possesses exactly five nonzero entries which correspond to the nonzero entries in a₀. The recovered amplitudes are very close to the initial amplitudes (it cannot be exact due to the added measurement noise) and to the ones produced by the reference digital solver. However, the LCA produces a sparse vector while the digital solver returns many small but nonzero entries that would have to be removed by postprocessing.

Fig. 4.

Plot of the evolution with respect to time of several LCA nodes u_k(t). The plain lines correspond to nodes that are active in the final solution and the dashed lines correspond to nodes that are inactive in the final solution.

Fig. 5.

Output a* of the LCA after convergence. Only nonzero elements are plotted. The fixed point reached by the system is very close to the initial sparse vector used to create the measurement vector (it cannot be exact due to noise). The solution is also very close to a standard digital solver [8] run using the same inputs. Note that the LCA produces many coefficients that are exactly zero (therefore not plotted).

To illustrate the global convergence behavior, we also ran the LCA for 30 randomly generated initial points. We selected two nodes from the final active set and plotted the trajectories in the space defined by those two nodes. Fig. 6 clearly shows that the solution is attractive for any of those initial points.

Fig. 6.

Trajectories of u(t) in the plane defined by two nodes chosen randomly from the active set. Trajectories are shown for 30 random initial states.

To illustrate the number of switches used by the system (see Theorem 2), we generate 1000 sparse vectors a₀ and measurements y and simulate the LCA dynamics. Fig. 7 shows a histogram of the number of switches needed for the system to converge. The figure illustrates that the number of switches before convergence of the neural network is finite and of the order of the dictionary size. This illustrates that this solver takes an efficient path toward the solution.

Fig. 7.

Histogram (in percentage) of the number of switches the LCA requires before convergence over 1000 trials.

B. Convergence Rate Results

To illustrate the convergence rate result in Theorem 3, it is necessary to find an expression for the convergence speed (1 – δ)/τ that appears in the exponential term in (20). This term bounds the error squared

$$\frac{1}{2}{\Vert u\left(t\right)-u^{\ast }\Vert }_2^2$$

which is normalized to have initial value at t = 0 of 1 and plotted using a log-scale on Fig. 8. Note that the constant δ defined in (15) depends on the sequence of active sets Γ_k visited by the system. However, it is very difficult to predict for a given input signal what sequence of active sets the algorithm is going to visit. To estimate this upper bound, we compute the constant δ using the matrix Φ_Γ* composed of the dictionary elements that are active in the final solution. The corresponding upper bound on the decay e^{–(1–δ*)t/τ} is plotted in Fig. 8. During the transient phase, the number of active nodes is actually larger and therefore we expect 1 – δ to be smaller than this estimate and the nodes to converge more slowly at some point during the transient phase. As a consequence, we keep track of the largest support visited by the network and compute the corresponding δ. This second upper bound e^{–(1–δ_max)t/τ} on the convergence rate is plotted on the same figure. As expected, the theoretical decay computed with the maximum support visited is an upper bound for the convergence speed. However, it can be seen that this estimate is very pessimistic and that the bound computed with the final active set is a better estimate. This simulation illustrates that the theoretical exponential convergence appears to capture the essential system behavior.

Fig. 8.

Convergence behavior of $(1∕2){\Vert u\left(t\right)-u^{\ast }\Vert }_2^2$. The dashed line shows the theoretical decay in (20) with δ* computed by using the final solution support. The dash-dot line shows the theoretical decay with δ_max computed on the largest support visited. While both estimates are showing theoretically correct behavior, the estimate of the rate based on δ* is more empirically accurate than the conservative estimate based on δ_max.

VI. Conclusion

This paper presented a mathematical analysis of the convergence properties and convergence rate of the LCA, a neural network designed specifically for the challenging sparse approximation problem. Despite a nonsmooth activation function and possibly singular interconnection matrix that prevent the application of existing analysis approaches, we have shown that the system is globally convergent to the optimal solution. In addition, under some mild assumptions on the solution, we have shown that the trajectories follow a reasonable path and reach the final active set in finite time. Finally, under slightly stronger assumptions on the problem specifics (applicable at least in CS recovery problems), we established that the LCA is exponentially convergent and with a convergence rate that depends on problem-specific parameters.

This collection of results and analysis leads us to conclude that performance guarantees can be made for the LCA system that make it plausible for implementation in engineering applications and as a model of biological information processing. Indeed, providing such guarantees makes it easier to justify the expense associated with developing analog VLSI implementations, which could eventually result in significant improvements to the speed and power consumption necessary for real-time signal processing applications. Our future work will concentrate on finding reasonable estimates of the theoretical convergence speed (especially in well-studied special cases such as CS recovery) and further characterizations of the LCA system dynamics that may open up new applications of this system for time-varying input signals.

Biography

Aurèle Balavoine (S'09) received the B.S. degree from Ecole Supérieure d'Electricité, Gif-sur-Yvette, France, in 2008, and the M.S. degree from the Georgia Institute of Technology, Atlanta, in 2009. She is currently pursuing the Ph.D. degree with the School of Electrical and Computer Engineering, Georgia Institute of Technology.

Her current research interests include sparsity-based signal processing, mathematical optimization, dynamical systems, and neural networks.

Justin Romberg (S'98–M'03–SM'12) received the B.S.E.E., M.S., and Ph.D. degrees from Rice University, Houston, TX, in 1997, 1999, and 2004, respectively.

He was a Researcher with Xerox PARC, Palo Alto, CA, in 2000, a Visitor with the Laboratoire Jacques-Louis, Lions, Paris, in 2003, and a Fellow with UCLA's Institute for Pure and Applied Mathematics, Los Angeles, CA, in 2004. He was a Post-Doctoral Scholar with the Department of Applied and Computational Mathematics, California Institute of Technology, Pasadena, from 2003 to 2006. He joined the faculty of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, in 2006, and is currently an Associate Professor and a member of the Center for Signal and Image Processing.

Dr. Romberg was a recipient of ONR Young Investigator Award in 2008 and the PECASE Award and a Packard Fellowship in 2009. He was named a Rice University Outstanding Young Engineering Alumnus in 2010. From 2008 to 2011, he was an Associate Editor for the IEEE Transactions on Information Theory.

Christopher J. Rozell (S'00–M'09–SM'12) received the B.S.E. degree in computer engineering and the B.F.A. degree in performing arts technology (music technology) in 2000 from the University of Michigan, Ann Arbor, and the M.S. and Ph.D. degrees in electrical engineering from Rice University, Houston, TX, in 2002 and 2007, respectively.

He was a Texas Instruments Distinguished Graduate Fellow with Rice University, and following graduate school was a Post-Doctoral Research Fellow with the Redwood Center for Theoretical Neurosciences, University of California, Berkeley. He joined the faculty at the Georgia Institute of Technology, Atlanta, in 2008, where he is currently an Assistant Professor with the School of Electrical and Computer Engineering, and a member of the Laboratory for Neuroengineering, and the Center for Signal and Image Processing. His current research interests include constrained sensing systems, sparse representations, statistical signal processing, and computational neuroscience.

Appendix A

Proof of Theorem 1

Building on the earlier definition of a subgradient to give a notion that nondifferentiable functions can still be well behaved, a function $g:X\to \mathbb{R}$ (where X is a Banach space) is said to be regular [40, Def. 2.3.4] at x in X if:

1. for all υ ∈ X, the usual one-sided directional derivative

   $$g^{\prime }(x;\upsilon )=\underset{t\downarrow 0}{\text{lim}}\frac{g(x+t\upsilon )-g\left(x\right)}{t}\text{exists};$$
2. for all υ ∈ X, g′(x; υ) = g°(x; υ), where g°(x; υ) is the generalized directional derivative

   $$g^{°}(x;\upsilon )=\underset{\begin{array}{c}\hfill y\to x\hfill \\ \hfill t\downarrow 0\hfill \end{array}}{\text{lim sup}}\frac{g(y+t\upsilon )-g\left(y\right)}{t}.$$

It can easily been seen that, since the function C(·) is defined from $\mathbb{R}$ to $\mathbb{R}$ and is differentiable on $\mathbb{R}\backslash \left\{0\right\}$, and the function T_λ(·) is continuous on all $\mathbb{R}$, then C(·) admits left and right derivatives and is clearly regular on $\mathbb{R}$. This implies that V(·) is regular on ${\mathbb{R}}^N$, and by [40, Prop. 2.3.3] we have that

$$\partial V\left(a\left(t\right)\right)=-{\Phi }^{T}y+{\Phi }^T\Phi a\left(t\right)+\lambda \partial C\left(a\left(t\right)\right)$$ (21)

where ∂C(a(t)) = [∂C(a₁(t)), . . . , ∂C(a_N(t))]^T. We also recall the following result [40, Th. 2.3.9 (iii)], which is a generalization of the chain rule for regular functions.

Lemma 2: Suppose that $V\left(a\right):{\mathbb{R}}^N\to \mathbb{R}$ is regular in ${\mathbb{R}}^N$ and that $a\left(t\right):[0,+\infty )\to {\mathbb{R}}^N$ is strictly differentiable on [0, +∞). Then, V(a(t)) is regular on ${\mathbb{R}}^N$, and we have

$$\frac{d}{dt}V\left(a\left(t\right)\right)={\zeta }^T\stackrel{.}{a}\left(t\right)\forall \zeta \in \partial V\left(a\left(t\right)\right).$$ (22)

Note that, from this theorem, since V(a(t)) is regular, we can choose any element in ∂V(a(t)) to compute the time derivative of V(·) along the trajectories of the neural network. Armed with these tools, we proceed with the proof of Theorem 1.

Proof of Theorem 1: Beginning with part 1 of the theorem, we first show that any fixed point of system (3) is a critical point of the objective in (1). From (11), any fixed point u* of (3) satisfies the relationship u̇(t) = 0. Let Γ_* be the active set at the fixed point u*. Equations (8) and (9) yield

$$-u_{{\Gamma }_{\ast }}^{\ast }+f\left(u_{{\Gamma }_{\ast }}^{\ast }\right)-{\Phi }_{\Gamma }^T{\Phi }_{\Gamma }{a}_{{\Gamma }_{\ast }}^{\ast }+{\Phi }_{{\Gamma }_{\ast }}^{T}y=0$$ (23)

$$-u_{{\Gamma }_{\ast }^c}^{\ast }-{\Phi }_{{\Gamma }_{\ast }^c}^T{\Phi }_{{\Gamma }_{\ast }}{a}_{{\Gamma }_{\ast }}^{\ast }+{\Phi }_{{\Gamma }_{\ast }^c}^{T}y=0.$$ (24)

According to (12), and using (21), a point a* is a critical point of V(·) if and only if

$${\Phi }^{T}y-{\Phi }^T\Phi a^{\ast }\in \lambda \partial C\left(a^{\ast }\right).$$ (25)

For the nodes in the active set n ∈ Γ_*, C(a_n) admits a usual gradient, as defined in (4), and thus (25) yields

$${\Phi }_{{\Gamma }_{\ast }}^{T}y-{\Phi }_{{\Gamma }_{\ast }}^T{\Phi }_{{\Gamma }_{\ast }}{a}_{{\Gamma }_{\ast }}^{\ast }=u_{{\Gamma }_{\ast }}^{\ast }-f\left(u_{{\Gamma }_{\ast }}^{\ast }\right).$$

This is the same as condition (23). For nodes in the inactive set ${\Gamma }_{\ast }^c$, we need to determine the subgradient of C(·) at zero. To do so, note that using (4) and the continuity of the function f(·) at λ [condition (6a)], we have

$$\underset{a\downarrow 0}{\text{lim}}\lambda \nabla C\left(a\right)=\underset{u\downarrow \lambda }{\text{lim}}u-f\left(u\right)=\lambda .$$

As a consequence, we find that

$$\underset{a\downarrow 0}{\text{lim}}\nabla C\left(a\right)=1\text{and}\underset{a\uparrow 0}{\text{lim}}\nabla C\left(a\right)=-1.$$

From the definition of the subgradient, these limits show that ∂C(0) = [–1, 1] . Using this, the condition in (25) restricted to the set of inactive nodes is equivalent to

$${\Phi }_{{\Gamma }_{\ast }^c}^{T}y-{\Phi }_{{\Gamma }_{\ast }^c}^T{\Phi }_{{\Gamma }_{\ast }}{a}_{{\Gamma }_{\ast }}^{\ast }\in [-\lambda ,\lambda ].$$

We immediately see that this condition is the same as (24), since by definition of the inactive nodes $u_{{\Gamma }_{\ast }^c}^{\ast }\in [-\lambda ,\lambda ]$. This shows that the fixed points a* coincide with the critical points of the objective function (1).

Moving on to establishing the convergence result in part 2 of the theorem, we first note that, from our analysis above, the same reasoning leads to the conclusion that

$$-\stackrel{.}{u}\left(t\right)=u\left(t\right)-f\left(u\left(t\right)\right)+{\Phi }^T\Phi a\left(t\right)-{\Phi }^{T}y\in \partial V\left(a\left(t\right)\right).$$ (26)

Using the chain rule (22) with ζ = –u̇(t) ∈ ∂V(a(t)) from (26) and using the expression in (7), we get the relationship

$$\begin{array}{cc}\hfill \frac{dV\left(a\left(t\right)\right)}{dt}& =-\stackrel{.}{u}{\left(t\right)}^T\stackrel{.}{a}\left(t\right)\hfill \\ \hfill & =-\stackrel{.}{u}{\left(t\right)}^T{F}^{\prime }\left(t\right)\stackrel{.}{u}\left(t\right)\hfill \\ \hfill & =-\sum _{n\in \Gamma }{f}^{\prime }\left(u_n\left(t\right)\right){\mid {\stackrel{.}{u}}_n\left(t\right)\mid }^2.\hfill \end{array}$$ (27)

This expression is valid for all time t ≥ 0. In addition, because the function f(·) satisfies (6b), f′(u_n(t)) > 0, and thus

$$\begin{array}{cc}\hfill \frac{dV\left(a\left(t\right)\right)}{dt}& \le 0\text{for all}t\ge 0,\text{and}\hfill \\ \hfill \frac{dV\left(a\left(t\right)\right)}{dt}& <0\text{for all}t\ge 0\mathrm{s}.\mathrm{t}.{\Vert {\stackrel{.}{u}}_{\Gamma }\left(t\right)\Vert }_2\ne 0.\hfill \end{array}$$

This means that V(a(t)) is nonincreasing for all t ≥ 0. Since V(a(t)) is continuous, bounded below by zero, and nonincreasing, V(a(t)) converges to a constant value V*, and its time derivative V̇(a(t)) tends to zero as t → ∞. Using (27) and (6b), we conclude that $\underset{t\to +\infty }{\text{lim}}{\Vert {\stackrel{.}{u}}_{\Gamma }\left(t\right)\Vert }_2=0$. As a consequence, we also have $\underset{t\to +\infty }{\text{lim}}{\Vert \stackrel{.}{a}\left(t\right)\Vert }_2=0$, so the outputs converge to the set E = {a : s.t. ȧ(t) = 0}, and the LCA outputs are quasi-convergent.

Moving on to part 3 of the theorem, we assume that the critical points of (1) are isolated. We need to show that both active and inactive nodes converge to a single fixed point. From part 2, we know that, since the nodes converge to E, after some time, the active nodes will be within a ball of radius R around one element a* ∈ E. However, since critical points of (1) are isolated, there exists a ball ${\mathcal{B}}_{∊}\left(a^{\ast }\right)$ of radius ε > 0 around a* that does not contain any critical point

$$a^{\ast }\in E\text{and}\forall a\in {\mathcal{B}}_{∊}\left(a^{\ast }\right),a\ne a^{\ast }\Rightarrow a\notin E.$$

Since the system is stable, we know that once the trajectory gets close enough (within a ball of radius R) to one element in E, it cannot leave a ball of radius around this fixed point [see (13)]. As a consequence, the outputs remain within the ball ${\mathcal{B}}_{∊}\left(a^{\ast }\right)$, which contains only the fixed point a*. This proves that the active nodes converge to the point a* in E

$$\underset{t\to +\infty }{\text{lim}}a\left(t\right)=a^{\ast }.$$ (28)

This implies that the ODE (3) can be written in terms of the distance $\tilde{a}\left(t\right)=a\left(t\right)-a^{\ast }$ of the outputs from the solution

$$\stackrel{.}{u}\left(t\right)=-u\left(t\right)-{\Phi }^T\Phi a^{\ast }+{\Phi }^{T}y+a^{\ast }-{\Phi }^T\Phi \tilde{a}\left(t\right)+\tilde{a}\left(t\right).$$

We let

$$u^{\ast }=-{\Phi }^T\Phi a^{\ast }+{\Phi }^{T}y+a^{\ast }$$

and rewrite the ODE (3) as

$$\stackrel{.}{u}\left(t\right)=-u\left(t\right)+u^{\ast }-\left({\Phi }^T\Phi -I\right)\tilde{a}\left(t\right).$$

Solving this ODE for all t ≥ 0 yields

$$u\left(t\right)=u^{\ast }+e^{-t}\left(u\left(0\right)-u^{\ast }\right)+e^{-t}{\int }_0^t{e}^s\left({\Phi }^T\Phi -I\right)\tilde{a}\left(s\right)ds.$$

While it is difficult to say anything directly about the trajectory of the system, it is helpful to consider a surrogate trajectory that is a straight line in the state-space u* + e^–t (u(0) – u*). This linear path obviously converges to the fixed point u*, and if we are able to show that the actual trajectory u(t) asymptotically approaches this idealized linear path, we will have established that the system converges to u*. To take this approach, we examine the quantity

$$h\left(t\right)=u\left(t\right)-u^{\ast }-e^{-t}\left(u\left(0\right)-u^{\ast }\right)$$

which is the deviation from the linear path. Consider the norm of this deviation

$$\begin{array}{cc}\hfill {\Vert h\left(t\right)\Vert }_2& ={\Vert u\left(t\right)-u^{\ast }-e^{-t}\left(u\left(0\right)-u^{\ast }\right)\Vert }_2\hfill \\ \hfill & ={\Vert e^{-t}{\int }_0^t{e}^s\left({\Phi }^T\Phi -I\right)\tilde{a}\left(s\right)ds\Vert }_2\hfill \\ \hfill & \le e^{-t}{\Vert {\Phi }^T\Phi -I\Vert }_2{\int }_0^t{e}^s{\Vert \tilde{a}\left(s\right)\Vert }_{2}ds.\hfill \end{array}$$

To show convergence to zero, we split the integral into two parts. Since $\tilde{a}\left(t\right)\underset{t\to +\infty }{\to }0$, then for any $\widetilde{∊}>0$, there exists a time t_c ≥ 0 such that $\forall t\ge t_c$, ${\Vert \tilde{a}\left(t\right)\Vert }_2\le \widetilde{∊}$. Moreover, since ${\Vert \tilde{a}\left(t\right)\Vert }_2$ is continuous and goes zero as t goes to infinity, it admits a maximum μ, $\forall t\in \mathbb{R}$. This yields, for all t ≥ 2t_c

$$\begin{array}{cc}\hfill {\Vert h\left(t\right)\Vert }_2& \le e^{-t}{\Vert {\Phi }^T\Phi -I\Vert }_2\mu {\int }_0^{t_c}{e}^{s}ds+e^{-t}{\Vert {\Phi }^T\Phi -I\Vert }_2\widetilde{∊}{\int }_{t_c}^t{e}^{s}ds\hfill \\ \hfill & \le {\Vert {\Phi }^T\Phi -I\Vert }_2\mu \left[e^{-t+t_c}-e^{-t}\right]+{\Vert {\Phi }^T\Phi -I\Vert }_2\widetilde{∊}\left[1-e^{-t+t_c}\right]\hfill \\ \hfill & \le {\Vert {\Phi }^T\Phi -I\Vert }_2\mu \left[e^{-t∕2}-e^{-t}\right]+{\Vert {\Phi }^T\Phi -I\Vert }_2\widetilde{∊}.\hfill \end{array}$$

Since the left term converges to 0 and $\widetilde{∊}$ can be chosen arbitrarily small, this shows that the trajectory u(t) converges to the trajectory u* + e^–t (u(0) – u*) as t goes to infinity, and thus we can conclude that $u\left(t\right)\underset{t\to +\infty }{\to }{u}^{\ast }$.

Because we have shown separately that both the active and inactive nodes converge for any initial state, it concludes our proof that the system is globally convergent.

Appendix B

Proof of Lemma 1

Proof: Each of the four cases will be treated separately.

1. For any ${\tilde{u}}_n\in \mathbb{R}$, $\text{let}{z}_n=\text{sign}\left({\tilde{u}}_n\right)$. Since the thresholding function is nondecreasing (6b), and T_λ(–u_n) = –T_λ(u_n) from (6a), we have

   $$\begin{array}{cc}\hfill z_n=\text{sign}\left({\tilde{u}}_n\right)& \Rightarrow 0\le z_n{\tilde{u}}_n\hfill \\ \hfill & \Rightarrow z_n{u}_n^{\ast }\le z_n{\tilde{u}}_n+z_n{u}_n^{\ast }\hfill \\ \hfill & \Rightarrow T_{\lambda }\left(z_n{u}_n^{\ast }\right)\le T_{\lambda }\left(z_n{\tilde{u}}_n+z_n{u}_n^{\ast }\right)\hfill \\ \hfill & \Rightarrow z_n{T}_{\lambda }\left(u_n^{\ast }\right)\le z_n{T}_{\lambda }\left({\tilde{u}}_n+u_n^{\ast }\right)\hfill \\ \hfill & \Rightarrow 0\le z_n\left[T_{\lambda }\left({\tilde{u}}_n+u_n^{\ast }\right)-T_{\lambda }\left(u_n^{\ast }\right)\right]\hfill \\ \hfill & \Rightarrow 0\le z_n{\tilde{a}}_n\hfill \\ \hfill & \Rightarrow \text{sign}\left({\tilde{a}}_n\right)=z_n=\text{sign}\left({\tilde{u}}_n\right).\hfill \end{array}$$
2. We can separate this proof into four cases. If $\mid {\tilde{u}}_n+u_n^{\ast }\mid \le \lambda$ and $\mid u_n^{\ast }\mid \le \lambda$, we have $\mid {\tilde{a}}_n\mid =\mid T_{\lambda }({\tilde{u}}_n+u_n^{\ast })-T_{\lambda }\left(u_n^{\ast }\right)\mid =0\le \alpha \mid {\tilde{u}}_n\mid$. If $\mid {\tilde{u}}_n+u_n^{\ast }\mid \le \lambda$ and $\mid u_n^{\ast }\mid >\lambda$, according to the mean value theorem, since the function f(·) is continuous on $[\text{sign}\left(u_n^{\ast }\right)\lambda ,u_n^{\ast }]$, differentiable on $(\text{sign}\left(u_n^{\ast }\right)\lambda ,u_n^{\ast })$ and $f\left(\text{sign}\left(u_n^{\ast }\right)\lambda \right)=0$, there exist $c\in (\text{sign}\left(u_n^{\ast }\right)\lambda ,u_n^{\ast })$ such that

   $$\begin{array}{cc}\hfill \mid {\tilde{a}}_n\mid & =\mid f\left(u_n^{\ast }\right)\mid =\mid f^{\prime }\left(c\right)\left(u_n^{\ast }-\text{sign}\left(u_n^{\ast }\right)\lambda \right)\mid \hfill \\ \hfill & =\mid f^{\prime }\left(c\right)\mid \left(\mid u_n^{\ast }\mid -\lambda \right)(\text{since}\mid u_n^{\ast }\mid >\lambda )\hfill \\ \hfill & \le \alpha \left(\mid u_n^{\ast }\mid -\lambda \right)\hfill \\ \hfill & \le \alpha \mid {\tilde{u}}_n\mid (\text{since}\mid u_n^{\ast }\mid -\mid {\tilde{u}}_n\mid \le \mid {\tilde{u}}_n+u_n^{\ast }\mid \le \lambda ).\hfill \end{array}$$

   If $\mid {\tilde{u}}_n+u_n^{\ast }\mid >\lambda$ and $\mid u_n^{\ast }\mid \le \lambda$, according to the mean value theorem, there exists $c\in (\text{sign}({\tilde{u}}_n+u_n^{\ast })\lambda ,{\tilde{u}}_n+u_n^{\ast })$ such that

   $$\begin{array}{cc}\hfill \mid {\tilde{a}}_n\mid & =\mid f({\tilde{u}}_n+u_n^{\ast })\mid \hfill \\ \hfill & =\mid f^{\prime }\left(c\right)\left({\tilde{u}}_n+u_n^{\ast }-\text{sign}\left({\tilde{u}}_n+u_n^{\ast }\right)\lambda \right)\mid \hfill \\ \hfill & =\mid f^{\prime }\left(c\right)\mid \left(\mid {\tilde{u}}_n+u_n^{\ast }\mid -\lambda \right)\hfill \\ \hfill & \le \alpha \left(\mid {\tilde{u}}_n\mid +\mid u_n^{\ast }\mid -\lambda \right)\le \alpha \mid {\tilde{u}}_n\mid .\hfill \end{array}$$

   Finally, if $\mid {\tilde{u}}_n+u_n^{\ast }\mid >\lambda$ and $\mid u_n^{\ast }\mid >\lambda$, according to the mean value theorem, there exists $c\in (u_n^{\ast },{\tilde{u}}_n+u_n^{\ast })$ such that $\mid {\tilde{a}}_n\mid =\mid f({\tilde{u}}_n+u_n^{\ast })-f\left(u_n^{\ast }\right)\mid =\mid f^{\prime }\left(c\right){\tilde{u}}_n\mid \le \alpha \mid {\tilde{u}}_n\mid$.
3. Using properties 1) and 2), we have

   $$\begin{array}{cc}\hfill {\tilde{a}}_{\mathcal{T}}^T{\tilde{a}}_{\mathcal{T}}& =\sum _{n\in \mathcal{T}}{\tilde{a}}_n{\tilde{a}}_n=\sum _{n\in \mathcal{T}}\mid {\tilde{a}}_n\mid \mid {\tilde{a}}_n\mid \hfill \\ \hfill & \le \sum _{n\in \mathcal{T}}\alpha \mid {\tilde{u}}_n\mid \mid {\tilde{a}}_n\mid =\alpha \sum _{n\in \mathcal{T}}{\tilde{u}}_n{\tilde{a}}_n=\alpha {\tilde{u}}_{\mathcal{T}}^T{\tilde{a}}_{\mathcal{T}}\hfill \\ \hfill & \le \sum _{n\in \mathcal{T}}\alpha \mid {\tilde{u}}_n\mid \alpha \mid {\tilde{u}}_n\mid ={\alpha }^2\sum _{n\in \mathcal{T}}{\tilde{u}}_n{\tilde{u}}_n={\alpha }^2{\tilde{u}}_{\mathcal{T}}^T{\tilde{u}}_{\mathcal{T}}.\hfill \end{array}$$
4. Since the soft-threshold function is nondecreasing, then the function $g_n\left(s\right)=T_{\lambda }(s+u_n^{\ast })-T_{\lambda }\left(u_n^{\ast }\right)$ is also nondecreasing. Moreover, g_n(0) = 0 and $g_n\left({\tilde{u}}_n\left(t\right)\right)={\tilde{a}}_n\left(t\right)$. As a consequence, we can bound the integral by

   $${\int }_0^{{\tilde{u}}_n\left(t\right)}{g}_n\left(s\right)ds\le \left(g_n\left({\tilde{u}}_n\left(t\right)\right)-g_n\left(0\right)\right){\tilde{u}}_n\left(t\right)={\tilde{a}}_n{\tilde{u}}_n.$$

   As a consequence

   $$\sum _{n=1}^N{\int }_0^{{\tilde{u}}_n\left(t\right)}{g}_n\left(s\right)ds\le \sum _{n=1}^N{\tilde{a}}_n{\tilde{u}}_n={\tilde{a}}^T\tilde{u}.$$