Absolute cross sections for electronic excitations of cytosine by low energy electron impact

Abstract

The absolute cross sections (CS) for electronic excitations of cytosine by electron impact between 5 and 18 eV were measured by electron-energy loss (EEL) spectroscopy of the molecule deposited at low coverage on an inert Ar substrate. The lowest EEL features found at 3.55 and 4.02 eV are ascribed to transitions from the ground state to the two lowest triplet 1 ³A′(π→π*) and 2 ³A′(π→π*) valence states of the molecule. Their energy dependent CS exhibit essentially a common maximum at about 6 eV with a value of 1.84 × 10⁻¹⁷ cm² for the former and 4.94 × 10⁻¹⁷ cm² for the latter. In contrast, the CS for the next EEL feature at 4.65 eV, which is ascribed to the optically allowed transition to the 2 ¹A′(π→π*) valence state, shows only a steep rise to about 1.04 × 10⁻¹⁶ cm² followed by a monotonous decrease with the incident electron energy. The higher EEL features at 5.39, 6.18, 6.83, and 7.55 eV are assigned to the excitations of the 3 ^{3, 1}A′(π→π*), 4 ¹A′(π→π*), 5 ¹A′(π→π*), and 6 ¹A′(π→π*) valence states, respectively. The CS for the 3 ^{3, 1}A′ and 4 ¹A′ states exhibit a common enhancement at about 10 eV superimposed on a more or less a steep rise, reaching respectively a maximum of 1.27 and 1.79 × 10⁻¹⁶ cm², followed by a monotonous decrease. This latter enhancement and the maximum seen at about 6 eV in the lowest triplet states correspond to the core-excited electron resonances that have been found by dissociative electron attachment experiments with cytosine in the gas phase. The weak EEL feature found at 5.01 eV with a maximum CS of 3.8 × 10⁻¹⁸ cm² near its excitation threshold is attributed to transitions from the ground state to the 1 ^{3, 1}A″(n→π*) states. The monotonous rise of the EEL signal above 8 eV is attributed to the ionization of the molecule. It is partitioned into four excitation energy regions at about 8.55, 9.21, 9.83, and 11.53 eV, which correspond closely to the ionization energies of the four highest occupied molecular orbitals of cytosine. The sum of the ionization CS for these four excitation regions reaches a maximum of 8.1 × 10⁻¹⁶ cm² at the incident energy of 13 eV.

I. INTRODUCTION

Nuclear medicine uses radionuclides (e.g., ⁶⁷Ga, ^99mTc, ¹¹¹In, ¹²³I, ¹²⁵I and ²⁰¹Tl) for diagnostic (i.e., medical imaging) as well as in targeted radionuclide therapy (TRT).^{1, 2} The first application requires radionuclides that decay with penetrating γ rays and/or β particles, which distribute their energies relatively homogeneously throughout and outside the body. In TRT the ultimate goal is to deliver, via suitable radiopharmaceutical carriers, a sterilizing amount of energy to all cancer cells in the body while sparing nearby healthy cells.³ Therefore, carriers containing radionuclides that emit weak β particles and/or short-range Auger electrons are preferred.⁴ When bound or incorporated into the DNA of cells, these radionuclides are highly radiotoxic as the emitted Auger electrons produce biological effects comparable to those induced by alpha particles, which have a high linear energy transfer.^{5, 6} It appears that an optimal TRT is not only limited to the design of suitable carriers, but also requires to quantify the energy imparted per unit mass (i.e., radiation dose) by such radionuclides at the single-cell level with emphasis on the DNA structure.

In conventional dosimetry, analytical and Monte Carlo methods are used to compute the radiation dose by fast primary particles (e.g., photons, electrons, and positrons) to different tissues and organs. Those calculations require the scattering cross sections (CS) as input data to describe all the collisions made by the primaries with the molecules of the biological media, particularly the water molecule.⁷ The same principle applies in TRT in that the absorbed dose must be calculated also from the scattering CS for the primary particles. However, in TRT most of the primary particles are Auger electrons that have energies lower than a few hundred eV. These low energy electrons (LEEs), which have very short ranges in biological media, generate a high density of energy deposits and clustered damage in the immediate vicinity of the radionuclides. Therefore, to carry out a dosimetry or more specifically a nanodosimetry of these radionuclides requires the knowledge of the scattering CS for LEEs interacting with the DNA constituents.

Several experimental studies have been carried out on electron impact on individual DNA bases to understand what fragments are generated. Most of them concern the formation of various anion fragments produced by dissociative electron attachment (DEA) to these molecules in gas phase^{8 – 19} and sublimated as thin films.^{20, 21} Few studies have examined their electronic and vibrational excitations by electron energy loss (EEL) spectroscopy in the gas phase.^{22 – 24} So far, not much attention have been devoted on the determination of the absolute CS values for these different collision processes. The reason for this may lie in the low energy range where both experiments and theoretical calculations are difficult to perform. In line with these requirements, a number of quantitative studies of the interaction of LEEs with DNA basis has been undertook recently by our group. More specifically, the absolute CS for vibrational and electronic excitations of thymine,^{25 – 27} pyrimidine,²⁸ and adenine²⁹ by electron impacts have been measured over the 1 – 12 eV incident electron energy range for the molecules deposited at very low coverage on a solid Ar substrate. Besides the reported CS values, these studies showed selective vibrational enhancements at different electron impact energies, thus indicating the formation of several transient anion states.

In the present paper, the absolute CS values to excite various electronic modes of cytosine by electron impact between 5 and 18 eV are determined for the molecule deposited at low coverage on an inert Ar substrate. The scattering model to extract the CS values is the same as in our previous work on pyrimidine²⁸ but the experimental method includes some improvements. In contrast to our previous works, the present EEL spectra at different incident electron energies and thus the electron impact energy dependences of the various CS are obtained for exactly the same cytosine coverage on the inert Ar substrate. The end result is an important reduction of the scatter that was present in our previous data and which was due to the use of a new molecular deposition for each of the incident energies. Also the cytosine coverage is calibrated directly in terms of molecular number density at the surface of the Ar substrate instead of the usual monolayer coverage, which introduces an additional systematic uncertainty about its true value. The present electronic excitation energies are compared to those that have been found by EEL spectroscopy and valence-shell photoelectron spectroscopy of cytosine in the gas phase as well as to the excitation values that have been reported from various electronic structure calculations of the molecule. The enhancements exhibited at specific energies in the CS are further discussed by comparing to the DEA experiments to cytosine in gas phase.

II. EXPERIMENT

The electron-scattering experiments were performed with a high-resolution electron-energy-loss (EEL) spectrometer described in detail previously.³⁰ The spectrometer is housed in a closed-cycle cryopumped UHV system³¹ at a typical base pressure of 5 × 10⁻¹¹ Torr. The substrate for sample deposition consists of a 0.0075 mm thick polycrystalline Pt ribbon (Goodfellow Cambridge Ltd., 99.95%) press fitted against the tip of the closed-cycle cryopump at 18 K. The Pt ribbon is cleaned by resistive heating in UHV at 1100 K for about 10 sec. The EEL spectra presented in this paper were recorded with the monochromator oriented near to the normal to the sample at θ₀ = 15° along with the analyzer fixed at θ_d = 45°. The combined resolution of the spectrometers was adjusted at 18 meV full width at half maximum (FWHM) for a transmitted current I_S of 0.26 nA, as measured by an electrometer connected to the Pt substrate. The incident electron energy E₀ was calibrated, within ± 0.1 eV with respect to the vacuum level, by measuring with the electrometer the onset of the transmitted current.³² The analyzer lenses were tuned for a maximum signal between 2 and 18 eV with only a fall off below 2 eV or in terms of energy loss within the highest 2-eV range. Yet this latter outcome was systematically corrected in the present work by comparing to a reference spectrum obtained by compiling several EEL spectra with the analyzer tuned at different low residual energies. The recordings were also obtained under sufficiently small electron exposures so as to make sample decomposition and/or charging due to the trapping of electrons or creation of holes in the sample negligible. These effects were monitored by comparing the EEL spectra and the low-energy electron transmission onsets during the course of an experiment.

Gaseous and liquid samples to be condensed on the Pt substrate were initially prepared in a gas-handling manifold described in detail previously.³⁰ In the present work, the amount of gas or vapor admitted in UHV and deposited on the substrate (ΔP) was further expressed in terms of an absolute surface number density (n_S) in the following manner. First, we determined the absolute pressure drop ΔP_Ar (i.e., 4 mTorr) in the manifold to grow a (111) monolayer of a solid film of Ar (Matheson of Canada Ltd., 99.9995%) on the Pt substrate.^{33, 34} Given the value of ΔP_Ar and taking the atomic density of an Ar monolayer (n_Ar) as that corresponding to a (111) plane in the bulk of solid Ar at 20 K (i.e., n_Ar = 8.167 × 10¹⁴ cm⁻²),^{35, 36} the ΔP for a gas or vapor was thus converted into a surface number density (n_S) with the relation n_S = (n_Ar/ΔP_Ar)ΔP.³⁷ The uncertainty in this n_S value arises essentially from the error in the individual pressure measurement ΔP at ±2.5% and in the value taken for n_Ar at ±5% for a combined uncertainty of ±10%.³⁸

Cytosine (Aldrich Chemical Ltd., 99%) was sublimated at a temperature of 90° under UHV condition with a double-stage oven system.²⁷ To prevent any insidious effect such as decomposition of the cytosine molecule by the Pt surface in the present experiment, a 3-layer film of Ar was systematically used as a spacer.³⁹ Since, it is generally accepted from VUV,⁴⁰ photoelectron,⁴¹ IR,⁴² and Raman⁴² spectroscopy studies that cytosine does not decompose upon heating up to 220°C in vacuum; the present sublimation temperature is expected to preserve the integrity of the molecule. After several days of experiments, the sample holder and the electron spectrometer needed to be heated at about 50°C during 48 hours in order to remove the insulating deposits that deteriorate the measurements.

The cytosine coverage was monitored in situs from the attenuation of the electron specular elastic reflectivity from the underlying Ar substrate, as described previously.²⁵ But in the present experiment, to obtain the cytosine coverage directly in terms of surface number density n_S, the attenuation of the specular intensity was compared to that caused by a similar molecule pyrimidine (Aldrich Chemical Ltd., 99%). Since pyrimidine is liquid above 22°C, it was first degassed by repeated freeze-thaw cycles under vacuum and its vapor condensed on the Ar substrate via the gas-handling manifold, which was heated around 30°C. The attenuation of the specular intensity I_R (ΔP) was thus measured as a function of ΔP of pyrimidine in the manifold. From fitting the I_R (ΔP) data normalized to the value at ΔP = 0 (i.e., I₀ R) with the following relation

$$I_R(\mathrm{\Delta }P)=I_{0}Rexp(-\mathrm{\Delta }P/\mathrm{\Delta }{P}_0),$$ (1)

the constant ΔP₀, which actually in absence of pile-up corresponds to the slightest coverage required to annihilate completely the specular intensity from the substrate, was deduced to be 0.873 mTorr (±2.5%). Finally, using the conversion factor n_Ar/ΔP_Ar = 2.04 × 10¹⁴ cm⁻²-mTorr⁻¹ (± 7.5%), both the ΔP scale and ΔP₀ were transformed into surface number densities n_S. The latter value for ΔP₀ is n_S = 1.78 × 10¹⁴ cm⁻² (±10%), which agree with the number density of 1.80 × 10¹⁴ cm⁻² for a single plane along the [001] direction in the pyrimidine crystal.^{43 – 45} In the present work, the coverage of cytosine was chosen with the normalized specular intensity attenuated to about 0.31 (±7.5%). From Eq. 1 this is equivalent to ΔP = 1.02 mTorr (± 9%). The latter uncertainty arises via Eq. 1 from the relative errors in the normalized specular intensity at ±7.5% and ΔP₀ at ±2.5%. Finally, given again the above conversion factor n_Ar/ΔP_Ar, this yields n_S = 2.08 × 10¹⁴ cm⁻² (±16.5%). Considering that similar values of 1.90 × 10¹⁴ and 2.17 × 10¹⁴ cm⁻² have been obtained by scanning tunneling microscopy on Au(111)^{46, 47} and molecular modeling based on van der Waals radii⁴⁸ for a monolayer of cytosine, the present value will be referred to for convenience as 1-layer coverage.

III. SCATTERING MODEL AND MEASUREMENT PROCEDURE

For an electron beam current I₀ of energy E₀ incident on a film of molecules deposited on an inert substrate, the scattering of electrons from the film can be described in terms of the multiple scattering theory developed previously.⁴⁹ However, when the thickness of the film is smaller than the electron mean free path, one may retain only the terms arising from single collisions within the film. Under this condition, it can be shown that the expression for the current of electrons measured by the analyzer in the backscattered direction θ_d after having transferred an energy E − E₀ into the film (i.e., EEL spectrum) reduces to²⁸

$$I({\theta }_d,E_0,E-E_0)\cong \frac{I_0({\theta }_d,E_0)}{cos{\theta }_0}{\sigma }_r(E_0,E-E_0)n_S.$$ (2)

Here I₀(θ_d, E₀) is defined as an effective incident electron current. The latter may be seen as the portion of the incident electron current I₀ that would be backscattered into the analyzer in the same direction θ_d by a model material having an elastic reflectivity equal to one (i.e., all incident electrons being scattered out of the film). In the present experiment, a value of 7400 counts s⁻¹ (± 7%) was obtained for I₀(θ_d, E₀) by depositing increasing amounts of pyrimidine or H₂O vapor on the Ar substrate and using the conservation law between the backscattered and transmitted current, as described in details previously.²⁸ The quantity σ_r(E₀, E − E₀) is the CS per unit energy transfer range for an electron of energy E₀ to deposit an energy E − E₀ in the film and be backscattered into the vacuum (i.e., integrated over the whole half-angular space). The value n_S is the surface number density of molecules on the substrate corresponding to the thickness of the film. Finally, the factor 1/cos θ₀ accounts for the projection of the incident electron beam section onto the film surface.

In practice several EEL spectra I(θ_d, E₀, E − E₀) are recorded for different E₀ in the direction θ_d on a sufficiently thin film. Given the above I₀(θ_d, E₀) along with n_S, the corresponding σ_r(E₀, E − E₀) are deduced from Eq.2. Each of the them are next fitted with multiple Gaussian functions to delimit the various excitation energy regions centered at about the energies hνi as

$${\sigma }_r(E_0,E-E_0)=\sum _i{a}_i(E_0)exp[-{(E-E_0+h{\nu }_i)}^2/b_i^2],$$ (3)

with b_i = δ_i/[2(ln 2)^½] and where a_i(E₀) is the amplitude and δ_i the FWHM of a Gaussian function i. Finally, the CS value to excite a molecule at about the energy hνi by electron impact is obtained from the area under the corresponding Gaussians distribution i, which is given analytically as

$${\sigma }_i(E_0)=a_i(E_0)b_i{\pi }^{1/2}.$$ (4)

In the case that an electron has the same probability to be scattered in the backward and forward direction with respect to the molecular film surface σ_i (E₀) accounts for half of the integral CS.

IV. RESULTS AND DISCUSSION

A. Electronic excitations

The cytosine molecule in its ground state may be considered to belong to the point group C_S, with a mirror plane that contains all the atoms of the molecule, except for the two hydrogens sticking out of the amino group. The electronic states can thus be classified as symmetric (A′) or antisymmetric (A″) with respect to this plane. Most of the valence excitations can be described by the promotion of an electron out of the four highest occupied molecular orbitals (MOs) into the three lowest unoccupied MOs.⁵⁰ The highest occupied MO (π_H) is a π-type orbital with large amplitude at the oxygen site. The second highest occupied MO (π_{H − 1}) is also of π-type. The third highest occupied MO (n_O) is an n-type orbital with large amplitude for the oxygen lone-pair orbital. The fourth highest occupied MO (n_N) is also of n-type, but the amplitude is concentrated on the nitrogen lone-pair orbital. As for the virtual MOs, the lowest unoccupied MO(π_L*) is a π-type orbital delocalized over the whole molecule. Following the same notation, the higher virtual MOs are denoted π_L+1*, π_L+2*, etc.⁵⁰

In view of the generally larger oscillator strength predicted for π → π* transitions,^{50 – 52} the most intense excitation bands observed at 4.54, 5.40, 6.07, and 6.67 eV in VUV absorption spectra of sublimed cytosine film,^{53, 54} are generally attributed to transitions from the ground state to the four lowest singlet ¹A′ (π → π*) states of the molecule.⁵² No evidence has been found for n → π* transitions, which are predicted to have very small oscillator strengths. However, a weak feature around 5.0 eV in circular dichroism spectra⁵⁵ has been interpreted to be the transition from the ground state to the lowest singlet ¹A″(n → π*) state of the molecule.⁵² In the present work, the EEL spectra should differ in many aspects from those recorded under optical conditions. More specifically, owing to the low incident electron energy and large scattering angle, the spectra are expected to be much more sensitive to symmetry- and spin-forbidden transitions (i.e., triplet states), as shown previously in the case of benzene⁵⁶ and pyrimidine.²⁸.

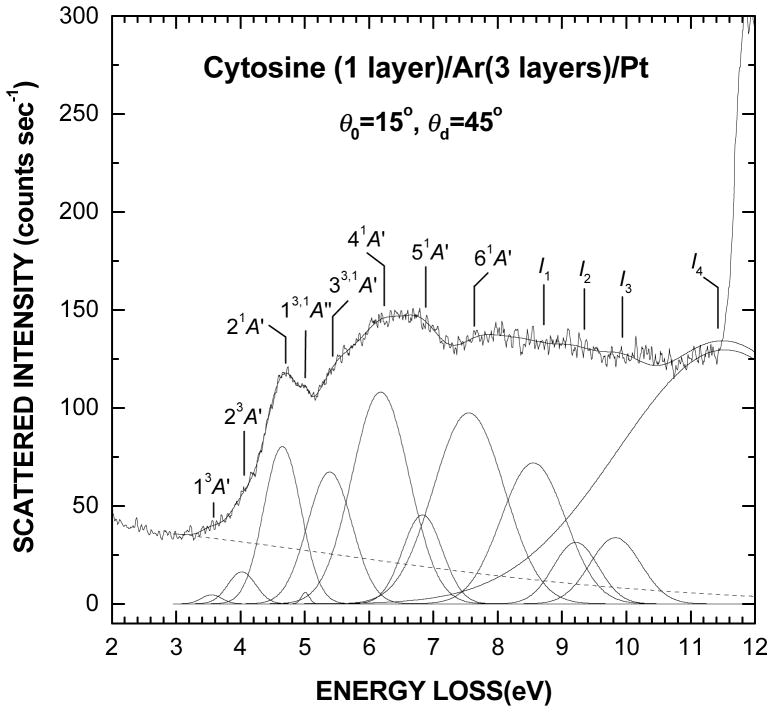
A survey electronic EEL spectrum in the range from 2 to 12 eV of a 1-layer film of cytosine deposited on the Ar substrate is shown in Fig. 1. This spectrum results more specifically from averaging ten different scans, which were recorded between E₀ = 9 and 18 eV. Besides, the EEL signal was found to be directly proportional to the amount of cytosine up to about one layer and then to saturate at higher coverage. The latter behavior is due to the finite total electron mean free path in the bulk of a film and beyond which the molecules cannot be detected efficiently. The thin continuous line superimposed on the spectrum results from curve fitting with multiple Gaussian functions to delimit the various transition regions, as shown in the bottom of Fig. 1. The dashed line accounts simply for the background contribution arising from multiple energy losses into the underlying substrate.⁵⁷ The present analysis suggests the existence of two small overlapping bands with maxima at 3.55 ±0.1 and 4.02 ±0.1 eV along with an excitation onset at about 3.2 eV. These bands, which are better revealed at low impact energy, are followed by five excitation bands at 4.65 ±0.05, 5.39 ±0.2, 6.18 ±0.05, 6.83 ±0.2 and 7.55 ±0.05 eV along with the presence of a small peak at 5.01 ±0.05 eV. The EEL signal between 8 and 11.5 eV, which arises mostly from the ionization of cytosine, is described here with four broad features around 8.55 ±0.1, 9.21 ±0.2, 9.83 ±0.2, and 11.53 ±0.3 eV. The sharp rise in the EEL intensity above 11.5 eV is due to electronic transitions in the Ar substrate (i.e., excitons)⁵⁸ and as such imposes an upper limit to the present investigated EEL range. The energies and FWHM of all excitation bands (i.e., Gaussians) in Fig. 1 are listed in Table I along with the reported excitation values from electronic structure calculations,^{50 – 52, 59} EEL spectra in gas phase²⁴ and vacuum ultraviolet (VUV) absorption spectra of sublimed films.^{53, 54}

Fig. 1.

Survey electronic EEL spectrum of one layer of cytosine deposited on a 3-layer spacer of Ar. This spectrum results from averaging the scattered intensities of ten spectra recorded for electron incident energies between E₀ = 9 and 18 eV. The thin solid line passing through the spectrum results from curve fitting with multiple Gaussian functions to delimit the different electronic transitions, as shown in the bottom of the figure. Their energy positions and widths are listed in Table I. The dashed line accounts simply for the background contribution arising from multiple energy losses in the substrate

TABLE I.

Electronic excited states of cytosine from ab initio calculations, electron energy loss (EEL) spectroscopy in the gas phase and vacuum ultraviolet spectroscopy (VUV) of sublimed films compared to EEL spectroscopy of cytosine deposited on an inert argon substrate. I₁, I₂, I₃, and I₄, represent the vertical ionization energies of the molecule. Values within parentheses are the FWHM of the excitation bands. All energies are in eV.

Theory					EEL		VUV
State	CC2a	DFTb	CASPT2c	DFTd	Gase	Filmf	Filmg	Filmh
1 3A′ (π → π*)	3.88			3.60	3.50	3.55 (0.37)
2 3A′ (π → π*)	4.71				4.25	4.02 (0.51)
2 1A′ (π → π*)	4.66	4.83	4.39		4.65	4.65 (0.68)	4.54 (0.60)	4.50
1 3A″ (n → π*)	4.79
1 1A″ (n → π*)	4.87	5.02	5.00			5.01 (0.15)
2 3A″ (n → π*)	5.09
2 1A″ (n → π*)	5.26	5.50	6.53
3 3A′ (π → π*)	5.27
3 1A′ (π → π*)	5.62	5.67	5.36		5.50	5.39 (0.81)	5.40 (0.87)
3 3A″ (n → π*)	5.67
3 1A″ (n → π*)	5.84	5.91
4 1A′ (π → π*)		6.60	6.16		6.20	6.18 (1.04)	6.07 (0.79)	6.18
5 1A′ (π → π*)			6.74		6.70	6.83 (0.73)	6.67 (0.79)
6 1A′ (π → π*)			7.61		8.00	7.55 (1.30)	7.35 (0.79)	7.5
I1						8.55 (1.18)		8.5
I2						9.21 (0.83)
I3						9.83 (0.93)
I4						11.53(3.91)

^aCalculated results from Reference 51.

^bCalculated results from Reference 50.

^cCalculated results from Reference 52.

^dCalculated results from Reference 59.

^eReference 24

^fThis work.

^gReference 53.

^hReference 54

The energies and relative magnitudes of the present EEL features bear the closest resemblance to those observed by EEL spectroscopy of cytosine in the gas phase.²⁴ In that work the first two features at 3.5 and 4.25 eV, which appear essentially at low impact energies and large scattering angles, have been attributed to triplet states. Since the present electron scattering conditions are similar to those conditions, the two lowest features at 3.55 and 4.02 eV in Fig. 1 can be immediately assigned to the excitation of the 1 ³A’(π → π*) and 2 ³A′(π → π*) triplet valence states of the molecule. In the gas phase, the next EEL features at 4.65, 5.5, 6.2, 6.7 and 8 eV, which are found at higher impact energies and smaller scattering angles, have been identified as dipole allowed transitions to singlet states.²⁴ Besides, their energy positions have been found only about 0.1 eV at higher energy than those of the VUV absorption bands in sublimed cytosine films.⁵³ Conversely, valence transitions that are electric-dipole allowed and exhibit large oscillator strengths may be shifted to lower energy by up to a few hundred meV in the condensed phase because of local crystal-field effects. Still, the slight differences found between some of our excitation energies and those reported in the gas-phase could be merely explained by the presence of triplet valence states lying at about the same energies, as suggested by the calculations on cytosine.⁵¹ Hence, in the present EEL spectrum, the peak seen at 4.65 eV can be immediately recognized as the transition from the ground state to the singlet 2 ¹A′ (π → π*) state, as in the gas phase. The small peak at 5.01 eV can be explained by the excitations of both the singlet 1 ¹A″ (n → π*) and triplet 1 ³A″ (n → π*) states, which have been calculated at about the same energy and to be separated by only about 0.2 eV.⁵¹ The following shoulder at 5.39 eV can be assigned to the excitation of the singlet 3 ¹A′ (π → π*) state along with some contribution from the triplet 3 ³A′ (π → π*) state that has been predicted at 5.27 eV.⁵¹ The maximum at 6.18 eV followed by the weak shoulder at 6.83 eV can be attributed to the 4 ¹A′(π → π*) and 5 ¹A′(π → π*) singlet states, respectively, similarly to the gas phase. Finally, the broad band at 7.55 eV can arise from the singlet 6 ¹A′(π → π*) state, which has been located around 8 eV in the gas phase and 7.35 eV in VUV of sublimed films.

In Fig. 1 the Gaussians labeled I₁, I₂, I₃, and I₄ at about 8.55, 9.21, 9.83, and 11.53 eV, respectively, stand for the ionization of the four highest occupied MOs (i.e., π_H, π_H−1, n_N, and n_O), which are also responsible for the valence excitations. In valence shell photoelectron spectrum of cytosine in the gas phase, the vertical ionization energies of the molecule in its ground state (i.e., binding energies) encompassing these MOs have been found at 8.89, 9.55, 9.89, and 11.64 eV along with a shallow shoulder at about 11.20 eV.⁴¹ For a monolayer film of cytosine deposited on solid Ar, these energies are expected to be lowered by a few hundred meV owing to the electronic polarization induced by the molecular cations (i.e., valence holes) at the surface of the substrate.⁶⁰

B. Electronic scattering cross sections

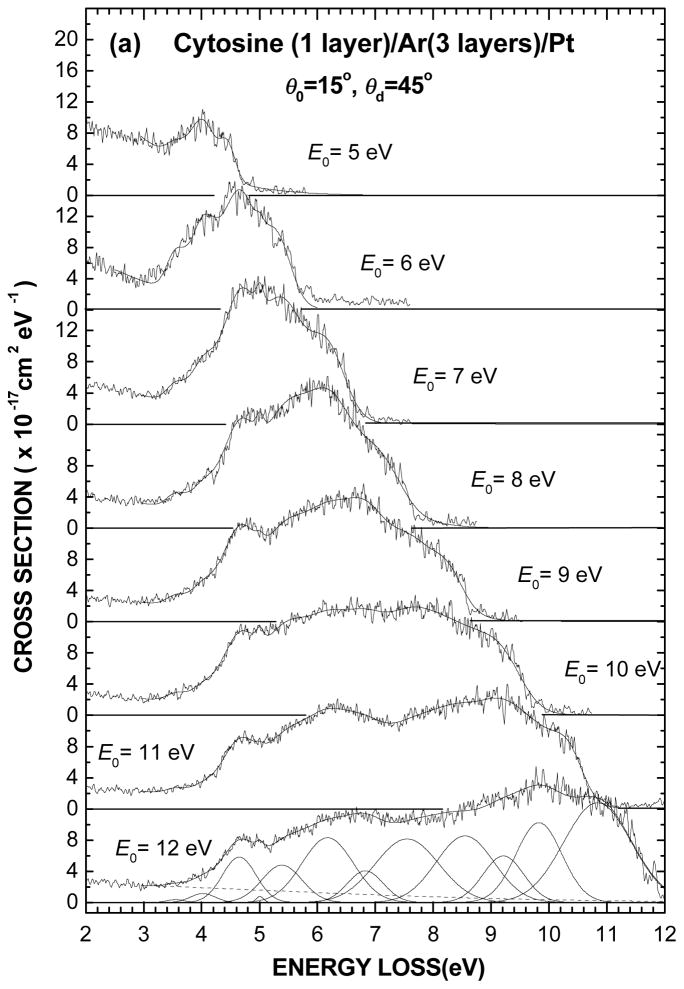
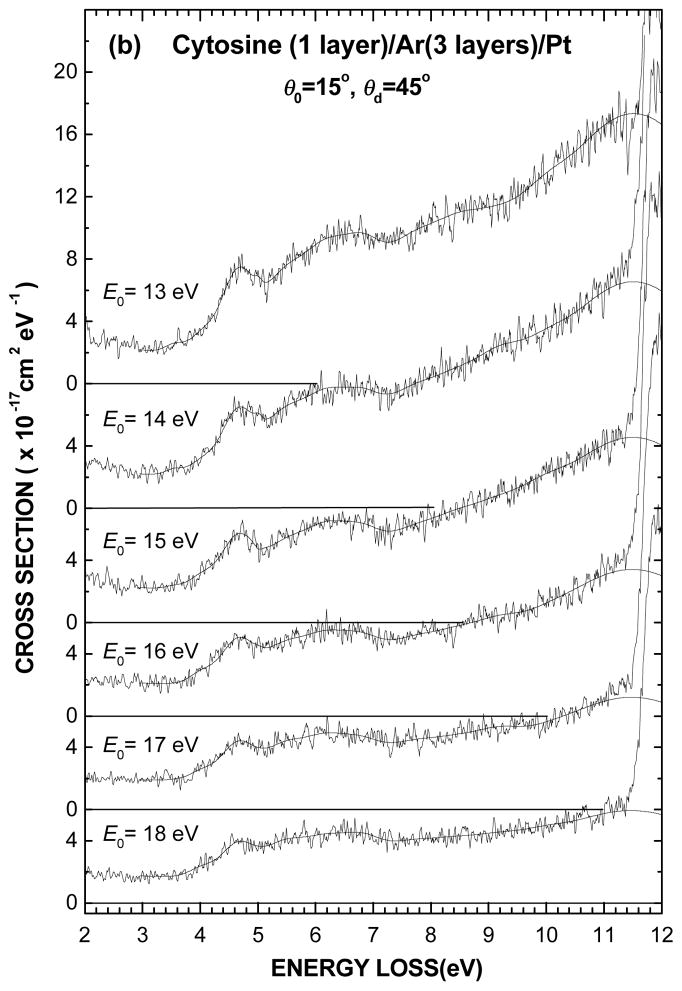
The electronic EEL spectra of 1-layer film of cytosine deposited on the Ar substrate are shown for different incident electron energies between 5 and 18 eV in Figs. 2(a) and (b). The present intensity scale results from normalizing to the effective incident current I₀(θ_d, E₀) and dividing by the molecular surface number density n_S, as prescribed by Eq. 2. The thin solid line passing through the experimental data results from curve fitting with the Gaussian functions whose energy positions and FWHM are given in Table I. These latter parameters, which define the various spectral regions pertaining to the electronic states, were kept fixed for all spectra whereas only the amplitude of the Gaussian functions was varied. As for the background signal in each spectrum, it was simply taken into account by fitting with a wide Gaussian distribution centered at zero energy loss and falling to zero at the highest energy loss, as shown by the dashed line in Fig. 1.

Fig. 2.

(a) Electronic EEL spectra of one layer of cytosine deposited on a 3-layer spacer of Ar for different incident electron energies E₀ from 5 to 12 eV and (b) from 13 to 18 eV. The vertical scale is normalized so as the integral over an energy-loss range can be expressed in terms of a cross section value. The thin solid line passing through each spectrum results from curve fitting with of the multiple Gaussians obtained in Fig. 1 by varying only their amplitudes (i.e., keeping their energy positions and widths fixed), as shown in the bottom of Fig. 2(a).

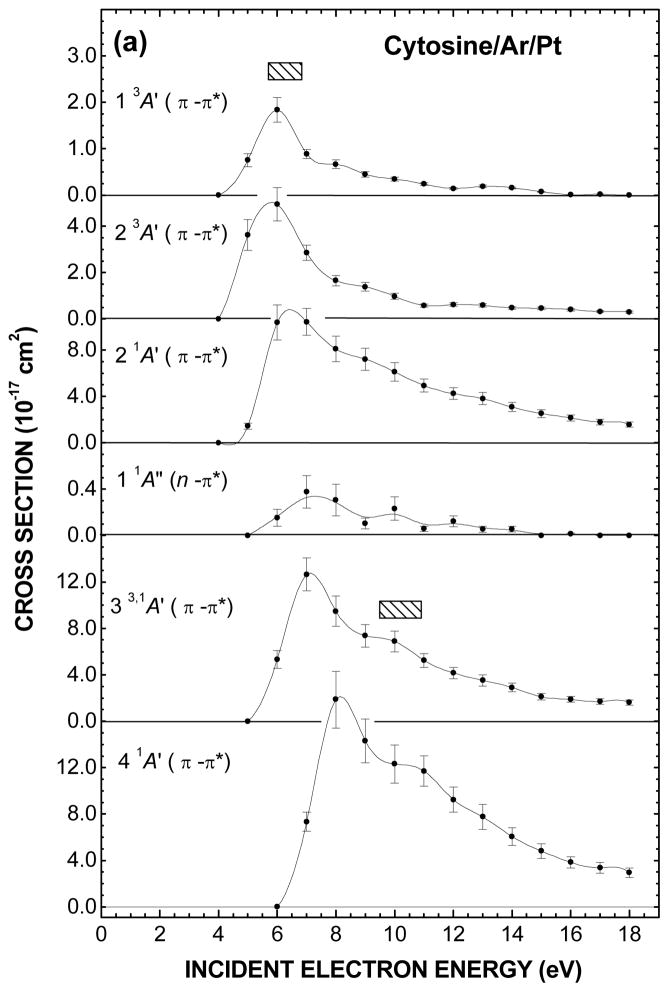
The electron impact energy dependences of the CS to excite various electronic states of cytosine are shown in Figs. 3(a) and (b) and their values listed in Table II. Here, for each of the incident energy E₀, they were obtained from integrating over their corresponding Gaussian energy distribution. The error bars about the data points, which amount to ± 13.5% on the whole, result only from the Gaussian curve fitting to the experimental spectra in Figs. 2(a) and (b). They do not include the systematic uncertainties arising from the calibration of the effective incident current I₀(θ_d, E₀) at ± 7% and the determination of the molecular coverage n_S at ± 16.5%. Actually, the latter two values apply only to the vertical scale of Figs. 3(a) and (b). Hence, considering their sum at ± 23.5% and the error bars; the total absolute error on the present CS values amount to ± 37%.

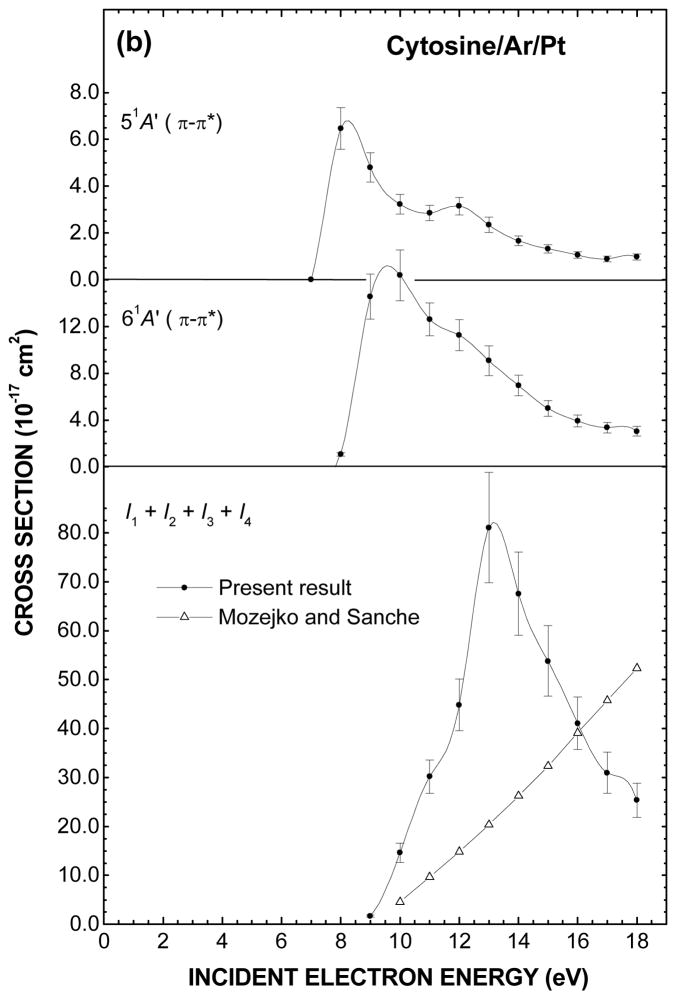
Fig. 3.

Fig. 3(a) and (b). Electron impact energy dependences of the cross sections to excite and ionize various electronic states of cytosine. The values of the cross sections resulting from fitting with multiple Gaussian functions are listed in Table II. The shaded rectangles in (a) represent the energy ranges of the core-excited electron resonances that have been observed in anion fragment yields in DEA experiments with cytosine in the gas phase (Ref. 14). Open triangle in the bottom of (b) is the total ionization cross section calculated by Mozejko and Sanche (Ref. 67).

TABLE II.

Cross section σ_ri (10⁻¹⁷ cm²) for electronic excitations of cytosine by electron impact at different energies E₀ (eV). The energy and FWHM of the Gaussian distributions corresponding to the excitation bands are reported in Table I.

	Electronic states
E0	1 3A′	2 3A′	2 1A′	1 1A″	3 1A′	4 1A′	5 1A′	6 1A′	I1	I2	I3	I4
5	0.76	3.62	1.42
6	1.84	4.94	10.36	0.15	5.33
7	0.89	2.85	10.42	0.38	12.65	7.33
8	0.67	1.65	8.08	0.31	9.48	17.87	6.47	1.08
9	0.45	1.39	7.20	0.11	7.37	14.31	4.81	14.56	1.70
10	0.35	0.98	6.10	0.23	6.88	12.31	3.23	16.37	10.31	4.30
11	0.24	0.58	4.92	0.06	5.23	11.70	2.85	12.62	12.86	6.05	8.24	3.05
12	0.14	0.62	4.24	0.12	4.16	9.24	3.15	11.26	10.71	5.25	10.18	18.69
13	0.19	0.58	3.80	0.05	3.51	7.75	2.34	9.08	6.73	1.41	1.85	71.09
14	0.16	0.48	3.08	0.06	2.91	6.06	1.67	6.95	5.22	1.85	1.57	58.95
15	0.07	0.46	2.52	0	2.10	4.81	1.32	4.99	3.98	1.11	1.34	47.39
16	0.01	0.40	2.14	0.01	1.87	3.84	1.06	3.91	2.87	0.90	0.60	36.72
17	0.02	0.32	1.79	0	1.70	3.36	0.89	3.35	2.35	0.84	0.42	27.36
18	0	0.30	1.56	0	1.62	2.96	0.97	3.04	2.10	0.61	0.67	21.98

The CS for the excitation of both 1 ³A′(π → π*) and 2 ³A′(π → π*) triplet valence states in Fig. 3(a) exhibits a common maximum at about 6 eV that declines steeply to almost zero at 18 eV. In contrast, the CS for the 2 ¹A′(π → π*) singlet valence state shows a relatively steep rise from its excitation threshold followed by a monotonous decrease keeping still a small value at 18 eV. The same general trend may be found for the 3 ¹A′(π → π*) and 4 ¹A′(π → π*) excitation CS except for the presence of shoulders around 10 eV and corresponding higher energy thresholds. The 1 ¹A″(n → π*) excitation CS, which is more than an order magnitude smaller than the other ones, is significant just in the first few eVs above its excitation energy threshold. In Fig. 3(b), the CS for the excitation of the 5 ¹A′(π → π*) state exhibits two maxima at 8 and 12 eV. An enhancement is also found around the latter energy in the 6 ¹A′(π → π*) excitation CS but more as a shoulder that is superimposed on a steep rise followed by a monotonous decrease.

Owing to the low incident electron energy E₀ and large scattering angle, the present electronic excitation CS should reflect short-range interactions, which include static-exchange and correlation effects as well as capture of the incident electron by a molecule (i.e., electron resonance). Electron exchange makes it possible to change the multiplicity of an electronic state by ±2, thus allowing for instance the transition from an initial singlet ground state to a final triplet excited state.⁶¹ Electron correlation effects at long range are responsible for the induced polarization interaction that arises from virtual excitation of optically allowed electronic transitions (i.e., associated with the dipole moment) of the molecule.⁶² When the incident electron energy E₀ exceeds the corresponding transition energies, the electron then suffers inelastic collisions, which transfer and partition its energy among the various electronic excitations. The latter effect dominates at high E₀ and small scattering angles and yield energy dependence CS for the dipole allowed transitions that fall off as E₀-1ln E₀.^{61, 63} Yet at high E_0, the CS values for optically forbidden transitions, such as those associated with the quadrupole moment, are much smaller and decrease with E₀ more strongly than in optically allowed case. ⁶¹

The present trend observed in the energy dependence of the CS for the singlet states (i.e., dipole allowed transitions) can be related to the kinematics of the electron-molecule collision.⁶³ Under the current scattering angle of 120°(i.e., θ₀ = 15°, θ_d = 45°), the electron wave-vector transfer associated for instance to a fixed energy transfer of 5 eV increases from 1.15 Å⁻¹ at the excitation energy threshold up to 3.5 Å⁻¹ at the incident electron energy E₀ of 18 eV. The same wave-vector transfer values would be achieved if E₀ was set to 200 eV and the scattering direction was varied from 9 to 28°. Since the CS for dipole allowed transitions are strongly forward peaked at such incident energy and thus decrease with increasing scattering angle, suggests that the present CS for the singlet components should reach a maximum slightly above their energy thresholds and then decrease accordingly with E₀. In contrast, if the scattering angle was 0° for the same energy transfer and incident electron energy range, then the minimum wave-vector transfer would decrease from 1.15 down to 0.33 Å⁻¹. In that case the measurement would reveal more and more the long-range part of electron-molecule interaction along with the CS increasing steadily with E₀. In fact, measurement of 0° and 180° differential cross sections for aromatic hydrocarbons (and other compounds), which has been performed in the gas-phase, indicates that the CS for the excitation of dipole allowed electronic transitions rise nearly linearly up to fairly high energies and show little structure.⁶⁴

The presence of enhancements at specific energies in the electronic excitation CS of a molecule is most likely due to the formation of core-excited electron resonances during the collision of an electron with the molecule.^{64, 65} Such a transient anion state, which is characterized by a lifetime much longer than the normal scattering time (i.e., ~ 10⁻¹⁶ s), arises from the capture of an extra electron into an empty MO (i.e., virtual orbital) of the molecule while the molecule is being excited into an electronic state, which is called the “parent state”. Alternatively, this compound state can be described as two particles in unoccupied MOs and a hole in one normally occupied MO. For sufficiently long capture time (i.e., ~ 10⁻¹³ – 10⁻¹⁴ s) and entirely repulsive anion state, the molecule can dissociate into an anion along with one or more neutral fragments (i.e., DEA) or else cleave. For a bonding potential-energy surface, DEA or cleavage may still occur but for the transient anion formed into the repulsive part lying above the dissociation limit. For shorter capture time (i.e., ~ 10⁻¹⁵ s), it may result an efficient displacement of the nuclei prior to electron autodetachment and the resonance may decay into the vibrationally excited ground state as well as allowed electronic states of the molecule.

The electron energy dependence for production of several anion fragments have been observed for cytosine in the gas phase^{8, 12, 14, 15, 19} and in the condensed phase as multilayer films.²¹ In the latter result only low mass fragment anions possessing sufficient kinetic energies to surmount the film-vacuum barrier due to the image force have been detected. The measurement of the H⁻, CN⁻, and O⁻/NH₂⁻ yields as a function of the electron impact energy, show resonance structures at about 9 and 20 eV, which are superimposed on a monotonous signal rise from about 12 eV. This rise is attributed to dipolar dissociation that results from excitation of a neutral electronic state dissociating into a stable anion and cation. In the gas-phase, many more fragment anions have been found below 12-eV impact energy, where essentially DEA is operative. Among these, the C₃H₃N₂⁻, C₃HN₂⁻, OCN⁻, CN⁻ and O⁻/NH₂⁻ fragments appear to be the most interesting with their energy dependent production yield showing resonances lying within the 5.7 – 6.8 eV and 9.5 – 10.9 eV range.¹⁴ The comparison between the latter two resonance ranges shown as shaded rectangles in Fig. 3(a) and the present enhancements around 6 and 10 eV in the electronic excitation CS suggests the existence of common precursor anion states decaying with certain probabilities into their parent states. As for the enhancements around 8 and 12 eV in the CS for the excitation of the 5 ¹A′(π → π*) state and which are not seen in DEA measurements in the gas phase, they might arise from shorter-lived core-excited resonance decaying mainly into their parent states.

The sum of the CS attributed to the ionization potential I₁, I₂, I₃, and I₄ (Table II) is shown in the bottom of Fig. 3(b). The CS rises steeply to a maximum of 8.1 × 10⁻¹⁶ cm² at the incident energy of 13 eV and then falls. This drop should not come as a surprise since the present analysis is limited to an EEL energy of 12 eV and thus ignores the contribution from the inner valence shell MOs, which have been found at about 12.93, 13.86, 14.94 and 18.02 eV in the gas phase.⁴¹ No experimental CS data for electron impact ionization of cytosine have been published. However, the total CS for electron impact ionization of DNA bases have been calculated for energies ranging from the ionization threshold up to a few thousand eV by several groups using semi-classical and binary-encounter-Bethe formalisms.^{66, 67} Such a computed CS by Mozejko and Sanche⁶⁷ for cytosine is shown in the bottom of Fig. 3(b). The present total CS, which may be seen to be linear the first few eVs above the ionization threshold, is about three times larger than the calculated one. Ionization potentials are lower in condensed phase owing to the electronic polarization induced by the positive ion in the surrounding medium. This however, can hardly explain the present much larger value. However, in an EEL spectrum recorded for incident electron energy E₀ just above an ionization threshold, it is impossible to distinguish between a scattered and an ejected electron. If the latter contributed to half of the ionization EEL signal (i.e., both electrons having about the same energy) the present ionization CS values would be twice too large.

V. SUMMARY

The electronic excitation energies of cytosine deposited on an inert Ar substrate compare favorably to those obtained by EEL spectroscopy of the molecule in the gas phase. The LEE scattering CS values were obtained with a better accuracy than before owing to essentially the use of the same cytosine coverage on the inert Ar substrate and of its calibration directly in terms of surface number density. The CS for some of them exhibits enhancement at specific energies that are similar to those that has been found in the DEA experiment to cytosine in gas phase. This finding suggests the presence of short-lived core-excited resonances decaying mainly into their parent states. The sum of the CS attributed to the ionization of the four highest occupied MOs is larger than the theoretical predictions for the total ionization CS within the first few eVs above the ionization threshold. This confirms that ionization of cytosine is an important dissipative process via which ionizing radiation degrade and is absorbed in DNA.

As explained in the introduction, our scattering LEE scattering CS values are directly related to dose calculation in TRT. Although, the contribution of LEEs with their short ranges (~ nm) is not required in the conventional dosimetry of fast primary particles in a macroscopic volume, such as an organ, the same is not true when considering dose and damage heterogeneities at the level of the cell nucleus, the chromosome, or the DNA. This situation is met, for example, when radiation dose is delivered with the concomitant administration of radiosensitizers or high molecular weight (i.e., high-Z) atoms that incorporate into DNA of the cancer cells (e.g., bromouridine and cis-platin). Under these conditions, the nanoscopic dose and the evaluation of DNA damage could both be underestimated in conventional dosimetry owing to the neglect of LEEs.