Differential proliferation rates generate patterns of mechanical tension that orient tissue growth

Abstract

Orientation of cell divisions is a key mechanism of tissue morphogenesis. In the growing Drosophila wing imaginal disc epithelium, most of the cell divisions in the central wing pouch are oriented along the proximal–distal (P–D) axis by the Dachsous-Fat-Dachs planar polarity pathway. However, cells at the periphery of the wing pouch instead tend to orient their divisions perpendicular to the P–D axis despite strong Dachs polarization. Here, we show that these circumferential divisions are oriented by circumferential mechanical forces that influence cell shapes and thus orient the mitotic spindle. We propose that this circumferential pattern of force is not generated locally by polarized constriction of individual epithelial cells. Instead, these forces emerge as a global tension pattern that appears to originate from differential rates of cell proliferation within the wing pouch. Accordingly, we show that localized overgrowth is sufficient to induce neighbouring cell stretching and reorientation of cell division. Our results suggest that patterned rates of cell proliferation can influence tissue mechanics and thus determine the orientation of cell divisions and tissue shape.

Introduction

Multi-cellular tissues must grow in a spatially coordinated manner to reach their correct size and shape. The final structure is a result of the combined patterns of cell divisions, cell death, cell-shape changes, and cell rearrangements (Lecuit and Le Goff, 2007). During the growth phase of development, the orientation of cell divisions can have a major influence on the shape and function of the final adult tissue (Gong et al, 2004; Ciruna et al, 2006; Keller, 2006). Morphogenesis then further sculpts this post-growth tissue mass through cell-shape changes and cell rearrangements (Lecuit and Le Goff, 2007; Keller et al, 2008; Aigouy et al, 2010; Bosveld et al, 2012) to produce a tissue of the correct final shape.

In Drosophila, the cells in the wing epithelium divide preferentially along the proximal–distal (P–D) axis to give rise to a wing that is more elongated in the P–D axis (Baena-López et al, 2005). Loss of the orientation of cell divisions during growth can lead to misshapen wings (Baena-López et al, 2005; Mao et al, 2011). The control of cell division orientation has been extensively studied, both in unicellular systems and in multi-cellular epithelial tissues. Several molecular pathways, including the Wnt-Fz and Dachsous-Fat-Dachs planar cell polarity pathways, have been implicated in the control of the mitotic spindle orientation (Quesada-Hernandez et al, 2010; Ségalen et al, 2010; Morin and Bellaïche, 2011). The role of the Dachsous-Fat pathway in mitotic spindle orientation has been shown to be due to its ability to polarize the unconventional myosin Dachs along the P–D axis (Mao et al, 2006, 2011).

Previous to these insights into the molecular control of cell division orientation, classical observations made over 150 years ago have suggested that cell geometry strongly dictates the mitotic cleavage plane (Hofmeister, 1863; Hertwig, 1893). Several studies have shown that cells align their mitotic spindle to their longest axis—a principle known as Hertwig’s rule (Hertwig, 1893; Strauss et al, 2006; Théry et al, 2007; Gibson et al, 2011; Minc et al, 2011)—and to their external force field (Fink et al, 2011). In a multi-cellular tissue such as a growing epithelium, each cell’s shape and division orientation is strongly influenced by the forces from neighbouring cells (Aegerter-Wilmsen et al, 2010; Gibson et al, 2011). The cellular packing geometries of the wing epithelium, like many other tissue types, consist mainly of hexagons with other polygons occurring less frequently (Gibson et al, 2006; Farhadifar et al, 2007; Patel et al, 2009; Aegerter-Wilmsen et al, 2010). In the wing disc, this geometry is further complicated by a gradient of cell shapes along the P–D axis (Jaiswal et al, 2006; Aegerter-Wilmsen et al, 2012).

The unconventional myosin Dachs can affect cell geometry by generating local force anisotropies in the cell, either leading to polarized cell divisions in the third instar wing disc or directing neighbour exchanges in the pupal notum (Mao et al, 2011; Bosveld et al, 2012). In the wing disc, Dachs biases cell elongation along the P–D axis, directing division proximo-distally. This is particularly evident in the shape of clones in the distal (centre) portions of the wing pouch, which are strongly elongated along the P–D axis (Figure 1A and B; Mao et al, 2006, 2011), a bias that disappears in the absence of Dachs polarization (Baena-López et al, 2005; Mao et al, 2011). Towards the proximal region (edge) of the wing pouch, this force of Dachs is less evident, despite a strongly polarized expression pattern (Mao et al, 2006; Brittle et al, 2012). Hence, other forces in the tissue must be more prominent in controlling cell geometry in the proximal edge regions of the wing disc. How these forces are generated and integrated to produce the patterned distribution of cell shapes in the wing disc is still unclear.

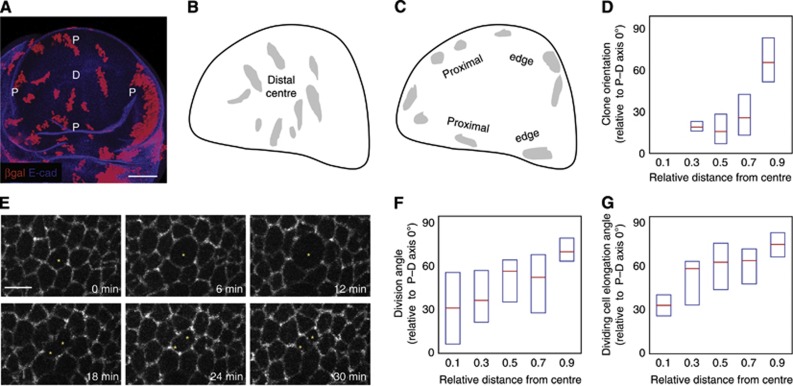
Figure 1.

Clone orientations and division orientations change along the P–D axis. (A) A wild-type (WT) wing disc containing clones expressing lacZ. D marks the distal (centre) of the wing disc and P marks the proximal ring (edge); scale=50 μm. The P–D axis during wing disc development is a radial axis. (B) Overlay of clones in the distal (centre) region from several wing discs. These are elongated along the P–D axis (radial). (C) Overlay of clones in the proximal (edge) region from several wing discs. These are elongated perpendicular to the P–D axis (circumferential). (D) The long axes of individual clones are oriented relative to the P–D axis at that position (perfect P–D alignment=0°) and plotted against relative distance from the centre to the first fold (edge) of the wing pouch. Box plots show median and first and third quartiles, n=119 clones, only clones with an elongation ratio of >1.25 are plotted. (E) Snapshots from a live-imaged Arm::GFP wing disc, scale=5 μm. 0 min shows the dividing cell (marked by an asterisk) immediately prior to mitosis. At 30 min, cytokinesis has completed and the two daughter cells are formed. (F) The alignment of the two daughter cells immediately after mitosis in live-imaged discs is oriented relative to the P–D axis and plotted against its relative distance from the centre to the first fold of the pouch. Box plots show median and first and third quartiles, n=110 dividing cells. Only mother cells with elongation ratios (long/short axis)>1.3 are plotted. (G) The long axis of each dividing cell immediately prior to mitosis in live-imaged discs is oriented relative to the P–D axis and plotted against its relative distance from the centre to the first fold (edge) of the pouch. Box plots show median and first and third quartiles, n=110 dividing cells. Only cells with elongation ratios (long/short axis)>1.3 are plotted.

Here, we use experimental observations, quantitative image analysis, and computational modelling to show that differential proliferation rates can generate global patterns of mechanical tension. In combination with local control of cell geometry, these global tension patterns can generate global cell-shape patterns, which then orient cell divisions and growth in a developing epithelium. Our results suggest a mechanism that links the cell division rates with the cell division orientations, such that a tissue can simultaneously control its size and shape during proliferative growth, building a pre-shaped tissue mass for morphogenesis movements to sculpt and amplify.

Results

Cell divisions are differentially oriented along the P–D axis

Although distal (central) clones predominantly grow along the P–D axis in the wing disc, clones in the proximal part of the pouch, and in the hinge regions of the wing disc, grow perpendicular to the P–D axis (Figure 1A–D), despite clear polarization of Dachs in this region (Mao et al, 2006; Brittle et al, 2012). This suggests that another mechanism overcomes Dachs-mediated orientation of cell divisions in the proximal wing. To investigate how the cell division orientations change along the P–D axis of the wing, we carried out live imaging of the proliferating wing imaginal disc (Figure 1E; Supplementary Movie 1). Since the hinge region is highly folded, we restricted our analysis of cell shapes and divisions to regions of the wing pouch up to the first fold of the wing, which becomes the future wing blade (see Figure 2B for example zones of interest and Supplementary Figure S1 for pupal and adult wings). As previously observed, cells in the distal region of the pouch divide with a strong bias along the P–D axis, but further from the distal-most point, this alignment becomes lost. Eventually, at the most proximal regions of the pouch, divisions are oriented with a bias perpendicular to the P–D axis, as observed using time-lapse videomicroscopy of wing discs cultured ex vivo (Figure 1E and F). These results are consistent with the changes in clone orientations along the P–D axis (Figure 1D). Since cells divide along their longest axis, we checked the elongation orientation of the dividing cells just prior to mitosis, and observed the same trend. Cells are elongated with a P–D axis bias in the distal region (centre) of the wing pouch, but become more imperfectly aligned with increasing distance away from the distal-most point, eventually becoming almost perpendicular to the P–D axis in the proximal-most outer rim of the wing pouch (Figure 1G).

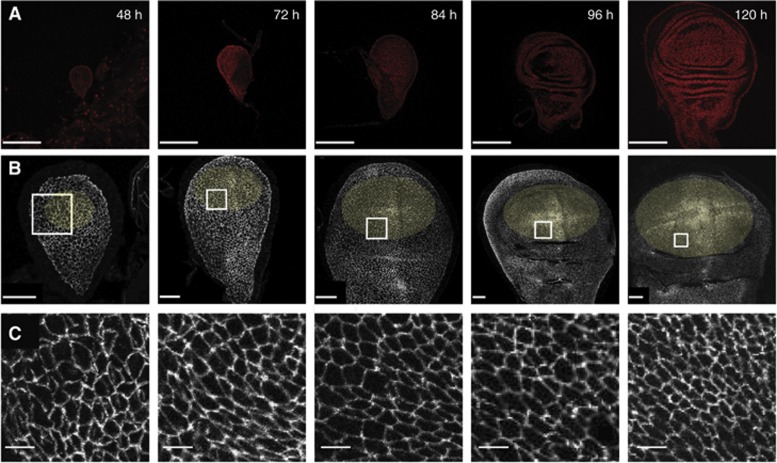
Figure 2.

Wing disc development. Confocal micrographs of wing discs fixed at the indicated ages after egg laying (AEL). (A) Hoechst staining labels nuclei. Scale=100 μm. (B) Wing discs expressing E-cadherin::GFP at endogeneous levels, marking the adherens junctions to show the apical cell geometries. Scale=20 μm. Yellow ellipses mark the areas of wing discs used for analysis. For 48–72 h wing discs, the Nubbin expression domain is used (Supplementary Figure S2), for older wing discs, an elliptical zone up to the first visible fold is used. (C) A magnified view of the white-square region marked in (B), scale=4 μm. Note that folds in the surface of the wing disc appear at ∼80 h AEL.

The epithelial geometry of the wing disc changes during growth

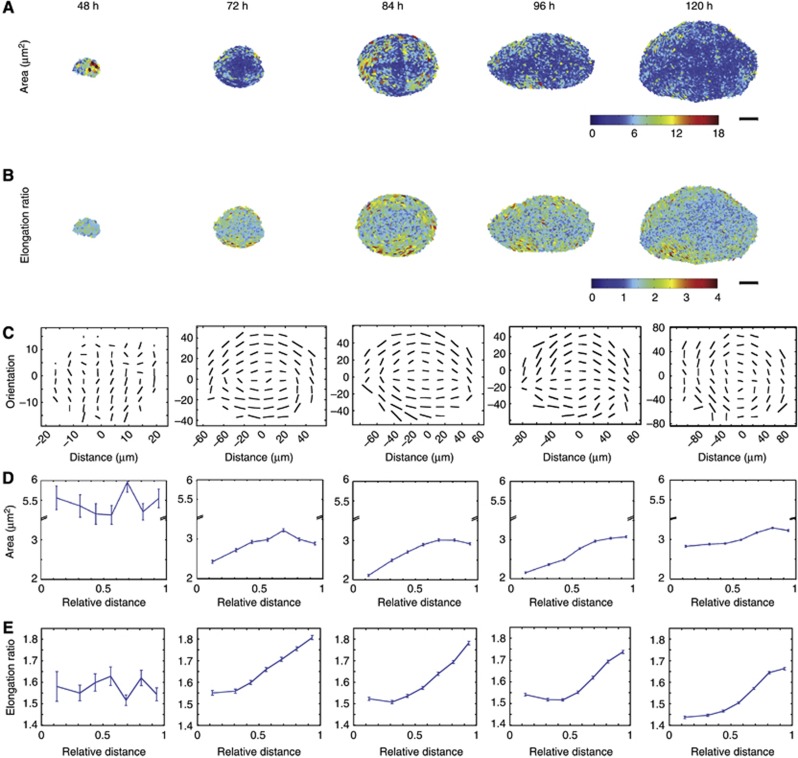
Since the epithelial geometry of the wing disc strongly dictates the cell division orientations, and thus the future growth patterns of the wing, we decided to investigate how the geometry of the epithelium changes during development. Previous work had suggested a gradient of cell area distributions along the P–D axis (Jaiswal et al, 2006; Aegerter-Wilmsen et al, 2012). We focussed on six developmental stages of the wing disc, from 48 h after egg laying (AEL) to 120 h AEL, when the larvae are about to pupate and the wing disc is ready to undergo pupal morphogenesis (Figure 2 and Supplementary Figure S4 for 60 h wing disc). We concentrated on how the apical area, elongation, and orientation of cells in the wing pouch (yellow highlighted areas) evolve, both in time and spatially, along the P–D axis. We used a custom-made image segmentation software to extract these features from these different stages of wing disc development (Figure 3; Materials and methods). The most striking emergence of non-uniformity in the apical epithelial pattern occurs from 48 h to 72 h AEL. At 48 h, the cells in the wing pouch show no measurable P–D bias in cell area and elongation (Figure 3D and E, 48 h). Their orientations are also mostly random at this stage (Figure 3C, 48 h). However, by 72 h, clear trends along the P–D axis are already visible. Overall, cells have a smaller apical area, but they are markedly larger in the proximal regions than in the distal regions, and become more elongated towards the proximal region (Figure 3D and E-72 h). The elongation orientation is also more defined at this stage, with more cells orienting perpendicular to the P–D axis as they become more proximal (Figure 3C-72 h; Supplementary Figure S3). This pattern is sustained throughout the next 48 h of growth, with little changes developing along the P–D axis, although at 96 and 120 h, the cells do become slightly less elongated (see Discussion).

Figure 3.

Quantification of cell geometries in the developing wing disc. (A) The individual cell areas extracted from segmented images of fixed single wing pouches at the shown ages AEL. Scale=25 μm. (B) The individual cell elongation ratios extracted from the same wings as (A). Scale=25 μm. (C–E) Averaged data from multiple wing discs: n=6 (48 h), n=12 (72 h), n=11 (84 h), n=12 (96 h), and n=10 (120 h). (C) Elongation orientation of cells averaged over a minimum of 10 cells. The length of the bar indicates the extent of elongation, and direction of the bar indicates orientation. (D) Mean apical area of cells plotted against its relative distance from the distal centre to the proximal edge of the pouch. Error bars indicate s.e.m. (E) Mean elongation ratios of cells plotted against its relative distance from the distal centre to the proximal edge of the pouch. Error bars indicate s.e.m.

Global non cell-autonomous forces account for higher tension in the peripheral cells

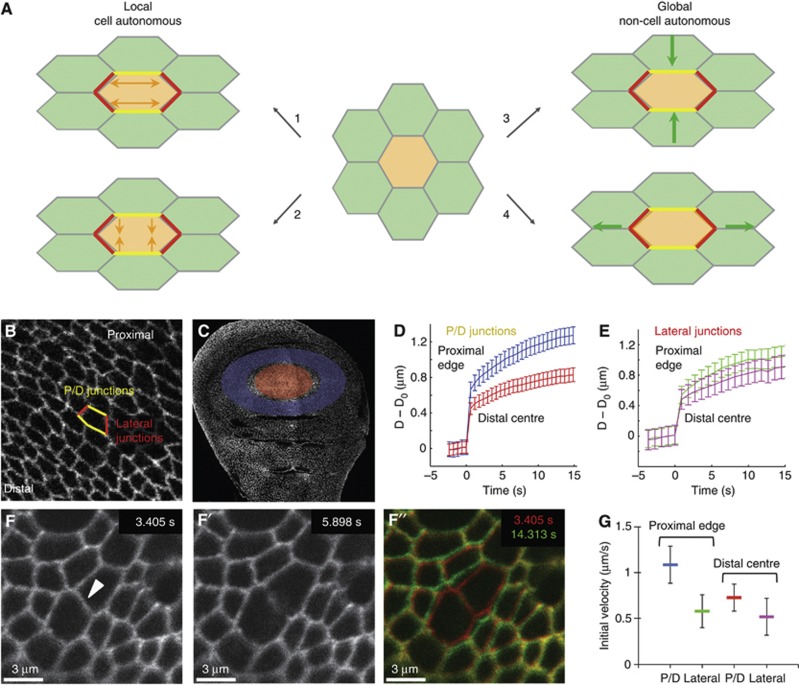
We wondered how this pattern of cell geometries along the P–D axis could arise, and whether it could be generated on a purely mechanical basis, without the cells having different genetic identities. From a physical perspective, in order for the proximal cells to elongate circumferentially more than the distal cells, they must be experiencing different force anisotropies. This could result from four distinct mechanisms (Figure 4A). The proximal cells could ‘autonomously’ either (1) extend their proximal/distal edges or (2) constrict their lateral edges (Figure 4A and B). On the other hand, they could either (3) be compressed or (4) stretched by tissue-wide forces (Figure 4A).

Figure 4.

Patterns of mechanical tension in the wing disc. (A) A schematic representation of the different mechanisms in which a cell (marked in orange) could elongate, starting from the isotropic configuration in the centre. (1) Local cell-autonomous extension of yellow junctions. (2) Local cell autonomous constriction of red junctions. (3) Global non cell-autonomous compression forces leading to constriction of the red junctions. (4) Global non cell-autonomous stretching forces leading to extension of yellow junctions. (B) In the wing disc, the junctions highlighted in yellow are the proximal/distal (P/D) junctions, and the junctions in red are the lateral junctions. The orientation of the wing disc is highlighted by the direction of the distal (centre) and the proximal (edge). (C) E-cadherin::GFP wing disc with the regions used for laser ablation in (D, E) highlighted. Red: distal centre, blue: proximal edge. (D) P/D junctions. Plot of increase in distance (μm) between the vertices of the cut junction (D−D₀) against time (s) after laser cut, mean±s.e.m. Blue=P/D junctions in the proximal (edge) region. Red=P/D junctions in the distal (centre). (E) Lateral junctions, as in (D). Green=lateral junctions in the proximal (edge) region. Magenta=lateral junctions in the distal (centre). (F–F′) Snapshots of an example laser ablation of a junction at the indicated time points (see Supplementary Movie 2). The cut was performed at 3.405 s and the recoil imaged for at least 15 s. (F″) An overlay of the junction before cut (red) and 11 s after cut (green) is shown. (G) The initial (maximum) recoil velocity of the vertices after the cut. Represented as mean±s.e.m. For cells at the proximal (edge) of the disc: P/D junctions (blue): velocity=1.09±0.20 μm/s, n=47; lateral junctions (green): velocity=0.58±0.18 μm/s, n=30. For cells at the distal centre: P/D junctions (red): velocity=0.73±0.16 μm/s, n=53; lateral junctions (magenta): velocity=0.52±0.2 μm/s, n=28. The average ratio of P/D to lateral junctions at the proximal edge is 1.87, higher than the average ratio of 1.4 at the distal centre of the pouch. Ablation experiments were performed at ∼100 h AEL.

To explore the first two possibilities, we examined the adherens junction component E-cadherin and Myosin-II, which are two key determinants of adhesion and cortical tension in this system (Lecuit, 2008). E-cadherin and Myosin-II light chain (Sqh) show no obvious anisotropies in their expression levels throughout the wing disc (Supplementary Figure S5A and B). However, phospho-Myo-II (p-Myo-II) stainings revealed higher myosin contractile activity on the proximal/distal edges of proximal cell, similar to Dachs polarization (Supplementary Figure S5C). This anisotropy in Myo-II activity would be expected to constrict the proximal/distal edges. However, since these are more elongated, and cell areas are larger, it is probable that p-Myo-II accumulation is in fact counterbalancing a stronger external force, suggesting that a non cell-autonomous global force is stretching the cells perpendicular to the P–D axis. Using laser ablation to reveal junctional tension (Farhadifar et al, 2007; Cavey et al, 2008), we could show that cells in the proximal region of the wing disc are under higher tension in their P/D junctions than their lateral junctions compared to cells in the distal centre of the wing (Figure 4B–G; Supplementary Movie 2). This result suggests that in the periphery of the wing disc, global forces are dominating the cell-shape changes.

Computational modelling predicts that differential proliferation rate is a key mechanism in generating global mechanical tension patterns

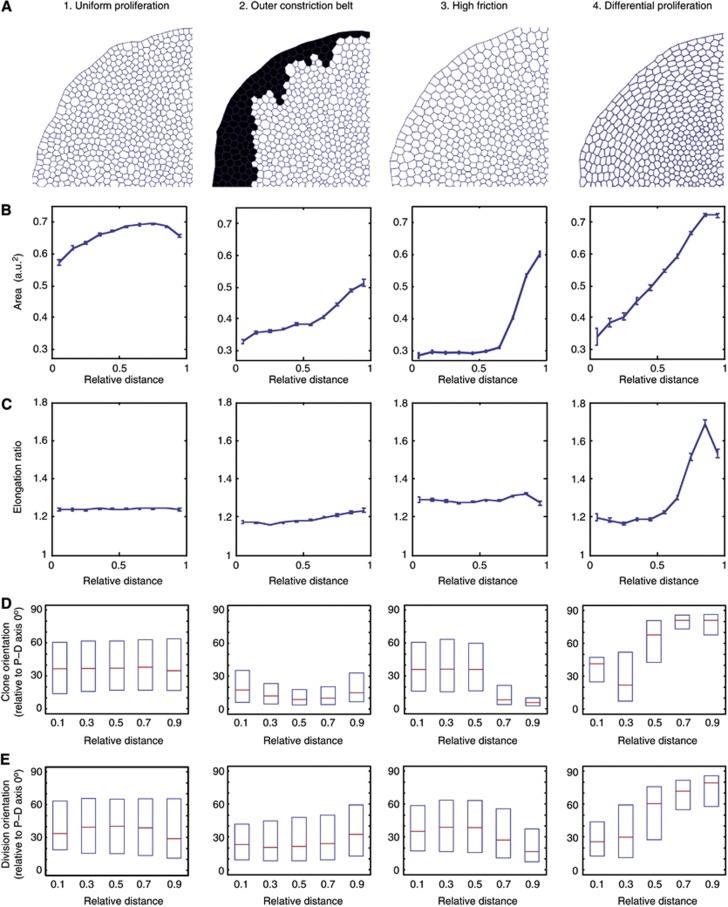
Using a computational vertex model, we explored different hypotheses for how this global force around the periphery of the wing disc could be generated (Farhadifar et al, 2007; Mao et al, 2011). We simulated each mechanism to investigate whether the in vivo epithelial pattern could emerge from the simple rules in the in silico model. As a baseline, we used conditions where the whole tissue had uniform properties—uniform proliferation rates and uniform (low) friction against the substrate. Even when this simulated tissue reached 10 000 cells, the cell geometries across the tissue remained uniform, and there were no changes in cell area or elongation along the (in silico) P–D axis (Figure 5A–C1). We also ‘induced’ clones in silico during the simulations and tracked cell division orientations, and neither showed orientation changes along the P–D axis (Figure 5D and E1; Supplementary Movie S3). Thus, there must be a difference in epithelial properties along the P–D axis for the epithelial geometry and the cell division orientations that we observe in vivo to emerge.

Figure 5.

Computational exploration of the different mechanisms that can generate global forces to elongate cells in the periphery of the disc. A radial (P–D) polarization of Dachs is applied to all simulations to mimic the in vivo Dachs polarization patterns. (A) Snapshots of a quadrant of the in silico wing discs after ‘60 h real time’ simulations (equivalent to between 2 and 10 h computational run time, depending on scenario). (B–E) All graphs show relative distance from the centre of the disc on the X axis. (B) Cell area (arbitrary units) at end point. Error bars represent s.e.m. (C) Cell elongation ratios at end point. Error bars represent s.e.m. (D) Clones are induced in silico and their elongation orientations (relative to the radial P–D axis) are recorded at end point. Plots show median and first and third quartiles. Note the baseline bias of orientations towards the P–D axis, due to Dachs. (E) Cell division orientations are tracked throughout the run. Showing median and first and third quartiles. See Supplementary Figure S6 for detailed analysis of cell elongation orientations. The profile of the steep differential proliferation in mechanism (4) is shown in Supplementary Figure S6D, top panel.

We reasoned that, as the tissue grows, cells need to slide outwards (Supplementary Movie 3), so if there is a physical constriction belt or barrier on the periphery preventing this outward growth, pressure would build-up from the centre, potentially building up peripheral tension on the outer cells. This belt could, for example, correspond to the pouch/hinge boundary, which is a deep, actin-rich indentation in the tissue and could therefore form a physical barrier. We simulated this outer constriction belt by setting the friction on the outermost ring of cells × 200 higher than the rest of the tissues, such that they would resist the outward growth motion of the tissue (black cells in Figure 5A2 and Supplementary Movie S4). The cell areas did show a graded decrease across the epithelium (compare Figure 5B1 with Figure 5B2), suggesting that the constriction belt is slowing the growth of the epithelium, more in the centre than at the edge. However, there were no significant differences in cell elongation across the epithelium (Figure 5C2), and any slight elongations near the edge were all parallel to the P–D axis, rather than perpendicular to it (Supplementary Figure S6B). Clones and cell divisions also do not show a gradual circumferentially bias (90° to P–D) towards the edges of the in silico wing disc (Figure 5D and E2). Hence, in this simulation, the constriction ring is providing a physical force that does affect cell size, but not the cell orientations and divisions, as observed in vivo. This is in agreement with the fact that folds develop around 80 h AEL, at which point we already observe cell-shape changes in the wing pouch (Figure 2).

Another possibility to explain the stretching of proximal cells is if the whole tissue experiences substantial friction against the substratum (i.e., the extracellular matrix). Indeed, depletion of Collagen IV had a profound effect on wing disc shape (Pastor-Pareja and Xu, 2011). Since the outer cells have to ‘slide’ more than the inner cells to accommodate tissue growth, this creates an effective friction gradient (higher on the outer cells and lower at the centre). When we introduced uniform higher friction (× 1000) into our model, which should mimic an in vivo friction gradient, we noticed a gradient of cell areas emerged along the P–D axis, similar to that observed in vivo (Figure 5B3; Supplementary Movie 5). However, the slight elongation of cells towards the edge (Figure 5C3) was oriented along the P–D axis, rather than perpendicular to it (Supplementary Figure S6C). This is also reflected in the clone and cell division orientations, which became even more biased along the P–D axis towards the edge of the disc (Figure 5D and E3). Thus, altering the friction levels also did not reproduce in vivo cell geometry and growth patterns.

Alternatively, we considered the idea that faster growth in the centre than in the periphery might also lead to a pressure build-up in the centre and generate a circumferential force on the peripheral tissue. Indeed, a previous modelling study had suggested that mechanical distortions can occur at the interface between quiescent and proliferating cell populations (Li et al, 2012). Simulations with differential proliferation rates along the P–D axis generated an epithelial geometry that closely resembles that of the real wing imaginal disc, with larger cells that are elongated perpendicular to the P–D axis towards the edge (Figure 5A, B, and C4; Supplementary Figure S6D). Clones and cell division orientations also show a gradual transition, showing a bias along the P–D axis in the centre, and a bias perpendicular to the P–D axis towards the edge of the disc (Figure 5D and E4; Supplementary Movie 6). Therefore, a higher proliferation rate in the distal (centre) of the tissue is able to generate mechanical force anisotropies along the P–D axis such that the proximal cells are stretched more along the circumference of the disc, which orients cell divisions and clonal growth.

Altering proliferation rates in vivo affects cell shape, junctional tension, and cell division orientation

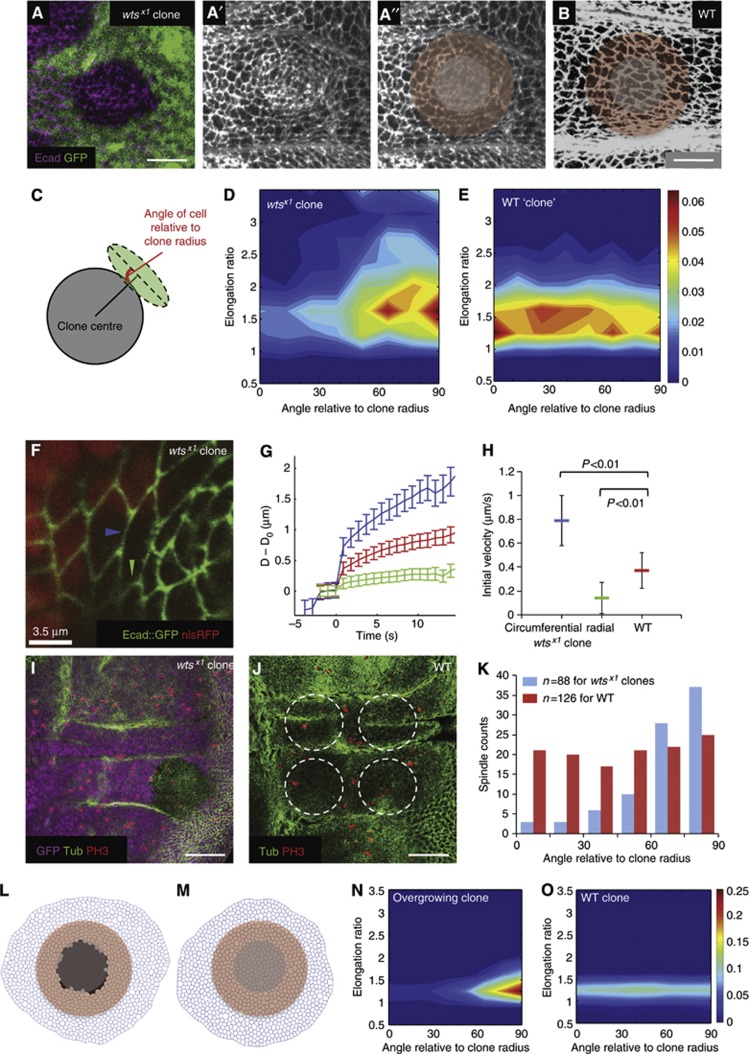
Although our in silico explorations suggested that differential proliferation rates are a major driving force for generating patterns of global mechanical anisotropies, we wanted to examine whether ectopically altering proliferation rates in vivo could induce the same effects on epithelial cells. We generated clones of fast-proliferating cells and measured the consequences of neighbouring cells, thus testing whether a local increase in growth rate is sufficient to induce tension in neighbouring slower proliferating cells. We performed these experiments in the hinge region of the wing, where the results are not complicated by the ‘endogeneous’ tension gradient we observe in the pouch. When we induced mutant clones for the Hippo pathway component warts (wts), which has been shown to result in tissue overgrowth (Justice et al, 1995; Xu et al, 1995) we observed considerable changes in neighbouring cells. Image segmentation shows that cells around the overgrowing clone become elongated perpendicular (circumferential) to the clone radius (Figure 6A–E). This alteration in cell elongation is correlated with increased tension in the circumferential junctions of wild-type cells surrounding the clone, but a decrease in tension of the radial junctions, as revealed by laser ablation (Figure 6F–H; Supplementary Movie 7). Accordingly, cell divisions around the clones are also reoriented perpendicular to the clone radius (Figure 6I–K). Together, these data show that in vivo, a local overgrowth can induce an increased tension in neighbouring cell junctions, which stretches cells and reorients divisions. This phenomenon is also reproducible in our in silico model where an acute local overgrowth can induce surrounding cells to become elongated perpendicular to the overgrowing clone (Figure 6L–O), see Materials and methods for details.

Figure 6.

The effect of altering proliferation rates in vivo. (A–A″) wts mutant clones marked by lack of nuclear GFP and stained for E-cadherin in the hinge region of the wing disc, scale=10 μm. A more basal GFP section is used to show the nuclear GFP signal. (A″) Schematic to represent the grey mutant cells removed from the cell-shape analysis and the surrounding red cells used in the analysis in (D). (B) The hinge region of a wild-type wing disc stained for E-cadherin, scale=10 μm. The red region is the corresponding control cells used for cell-shape analysis in (E). (C) Scheme of how the cell shapes around the clones are quantified (see Materials and methods). (D) Cell-shape analysis of cells surrounding wts clones (n=5 clones). Majority of cells around the clone are elongated circumferentially around the clone (tangential). (E) Cell-shape analysis of cells surrounding WT ‘clones’ (n=5 clones, each in the corresponding regions to each wts mutant clone). Cells are less elongated and show no specific orientation patterns. (F) A wts mutant clone marked by the absence of nuclear RFP and simultaneously expressing an E-cadherin::GFP transgene to allow live imaging of cell junctions for laser ablation. The blue arrowhead marks a typical circumferential junction of a wild-type cell bordering the mutant clone that was cut for the analysis (see Supplementary Movie 7). The green arrowhead marks a typical radial junction as used in the analysis. (G) Plot of increase in distance (μm) between the vertices of the cut junction (D−D₀) against time (s) after laser cut, mean±s.e.m. Blue=circumferential junctions of wild-type cells surrounding wts mutant tissue, green=radial junctions of wild-type cells surrounding wts mutant tissue, red=wild-type hinge junctions. (H) The initial (maximum) recoil velocity of the vertices after the cut. Represented as mean±s.e.m. For circumferential junctions surrounding wts mutant tissue (blue), velocity=0.79±0.21 μm/s, n=39 junctions; for radial junctions surrounding wts mutant tissue (green), velocity=0.14±0.13 μm/s, n=30 junctions; for WT hinge junctions (red), velocity=0.37±0.15 μm/s, n=50 junctions. (I) wts mutant clone (lack of GFP) stained for tubulin and PH3 to identify mitotic spindle orientation, scale=50 μm. Only spindles close to clone boundaries are used for analysis in K (see Materials and methods). (J) A WT wing disc stained for tubulin and PH3, scale=50 μm. Circles show typical control ‘clone’ regions used for WT hinge spindle analysis. (K) Spindles surrounding wts mutant clones (blue) are oriented more circumferentially around the clone (tangential), whereas spindles in WT hinges show no orientation bias. (L) In silico simulation of an acute overgrowing clone (black cells) in wild-type tissue. (M) Control simulation where there is no acute overgrowing clone. (N) Cells surrounding the overgrowing clone (pink cells in L) elongate perpendicular to the clone radius. (O) Without acute overgrowth, cells show no elongation bias around the ‘clone’.

Differential proliferation rates occur in the early wing disc during normal development

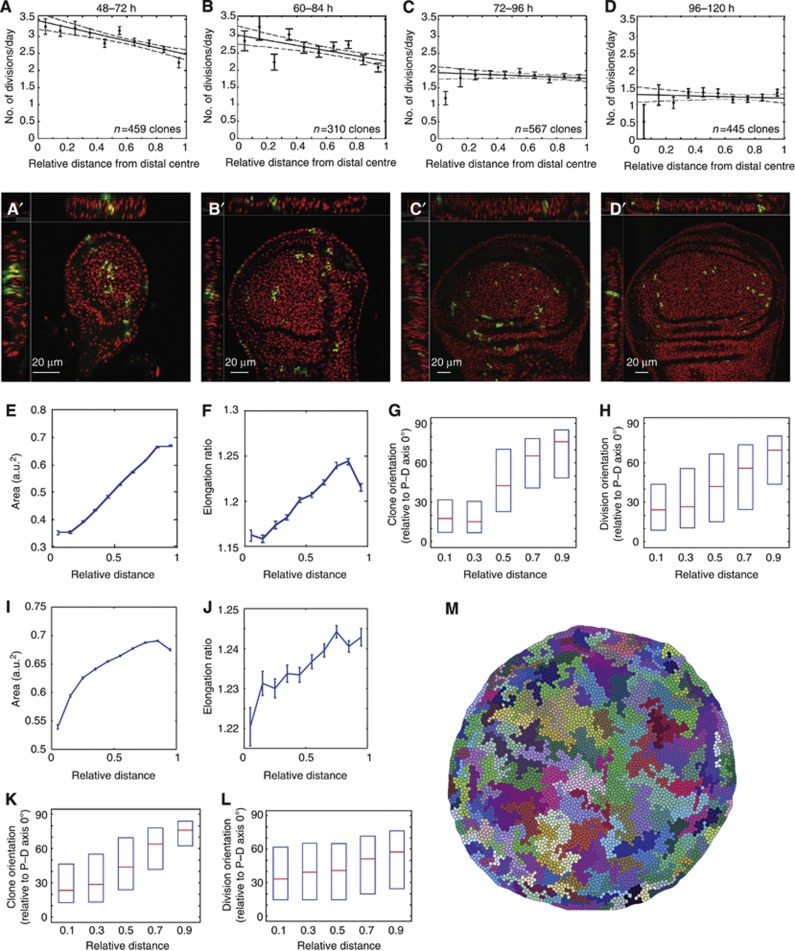
To determine whether differential proliferation does indeed occur in the wing disc, we measured in detail the spatial and temporal patterns of proliferation rates in the wing disc, with particular emphasis on how the pattern changes along the P–D axis. Although many previous reports have found that proliferation rates are largely uniform in the wing disc (Schwank et al, 2011; Wartlick et al, 2011), these were mainly measured towards the end of wing disc development. We were particularly interested in the earlier stages, during 48–72 h of development AEL, since it is between these stages that we observe the largest change in epithelial geometry in the wing disc (Figure 3). We focussed our analysis on four 24-h developmental periods (Figure 7A–D) and measured how clones grew in different regions of the wing pouch during each of these 24-h periods. GFP-labelled clones were induced at 48, 60, 72 or 96 h AEL, and wing discs were dissected precisely 24 h later (see Materials and methods for details). The number of cells in each clone was then counted in 3D to ensure that even the nuclei that were tightly packed on top of each other were counted, a particular problem in the distal centre region of the densely packed pseudo-stratified epithelium (see Figure 7A′–D′). Simple 2D projections would result in an underestimation of cell numbers. Only clones up to the first fold of the wing pouch were included in the analysis.

Figure 7.

Differential proliferation rates measured in vivo are sufficient to orient divisions and clonal growth. (A–D) Proliferation rates (number of divisions/day) for the different 24 h developmental time windows are shown. Individual points are mean±s.e.m. Dotted lines show 95% confidence intervals of the fit of the proliferation profiles. (A′–D′) An example of wing discs used for the proliferation rate analysis showing 3D views. Green=GFP expressing clones. Red=Hoechst stain for nuclei. (E–H) Analysis of cell area, elongation ratio, clone orientation, and cell division orientations, when using a shallow differential proliferation for ‘60 h real time’ simulations. See Supplementary Figure S6E for proliferation profile used. This shallow profile is sufficient to produce the correct trends in cell behaviours as in vivo. (I–M) Analysis of the ‘in vivo mimicking’ simulation. The exact spatial and temporal changes in proliferation profiles as measured in vivo are used for ‘72 h real time’ simulations. A uniform array of about 150 cells is used as the 48-h starting configuration (as in vivo; Figure 3). Clones are ‘induced’ at 48 h. Differential proliferation occurs until 84 h, followed by uniform proliferation, using the rates measured in (A–D). Cell areas (I), cell elongation ratios (J), and clone orientations (K) at the end (120 h). Cell divisions throughout the run are tracked (L). Box plots show median and first and third quartiles. (M) Snapshot of the end point showing the pattern of clonal growth that closely matches that of in vivo clones.

In early (second instar) discs (48–72 h AEL), there is clearly a range of clone sizes, which is consistent with previous findings (González-Gaitán et al, 1994; Milán et al, 1996). When we plotted the cell proliferation rates (number of divisions per day) as a function of the clone’s distance from the distal centre of the pouch, we found that proliferation was significantly faster in distal centre region of the pouch than in the proximal edge region (Figure 7A). In the distal centre, an average of 3.5 divisions per day was measured, and at the proximal edge, 2.5 divisions per day. This range is consistent with reports of the average cell doubling times at this early stage being around 6 h (Martín et al, 2009) to 10 h (Johnston and Sanders, 2003). For the period of 60–84 h, the proliferation differential is still detectable, but has dropped to only 3 divisions per day in the centre. During 72–96 h, proliferation rates drop throughout the pouch to a uniform 2 divisions per day and decrease further during 96–120 h to about 1.2 divisions per day, both of which are in agreement with previous measurements (Neufeld et al, 1998; Martín et al, 2009; Aliee et al, 2012). Statistical analysis of these two later periods shows that the data are consistent with a uniform proliferation profile (apart from the known zones of non-proliferation at the dorsal–ventral boundary of the disc (O'Brochta and Bryant, 1985; Johnston and Edgar, 1998)) as also measured in previous studies (Schwank et al, 2011; Wartlick et al, 2011). This is also consistent with the lack of significant changes in the epithelial geometry during 72–120 h of wing disc growth. Note that from 60 h to 84 h, there is a significant progression in cell profile changes, reflecting the proliferation differential that is still occurring during this 24 h developmental window (compare Supplementary Figure S4C and D with Figure 3D and E, 84 h). Hence, there is a pattern of differential proliferation along the P–D axis in the wing disc that is maximal during 48–72 h of development (which then slowly equilibrates), consistent with the emergence of non-uniformity in the epithelium during this period, and with the in silico simulations.

In vivo spatial and temporal patterns of proliferation rates can generate wild-type growth patterns in silico

Since the in vivo proliferation differential is shallower than the steep differential used in the initial exploration (Figure 5; Supplementary Figure S6), we wanted to investigate whether a gentle differential similar to that observed in vivo could also generate sufficient global tension anisotropies to produce the correct cell geometries and growth patterns in the wing disc. When we simulated the growth with a gentle proliferation differential over the whole ‘60-h real time’ growth period (Supplementary Figure S6E top), the correct trends in cell area and cell elongation ratio still occurred (Figure 7E and F), with the cells getting larger and more elongated towards the edge. The orientation of the elongation also becomes more perpendicular to the P–D axis towards the proximal edge (Supplementary Figure S6E, bottom two panels). The correct trends for clone orientations and cell divisions also occurred, with orientations becoming gradually less P–D axis oriented away from the distal centre (Figure 7G and H).

To address whether just an initial period of differential proliferation can be sufficient to generate the growth patterns in the wing disc, we simulated 48–120 h of wing growth by having differential proliferation rates as in vivo during 48–84 h of growth, and then uniform proliferation for 84–120 h (see Supplementary Materials and Methods for details). This still gave us the same cell area and elongation trends (Figure 7I and J). The clones also closely resembled that of wild-type wing disc—elongated along the P–D axis in the distal centre, and perpendicular to P–D in the proximal edge (Figure 7K and M; Supplementary Movie 8). To confirm that this is indeed due to the orientation of cell divisions, we also tracked all cell divisions during this 72 h of growth, and the same gradual trend was observed (Figure 7L). Hence, the in vivo spatial and temporal patterns of proliferation rates can generate sufficient global patterns of tension to drive the correct orientation of cell divisions and tissue growth.

Discussion

Our findings indicate that cell geometries in the wing disc result from a balance between local cell autonomous forces and global non cell-autonomous forces. We show that the global force anisotropy in the wing disc is primarily due to differential proliferation, with the distal centre growing faster than the proximal edge of the wing disc. Indeed, ectopic localized overgrowth results in stretching of neighbouring cells and reorientation of cell divisions perpendicular to the overgrowing clone. This finding supports our model that the proliferation gradient observed in early wing imaginal discs acts as a driving force for increased peripheral tension. Myo-II recruitment to actin filaments can be promoted by tension, possibly though stretch-induced increase in Myo-II/actin association (Kovacs et al, 2007; Fernandez-Gonzalez et al, 2009; Uyeda et al, 2011; reviewed in Fernandez-Gonzalez and Zallen, 2009). It is therefore possible that Myo-II is stabilized at the P–D junctions to counterbalance global tissue forces. Increased p-Myo-II (Supplementary Figure S5) along with increased Dachs through Dachsous/Fat signaling could combine at the P–D junctions to allow the distal cells to continue to elongate and divide along the P–D axis while preventing the proximal cells from becoming excessively stretched, thus maintaining tissue integrity.

Our mathematical model suggests that a central (distal) to edge (proximal) proliferation gradient such as that observed in vivo is sufficient to drive cell elongation and orient cell division in the periphery of a tissue. Interestingly, although the in vivo mimicking model (Figure 7) accurately reproduces the in vivo trends in cell elongation and oriented cell division, the quantitative extent of elongation and division orientation bias is weaker in the model. We were interested in understanding the basis for this difference, leading us to compare the patterns of cell–cell neighbour exchanges (Lecuit and Lenne, 2007) in the model and in vivo using cell tracking of cultured wing discs (Supplementary Figures S7 and S8, Supplementary Movie 9; Supplementary Materials and methods). We observed that T1 transitions in the model are very rapid and stable, whereas in the developing wing disc this process is very slow. The situation in the larval wing disc is in contrast to the ‘decisive’ manner in which cell–cell rearrangements occur in situations such as germ-band extension in the embryo, which involves active shrinkage of certain junctions (Bertet et al, 2004; Zallen and Wieschaus, 2004). This suggests that cells in the model can rapidly disperse excess tension by exchanging neighbours, where wing disc cells cannot do. This explains why the extent of proximal cell stretching, and therefore the bias in cell division orientation is less pronounced in silico than in vivo. It is impossible to prevent this rapid remodelling within the current implementation of the Vertex model. Future models should therefore be developed where the cell–cell plasticity of the tissue can be modulated to match that observed in vivo, perhaps by adding apposed membranes and representing the activity of adhesion molecules such as E-cadherin.

Recent theoretical work has suggested that a mechanical feedback control of proliferation is a likely mediator of terminal proliferation arrest during wing disc development (Shraiman, 2005; Aegerter-Wilmsen et al, 2007; Hufnagel et al, 2007; Aegerter-Wilmsen et al, 2012). In particular, the pattern of compression in the centre and stretching in the periphery has been proposed to account for equilibrating the differences in pro-growth signals between the centre of the pouch (distal), where cells are exposed to high levels of the Dpp and Wg morphogens versus the periphery (proximal) where cells are exposed to lower morphogen levels (Aegerter-Wilmsen et al, 2012). The pro-growth transcriptional co-activator Yorkie (YAP in mammals), which has been reported to respond to a cell’s mechanical environment (Dupont et al, 2011; Fernandez et al, 2011; Sansores-Garcia et al, 2011; Wada et al, 2011), has been suggested as a growth-regulatory sensor of these physical inputs (Aegerter-Wilmsen et al, 2012). While this is an attractive hypothesis, it was unclear how the patterns of stretch and compression observed in late discs arise in the first place. Our data suggest that early differences in proliferation rates in the centre versus the periphery likely account for these patterns, which might feedback to increase proliferation in stretched outer cells, leading to proliferation rate equilibration (as we and others observe in later stages—see Figure 7C and D). The gradual, albeit slight, decrease in cell elongations observed towards the later stages of wing disc development (Figure 3E) may reflect a possible outcome of this feedback mechanism. The combined chemical and physical feedback control of proliferation rates should result in a more robust output of both growth rates and growth orientations. Further experiments are needed to show that there is indeed a physical feedback control of growth operating in the wing disc.

Our work suggests that small spatial differences in proliferation rates can lead to anisotropies in global tissue mechanics, which will drive epithelial patterning, and control future cell division orientations and hence tissue shape. In addition to cell shape and arrangement changes, this provides an elegant mechanism to sculpt tissue shape during growth and morphogenesis.

Materials and methods

Drosophila strains and genetics

Drosophila stocks were obtained from Bloomington stock centre, unless otherwise stated. Genotypes used are yw hs.flp/+;;actin.FRT.CD2.FRT lacZ/+ (Figure 1A); w; Armadillo::GFP (Figure 1E); w; E-cadherin::GFP (Figures 2 and 4, gift from Yang Hong (Huang et al, 2009); yw;; FRT82B wts^X1/TM6b (Figure 6, gift from Tian Xu; Xu et al, 1995); yw hs.flp;; FRT82B Ubi-GFP-nls (Figure 6); yw hs.flp; E-cadherin::GFP; FRT82B Ubi-mRFP-nls (Figure 6, self-generated); yw hs.flp/+;;actin.FRT.CD2.FRT UAS.GFP/+ (Figure 7). Clones marked by expression of actin.lacZ were induced at 48–72 h AEL by a 10-min heat shock to induce in cis FLP/FRT-mediated recombination. FRT82B wts^X1mitotic recombination clones were induced by a 15-min heat shock.

Immunohistochemistry

Discs were fixed for 30 min in 4% paraformaldehyde in PBS, washed with PBT (PBS, 0.3% Triton X-100), blocked with PBT+0.1% BSA, and stained with primary and fluorescently conjugated secondary antibodies (Molecular Probes and Jackson ImmunoResearch) with additional PBT washes. Primary antibodies used are rat anti-E-cad (Developmental Studies Hybridoma Bank), rabbit anti-βgal (Cappel), mouse anti-Tubulin (Sigma), and rabbit anti-PH3 (Millipore).

For E-cadherin::GFP and yw hs.flp/+;;actin.FRT.CD2.FRT UAS.GFP/+, discs were washed in PBS after fixing, stained with Hoechst (Molecular Probes) to label the nuclei, and mounted after washing in PBS. Care was taken to preserve the discs’ native shape by using double-sided tape spacers between the slide and the coverslip, when necessary.

Precise staging of wing disc development

For precise staging of wing disc development, 6 h egg lays were grown at 25°C and larvae were dissected at the indicated times AEL. To correct for slight ageing variations due to food, all wing discs were aged again according to their area post-imaging, using the growth curve generated in Bittig et al (2009) as a reference. The area ranges (μm²) used to group the wing discs were 48 h: <5000, 60 h: 5000–9000, 72 h: 9000–20 000, 84 h: 20 000–30 000, 96 h: 30 000–50 000, and 120 h: >50 000. Since the discs were used for either cell-shape extraction or clone size counting, the discs were not excessively flattened, and maintain their dome-like 3-dimensional structure, so the areas (in 2D) of the 96-h and 120-h wing discs may appear smaller than published results.

Proliferation rate analysis

Discs were staged and aged as above. The following regimes were used for the different time windows to ensure correct clone density (all heat shocks were at 37°C):

 48–72 h and 60–84 h rates: heat shock at 48 or 60 h AEL for 7 min, dissect 24 h later.

 72–96 h and 96–120 h rates: heat shock at 72 or 96 h AEL for 5 min, dissect 24 h later.

 The number of nuclei in each clone was counted manually using a tailor-made 3D viewer and a cell counting tool in Matlab to ensure that all nuclei were visible and could be easily counted. Simple 2D Z projections and clone area estimates would often underestimate the number of nuclei in the clone, as many are densely packed on top of each other in this pseudo-stratified epithelium (see Figure 7). This is particularly a problem in the centre of the disc where the nuclei are more densely packed. The number of divisions per day=log₂ (number of cells in clone after 24 h). The edge of the pouch (up to the first fold) is also marked during the analysis, hence the relative position of each clone in each disc can be calculated.

Fixed sample imaging

Fluorescent imaging of fixed samples was performed with a Leica SP5 laser scanning confocal microscope. For discs used in cell shape and proliferation rate analysis, Z intervals of 0.5–1 μm were used to achieve sufficient Z-resolution.

Live imaging

Live imaging of armadillo::GFP or E-cadherin::GFP wing discs was performed with a Perkin-Elmer Spinning Disc microscope as in Mao et al (2011). In order to simultaneously capture cell divisions at the distal centre and the proximal edge of the wing pouch, the field of view was focussed on either the dorsal or ventral half of the wing disc (at 100 h AEL) with a × 60 lens, see Supplementary Movie S1.

Laser ablation

Laser ablation was performed on wing discs at ∼100 h AEL using a Zeiss LSM780 inverted two-photon microscope with a Chameleon Ultra II laser (Coherent) tuned to 730 nm at 20–50% power (depending on the output of the 3W laser). The ablation pixel dwell time was typically around 16 μs, with × 40 water lens and × 10–14 digital zoom. The time-lapse sequence was acquired using the inverted Zeiss LSM 780 (single photon) scanning confocal with 0.7 s lapse interval, either in single channel mode (when just imaging Ecad::GFP) or in double channel simultaneous scanning (when imaging RFP and Ecad::GFP for the wts clone analysis).

For the wts clone experiments, since the nuclear RFP clonal marker is more basal than the apical Ecad::GFP signal, the correct junctions bordering the mutant and wild-type tissues were first identified by scanning basally at the level of the RFP marker, and then moved to the junctional Ecad::GFP level for the ablation. After ablation, the focus was moved more basally again (while still imaging the same time-lapse sequence) to confirm that the junction ablated is indeed at the clone boundary (see Supplementary Movie 7).

To analyse the tension patterns in the wild-type hinge regions, junctions of different anterior–posterior or dorsal–ventral orientations in both hinges were ablated and analysed separately (as four different populations). They did not show significant differences in their tension profiles, and the data sets were thus pooled to generate Figure 6G and H. The same procedure was applied to the junctions affected by the wts clones in the hinge region.

Analysis of orientation of cell divisions and clone shapes with respect to the P–D axis

Systematic definition of P–D axis was done as in Mao et al (2011). Statistical analyses of the orientation of clone shapes and cell divisions were performed with a tailor-made software in Matlab. The user defined the distal most segment of the wing pouch as two points along the dorsal–ventral boundary, which also defines the centre of the disc. The user also marked the edge of the pouch (up to the first fold) to define the maximum distance from the centre. The user manually traced the outlines of clones, dividing cells (immediately prior to mitosis), and the positions of the daughter cells. Ellipses were then fitted around the clones and cells, and their main axes and centres were used to calculate angles (relative to its theoretical P–D angle at that location) and its relative distance from the centre.

Automated image segmentation of cell geometries in wing discs and cell tracking

Please see Supplementary Materials and Methods and Supplementary Figure S7 for details of the technique.

Analysis of the shape of cells surrounding wts loss of function clones

In order to analyse the effect of overgrowth induced by wts loss of function clones on their neighbouring cells, we used our automated image segmentation software to extract the cell outlines of cells surrounding the clones. We removed the cells actually in the clone (marked by lack of GFP), and segmented up to five rows of cells beyond the clone (or until the hinge cleft, red zone Figure 6A″). Each cell’s elongation ratio was calculated, and the angle of its major axis relative to the radius of the clone was also calculated (Figure 6C). For each clone, we picked the corresponding region of a wild-type disc and drew a mock ‘clone’ of the same size and shape in the same position. We removed the cells in the ‘clone’ and segmented and analysed the cell shapes (up to five rows again) surrounding the ‘clone’. Each cell’s elongation ratio and angle relative to the ‘clone’ radius was analysed as for the wts clones. For each of the five wts clones analysed, and for the five corresponding control ‘clones’, the data were indistinguishable, and thus pooled.

In silico overgrowing clones analysis

In order to mimic the in vivo wts loss of function experiments, simulated WT tissue was grown in silico until it reached a size of ∼1000 cells, at which point an overgrowing cell line was introduced into the centre of the tissue (cell cycle 5 times faster than WT). The simulation was then left to run for a further 4 h until the clones reached a size similar to the in vivo clones (∼100 cells). Control simulations were performed by starting from the same WT tissue at ∼1000 cells and then letting the tissue grow for a further 4 h as was done for the fast-growing clones. The snapshots of the simulated overgrowing clones were then fed into the same algorithm as was used in the in vivo case to measure the cell orientation and elongation ratio of the cells around the clones.

Analysis of mitotic spindle orientation (cell division orientation) of cells surrounding wts loss of function clones

We modified the above clone shape and cell division analysis software in Matlab for spindle analysis. For the wts clones, the user clicks on the centre of the clones. We then analysed the orientation of the spindles that are on or close to the clone boundary, since only these cell shapes are affected. When the user clicks on the two ends of the mitotic spindle to define the spindle angle, the spindle orientation is calculated relative to the radius of the clone (as for the cell-shape orientation above). As it is almost impossible to have a control disc with a WT clone in the same geometric position that also has mitotic spindles bordering the clone, we analysed whether the hinge spindle orientation has any natural patterns, which turned out not to be the case (Figure 6K, red bars). Since most of the wts clones were in roughly the positions highlighted in Figure 6J, we decided to use these as our mock ‘clonal’ centres and analysed the spindle orientations of spindles close to these four ‘centres’.

Computer model

The vertex model adapted from Farhadifar et al (2007), and modified in Mao et al (2011), was used. See Supplementary Materials and methods for details.