Analyzing Recurrent Event Data With Informative Censoring

Abstract

Recurrent event data are frequently encountered in longitudinal follow-up studies. In statistical literature, noninformative censoring is typically assumed when statistical methods and theory are developed for analyzing recurrent event data. In many applications, however, the observation of recurrent events could be terminated by informative dropouts or failure events, and it is unrealistic to assume that the censoring mechanism is independent of the recurrent event process. In this article we consider recurrent events of the same type and allow the censoring mechanism to be possibly informative. The occurrence of recurrent events is modeled by a subject-specific nonstationary Poisson process via a latent variable. A multiplicative intensity model is used as the underlying model for nonparametric estimation of the cumulative rate function. The multiplicative intensity model is also extended to a regression model by taking the covariate information into account. Statistical methods and theory are developed for estimation of the cumulative rate function and regression parameters. As a major feature of this article, we treat the distributions of both the censoring and latent variables as nuisance parameters. We avoid modeling and estimating the nuisance parameters by proper procedures. An analysis of the AIDS Link to Intravenous Experiences cohort data is presented to illustrate the proposed methods.

1. INTRODUCTION

Recurrent event data are frequently encountered in longitudinal follow-up studies. In such a study, the observation of recurrent events could be terminated at or before the end of the study. For example, the recurrent events could be multiple occurrences of hospitalizations from a group of patients, and the observation of the repeated hospitalization process could be terminated by the end of the study, patient dropout, loss to follow-up, or patient death.

To analyze recurrent event data, the focus can be placed on time-between-events or time-to-events models. When time between events is the variable of interest, various approaches have been proposed for survival function estimation based on multiple events of different types (Visser 1996; Wang and Wells 1997; Huang and Louis 1998; Lin, Sun, and Ying 1999;), or same type (Wang and Chang 1999), and for regression analysis (Gail, Santner, and Brown 1980; Prentice, Williams, and Peterson 1981; Chang and Wang 1999, Huang 2000). In this article we consider recurrent events of the same type and focus on time-to-events models. In the literature, time-to-events models were studied in the important articles of Prentice et al. (1981) and Andersen and Gill (1982) under either a Poisson-type process assumption or the requirement that the event history be a part of the conditional statistics of the occurrence probability of recurrent events. The independent increment assumption of the Poisson-type process was relaxed by Lawless and Nadeau (1995) in the estimation of the cumulative rate function, and by Pepe and Cai (1993) and Lin et al. (2000) for robust inferences of semiparametric regression models. The methodological procedures considered by these authors are based on the concept of risk sets where independent censoring is required for the validity of the methods. In many applications, however, censoring could be caused by informative dropouts or failure events, and it is unrealistic to assume independence between the censoring mechanism and the recurrent event process. A successful attempt to resolve the informative censoring problem was made by Lancaster and Intrator (1998). Using panel data to motivate the research, they considered joint parametric modeling of recurrent event and survival data and illustrated their methods with an analysis of data from a human imunodeficiency virus (HIV) study. Examples motivated by econometric applications can be found in the book by Lancaster (1990) and references therein.

In this article we model the occurrence of recurrent events by a subject-specific nonstationary Poisson process via a latent variable. In Section 2 we introduce a multiplicative intensity model as the underlying model for nonparametric estimation of the cumulative rate function. The multiplicative intensity model is extended to a semiparametric regression model by taking the covariate information into account. We develop statistical methods and theory for estimating the cumulative rate function and regression parameters in Sections 3 and 4. As a major feature of this article, we treat both the distributions of the censoring and latent variables as nuisance parameters. We avoid modeling and estimating the nuisance parameters by the proposed procedures. In Sections 5 and 6 we present simulation and an analysis of data from the AIDS Link to Intravenous Experiences (ALIVE) cohort study as a means of illustrating the proposed methods. We conclude with a discussion in Section 7.

2. INFORMATIVE CENSORING MODELS

Suppose that research interest is focused on the occurrence rate of recurrent events in the time interval [0, T₀], where the constant T₀ > 0 is determined with the knowledge that recurrent events could potentially be observed up to T₀. Let N(t) denote the number of recurrent events occurring at or before t, t ≥ 0. The rate function (RF) of a continuous recurrent event process at t, t ∈ [0, T₀], is defined as

$$\lambda (t)=\underset{\mathrm{\Delta }\to 0^{+}}{\text{lim}}\frac{\mathrm{P}\mathrm{r}(N(t+\mathrm{\Delta })-N(t)>0)}{\mathrm{\Delta }}.$$

The RF is conceptually and quantitatively different from the intensity function of a point process; the RF is defined as the occurrence rate of recurrent events unconditional on the event history, whereas the intensity function is the occurrence rate conditional on the event history. In general, the RF gives more direct interpretations for identifying risk factors, and the use of it is preferred over the intensity function in many applications. Further, define the cumulative rate function (CRF) as $\mathrm{\Lambda }(t)={\int }_0^t\lambda (u)du$. Let Y* be the censoring time at which the observation of the recurrent event process is terminated. Because only the occurrence rate in the time interval [0, T₀] is of interest, recurrent event data beyond T₀ will not be useful in the analysis. Thus further define Y = min(Y*, T₀) as the new censoring time to be used in the proposed models and methods.

Model A. Consider a multiplicative intensity model, termed Model A, which assumes the following conditions:

• A1. There exists a nonnegative valued latent variable Z so that, conditioning on Z = z, N(t) is a nonstationary Poisson process with the intensity function zλ₀(t), where the baseline intensity λ₀(t) is a continuous function.

• A2. Conditioning on z, N(·) is independent of Y.

Model A is partly motivated by the model introduced by Lancaster and Intrator (1998), who established inferences with parametric modeling of recurrent event and survival data. In contrast to their parametric inferences, our intention here is to develop nonparametric and semiparametric inferences of recurrent event data under the specified models.

Assumption A1 assumes a multiplicative intensity model in which the latent variable Z acts as a multiplicative random effect or frailty. Under A1, a large value of z implies frequent occurrences of recurrent events, and a small z implies less frequent occurrences of events. Conditional on z, the intensity function is the same as the RF because of the independent increment property of Poisson processes. Unconditonal on z, the RF is λ(t) = E[Zλ₀(t)] = μ_zλ₀(t), with μ_z = E[Z], and the CRF is Λ(t) = μ_zΛ₀(t). Under A2, the censoring time Y is allowed to depend on the latent variable Z, and this substantially relaxes the usual requirement that N be independent of Y in an independent censoring model. Although A2 specifies only a simple structure of informative censoring, it is generally enough to handle the situation when the censoring is caused by two types of mechanisms. For instance, suppose that $Y_0^{*}$ represents a noninformative censoring time (such as time to the end of study) that is independent of N(·), and $Y_1^{*}$ represents an informative censoring time that is independent of N(·) given Z = z. Then both $Y^{*}=\text{min}(Y_0^{*},Y_1^{*})$ and Y = min(Y*, T₀) are independent of N(·) given Z = z.

Assumptions A1 and A2 form the basic model for one-sample estimation of Λ(t) that we consider in Section 3. In some applications RF would be preferred over CRF, because it describes the instantaneous risks of recurrent events. Under A1 and A2, nonparametric estimation of the RF can be developed by smoothing techniques, such as the kernel methods (Chiang and Wang 2000).

Model B. Let X be a 1×p vector of covariates. To explore the association between X and N(·), we extend model A to model B. In Section 4 we study estimation procedures with this extended model. Model B assumes the following conditions:

• B1. There exists a nonnegative valued latent variable Z so that, conditioning on (x, z), N(t) is a nonstationary Poisson process with the intensity function zλ₀(t)e^xβ, where β is a p x 1 vector of parameters and the baseline intensity λ₀(t) is a continuous function. The latent variable Z satisfies E[Z|x] = 1.

• B2. Conditioning on (x, z), N(·) is independent of Y.

Assumption B1 implies the marginal proportional rate function,

$$\lambda (t|x)={\lambda }_0(t)e^{x\beta }.$$ (1)

Note that Assumption B1 can be equivalently stated as follows:

B1*. There exists a nonnegative valued latent variable Z so that, conditioning on (x, z), N(t) is a nonstationary Poisson process with intensity function zλ₀(t)e^xθ₁, where θ₁ is a p×1 vector of parameters and the baseline intensity λ₀(t) is a continuous function. The expected value of Z given x is E(Z|x) = e^xθ₂ with θ₂ a 1×p vector of parameters.

Under the alternative statement B1*, the validity of (1) follows because λ(t|x) = E[Zλ₀(t)e^xθ₁|x] = λ₀(t)e^xβ, where β = θ₁ + θ₂. For ease of discussion, we use the parameterization under B1 and B2 rather than B1* and B2. Note that, similar to the structure of model A, conditional on z, the intensity function zλ₀(t)e^xβ is also the rate function. Further, it can be easily shown that the parameters θ₁ and θ₂ are not identifiable, but that β = θ₁ + θ₂ is identifiable.

The marginal proportional rate function in (1) was studied by Pepe and Cai (1993) and Lin et al. (2000) in independent censoring models subject to different levels of model assumptions. The proportional rate function in (1) is the focus of interest for our regression inferences. This function has the direct interpretation as the average occurrence rate of recurrent events at t conditional only on x; for instance, x could be a treatment indicator, and (1) is used to identify the population-average treatment effect.

3. MODEL A: ESTIMATING THE CUMULATIVE RATE FUNCTION

Assume the validity of model A. For subject i, i = 1, 2, …, n, let y_i denote the observed censoring time and let t_i1 ≤ ⋯ ≤ t_{i, mi} be the observed event times with m_i defined as the index for the last event occurring at or before y_i. Assume that the observations from the n subjects are iid copies generated by model A.

In an independent censoring model, a risk set at t can be defined as {i : y_i ≥ t}; that is, the class of subjects who are under observation at t. Let R(t) be the number of subjects in the risk set at t. Because the censoring is independent of the recurrent event process, the risk set at t forms a random sample from the risk population, and thus Λ(t) can be estimated by the empirical measure of event times with R(t) serving as the time-dependent sample size:

$$\sum _{i=1}^n\sum _{j=1}^{m_i}\frac{I(t_{ij}\le t)}{R(t_{ij})}.$$ (2)

This estimator was studied by Nelson (1988) and Lawless and Nadeau (1995). Although the assumptions required to validate this estimator are rather unrestrictive, independent censoring is necessary in the estimation procedures. Under A1 and A2, because the sampling of the risk sets is allowed to depend on the value of of z_i, the risk sets could be biased for the estimation of marginal parameters, and thus the estimator in (2) is inappropriate for estimating the CRF. In this section we propose a bias-adjusted method for estimating the CRF.

Define the density function

$$f(t)=\frac{{\lambda }_0(t)I(0\le t\le T_0)}{{\mathrm{\Lambda }}_0(T_0)}=\frac{z_i{\lambda }_0(t)I(0\le t\le T_0)}{z_i{\mathrm{\Lambda }}_0(T_0)}$$

as the normalized function for both the baseline intensity, λ₀(t), and the subject-specific intensity, z_i λ₀(t), when z_i > 0. This density function, or the corresponding cumulative distribution function F(t), can be thought of as a shape function in the model.

If we consider a fully parameterized model in which the parametric forms of λ₀ and the joint distribution of (Z, Y) are specified, then the full likelihood can be used for the estimation of model parameters. Here we consider the model under A1 and A2, where the distributions of Z and Y are treated as nuisance parameters and λ₀ is left as an unspecified continuous function. With the involvement of the nuisance parameters, the full likelihood approach is generally difficult for both computation and inferences. Instead of the full likelihood approach, a conditional likelihood will be useful in the estimation procedures. For subject i, conditional on (Y_i, Z_i, m_i), the event times (t_i1, t_i2, …, t_{i, mi}) are the order statistics of a set of iid random variables with the density function f(t)I(0 ≤ t ≤ y_i)/F(y_i) (Ross 1983). The conditional likelihood function can be derived as

$$L_c=\prod _{i=1}^{n}p(t_{i1},t_{i2},\dots ,t_{i,m_i}|y_i,z_i,m_i)=\prod _{i=1}^n\{m_i!\prod _{j=1}^{m_i}\frac{f(t_{ij})}{F(y_i)}\}\propto \prod _{i=1}^n\prod _{j=1}^{m_i}\frac{f(t_{ij})}{F(y_i)}.$$ (3)

The conditional likelihood L_c involves only the shape function F (or f) and does not require information of the unobserved {z_i}. The likelihood function L_c in (3) is a particular case of nonparametric likelihood for right-truncated data where the truncation time for t_ij is y_i. The distribution function F(t) can be estimated by the nonparametric maximum likelihood estimator F̂(t). Under regularity conditions, the estimator F̂(t) is known to have a simple product-limit representation,

$$\mathrm{F̂}(t)=\prod _{s_{(l)}>t}(1-\frac{d_{(l)}}{N_{(l)}}),$$ (4)

where {s_(l)} are the ordered and distinct values of the event times {t_ij}, d_(l) is the number of events occuring at s_(l), and N_(l) is the total number of events with event time and censoring time satisfying t_ij ≤ s_(l) ≤ y_i.

The CRF Λ(t) is related to F through the formulation Λ(t) = F(t)Λ(T₀), where the parameter Λ(T₀) can be interpreted as the average number of recurrent events occurring in [0, T₀]. The CRF can be estimated nonparametrically, as discussed later. Conditioning on (y_i, z_i), the number of the observed events, m_i, has expected value z_iΛ₀(y_i). The ratio of m_i to F(Y_i) projects the the number of events in [0, T₀], and the expected value of the projected number is Λ(T₀):

$$E[m_i{F}^{-1}(Y_i)]=E[E[m_i{F}^{-1}(Y_i)|Y_i,Z_i]]=E[Z_i{\mathrm{\Lambda }}_0(Y_i)F^{-1}(Y_i)]=E[Z_i{\mathrm{\Lambda }}_0(T_0)]=\mathrm{\Lambda }(T_0).$$

Substituting F̂(t) for F̂(t), estimators for Λ(T₀) and Λ(t) can be constructed as

$$\mathrm{\Lambda ̂}(T_0)=\frac{1}{n}\sum _{i=1}^n{m}_i{\mathrm{F̂}}^{-1}(Y_i)$$ (5)

and

$$\mathrm{\Lambda ̂}(t)=\mathrm{F̂}(t)\mathrm{\Lambda ̂}(T_0)$$ (6)

Although it is straightforward to derive F̂(t) from the conditional likelihood L_c, the existing asymptotic properties of the truncation product-limit estimator (Woodroofe 1985; Wang, Jewell, and Tsai 1986, among others) were developed for independent truncation data and are not readily applicable to correlated recurrent event data. An independent truncation model typically involves a failure time and a truncation time, where the failure time variable is independent of the truncation time variable. For recurrent event data, the model setting apparently changes, and thus different considerations must be integrated into the large-sample theory. In the Appendix we derive an asymptotic representation of F̂(t) and use this representation to study the asymptotic properties of Λ̂(T₀) and Λ̂(t). The properties of the nonparametric estimators in (5) and (6) are stated in Theorem 1. The details of the proof of Theorem 1 are included in the Appendix.

Let W represent the joint distribution function of (Y, Z) and define G(u) = ∫ zI(y ≥ u)dW(y, z).

Theorem 1. Assume that (a) Λ₀(T₀) > 0, (b) Pr(Y* ≥ T₀, Z > 0) > 0, and (c) G(u) is a continuous function for u ∈ [0, T₀]. As n → ∞, n^1/2{Λ̂(T₀) − Λ(T₀)} converges weakly to a normal distribution with mean 0 and variance $\mathrm{E}[c_i^2]$, where c_i is as defined in the Appendix. As n →∞, for inf{y : Λ₀(y) > 0} < t ≤ T₀, n^1/2{Λ̂(t) − Λ(t)} converges weakly to a normal distribution with mean 0 and variance $\mathrm{E}[d_i^2(t)]$ where d_i(t) is as defined in the Appendix.

4. MODEL B: MARGINAL REGRESSION

Assume that model B holds. In this section we consider estimation of the parameter β of the marginal proportional rate function in (1). Under model B, the density function

$$f(t)=\frac{{\lambda }_0(t)I(0\le t\le T_0)}{{\mathrm{\Lambda }}_0(T_0)}=\frac{z_i{\lambda }_0(t)e^{x_i\beta }I(0\le t\le T_0)}{z_i{\mathrm{\Lambda }}_0(T_0)e^{x_i\beta }}$$

remains as the shape function for the subject-specific intensity, z_iλ₀(t)e^x_iβ, when z_i > 0. Similar to the earlier argument, the conditional likelihood L_c is the probability density of {(t_i1, t_i2, …, t_{i, mi})} given {(m_i, y_i, z_i, x_i)}:

$$L_c\propto \prod _{i=1}^n\prod _{j=1}^{m_i}\frac{f(t_{ij})}{F(y_i)}.$$

Conditioning on (x_i, y_i, z_i), the expected value of m_i is z_iΛ₀(y_i)exp(x_iβ). Thus

$$\mathrm{E}[m_i{F}^{-1}(Y_i)|x_i]=\mathrm{E}[\mathrm{E}[m_i{F}^{-1}(Y_i)|Y_i,Z_i]|x_i]=\mathrm{E}[Z_i{e}^{x_i\beta }{\mathrm{\Lambda }}_0(Y_i)F^{-1}(Y_i)|x_i]=e^{x_i\beta }\mathrm{E}[Z_i|x_i]{\mathrm{\Lambda }}_0(T_0)=e^{x_i\beta }{\beta }_0$$

with β₀ = Λ₀(T₀). A class of unbiased estimating equations can be defined as

$$n^{-1}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t(m_i{F}^{-1}(y_i)-e^{{\mathrm{x̄}}_i\gamma })=0,$$ (7)

where x̄_i = (1, x_i), γ^t = (lnβ₀, β^t), and w_i is a weight function depending on (x_i, γ, F).

In the case where F is known, the optimal weight for achieving finite-sample or large-sample efficiency is w_i = e^x̄_iγ/E[(m_iF⁻¹(y_i) − e^x̄_iγ)²]. In the special case where Z_i = 1 and Pr(Y_i = T₀) = 1, the optimal weight is w_i = 1 because the expectation and variance of m_i are the same for the Poisson distribution. In this case, (7) coincides with the likelihood score equation for Poisson count data; that is, ${\sum }_i{\mathrm{x̄}}_i^t(m_i-e^{{\mathrm{x̄}}_i\gamma })=0$. Under model B, the distribution function F is unknown, and thus we replace F in (7) by F̂. A class of estimating equations for estimating γ is defined as

$$n^{-1}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t(m_i{\mathrm{F̂}}^{-1}(y_i)-e^{{\mathrm{x̄}}_i\gamma })=0.$$ (8)

In the Appendix we show that the solution of (8), γ̂, has the property that $\sqrt{n}(\mathrm{\gamma ̂}-\gamma )$ converges weakly to the multivariate normal (MVN) distribution,

$$\sqrt{n}(\mathrm{\gamma ̂}-\gamma )\stackrel{d}{\to }\mathrm{M}\mathrm{V}\mathrm{N}(0,{\psi }^{-1}\mathrm{\Sigma }{({\psi }^t)}^{-1}),$$ (9)

where ψ and Σ are as specified in the Appendix. Based on the formulation F(t) = Λ₀(t)/β₀, the baseline CRF can be estimated by Λ̂₀(t) = exp(γ̂₁) F̂(t). When $n\to \infty ,\sqrt{n}({\mathrm{\Lambda ̂}}_0(t)-{\mathrm{\Lambda }}_0(t))$ converges weakly to a normal distribution. Details of the derivation of the asymptotic normality are given in the Appendix.

As an alternative procedure, an estimating equation can be written as

$$n^{-1}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t\{\sum _{k=1}^n\sum _{j=1}^{m_k}I(t_{kj}\le y_i)[N_i(t_{kj}){\mathrm{F̂}}^{-1}(t_{kj})-e^{{\mathrm{x̄}}_i\gamma }]\}=0.$$

This estimating equation is constructed through the steps used for forming (8), but instead of using count information only at {y_i}, it collects information from all of the event times {t_ij}, because at these points the values of F and N_i could change. Although this approach might produce more efficient estimation results, it is not explored here because computationally and inferentially it is much more complicated than (8).

5. MONTE CARLO SIMULATION

We examine the finite-sample properties of the proposed estimators through a Monte Carlo simulation. In particular, we generate data with structure similar to the inpatient care data from the AIDS Link to Intravenous Experiences (ALIVE) cohort study (Vlahov et al. 1991).

Let {X_i} be iid Bernoulli random variables. Conditioning on x_i, the latent variable Z_i is defined as $Z_i=\text{exp}(-x_i\times \text{ln}(2.75))Z_i^{*}$, where $Z_i^{*}$ is distributed with density

$$f(z^{*}|x_i)=(1-x_i)I(.5\le z^{*}\le 1.5)+\frac{x_i}{2.5}I(1.5\le z^{*}\le 4),$$

where I(·) is an indicator function. It can be verified that E[Z_i|x_i] = 1.

Two simulations are conducted: (a) Pr(X_i = 0) = 1 and (b) Pr(X_i = 1) = Pr(X_i = 0) = .5. For each simulation, data are repeatedly generated 500 times, and each simulated data set consists of information from 400 independent nonstationary Poisson processes {N_i(t)}, t ∈ [0, 10], with the corresponding intensity function z_iλ₀(t)exp(x_i), where

$${\lambda }_0(t)=.6+\frac{{(t-6)}^3}{360}.$$

Therefore, the marginal proportional rate model is given by

$$\lambda (t|x_i)={\lambda }_0(t)\text{exp}(x_i\beta ),$$

with β = 1. Here the baseline intensity function λ₀(t) is chosen to simulate the situation where the occurrence rate of recurrent events increases over time. Conditioning on (x_i, z_i), the censoring time Y_i is designed to be independent of N_i(·) and is distributed as a truncated distribution of the exponential distribution exp(z_i/10). This truncated distribution ranges from 1 to 10 and has density

$$f_{Y|(x_i,z_i)}(y)=\frac{.1z_i\text{exp}(-.1z_{i}y)}{\text{exp}(-.1z_i)-\text{exp}(-z_i)}I(1\le y\le 10).$$

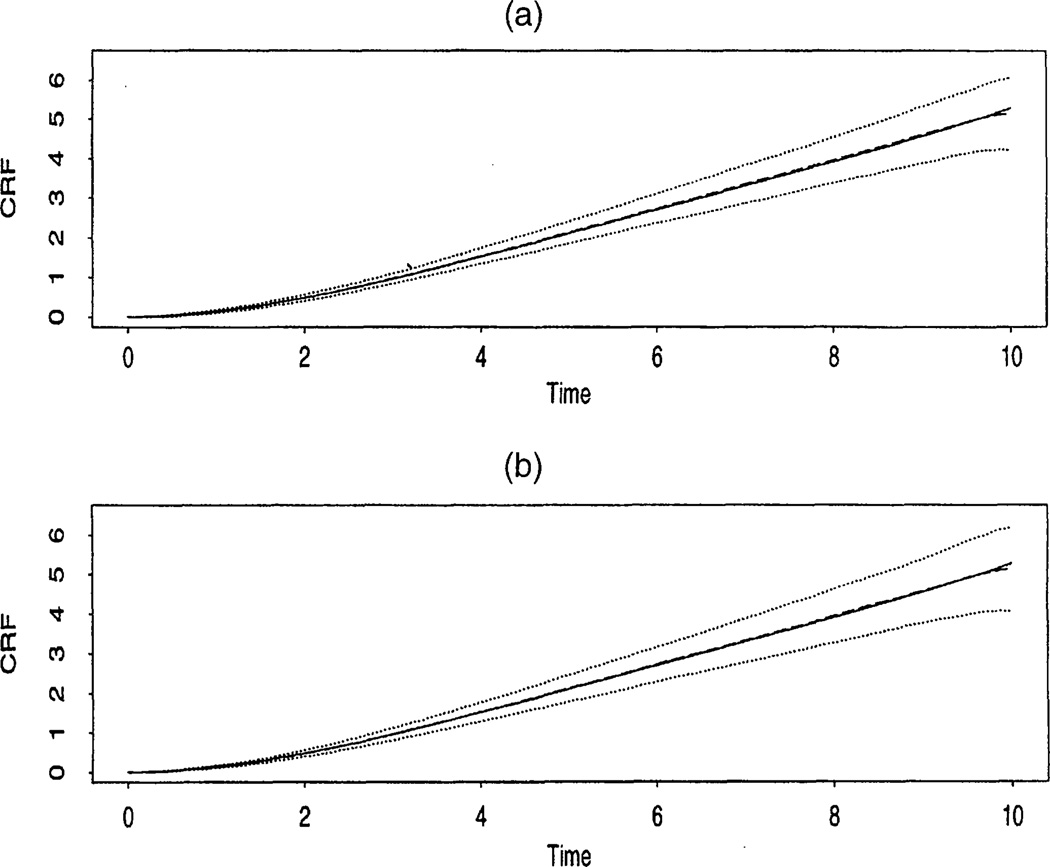
Under simulation model (a), note that Λ(t) = Λ₀(t). The estimated CRF, Λ̂(t), is computed based on simulated data. For simulation (b), the estimated curve, Λ̂₀(t), and the estimates β̂₀, and β̂ are computed. Based on 500 simulated datasets, the average of the estimated CRF Λ̂(t) from simulation (a) is shown in Figure 1(a), and the average of the estimated baseline CRF, Λ̂₀(t), from data of simulation (b) is presented in Figure 1(b). Note that the two estimates are close to each other, and each serves as a good estimate of Λ̂₀(t). Also, the averages of the estimates β̂₀ and β̂ are 5.35 and 1.01, which are close to the true parameters β ₀ = 5.28 and β = 1.00, with standard errors of .6448 and .0993. To evaluate the validity of the estimators, 95% bootstrap confidence intervals for Λ₀(t), β₀, and β₁ are produced based on 200 bootstrap replications. Table 1 summarizes the empirical coverage probabilities of 95% bootstrap intervals for Λ₀(t), computed over the 500 simulated samples, at selected time points. The empirical coverage probabilities 95% bootstrap intervals for β̂₀ and β̂₁ are .924 and .948. These coverage probabilities are generally close to the nominal level.

Figure 1.

(a) The Real CRF Λ(t) (———), Estimated CRF Λ̂ (t) (– – – – –), and 95% Bootstrap Confidence Intervals (⋯⋯), (b) The Real Baseline CRF Λ₀(t) (———), Estimated Baseline CRF Λ̂₀(t) (– – – – –), and 95% Bootstrap Confidence Intervals (⋯⋯).

Table 1.

The Empirical Coverage Probabilities of the 95% Bootstrap Confidence Intervals for Λ₀(t)

Time point	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0	9.0
Coverage probability	.942	.950	.936	.942	.930	.944	.944	.950	.932

6. A DATA EXAMPLE

The dataset considered here is from the ALIVE cohort study, which includes the information of inpatient admissions, race, and HIV status collected from a group of intravenous drug users in Baltimore. Repeated hospitalizations were systematically recorded since July 16, 1993. In this section we analyze hospitalization data collected after August 1, 1993, to ensure better quality of data. In particular, we use hospitalization data observed between August 1, 1993, and December 31, 1997, from 715 intravenous drug users in the analysis. Each subject is labeled by black or nonblack and by HIV-negative or HIV-positive defined at 0 (August 1, 1993). Those HIV-negative drug users defined at 0 who became HIV-positive during the study period (21 in total) are excluded from our data analysis.

The main objective here is to estimate the CRF Λ(t) of hospitalization over time, and the effects of race and HIV status on the occurrence rate function. Let t_ij, i = 1, …, 715, j = 1, …, m_i be the time from August 1, 1993, to the jth inpatient admission. Let y_i denote the time of the last visit recorded by the study before December 31, 1997, let T₀ denote the maximum time of y_i’s, let x_i1 denote the black–nonblack indicator, and let x_i2 denote the HIV status with 1 indicating HIV-positive and 0 indicating HIV-negative drug users. Here Λ₀(t) is interpreted as the baseline CRF for the nonblack and HIV-negative drug users, and β = (β₁, β₂) are regression parameters for the black–nonblack and HIV status indicators in the proportional rate function, (1).

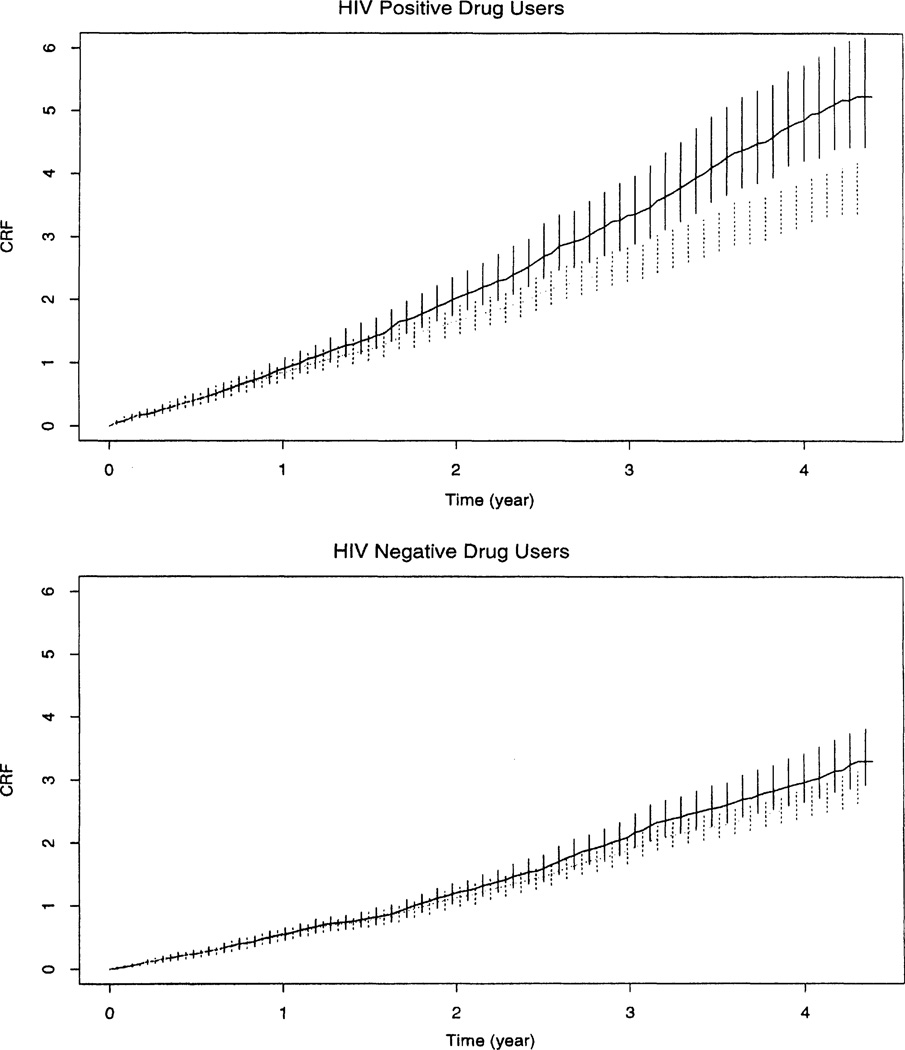
Before fitting the data by model B, we compute the non-parametric estimates of CRF in (2) and (6) for HIV-positive and HIV-negative drug users. The estimator in (2) is referred to as the “risk-set method” and that in (6) as the “proposed method.” Figure 2 shows the estimated CRF for these two groups. Clearly, the hospitalization rate estimated by the proposed method is much higher than that estimated by the risk-set method for HIV-positive drug users. The two estimates produce similar curves for the HIV-negative drug user group. Also, HIV-positive drug users appear to have a higher hospitalization rate than HIV-negative drug users under both approaches. The result suggests the possibility of heavy informative censoring from the HIV-positive users. Moreover, the ALIVE investigators indicated that the censoring among HIV-positive users is likely to be caused by informative dropouts from sicker HIV-positive users.

Figure 2.

The Estimated CRF for HIV-Positive and HIV-Negative User Groups With 95% Bootstrap Confidence Intervals for (⋯⋯) Risk-Set Method; –––– Proposed Method.

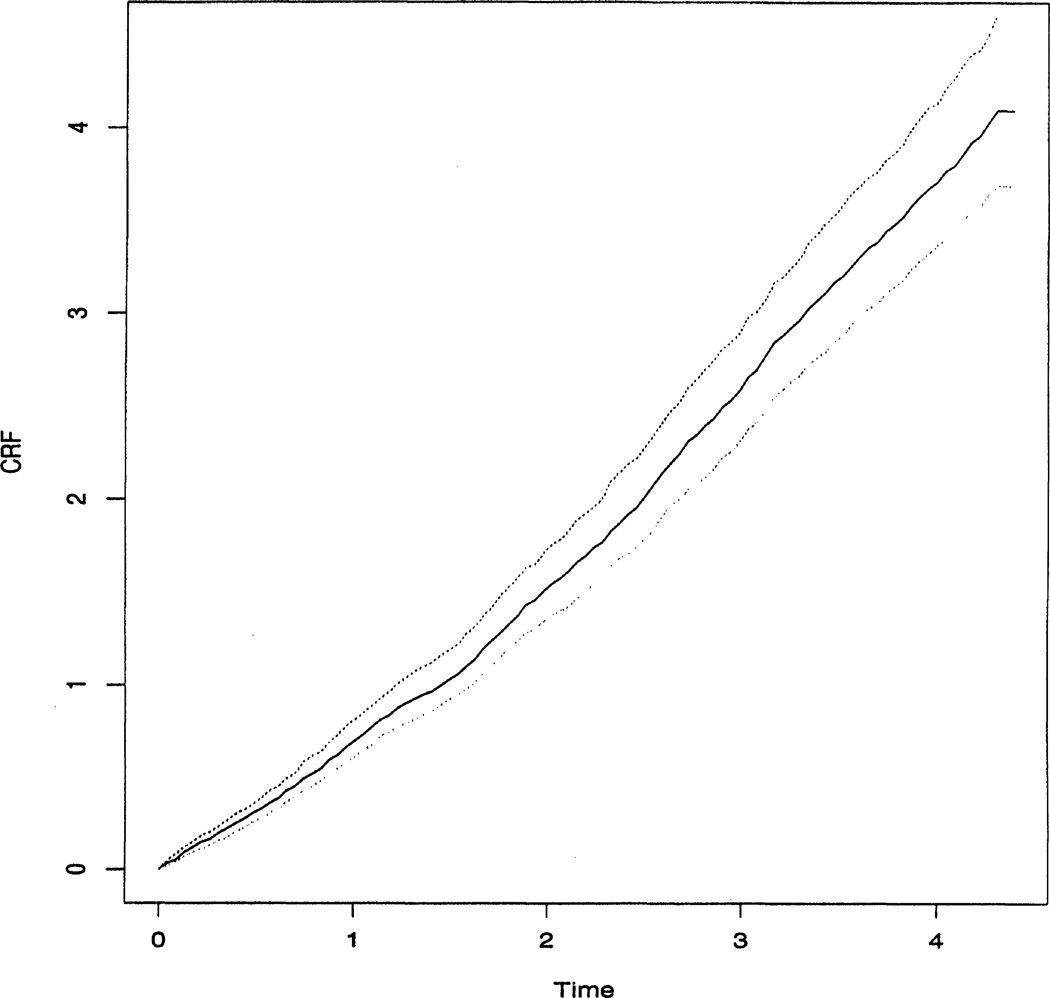
In the marginal proportional rate model, the estimated β̂₁ and β̂₂ are −.0510 and .4955 with the corresponding 95% bootstrap percentile confidence intervals (−.3115, .2554) and (.3185, .7209). The regression result suggests that the race indicator is not associated with the hospitalization pattern of drug users. The hospitalization occurrence rate of HIV-positive drug users is about 1.64 [≈ exp(.4955)] times as much as the rate of HIV-negative drug users. This is consistent with the observation from the CRF estimates. Figure 3 shows the estimated CRF Λ̂₀(t) with 95% bootstrap percentile confidence intervals for the baseline CRF Λ₀(t) for the nonblack and HIV-negative drug users. This estimated CRF is close to a straight line, suggesting that the occurrence rate function λ₀(t) approximates a constant over time.

Figure 3.

The Estimated Baseline CRF, Λ̂₀(t), With 95% Bootstrap Confidence Intervals.

7. DISCUSSION

In this article we have developed nonparametric and semiparametric methods for estimating the CRF and regression parameters based on recurrent event data in informative censoring models. We adopted a multiplicative intensity function as the underlying model for the proposed methodologies.

Marginal parameters such as the CRF or the proportional rate function in (1) are particularly useful in analysis for identifying treatment-effect or population-based risk factors. We used a latent variable in models A and B to characterize the heterogeneity among subjects, but treated the latent variable itself as a nuisance. The inferences that we have developed here focus on marginal parameters induced from models A and B.

While serving as a nonstringent model for informative censored data, the multiplicative intensity model, A1 (and B1), relies on two conditions: a subject-specific Poisson process assumption and invariance of the shape function f. To apply the proposed methodologies, one should examine both conditions with care. Generally, for continuous event times, model A1 (B1) would be approximately valid when the latent variable z_i (and e^x_iβ) influences the intensity function multiplicatively and z_i is the only factor that explains the heterogeneity from different subjects (besides x_i). There are of course situations in which the indicated conditions are not satisfied and an alternative model serves as a better choice. For instance, a possible alternative model would be to replace the multiplicative intensity function in A1 by an additive intensity function, z_i + λ₀(t), with z_i denoting a latent variable; or, as a more general version of A1, one could consider the subject-specific intensity model $z_i^{(1)}{\lambda }_0(z_i^{(2)}t)$, where $(z_i^{(1)},z_i^{(2)})$ is a pair of nonnegative valued latent variables. In the latter case, both the magnitude and shape of the intensity function vary with subjects. For future research, it will be of interest to explore rigorous methods to verify the validity of the proposed models.

The proposed models for informatively censored data certainly have their competitors. In particular, at the price of fully parameterizing the model, the likelihood approach of Lancaster and Intrator (1998) would lead to inferences of the joint structure of recurrent and survival events. Or, in a semiparametric setting, an alternative way to deal with the problem of informative censoring is to model the censoring time using observable covariate information and adopt local efficient estimation techniques of Bickel, Klaassen, Ritov, and Wellner (1993) and Robins and Rotnitzky (1992). At the price of modeling the censoring mechanism with proper covariate information, this approach is expected to achieve optimal estimation efficiency subject to the specified models. In our case, given the complexity of recurrent event data, we suspect that it will be difficult to find or study such estimation procedures. In practice, using the techniques of Bickel et al. might be difficult because the computation usually involves all of the underlying nonparametric and parametric parameters. In contrast, our estimators have simplicity, robustness, and decent efficiency, although they might not be the optimal choices.

The proposed methodologies have pros and cons compared to the “risk-set methods” mentioned in Section 3. In independent censoring models, the risk-set approaches are more efficient for analyzing recurrent event data. These approaches require less restrictive assumptions and allow for time-dependent covariates in the marginal proportional rate model (Lin et al. 2000). Regardless of the advantages, however, the validity of the risk-set methods relies heavily on the independent censoring assumption, which may not hold in some studies. In contrast, the proposed methods have the advantage of handling informative censoring without specifying distributional assumptions on the censoring and latent variables.

APPENDIX: PROOFS

Proof of Theorem 1

We first derive an iid representation of $\sqrt{n}(\mathrm{F̂}(t)-F(t))$. Based on this representation and the delta method, we can prove the asymptotic normality properties of $\sqrt{n}(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))$ and $\sqrt{n}(\mathrm{\Lambda ̂}(t)-\mathrm{\Lambda }(t))$. Recall that

$$G(u)=\int zI(y\ge u)dW(y,z),$$

and define

$$Q(u)={\int }_0^{u}G(\upsilon )d{\mathrm{\Lambda }}_0(\upsilon ),R(u)=G(u){\mathrm{\Lambda }}_0(u),\mathrm{Q̂}(u)=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{m_i}I(T_{ij}\le u),$$

and

$$\mathrm{R̂}(u)=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{m_i}I(T_{ij}\le u\le Y_i).$$

Note that Q̂(u) and R̂(u) are unbiased estimators for Q(u) and R(u), because

$$\mathrm{E}[\sum _{j=1}^{m_i}I(T_{ij}\le u\le Y_i)]=\mathrm{E}[I(Y_i\ge u)\mathrm{E}(N_i(u)|Z_i,Y_i)]=\mathrm{E}[I(Y_i\ge u)Z_i{\mathrm{\Lambda }}_0(u)]=G(u){\mathrm{\Lambda }}_0(u)$$

and

$$\mathrm{E}[\sum _{j=1}^{m_i}I(T_{ij}\le u)]=\mathrm{E}\left[\mathrm{E}\right[\sum _{j=1}^{m_i}I(T_{ij}\le u)|z_i,Y_i)\left]\right]=\mathrm{E}[Z_i{\mathrm{\Lambda }}_0(u\wedge Y_i)]=\mathrm{E}[{\int }_0^u{Z}_{i}I(Y_i\ge \upsilon )d{\mathrm{\Lambda }}_0(\upsilon )]=Q(u).$$

Further,

$$-\text{ln}F(t)={\int }_t^{T_0}\frac{dF(u)}{F(u)}={\int }_t^{T_0}\frac{dQ(u)}{R(u)}.$$

Note that assumptions (a) and (b) imply that R(T₀) > 0. Thus for any constant τ > inf{y : Λ₀(y) > 0}, one has R(u) > 0 for τ ≤ u < T₀. As n → ∞, Q̂(u) and R̂(u) converge almost surely to Q(u) and R(u) uniformly in u ∈ [τ, T₀]. Thus, by approximation techniques for product-limit estimators and the inequality 0 < − ln(1 − u⁻¹)−u⁻¹ < u⁻¹ (u − 1) ⁻¹, for u > 1, we can derive

$$-\text{ln}\mathrm{F̂}(t)-{\int }_t^{T_0}\frac{d\mathrm{Q̂}(u)}{\mathrm{R̂}(u)}\to 0\text{almost surely for each}t\in [\tau ,T_0].$$

Further, for t ∈ [τ, T₀],

$$\mathrm{F̂}(t)=\text{exp}(-{\int }_t^{T_0}\frac{d\mathrm{Q̂}(u)}{\mathrm{R̂}(u)})+o_p(n^{-1/2})$$

and

$${\int }_t^{T_0}\frac{d\mathrm{Q̂}(u)}{\mathrm{R̂}(u)}={\int }_t^{T_0}\frac{dQ(u)}{R(u)}-{\int }_t^{T_0}\frac{(\mathrm{R̂}(u)-R(u))dQ(u)}{R^2(u)}+{\int }_t^{T_0}\frac{d(\mathrm{Q̂}(u)-Q(u))}{R(u)}+o_p(n^{-1/2})=-\text{ln}F(t)-\frac{1}{n}\sum _{i=1}^n{b}_i(t)+o_p(n^{-1/2}),$$

where

$$b_i(t)=\sum _{j=1}^{m_i}\{{\int }_t^{T_0}\frac{I(T_{ij}\le u\le Y_i)dQ(u)}{R^2(u)}-\frac{I(t<T_{ij}\le T_0)}{R(T_{ij})}\},$$

and it can be seen from the foregoing formulation that b_i(t) has zero expectation and

$$\mathrm{F̂}(t)-F(t)=\frac{1}{n}\sum _{i=1}^{n}F(t)b_i(t)+o_p(n^{-1/2}).$$

Further observe

$$\sqrt{n}(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))=n^{-1/2}\sum _{i=1}^n{m}_i(\frac{1}{\mathrm{F̂}(Y_i)}-\frac{1}{F(Y_i)})+n^{-1/2}\sum _{i=1}^n(\frac{m_i}{F(Y_i)}-\mathrm{\Lambda }(T_0))=I+II.$$

Let H be the joint probability measure of (m, y) and let Ĥ be the corresponding empirical measure for H. Then

$$I=-\sqrt{n}\int \frac{m(\mathrm{F̂}(y)-F(y))dĤ(m,y)}{F^2(y)}+o_p(1)=-\sqrt{n}\int m{F}^{-2}(y)(\mathrm{F̂}(y)-F(y))dH(m,y)+o_p(1)=-\sqrt{n}\sum _{i=1}^n\int \frac{m{b}_i(y)dH(m,y)}{F(y)}+o_p(1).$$

Let

$$c_i=-\int \frac{m{b}_i(y)dH(m,y)}{F(y)}+\frac{m_i}{F(Y_i)}-\mathrm{\Lambda }(T_0).$$

Then c_i has zero expectation and $\sqrt{n}(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))=I+II=n^{-1/2}{\sum }_i{c}_i+o_p(1)$. Thus $\sqrt{n}(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))$ is asymptotically normally distributed with mean 0 and variance $\mathrm{E}[c_i^2]$. For t ∈ [τ, T₀],

$$\sqrt{n}(\mathrm{\Lambda ̂}(t)-\mathrm{\Lambda }(t))=\sqrt{n}\mathrm{F̂}(t)(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))+\sqrt{n}\mathrm{\Lambda }(T_0)(\mathrm{F̂}(t)-F(t))=\sqrt{n}F(t)(\mathrm{\Lambda ̂}(T_0)-\mathrm{\Lambda }(T_0))+\sqrt{n}\mathrm{\Lambda }(T_0)(\mathrm{F̂}(t)-F(t))+o_p(1)=n^{-1/2}\sum _{i=1}^n{d}_i(t)+o_p(1),$$

where d_i(t) = F(t){c_i + Λ(T₀)b_i(t)}. It can be shown that d_i(t) has zero expectation for each t ∈ [0, T₀]. By the central limit theorem, $\sqrt{n}(\mathrm{\Lambda ̂}(t)-\mathrm{\Lambda }(t))$ converges weakly to the normal distribution with mean 0 and variance $\mathrm{E}[d_i^2(t)]$.

Proof of (9)

The estimating function on the left side of (8) can be expressed as

$$\frac{1}{n}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t(\frac{m_i}{\mathrm{F̂}(y_i)}-\frac{m_i}{F(y_i)})+\frac{1}{n}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t(\frac{m_i}{F(y_i)}-e^{{\mathrm{x̄}}_i\gamma })=-\frac{1}{n}\sum _{i=1}^n\int \frac{w{\mathrm{x̄}}^{t}m{b}_i(y)dV(w,\mathrm{x̄},m,y)}{F(y)}+\frac{1}{n}\sum _{i=1}^n{w}_i{\mathrm{x̄}}_i^t(\frac{m_i}{F(y_i)}-e^{{\mathrm{x̄}}_i\gamma })=\frac{1}{n}\sum _{i=1}^n{e}_i+o_p(n^{-1/2}),$$

where V is the joint probability measure of (w, x̄, m, y) and

$$e_i=-\int \frac{w{\mathrm{x̄}}^{t}m{b}_i(y)dV(w,\mathrm{x̄},m,y)}{F(y)}+w_i{\mathrm{x̄}}_i^t[m_i{F}^{-1}(y_i)-\text{exp}({\mathrm{x̄}}_i\gamma )].$$

Then, by standard procedures, we can show that $\sqrt{n}(\mathrm{\gamma ̂}-\gamma )=n^{-1/2}{\psi }^{-1}{\sum }_i{e}_i+o_p(1)$ with ψ = E[−∂e_i/∂γ]. Therefore, $\sqrt{n}(\mathrm{\gamma ̂}-\gamma )$ converges weakly to the multivariate normal distribution with mean 0 and variance-covariance matrix ψ⁻¹Σ(ψ^t)⁻¹, where Σ represents the variance-covariance matrix of e_i.

Asymptotic Normality of $\sqrt{n}({\mathrm{\Lambda ̂}}_0(t)-{\mathrm{\Lambda }}_0(t))$

The asymptotic normality of $\sqrt{n}({\mathrm{\Lambda ̂}}_0(t)-{\mathrm{\Lambda }}_0(t))$ relies on nomality properties of F̂(t) and γ̂₁. Using similar steps as in the proof of Theorem 1, by substituting Z exp(Xβ) for the latent variable Z in the definition of G, the iid representation of $\sqrt{n}(\mathrm{F̂}(t)-F(t))$ remains the same as F̂(t) − F(t) = n⁻¹ ∑_i F(t)b_i(t) + o_p(n^−1/2). Thus

$$\sqrt{n}({\mathrm{\Lambda ̂}}_0(t)-{\mathrm{\Lambda }}_0(t))=\sqrt{n}\mathrm{F̂}(t)(\text{exp}({\mathrm{\gamma ̂}}_1)-\text{exp}({\gamma }_1))+\sqrt{n}\text{exp}({\gamma }_1)(\mathrm{F̂}(t)-F(t))=\sqrt{n}F(t)(\text{exp}({\mathrm{\gamma ̂}}_1)-\text{exp}({\gamma }_1))+\sqrt{n}\text{exp}({\gamma }_1)(\mathrm{F̂}(t)-F(t))+o_p(1)=n^{-1/2}F(t)\text{exp}({\gamma }_1)\sum _{i=1}^n\{f_i+b_i(t)\}+o_p(1),$$

where f_i is the first entry of the vector function ψ⁻¹e_i. It follows that $\sqrt{n}({\mathrm{\Lambda ̂}}_0(t)-{\mathrm{\Lambda }}_0(t))$ converges weakly to the normal distribution with variance F²(t) exp(2γ₁)E[(f_i + b_i (t))²].