A Critical Test of the “Tunneling and Coupled Motion” Concept in Enzymatic Alcohol Oxidation

Abstract

The physical mechanism of C-H bond activation by enzymes is the subject of intense study and we have tested the predictions of two competing models for C-H activation in the context of alcohol dehydrogenase. The kinetic isotope effects (KIEs) in this enzyme have previously suggested a model of quantum mechanical tunneling and coupled motion of primary (1°) and secondary (2°) hydrogens. Here we measure the 2° H/T KIEs with both and H and D at the 1° position and find that the 2° KIE is significantly deflated with D-transfer, consistent with the predictions of recent Marcus-like models of H-transfer. The results suggest that the fast dynamics of H-tunneling result in a 1° isotope effect on the structure of the tunneling ready state: the trajectory of D-transfer goes through a shorter donor-acceptor distance than that of H-transfer.

Alcohol dehydrogenase (ADH) is an important model system for studying the physical processes involved in enzyme-catalyzed hydrogen transfers. ADH catalyzes the oxidation of alcohol using a nicotinamide cofactor (Scheme 1), and this reaction has provided many surprising experimental results that have caused the enzymology community to rethink many facets of enzymology.^1,2

Scheme 1.

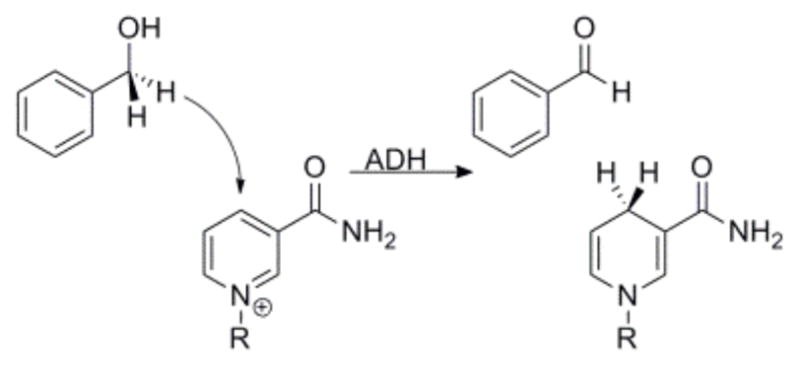
The reaction catalyzed by ADH (using benzyl alcohol as an alternative substrate). R= adenine diphosphate ribosyl-.

One of the most significant concepts to come out of work on ADH is the notion of “quantum mechanical tunneling and coupled motion” between primary (1°) and secondary (2°) hydrogens. The theory of tunneling and coupled motion (Figure 1a) posits that the reaction coordinate for hydride transfer involves motion of both the 1° and 2° hydrogens, and that together, the hydrogens tunnel through the reaction barrier.^3–7 At its time this concept seemed to be in accordance with some surprising KIE data, and additional KIE experiments⁸ apparently confirmed one of the model’s most significant predictions, that Swain-Schaad Exponents (SSEs) would be inflated. The SSE is the relationship between KIEs using different combinations of isotopes of hydrogen.⁹ A simple derivation making the assumptions of semiclassical transition state theory, no tunneling, and harmonic vibrational frequencies, showed that the SSE should be a constant, regardless of what reaction is studied or which atom is isotopically labeled:⁹

Figure 1.

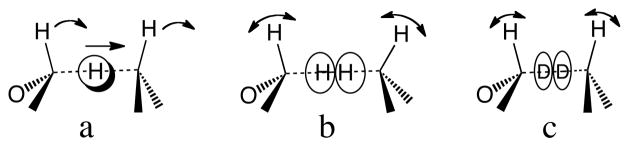
Schematic illustration of the differences between the two models in question: a) The traditional model of tunneling and coupled motion, where the arrows represent the coupled motion of the 1° and two 2° hydrogens at the TS. As these three atoms constitute a normal mode, isotopic substitution of any of them will alter the KIE on the others. b) By the proposed model, since H’s wavefunction is more diffuse than D’s, its TRS (see figure 2) is more “dissociated”. The double-headed arrows represent the change in vibrational ZPE from ground state to TRS, which determine the 2° KIEs. c) Since D’s wavefunction is more localized than H at the TRS, its TRS is more “associated”, leading to suppression of the change in vibrational ZPE from ground state to TRS, and thus deflated 2° KIEs.

$$\mathit{SSE}=\frac{ln(\frac{k_H}{k_T})}{ln(\frac{k_D}{k_T})}=3.3$$ [1]

where k_i is the rate with isotope i. Since Klinman and co-workers found that the relationship was extraordinarily inflated for 2° KIEs in yeast ADH (yADH),⁸ inflated SSEs have been cited prolifically as evidence for tunneling and coupledmotion.^1,10 A computational study,^11,12 provided the first quantitative explanation of ADH KIEs and additional insight, although these studies focused on the horse ADH, where kinetic complexity masks the intrinsic KIEs and mSSEs.¹³

Perhaps due to the relative ease of synthesizing the necessary isotopically labeled materials, the particular experiments that showed the inflated 2° SSEs (in yeast,⁸ as well as other ADHs^14,15) were mixed-labeling experiments,¹⁶ where the 2° H/T KIE was measured with H at the 1° position, but the 2° D/T KIE was measured with D at the 1° position. Thus, the experiments measured the mixed-labeling 2° SSE (mSSE):

$$\mathit{mSSE}=\frac{ln(\frac{k_{HH}}{k_{HT}})}{ln(\frac{k_{DD}}{k_{DT}})}$$ [2]

where k_ij is the rate with isotope i at the 1° position and isotope j at the 2° position. According to semi-classical transition state theory and the Bigeleisen equation,¹⁷ the mSSE should equal the SSE, since the rule of the geometric mean (RGM) states that there are no isotope effects on isotope effects.^18,19 Nonetheless, one of the great mysteries has been why inflated SSEs have appeared in so few other systems,²⁰ despite evidence that tunneling is important to most or all H-transfers.

An analysis of the inflated mSSEs from many different ADHs showed that the source of the inflation was not that the 2° H/T KIE was inflated, as expected from the traditional model of tunneling and coupled motion, but the D/T KIEs were deflated:²¹ The data suggested that the shorter donor-acceptor distance (DAD) necessary for D-tunneling caused steric hindrance between the substrates to inhibit rehybridization of the donor carbon, thus deflating the 2° KIEs. A recent experimental study of the yADH reverse reaction led to QM calculations that explained all 2° KIEs and most other data on the C-H activation for this enzyme.²² A critical component in these calculations was a shorter DAD for D-transfer than for H-transfer, which is a component of large-curvature tunneling models.²³ It is important to note that ref 24 indicated that the theoretical treatment of such reactions by Truhlar and Gao encapsulates all the components of the Marcus-like models and does not contradict such phenomenological models. In addition to increased steric hindrance, at the shorter DAD the transferred particle is less delocalized (the donor and acceptor wells are closer to one another), so the probability density of that particle in the vicinity of the 2° hydrogen is increased, leading to larger ZPE and smaller KIEs at the 2° position. These calculations were based on Marcus-like models of hydrogen tunneling (Figure 2), which have found great use in rationalizing both 2° and 1° KIEs and their temperature dependence.^25–31 Marcus-like models explain C-H activation in terms of a separation between heavy atom motion and hydrogen tunneling and give a rate constant (k) of the form

Figure 2.

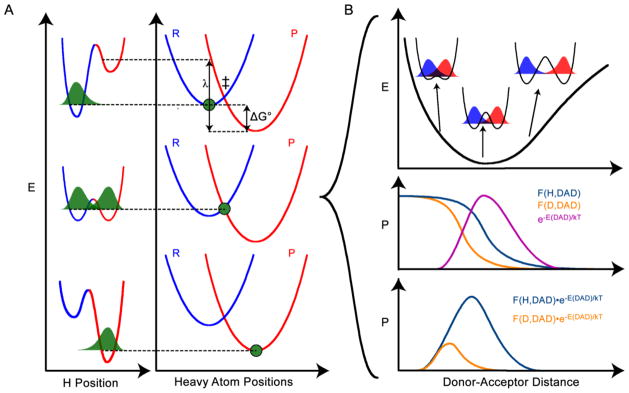
Marcus-like model of H-tunneling. A) The top, middle, and bottom panels show three stages of the reaction in two designated coordinates: the H position, and the positions of the heavy atoms that modulate the potential surfaces (reactant surface is blue and product surface is red) for the transferred H. In the top panel, the heavy atoms are in a position such that the zero point energy (ZPE) of the H is lower in the reactant well, so the H-wavefunction (green) is localized there. In the middle panel, the heavy atoms have rearranged to a tunneling ready state (TRS, ‡), where the ZPE for the transferred H is equal in the reactant and product wells and the H-wavefunction (including contributions from any motions coupled to the H-position) can tunnel through the barrier. The rate of reaching this tunneling ready state depends on the reaction driving force (ΔG°) and the reorganization energy (λ). In the bottom panel, the heavy atoms have rearranged further, making the ZPE of the product lower than the reactant, and thus trapping the transferred H in the product well. B) At the TRS (middle panel of A) fluctuations of the DAD affect the tunneling probability. The top panel shows a free energy surface for the designated DAD coordinate, indicating the different levels of reactant-product wavefunction overlap at different DADs. At short enough DAD, the ZPE of the transferred particle may be above the barrier, but this leads to very small 1° KIEs and does not appear to be the case for ADH. The middle panel shows the Boltzmann probability distribution of the system being at any given DAD (magenta), along with the tunneling probabilities of H and D as a function of DAD (orange and purple, respectively). The bottom panel shows the product of the Boltzmann factor and the tunneling probability for each particle, yielding the probability of a reactive trajectory as a function of DAD. Panel B illustrates that the reactive trajectories for H and D go through different average DADs, constituting an isotope effect on TRS structure. In ADH, the difference in average DAD for hydride transfer vs. deuteride transfer, which was estimated as 0.2 Å, leads to differences in 2° KIEs when the transferred isotope is different.²²

$$k=\frac{{\mid V\mid }^2}{\hslash }\sqrt{\frac{\pi }{\lambda k_{B}T}}{e}^{-\frac{{(\mathrm{\Delta }{G}^{\circ }+\lambda )}^2}{4k_{B}T\lambda }}{\int }_0^{\infty }F(m,\mathit{DAD})e^{-E(\mathit{DAD})/k_{B}T}\mathit{dDAD}$$ [3]

The factors in front of the integral give the rate of reaching a tunneling ready state (TRS) based on the electronic coupling between reactants and products (V), the reaction driving force (ΔG°), and the reorganization energy (λ). A TRS is a point of transient degeneracy between reactants and products, where the H can tunnel while still conserving energy. The process of reaching a TRS is depicted in Figure 2a. The integral computes the probability of transmission to products once the system reaches a TRS (Figure 2b). This probability is based on the probability of tunneling as a function of mass and DAD, F(m,DAD), and a Boltzmann factor giving the probability of being at any given DAD. Integrating over all DADs gives the overall probability of transmission to products. The free energy surface dictating the reaction depends on the nature of the substrates, as well as the enzyme environment, though we note that eq. 3 assumes thermal equilibrium (i.e., no non-statistical dynamics). This kind of model proposes that all isotopes of H react by tunneling, but expects that the trajectory of heavier isotopes will pass through a shorter DAD (Figure 2b).

So far, all the experimental evidence supporting this explanation was quite complex and thus indirect.^{3,8,14,15,22,32,33} Here we have conducted one of the simplest possible tests of the predictions of that model: we have measured the 2° H/T KIEs on the oxidation of benzyl alcohol with both H- and D-transfer (Table 1). This experiment directly tests the effect of the 1° (transferred) isotope on the 2° KIEs (the RGM) without the many possible effects of assessing it from mixed labeling measurements (Eqs 2 and 4). The usefulness of directly measuring k_DH/k_DT was initially suggested by simple calculations of coupling between the 1° and 2° C-H bonds,³⁴ but has not yet been attempted experimentally due to the required stereospecific labeling pattern. The new measurement was made possible by the chemoenzymatic synthesis of 7R-[²H]-phenyl-[¹⁴C]-benzyl alcohol, which had previously been attempted for over 10 years (see Supporting Information and ref ³⁵). We measured the KIEs competitively using the same conditions as in previous studies on yADH (25° C, pH 8.5),^8,32 and the results (Table 1) are qualitatively consistent with the predictions based on both 1°–2° coupled motion³⁴ and Marcus-like models.^21,22 Specifically, the 2° KIE is significantly deflated with D-transfer versus H-transfer (1.30 ± 0.02 and 1.18 ± 0.03 with H- and D-transfer, respectively). Together with the value of the 2° D/T KIE with D-transfer (1.03 ± 0.01),⁸ our measurements yield the SSE_D:

$${\mathit{SSE}}_D=\frac{ln(\frac{k_{DH}}{k_{DT}})}{ln(\frac{k_{DD}}{k_{DT}})}$$ [4]

where, as in Eq 2, k_ij is the rate with isotope i at the 1° position and isotope j at the 2° position. The value we obtain for SSE_D (5.6 ± 2.0) is slightly higher than values calculated for the SSE_D,^22,34 but it is within the (larger) range calculated by models that have dispensed with some simplifying assumptions.^16,36,37

Table 1.

2° KIEs and SSEs on oxidation of benzyl alcohol by yADH

	Measured	Predictedd	Predictede
kDH/kDT	1.18 ± 0.03a	1.11	1.12
kHH/kHT	1.30 ± 0.02a&b	1.32	1.33
kDD/kDT	1.03 ± 0.01c	1.03	1.04
mSSE	8.9 ± 3.0	9.4	7.7
SSED	5.6 ± 2.0	3.4	2.9

^aThis work.

^bAlso measured in refs 8 and 33, and all measurements are within error of one another.

^cRef 8.

^dRef 22.

^eRef 34.

This measurement directly confirms that the inflated mSSE comes from a deflation of 2° KIEs when D is at the 1° position, as originally suggested in ref 21. Furthermore, this measurement reveals that the deflation of the 2° KIEs with D-transfer is not unique to D/T KIEs, as observed before, but is a general phenomenon reflecting the suppression of donor rehybridization at the TRS due to the close proximity of the H-acceptor. Both refs 34 (using a truncated Bell correction³⁸) and 22 (using a Marcus-like model) suggested a critical role for H-tunneling in predicting this breakdown of the RGM and the two studies made similar predictions for the value of the 2° H/T KIE with D-transfer, which we have measured here for the first time (Table 1). Nonetheless, the Marcus-like model has several advantages. First, the Bell-type corrections used in early models of tunneling and coupled motion^5,7,34,39 cannot account for temperature independent KIEs when reaction rates are temperature dependent.^10,14,40 This, however, is precisely the observed behavior of many enzyme reactions,^1,2,41 including that of a thermophilic ADH, which also showed inflated mSSEs.¹⁴ In fact, ref 34 stated explicitly that the temperature dependence of KIEs in that model was steeper than the observed data.⁸ Additionally, the nature of the coupling between vibrational modes in that study was vague and difficult to interpret. Thus, the more recent Marcus-like model that can account for all of the behavior of these reactions within an intuitively satisfying model is more compelling.

Marcus-like models originally arose out of the need to explain the temperature dependence of 1° KIEs,^25–29 but they describe a mechanism for C-H bond activation which, if right, should also account for 2° KIEs. Thus far, though, very little work has attempted to test the predictions of Marcus-like models in the context of 2° KIEs.^21,22,42 The experiments here directly demonstrate the deflation of 2° KIEs for D-transfer relative to H-transfer. Since the current experiment does not involve mixed labeling, it directly reveals the source of one of the most puzzling results for 2° KIEs (inflated mSSEs), and contributes strong support for the mechanism of C-H activation described by Marcus-like models. In this mechanism, H-tunneling is modulated by the “heavy atoms” coordinate that tunes the transient degeneracy necessary for tunneling. Once degeneracy is achieved, the transferred atom can tunnel to products with efficiency dependent on its mass and the DAD. Since the DAD must be shorter for D to tunnel than for H to tunnel, the average DAD of transfer is shorter with D than with H (Figure 2b).

In summary, the ADH reaction with H-transfer effectively goes through a different TRS than the reaction with D-transfer. The electronic potential surface is the same for the two reactions, consistent with the Born-Oppenheimer approximation, but the dynamics of nuclear tunneling contribute to the reaction’s bottleneck (i.e., the point along the reaction coordinate with the lowest flux of forward trajectories, analogous to the variational transition state).^24,43 One can describe this result as an isotope effect on the structure of the TRS. In a general sense, it is perhaps not surprising that the dynamics of H-tunneling contribute to the rate limitation of the H-transfer step, but here we have demonstrated clearly that this dynamic bottleneck⁴⁴ has important implications for the structure of the TRS. Furthermore, we have shown that 2° KIEs provide important information to determine the structure of a TRS. In contrast to 1° KIEs, though, 2° KIEs are only indirectly affected by tunneling: they are a manifestation of isotopic differences in the structural rearrangement necessary to reach the TRS (differences in ZPE contributions to ΔG° and λ of eq. 3). The structural information provided by 2° KIEs has been very useful in developing powerful transition state analog inhibitors for enzymes that catalyze heavy atom bond cleavages,⁴⁵ and now the door is open to use analogous methods for enzymes that catalyze H-transfers.