Minimization of bovine tuberculosis control costs in US dairy herds

Abstract

The objective of this study was to minimize the cost of controlling an isolated bovine tuberculosis (bTB) outbreak in a US dairy herd, using a stochastic simulation model of bTB with economic and biological layers. A model optimizer produced a control program that required 2-month testing intervals (TI) with 2 negative whole-herd tests to leave quarantine. This control program minimized both farm and government costs. In all cases, test-and-removal costs were lower than depopulation costs, although the variability in costs increased for farms with high holding costs or small herd sizes. Increasing herd size significantly increased costs for both the farm and the government, while increasing indemnity payments significantly decreased farm costs and increasing testing costs significantly increased government costs. Based on the results of this model, we recommend 2-month testing intervals for herds after an outbreak of bovine tuberculosis, with 2 negative whole herd tests being sufficient to lift quarantine. A prolonged test and cull program may cause a state to lose its bTB-free status during the testing period. When the cost of losing the bTB-free status is greater than $1.4 million then depopulation of farms could be preferred over a test and cull program.

Introduction

Bovine tuberculosis (bTB) is a disease of ruminants and cervids caused by chronic infection with Mycobacterium bovis. It is extremely rare in US cattle, with an estimated prevalence of 0.0006% herds in 2007 (USDA:APHIS:VS, 2009a). Between 2001 and 2009, approximately $342 million was spent on national bTB surveillance and control (USDA:APHIS:VS, 2009b). This number is likely to rise as costs of indemnity increase due to depopulation with larger herds sizes (USDA:APHIS:VS, 2007). For these reasons, Veterinary Services, a branch of the USDA Animal and Plant Health Inspection Service, recently recommended changes to the national bTB control program, including a need to prioritize selective animal removal and develop test-and-removal protocols (USDA:APHIS:VS, 2009b).

The USDA has proposed to control bTB in areas designated as bTB-free primarily using slaughter house surveillance and a pulsed test-and-remove strategy, in which the entire herd is tested at one time and all positive animals are culled, although a minimum level of herd surveillance may be required for herd accreditation, between-state animal movement, or the requirements defined in the Grade ‘A’ Pasteurized Milk Ordinance (USDA:APHIS:VS, 2010). Currently, after infected animals are identified at the slaughter house, the source herd will be placed under quarantine and a whole-herd test (WHT) will be performed. In this WHT, all animals are tested with the caudal fold test (CFT). All CFT+ animals will be tested with either the comparative cervical test (CCT) or the interferon gamma assay, and all test-positive animals will be slaughtered and tested post-mortem by histopathology and mycobacterial culture, with PCR of all acid-fast stains and cultured organisms. This process will be repeated at intervals of at least 2 months until the WHT is negative (no PCR-positive samples or all cows are CFT or CCT negative) for a pre-defined number of WHTs. Under current rules (USDA:APHIS:VS, 2005), herds are required to have 8 negative WHTs before being declared bTB negative again. The testing intervals (T_ti) of these 8 WHTs are such that there are 60 days between the first 4 tests, 180 days between the 4^th and 5^th test, and 12 months between the remaining tests. All WHT prior to 2 negative WHTs under the current plan require postmortem inspection of all CFT+ animals. Deviations from this protocol have been allowed in the past on a case-by-case basis. Depopulated herds are currently required to have 2 negative annual WHTs, starting 6 months after repopulation.

While the costs associated with depopulating bTB-infected dairy herds have been previously calculated (Wolf et al., 2000), the costs associated with the new test-and-remove strategy have not been quantified. Our previous work has detailed the costs associated with a WHT, assuming that all animals are bTB-negative (Dressler et al., 2010). We have also previously developed a stochastic discrete-time model for the spread and control of bTB in US herds (Smith et al., 2013). This model (Smith et al., 2013) has been validated against both an uncontrolled outbreak in a US beef herd (Perumaalla et al., 1999) and 10 controlled outbreaks in US dairy herds (USAHA, 2008). In the model, there are 2 user-defined control variables that will represent regulatory control programs: the testing interval (T_ti), and the number of negative WHTs required for clearance (N_WHT).

The purpose of this study is to find the economic optimal control for minimizing the separate government and farmer costs of controlling a bTB outbreak in individual states that are currently bTB-free, using California (CA) and New York (NY) as examples. This optimal cost will be compared to the cost of depopulation to determine the break-even point at which depopulation is economically justifiable.

Materials and Methods

Our previously-defined model (Smith et al., 2013) served as the basis for the economic model described below. Briefly, we implemented a stochastic (τ-leap) state transition model (Gillespie, 2001) with 4 compartments: Susceptible (S), Exposed (E), Reactor (R), and Infectious (I). Animals in the S category can become latently infected (exposed, E) at the frequency-dependent transmission rate β(N)SI/N, where β(N) is the population-dependent (N) transmission coefficient. Latent animals become detectable (reactors, R) with ante-mortem tests at rate γ, and reactors become infectious (I) at rate η. New susceptible animals enter the herd at rate μN(t), and all animals could be culled at rate μN(t)/N* where N* is the ideal herd size. The outbreak was initiated with 1 latent infected animal.

We assumed that animals in the R and I compartments can be detected at slaughter with imperfect sensitivity, and that such detection will trigger an immediate WHT. We have assumed that the herd will be tested using the CFT alone during the removal phase (all testing up to and including the second negative WHT) and using the CFT followed by the CCT during the validation phase (all testing after the second negative WHT). All animals in the R and I categories could be detected by the WHT during the removal phase with probability Se_CFT and during the validation phase with probability Se_CFT*Se_CCT, the product of the sensitivity of the 2 ante-mortem tests, with Se_CCT defined as the sensitivity of the CCT in CFT+ animals. Animals in the S and E categories could be removed from the herd during the removal phase with probability 1-Sp_CFT and during the validation phase with probability (1-Sp_CFT)*(1-Sp_CCT), the product of the complements of the specificity of the 2 ante-mortem tests, with Sp_CCT defined as the specificity of the CCT in CFT+ animals. We assumed perfect sensitivity and specificity for enhanced post-mortem inspection and PCR after a positive ante-mortem test result. A WHT was considered negative if all animals tested by post-mortem inspection and PCR were negative; that is, if all animals tested by post-mortem inspection were uninfected (in the S category) or had undetectable infections (in the E category). A herd was modeled to receive WHTs at the time interval T_ti until the number of consecutive negative WHTs was equal to N_WHT; the minimum T_ti is 60 days (2 months). The model was run until the herd was both infection-free (no bTB-infected animals) and declared to be free of bTB infection (undetected or detected with the validation phase completed), or until 10 years had passed with the herd remaining infected with bTB, whichever occurred first. All biological model parameters are shown in Table 1.

Table 1.

Parameter symbols, values, and sources used in the biological model for bovine tuberculosis spread in a US cattle herd.

Parameter	Description	Value (range)	Source
SpCFT	Specificity of caudal fold test	0.968 (0.755–0.99)	(De la Rua-Domenech et al., 2006)
SpCCT	Specificity of comparative cervical test	0.995 (0.788–1)	(De la Rua-Domenech et al., 2006)
SeCFT	Sensitivity of caudal fold test to infectious or reactor cattle	0.839 (0.632–1)	(De la Rua-Domenech et al., 2006)
SeCCT	Sensitivity of comparative cervical test	0.935 (0.75–0.955)	(De la Rua-Domenech et al., 2006)
Sepm	Sensitivity of post-mortem inspection to infectious or reactor cattle	0.55 (0.285–0.95)	(Asseged et al., 2004)
SePCR	Sensitivity of enhanced post- mortem inspection to infectious or reactor cattle	1 (0.8–1)	assumed
Ttt	Test turn-around time	10 days (6–14)	(Dressler et al., 2010)
β	Transmission rate	0.01/year (0.004–0.028)	(Barlow et al., 1997)
γ	Progression rate, latent to reactor	8.32/year (8.32–26.07)	(Kao et al., 1997)
η	Progression rate, reactor to infectious	0.347/year (0.347–4.06)	(Kao et al., 1997)
μ	Normal replacement rate	0.33/year (0.2–0.4)	(USDA:APHIS:VS, 2005b)
μd	Culling rate	μN/N*	calculated

Economic model

The calculation of the costs to be minimized was based on Dressler et al. (2010), but divided into costs for the average farm and costs for the government (state and federal combined). The parameters used for the economic analysis are shown in Table 2.

Table 2.

Parameter symbols, values, and sources used in the economic model for the cost of bovine tuberculosis control in a US cattle herd.

Parameter	Description	Value (range)	Source
A	Skin test administration cost	$7.13/cow (5.77–11.33)	(Buhr et al., 2009)
M&	Miles traveled by veterinarian	50 miles	Assumed
		(5–609)	California
		(5–356)	New York
MR^	Mileage rate	$0.55/mile (0.445–0.585)	(IRS, 2008)
pPCR	Price of histology, culture, and PCR test	$271.25/cow (217–325.5)	(USAHA, 2004)
N	Herd size	cows	state-specific (USDA, 2010)
		999 (500–3500)	California
		132 (50–3000)	New York
$ Foregone	Foregone future income due to premature culling	$965/cow (0–3600)	(Groenendaal et al., 2002)
Indemnity	Price paid per animal for culling due to test-positive result	Replacement + $ Foregone + Extra Indemnity	assumed
Extra Indemnity	Indemnity paid per animal above the cost incurred by the culling	0 (−$250–$250)	(USAHA, 2008)
Disposal	Cost per animal of shipping and disposing of infected cattle	$75 (60–90)	(Buhr et al., 2009)
Replacement+	Cost of replacing an animal culled due to CCT+ result	$/cow	state-specific (NASS, 2012)
		1300 (1200–1650)	California
		1460 (1200–1650)	New York
Salvage+	Value of an adult cull animal	$/cow	state-specific (NASS, 2012)*
		832 (445–1043)	California
		484 (445–1043)	New York
% Sold	Proportion of the herd sold as pregnant heifers	1%/month (0.8–1.2)	user-defined
Milk Profit^	Monthly operating profit for a farm (not including overhead costs)	$/cow/month	state-specific (USDA:ERS, 2012)
		141.65 (−814.12–957.30)	California
		220.85 (−201.91–557.66)	New York
Disinfection	Cost of disinfecting a farm after depopulation	$500 (400–600)	(Buhr et al., 2009)
% Loss	Proportional decrease in operating profit during repopulation	10% (2–12)	user-defined

^&Maximum value is the travel distance between the state capitol and the most distant major city.

^{^}Range is the minimum and maximum value across 5 years

⁺Range is the minimum and maximum value across all states

^*Assumes that the reported value of cattle sold is from culled cattle only, with an average culling rate of 30%/year

Government-level

At the government level, the cost of an outbreak consisted primarily of testing and indemnity expenses; the cost of a state-wide movement ban was not considered, nor were cleanup or transportation costs, as these costs vary widely and are difficult to estimate. Thus, the total cost was calculated as:

$$\begin{array}{l}{\mathit{costs}}_{\mathit{gov}}=N_{\mathit{WHT}}\ast c(\mathit{CFT})+{\sum }_{t}c\left(\mathit{CCT}\mid N_{\mathit{CCT}}(t)\right)+{\sum }_{t}c\left(\mathit{PCR}\mid N_{\mathit{slaughter},R,I}(t)\right)+\\ \mathit{cul}{l}_{I,R}(t)\ast \mathit{indemnity}+{\mathit{cull}}_{S,E}(t)\ast (\mathit{indemnity}-\mathit{salvage})\end{array}$$ [1]

where N_WHT is the number of WHTs given to all animals and N_CCT(t) and N_{slaughter,{R,I}}(t) are the total numbers of animals tested by CCT and by PCR, respectively, over the course of a testing period t, where it is assumed that only animals in the R and I classes will have gross lesions at slaughter requiring PCR testing. The number of detectable and undetectable animals culled due to positive tests are cull_I,R and cull_S,E, respectively. The cost of each CFT is represented by c(CFT),

$$c(\mathit{CFT})=A\ast N+2(M\ast MR)$$ [2]

with all variables as described in Dressler et al. and in Table 2. Briefly, A is the cost of administering the test per animal, M is the miles traveled by the veterinarian performing the test, and MR is the cost of traveling per mile. During the validation phase, all CFT-positive animals at time t were tested by CCT at cost c(CCT|N_CCT(t)), where N_CCT(t) is equal to the number of CFT-positive animals at time t and

$$c\left(\mathit{CCT}\mid N_{\mathit{CCT}}(t)\right)=A\ast N_{\mathit{CCT}}(t)+2(M\ast MR)$$ [3]

All CCT+ animals were then culled (in equation [1], cull_I,R(t) + cull_S,E(t)). During the removal phase, all CFT+ animals were culled (in equation [1], cull_I,R(t) + cull_S,E(t)). The expenses for the number of animals culled (in equation [1]) were the cost of indemnity in all animals culled (cull_I,R + cull_S,E) plus the cost of PCR in animals with gross lesions (cull_I,R), less the salvage value of animals without gross lesions (cull_S,E),

$$c\left(\mathit{PCR}\mid N_{\mathit{slaughter},R,I}(t)\right)={\mathit{cull}}_{R,I}(t)\ast [p_{\mathit{PCR}}+\mathit{indem}+\mathit{disposal}]+{\mathit{cull}}_{S,E}(t)\ast [\mathit{indem}-\mathit{salvage}]$$ [4]

where indem is the indemnity amount paid for each animal culled for tuberculosis, disposal is the cost of transporting and disposing of positive animals, and p_pcr is the cost of testing gross lesions by histopathology and PCR. It is assumed that only animals culled by testing in the Reactor and Infectious categories, cull_R,I, would have gross lesions. The number of animals culled by testing in the Susceptible and Latent categories is represented by cull_S,E and salvage is the value of their carcasses. Salvage value was calculated from published values of cattle sold by state.

Under current rules, the value of indemnity is officially 100% of the fair market value, minus salvage and plus disposal costs, up to $3,000 per animal (USDA:APHIS:VS, 2010). This value will change for each animal, but an average for the herd may be considered. For instance, in a New Mexico herd of 1500 cows, indemnity for depopulation in 2002 was calculated to cost $3,750,000, or $2,500/animal (USAHA, 2008; Wolf et al., 2000); during that year in New Mexico, replacement cost was approximately $1675/animal (National Agricultural Statistics Service, 2003), so the total indemnity was similar to the replacement cost plus the assumed $965/animal (Groenendaal et al., 2002) cost of early culling ($ Foregone, in equation [5] below). We can therefore assume that indemnity would remain approximately equal to the replacement cost plus the cost of early culling (the total cost to the farm of losing the animal). This maintains the observed relationship between indemnity and contemporary farm-level slaughter costs, in which values approach parity.

Farm-level

At the farm level, the cost of an outbreak included replacement costs, decrease in milk sold, and a holding cost due to quarantine. We assume a simple cost structure,

$${\mathit{costs}}_{\mathit{farm}}={\sum }_t\left[{\mathit{cull}}_{S,E}(t)+{\mathit{cull}}_{I,R}(t)\right]\ast [\$\mathit{Foregone}+\mathit{replacement}-\mathit{indem}]+c(\mathit{holding})$$ [5]

where $ Foregone is the cost of the money foregone by early culling of a CCT⁺ animal (cull_S,E+cull_R,I, from equation [1]), assuming that replacements are able to enter the herd immediately. The cost of replacing animals culled is represented as replacement, and indem is as defined above.

We considered 3 situations with regards to holding costs: no loss due to quarantine, fixed costs, and monthly losses. Fixed costs are used to represent herds in which off-site heifer rearing is used; upfront costs associated with calf housing ($housing in equation [6]) will be required, but operating costs were assumed to be unchanged. With monthly losses, the least common scenario, we assumed that a proportion of pregnant heifers would have been sold each month as surplus. The holding cost during the quarantine period therefore consisted primarily of lost sales. Thus, the cost of quarantine in equation [5] was

$$c(\mathit{holding})=\$\mathit{housing}+{\sum }_{t=1}^q\%\mathit{sold}\ast (\mathit{replacement}-\mathit{salvage})\ast N(t)$$ [6]

where %sold is the proportion of the herd sold each month as pregnant heifers, salvage is the salvage value of an adult cow, N is the herd size, and q is the number of months the herd spends in quarantine. In this situation, we assumed that the heifers would replace older cows, which would be culled.

Simulation

The model was first simulated at a range of T_ti and N_WHT values, with 1,000 iterations at each combination of parameters. Farm and government level cost distributions (equations [1] and [5]) were recorded for each combination of parameters.

Sensitivity Analysis

A global sensitivity analysis was performed using Latin Hypercube sampling on all 24 parameters with 100 model runs of 1000 iterations each, with iterations in which herds were undetected discarded. Parameters were varied over an expected range based on the literature; if a range for a parameter was not available in the literature, it was varied over +/− 20% of its base value (in Tables 1 and 2). The partial rank correlation coefficient for mean cost was calculated for each of the 3 scenarios (government, equation [1]; farm with no holding cost, equation [5] with equation [6] set to 0; and farm with varied holding cost, equation [5] with equation [6] added). Effects were assumed to be significant at the α=0.05 level.

Stochastic Optimization

First, we examined the results of the original simulation for first-order dominance in either cost distribution (farm, equation [5], and government, equation [1], level). When first order dominance was not obtained leading to a dominant action, we utilized a global non-parametric optimization algorithm developed by Andradottir (1996) to obtain an optimal action. In this method, the goal is

$${min}_{v\in V}f(v)=E[X_v]$$ [7]

where X_v is a sequence of random variables (in this case, the cost of bTB control, either equation [1] or equation [5] depending on the focus of the optimization), but E[X_v] is unknown due to the stochastic nature of the system. Given that V is a vector of possible variable sets (in our case, a matrix of {T_ti, N_WHT} combinations), we selected a single point v and choose another point v′ at random. The simulation was iterated once for each variable set chosen, and the costs (f(v) and f(v′)) were calculated. The combination of T_ti and N_WHT producing a lower cost was chosen, and the process was repeated starting with the chosen random value. After a sufficient number of iterations, the point visited most often is the global optimizer.

The model described above was optimized separately for government (equation [1]) and farm costs (equation [5]), assuming c(holding)=0 (equation [6] set to 0), T_ti={2:12}, and N_WHT={1:8}. The optimizer was run for 1 million iterations each.

Cost of depopulation

The alternative to test and slaughter is the current practice of farm depopulation. Government costs under depopulation are a simple linear function of herd size, less the salvage value of PCR-negative animals.

$${\mathit{cost}}_g(\mathit{depop},t)=N_{I,R}(t)\ast (\mathit{indemnity}+p_{\mathit{PCR}}+\mathit{disposal})+N_{S,E}(t)\ast (\mathit{indemnity}-\mathit{salvage})+{\mathit{cost}}_g(\mathit{test})+\mathit{disinfection}$$ [8]

where cost_g (test) is the cost of 2 annual WHTs in an uninfected herd, as in equations [2] and [3] for a herd in the validation phase, and disinfection is the cost of cleaning the farm after depopulation. Farm costs of depopulation were adapted from Wolf, Harsh, and Lloyd (2000) as

$${\mathit{cost}}_f(\mathit{depop})=\mathit{CRV}(t)+\mathit{NMP}(t)+c(\mathit{holding})$$ [9]

where CRV is the cattle replacement value assuming that calves and yearlings can be replaced at no loss,

$$\mathit{CRV}=N(t)\ast (\mathit{replacement}+\$\mathit{Foregone}-\mathit{indemnity})$$ [10]

NMP is the net milk profit lost,

$$\mathit{NMP}=\left[{(\mathit{Milk}\mathit{Profit})}_q+{(\mathit{Milk}\mathit{Profit})}_r\ast \%\mathit{loss}\right]\ast N(t)$$ [11]

c(holding) is as defined in equation [6], assuming that the quarantine period q is equal to the season of repopulation, s, and cull_S,E,R,I is the number of animals culled by the 2 annual WHTs following repopulation. We defined (Milk Profit)_q in equation [11] as the profit from milk produced during the season of quarantine, q, in the most recent year. Milk Profit was assumed to be the value of milk ($/cwt) (National Agricultural Statistics Service, 2012a) less the operating costs ($/cwt) (USDA:ERS, 2012) times the production per cow (cwt/cow) (National Agricultural Statistics Service, 2012b); all values were averaged at the state level over the years 2006 to 2010. The %loss in equation [11] was the assumed proportional loss of production during the period of repopulation, r.

We compared the distribution of the cost of depopulation (equations [8] and [9]) to the distribution of the costs of the optimal test-and-remove plan (equations [1] and [5]) across a spectrum of herd sizes (100 to 10,000 head), variable monthly losses per animal due to quarantine ($0 to $1,000), and variable average indemnity values ($500 to $2,500). Comparisons were made for both farm-level and government-level costs.

The model and all analyses were programmed in R 2.12.2¹, which was accessed through the Revolution R Analytics 4.3.0 interface².

Results

The system was optimized separately for the farm and government level costs. The optimizer visited each value of T_ti between 2 and 4 for more than 10,000 of the 1,000,000 iterations for both farm and government level analyses, with a preference for 2 at 15.8% of iterations. There was a strong preference for fewer N_WHT, with 2 visited by 95.9% of iterations.

The range of mean government and farm costs in CA across T_ti and N_WHT is shown in Figure 1. These costs increase significantly as the required number of tests increase for clearance but change little over the number of testing intervals. Government costs are much more sensitive to N_WHT than to T_ti. Although not shown for brevity, similar relationships are seen in NY herds.

Figure 1.

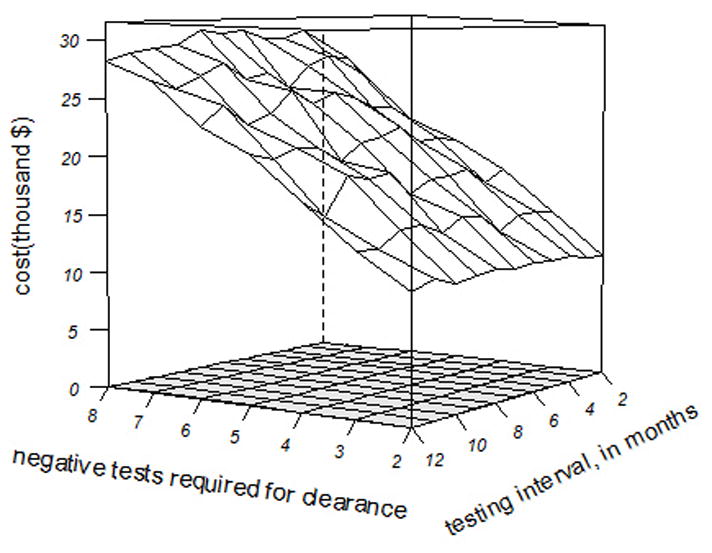
Mean cost per farm for the government to control a bovine tuberculosis outbreak in an average California dairy herd, by the interval of whole-herd tests and the number of negative whole-herd tests needed to declare the herd to be clear of infection.

The results of the sensitivity analysis for CA herds are shown in Figure 2, where the partial rank correlation coefficient of parameters on costs are listed. The most important parameters for government costs (equation [1]) are herd size (N), per-animal testing costs (A), the specificity of CCT tests, and the number of miles traveled by the vet administering tests (M), an increase of any of which causes an increase in government costs. The most important parameter influencing farm costs (equation [5]) is indemnity, an increase of which decreases farm costs, followed by herd size (N), the monthly loss/animal due to quarantine (L), and the specificity of the CFT (Sp_CFT), an increase of any which causes an increase in farm costs. If monthly loss/animal due to quarantine is restricted to 0, only indemnity significantly affects farm costs. The results for NY herds are similar.

Figure 2.

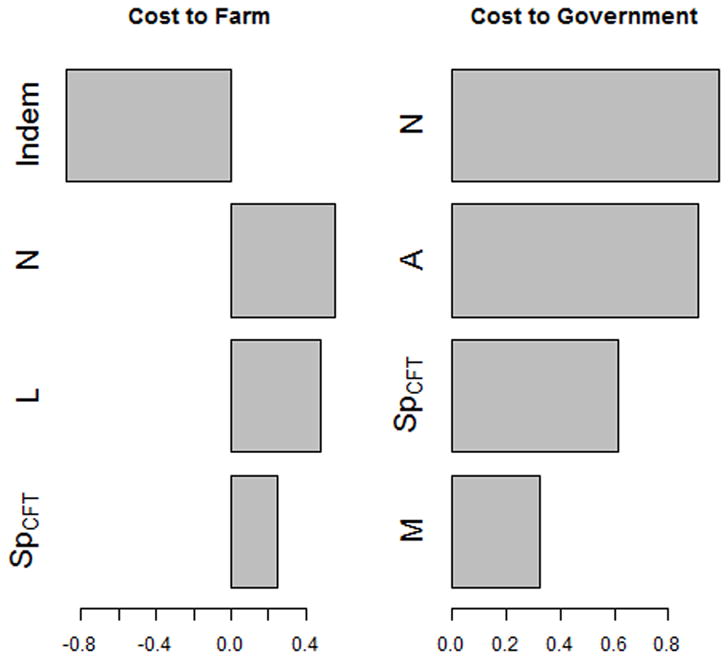
Partial rank correlation coefficient values from a global sensitivity analysis of all parameters used in the model of bovine tuberculosis control costs for an average dairy herd in California (Tables 1 and 2) under the optimal test-and-removal program, which consists of a 2 month testing interval with 2 negative whole-herd tests required to declare the herd free of infection. Only parameters with α<0.1 with the Bonferroni correction are shown. Indem is the indemnity cost per animal, N is the herd size, L is the monthly loss due to quarantine, Sp_CFT is the specificity of the CFT, A is the skin test administration cost per animal, and M is the number of miles traveled by the vet administering the skin test.

The distributions of the difference in government costs between depopulation (equation [8]) and either optimal test-and-remove or the current test-and-remove program (equation [1]) in the same herds are shown in Figure 3a for CA, and the distributions of the difference in farm costs between depopulation (equation [9]) and test-and-remove under the optimal program for 3 values of L and the current test-and-remove program (equation [5]) are shown in Figure 3b for CA. The distributions for NY herds are not shown but are similar, except with a lower mean.

Figure 3.

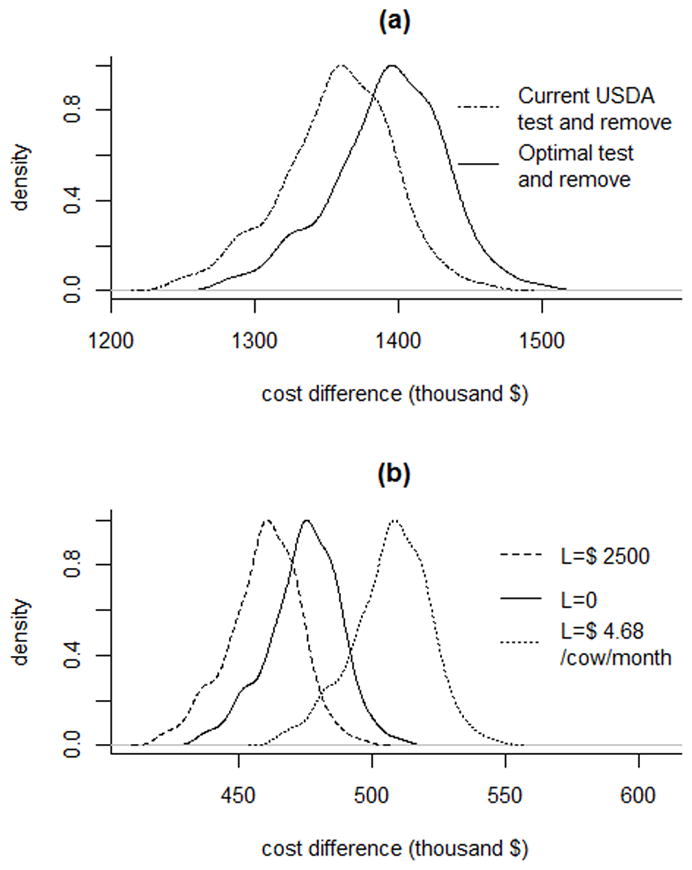
Distribution of cost differences for control of a bovine tuberculosis outbreak in an average California dairy herd under depopulation when compared to the optimized or current test-and-removal programs, observed for the government (a) and farm (b); depopulation refers to removal and replacement of all animals followed by a 2-year quarantine with annual testing, while the optimal test-and-remove program consists of a 2 month testing interval with 2 negative whole-herd tests required to declare the herd free of infection. For the government, the current USDA test and remove plan (dot-dash line) is compared to the optimal test and remove plan (solid line) For farms, the optimal test and remove plan is compared when the cost of quarantine (L) is allowed to be 0 (solid line), a fixed value ($2,500, dashed line), or a time-dependent variable cost ($4.68/cow/month, dotted line).

The distribution of the difference between the costs for depopulation and optimal test and removal, proportional to herd size, is shown for a range of CA herd sizes in Figure 4 a and b for government (equation [8]-equation [1]) and farm (equation [9]-equation [5]) levels, respectively. Variability is highest in small herds for both government and farm costs, but the mean cost/animal is unchanged across herd sizes.

Figure 4.

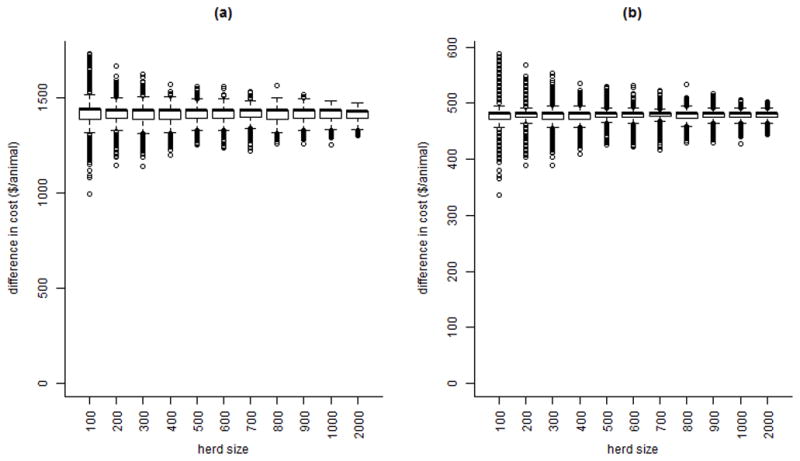
The distribution of the difference between depopulation costs and optimal test-and-remove costs for a bovine tuberculosis outbreak in an average California dairy herd, for government-level costs (a) and farm-level costs (b), across a range of herd sizes; depopulation refers to removal and replacement of all animals followed by a 2-year quarantine with annual testing, while the optimal test-and-remove program consists of a 2 month testing interval with 2 negative whole-herd tests required to declare the herd free of infection. The black line is the median, the box contains the interquartile range (IQR), the whiskers contain the largest and smallest observations within 1.5IQR of the upper and lower quartiles, respectively, and the dots are outliers.

The difference in farm level costs between depopulation and optimal test and remove (equation [9]-equation [5]) are shown in Figure 5 for a range of L, the cost/animal/month due to quarantine. The variability and size of the difference both increase with an increase in L. The difference in farm (equation [9]-equation [5]) and government (equation [8]-equation [1]) level costs between depopulation and optimal test and remove is shown in Figure 6 for a range of indemnity values; for farms, an increase in indemnity over culling costs results in a lower (but still positive) mean break-even cost for depopulation compared to test and removal.

Figure 5.

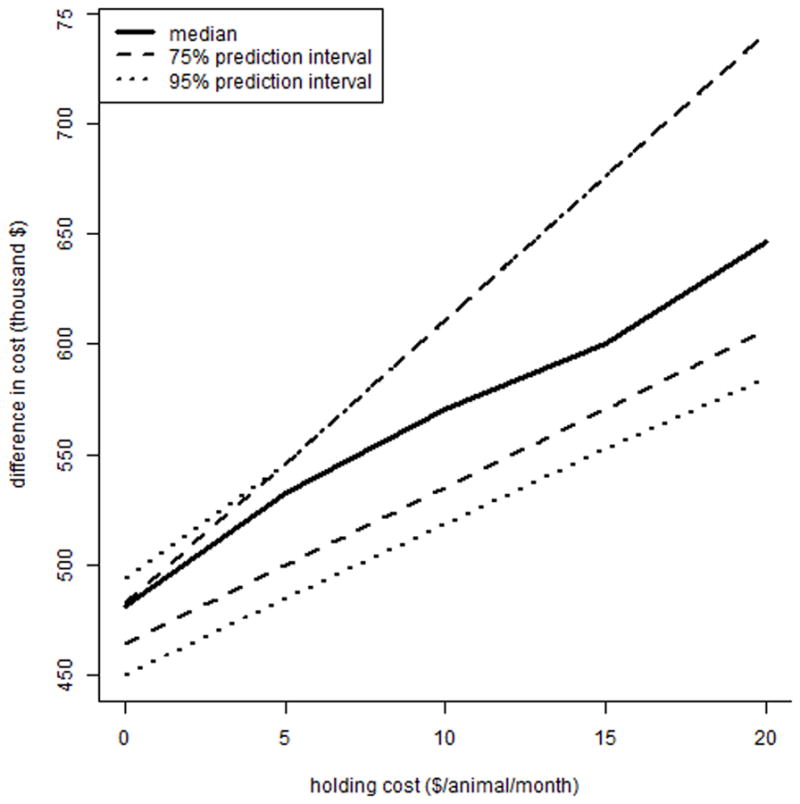
The median, 75%, and 95% prediction intervals of the difference between depopulation costs and optimal test-and-remove costs for a bovine tuberculosis outbreak in an average California dairy herd, for farm-level costs, across a range of quarantine holding costs. Depopulation refers to removal and replacement of all animals followed by a 2-year quarantine with annual testing, while the optimal test-and-remove program consists of a 2 month testing interval with 2 negative whole-herd tests required to declare the herd free of infection.

Figure 6.

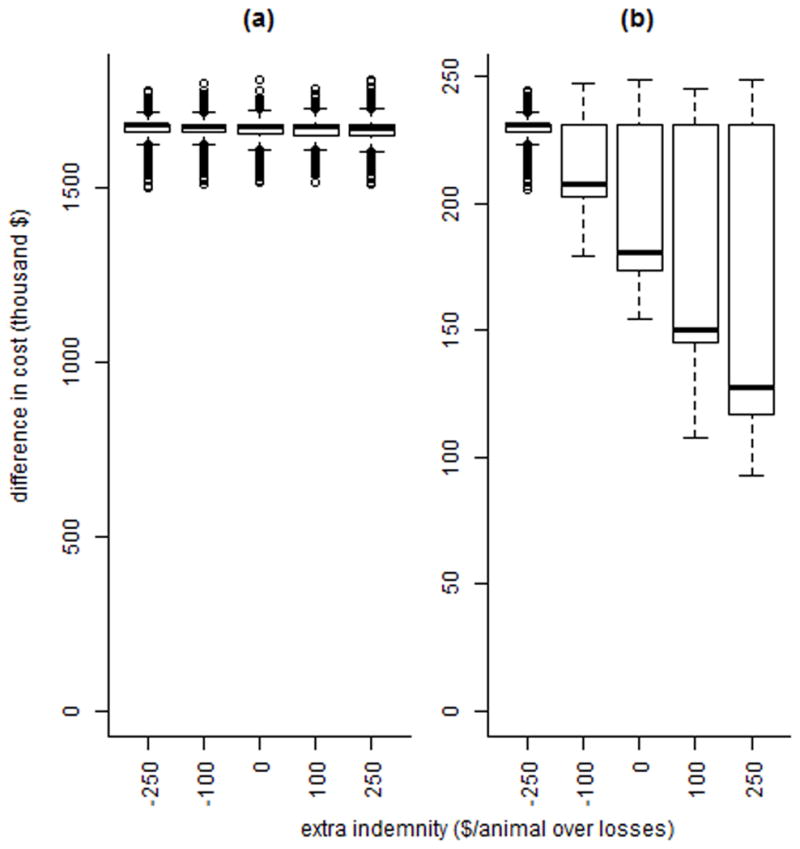
The distribution of the difference between depopulation costs and optimal test-and-remove costs for a bovine tuberculosis outbreak, for government-level costs (a) and farm-level costs (b), across a range of extra indemnity values, where extra indemnity is the difference between indemnity offered per animal and the farm’s losses and replacement costs due to culling. Depopulation refers to removal and replacement of all animals followed by a 2-year quarantine with annual testing, while the optimal test-and-remove program consists of a 2 month testing interval with 2 negative whole-herd tests required to declare the herd free of infection. The black line is the median, the box contains the interquartile range (IQR), the whiskers contain the largest and smallest observations within 1.5IQR of the upper and lower quartiles, respectively, and the dots are outliers.

As the average amount of indemnity per animal rises, the cost of depopulation increases for the government and decreases for the farm (results not shown); for a low average indemnity value, the government costs are lower for depopulation than for test and remove. However, the farm cost of depopulation is much higher in that circumstance than under higher indemnity values.

Discussion

The stochastic model for the cost of controlling a bovine tuberculosis outbreak at the government level predicts that the optimal control, in most cases, is a test-and-removal program with a 2 month testing interval and requiring 2 negative WHTs to declare the herd free of infection.

The goal of this study was to determine the point at which depopulation of a herd is preferable to test-and-removal. However, the study found that, on average, the cost of depopulation is always greater than the cost of test-and-removal under reasonable parameter values. The difference in cost varies with quarantine costs and indemnity values, but the cost of depopulation is never less than the cost of test-and-removal.

The finding that only 2 negative WHTs are needed to declare the herd free of infection is not consistent with modern policies for bTB eradication in many high-income countries. The fear is that undetected animals may cause a recurrent outbreak in a herd prematurely declared free of infection. In New Zealand, skin testing programs are based on prevalence, with higher prevalence herds requiring more stringent testing to be declared free of infection (Ryan et al., 2006). The prevalence within those herds, however, may be related to local endemically infected wildlife populations (Livingstone et al., 2006). Likewise, Great Britain and Northern Ireland have observed repeat outbreaks in herds under similar test-and-removal programs (2 to 3 negative WHT using only the CCT, with 6 and 12 month intervals, to be declared free of infection). Although farm-specific characteristics have been found to be related to recurrent outbreaks in Great Britain, and those outbreaks may have been caused by within-herd persistence (Karolemeas et al., 2011), many of these outbreaks are likely due to reintroduction from wildlife or imported cattle (Abernethy et al., 2013; Conlan et al., 2012). We are not including reintroduction from wildlife or imported cattle in our model as the data available to us indicate that reintroduction from these sources is not a concern for the herds considered in this study. Another factor in repeat outbreaks is the prevalence within the herd at the time of detection. In Australia, for instance, most detected herds had no secondary infections, indicating that fewer than the 4 negative WHTs required to declare a herd free of infection would have been necessary in most cases (Radunz, 2006). One study has found that a number of herds in Ireland were found to be infected only 6 months after being declared clear by a test-and-removal program similar to that being proposed in this study, but few of those herds had a low apparent prevalence (Wolfe et al., 2010). A study in Scotland found that there was heterogeneity in breakdown size, so the majority of homegrown reactors may have come from a few herds with large breakdowns (Gates et al., 2013). In the US, by contrast, outbreaks tend to involve very few infected animals; however, it should be noted that herds with a higher apparent prevalence at detection may require more careful post-outbreak monitoring.

The results generated by the model rely heavily on the parameter values provided, which are often specific to a farm and state. The global sensitivity analysis shows that 6 parameters drive the model results. Both the government level and the farm level show costs increasing with herd size, primarily because many costs (i.e., testing, quarantine, and indemnity) are calculated per animal. As indemnity increases, farm level costs decrease due to overcompensation for lost animal value. However, farm level costs increase with rising costs due to quarantine, as the model assumes a minimum of 4 months in quarantine. It is interesting that increasing the specificity of CFT would increase the cost to both the farm and the government. Although the number of latently infected animals which are falsely identified and removed would be decreased, leaving the latently infected animals in the herd longer increases the likelihood of further secondary infections and more positive WHTs, thereby increasing the duration of the infection in the herd and requiring more costly tests and culling. Both the test administration cost and the distance traveled to administer the tests were directly related to the government level costs, as they increased the cost of the WHTs. Despite the broad range of sensitivity values for post-mortem inspection and PCR, that parameter did not significantly impact the cost to the farm or the government, which justifies the simplifying assumption of perfect sensitivity and specificity throughout the rest of the study.

This model considered only the use of CCT for follow-up antemortem testing of CFT+ animals. In some areas, including many states experiencing bTB outbreaks, the interferon gamma assay is preferred because it decreases the number of farm visits and animal handling events, which could decrease the on-farm testing cost and increase the safety of animals and test administrators.

However, the interferon gamma assay has a slightly lower sensitivity and specificity (De la Rua-Domenech et al., 2006), which could increase false positive culling and delay detection of positive animals, and a high laboratory cost. A decision tree analysis in the UK found that using the interferon gamma assay in place of the CCT would dramatically increase the cost of bTB control in all herds, even if the laboratory cost of the interferon gamma assay was greatly reduced (Christiansen et al., 2002). Thus, we focused our models on the use of CCT; future work may include the interferon gamma assay as an option in this simulation model, but it is unlikely to be preferred economically due to the poorer performance and higher cost.

We also assumed that all test results were independent, despite animals being tested multiple times; a false-negative test result may be caused by an animal’s immune status or prior exposure to other mycobacteria, leading to more false-negative tests. However, we found that most infected animals were removed from the herd within 2–3 WHTs, indicating that very few infected animals were tested multiple times after leaving latency. In order to consider the effect of factors decreasing the sensitivity of the skin test in individual animals, an agent-based model would be required, as a compartmental model such as this is unable to account for such heterogeneity in individuals (Keeling and Rohani, 2008).

While this model attempts to take into account all aspects of the direct cost of bTB outbreaks, there are indirect costs that can be difficult to measure and that were not taken into account in the current study. Two specific indirect costs should be considered when interpreting the results of this study for government-level optimization. First, the model assumes that the presence of a bTB-positive herd generates no externality cost to the state or the state’s wider cattle industry. Currently, only depopulation will guarantee that result; test and removal may result in a state’s bTB status being downgraded from Accredited Free to Modified Accredited or Modified Accredited Advanced (USDA:APHIS:VS, 2005), although this may change when new BTB program standards are adopted (USDA:APHIS:VS, 2009b). Such a downgrade could cost the state’s cattle industry through a loss of exports, and cost the state through increased surveillance requirements. Second, the model assumes that the outbreak is contained within one herd and that spread to other herds and/or wildlife will not occur during the quarantine period. If quarantine is not 100% effective at containing the outbreak, the state could suffer losses controlling the secondary outbreaks. In either of these 2 cases, depopulation could become preferable to test-and-removal, and shorter testing intervals are likely to be preferred, especially in major dairy states. In states with small dairy industries these 2 situations might incur minor costs, such that test-and-removal would clearly be preferred over depopulation. The break-even cost for these externalities can be assumed to be the difference between depopulation and test and removal costs at the government level.

Due to the stochasticity of the model, the variability of costs decreased with herd size and increased with average indemnity and with holding costs. In smaller herds, a single secondary infection has a much greater effect on the cost/animal, as there are additional costs (primarily further testing visits) associated with a secondary infection. Stochasticity also means variation in the number of animals removed by testing (due to variation in false positive results) and in the number of months in quarantine (due to variation in true positive results, the number of secondary infections, and the time at which secondary infections become detectable). These numbers increase the cost multiplicatively with indemnity and holding costs, respectively.

Conclusion

Our model predicts that WHTs at a 2 month interval, with 2 negative WHTs required to declare a herd bTB-free, is the economically optimal control strategy in most scenarios. This would greatly decrease the cost of bTB control in individual herds in the US which now relies upon depopulation of the herd or extended testing programs. However, depopulation may be preferred if the loss of a state’s bTB-free status is sufficiently costly.