Factorial Structure of the Brief Symptom Inventory (BSI)-18 among Chinese Drug Users

Abstract

BACKGROUND

Although the Brief Symptom Inventory-18 (BSI-18) has been widely used for mental health screenings in both clinical and non-clinical populations, the validation of its application to Chinese populations has been very limited. The objective of this research is to assess the factorial structure of the BSI-18 within a Chinese drug using population.

METHODS AND RESULTS

A total sample of 303 drug users recruited via Respondent Driven Sampling (RDS) from Changsha, China was used for the study. Our results show: 1) The BSI-18 item scores are highly skewed; 2) With dichotomous items measures (1-problem at least moderately caused respondent discomfort during the past week; 0-otherwise), our findings support the designed 3-factor solution of the BSI-18 (somatization, depression, and anxiety); 3) The BSI-18 has a hierarchical factorial structure with 3 first-order factors and an underlying second-order factor (general psychological distress); 4) Tentative support should also be given to a single dimension of general psychological distress in Chinese drug using populations. Our study recommends a useful alternative approach for evaluating the factorial structure of the BSI-18 – i.e. CFA with dichotomous item measures. Both the total BSI-18 score and the three subscales (SOM, DEP, and ANX) can be used in applications of the BSI-18.

CONCLUSION

Overall, our findings suggest the BSI-18 is useful with Chinese drug users, and shows potential for use with non-Western and substance using populations more generally.

1. INTRODUCTION

Numerous epidemiological studies have demonstrated interconnections between substance use and mental health (e.g. Kessler et al., 1996; Grant et al., 2004). Considering this, the measurement of mental health within substance using populations remains a key issue. Comprehensive assessments of psychiatric symptoms can be time-consuming and burdensome. In some studies, such assessments also prove more extensive than necessary for study completion. As such, effective, precise, and efficient measures of mental health are of significant interest to substance use researchers throughout the world. Considering global population trends and shifts in global drug markets, it is imperative to identify measures that can be utilized within a variety of nations. While the BSI-18 has been increasingly utilized, its application to populations outside Western nations is less well validated. Given the increasing use of this measure in substance use research in other regions, it is important to assess its factorial structure in other populations to more fully evaluate its validity.

1.1 Brief Symptom Inventory and Substance Use

The Brief Symptom Inventory (BSI; Derogatis and Spencer, 1983) has been widely used to assess mental health in both clinical and non-clinical populations, including studies of drug users. These focus on a wide range of substances from methamphetamine (Booth et al., 2006) to cocaine (Magura et al., 1998) to ecstasy (Soar et al., 2006), and also studies of residential therapeutic communities (Metrikin et al., 2003). Additionally, the BSI has been used to assess mental health in varying types of drug use research including therapy for couples in treatment (Li et al., 2007), clinical studies of pharmacotherapy for dependent individuals (Meredith et al., 2007), and studies of anti-retroviral adherence among drug users (Knowlton et al., 2006). It has also been useful for screening substance abuse treatment clients for mental health symptoms (Royse and Drude, 1984). In sum, the BSI is a widely adopted measure that has demonstrated considerable utility in research and clinical practice related to substance use. The BSI-18 has demonstrated similar potential for drug using populations (Wang et al., 2010).

1.2. Assessments of the BSI and BSI-18

Based upon clinical conceptualizations of psychological disorders, the original BSI has 53 items designed to assess nine distinctive psychological domains: (somatization, obsessive– compulsive disorder, interpersonal sensitivity, depression, anxiety, hostility, phobic anxiety, paranoid ideation, and psychoticism (Derogatis, 1993). However, studies have shown inconsistent dimensional structures for the BSI with a varying number of dimensions (Hayes, 1997; Johnson et al., 1996; Kellett et al., 2004; Ruiperez et al., 2001). For example, Piersma and colleagues’ study (1994) with a sample size of 217 suggested that the BSI provides only a unidimensional measure of general psychological distress.

While the original BSI has good psychometric properties including high internal consistency and test-retest reliability (Derogatis and Spencer, 1983; Derogatis, 1993), its factorial structure remains difficult to test. A commonly used rule of thumb for structural equation modeling is 10 cases/observations per indicator variable (Nunnally, 1967) or 5–10 cases/observations per free parameter (Hoogland and Boomsma, 1998). With 53 items, a large sample is needed for factor analysis of the BSI. In addition, an instrument with multiple scales and many items often proves difficult with validation of its factorial structure in CFA modeling. Even when Cronbach’s alphas are high for the scales under study, the CFA model may not fit the data well unless some cross-factor loadings and error covariances are specified. Theoretically speaking, in CFA modeling, each item should be loaded only on its theoretical underlying factor(s) and items should be independent of each other once they are loaded to their underlying factors. Cross-factor loadings and error covariances are allowable only if they can be appropriately explained.

Similar concerns regarding these issues pertain less to the BSI-18, a shorter version used to screen for the most common psychiatric problems: somatization (SOM), depression (DEP), and anxiety (ANX), as the instrument has less heterogeneity (Derogatis, 2001). Indeed, the reduction to its 18-item format was also intended to improve structural validity through an instrument with fewer domains (Derogatis, 2001). Because of its simplicity, the BSI-18 is a useful measure to screen for psychiatric symptoms in a wide range of populations. Three theoretically defined dimensions of the BSI-18 were confirmed by Derogatis (2001) using principal components analysis. Importantly, the BSI-18 also permits considerations of a hierarchical structure, a matter of increasing interest for the assessment of mental health (Watson, 2005), and health outcomes more generally (Reise et al., 2007). This permits the consideration of generalized distress underlying the three specified psychiatric symptoms.

The three dimensions of the BSI-18 focus on the most commonly experienced mental health concerns (DEP, SOM, and ANX), thus making it useful for mental health assessments in community samples. Given its efficiency, this streamlined instrument is particularly useful for assessments in which mental health is not the primary outcome of interest, such as those in which common psychiatric symptoms may be associated with substance use. Several investigations of the BSI-18 have validated the originally designed three-dimensional structure (Durá et al., 2006; Andreu et al., 2008; Franke et al., 2011; Petkus et al., 2010; Wang et al., 2010; Wiesner et al., 2010). However, an alternative 4-factor model with factors DEP, SOM, Agitation (AGI), and Panic (PAN) has been suggested, as well as a 4-factor model that considers the original 3 dimensions plus suicidal ideation (Zabora et al., 2001). Yet, some have indicated that support for this 4-factor model is weak, particularly one with suicidal ideation given that it is based upon a single item, and thus the 3-factor model is preferable (Recklitis et al., 2006). Others have suggested that the BSI-18 is best used to measure a single dimension of general psychological distress (GPD; Asner-self et al., 2006; Prelow et al., 2005). Many of these studies have focused on clinical samples (e.g., Andreu et al., 2008; Durá et al., 2006; Franke et al., 2011; Petkus et al., 2010; Recklitis et al., 2006; Zabora et al., 2001); thus, further studies within community samples are warranted. Given these considerations, it remains important to further investigate whether the BSI-18 provides a hierarchical measure of both general psychological distress and individual dimensions of mental health, particularly in community samples.

1.3 Current Study

To further strengthen efforts to address the methodological challenges related to the measurement of mental health symptoms among substance users, the present study addresses the properties of the BSI-18 within a Chinese drug using population. Specifically, we report the details of an assessment of the factorial structure of this instrument in order to evaluate the extent to which the BSI-18 provides a precise and robust means to measure mental health among Chinese drug users in accordance with a hierarchical conceptualization of mental health. Testing the measure within this population also allows us to assess the validity of the BSI-18 within non-English speaking and non-Western populations.

2. METHODS

2.1 Sample

A total of 303 drug users were recruited in Changsha, China during 2010 and 2011. Study eligibility included: being 18 or older; methamphetamine use during the past 30 days; residence in Changsha; and the capacity to consent to research participation. Respondent-driven sampling (RDS), widely applied to hidden populations, was used for sample recruitment (Heckathorn, 1997, 2002; Wang et al., 2005, 2007). To initiate the RDS process, ethnographic methods were used to recruit 20 “seeds” within community settings. After having finished the survey, each seed was provided three confidentially linkable referral coupons in addition to the incentive received for their own participation (150 Yuan [∼$23 USD]). Each time a network member enrolled and presented a numerically-coded coupon, the “seed” received an incentive (50 Yuan [∼$8 USD]) for facilitating participation. The enrolled recruit then also received three referral coupons and was offered the same incentives as the “seed” to stimulate enrollment among network members. Peer recruitment with referral coupons and the dual incentives were employed to help reduce volunteerism and masking effects during the recruitment process (Heckathorn, 1997, 2002). The process continued through successive waves to build momentum within the networks to foster participation. Assessments of sample composition indicate that the sample extended through numerous waves and converged to equilibrium during the course of recruitment. All consent procedures conformed to IRB approval.

2.2 Measures

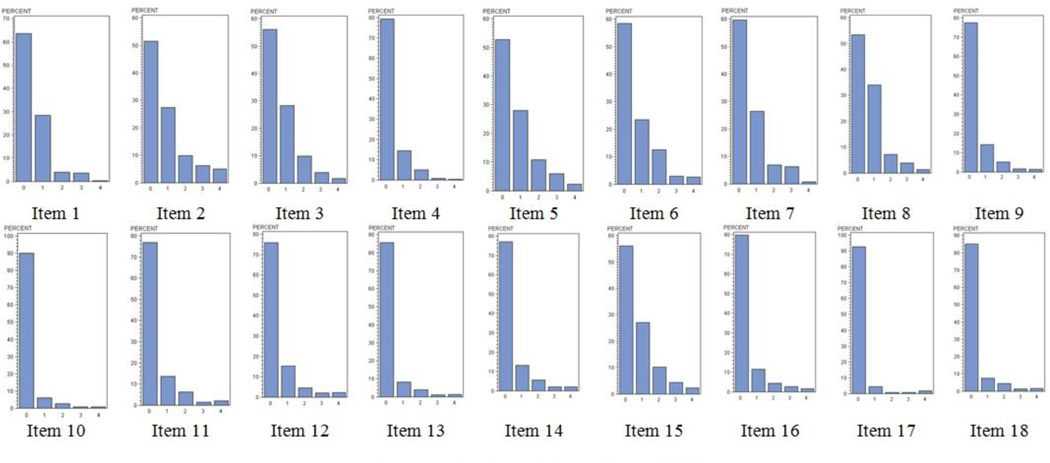
The BSI-18 items were designed to measure three dimensions of psychiatric disorders: somatization (SOM), depression (DEP), and anxiety (ANX). Each subscale included six items. BSI-18 items are rated on a 5-point, Likert scale: 0- not at all; 1- a little bit; 2- moderately; 3-quite a bit; 4-extremely. The items were translated from English to Chinese by using the back translation method by bilingual research team members. In applications of the BSI-18, item scores are usually treated as continuous measures to generate subscale scores or conduct factor analysis. The BSI-18 items scores in the present study are highly skewed with very few cases having responses 3 (quite a bit) or 4 (extremely; see Figure 1), and our preliminary analyses show that no CFA models fit the data even though robust ML estimator (e.g., MLR) was used to handle multivariate data non-normality in modeling. As such, we recoded all items as dichotomous measures: item responses were coded 1 if the problem at least moderately caused the respondent discomfort during the past week, otherwise coded 0. The dichotomous measures are meaningful indicators of whether symptoms caused at least moderate discomfort.

Figure 1.

Frequencies of the BSI-18 Item Scores.

2.3 Analytical Methods

Having recoded the BSI-18 items as dichotomous measures, the Kuder-Richardson Formula 20 (KR-20), a non-parametric equivalent to Cronbach’s α, was used to evaluate their internal consistency (Fleming et al.,1976; Ghiselli et al., 1981; Cortina, 1993). A KR-20 coefficient ≥ 0.60 is considered to indicate that the measure is internally consistent (Allen et al., 2000).

When categorical indicators/items are involved in CFA, instead of the variances/covariances of the observed items, the correlations between the unobserved latent continuous variable y^*s underlying the observed categorical items are analyzed. When one of the items is continuous and another is an ordered categorical measure, the latent correlation is polyserial correlation; the latent correlation is polychoric correlation for two categorical indicators; tetrachoric correlation for two dichotomous indicators; and biserial correlation for one continuous and one dichotomous indicator (Jöreskog and Sörbom, 1988; Brown, 2006). For the CFA models in this study, tetrachoric correlations were analyzed, using WLSMV that uses diagonal of the weight matrix (i.e., the inverse of the asymptotical variance/covariance matrix of the latent correlations) for parameter estimation and the entire weight matrix for standard error estimation. The estimated tetrachoric correlations ranged from 0.36 to 0.85.

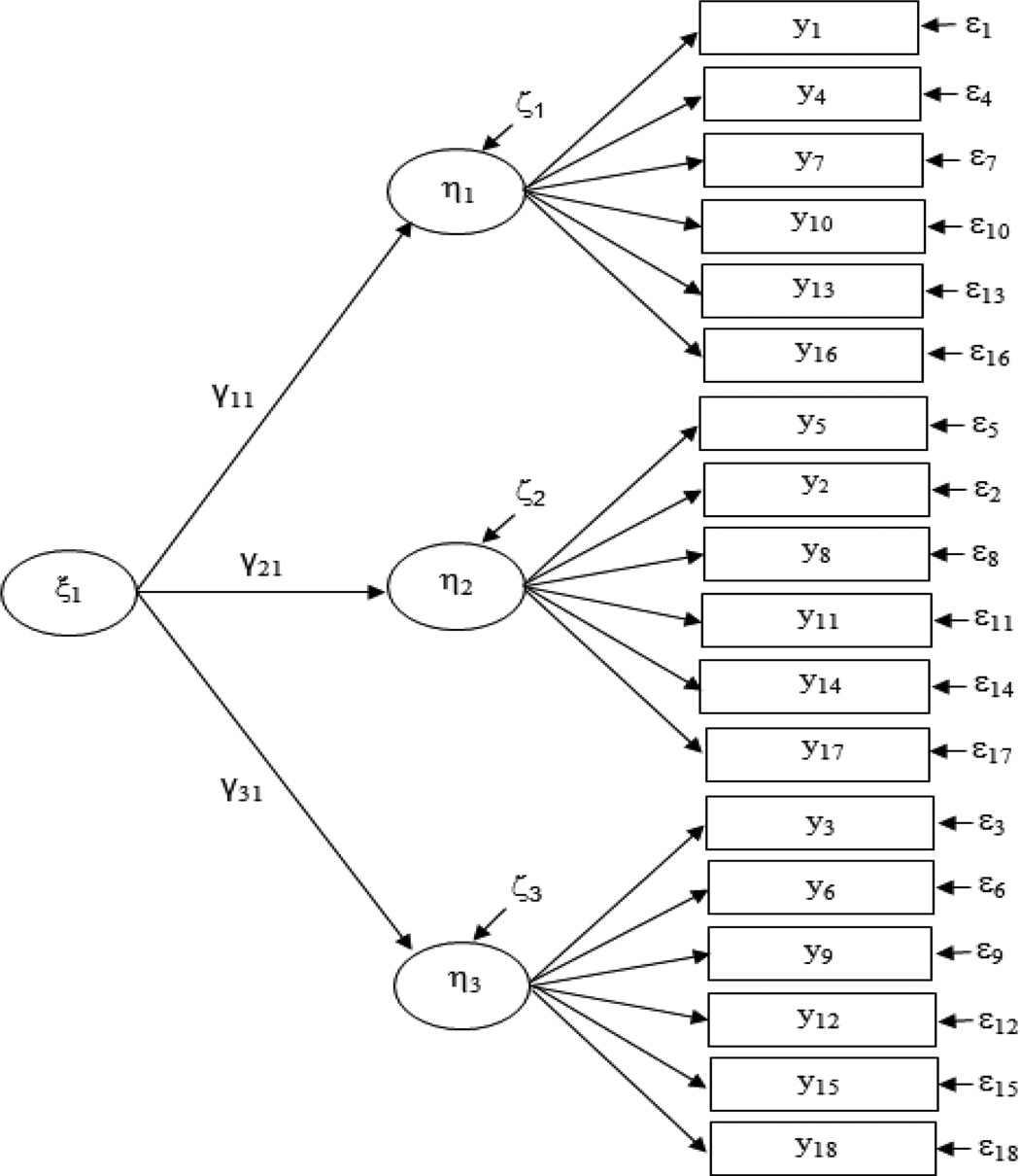
Various factorial solutions, including a single factor, three factors, and four factors, were tested. The first-order factors (e.g., SOM, DEP and ANX in the 3-factor CFA; SOM, DEP, AGI, and PAN in the 4-factor CFA) were highly correlated with each other (the correlation between the factors ranges from 0.88 to 0.98 in our sample). When a measurement instrument assesses several highly related domains, two alternative approaches within confirmatory factor analysis (i.e., the second-order CFA and the bifactor CFA) could be applied for modeling. Bifactor moels have become increasingly used to resolve dimensionality issues (Reise et al., 2007), yet secondorder models provide an appropriately comparable approach. The second-order model is more familiar to researchers as they have been applied in a wider variety of substantive areas, such as personality (DeYoung et al., 2002), self-concept (Marsh et al., 2002), and psychological well-being (Hills and Argyle, 2002). In the present study, we hypothesize that general psychological distress would account for the covariance among the first-order factors. Thus, second-order CFA models based on the three- and four-factor models were then tested to account for a hierarchical factorial structure of the BSI-18. A broader measure of GPD was specified as a second-order factor underlying the first-order factors (see Figure 2). On the basis of second-order CFA model, the relationships of the observed items with the first-order and second-order factors were further evaluated using Schmid and Leiman (1957) transformation. The basic idea of Schmid and Leiman transformation is to decompose the total explained item variance (as the observed items are dichotomous measures, the explained variance in an item is not the proportion of variance in the observed binary item, but in the corresponding latent reponse variably y) into two components: variance explained by second-order factors, and variance explained by first-order factors (Brown, 2006; Wang and Wang, 2012).

Figure 2.

Second order CFA of BSI-18.

Note: The latent response variable y^*s, corresponding to the observed dichotomous items, are not shown here for visual clarity.

The CFA models with dichotomous indicators were estimated using WLSMV, and mean and covariance structures (MACS) were analyzed. All models were estimated without specifying cross-factor loadings and error covariances. For model fit evaluation, the chi-square statistic is one conventional test of model fit in SEM. Because chi-square is defined as a (N-1) times the fitting function (Jöreskog, 1969; in most SEM computer programs, model chi-square is defined as χ² = f_ML(N-1), but it is defined as χ² = f_ML(N) in Mplus), it is highly sensitive to sample size; i.e., the larger the sample size, the more likely model rejection will occur. To address this limitation of the chi-square test, a number of model fit indexes have been developed for model fit tests. In this study, we report several model fit indices commonly reported in SEM applications: the comparative fit index (CFI; Bentler, 1990), the Tucker-Lewis index (TLI; Tucker and Lewis, 1973), the Nonnormed Fit Index (NNFI; Bentler and Bonett, 1980), root mean square error of approximation (RMSEA; Steiger, 1990; Browne and Cudeck, 1992), and the weighted root-mean-square residual (WRMR; Muthén and Muthén, 1998–2004). The cutoff value for CFI and TLI is usually 0.90, but higher values (e.g., ≥0.95) have been considered as the cutoff value in recent years. WRMR value of 1.0 or lower is considered good fit (Yu, 2002). The values of RMSEA are often interpreted as: 0-perfect fit; <0.05=close fit; 0.05–0.08=fair fit; 0.08–0.10=mediocre fit; and >0.10=poor fit (Browne and Cudeck 1993; Byrne, 1998). Hu and Bentler (1999) suggest RMSEA <= 0.06 as the cutoff for good model fit. RMSEA is the only model fit index so far that provides a confidence interval around its calculated value. In a well-fitting model, the lower 90% confidence limit includes or is close to 0, while the upper limit is less than 0.08. In addition, a test of close-fit for null hypothesis (H₀: RMSEA <=0.05) is also important. If the p-value of the close-fit test is greater than 0.05, then we cannot reject the null hypothesis, therefore, the specified model has a “close fit.” It is notable that no single index should be relied upon exclusively for evaluating model fit. Instead, model fit evaluation should be based on multiple indices in order to avoid inaccurate conclusions (Bollent, 1989; Bentler, 2007). In this regard, we considred a broad array of fit indices to assess model fit. All CFA models were estimated using Mplus 6.12 (Muthèn and Muthèn, 1998–2010).

Kim’s method (Kim, 2005) that is based on testing model's overall fit was used to estimate sample size for the CFA models under study (Kim’s equation of estimating sample size for SEM based on model fit index RMSEA is: ${\mathrm{N}}_{\text{RMSEA}}=\frac{\lambda }{{\text{RMSEA}}^2·\mathit{\text{df}}}+1,$ where d.f is model degree of freedom, λ the estimated chi-square noncentrality parameter given a d.f. and statistical power; e.g., 0.80)

Though the sample size (N=303) is moderate, statistical power is large enough for our CFA models to achieve a good model fit (RMSEA=0.05) given a statistical power of 0.80 at 0.05 level: the estimated sample size for the single-factor CFA, first- and second-order 3-factor CFA (the d.f. is the same for the first- and second-order 3-factor CFA models), first-order 4-factor CFA, and second-order 4-factor CFA models are n=137, 140, 141, and 139, respectively.

3. RESULTS

Socio-demographic characteristics and recent drug use practices are shown in Table 1. The sample was dominated by Han nationality (98%) and males (87.1%), which cohere with many studies of drug users in China. The participants were relatively young with a mean age of 29.9 (SD=7.6). A majority had less than a high school education (59.7%). In the sample, 42.6% were currently married, 44.2% had children, and only 38.6% were full-time employees. In regard to frequency of recent methamphetamine use, 23.8% reported using meth on more than 30 days, 31.4% used on 10–30 days, and 44.9% used meth on less than 10 days, thus indicating a range of drug use patterns within the sample.

Table 1.

Descriptive statistics of socio-demographics and current drug use (N=303)

Variable	N (%)
Socio-Demographics
Age
<20	19 (6.3)
20–29	152 (50.2)
30–39	94 (31.0)
40+	38 (12.5)
Gender
Male	264 (87.1)
Female	39 (12.9)
Ethnicity
Han	297 (98)
Ethnic Minority	6 (2)
Employment Status
Full-time	117 (38.6)
Part-time	84 (27.7)
Student	7 (2.3)
Unemployed	95 (31.4)
Relationship Status
Married	129 (42.6)
Domestic Partner	13 (4.3)
Steady Boyfriend/Girlfriend	75 (24.8)
Single	74 (24.4)
Divorced	11 (3.6)
Widowed	1 (0.3)
Parental Status
Children	134 (44.2)
Without Children	169 (55.8)
Education
<High School	181 (59.7)
High School	75 (24.8)
Some College	33 (10.9)
Bachelor's +	14 (4.6)
Drug Use in the Past three Months
Methamphetamine
<10 Days	136 (44.9)
10–30 Days	95 (31.4)
>30 Days	72 (23.8)
Marijuana
Never	296 (97.7)
Ever	9 (3.0)
Opium
Never	302 (99.7)
Ever	2 (0.7)
Heroin
Never	298 (98.4)
Ever	11 (3.6)
Ecstasy
Never	300 (99.0)
Ever	4 (1.3)
Ketamine
Never	302 (99.7)
Ever	65 (21.5)
Cocaine
Never	303 (100.0)
Ever	0 (0.0)
Other Drugs*
Never	289 (95.4)
Ever	14 (4.6)

Note.

^*Use other drugs, e.g., methadone, buprenorphine, diazepam, tramadol etc.

Table 2 shows the descriptive statistics of the dichotomous measures of the BSI-18 items by subscale and general psychological distress (GPD), as well as their internal consistency measured by KR-20 (analogous to Cronbach's α). The KR-20 coefficients are high, ranging from 0.76 to 0.83 for the composite measure of SOM, DEP, and ANX, and over 0.90 for GPD, demonstrating good internal consistency. Our results show that the three original scales and the total score of the BSI-18 had good reliability within the sample of Chinese drug users.

Table 2.

Descriptive statistics of the BSI-18 items (N=303)

Item	Item #	N (%)
Somatization (SOM)		(KR-20=0.76)
Faintness	1	24 (7.9)
Chest pains	4	18 (5.9)
Nausea	7	55 (18.2)
Short of breath	10	12 (4.0)
Numb or tingling	13	19 (6.3)
Body weakness	16	26 (8.6)
Depression (DEP)		(KR-20=0.77)
Lonely	5	58 (19.1)
No interest	2	64 (21.1)
Blue	8	38 (12.5)
Worthlessness	11	29 (9.6)
Hopelessness	14	29 (9.6)
Suicidal thoughts	17	9 (3.0)
Anxiety (ANX)		(KR-20=0.83)
Nervousness	3	47 (15.5)
Tense	6	55 (18.2)
Scared	9	25 (8.3)
Panic episodes	12	27 (8.9)
Restlessness	15	51 (16.8)
Fearful	18	22 (7.3)
General Psychological Distress (GPD)	1–18	(KR-20=0.91)

Note.

KR-20: The Kuder Richardson Coefficient of reliability, which is non-parametric equivalent to Cronbach’s α.

Table 3 shows the model fit statistics/indexes for the single-factor, 3-factor (i.e., SOM, DEP, and ANX) and 4-factor (i.e., SOM, DEP, ANX, and PAN) CFA models, as well as 3- and 4-factor second-order CFA models. The results show that all models, including the single-factor model, fit the data very well: CFI and TLI are above 0.95, RMSEA≤0.06, Close-fit test P-value>0.05, and WRMR<1.00. While a significant model χ² statistic does not necessarily indicate bad model fit, an insignificant chi-square statistic is appreciable. All our model χ² statistics, except for the single-factor CFA model, are not statistically significant. Although the model χ² of the single-factor CFA is statistically significant (P=0.033), its other model fit indices (e.g., CFI=0.99, TLI=0.99, RMSEA=0.03 (90% C.I.: 0.01, 0.04), Close-fit test P =0.998, and WRMR=0.81) indicate the model fit is acceptable.

Table 3.

Goodness-of-fit statistics/indices for CFA models¹

Model	χ2	d.f.	P	CFI	TLI	RMSEA (90% C.I.)	WRMR
First-order CFA
1 Factor	166.53	135	0.033	0.989	0.988	0.028 (0.008, 0.041) Close-Fit P=0.999	0.814
3 Factors	152.03	132	0.112	0.993	0.992	0.022 (0.000, 0.037) Close-Fit P=1.000	0.753
4 Factors	145.98	129	0.145	0.994	0.993	0.021 (0.000, 0.036) Close-Fit P=1.000	0.720
Second-order CFA
3 Factors	152.03	132	0.112	0.993	0.992	0.022 (0.000, 0.037) Close-Fit P=1.000	0.753
4 Factors2	145.81	132	0.194	0.995	0.994	0.019 (0.000, 0.034) Close-Fit P=1.000	0.725

Note.

¹All models were estimated using WLSMV in Mplus. No cross-loadings and measurement error covariances were specified in the models.

²The residual variance of factor Agitation was fixed to 0 to avoid a negative residual variance in model estimation.

CFI: Comparative fit index.

TLI: Tucker-Lewis index.

RMSEA: Root mean square error of approximation.

WRMR: Weighted root mean square residual.

As other studies have shown (Derogatis, 2001; Recklitis et al., 2006; Wang et al., 2010), our results support the original 3-factor design of the BSI-18 because: 1) conceptually speaking, two factors (panic and agitation; in the 4-factor model, factor loadings of items of the panic factor were 0.91, 0.92 and 0.94 for Item 9 (Scared), Item 12 (Panic episodes) and Item 18 (Fearful), respectively, and another factor underlying agitation symptoms has factor loadings of 0.90, 0.91, and 0.83 for Item 3 (Nervousness), Item 6 (Tense), and Item 15 (Restlessness), respectively). In the 4-factor model can be considered anxiety (Derogatis, 2001); and 2) there was hardly any difference between our 3- and 4-factor models regarding the model fit indexes. Given similar model fit, the more parsimonious model is typically preferable.

Selected results of the second-order CFA model with 3 first-order factors are shown in Table 4. All the items are highly loaded onto their underlying first-order factors; and the first-order factors (i.e., SOM, DEP, and ANX) are highly loaded onto the second-order factor (GPD). The proportions of variance in the first-order factors explained by the second-order factors are 0.82, 0.95, and 0.99, respectively, indicating that the higher-order solution provides a good account for the covariances among the first-order factors.

Table 4.

Results of Second-Order 3-Factor CFA Model¹³

Item	Item#	SOM	DEP	ANX
Faintness	1	0.77
Chest pain	4	0.84
Nausea	7	0.66
Short of breath	10	0.99
Numb or tingling	13	0.95
Body weakness	16	0.85
Lonely	5		0.81
No interest	2		0.81
Blue	8		0.86
Worthlessness	11		0.91
Hopelessness	14		0.83
Suicidal Thoughts	17		0.85
Nervousness	3			0.90
Tense	6			0.91
Scared	9			0.86
Panic episodes	12			0.88
Restlessness	15			0.83
Fearful	18			0.91
			GPD
SOM			0.91
DEP			0.97
ANX			0.98
Model Fit		CFI=0.99, TLI=0.99, RMSEA=0.02 (90% C.I.: 0.00, 0.04), Close-Fit Test P-value=1.00 WRMR=0.75

Note.

^*The first item of each factor was treated as the marker indicator by default in Mplus. Switching marker indicator does not change the model results. Results reported in the table are based on a completely standardized solution.

Table 5 shows the Schmid-Leiman transformation of the second-order CFA model estimates. Columns A and B are standardized first- and second-order factor loadings, respectively, for each observed BSI-18 item. Column C, the squared value of Column A, represents the total variance of the unobserved response variable y^* explained by the factors. The factor loading of an item onto the second-order factor can be calculated as the product of the standardized first- and second-order factor loadings; and the squared value of this product is the variance of y^* explained by the second-order factor (Column D). Knowing the total explained variance and the variance explained by the second-order factor, the variance of y^* explained by the first-order factor can be readily calculated (Column G); and (one minus the total explained variance) is the residual variance (Column H). As such, the variance of the unobserved response variable y^* is decomposed into three components: variance explained by the second-order factor (GPD), variance explained by a first-order factor (SOM, DEP, or ANX), and residual variance. The results show that a substantial portion of the variance of y^* corresponding to each BSI-18 item was explained by its underlying factors: 44% to 98% for the SOM items, 66% to 83% for the DEP items, and 69% to 83% for the ANX items (see Column C). However, the variances of y^* were not much explained by the first-order factors (SOM, DEP, or ANX), but by the secondorder factor, general psychological distress. For example, 78 % (Column D) of the variance of y^* corresponding to Item Y₃ were explained by the second-order factor, only 3% (Column G) were explained by its underlying first-factor (i.e., ANX), and the unexplained variance or residual variance of Y₃ is 19% (Column H).

Table 5.

Schmid-Leiman Transformation of the Second-order CFA Model Estimates^*

	A	B	C	D	E	F	G	H
Item	First-order Factor Loading	Second-order Factor Loading	Total Variance** Explained by Factors (A2)	Item Variance** Explained by Second- order Factor (A*B)2	SQRT of Unexplained Variance of First-order Factor $\sqrt{(1-{\mathrm{B}}^2)}$	Residualized First-order Factor Loading (A*E)	Item Variance** Explained by First- order Factor (F2)	Item Variance** Not Explained by Factors [1-(D+G)]
SOM
Y1	0.77	0.91	0.59	0.49	0.41	0.32	0.10	0.41
Y4	0.84	0.91	0.71	0.58	0.41	0.34	0.12	0.30
Y7	0.66	0.91	0.44	0.36	0.41	0.27	0.07	0.57
Y10	0.99	0.91	0.98	0.82	0.41	0.41	0.17	0.01
Y13	0.95	0.91	0.90	0.75	0.41	0.39	0.15	0.10
Y16	0.85	0.91	0.72	0.60	0.41	0.35	0.12	0.28
DEP
Y5	0.81	0.97	0.66	0.62	0.24	0.19	0.04	0.34
Y2	0.81	0.97	0.66	0.62	0.24	0.19	0.04	0.34
Y8	0.86	0.97	0.74	0.70	0.24	0.21	0.04	0.26
Y11	0.91	0.97	0.83	0.78	0.24	0.22	0.05	0.17
Y14	0.83	0.97	0.69	0.65	0.24	0.20	0.04	0.31
Y17	0.85	0.97	0.72	0.68	0.24	0.20	0.04	0.28
ANX
Y3	0.90	0.98	0.81	0.78	0.20	0.18	0.03	0.19
Y6	0.91	0.98	0.83	0.80	0.20	0.18	0.03	0.17
Y9	0.86	0.98	0.74	0.71	0.20	0.17	0.03	0.26
Y12	0.88	0.98	0.77	0.74	0.20	0.18	0.03	0.23
Y15	0.83	0.98	0.69	0.66	0.20	0.17	0.03	0.31
Y18	0.91	0.98	0.83	0.80	0.20	0.18	0.03	0.17

Note.

^*Results are based on completely standardized solution.

^**The variance of the unobserved continuous response variables y^*.

4. DISCUSSION

Although the BSI-18 has been widely used, the validation of its application to Chinese populations and to substance using populations in non-Western settings has been limited, e.g., one study of patients undergoing renal transplantation (Liang and Gou, 2006), and another focused on elderly inpatients (Yang et al., 2012). Although the global BSI-18 and its three subscales all demonstrated appropriate Cronbach’s α in these studies, its factorial structure was not examined. The relatively low use of the BSI-18 in China indicates that proper validation of the BSI-18 in Chinese may be necessary prior to wider use. The present study is the first time, to our knowledge, to conduct a systematic test of the factorial structure of the BSI-18 among individuals in a health study in China. It is also an important step in the validation of the BSI-18 for substance using populations in other non-Western settings.

By decomposing the variance of the unobserved response variable y^*, we found that the variance of y^* corresponding to the BSI-18 items were not much explained by the first-order factors (SOM, DEP, or ANX), but primarily by the second-order factor. Similar to the findings of some other studies (Asner-self et al., 2006; Prelow et al., 2005), our results imply that the BSI-18 items lie more in their contribution to the general psychological distress. Thus, tentative support may be given to a single dimension of general psychological distress in this sample of drug users in China. As a matter of fact, the single-factor solution has good fit to the data in our study. In this regard, while the individual sub-scales retain utility within these populations, the BSI-18 may contribute more to the assessment of general mental health impairment, as the generalized psychological distress underlies the three specified psychiatric symptoms. Overall, our results indicate that the BSI-18’s focus on the most commonly experienced mental health concerns (DEP, SOM, and ANX) and the ability to assess a broader dimension of mental health impairment, make it useful for mental health assessments in community samples.

Importantly, our study also recommends a useful alternative approach for evaluating the factorial structure of the BSI-18. The BSI-18 items are measured on a 5-point Likert scale, and are often not normally distributed (e.g., Recklitis et al., 2006; Wang et al., 2010). Our findings demonstrate the utility of dichotomous indicators in such instances. When items are moderately skewed, the maximum likelihood (ML) method will produce biased estimates of fit (Chou et al., 1991; Curran et al., 1996; Muthén and Kaplan, 1985). To accommodate data non-normality, robust maximum likelihood estimators (e.g., MLR, MLM) can be used to adjust the model chisquare and provide robust standard errors that are used to conduct significance testing for individual parameter estimates (Muthèn and Muthèn, 1998–2010). Studies of the factorial structure of the BSI-18 have shown that using robust estimator for model estimation improves model fit (Wang et al., 2010; Wang and Wang, 2012). However, with highly skewed BSI-18 measures in the present study (see Figure 1), none of the CFA models with the original BSI-18 measures, including the single factor, 3-, and 4-factor CFA models, fit the data well, even with the robust estimator for model estimation. Thus, in the present study, CFA with dichotomous items were used to test the factorial structure of the BSI-18, and the models fit the data very well. Our results support the findings of a similar application of the BSI-18 to drug users in the U.S. (Wang et al., 2010); that is, the BSI-18 has a 3-factor structure (SOM, DEP, and ANX) with an underlying second-order factor (GPD).

4.1 Limitations

Although our findings demonstrate the BSI-18’s potential utility with drug using populations and non-Western populations, we must consider some limitations. First, though statistical power is large enough for the CFA model under study, the sample size is moderate and may limit our practice of structural equation modeling where the CFA model is used as a measurement model. Second, RDS was used for participant recruitment. Though RDS is a widely used sampling method for hidden populations and is better than convenience sampling (Heckathorn, 1997, 2002), a RDS sample is not a random sample; thus, our sample may not be totally representative of the target population. Third, the data used for analysis were self-reported, and thus might contain potential information bias. Fourth, the BSI-18 items were recoded as dichotomous measures in this study because the BSI-18 item responses in our sample were highly skewed with empty cells or small cell frequencies in some items. The factors that account for the skewness of the distributions are unclear and need to be further explored. Although it is sometimes desirable or useful to transform continuous or ordinal measures into dichotomous measures for analysis (McFall and Treat, 1999), such transformation may result in losing information (Watson, 2005). However, studies that have used the BSI-18 with Chinese students suggest no culturally influenced response patterns (Wang and Mallinckrodt, 2006; Wang et al., 2012), and we are unaware of response styles unique to Chinese individuals that would yield such results. Finally, the present study was based on one sample of drug users from central China. More studies using samples from different populations are needed to confirm our findings and have a better understanding of its factorial structure. In future studies, scholars should examine factorial structure invariance of the BSI-18, using multi-group CFA models, to confirm that the instrument is valid in drug-using populations in different locations.

4.2 Conclusions

Our analyses present several interesting findings with respect to the utility of the BSI-18 with Chinese drug using populations. First, our study recommends a useful alternative approach for evaluating the factorial structure of the BSI-18; that is, CFA with dichotomous item measures when CFA with the original ordinal item measures does not fit data. Second, although the BSI-18 has valid factorial structure with 3 factors, it is also intended to measure general psychological distress. As such, both the total BSI-18 score and the three subscales (SOM, DEP, and ANX) can be used in applications of the BSI-18. Overall, our findings indicate that the BSI-18 is useful within Chinese populations, and shows great potential for use with non-Western substance using populations more generally.