Improved fracture risk assessment based on nonlinear micro-finite element simulations from HRpQCT images at the distal radius

Abstract

More accurate techniques to estimate fracture risk could help reduce the burden of fractures in postmenopausal women. Although micro-finite element (µFE) simulations allow a direct assessment of bone mechanical performance, in this first clinical study, we investigated whether the additional information obtained using geometrically and materially nonlinear µFE simulations allows a better discrimination between fracture cases and controls. We used patient data and high-resolution peripheral quantitative computed tomography (HRpQCT) measurements from our previous clinical study on fracture risk which compared 100 postmenopausal women with a distal forearm fracture to 105 controls. Analyzing these data with the nonlinear µFE simulations, the odds ratio (OR) for the factor-of-risk (yield load divided by the expected fall load) was marginally higher (1.99; 95% CI, 1.41–2.77) than for the factor-of-risk computed from linear µFE (1.89; 95% CI, 1.37–2.69). The yield load and the energy absorbed up to the yield point as computed from nonlinear µFE were highly correlated with the initial stiffness (R², 0.97 and 0.94, respectively) and could therefore be derived from linear simulations with little loss in precision. However, yield deformation was not related to any other measurement performed and was itself a good predictor of fracture risk (OR, 1.89; 95% CI, 1.39–2.63). Moreover, a combined risk score integrating information on relative bone strength (yield load-based factor-of-risk), bone ductility (yield deformation) and the structural integrity of the bone under critical loads (cortical plastic volume) improved the separation of cases and controls by one third (OR, 2.66; 95% CI, 1.84–4.02). We therefore conclude that nonlinear µFE simulations provide important additional information on the risk of distal forearm fractures not accessible from linear µFE nor from other techniques assessing bone microstructure, density or mass.

Introduction

Osteoporosis is associated with impaired bone strength that leads to a higher incidence of fractures, thereby causing high morbidity and large health care costs (1,2). Therefore, the aim is to diagnose bone loss early and initiate treatment strategies before fractures occur. The standard clinical assessment currently is based on areal bone mineral density (aBMD) as measured by dual-energy X-ray absorptiometry (DXA) and is thereby limited to detecting differences in bone mass (3). To capture the variability in bone quality (4), significant efforts have been devoted to augmenting DXA measurements with information on bone microstructure and its functional competence (5). In vivo high-resolution peripheral quantitative computed tomography (HRpQCT) measurements provide an accurate reconstruction of bone microstructure and, together with 3D histomorphometric parameters derived from the HRpQCT images, allow a detailed analysis of bone microarchitecture (6,7). Furthermore, using such data in mechanical finite element (FE) simulations provides a way to assess bone strength more directly. In particular, linear-elastic microstructural FE (µFE) based on the segmented bone microstructure has been widely used to estimate bone strength (8–14). However, the resulting stiffness was typically correlated highly with bone mass and density. Consequently, the factor-of-risk defined as the ratio of the estimated fall load over the bone strength computed by linear µFE was unable to contribute significantly over densitometry-based measures to distinguish women with distal forearm fractures from controls (14).

One possible conclusion is that not only stiffness but also the ability of the bone to undergo deformation and absorb energy should be considered important contributors to distal forearm fracture risk. Nonlinear µFE can accurately and reproducibly account for materially nonlinear effects such as plastic deformations and geometrically nonlinear effects, particularly the bending of the bone microstructure under load (15). Therefore, nonlinear µFE can be used to simulate, for example, the onset of yielding. The complexity of nonlinear µFE simulations has evolved over time such that the majority is now geometrically and materially nonlinear, as in this study. Furthermore, the development of efficient parallel solvers for large nonlinear FE problems and the availability of high performance computer clusters allow nonlinear µFE simulations to be used also in large clinical trials.

In this first application of nonlinear µFE in a clinical setting, we investigated whether materially and geometrically nonlinear µFE simulations can improve the estimation of patient-specific distal forearm fracture risk. For this, we tested the ability of nonlinear µFE simulations in addition to aBMD, HRpQCT bone histomorphometric parameters and linear µFE to distinguish between 100 postmenopausal women with a distal forearm fracture (cases) and 105 controls from a previously published study (14). We hypothesized that nonlinear µFE, in particular yield deformation and the energy dissipated before bone yielding, contribute important additional information with which to assess fracture risk.

Materials and methods

Patient data and previous analyses

The patient data originated from a previously published study (14) on 100 postmenopausal women who were newly diagnosed with a distal forearm fracture. The 105 postmenopausal controls were frequency matched based on the expected age distribution of forearm fractures in that community (16). None of the controls had a history of a typical osteoporotic fracture. It was reported previously that fracture cases and controls had identical average heights and similar weights, as well as body mass index. As a consequence, only skeletal variables discriminated cases from controls (14). HRpQCT measurements were performed at the non-dominant (or unfractured) wrist using an XtremeCT device (Scanco Medical AG, Brüttisellen, Switzerland), yielding a tomographic image composed of 110 slices with an isotropic voxel size of 82 µm. The study was approved by Mayo Clinic's Institutional Review Board, and anonymized data were used in the present analysis.

Nonlinear µFE analysis

The µFE models of the bone microstructure were created with a direct voxel to element conversion from HRpQCT image voxels (17). We adapted the elastic modulus of the bone elements to the local density in the HRpQCT image. An elastoplastic material model with a constant yield strain was employed for the bone, while marrow was modeled with a hyperelastic material model (15).

The gray-scale value in the Gaussian filtered HRpQCT image (σ = 1.2, support = 2) was first converted to apparent density (ρ_app) according to the measurement calibration record (18) and, second, to a local elastic modulus (E) using the relation by Morgan et al (19) for the femoral neck, E(ρ_app)=6850 ρ_app^1.49. Bone tissue was modeled as an elastoplastic material with a von Mises yield criterion. A constant yield strain of 0.75% was assumed (20), and the hardening modulus was set to the elastic modulus of collagen (H = 2 MPa) (21). A constant Poisson’s ratio (ν) of 0.3 was used for the bone. The voids in the bone were assumed to be filled by bone marrow and were modeled as neo-Hookean hyperelastic material, with E = 2 MPa and ν = 0.167 (22). The hyperelastic material was necessary to cope with the large strains occurring in this comparably soft material. Furthermore, finite deformations were assumed to account for bending modes in the bone microstructure (23,24). An axial compression by 1.5% of the original height was simulated in 15 increments of 0.1% deformation each.

We used a newly developed, fully nonlinear, parallel FE solver (ParFEnl) (15) with a full Newton-Raphson scheme and an algebraic multigrid preconditioner that was built based on the linear solver ParFE (25). The nonlinear simulations were performed on a CRAY XE6 computer at the Swiss National Supercomputing Centre (CSCS, Lugano, Switzerland), composed of compute nodes with 2 16-core AMD Opteron Interlagos processors running at 2.1 GHz and 32 Gigabytes of memory per node. The simulations with 2.4 to 6.1 Mio elements were run in parallel on 5 compute nodes with 160 CPUs in total and took between 1.1 and 6 hours per sample. The entire study comprised a total of 205 nonlinear simulations and required about 150'000 CPU-hours.

In nonlinear FE simulations, the entire load-displacement curve may be evaluated. Stiffness was computed from the first load increment. We defined the yield point according to the 0.2% offset criterion (15). The load at the yield point was used as a surrogate for bone strength, the deformation as a surrogate for ductility and the energy dissipated until the yield point as a surrogate for toughness. The factor-of-risk for fracture was computed based on the yield load. From the individual’s height, the expected load for a fall on the outstretched arm was computed as $F_{\mathit{\text{fall}}}={670}^{Ns}/m·\sqrt{2·9.81·\mathit{\text{height}}/2}$ (26). The yield factor-of-risk was computed as F_fall divided by the yield load. Furthermore, to assess the structural integrity of the deformed bone, we calculated the amount of cortical bone that was in the plastic phase at 1 % compressive deformation.

In vitro validation

To assess the accuracy of the nonlinear µFE simulations and to determine whether the simulated yield point could be used to approximate the point of failure, we compared the simulations to biomechanical tests on entire cadaveric forearms (27). The samples were provided by the Ludwig-Maximilian-University (LMU), Munich and were donated in accordance with German legislative requirements. The samples were imaged using a prototype HRpQCT scanner (Scanco Medical AG, Brüttisellen, Switzerland) at a resolution of 89 µm in plane and a slice thickness of 92 µm in accordance with the manufacturer’s recommendation for in vivo measurements. The intact forearms were then subjected to displacement-controlled compressive loading up to failure (8). We selected 20 out of 100 samples (10 male, 10 female, age 83.6±9.1 years) with minimal drops during the main loading phase to reduce the impact of the surrounding soft-tissue. The material properties and loading conditions of the µFE models were defined as described above. Using linear regression analysis and Student’s t-test, we found a high correlation (R = 0.82, p < 0.001) between the simulated yield load and the experimental failure load, which was defined as the maximum load before a reduction of the reaction force by at least 30%. Furthermore, we observed a correlation (R = 0.60, p < 0.001) between the simulated yield deformation and the deformation measured in the experiment from the beginning of the linear region up to the point of failure. Lastly, a correlation (R = 0.79, p < 0.001) was found between the simulated energy dissipated before yielding and the energy absorbed by the forearm, which was measured from the area under the load-displacement curve between the onset of the linear region and failure. These correlations are within the same range as found between linear µFE simulations and the compressive strength of entire forearms (8,27). However, it has been shown for both linear and nonlinear µFE simulations that much higher correlations can be achieved when using well controlled boundary conditions and when only a section of the bone is tested (10,28).

Statistical analysis

All statistical analyses were performed with R (29), using a significance level of 0.05. In the descriptive statistics, the variables were summarized with means and standard deviations. An approximately normal distribution was confirmed for all variables using a Kolmogorow-Smirnow test. The differences between fracture cases and controls were indicated as percent differences and standard (z) scores and were assessed by a Student’s t test. Odds ratios (OR) per SD decrease derived from logistic regression models were used to measure the relative fracture risk associated with the respective variable; OR for the factor-of-risk and for the cortical plastic volume were indicated per SD increase. Differences in OR were assessed using Wald chi-squared tests on the logistic regressions. Standard receiver operating curves (ROC) and areas under the curve (AUC) were computed for all variables as an alternative measure of the ability to distinguish cases and controls. Furthermore, correlations between the variables were computed using linear regression in order to measure the amount of independent information contained in the results of the nonlinear µFE simulations. Finally, a combined risk score was defined starting with yield factor-of-risk and forward selection of further factors, provided they added significant independent information to differentiate cases from controls. For this, the individual variables were normalized as z-scores, and their weight was computed from the logistic regression.

Results

As was seen in the previous study (14), most variables differed significantly between distal forearm fracture cases compared to controls (Table 1). The exceptions were the slope in the yield point and the cortical plastic volume. In terms of standard (z-)scores, the biggest difference was found in the yield-based factor-of-risk (0.75). However, according to the Student's t-test, the most significant difference was in yield deformation (p<0.0001).

Table 1.

Comparison of Bone Density, Microstructure and Mechanical Variables for Distal Forearm Fracture Cases and Controls

	Total	Controls	Cases	Difference
	Mean±SD	Mean±SD	Mean±SD	%	z-Score
Stiffness (kN/mm)	71.231±21.006	76.436±21.681	65.766±18.883	16.2	−0.49***
Yield deformation (%)	0.747±0.033	0.757±0.031	0.738±0.032	2.5	−0.60***
Yield load (N)	3483.7±1166.1	3795.0±1227.3	3156.9±1004.3	20.2	−0.52***
Yield energy (mJ)	179.36±65.42	197.46±69.68	160.35±54.83	23.1	−0.53***
Yield slope (kN/mm)	13.388±3.817	13.825±3.787	12.930±3.814	6.9	−0.24
Yield factor-of-risk	0.858±0.328	0.771±0.240	0.950±0.380	−18.9	0.75***
Cortical plastic volume (%)	11.866±3.010	12.016±3.105	11.709±2.916	2.6	−0.1

^*p < 0.05,

^**p < 0.01,

^***p < 0.001

Analogously, the ORs were very similar for many variables (Table 2). The highest ORs were found for yield-based factor-of-risk (1.99; 95% CI,1.41–2.91), but almost equally high ORs resulted for other variables from the nonlinear µFE simulations such as yield energy (1.95; 95% CI, 1.41–2.77) and yield deformation (1.89; 95% CI, 1.39–2.63). Also important were factors describing the bone microstructure (SMI, 1.86; 95% CI, 1.37–2.59), density measures based on HRpQCT imaging such as radius trabecular volumetric BMD (vBMD) (1.86, 95% CI, 1.37–2.58), and some linear µFE simulations (e.g., linear factor-of-risk, 1.89, 95% CI, 1.37–2.69). The comparable performance was also reflected in the respective AUC values (Table 2).

Table 2.

Odds Ratios (OR) for Distal Forearm Fracture per SD Decrease in Key Variables

	OR (95% CI)	AUC
Stiffness	1.76 (1.30–2.44)	0.63
Yield deformation	1.89 (1.39–2.63)	0.66
Yield load	1.87 (1.37–2.64)	0.65
Yield energy	1.95 (1.41–2.77)	0.65
Yield slope	1.27 (0.96–1.70)	0.57
Yield factor-of-risk	1.99 (1.41–2.91)	0.65
Cortical plastic volume	0.90 (0.68–1.19)	0.49

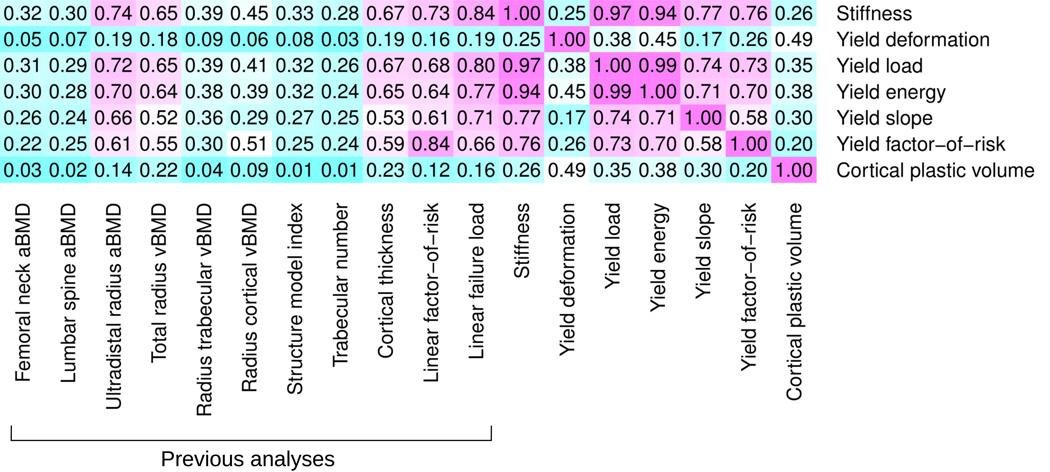
However, many of the variables were mutually correlated (Figure 1) and contained only a limited amount of independent information. In particular, yield load was highly correlated with bone stiffness (R² = 0.97). Also, yield energy was largely determined by initial stiffness (R² = 0.94). However, other variables, in particular yield deformation and the cortical plastic volume, correlated little with the other assessments of bone density, microstructure and mechanical performance.

Figure 1.

Mutual linear correlation between the variables analyzed in this study indicated as coefficients of determination (R²). Magenta indicates high correlation and cyan low correlation. In particular the yield deformation and the cortical plastic volume were independent of any other variable, including measurements from DXA, as well as bone density and microarchitecture from HRpQCT scans.

In a multivariate analysis starting with yield factor-of-risk, yield deformation was the best predictor of fracture risk. As a third and last factor, cortical plastic volume was able to provide significant independent information (Figure 2). All other variables were no longer significant. With the weights of the individual factors computed from the logistic regression and a normalization of the risk score to have a mean value of 0 and a standard deviation of 1, we arrived at the following model:

$$\text{RiskScore}=\frac{(-0.63·Y_{\text{FOR}}+0.78·Y_D-0.65·Ct.Pl.V)}{0.98},$$

where Y_FOR denotes the yield factor-of-risk, Y_D the yield deformation and Ct. Pl. V the cortical plastic volume at 1% deformation, with all factors normalized as z-scores.

Figure 2.

Large plastic regions in the cortical bone.

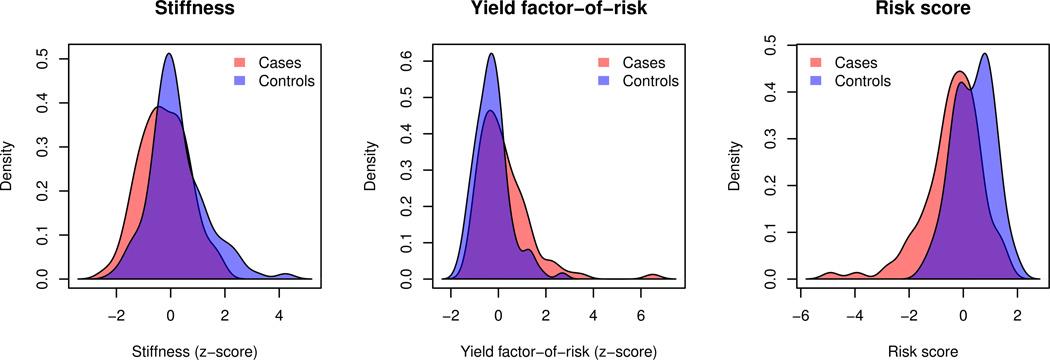
This risk score allowed a significantly more accurate estimation of the patient's risk for Colles' type distal forearm fractures compared to the yield-based factor-of-risk alone (p<0.05), as the odds ratio was increased by one third from 1.99 (95% CI, 1.41–2.91) to 2.66 (95% CI, 1.84–4.02) and the AUC from 0.65 to 0.71. The better separation of the fracture cases and controls was also reflected in the histograms of the stiffness, the yield factor-of-risk and the risk scores (Figure 3).

Figure 3.

Histograms of stiffness (left), yield factor-of-risk (center) and risk score (right) for forearm fracture cases and controls.

Discussion

In this first application of nonlinear µFE in a clinical study of distal forearm fracture risk, we found that nonlinear µFE provided important additional information on fracture risk that was not available from linear µFE or from other measures of bone microarchitecture, density and mass. The best individual variables from the nonlinear simulations were only marginally better predictors for fracture risk than the linear simulations and were similar to aBMD. However, a risk score combining information on the factor-of-risk computed from the yield load, the yield deformation and the cortical plastic volume yielded a significantly better estimation of the fracture risk than factor-of-risk alone.

These findings are in contrast to a previous study on the same subjects (14), which concluded that the fracture risk assessment based on DXA measurements could only marginally be improved upon by information on the bone microstructure. The OR for DXA-derived femoral neck aBMD (2.0; 95% CI, 1.4–2.8) reported in the previous study on the same dataset was marginally higher than the factor-of-risk based on the yield load. However, other studies have not found DXA measurements at the hip to be the best single predictor of distal radius fracture risk (11–13,30,31).

We found that yield load was highly correlated with stiffness, inferring that yield factor-of-risk can be approximated from stiffness. Furthermore, the energy absorbed before yield could also be approximated by stiffness. This was mostly because of the larger variability in stiffness and yield load compared to yield deformation, confirming experimental and computational studies (18,20,21,32–34). On the other hand, yield deformation was independent of all other variables analyzed in this and in the previous study (14). The assumption of a constant yield strain led to very small deviations in the yield deformation. However, these variations were due to the specific bone microarchitecture and geometry. Consequently, information on the ductility up to the onset of yielding can only be computed from nonlinear µFE and not derived from other techniques. In addition, cortical plastic volume was only slightly correlated with yield deformation and yield load.

The combined risk score linked information on yield factor-of-risk, yield deformation and cortical plastic volume and thereby allowed a significantly better discrimination of fracture cases from controls. The yield factor-of-risk measured bone strength in relation to the expected loads for a fall on the outstretched arm from standing height, with a higher factor-of-risk reflecting an increased risk of distal forearm fracture. In addition, yield deformation introduced information on the ductility of the bone, i.e., the risk of fracture was higher in bones that were only able to undergo little deformation before yielding. Lastly, the cortical plastic volume added information on the structural integrity of the bone under critical loads. At 1% compression, there were isolated and rather small regions of cortical bone loaded beyond elastic range in some bones, while in others large portions of the cortical bone were plastically deformed. Apparently, such large regions of cortical bone loaded beyond the yield stress impaired the mechanical stability of the bone and thereby increased the risk of distal forearm fractures. However, the cortical plastic volume was only significantly different in cases and controls when they were adjusted for yield deformation or yield deformation and yield factor-of-risk.

Furthermore, we assessed which of the techniques used in this and in the previous study (14) provided significant additional information independent of the other techniques. DXA measurements provided significant independent information. Also, nonlinear µFE simulations yielded important additional information that was not possible with any of the other techniques (p<0.001). On the other hand, bone microstructure and linear µFE analysis together did not contribute significantly when adjusted for DXA and nonlinear µFE. In case a choice can be made to perform either DXA or HRpQCT measurements on patients, our results suggest using HRpQCT, since the derived information on the bone microstructure (morphometry) and mechanical performance (nonlinear µFE) allow a better prediction of fracture risk for forearm fractures than DXA measurements alone.

The nonlinear µFE simulations, however, depend on the availability of the appropriate computational resources to be able to routinely obtain nonlinear µFE models in the clinical setting, which may soon be entirely feasible given the pace of developments in computing hardware. The current hardware requirements to conduct these simulations today (160 CPU cores, 160 GB of memory and a few hours to complete the simulations) necessitate a medium size computer cluster. While hardware performance is expected to keep increasing at the current rate, the costs of the computer hardware as well as the running costs are expected to decrease at a similar rate. Moreover, the presented workflow is fully automated and requires no user interaction. On the other hand, nonlinear µFE simulations can provide a basis to better understand the function of the bone microarchitecture under critical loads. Besides providing information on apparent mechanical properties, these simulations could also be used to investigate the local accumulation of plastic deformations at the microstructural level.

In this study, the elastic modulus of the individual elements was computed from the local density in the calibrated HRpQCT images. As a consequence, it was not necessary to segment the bone microstructure, which is very sensitive to partial volume effects due to the limited resolution of 82 µm. As in simulations on the segmented bone microstructure with a homogeneous elastic modulus, there is no consensus on the relationship between density and modulus (18). Essentially, there are two approaches: Either a relationship originally established for lower resolutions and FE models that are not resolving the microstructure is used (19), as in this study, or the relationship between density and elastic modulus is formulated only to compensate the partial volume effects as suggested by Homminga et al. (35). In the present study, µFE simulations with a density-derived elastic modulus yielded similar, but not identical, results compared to µFE on the segmented microstructure. We found a high correlation between the stiffness computed by linear FE on the segmented microstructure and a modulus computed from the local density. Furthermore, the results also differed in magnitude. The stiffness computed here was 40% higher than the stiffness computed previously with a homogeneous elastic modulus (15).

One of the limitations of this study was that the maximal load was not computed. Effectively, there were two reasons for this: Firstly, simulations up to the maximal load require considerably more computational resources since the computation time increases progressively with larger deformations. Secondly, simulations beyond the yield point would probably require more complex material models. The elastoplastic material model with a von Mises yield criterion used in this study has been able to approximate the onset of yielding, although the difference in yield strain in tension and compression is neglected (36,37). However, the von Mises yield criterion was defined to approximate the behavior of metals, and it is unlikely that plastic hardening in bone is independent of a volume change. Instead, for simulations of the post-yield behavior of bone, more realistic material models would be required that capture the effects of microdamage. Furthermore, the material model does not consider potential differences in the density relationship of cortical and trabecular bone and assumes a constant yield strain for all bone compartments and all patients. Moreover, very simplistic boundary conditions were used that resemble in vitro plate-to-plate compression tests, but not necessarily the loading during a fall on the outstretched arm. A further limitation is the fact that ORs may not be directly comparable between different studies (11,12,14,30,31), although the study designs were very similar and the measurement techniques were well standardized and shown to be highly reproducible (6,7). Possibly, the rather large variation in ORs reported in different studies is due to different inclusion and exclusion criteria or to inherent variations between different study populations. Finally, the results that we found in this cross-sectional study need to be tested in a prospective clinical study.

In conclusion, we found that nonlinear µFE simulations provided additional information on the risk of distal forearm fractures that was not accessible from linear µFE or from the other techniques assessing bone microstructure, density or mass. In terms of the individual predictors, the nonlinear simulations were only marginally better than the linear simulations and similar to aBMD. However, using a risk score including the factor-of-risk based on the yield load, yield deformation and the cortical plastic volume, we were able to significantly improve estimation of the fracture risk by one third compared to any single factor.