Polarisation Dynamics of Vector Soliton Molecules in Mode Locked Fibre Laser

Abstract

Two fundamental laser physics phenomena - dissipative soliton and polarisation of light are recently merged to the concept of vector dissipative soliton (VDS), viz. train of short pulses with specific state of polarisation (SOP) and shape defined by an interplay between anisotropy, gain/loss, dispersion, and nonlinearity. Emergence of VDSs is both of the fundamental scientific interest and is also a promising technique for control of dynamic SOPs important for numerous applications from nano-optics to high capacity fibre optic communications. Using specially designed and developed fast polarimeter, we present here the first experimental results on SOP evolution of vector soliton molecules with periodic polarisation switching between two and three SOPs and superposition of polarisation switching with SOP precessing. The underlying physics presents an interplay between linear and circular birefringence of a laser cavity along with light induced anisotropy caused by polarisation hole burning.

Soliton is a stable self-reinforcing solitary wave that maintains its shape while it travels and interacts with other solitons. This fundamental concept in mathematics and physics was firstly introduced by Norman Zabusky and Martin Kruskal in 1965 and since then has spread all around such fields of science as physics of plasma, optics, laser physics, biology, field theory, chemistry, hydrodynamics, and many other fields¹. In mode-locked lasers (MLLs), the concept of dissipative solitons (DS) is used to describe a train of short pulses with specific shape defined by a complex interplay and balance between the effects of gain/loss, dispersion, and nonlinearity¹,². With increased gain in active medium, the fundamental soliton becomes unstable and more complex waveforms can appear, viz. multi-pulsing³,⁴, harmonic mode locking⁵, bound states (BSs)¹,²,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸, and soliton rain¹,¹⁹. The bound states originate from balance of repulsive and attractive forces between solitons caused by Kerr nonlinearity and dispersion that can result in tightly BSs in terms of fixed and discrete separations and phase differences of 0, π, or ±π/2. The tightly BS solitons have been experimentally observed in nonlinear polarization rotation, figure-of-eight, carbon nanotubes (CNT) and graphene based mode locked fibre lasers⁸,⁹,¹⁰,¹¹,¹²,¹⁶,¹⁷,¹⁸. In addition, various types of different bound states have been studied theoretically and experimentally including vibrating bound states, oscillating bound states²,¹³, bound states with flipping and independently evolving phase¹⁴,¹⁵. Stable bound states – soliton molecules can be used for coding and transmission of information in high-level modulation formats when multiple bits are transmitted per clock period, increasing capacity of communication channels beyond binary coding limits²⁰,²¹,²²,²³,²⁴.

Recently, the vector nature of dissipative solitons has been exploited to reveal polarisation dynamics of DSs or so-called vector dissipative solitons (VDSs)⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³,³⁴.The stability of VDSs at the different time scales from femtosecond to microseconds is an important issue to be addressed for increased resolution in metrology³⁵, spectroscopy³⁶ and suppressed phase noise in high speed fibre optic communication³⁷. In addition, there is a considerable interest in achieving high flexibility in generation and control of the dynamic SOPs in the context of trapping and manipulation of atoms and nanoparticles³⁸,³⁹,⁴⁰, control of magnetization⁴¹, and secure communications⁴². In our previous publications we have already studied experimentally the conditions for emerging and suppression of VDSs for fundamental and multi-pulse regimes, viz. VDSs with SOPs locked, pulse-to-pulse polarisation switched and cyclically evolving⁴,³³,³⁴. In this work we study for the first time SOP dynamics for vector dissipative soliton molecules. Among the aforementioned applications of controllable SOP dynamics, vector soliton molecules are of a special high interest for telecommunications applications in the context of increased capacity in fibre optic telecommunications based on polarisation division multiplexing (PDM) quadrature phase shift keying (PDM-QPSK), polarisation switched QPSK (PSQPSK)⁴³, and modified coded hybrid subscriber/amplitude/phase/polarisation (H-SAPP) modulation schemes⁴⁴.

In this paper, we present the first experimental results on SOP evolution of tightly BSs – vector soliton molecules with fixed delay and phase differences of π/2 and π along with interleaved BSs with phase differences π/2 and π. Unlike polarisation dynamics of vector solitons on the Poincaré sphere demonstrated by Akhmediev, Soto-Crespo²⁶ and Komarov et al.⁴⁵, we study experimentally how polarisation hole burning in an active medium⁴⁶,⁴⁷,⁴⁸,⁴⁹ contributes to the polarisation dynamics. All results are obtained based on inline polarimeter (OFS TruePhase IPLM) optimised for high-speed operation⁵⁰,⁵¹,⁵².

Results

Tightly bound solitons – soliton molecules

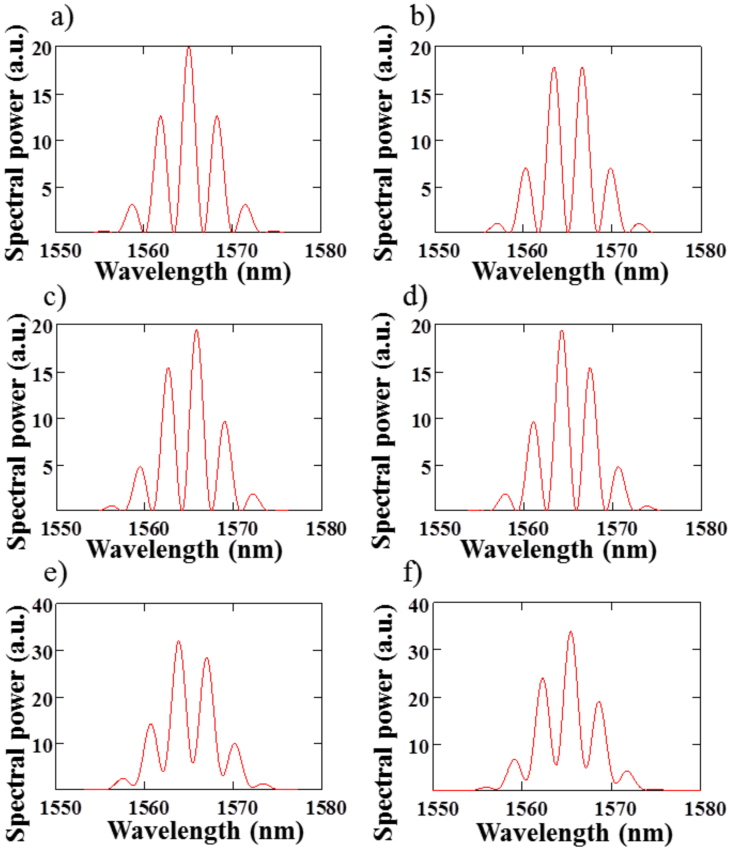
Bound state solitons pulse separation and a phase shift can be determined using optical spectra analysis. When two-soliton bound state has pulse separation τ and a phase shift φ, the amplitude of BS can be found as f(t) + f(t + τ)exp(iφ) and the corresponding optical spectrum can be presented as follows¹⁸:

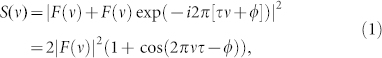Here F(ν) = FFT(f(t)). The results for different phase shifts are shown in Fig. 1 (a–d). As follows from Fig. 1(a–d), optical spectrum is modulated with the frequency Δν = 1/τ, symmetry of spectrum is phase shift dependent, and the spectral power in minima is close to zero. In some experiments a loss of contrast in the spectral fringes was associated with so-called vibrating solitons where pulse separation is oscillating¹³. However, when the MLL can support interleaving of two two-pulse bound states with different phase shifts (0 and −π/2 or π and π/2) based on harmonic mode locking at doubled frequency, the contrast of fringes is also reduced as shown in Fig. 1 (e, f). For MLLs with anomalous dispersion, pulse shape is a hyperbolic-secant-squared giving a time-bandwidth product of 0.315. So pulse width ΔT and pulse separation τ can be estimated from an optical spectrum as

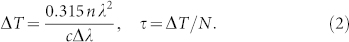Here n = 1.44 is a refractive index of silica fibre, λ is the central wavelength in optical spectrum, c is the speed of light, and N is the number of minima in optical spectrum. The obtained metrics will be used further to identify soliton molecules (tightly bound state solitons) in terms of pulse separation and phase shifts.

Figure 1. (a–d) Spectra of two-soliton bound states with phase shift of: (a) 0, (b) π, (c), −π/2, (d) π/2; (e, f) interleaving of two-soliton bound states with phase shifts of: (e) 0 and −π/2, (f) π and π/2.

Experimental setup and results

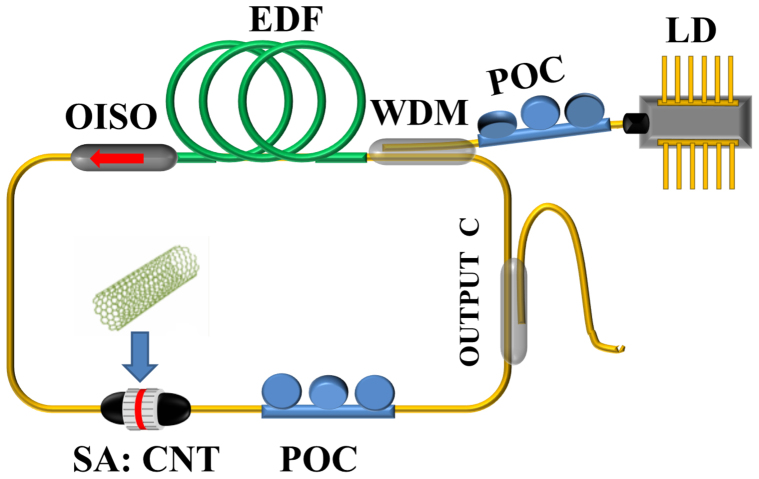
The ring cavity fibre laser (total cavity length of 7.83 m) shown in Fig. 2 includes high concentration erbium doped fibre (2 m of LIEKKI™ Er80-8/125), single mode (SM) fibre with anomalous dispersion, polarisation controllers (POCs), a wavelength division multiplexing (WDM) coupler, an optical isolator (OISO), a fast (370 fs relaxation time) saturable absorber in the form of carbon nanotubes (CNT) doped polymer film, and an output coupler. The cavity is pumped via 980/1550 WDM by a 976 nm laser diode (LD) with a maximum current of about 355 mA which provides 170 mW of optical power³³,³⁴. The laser output is analysed with the help of the optical spectrum analyser (ANDO AQ6317B) and the inline polarimeter (OFS TruePhase IPLM with resolution of 2 ns and the number of samples was 10 M)⁵¹,⁵². IPLM measured the normalized Stokes parameters s₁, s₂, s₃ and degree of polarization (DOP) which are related to the output powers of two linearly cross-polarized SOPs 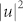and 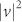, and phase difference between them Δφ as follows:

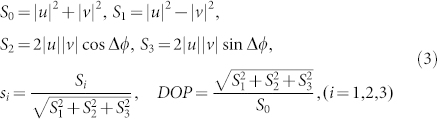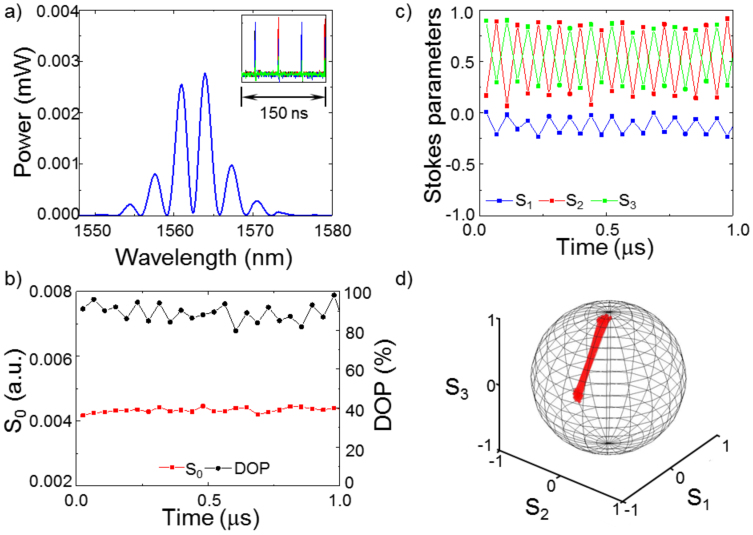
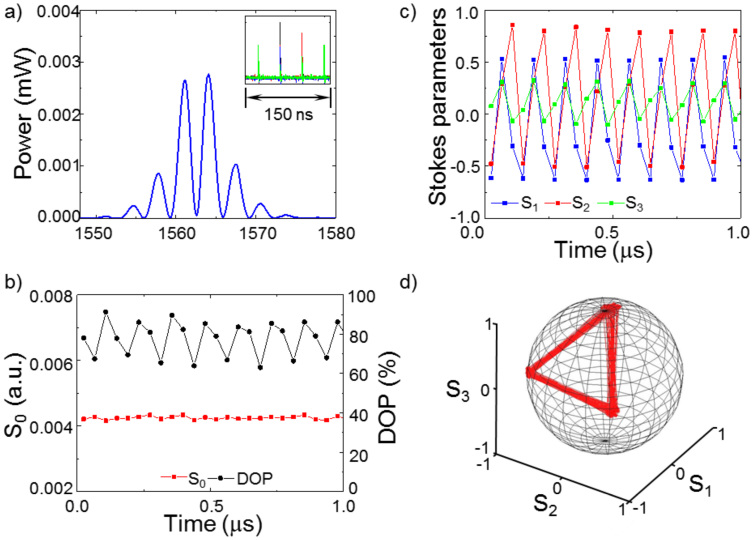
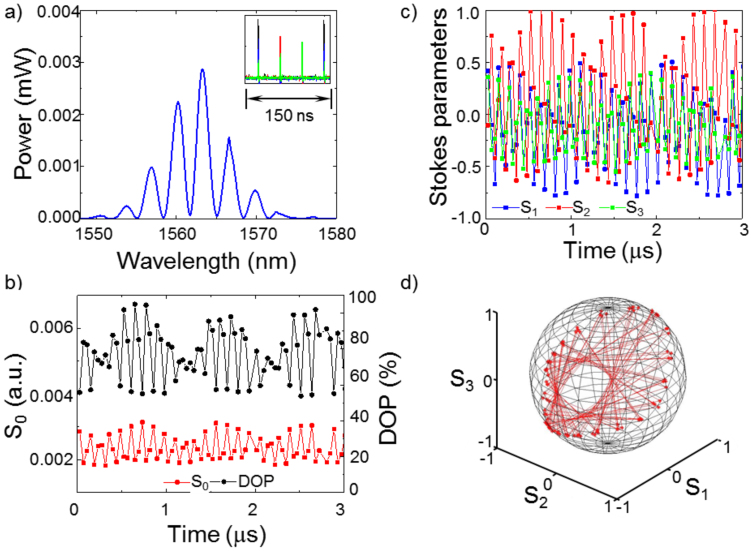
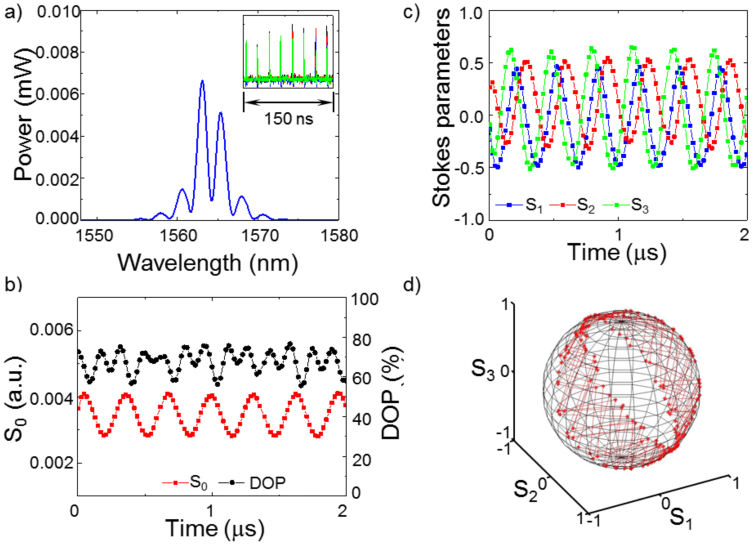
optimised for the high-speed operation; for further details see below in Methods. In this experiment, pump current was about 300 mA, and the in-cavity and pump polarisation controllers have been tuned to obtain the polarisation attractors shown in Figs. 3,4,5,6. Fig. 3(a) shows a spectrum of tightly two-pulse bound state soliton with phase shift of π according to Fig. 1 (b). The corresponding pulse train with the period of 38.9 ns is collected from four polarimeter detectors is shown in insert to Fig. 3 (a). The polarisation dynamics shown in Fig. 3(b–d) take the form of polarisation switching between two SOPs with period equal to two pulse round trips in the laser cavity. DOP oscillations around the value of 90% have also been observed (Fig. 3 (b)). In view of detector integration time (2 ns) being longer than the pulse separation (2 ps), high value of DOP indicates that bound solitons have the same SOP otherwise DOP will be close to zero for the case of orthogonal SOPs. The total laser power (S₀ in Fig. 3(b)) is constant within ±5% precision. Pulse width and pulse separation have been found from Fig. 3 (a) as 370 fs and 1.5 ps. Contrast of spectral fringes in Fig. 3 (a) is high and the pulse separation is less than five pulse widths, therefore BS is a tightly bound soliton with fixed phase shift and pulse separation⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸. Fig. 4 shows the other type of polarisation dynamics of bound state soliton. The spectrum in Fig. 4 (a) is similar to the previous one shown in Fig. 3(a) and so BS is a tightly bound soliton with fixed phase shift of π and pulse separation of 1.5 ps⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸. In this case, the variations of the total laser power were less than 5% (Fig. 4 (b)). DOP oscillates around the value of 80% with the period equal to three cavity round trips (Fig. 4 (b)). Stokes parameters s₁, s₂, s₃ oscillate with the lowest, intermediate and highest values corresponding to each of the localized SOPs shown in Fig. 4 (d). Spectra in Figs. 3 (a) and 4 (a) demonstrate the presence of slight asymmetry. It can be caused by hopping between π- and −π/2-shifted bound states that arises from changing the erbium gain spectrum under long-term fluctuations of ambient temperature¹⁸. High contrast of spectral fringes and small asymmetry of spectrum indicates that lifetime in π-shifted BS is much longer than lifetime in −π/2-shifted BS. Otherwise, the spectrum takes the form shown in Fig. 5 (a), i.e. it is close to the −π/2-shifted tightly BS with pulse width of 370 fs and pulse separation of 1.5 ps. Output power and DOP oscillations with two periods of 3 and 20 round trips as shown in Fig. 5 (b). SOP evolution takes the form of superposition of switching between three SOPs with a precession of these SOPs along a circle trajectory located on Poincaré sphere with the periods of 3 and 20 round trips (Fig. 5 (c, d)).

Figure 2. Erbium doped fiber laser mode-locked with carbon nanotubes.

A ring cavity fibre laser comprises high concentration erbium doped fibre (EDF), polarisation controllers (POCs), wavelength division multiplexing (WDM) coupler, optical isolator (OISO) to provide unidirectional lasing, saturable absorber in the polymer film with carbon nanotubes (SA: CNT), and output coupler (OUTPUT C). The cavity is pumped via 980/1550 WDM by 976 nm laser diode (LD). Output lasing has been analysed with an optical spectrum analyser (OSA), and in-line polarimeter (IPLM). The resolution of IPM was 2 ns and the number of samples was 10 M.

Figure 3. Polarisation dynamics of bound state soliton in the form of polarisation switching between two SOPs.

(a) Output optical spectrum indicates π shift bound state with 370 fs pulse width and 1.5 ps pulse separation; inset: pulse train with period of 40 ns collected from four polarimeter photodetectors; (b) total optical power (red squares) and DOP (black circles); (d) Stokes parameters on the Poincaré sphere. Each point in Fig. (b)–(d) corresponds to a single laser pulse.

Figure 4. Polarisation dynamics of bound state soliton in the form of polarisation switching between three SOPs.

(a) Output optical spectrum indicates π shift bound state with 370 fs pulse width and 1.5 ps pulse separation; inset: pulse train with period of 40 ns collected from four polarimeter photodetectors; (b) total optical power (red squares) and DOP (black circles); (d) Stokes parameters on the Poincaré sphere. Each point in Fig. (b)–(d) corresponds to a single laser pulse.

Figure 5. Polarisation dynamics of bound state soliton in the form of superposition of polarisation switching between three SOPs and SOP precession.

(a) Output optical spectrum indicates −π/2 shift bound state with 370 fs pulse width and 1.5 ps pulse separation; inset: pulse train with period of 40 ns collected from four polarimeter photodetectors; (b) total optical power (red squares) and DOP (black circles); (d) Stokes parameters on the Poincaré sphere. Each point in Fig. (b)–(d) corresponds to a single laser pulse.

Figure 6. Polarisation dynamics of bound state soliton in the form of superposition pfpolarisation switching between two SOPs of two interleaved BSs and SOP precession.

(a) Output optical spectrum indicates interleaved BSs with phase shifts of π/2 and π, 740 fs pulse width and 1.5 ps pulse separation; inset: pulse train of harmonically mode locked operation with period of 20 ns collected from four polarimeter photodetectors; (b) total optical power (red squares) and DOP (black circles); (d) Stokes parameters on the Poincaré sphere. Each point in Fig. (b)–(d) corresponds to a single laser pulse.

There are two scenarios resulting in bound state with pulse width of 740 fs and pulse separation of 1.5 ps shown in Fig. 6 (a–d). The first one presents a harmonically mode locked vibrating BS with the period of half round trip (insert to Fig. 6 (a))¹³. As follows from Fig. 6 (a), insert and Fig. 1 (e), the second scenario is an interleaving of independent tightly bound states with phase shifts of π/2 and π resulting in the same type of harmonic mode locking. The SOPs of two interleaved BSs can be slightly different and so we observe superposition of the SOP switching with precession along the cyclic trajectory on the Poincaré sphere with the period of 14 round trips (Fig. 6 (c, d)).

Discussion

As shown by Akhmediev, Soto-Crespo²⁶ and Komarov et al.⁴⁵, the eigenstates for a fibre with the linear birefringence and circular birefringence can be found as follows (Fig. 7 (a)):

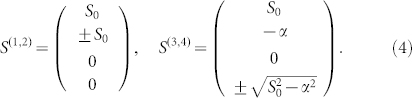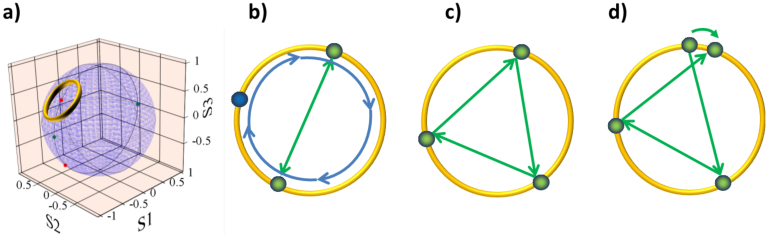
Here S₀ = const and α is determined by the ratio of linear to circular birefringence strength. In our case, the linear and circular birefringenceis are controlled by the in-cavity polarisation controller. The rate of excitation migration is very high in LIEKKI™ Er80-8/125 used herein due to the high concentration of erbium ions and so the anisotropy induced by pump light is supressed⁴⁶,⁴⁷. Polarisation hole burning⁴⁶,⁴⁷,⁴⁸,⁴⁹ changes the active medium anisotropy (both linear and circular) and so pulse SOP is located on a circle as shown in Fig. 7 (a). If pulse-to-pulse power is constant and the beat length in the anisotropic cavity is equal to the round trip distance then the pulse SOP is fixed and so vector soliton is polarisation locked³³,³⁴ (Fig. 7 (b)). In the case of round trip distance being equal to half or third of beat length, the SOP is reproduced in two (Fig. 7 (b)) or three (Fig. 7 (c)) round trips; therefore, polarisation switching takes the forms shown in Figs. 3 (d) and 4 (d). The depth of the hole in the orientational distribution of inversion is proportional to the laser power and so with periodic oscillations of the output power (Fig. 5 (b)) light induced anisotropy in an active medium will be periodically modulated⁴⁶,⁴⁷,⁴⁸,⁴⁹. In this case, if the round trip is equal to the one third of beat length then SOP after three round trips will deviate slightly from the initial one as shown in Figs. 5 (d) and 7 (d) and can be reproduced only for the period of pulse power oscillations (Fig. 5 (d)). The same holds true for the case of two interleaved BSs with slightly different SOPs that results in superposition of the SOP switching with precession along the cyclic trajectory on the Poincaré sphere with the period of 14 round trips (Fig. 6 (c, d)).

Figure 7. Pulse-to-pulse evolution of states of polarisation in the mode locked laser cavity.

(a) green and red points corresponds to eigenstates of anisotropic cavity, circle is a trajectory of SOP evolution; (b) round trip is equal to the beat length (blue circle) and a half of beat length (green circles); (c) round trip is equal to one third of beat length (green circles); (d) pulse power is slowly oscillating and round trip is equal to one third of beat length (green circles).

Thus, optimisation of inline polarimeter (OFS TruePhase IPLM) for the high-speed pulse-to-pulse SOP measurements operation allowed us to reveal new types of vector soliton molecules shown in Figs. 3–6. By unveiling the origin of new types of unique states of polarisation evolving on very complex trajectories, our experimental studies can find applications in the context of design of new types of lasers with controlled dynamical states of polarisation and increased capacity in fibre optic telecommunications based on polarisation division multiplexing (PDM) quadrature phase shift keying (PDM-QPSK), polarisation switched QPSK (PSQPSK)⁴³, and modified coded hybrid subscriber/amplitude/phase/polarisation (H-SAPP) modulation schemes⁴⁴. The obtained results can also find applications in nano-optics (trapping and manipulation of nanoparticle and atoms¹⁷,¹⁸,¹⁹), and spintronics (vector control of magnetization²⁵).

Methods

Polarimeter principle of operation and design

Conceptually, the most straight forward solution for polarimetry is to measure Stokes vector directly [P, P_h-P_v, P₄₅-P₁₃₅, P_r-P_l], where P is the total signal power and P_h, P_v, P₄₅, P₁₃₅, P_r, P_l are powers measured after ideal horizontal, vertical, 45, 135, right circular, left circular polarizers respectively. However, the practical realization is difficult as a large number of high quality polarizers and waveplates are required⁵⁰.

An alternative solution is to use 4 polarisation sensitive detectors to measure the light in the direction of 4 non-coplanar Stokes vectors, ideally forming a tetrahedron⁵¹,⁵². Then, the Stokes vector S can be calculated by multiplying a 4 × 4 calibration matrix C to the 4 × 1 detector vector D

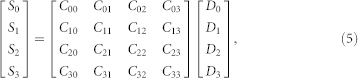where C_ij are the elements of the calibration matrix, S_i are the Stokes parameters and D_i are the powers measured by each detector. This approach requires no moving parts and minimizes the number of required detectors. This configuration was realized in the OFS TruePhase IPLM polarimeter⁵¹,⁵².

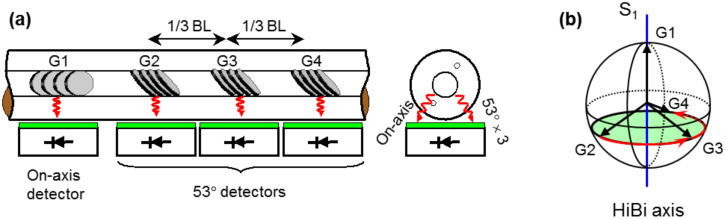
The schematic diagram of IPLM polarimeter and its principle of operation are shown in Fig. 8 (a) and (b) respectively. Four fibre Bragg gratings are written in the core of OFS TruePhase polarisation maintaining (HiBi) fibre. The gratings have a 45° blaze angle with respect to the fibre axis. The longitudinal period of the grating along the fibre is roughly 1.07 μm so that core light at 1.55 μm is phase matched to orthogonally scattered light. The 45° blaze angle ensures a highly directional orthogonal scattering with the maximum strength. The orthogonal scattering geometry also provides the polarisation sensitivity. As the induced dipoles are aligned orthogonally to the scattering direction, the strength of the light polarized parallel to the plane of scatter is minimal. Since the interaction length between the intra-core light and the orthogonally propagating light is on the order of the core diameter, the scattering is insensitive to wavelength over tens of nanometers. Hence, these gratings act as broadband, highly polarisation sensitive optical taps with the intensity of the scattered light proportional to a projection of the signal polarisation onto the polarisation state defined by the grating.

Figure 8.

(a) Schematic diagram of the IPLM polarimeter. (b) Principle of operation of the device.

The first grating is aligned to the HiBi axis of the fibre (the on-axis grating) and 3 other gratings are rotated by 53° with respect to the HiBi axis (the off-axis gratings). The distance between on-axis and off-axis gratings is arbitrary, however it should be minimized in order to reduce the overall birefringence of the device. The separation between 3 off-axis gratings is 1/3 of the fibre beat length (4.8 mm/3 in this case). The 53° rotation between gratings result in 106° angle in Stokes space between the light scattered by the on-axis and the off-axis gratings. The separation between the off-axis gratings of 1/3 of the beat length results in 120° angular rotation about the HiBi axis in Stokes space. Thus, the on-axis grating scatters linearly vertically polarized light and the off-axis gratings project the light onto the circle parallel to the equator with the 120° separation between the light scattered by each of the off-axis gratings, forming a tetrahedron in the Stokes space as shown in Fig. 8b. This configuration gives the best noise performance of the polarimeter and also results in the lowest PDL of the device⁵¹. In this polarimeter all gratings are 300 μm long and have strength of approximately 1% and the bandwidth of more than 200 nm. The fibre was glued on top of 4 InP 300 μm wide photodetectors using index matching epoxy. The device has an insertion loss of less than 0.5 dB and polarisation dependent loss (PDL) less than 0.1 dB. The detectors and grating assembly (polarimeter optical head) is packaged in a high-speed package with SMA connectors for each detector. The photodiode biasing circuit was optimised to obtain the maximal electrical bandwidth of the device, which was characterized using a lightwave network analyser by launching modulated light and measuring the frequency response of each detector. The resultant 3 dB electrical bandwidth was 550 MHz with a variation of bandwidth from detector to detector of ±20 MHz and a frequency response difference less than 0.7 dB corresponding to a maximum frequency dependent degree of polarisation (DOP) error of around ±4%.

As discussed earlier, in order to convert detectors values into Stokes vector components, a 4 × 4 calibration matrix is required. One way to compute a polarimeter calibration matrix is to launch 4 known non-degenerate SOPs and compute the C matrix as:

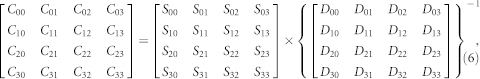where C_ij are the elements of the calibration matrix, S_ij are the Stokes vectors and D_ij are the measured scattered powers. Although, this technique is relatively simple and robust, it requires another calibrated reference polarimeter or generator of known SOPs, i.e. referenced procedure. A more attractive alternative is a reference-free calibration procedure. Such a calibration procedure relies on the imposition of a constraint on the input signals used to perform the calibration. The simplest and most robust constraint is to use signals with DOP = 1. This condition is relatively easy to verify in narrow linewidth lasers and can be transported over long lengths of fibre without significant degradation. The calibration matrix of the polarimeter is then adjusted so that measurements made at the polarimeter match the constraint on the input polarisations. While this procedure can be effective, a more accurate calibration may be obtained if power is also measured. The reference-free calibration procedure requires several polarisation states to be launched into the device. For each of these, the detector values D_ij and power P_j are measured, so, the 4 × N matrix of detector values and N power values are obtained. The calibration then has two steps. Firstly, the top row of the calibration matrix is fit to the measured power data P_j. The power is the same as S₀ and is determined by the top row of the calibration matrix.

Thus, the first row C_0n must be adjusted to minimize

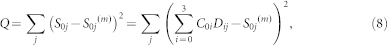where 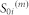are the measured power values. The elements of the first row of C can then be computed through a matrix multiplication:

where

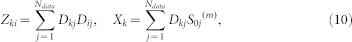where N_data is the total number of data points.

At this stage the first row of the calibration matrix is determined and will be treated as a constant. It contains the power scaling factors relating the detector voltages to the measured power. It also reflects any residual PDL in the optical path between the detectors and the power measurement. The lower 12 elements of C are then adjusted to minimize the DOP difference for all calibration SOPs. This can be accomplished with a nonlinear least squares fitting routine that minimizes Q:

Q is related to (DOP² − 1)² and is an internal metric of the accuracy of the calibration.

Since this is a nonlinear least squares fit, it is useful to obtain an appropriate first guess that is as accurate as possible. For this purpose, the ideal calibration matrix for a polarimeter that measures projections onto a tetrahedron on the Poincare sphere is used. This matrix assumes perfect polarizers and unity gains:

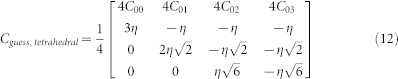where η is an average scale factor equal to the average of the first row.

The resulting solution for C is still degenerate under Stokes rotations. However, such rotations are not important for measurement of power, DOP and differential changes of the SOP. If an absolute reference is required, it may be obtained in several ways. One of the simplest references is to adjust the HiBi axis of our polarimeter fibre, as detector number one is on-axis and represents a projection onto S₁.

To measure fast changes of the SOP of the laser, four detector voltages were recorded simultaneously using an oscilloscope (Tektronix DPO7254). The data collected from the oscilloscope was filtered with a Hanning filter and the Stokes parameters were calculated for each laser pulse.

Author Contributions

S.V.S. initialised work and made a major contribution to the interpretation of results and manuscript writing; V.M., B.R. and P.S.W. contributed to the description of fast polarimeter; V. Ts. made experiments with polarimeter, Ch. Mou developed a mode locked laser; CNT films has been manufactured by A.R.; S.K.T. participated in the analysis and interpretation of the results; all authors contributed to the manuscript writing and reviewed the manuscript.