Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 6;3:3150. doi: 10.1038/srep03150

Surface Hall Effect and Nonlocal Transport in SmB6: Evidence for Surface Conduction

D J Kim 1,2, S Thomas 1,2, T Grant 1, J Botimer 1, Z Fisk 1, Jing Xia 1,a
PMCID: PMC3818682  PMID: 24193196

Abstract

A topological insulator (TI) is an unusual quantum state in which the insulating bulk is topologically distinct from vacuum, resulting in a unique metallic surface that is robust against time-reversal invariant perturbations. The surface transport, however, remains difficult to isolate from the bulk conduction in most existing TI crystals (particularly Bi2Se3, Bi2Te3 and Sb2Te3) due to impurity caused bulk conduction. We report in large crystals of topological Kondo insulator (TKI) candidate material SmB6 the thickness-independent surface Hall effects and non-local transport, which persist after various surface perturbations. These results serve as proof that at low temperatures SmB6 has a metallic surface that surrounds an insulating bulk, paving the way for transport studies of the surface state in this proposed TKI material.

Recently discovered1,2,3,4,5,6,7 three-dimensional (3D) topological insulators (TI) have generated great excitement. Strong spin-orbit coupling in a TI gives rise to a non-trivial and robust conducting surface state4,5, reminiscent of the edge channel8,9 found in quantum Hall (QH)10,11 and quantum spin Hall (QSH)12,13 states. However, such surface transport properties have remained challenging to separate from residual bulk impurity conduction14,15,16,17 despite rapid recent improvements7,18,19,20,21, promoting us to search for TI materials with better bulk insulation. More importantly, most theoretical and experimental efforts to date have been dedicated to materials with the underlying physics of non-interacting electrons1,4,5,12. A big question thus concerns the role of electron interaction and competing orders in new TI materials with strong correlation, from which new types of topological phases are expected to emerge4,5.

Recent seminal theoretical works22,23 have predicted in the strongly correlated material SmB6 the existence of a topological insulator phase: topological Kondo insulator (TKI). SmB6 is a heavy fermion material first studied 40 years ago24. In SmB6, highly renormalized f-electrons hybridize with conduction electrons and form a completely filled band of quasiparticles with a transport excitation gap Δ of about 40 Kelvin. However, its many exotic properties25,26,27 still defy a satisfactory understanding within the framework of conventional insulators. One of these mysteries is the peculiar residual conduction at the lowest temperatures. Behaving electronically like an insulator at high temperatures, at low temperature its resistance mysteriously saturates: a curiosity that is usually attributed to the existence of density of states within the band gap. According to the recent TKI theory22,23,28,29, the hybridization and odd parity wavefunction lead to strong spin-orbit coupling in SmB6 and give rise to a topological surface state, which naturally explains the origin of the in-gap state and pinpoints its location to be on the surface of SmB6. Our recent capacitance measurements on high quality SmB6 crystals revealed intriguing anomalous capacitance effects30 that could be explained by assuming the in-gap-states exist on the surface. In this paper we present evidence of thickness-independent surface Hall effect and nonlocal transport in high quality SmB6 crystals of various geometries and from different growth batches. These results reveal in SmB6 an insulating bulk and a conducting surface.

Results

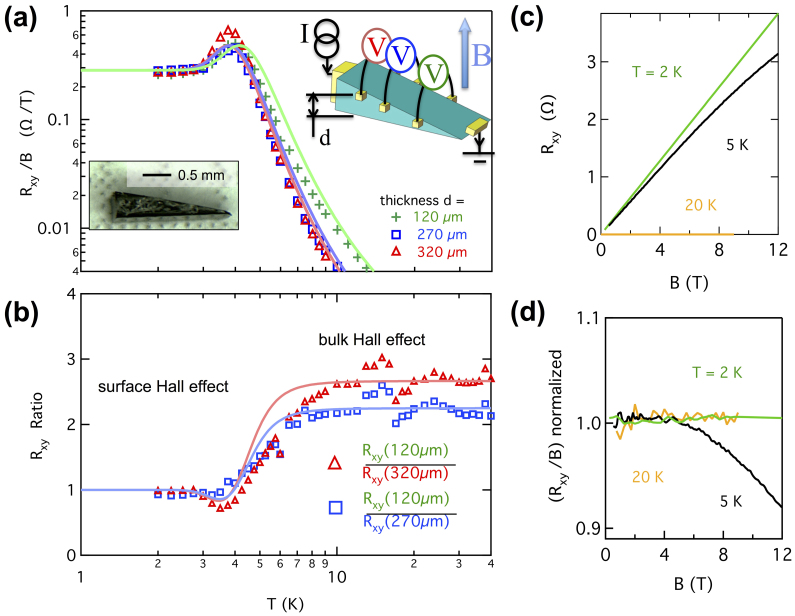
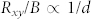Hall effect measurements were carried out in wedge-shaped SmB6 crystals. As depicted in the inset in Fig. 1(a), the sample is placed in a perpendicular magnetic field Inline graphic and current I flows between the two ends of the wedge. The Hall resistances Rxy = Vxy/I are measured at different thicknesses d to distinguish between surface and bulk conduction. For bulk conductionInline graphic, while Rxy/B is d-independent if surface conduction dominates. In both cases, one can define a Hall coefficient RH = Ey/jxB independent of B, where jx is the current density (surface or bulk) and Ey is the transverse electric field. The Hall voltage Vxy is found to be linear with B (Fig. 1(c) (d)) at small fields at all temperatures, but becomes significantly nonlinear for larger fields around 5 K, indicating a temperature regime of multichannel conduction. At high (20 K) or low (2 K) temperatures, the extreme linearity of the Hall effect indicates single channel conduction, either from the bulk or surface. For the simplest case of one surface conduction channel (top and bottom surfaces combined) and one bulk channel with Hall coefficients RHS, RHB and resistivity ρS, ρB respectively, the Hall resistance Rxy at magnetic field B is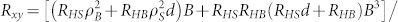 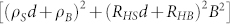Inline graphic Inline graphic. Nonlinearity is expected at large B, but at small fields it simplifies to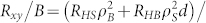 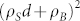Inline graphic Inline graphic, which indeed gives thickness-independent Rxy/B = RHS if the surface channel dominates (i.e. ρB ≫ ρSd). From B < 1 T data we extract the value Rxy/B at various temperatures T. Representative results in sample S1 are plotted in Fig. 1(a) for d = 120, 270, and 320 μm respectively, showing clearly that while at high temperatures Rxy/B differ at different d, they converge to a same universal value of 0.3 Ω/T below 4 Kelvin, consistent with surface conduction. Since more than one surface channels may exist, as predicted by theory28,29, it is difficult to quantitatively extract the surface carrier density and mobility at this stage. Replotting the Hall resistance ratios Rxy(d1)/Rxy(d2) in Fig. 1(b), we found these ratios to be equal to d2/d1 at high T and become unity at low T, proving the crossover from 3D to 2D Hall effects when T is lowered. The temperature dependence is well described by a two-channel (bulk and surface) conduction model in which the bulk carrier density decreases exponentially with temperature with an activation gap Δ = 38 K. Using this simple model, we could reproduce the curious “peak” in Rxy/B at 4 K (solid lines in Fig. 1(a)), which lacks31 a good explanation until now. Low temperature surface-dominated conduction would also give rise to a longitudinal resistance Rxx that is independent of sample thickness, which we have demonstrated recently32.

Figure 1. Surface Hall effect.

Figure 1

Open in a new tab

(a), Markers, Hall resistances Rxy divided by magnetic field B versus temperature T at three different thicknesses d in a wedge shaped sample S1. Lines are simulations using a two conduction channel model (see text). Left inset, picture of the crystal before wiring. Right inset, measurement schematic. (b), Markers, ratios between Hall resistances Rxy at different d, showing the transition from bulk to surface conduction as temperature is lowered. Lines are calculated from simulations as in (a). (c), Rxy versus B at various T for d = 120 μm, showing nonlinearity at around 5 K. (d), Rxy/B normalized to small field values to demonstrate the nonlinearity.

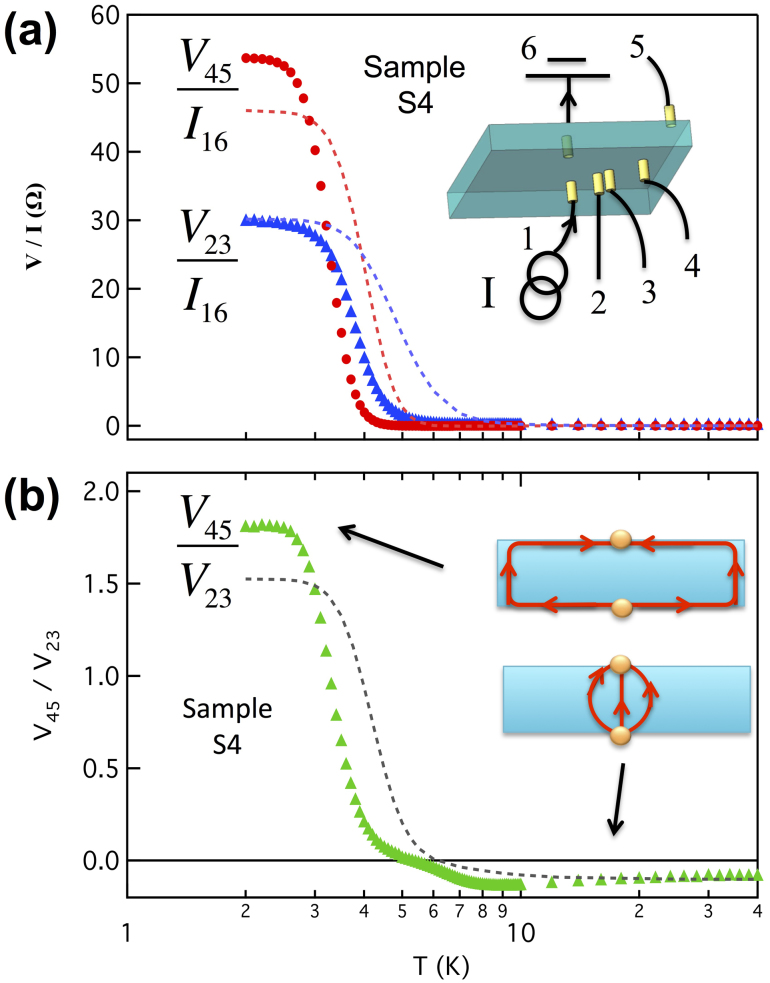
Surface dominated conduction could also be demonstrated at zero magnetic field with so-called “non-local” transport in the spirit of nonlocal transport experiments performed in QH10,11 and QSH12,13 states that have served as evidence8,9 for the existence of the topological edge states that are one-dimensional analogues to the surface state in a TI. The highly metallic surface conduction in a TI would necessarily invalidate Ohm's law and introduce large nonlocal voltages, which we have indeed found in SmB6 samples. Fig. 2(a) shows a schematic of the nonlocal measurement in sample S4. Current I16 flows between current leads 1 and 6 at the center on opposite faces of the crystal. Contacts 2 and 3 are located close to contact 1 for the detection of “local” voltage V23. Contacts 4 and 5 are put near the sample edge far away from the current leads to detect “nonlocal” voltage V45. As shown in the inset in Fig. 2(b), in the case of bulk conduction, current will concentrate in the bulk near the current leads 1 and 6, resulting in negligibly small nonlocal voltage (V45 ≪ V23). If surface conduction dominates, however, current will be forced to flow between contacts 1 and 6 via the surface, making V45 larger. Fig. 2(a) shows as a function of temperature the measured V45 and V23 divided by I16, both agreeing qualitatively with our finite element simulations (Supplementary Information) incorporating the aforementioned simple model. The ratio V45/V23 is replotted in Fig. 2(b). At low temperature, when surface conduction dominates, the nonlocal voltage V45 becomes large and even surpasses the local voltage V23. Above T = 5 K, when bulk conduction dominates, the magnitude of V45/V23 is very small. The negative sign of V45/V23 is due to the small misalignment of contacts (Supplementary Information). The change of both magnitude and sign of V45/V23 is reproduced by our simulation and highlights the distinction between high T bulk conduction and low T surface conduction.

Figure 2. Nonlocal transport due to surface conduction.

Figure 2

Open in a new tab

(a), Markers, nonlocal resistance V45/I16 and local resistance V23/I16 versus temperature T. Dashed lines are finite element simulations. Inset is a schematic of the measurement configuration on sample S4. (b), Ratio between nonlocal and local voltages V45/V23 versus T. Dashed lines are finite element simulations. Inset, cartoons for current distribution in sample cross-section for surface and bulk dominated conductions.

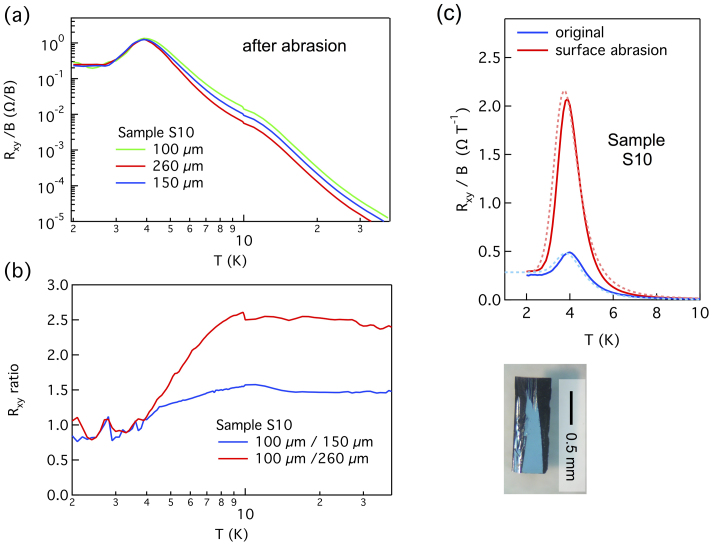
An important aspect of TI is the topological protection of the surface state against time-reversal invariant perturbations. The robustness against perturbation distinguishes a topological surface state from “accidental” surface conduction4,5. We found that the above surface Hall effect and nonlocal transport are recurrent phenomena in various samples and persist after chemical and mechanical sample treatments. We have mechanically cut and scratched the surface of sample S10 (Fig. 3 inset) and performed Hall measurements before and after surface abrasion. We found that the low temperature Hall resistance Rxy/B remained unchanged (Fig. 3(c)), indicating that the surface carrier density nS was not affected by abrasion. The abrasion does reduce the surface mobility μS though, as reflected by the height of Rxy/B “peak” at T = 4 K, presumably due to greatly enhanced geometric roughness. As shown in Fig. 3 (a) (b), the surface dominated conduction persists after abrasion, as demonstrated by the thickness-independent Hall effect below 4 K.

Figure 3. Surface conduction after surface treatments.

Figure 3

Open in a new tab

(a), Markers, Hall resistances Rxy divided by magnetic field B versus temperature T at three different thicknesses d in a wedge shaped sample S10, after intentional chemical etching and cutting. (b), Markers, ratios between Hall resistances Rxy at different d, showing the transition from bulk to surface conduction as temperature is lowered. (c), Solid lines, Hall resistance Rxy divided by magnetic field B versus temperature T, before and after surface abrasion. Dashed lines are simulations assuming abrasion only reduces the effective surface mobility μS. Inset, picture of sample S10 during abrasion.

Discussion

The experimental identification of thickness-independent surface Hall effect and nonlocal transport serve as strong evidence that SmB6 has a metallic surface state surrounding an insulating bulk at low temperatures. The characterization of energetics of the surface state and hence direct tests of the topological nature, however, awaits future investigations using energy and spin resolved techniques like ARPES2,3 and STM33,34. Recent ARPES35,36,37, quantum oscillation38 and STM measurements39 have provided further evidence of surface conduction, as well as insights of the surface electronic structure. Recent transport measurements with doped SmB6 samples32 have demonstrated that the surface conduction persists after non-magnetic doping but is destroyed by magnetic doping, as expected from a topological surface state protected by time-reversal-symmetry. Transport experiments40 at lower temperatures have revealed the weak-anti-localization effect, which is expected from a spin-momentum-locked topological surface state. Unlike weakly interacting TI materials, the strong electron correlation in SmB6 could give rise to exotic emergent phases4,5 with exciting new physics.

Note added: During initial submission of the manuscript, we became aware of a related work41 in which evidence for surface conduction was provided in a SmB6 sample with contacts arranged in a unique configuration, and a point contact measurement42 that excludes the possibility that the in-gap state is located in the bulk of SmB6.

Methods

High quality SmB6 crystals were grown using the aluminium flux method. The surfaces of these crystals were carefully etched using hydrochloric acid and then cleaned using solvents to remove possible oxide layer or aluminium residues. These crystals are then inspected using X-ray analysis to make sure SmB6 is the only content. Samples used in the experiments were made from these crystals either by mechanical cleaving or polishing using polishing films containing diamond particles. The exposed surfaces are (100) planes. Gold and platinum wires are attached to the samples using micro spot welding and/or silver epoxy, with no discernable differences in measurements. Low frequency transport measurements were carried out in dilution fridges and helium cryostats using either standard low frequency (37 Hz) lock-in techniques with 50 nA excitation currents or with a resistance bridge.

Author Contributions

J.X. conceived the project. D.J.K., T.G. and Z.F. grew the crystals. D.J.K., S.T., J.B., and J.X. fabricated the samples and performed the measurements. T.G. performed X-ray analysis of the crystals. S.T. and J.X. performed the simulations. All authors analysed the data and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplemental information

srep03150-s1.pdf (3.3MB, pdf)

Acknowledgments

We thank T.H. Geballe and A. Kapitulnik for useful discussions. This work was supported by UC Irvine CORCL Grant MIIG-2011-12-8, Sloan Research Fellowship #BR2013-116 (J. X.). Crystal growth was supported by NSF grant #DMR-0801253.

References

  1. Fu L. & Kane C. L. Topological insulators with inversion symmetry. Phys. Rev. B. 76, 045302 (2007). [Google Scholar]
  2. Hsieh D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008). [DOI] [PubMed] [Google Scholar]
  3. Chen Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009). [DOI] [PubMed] [Google Scholar]
  4. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  5. Hasan M. & Kane C. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  6. Roy R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B. 79, 195322 (2009). [Google Scholar]
  7. Brune C. et al. Quantum Hall effect from the topological surface states of strained bulk HgTe. Phys. Rev. Lett. 106, 126803 (2011). [DOI] [PubMed] [Google Scholar]
  8. McEuen P. et al. New resistivity for high-mobility quantum Hall conductors. Phys. Rev. Lett. 64, 2062–2065 (1990). [DOI] [PubMed] [Google Scholar]
  9. Roth A. et al. Nonlocal transport in the quantum spin Hall state. Science 325, 294–297 (2009). [DOI] [PubMed] [Google Scholar]
  10. Klitzing von K., DORDA G. & Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980). [Google Scholar]
  11. Tsui D. C., Stormer H. L. & Gossard A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982). [Google Scholar]
  12. Bernevig B. A., Hughes T. L. & Zhang S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006). [DOI] [PubMed] [Google Scholar]
  13. Koenig M. et al. Quantum spin hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007). [DOI] [PubMed] [Google Scholar]
  14. Peng H. et al. Aharonov-Bohm interference in topological insulator nanoribbons. Nat. Mater. 9, 225–229 (2009). [DOI] [PubMed] [Google Scholar]
  15. Checkelsky J., Hor Y., Cava R. & Ong N. Bulk band gap and surface state conduction observed in voltage-tuned crystals of the topological insulator Bi2Se3. Phys. Rev. Lett. 106, 196801 (2011). [DOI] [PubMed] [Google Scholar]
  16. Analytis J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nat. Phys. 6, 960–964 (2010). [Google Scholar]
  17. Taskin A. & Ando Y. Quantum oscillations in a topological insulator Bi1−xSbx. Phys. Rev. B. 80, 085303 (2009). [Google Scholar]
  18. Ren Z., Taskin A. A., Sasaki S., Segawa K. & Ando Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B. 82, 241306 (2010). [Google Scholar]
  19. Jia S. et al. Low-carrier-concentration crystals of the topological insulator Bi2Te2Se. Phys. Rev. B. 84, 235206 (2011). [Google Scholar]
  20. Xiong J. et al. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity. Physica E 44, 917–920 (2012). [Google Scholar]
  21. Xiong J. et al. High-field Shubnikov-de Haas oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B. 86, 045314 (2012). [Google Scholar]
  22. Dzero M., Sun K., Galitski V. & Coleman P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010). [DOI] [PubMed] [Google Scholar]
  23. Dzero M., Sun K., Coleman P. & Galitski V. Theory of topological Kondo insulators. Phys. Rev. B. 85, 045130 (2012). [DOI] [PubMed] [Google Scholar]
  24. Menth A., Buehler E. & Geballe T. Magnetic and semiconducting properties of SmB6. Phys. Rev. Lett. 22, 295–297 (1969). [Google Scholar]
  25. Nickerson J. et al. Physical properties of SmB6. Phys. Rev. B. 3, 2030–2042 (1971). [Google Scholar]
  26. Barla A. et al. High-pressure ground state of SmB6: electronic conduction and long range magnetic order. Phys. Rev. Lett. 94, 166401 (2005). [DOI] [PubMed] [Google Scholar]
  27. Derr J. et al. From unconventional insulating behavior towards conventional magnetism in the intermediate-valence compound SmB6. Phys. Rev. B. 77, 193107 (2008). [Google Scholar]
  28. Lu F., Zhao J., Weng H., Fang Z. & Dai X. Correlated topological insulators with mixed valence. Phys. Rev. Lett. 110, 096401 (2013). [DOI] [PubMed] [Google Scholar]
  29. Alexandrov V., Dzero M. & Coleman P. Cubic topological Kondo insulators. arXiv:1303.7224 (2013). [DOI] [PubMed] [Google Scholar]
  30. Kim D., Grant T. & Fisk Z. Limit cycle and anomalous capacitance in the Kondo insulator SmB6. Phys. Rev. Lett. 109, 096601 (2012). [DOI] [PubMed] [Google Scholar]
  31. Cooley J., Aronson M., Fisk Z. & Canfield P. SmB6: Kondo insulator or exotic metal? Phys. Rev. Lett. 74, 1629–1632 (1995). [DOI] [PubMed] [Google Scholar]
  32. Kim D. J., Xia J. & Fisk Z. Topological surface state in the Kondo insulator samarium hexaboride. arXiv:1307.0448 (2013). [DOI] [PubMed] [Google Scholar]
  33. Alpichshev Z. et al. STM imaging of electronic waves on the surface of Bi2Te3: topologically protected surface states and hexagonal warping effects. Phys. Rev. Lett. 104 (2010). [DOI] [PubMed] [Google Scholar]
  34. Roushan P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009). [DOI] [PubMed] [Google Scholar]
  35. Neupane M. et al. Surface electronic structure of a topological Kondo insulator candidate SmB6: insights from high-resolution ARPES. arXiv:1306.3678 (2013). [DOI] [PubMed] [Google Scholar]
  36. Jiang J. et al. Observation of in-gap surface states in the Kondo insulator SmB6 by photoemission. arXiv:1306.5664 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Xu N. et al. Surface and bulk electronic structure of the strongly correlated system SmB6 and implications for a topological Kondo insulator. arXiv:1306.3678 (2013). [Google Scholar]
  38. Li G. et al. Quantum oscillations in Kondo insulator SmB6. arXiv:1306.5221 (2013). [Google Scholar]
  39. Yee M. M. et al. Imaging the Kondo insulating gap on SmB6. arXiv:1308.1085 (2013). [Google Scholar]
  40. Thomas S. et al. Weak antilocalization and linear magnetoresistance in the surface state of SmB. arXiv:1307.4133 (2013). [Google Scholar]
  41. Wolgast S. et al. Low temperature surface conduction in the Kondo insulator SmB6. arXiv:1211.5104 (2012). [Google Scholar]
  42. Zhang X. et al. Hybridization, inter-ion correlation, and surface states in the Kondo insulator SmB6. Phys. Rev. X 3, 011011 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplemental information

srep03150-s1.pdf (3.3MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES