Abstract
Objective
Understanding coronary artery mass transport allows researchers to better comprehend how drugs or proteins move through, and deposit into, the arterial wall. Characterizing how the convective component of transport changes based on arterial location could be useful to better understand how molecules distribute in different locations in the coronary vasculature.
Methods and results
We measured the mechanical properties and wall fluid flux transport properties of de-endothelialized (similar to post-stenting or angioplasty) left anterior descending (LADC) and right (RC) porcine coronary arteries along their arterial lengths. Multiphoton microscopy was used to determine microstructural differences. Proximal LADC regions had a higher circumferential stiffness than all other regions. Permeability decreased by 198% in the LADC distal region compared to other LADC regions. The RC artery showed a decrease of 46.9% from the proximal to middle region, and 51.7% from the middle to distal regions. The porosity increased in the intima between pressure states, without differences through the remainder of the arterial thickness.
Conclusions
We showed that the permeabilities and mechanical properties do vary in the coronary vasculature. With variations in mechanical properties, overexpansion of stents can occur more easily while variations in permeability may lead to altered transport based on location.
Keywords: Coronary, Permeability, Mechanical, Transport, Porohyperelastic
1. Introduction
While the expansion of coronary artery intervention into catheter-based methods has improved treatment success, failure mechanisms still exist for this therapy (AHA, 2010). The primary post-procedural failure mechanisms associated with this therapy include restenosis and thrombosis (Koskinas et al., 2012). Coronary artery disease and intervention is a critical focus area for many researchers given the severity, complications, and frequency of the disease (AHA, 2010; Gijsen et al., 2008; Hwang and Edelman, 2002; Hwang et al., 2001; Kabir et al., 2011; Sastry and Morice, 2010).
There have been numerous studies in which the delivery of coronary stents and the post-implantation functionality of these devices has been investigated from a biomechanical point of view (Feenstra and Taylor, 2009; Garasic et al., 2000; Gijsen et al., 2008; Himburg et al., 2004; Holzapfel et al., 2005; Lally et al., 2005). For example, finite element analysis has offered insight into the vascular injury induced from the stenting procedure on the wall. Such studies have examined vascular wall stress and contact area as it relates to coronary artery stents. This implies that biomechanical forces play a role in the vascular injury that can potentiate restenosis (Gijsen et al., 2008; Lally et al., 2005; Linxia Gu et al. (2010). Mass transport studies have been another area of focus. Mass transport studies can provide insight into disease etiology by studying transport of lipoproteins. In addition to understanding low density lipoprotein transport in vascular tissue (Rubboli et al., 2003;Soulis et al., 2010), mass transport (diffusive and/or convective) studies have been used to better understand pharmaceutical delivery in drug-eluting stents (DESs) (Feenstra and Taylor, 2009;Hwang et al., 2001, 2003). Such studies have shown that transport can change in tissue with induced strain through porosity alterations during induced mechanical load (Wu et al., 2009). This transport change can happen through alterations in convective (fluid-velocity driven) or diffusive (Brownian-motion driven) properties. Changes in transport can also be affected by alterations to endothelial cell permeability under different mechanical or chemical states (Himburg et al., 2004; Shepard et al., 1989; Yan et al., 2005). These alterations in endothelial cell permeability are not as relevant in situations where the endothelium has been disrupted, such as balloon angioplasty or stenting. The denuded endothelium results in a removed barrier for transport and therefore increased fluid permeation and solute transport into the arterial wall (Lovich et al., 1998).
In has been previously shown that the Peclet number is an important determining factor in the final distribution of species concentrations (Hwang et al., 2001). The Peclet number describes the relative influences of convective to diffusive transport. The importance of convection, in particular, becomes higher in scenarios where hydrophilic compounds (e.g., heparin) are transported (Lovich et al., 1998). The importance of permeability and convective transport is further accentuated in the absence of an endothelium, where it has been previously shown that the endothelium governs the deposition of molecules in the arterial wall by decreasing the hydraulic flow through the wall (Lovich et al., 1998).
Determining how a molecule moves through the arterial wall requires a thorough understanding of the interactions in an individual stent and tissue system, in addition to the coupled affects between the two. Several computational models have examined convective and diffusive transport through coronary arteries by either measuring transport properties on their own, or by taking previously published values and simulating the interactions computationally (Ayyalasomayajula et al., 2010; Feenstra and Taylor, 2009; Levin et al., 2004; Simon et al., 1998a,1998b).
One method of evaluating convective properties of tissues, specifically, is to measure their porohyperelastic properties (Vande Geest et al., 2011). A porohyperelastic analysis predicts interstitial fluid velocity as a function of the interstitial fluid pressure and mechanical deformation of the permeating material, as governed by the laws of the conservations of momentum and mass (Feenstra and Taylor, 2009; Simon et al., 1998a,1998b). To utilize this type of analysis, experimental input is needed as driven from the material laws (Feenstra and Taylor, 2009). In order to perform porohyperelastic analyses, the permeability as described in Darcy’s Law needs to be determined along with the mechanical properties (Ayyalasomayajula et al., 2010; Simon et al., 1998a). Utilizing mechanical properties in the fluid transport analysis, as is done in a porohyperelastic analysis, allows researchers to predict how vessel dimensions and void ratios change between pressure states, and how these changes translate to alterations in the convective fluid flow.
When looking at the tissue-DES interactions, there have been some studies indicating that restenosis is different based on location in the coronary vasculature (Ashby et al., 2002; Kang et al., 2011; Serruys et al., 2004). One study showed that the rate of restenosis differed between the proximal left anterior descending coronary (LADC) and right coronary (RC) arteries with rates of 68% and 19% respectively (Kang et al., 2011). Prior to the use of stenting, the procedure of angioplasty used a balloon catheter to forcibly open the vessel, thus introducing vessel injury and restenosis. In another study, this procedure resulted in restenosis rates of 37% in proximal LADC arteries versus 26% in the middle and distal LADC regions (Roubin et al., 1987). Concerning the RC arteries: the proximal and middle regions exhibited restenosis rates of 28% when compared to the distal region at 19% (Roubin et al., 1987). It should be noted that these results were in the absence of a stent. This could potentially be due to differences in transport thus allowing relatively different amounts of pro-proliferative and atherogenic molecules into the arterial wall. This is a vessel response (as opposed to the stent-vessel system) indicating that variations in this response can be a function of vessel location. While the location is not necessarily causative, the evaluation of the location dependent porohyperelastic properties can be used to investigate how species transport occurs as a function of location in the coronary vasculature. Therefore, the purpose of this manuscript is to determine the deformationally dependent fluid transport properties of porcine LADC and RC arteries and how these properties change along the arterial length.
2. Materials and methods
2.1. Transport theory
The total mass transport through a deformable porous media is governed by the relative contributions of diffusion and convection; coupled through the Eulerian isotropic Fick’s law (Eq. (1)) (Vande Geest et al., 2011):
| (1) |
where is the relative diffusive flux of the species [mol/m2_s], c is the concentration [mol/m3], xi is the deformed position coordinate [m], bcf is a convective transport parameter, kff is the hydraulic permeability [m4/N_s], and pf is the interstitial pore fluid pressure [Pa]. To determine how convective transport could influence total transport, the second term on the right hand side of Eq. (1) is considered. Fluid transport in a porous media, as implemented in ABAQUS, is governed by Darcy’s law (slow flow through a porous medium, Eq. (2)), which is a reduction of Forchheimer’s law (high flow through a porous medium) (Abaqus, 2009)
| (2) |
where fi is the volumetric flow rate per unit area [m/s], is the permeability [m/s], and γw is the specific weight of the permeating fluid [N/m3]. The value of can be converted to kff (from Eq. (1)) by , where g and ρ are gravity and the density of the fluid, respectively. Note that in the data processing used in this manuscript the permeability is assumed to be isotropic. The apparent relative fluid velocity of the permeating fluid is represented as
| (3) |
where n is the porosity (represented as the volume of the fluid divided by the total material volume), is the velocity of the fluid in the entire continuum [m/s], and vi is the velocity of the solid [m/s].
Porohyperelastic analysis follows the governing laws of the conservation of linear momentum (∂σij/∂xj = 0, where σij is the Cauchy stress tensor), conservation of mass (, where Dkk = ∂vk/∂xk), and the effective stress law (Hofma et al., 2006) (, where is the total Cauchy stress and is the effective Cauchy stress in the solid) (Simon et al., 1998a,1998b; Vande Geest et al., 2011). The effective Cauchy stress is related to the effective 2nd Piola Kirchhoff stress tensor (Seff) through (Hearn, 1997)
| (4) |
where J is the determinant of the deformation gradient tensor (F).
Note that our approach is in contrast to many previous studies (Filipovic et al., 2011; McGinty et al., 2011; Zhu et al., 2012), where the fluid transport is assumed to be constant. The porohyperelastic approach, via the use of kffdpf/dxi instead of a constant velocity term as in the standard convection–diffusion equation (Byron Bird et al., 2001), along with the right hand term of effective stress law, couples the deformation of the porous media to the observed convective transport.
2.2. Sample preparation
Testing occurred according to approved protocols with the University of Arizona Institutional Animal Care and Use Committee. Porcine hearts (n=5) were acquired within 30 min of slaughter from the University of Arizona Meat Sciences Laboratory. Samples were taken only from barrow pigs weighing approximately 311±41 lbs (live weight) at ages of 5–7 months old. Hearts were measured across their major axes: apex to coronary ostia (ACO), transverse at the auricles (TAA), and sagittal at the ostial level (SOL) (Crick et al., 1998;Skwarek et al., 2006). Hearts with dimensions outside of the mean (ACO=129, TAA=91, SOL=76 mm) by more than 10% were not used. The weight of each heart was not used to determine which samples to test due to potential error from the blood in the heart (e.g., ventricles, vessels, etc.) (Crick et al., 1998; Skwarek et al., 2006).
The LADC and RC arteries were located and marked at several locations along the axial length with a cyanoacrylate/ceramic powder mix. Suture lines were placed along the surface of the arteries on the outside of the heart and cut between marker sets. The arteries were removed from the heart and suture lines replaced and cut again between markers. The ratio of the length of the suture lines before and after removing the arteries provided the in-myocardium prestretch measurements of the artery segments (λZ–pre). After removal of extraneous tissue (e.g., fat, adventitia) the vessel segments were cut into thirds (proximal, middle, and distal regions) then prepared for either tubular biaxial tensile testing or permeability testing Keyes et al. (2011a). All testing occurred at 37±0.6 °C either through warming the testing bath directly or cycling warm water through the bath. Prior to mounting the vessels in testing fixtures, the vessels were mechanically de-endothelialized by rubbing the intimal surface gently with non-serrated forceps and confirming with Trypan blue after testing (data not shown). This was to ensure convective transport was measured through the arterial wall in a situation where the endothelium is damaged (e.g., interventional scenarios) (Caramori et al., 1999; Hofma et al., 2006).
2.3. Tubular biaxial tensile testing
The samples were tested as previously shown by our laboratory (Keyes et al., 2011a). Briefly, samples were cannulated and attached to the testing fixture. The testing fixture, once mounted in the testing bath, allows the tubular tissue specimen to be simultaneously pressurized and axially stretched (Keyes et al., 2011a,2011b). The sample was marked with two small black cyanoacrylate/ceramic powder dots to allow the axial displacement to be tracked over the course of the test. The sample was cycled through five stretch (to λZ–pre) and pressure (to 130 mmHg) cycles as preconditioning prior to beginning data collection. Samples were pressurized to 0, 70, or 130 mmHg then stretched from zero to λZ–pre cyclically at each pressure state to determine circumferential stress at different axial stretches. Correspondingly, the sample was held constant at three different axial stretches based on the prestretch measurements (λZ–pre=1, 1.15, or 1.40) and inflated from 0–130 mmHg cyclically at each stretch state to determine axial stress at each pressure state. The diameter, axial stretch, pressure, and axial force were acquired over the course of the tests. Inner diameter was determined at the different vessel mechanical configurations with multiphoton microscopy. These values were used in Eqs. (5 and 6) to determine the circumferential and longitudinal 2nd Piola Kirchhoff stresses, Sθθ and SZZ, respectively; Green’s strains for the two directions were calculated with Eqs. (7 and 8) (Hearn, 1997)
| (5) |
| (6) |
| (7) |
| (8) |
where r is the current radius, p is the intraluminal pressure, Fzz is axial force, A is the longitudinal cross section, λz is the longitudinal stretch, and ro is the undeformed outer radius. These equations are assuming a thin-walled vessel (thickness/diameter<0.1). Note that these equations neglect shear.
2.4. Permeability testing
Permeability testing was done similar to that previously described by (Simon et al., 1998b). Vessel sections were cannulated noting the locations of branching segments. The cannulas were placed to ensure no water leaked from the vessel, cannula assembly, or branching arteries. They were attached with cyanoacrylate at the cannula point, and tied with suture. The distance between sutures provided the permeation area (factored into fi in Eq. (2)). Histology measurements provided the undeformed cross-sectional geometries of the samples. One cannula was attached via silicone tubing to a glass capillary (2.419e–7 m2 cross section); the glass capillary was attached via silicone tubing to a pressure head filled with saline. Water was cycled through the vessel to flush any air from the system. The fluid exit cannula was sealed with a plugged silicone tube.
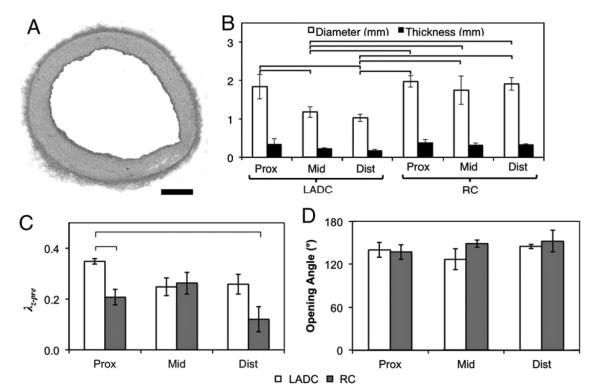
The prepared vessel was stretched to λZ–pre, glued down to a petri dish in the in vivo stretch configuration, and filled with 37 °C PBS to prepare for testing. The pressure head was raised to 70, 100, or 130 mmHg, and a bubble was inserted into the capillary tube by disconnecting the tube from the silicone, then lifting it slightly to insert a small air bubble (~1 ml). After this, the capillary was reattached to the system, sealing the bubble in the capillary inline with the cannulated vessel. Pressure was allowed to equibrilate, and the vessel allowed to consolidate under pressure for 30 min. After this, an image was taken of the bubble at different time-points depending on the velocity of the bubble. This typically happened every 30 min for the coronary artery samples until the bubble reached the end of the capillary. Bubble movement in the capillary indicated volumetric flow into the arterial wall. The bubble velocity was used to optimize for the permeability (discussed in Data Reduction). After testing was complete, the vessel segments were splayed open in Ca2+-free PBS to look at potential changes in opening angle based on location. A neighboring section was fixed in 2% paraformaldehyde, paraffin embedded, stained with H&E to help identify morphology, and cut normal to the vessel axis to determine the cross section dimensions (Fig. 1).
Fig. 1.
(A) Histological cross section (scale bar=0.25 mm). (B) Dimensions of the vessel segments. (C) Axial prestrain measured with sutures between marker points. (D) Opening angle between locations (p=NS). Bars p<0.05.
2.5. Microstructural analysis
To determine whether differences in permeability had a relationship to changes in microstructure, a tubular biaxial testing device was used in conjunction with a multiphoton microscope, as previously described (Keyes et al., 2011a,2011b). Three of the tested vessel segments and two fresh samples were held at λZ–pre and imaged at pressures of 0, 70, and 130 mmHg. Excitation wavelength was 780 nm, and the laser had 36 mW of power with linear scaling to 51 mW as the focus moved through the thickness. This allowed for deeper imaging through the vessel wall. Second harmonic generated light from collagen was collected along with autofluorescent light from elastin. To determine how the void ratio through the thicknesses changed, the images were analyzed by combining the two channels and thresholding the images by using the entropy maximizing routine in Matlab. The dark and light pixels were counted to determine the void ratios (e) (Eq (9)). In Eq (9), Vvoids is the volume of the voids, and Vsolid the volume of the solid. The collagen and elastin orientation was also analyzed in the images of the vessels at 130 mmHg as previously shown (Kirkpatrick et al., 2007). In addition, the vessel thicknesses at the different pressure states were examined by looking at the orthogonal projections of the image stacks. This provides an indication of the volumetric behavior, or compressibility, of the tissue.
| (9) |
2.6. Data reduction
Data was fit to a Fung-type orthotropic effective strain energy density from ABAQUS 6.9-1 (Eq. (10)). The second Piola-Kirchhoff stress was evaluated with Eq. (11)
| (10) |
| (11) |
where c, A1, A2, A3, and D are the material constants, and are the components of the deviatoric Green’s strain tensor. Each biaxial tensile testing dataset was simultaneously fit in a multidimensional nonlinear regression fashion to the Fung-type effective strain energy density with SigmaStat 3.5 in the circumferential and longitudinal directions assuming an incompressible model (D=0). Following this initial fit, a Matlab-ABAQUS optimization routine was performed that used the optimization constants from the incompressible solution from SigmaStat as the initial guesses (Vad et al., 2010). Optimization was performed using the fminsearch routine in Matlab. This is an unconstrained nonlinear optimization approach (Nelder–Mead simplex algorithm) (MathWorks, 2012). A series of constants were guessed from the starting point determined earlier in SigmaStat, and the optimization routine continued until the sum of the square of the residuals (differences between the experimental and computational results), or difference between sequential guesses, were minimized to <1e–12 for mechanical results and <1e–20 for fluid transport. The finite element model was a 1/20 circumferential symmetry model with six elements through the thickness. The same nodal separation was used in the axial and circumferential direction as was through the thickness. The mesh was chosen through a convergence study examining the components of the relative fluid velocity after consolidation, stress, and strain. Through the thickness: relative fluid velocity, stress, and strain components did not vary by more than 0.01% with four or more elements. Circumferentially and longitudinally the element size could have been more coarse, however, a finer mesh was determined to not be detrimental to the analysis time. The unconstrained nonlinear optimization program modified all constants, in an automated fashion, until the mechanical behaviors from the tubular biaxial testing and multiphoton imaging (thickness measurements) matched the finite element result.
The automated optimization procedure was performed for the cumulative dataset from each arterial section. Material constants were reported for the respective sections along with the 95% confidence intervals. The maximum tangential modulus (MTM) of a pressure-inflation upcycle at λZ–pre was used to determine relative differences in vessel circumferential stiffness between groups. Correspondingly, the MTM of the axial stretch upcycle at 70 mmHg internal pressure was used to determine differences in vessel axial stiffness between groups.
To determine the permeability, a similar ABAQUS-Matlab routine was run that couples the porohyperelastic analysis in a similar unconstrained nonlinear optimization routine (Vad et al., 2010). This was done as opposed to simply fitting the water flux to the Darcy equation because the mechanical properties can be incorporated. The mechanical properties allows for the implementation of the proper geometrical shape in the simulation. The shape change induced from the mechanical loads (pressure and axial stretch) will change the length scales used in the model. The model is again a section of tube driven by dimensions from the vessel section that was tested (diameter, thickness, length), and meshed with C3D8RP elements for a porohyperelastic analysis. Boundary conditions were applied by fixing one end, stretching the other to λZ–pre, and applying pore and mechanical pressures matching that of the individual tests that were run. The mechanical properties corresponding to the individual tested vessel segment was used in the optimization routine. After the analysis was completed, the relative fluid velocity, vfr, was read into Matlab from the ABAQUS results file. This was compared to a target vfr from the wet-laboratory bubble-velocity. The target vfr is the volume flux from the experiment (related to fi), divided by the permeation area (luminal surface area of the tested section). The was altered in a similar optimization routine as was used for the mechanical properties until the experimental fluid velocity matched the computational simulation. The final reported permeabilities are those from ABAQUS in units of meters/second.
2.7. Statistical analysis
ANOVA in one, two, and three way interactions were used to determine if differences exist in any experimental endpoint as a function of pressure (0, 70, 130 mmHg), arterial section (proximal, middle, distal), artery (LADC, RC), or any combination of the three. A Bonferroni adjustment was done to determine any pair-wise significance. Values of p<0.05 were considered significant. Water flux and permeability are reported as the overall mean (all pressures and samples from a specific section) plus/minus the standard deviation. The mechanical constitutive constants are reported as the 95% confidence bounds. Bar plots are represented as the mean with standard deviation error bars.
3. Results
3.1. Tubular biaxial testing
Axial prestretch was statistically larger in the proximal LADC artery compared to middle and distal regions (Fig. 1). The RC arteries showed a decreasing trend along the length, as well. The opening angle measurements showed no statistical difference between sections (Fig. 1). The mean opening angle for all groups was 141.3±9.9°.
The Fung constants for the cumulative fits are shown in Table 1. The circumferential MTMs of the LADC artery showed a statistically significant decrease in MTM moving from the proximal to middle region of 45.6%, and 62.7% from the middle to distal region (Fig. 2). The MTMs of the RC artery showed the same trend, however, with a change of 71.3% from the proximal to middle region, and 30.6% from the middle to the distal region. In addition, the RC arteries demonstrated an overall higher circumferential compliance than the LADC arteries (p<0.05).
Table 1.
Fung constants for each section (Values are mean±95% CI).
| Vessel segment | c (kPa) | A 1 | A 2 | A 3 | D (Pa−1) |
|---|---|---|---|---|---|
| LADC | |||||
| Proximal | 445±48 | 1.40±0.11 | 0.99±0.05 | 0.47±0.05 | 2.2E–08±1.2E–09 |
| Middle | 160±14 | 5.30±0.41 | 1.60±0.21 | 1.49±0.21 | 6.9E–09±3.1E–10 |
| Distal | 162±14 | 2.79±0.23 | 5.19±0.40 | 0.55±0.04 | 7.0E–09±4.9E–10 |
| RC | |||||
| Proximal | 439±41 | 0.99±0.13 | 1.33±0.09 | 0.32±0.02 | 7.8E–07±2.0E–08 |
| Middle | 61±4 | 4.51±0.08 | 5.50±0.09 | 2.61±0.22 | 8.1E–07±4.5E–08 |
| Distal | 61±5 | 0.96±0.14 | 13.10±0.10 | 1.72±0.01 | 9.0E–07±6.8E–08 |
Fig. 2.

Top: Axial maximum tangential modulus at 70 mmHg. Bottom: Circumferential maximum tangential modulus at in situ axial stretch. Bars indicate pair-wise significance to p<0.05.
The axial MTMs showed a different trend, with increasing stiffness along the LADC and RC arteries. The LADC showed an increase of 605.9% from the proximal to middle regions, and 2.8% from the middle to distal regions (not significant). The RC showed an increase of 22.8% from the proximal to middle region, and 127.7% from the middle to distal regions. Similar to the circumferential MTMs, the LADC did generally have higher stiffness compared to the RC arteries (one-way ANOVA p<0.05). In addition to the differences in the stiffness between regions, the different regions exhibited different levels of anisotropy as determined by the ratio of the MTMs in the circumferential to axial directions. The LADC proximal region had the highest level of anisotropy with a value of 2.4 for the ratio of MTMcirc/MTMaxial with all other LADC regions falling below 0.2. The RC proximal region had a value of 1.0 with all other regions falling below 0.3.
3.2. Permeability
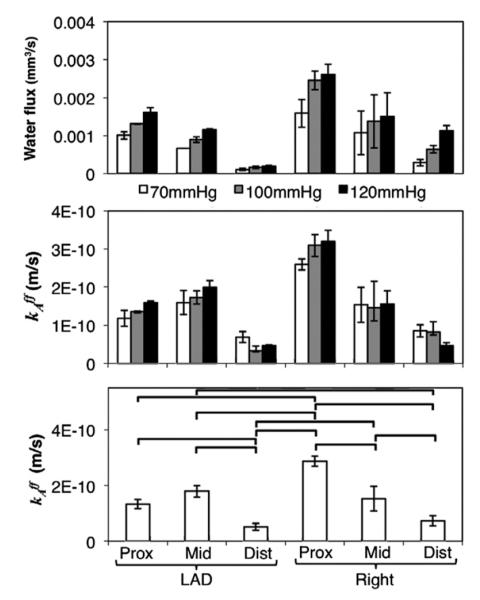
The permeability showed differences based on vessel location, as well. Generally, an increase in flux meant an increase in permeability of the segment, however, the differences in flux did not correspond to a direct-ratio change in permeability (i.e., a doubling in flux did not result in an exact halving of the permeability). This is primarily due to the vessel deformation during stretching and pressurization. In other words, this is due to differences in mechanical properties of the individual sections. Permeability was statistically smaller in the distal region of the LADC compared to the proximal and middle regions by 198% (Fig. 3). The RC artery showed a statistically significant decreasing trend, as well, with a decrease of 46.9% from the proximal to middle region, and 51.7% from the middle to distal regions. A three-way ANOVA showed statistical differences based on the artery (p<0.02), section (p<0.01, and the interaction between artery and section (artery section, p<0.01). The pressure, artery pressure interaction, section pressure interaction, and artery section pressure interactions were not significant (p>0.6).
Fig. 3.
Top: Volume flow rate for each vessel section at each test pressure. Middle: Permeability from the optimization routine for each section. Bottom: Permeability (averaged for all samples and pressures) for each section. Bars p<0.05.
3.3. Microstructural analysis
Microstructural analysis showed that during pressurization the collagen realigned and uncrimped without a change in void ratio (Fig. 4). The elastin however, exhibited realignment and changes to void ratio between pressure states. This occurred mainly at the intima. Qualitatively, the elastin bands closer to the intima showed the largest change in void. These larger bands exhibited a smaller degree of elastin sinuosity as the samples were pressurized with the width of the bands becoming smaller. This band lateral shrinking resulted in the exposure of voids. These larger bands were not seen outside of the intima.
Fig. 4.
Top row: Representative collagen orientation at 40% through the vessel wall (from the lumen) for a left proximal region. Note the uncrimping from 0 and 70 to 130 mmHg. Middle row: Representative elastin orientation for the same vessel at the intima. The white arrows are indicative of elastin bundles that exhibited the majority of the void ratio changes. Note how the image at 0 mmHg has elastin folding as indicated by the bright and dark bands in the elastin macrobundles. Bottom row: Thresholding of the elastin images showing the increase in void. Scale bar is 50 μm.
Deeper into the wall past the intima, the elastin was present as thinner fiber bundles as opposed to bands. The adventitia had a combination of collagen and elastin without noticeable organization and smaller voids with pores that did not open noticeably upon pressurizing the specimens.
Examining the differences between arteries, the LADC sections all had similar large bands that underwent changes in void at the intima. This was also seen in the proximal RC artery regions. The middle and distal regions had far smaller bands, and therefore smaller voids that opened up.
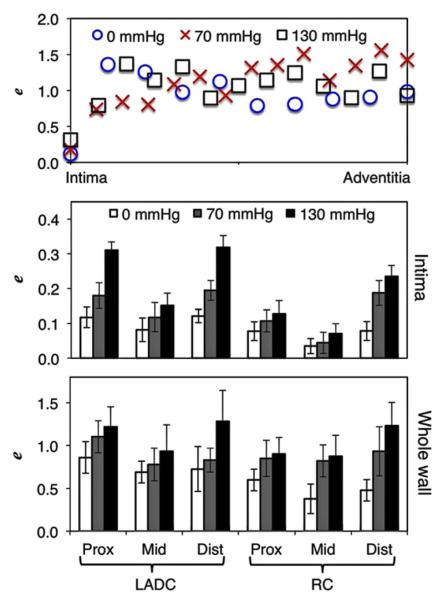
Fig. 5 shows an example of how void ratio changes through the depth along with the quantified void ratios averaged through the depth, and another panel for just the intima. The void ratios of the intima when analyzed via a three-way ANOVA showed significance between the artery, section, and pressure (all p<0.02). All other ANOVA interactions were p>0.1. The void ratios as binned through the entire thickness, when analyzed via three-way ANOVA showed no significance, presumably because beyond the intima the voids did not appear to change through the thickness. Between pressures, through the entire thickness, the p value for void was the lowest (p<0.09), all other ANOVA sources and interactions were p>0.2.
Fig. 5.
Top: Void ratio variation through the vessel thickness of a representative proximal LAD. Middle: Void ratio of just the intima at each pressure for the different segments. Bottom: Average void ratio through the entire thickness for each of the segments.
The orientation analyses indicated that differences existed based on location for each vessel in the in situ axial length state and at 130 mmHg internal pressure. The LADC proximal arteries showed a higher degree of collagen preferential alignment in the circumferential direction than the middle and distal sections by 21° after pressurizing the vessels. This correlates with the mechanical testing data showing that the proximal sections were more stiff in the circumferential direction than the middle and distal sections. The elastin had a similar trend, with the middle and distal regions having similar orientations (18° and 36° more axial, respectively), and the proximal region being more circumferentially aligned (45° offset from the circumferential direction). The proximal and distal RC regions had similar collagen profiles (62° and 60° more axial, respectively), however, the elastin in the proximal region was more spread in its orientation by 9°. The RC middle section showed a rather flat orientation profile (no definitive preferred orientation) in both the elastin and collagen channels. This could potentially be responsible for this section having the smallest average stiffness between the axial and circumferential directions.
4. Discussion
In this study we showed how the deformationally dependent fluid transport properties of coronary arteries varies between the two most frequently stented coronary arteries (LADC and RC) and down their axial lengths. The data showed that down the LADC artery, convective transport trended higher from the proximal to middle regions, and then dropped by more than half beyond the middle region. In the RC arteries, the permeability trended downward, decreasing by more than three-fold from the proximal to distal regions. In addition, we showed that the mechanical properties of the various sections showed differences, and that the void ratios through the thicknesses of the arteries did not change significantly between sections. However, the void ratios of the intima did change significantly between sections, arteries, and pressures. This shows that a significant contributor to alterations in convective transport based on different intraluminal pressures could be the elastin in the intima of de-endothelialized vessels serving as a governor for convective transport. Since convective fluid transport through the arterial wall can be a significant contributor to transport, the variations in the properties between sections could possibly result in changes in expected clinical concentrations of pharmaceuticals in those areas (Lovich et al., 1998). This can also apply to predictions of the levels of biological molecules, for example it has been shown that endothelium-derived relaxing factor can interact differently with proximal versus distal canine coronary arteries (Hoeffner et al., 1989).
Mechanical testing of coronary arteries has been done through various testing techniques, and on different species (human, pig, dog) (Holzapfel et al., 2005; Lally et al., 2004;Ozolanta et al., 1998; van Andel et al., 2003; Veress et al., 2002;Wang et al., 2006; Zemanek, 2009). It has been shown that not only do the properties change between species, but the mechanical properties and extracellular matrix components change between vessels (Humphrey et al., 2009). For instance, van Andel et al. reported similar mechanical properties of their porcine LADC arteries when comparing to the proximal and middle regions of LADC arteries in our study (van Andel et al., 2003). In addition, they showed there was not significant pairwise significance when comparing between LADC and RC sections, which we saw in the circumferential MTMs of all sections except the proximal LADC region. Vessels showing differences in stiffness based on location can have implications in percutaneous intervention. It has been shown that balloon over-inflation and stent–tissue interactions during deployment can influence how much injury occurs to the coronary artery (Garasic et al., 2000). Vessel compliances determine how much mechanical feedback, or resistive force to deployment, exists in the targeted arteries. The mechanical properties can also dictate how void ratios and length scales change in different vessel mechanical conditions.
The coupled determination of the convective transport properties with the mechanical properties has not been as thoroughly studied. Values are especially vacant in regard to porcine coronary artery permeability, although other authors have reported permeability of other arteries through the use of radiolabeling, fluorescent dye tracking, or bubble-velocity tracking (Creel et al., 2000; Hwang et al., 2001; Lovich et al., 1998; Simon et al., 1998a; Tzafriri et al., 2009). Other researchers that have investigated the permeability of coronary artery walls have looked at wall permeability with endothelial cell permeability playing a major role in determining transport, especially in regard to LDL accumulation in the artery (Sill et al., 1995). Our study reports values of permeabilities for arteries without an endothelium, which is especially relevant in cases of endothelial disruption (Ku et al., 1993). Shou et al. reported hydraulic conductivity values for rat aortas with and without the endothelial layer (Shou et al., 2006). Mathematically, the hydraulic conductivity is represented as fi=Lp*ΔP, where Lp is the hydraulic conductivity. Their values of Lp for the deendothelialized arteries (3e–7 cm/(s mmHg)) matches very closely with the distal regions of both arteries tested in our study (<10% difference). Their study also reported that when including the endothelium, they saw Lp values approximately five times lower (Shou et al., 2006). Knowing how permeability varies between vessel regions can help clinicians determine how species transport may vary between targeted therapy regions, especially after an interventional procedure that denudes the endothelium.
While our study reports on how convective transport varies between arteries and locations, the study did have several limitations. For instance, residual stresses in the circumferential and torsional directions were not incorporated during the finite element simulations to optimize for the permeability (Chuong and Fung, 1986; Wang et al., 2006). In addition, the use of tubular pressure-inflation testing as opposed to planar biaxial testing has errors associated with the fact that researchers consider the tube as stress free in the creation of the constitutive models for use in the finite element routines. This could result in inaccurate stress distributions through the wall. Although, it could be argued that the pressure-inflation data is more important because the pressure-inflation data best relates to the length-scale and void ratio changes. We also used the thin-walled and plane strain assumptions in the calculation of stresses and strains. We deemed this valid as the average radius-to-wall thickness ratio is greater than ten (Doyle and Dobrin, 1973). In using the plane strain assumption we calculate radial behavior based on what was measureable in the circumferential and longitudinal directions, and how the thickness changed between stress states. The measurement of strain behavior through the radial thickness could give potentially a more accurate model, however, considering the thin-walled nature of the tested vessels and moderate strain stiffening behavior, the radial distributions of the strain profile can be depicted via the use of the assumptions we have made. A source of error is also the geometry used. The average thickness and diameter of the vessel segments were used, however, the arteries are all slightly nonhomogeneous in these dimensions (Raghavan et al., 2004; Veress et al., 2002). Another drawback is the use of animals from a slaughterhouse. While we were careful to accept only those animals of certain ages and weights with similar environmental backgrounds and heart sizes, the study could have potentially been more accurate using a more controlled, bred-for-science, animal source. In addition, testing vessels in situ after removal from the heart negates any influence of fat, pericardium, and adventitia. We deemed this necessary because we wanted to test for microstructure through the entire thickness and any tissue outside of the intima and media would make that impossible due to the depth limitations of multiphoton microscopy.
Understanding transport based off of the properties reported in this manuscript in an in vivo situation would require advanced finite element studies. This is especially important considering the pulsatile nature of the cardiac cycle. Over the course of the cycle the vessel will undergo myocardial-influenced deformation and changes in the deformationally dependent permeability. Modeling the entire tissue with input from non-invasive imaging modalities to capture all surrounding tissue could potentially provide researchers with information in regard to how pulsatility affects transport in vivo. The difference in pulsatile versus steady state transport is an area of ongoing research in our laboratory.
We showed here that the two most frequently stented coronary arteries exhibit not only differences in permeability, mechanical properties, and void ratio behavior between the arteries, but also along the arterial length. These changes, when coupled to analyses where scientists are examining total diffusive and convective mass transport, could potentially influence total molecule transport, as determined by the relative influences of the different transport parameters (e.g., Peclet number). Our laboratory is currently investigating these other influences on transport for coronary arteries, and how these different influences alter total vessel wall concentrations based on location. While the location is not directly causative, this study can guide future studies on what factors underlie the differences we reported (e.g., microstructure, crosslinking, etc.). Knowing further information on how these properties change based on location could potentially guide therapy to account for relative differences in the porohyperelastic and mass transport characteristics.
5. Conclusions
Overall, we showed how the deformationally dependent fluid transport properties of porcine coronary arteries change, not just between arteries, but along their arterial length. Decreases in permeability between regions can diminish the amount of expected drugs to non-optimal levels, whereas increases may allow higher levels of LDL to distribute into the arterial wall. The differences presented here could be useful to guide future studies and therapies to ensure species are optimally delivered to their desired locations.
Acknowledgments
The authors would like to thank the University of Arizona Meat Sciences Laboratory for help in sample acquisition.
Sources of funding The Advanced Intravital Microscope was funded through a NIH/NCRR 1S10RR023737-01. This work is supported, in parts, by the National Institutes of Health Cardiovascular Biomedical Engineering Training Grant (T32 HL007955), an American Heart Association (AHA) Predoctoral Fellowship (11PRE7730024 to JTK), Achievement Rewards for College Scientists (ARCS; Mary Ann White Memorial Scholarship to JTK), and an AHA Grant-in-Aid (10GRNT4580045 to JPVG).
Footnotes
Disclosures None.
REFERENCE
- ABAQUS I. Abaqus Version 6.9 Documentation. In: Systemes D, editor. Dassault Systemes. Velizy-Villacoublay; France: 2009. [Google Scholar]
- Ashby DT, Dangas G, Mehran R, Lansky AJ, Narasimaiah R, Iakovou I, Polena S, Satler LF, Pichard AD, Kent KM, Stone GW, Leon MB. Comparison of clinical outcomes using stents versus no stents after percutaneous coronary intervention for proximal left anterior descending versus proximal right and left circumflex coronary arteries. American Journal of Cardiology. 2002;89:1162–1166. doi: 10.1016/s0002-9149(02)02297-x. [DOI] [PubMed] [Google Scholar]
- AHA . Heart Disease & Stroke Statistics: 2010 Update At-A-Glance. American Heart Association; 2010. [Google Scholar]
- Ayyalasomayajula A, Vande Geest JP, Simon BR. Porohyperelastic finite element modeling of abdominal aortic aneurysms. Journal of Biomechanical Engineering. 2010;132:104502. doi: 10.1115/1.4002370. [DOI] [PubMed] [Google Scholar]
- Byron Bird R, Lightfoot WES, Edwin N. Transport Phenomena. Second ed Wiley; New York: 2001. [Google Scholar]
- Caramori PR, Lima VC, Seidelin PH, Newton GE, Parker JD, Adelman AG. Long-term endothelial dysfunction after coronary artery stenting. Journal of the American College of Cardiology. 1999;34:1675–1679. doi: 10.1016/s0735-1097(99)00411-8. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. On residual stresses in arteries. Journal of Biomechanical Engineering. 1986;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- Creel CJ, Lovich MA, Edelman ER. Arterial paclitaxel distribution and deposition. Circulation Research. 2000;86:879–884. doi: 10.1161/01.res.86.8.879. [DOI] [PubMed] [Google Scholar]
- Crick SJ, Sheppard MN, Ho SY, Gebstein L, Anderson RH. Anatomy of the pig heart: comparisons with normal human cardiac structure. Journal of Anatomy. 1998;193(Pt 1):105–119. doi: 10.1046/j.1469-7580.1998.19310105.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle JM, Dobrin PB. Stress gradients in the walls of large arteries. Journal of Biomechanics. 1973;6:631–639. doi: 10.1016/0021-9290(73)90019-5. [DOI] [PubMed] [Google Scholar]
- Feenstra PH, Taylor CA. Drug transport in artery walls: a sequential porohyperelastic-transport approach. Computer Methods in Biomechanics and Biomedical Engineering. 2009;12:263–276. doi: 10.1080/10255840802459396. [DOI] [PubMed] [Google Scholar]
- Filipovic N, Rosic M, Tanaskovic I, Parodi O, Fotiadis D. Computer Simulation and Experimental Analysis of LDL Transport in the Arteries. Conference proceedings; Annual International Conference of the IEEE Engineering in Medicine and Biology Society; IEEE Engineering in Medicine and Biology Society; 2011. pp. 195–198. Conference 2011. [DOI] [PubMed] [Google Scholar]
- Garasic JM, Edelman ER, Squire JC, Seifert P, Williams MS, Rogers C. Stent and artery geometry determine intimal thickening independent of arterial injury. Circulation. 2000;101:812–818. doi: 10.1161/01.cir.101.7.812. [DOI] [PubMed] [Google Scholar]
- Gijsen FJ, Migliavacca F, Schievano S, Socci L, Petrini L, Thury A, Wentzel JJ, van der Steen AF, Serruys PW, Dubini G. Simulation of stent deployment in a realistic human coronary artery. Biomedical Engineering Online. 2008;7:23. doi: 10.1186/1475-925X-7-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hearn E. Mechanics of Materials Volume 1, Third Edition: An Introduction to the Mechanics of Elastic and Plastic Deformation of Solids and Structural Materials. 1997;v. 1 [Google Scholar]
- Himburg HA, Grzybowski DM, Hazel AL, LaMack JA, Li XM, Friedman MH. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. American Journal of Physiology Heart and Circulatory Physiology. 2004;286:H1916–1922. doi: 10.1152/ajpheart.00897.2003. [DOI] [PubMed] [Google Scholar]
- Hoeffner U, Boulanger C, Vanhoutte PM. Proximal and distal dog coronary arteries respond differently to basal EDRF but not to NO. The American Journal of Physiology. 1989;256:H828–831. doi: 10.1152/ajpheart.1989.256.3.H828. [DOI] [PubMed] [Google Scholar]
- Hofma SH, van der Giessen WJ, van Dalen BM, Lemos PA, McFadden EP, Sianos G, Ligthart JM, van Essen D, de Feyter PJ, Serruys PW. Indication of long-term endothelial dysfunction after sirolimus-eluting stent implantation. European Heart Journal. 2006;27:166–170. doi: 10.1093/eurheartj/ehi571. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. American Journal of Physiology Heart and Circulatory Physiology. 2005;289:H2048–2058. doi: 10.1152/ajpheart.00934.2004. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Eberth JF, Dye WW, Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. Journal of Biomechanics. 2009;42:1–8. doi: 10.1016/j.jbiomech.2008.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang CW, Edelman ER. Arterial ultrastructure influences transport of locally delivered drugs. Circulation Research. 2002;90:826–832. doi: 10.1161/01.res.0000016672.26000.9e. [DOI] [PubMed] [Google Scholar]
- Hwang CW, Wu D, Edelman ER. Physiological transport forces govern drug distribution for stent-based delivery. Circulation. 2001;104:600–605. doi: 10.1161/hc3101.092214. [DOI] [PubMed] [Google Scholar]
- Hwang CW, Wu D, Edelman ER. Impact of transport and drug properties on the local pharmacology of drug-eluting stents. International Journal of Cardiovascular Interventions. 2003;5:7–12. doi: 10.1080/14628840304614. [DOI] [PubMed] [Google Scholar]
- Kabir AM, Selvarajah A, Seifalian AM. How safe and how good are drug-eluting stents? Future Cardiology. 2011;7:251–270. doi: 10.2217/fca.11.1. [DOI] [PubMed] [Google Scholar]
- Kang SJ, Mintz GS, Park DW, Lee SW, Kim YH, Whan Lee C, Han KH, Kim JJ, Park SW, Park SJ. Mechanisms of in-stent restenosis after drug-eluting stent implantation: intravascular ultrasound analysis. Circulation Cardiovascular Interventions. 2011;4:9–14. doi: 10.1161/CIRCINTERVENTIONS.110.940320. [DOI] [PubMed] [Google Scholar]
- Keyes JT, Borowicz SM, Rader JH, Utzinger U, Azhar M, Vande Geest JP. Design and demonstration of a microbiaxial optomechanical device for multiscale characterization of soft biological tissues with two-photon microscopy. Microscopy and Microanalysis. 2011a;17:167–175. doi: 10.1017/S1431927610094341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keyes JT, Haskett DG, Utzinger U, Azhar M, Vande Geest JP. Adaptation of a planar microbiaxial optomechanical device for the tubular biaxial microstructural and macroscopic characterization of small vascular tissues. Journal of Biomechanical Engineering. 2011b;133:075001. doi: 10.1115/1.4004495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick ND, Andreou S, Hoying JB, Utzinger U. Live imaging of collagen remodeling during angiogenesis. American Journal of Physiology Heart and Circulatory Physiology. 2007;292:H3198–3206. doi: 10.1152/ajpheart.01234.2006. [DOI] [PubMed] [Google Scholar]
- Koskinas KC, Chatzizisis YS, Antoniadis AP, Giannoglou GD. Role of endothelial shear stress in stent restenosis and thrombosis: pathophysiologic mechanisms and implications for clinical translation. Journal of American College of Cardiology. 2012;59:1337–1349. doi: 10.1016/j.jacc.2011.10.903. [DOI] [PubMed] [Google Scholar]
- Ku DD, Zaleski JK, Liu S, Brock TA. Vascular endothelial growth factor induces EDRF-dependent relaxation in coronary arteries. The American Journal of Physiology. 1993;265:H586–592. doi: 10.1152/ajpheart.1993.265.2.H586. [DOI] [PubMed] [Google Scholar]
- Lally C, Dolan F, Prendergast PJ. Cardiovascular stent design and vessel stresses: a finite element analysis. Journal of Biomechanics. 2005;38:1574–1581. doi: 10.1016/j.jbiomech.2004.07.022. [DOI] [PubMed] [Google Scholar]
- Lally C, Reid AJ, Prendergast PJ. Elastic behavior of porcine coronary artery tissue under uniaxial and equibiaxial tension. Annals of Biomedical Engineering. 2004;32:1355–1364. doi: 10.1114/b:abme.0000042224.23927.ce. [DOI] [PubMed] [Google Scholar]
- Levin AD, Vukmirovic N, Hwang CW, Edelman ER. Specific binding to intracellular proteins determines arterial transport properties for rapamycin and paclitaxel. Proceedings of the National Academy of Sciences of United States of America. 2004;101:9463–9467. doi: 10.1073/pnas.0400918101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linxia Gu SZ, Muttyam Aswini K., Hammel James M. The relation between the arterial stress and restenosis rate after coronary stenting. Journal of Medical Devices. 2010;4:7. [Google Scholar]
- Lovich MA, Philbrook M, Sawyer S, Weselcouch E, Edelman ER. Arterial heparin deposition: role of diffusion, convection, and extravascular space. The American Journal of Physiology. 1998;275:H2236–2242. doi: 10.1152/ajpheart.1998.275.6.H2236. [DOI] [PubMed] [Google Scholar]
- MathWorks I. MATLAB R2012a Documentation. 2012 [Google Scholar]
- McGinty S, McKee S, Wadsworth RM, McCormick C. Modelling drug-eluting stents. Mathematical Medicine and Biology: A Journal of the IMA. 2011;28:1–29. doi: 10.1093/imammb/dqq003. [DOI] [PubMed] [Google Scholar]
- Ozolanta I, Tetere G, Purinya B, Kasyanov V. Changes in the mechanical properties, biochemical contents and wall structure of the human coronary arteries with age and sex. Medical Engineering and Physics. 1998;20:523–533. doi: 10.1016/s1350-4533(98)00050-2. [DOI] [PubMed] [Google Scholar]
- Raghavan ML, Trivedi S, Nagaraj A, McPherson DD, Chandran KB. Three-dimensional finite element analysis of residual stress in arteries. Annals of Biomedical Engineering. 2004;32:257–263. doi: 10.1023/b:abme.0000012745.05794.32. [DOI] [PubMed] [Google Scholar]
- Roubin GS, King SB, 3rd, Douglas JS., Jr. Restenosis after percutaneous transluminal coronary angioplasty: the Emory University hospital experience. American Journal of Cardiology. 1987;60:39B–43B. doi: 10.1016/0002-9149(87)90482-6. [DOI] [PubMed] [Google Scholar]
- Rubboli A, Euler DE, Sangiorgio P, Casella G, La Vechia L, Fontanelli A, Bracchetti D. Association of cholesterol levels and occurrence of angiographically detectable endothelial disruption during coronary angioplasty. Clinical Cardiology. 2003;26:336–340. doi: 10.1002/clc.4950260708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sastry S, Morice MC. Are drug-eluting stents safe and effective in the long term? Arquivos Brasileiros de Cardiologia. 2010;95:663–670. doi: 10.1590/s0066-782x2010001500016. [DOI] [PubMed] [Google Scholar]
- Serruys PW, Degertekin M, Tanabe K, Russell ME, Guagliumi G, Webb J, Hamburger J, Rutsch W, Kaiser C, Whitbourn R, Camenzind E, Meredith I, Reeves F, Nienaber C, Benit E, Disco C, Koglin J, Colombo A. Vascular responses at proximal and distal edges of paclitaxel-eluting stents: serial intravascular ultrasound analysis from the TAXUS II trial. Circulation. 2004;109:627–633. doi: 10.1161/01.CIR.0000112566.87022.32. [DOI] [PubMed] [Google Scholar]
- Shepard JM, Moon DG, Sherman PF, Weston LK, Del Vecchio PJ, Minnear FL, Malik AB, Kaplan JE. Platelets decrease albumin permeability of pulmonary artery endothelial cell monolayers. Microvascular Research. 1989;37:256–266. doi: 10.1016/0026-2862(89)90044-7. [DOI] [PubMed] [Google Scholar]
- Shou Y, Jan KM, Rumschitzki DS. Transport in rat vessel walls. I. Hydraulic conductivities of the aorta, pulmonary artery, and inferior vena cava with intact and denuded endothelia. American Journal of Physiology Heart and Circulatory Physiology. 2006;291:H2758–2771. doi: 10.1152/ajpheart.00610.2005. [DOI] [PubMed] [Google Scholar]
- Sill HW, Chang YS, Artman JR, Frangos JA, Hollis TM, Tarbell JM. Shear stress increases hydraulic conductivity of cultured endothelial monolayers. The American Journal of Physiology. 1995;268:H535–543. doi: 10.1152/ajpheart.1995.268.2.H535. [DOI] [PubMed] [Google Scholar]
- Simon BR, Kaufmann MV, McAfee MA, Baldwin AL. Porohyperelastic finite element analysis of large arteries using ABAQUS. Journal of Biomechanical Engineering. 1998a;120:296–298. doi: 10.1115/1.2798315. [DOI] [PubMed] [Google Scholar]
- Simon BR, Kaufmann MV, McAfee MA, Baldwin AL, Wilson LM. Identification and determination of material properties for porohyperelastic analysis of large arteries. Journal of Biomechanical Engineering. 1998b;120:188–194. doi: 10.1115/1.2798301. [DOI] [PubMed] [Google Scholar]
- Skwarek M, Grzybiak M, Kosinski A, Hreczecha J. Basic axes of human heart in correlation with heart mass and right ventricular wall thickness. Folia Morphol (Warsz) 2006;65:385–389. [PubMed] [Google Scholar]
- Soulis JV, Fytanidis DK, Papaioannou VC, Giannoglou GD. Wall shear stress on LDL accumulation in human RCAs. Medical Engineering and Physics. 2010;32:867–877. doi: 10.1016/j.medengphy.2010.05.011. [DOI] [PubMed] [Google Scholar]
- Tzafriri AR, Levin AD, Edelman ER. Diffusion-limited binding explains binary dose response for local arterial and tumour drug delivery. Cell Proliferation. 2009;42:348–363. doi: 10.1111/j.1365-2184.2009.00602.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vad S, Eskinazi A, Corbett T, McGloughlin T, Vande Geest JP. Determination of coefficient of friction for self-expanding stent-grafts. Journal of Biomechanical Engineering. 2010;132:121007. doi: 10.1115/1.4002798. [DOI] [PubMed] [Google Scholar]
- van Andel CJ, Pistecky PV, Borst C. Mechanical properties of porcine and human arteries: implications for coronary anastomotic connectors. The Annals of Thoracic Surgery. 2003;76:58–64. doi: 10.1016/s0003-4975(03)00263-7. discussion 64-55. [DOI] [PubMed] [Google Scholar]
- Vande Geest JP, Simon BR, Rigby PH, Newberg TP. Coupled porohyperelastic mass transport (PHEXPT) finite element models for soft tissues using ABAQUS. Journal of Biomechanical Engineering. 2011;133:044502. doi: 10.1115/1.4003489. [DOI] [PubMed] [Google Scholar]
- Veress AI, Weiss JA, Gullberg GT, Vince DG, Rabbitt RD. Strain measurement in coronary arteries using intravascular ultrasound and deformable images. Journal of Bio-mechanical Engineering. 2002;124:734–741. doi: 10.1115/1.1519279. [DOI] [PubMed] [Google Scholar]
- Wang C, Garcia M, Lu X, Lanir Y, Kassab GS. Three-dimensional mechanical properties of porcine coronary arteries: a validated two-layer model. American Journal of Physiology Heart and Circulatory Physiology. 2006;291:H1200–1209. doi: 10.1152/ajpheart.01323.2005. [DOI] [PubMed] [Google Scholar]
- Wu PI, Minisini S, Edelman ER. Intramuscular drug transport under mechanical loading: resonance between tissue function and uptake. Journal of Controlled Release. 2009;136:99–109. doi: 10.1016/j.jconrel.2009.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan S, Chai H, Wang H, Yang H, Nan B, Yao Q, Chen C. Effects of lysophosphatidylcholine on monolayer cell permeability of human coronary artery endothelial cells. Surgery. 2005;138:464–473. doi: 10.1016/j.surg.2005.06.027. [DOI] [PubMed] [Google Scholar]
- Zemanek M.B.Jirl, Detak Michal. Biaxial tension tests with soft tissues of arterial wall. Engineering Mechanics. 2009;16:8. [Google Scholar]
- Zhu X, Pack DW, Braatz RD. Modelling intravascular delivery from drug-eluting stents with biodurable coating: investigation of anisotropic vascular drug diffusivity and arterial drug distribution. Computer Methods in Biomechanics and Biomedical Engineering. 2012 doi: 10.1080/10255842.2012.672815. [DOI] [PMC free article] [PubMed] [Google Scholar]