Estimates of age-specific reductions in HIV prevalence in Uganda: Bayesian melding estimation and probabilistic population forecast with an HIV-enabled cohort component projection model

Abstract

BACKGROUND

Much of our knowledge of the epidemiology and demography of HIV epidemics in Africa is derived from models fit to sparse, non-representative data. These often average over age and other important dimensions, rarely quantify uncertainty, and typically do not impose consistency on the epidemiology and the demography of the population.

OBJECTIVE

This work conducts an empirical investigation of the history of the HIV epidemic in Uganda and Tanzania through the late 1990s, focusing on sex-age-specific incidence, uses those results to produce probabilistic forecasts of HIV prevalence ten years later, and compares those to measures of HIV prevalence at the later time to describe the sex-age pattern of changes in prevalence over the intervening period.

METHODS

We adapt an epidemographic model of a population affected by HIV so that its parameters can be estimated using both the Bayesian melding with IMIS estimation method and maximum likelihood methods. Using the Bayesian version of the model we produce probabilistic forecasts of the population with HIV.

RESULTS

We produce estimates of sex-age-specific HIV incidence in Uganda and Tanzania in the late 1990s, produce probabilistic forecasts of the HIV epidemics in Uganda and Tanzania during the early 2000s, describe the sex-age pattern of changes in HIV prevalence in Uganda during the early 2000s, and compare the performance and results of the Bayesian and maximum likelihood estimation procedures.

CONCLUSIONS

We demonstrate that: (1) it is possible to model HIV epidemics in Africa taking account of sex and age, (2) there are important advantages to the Bayesian estimation method, including rigorous quantification of uncertainty and the ability to make probabilistic forecasts, and (3) that there were important age-specific changes in HIV incidence in Uganda during the early 2000s.

1. Introduction

This work makes two main contributions. The first is an empirical investigation of the history of the HIV epidemic in East Africa. We replicate the work of Heuveline (2003) to estimate sex-age-specific HIV incidence and prevalence in Tanzania and Uganda in the mid-to-late 1990s using our modified version of his HIV-enabled cohort component model of population projection (HCCMPP). Then assuming no change in incidence, we make probabilistic forecasts of those HIV-infected populations and compare them with the empirical estimates from the HIV/AIDS Indicator and Demographic and Health Surveys about ten years later. The second contribution is an adaptation and implementation of the Bayesian melding with IMIS estimation procedure (Poole and Raftery 2000; Raftery and Bao 2010) to work with the HCCMPP. This Bayesian method has important advantages compared to the maximum likelihood approach used by both Heuveline and ourselves in previous work (Thomas and Clark 2011), including the ability to produce probability distributions of the estimated parameters and model outputs which can be used for inference and projection.

HIV affects both mortality (increases) and fertility (decreases) and consequently has important effects on population growth and the sex and age composition of a population (UNAIDS 2009a). The fundamental process in an HIV epidemic is transmission of the virus – how and between whom. The details of the transmission dynamics determine who is infected and at what age, and this then determines, with a delay, who is sick and dying at a given age. A fuller understanding of the biological and behavioral determinants of transmission would give us the ability to design effective prevention interventions that target specific mechanisms, situations and people.

It follows then that the most valuable indicator of an HIV epidemic is incidence, the ratio of new cases to those at risk of infection (Hallett, White, and Garnett 2007; Bongaarts et al. 2008). Beyond an understanding of the dynamics of the epidemic as a whole, and in order to design and monitor well-targeted, effective and affordable interventions, it is necessary to refine measures of incidence by at least sex and age. The problem is that HIV incidence is extremely difficult and expensive to measure because it involves long-term follow up of a large number⁴ of HIV negative people (see for example: Mbulaiteye et al. 2002; Wambura et al. 2007). There is a promising test for recency of HIV infection being developed and tested, but so far it is difficult to calibrate the results accurately (Parekh et al. 2004; McDougal et al. 2006; McWalter and Welte 2009, 2010). This leaves only one widely applicable option for learning about HIV incidence: mathematical modeling.

Mathematical and computational models of HIV epidemics (see, for example: Anderson, 1988; Hallett et al., 2006; Cassels, Clark, and Morris, 2008; Hallet et al., 2008a, 2008b; Granich et al., 2009) represent populations and the mechanisms that transmit the HIV from one (type of) person to another. Essentially they perform either or both of two tasks: to estimate parameter values or to project the population forward in time in order to make predictions or investigate different scenarios. ‘Parameters’ in this sense are variables whose values govern the behavior of the model; incidence (or something closely related) is often a variable in these models. Used in estimation mode, the objective is to find values of the parameters that produce model outputs that match a set of empirical values. Because HIV prevalence is comparatively easy and cheap to measure, models are often fit or estimated to match prevalence. In projection mode the model outputs themselves are the quantities of interest.

We use a mathematical model of a population with HIV to do both estimation and projection. First we estimate the model parameters necessary for the modeled population to closely match the HIV prevalence in a variety of study populations in Tanzania, Uganda and Burundi (East Africa) in the early-to-mid 1990s. This provides us with the trend and age-pattern of HIV incidence from the beginning of the epidemic up to then that are necessary to create the age-patterns of prevalence observed in each study population. We then move to projection mode and hold HIV incidence constant in each sex-age group and project the populations of Tanzania and Uganda forward in time until we have new representative measures of HIV prevalence from the HIV/AIDS Indicator and Demographic and Health Surveys, and at that time we compare our projected HIV prevalence to the estimates from the surveys. HIV prevalence is determined by both incidence and survival of the infected population. Since we have no reason to believe that mortality has increased (which would reduce HIV prevalence), declines in HIV prevalence are most likely attributable to declines in HIV incidence.⁵

Estimates and outputs from models like ours often appear as single numbers without corresponding measures of uncertainty or precision, or if they do have these, they are constructed in an ad hoc fashion. We address this problem by employing the Bayesian melding with IMIS method (Poole and Raftery 2000; Raftery and Bao 2010) which has the ability to properly quantify uncertainty in the estimated parameters and all of the model outputs, including HIV incidence, prevalence, age structures, etc. We use the estimated probability distributions of parameters and model outputs to confirm that significant, age-specific changes occurred in HIV prevalence and incidence in Uganda during the late 1990s.

2. Background

The most important indicator of an HIV epidemic is incidence, the rate at which uninfected members of the population become infected. The logistic and economic difficulties of measuring and tracking HIV incidence motivates the use of a modeling approach to study changes and variation in HIV incidence. Thus, we focus our attention here on the implementation of new infections in the HCCMPP and how this relates to the more recent empirical record. Palloni (1996) points out that in a demographic model with HIV/AIDS the force of infection that produces the current level of prevalence should depend on the past level of prevalence. This endogeneity of HIV incidence is not modeled directly in the HCCMPP; instead, a simple approximation is used to provide a plausible trend in HIV incidence. Heuveline (2003) adopted a gamma curve to determine the incidence trend, a strategy also used in previous models of HIV/AIDS epidemics (e.g., Chin and Lwanga 1991; Salomon and Murray 2001). Additional parameters are included in the HCCMPP to allow the risk of infection to vary by age, sex, and location, but the underlying trend is the same. In other words, the levels are estimated and the pattern over time is fixed.

While the fixed gamma curve used by Heuveline (2003) may provide a plausible course of development for an HIV epidemic, there has been little (if any) validation of this assumption. In the face of such model uncertainty the usual practice is to turn to the empirical record for guidance. In the present case, however, the available evidence is fairly limited, as there are few studies that provide information on the trends of HIV incidence in sub-Saharan Africa. Among the exceptions is Mbulaiteye et al. (2002) who tracked HIV incidence in a cohort study carried out in Masaka, Uganda from 1989 to 1999, and found evidence of a decline over that period. However, a study by Kamali et al. (2000) in the same area produced estimates of incidence by sex and age that illustrated how difficult it is to identify trends and differences, given the large amount of uncertainty around the point estimates when disaggregating the population by sex and age. In an open-cohort study carried out at a demographic surveillance system in rural Tanzania, Wambura et al. (2007) collected data on HIV incidence by village type, sex and age with serosurveys conducted in 1994–1995, 1996–1997, 1999–2000, and 2003–2004.⁶ The three point estimates of HIV incidence for the intervals between the serosurveys suggested differences in the trends for men and women in roadside villages, as well as between women living in remote rural villages and those living in roadside villages. Among men living in roadside villages, there was a significant increase in the crude incidence rate from the first to the second estimate, while the third point estimate did not differ from the second. A similar trend was found for both men and women living in remote villages, but the level of incidence was significantly lower than that of men in roadside villages for each time period. The trend among women in the roadside villages differed significantly in each time period with an increase followed by a decline in crude incidence. Wambura et al. (2007) also explored HIV incidence trends by broad age groups for men and women in different locations. Although the uncertainty around the point estimates makes it difficult to draw conclusions, the results do motivate the hypothesis that the incidence trends may differ by age, sex, and location.

In addition to direct measures of HIV incidence, there are other sources that provide information about the trends over time. One suggested option is to use HIV prevalence among women aged 15–24 years who attend antenatal clinics (UNAIDS 2009b). The underlying logic is that these young women have only been exposed to the risk of infection via heterosexual transmission for a short period of time, and thus those who are HIV positive are likely to have been infected fairly recently, with a very small percentage dying from AIDS. While this metric may serve as a useful means for monitoring the epidemic, it provides little information about HIV incidence at older ages (see also Wawer et al. 1997; Ghys, Kufa, and George 2006; Żaba, Boerma, and White 2000). Another potentially helpful source of information includes the hypotheses explored with other epidemiological and demographic models of HIV/AIDS. For example, Gregson et al. (1997) describe the predictions of a model that fit the so-called HIV-1 hypothesis, which posits a pattern of sexual behavior in rural areas where men are typically infected first, perhaps while working in an urban center or town, and then infect their female partners. This pattern of sexual mixing may result in different trends in HIV incidence between men and women, or differences between urban and rural areas. Results from other models suggest that the peak in HIV incidence occurs earlier than what is produced from the gamma curve used in the HCCMPP (Stoneburner et al. 1996; Salomon and Murray 2001).

These various sources of information concerning the trends in HIV incidence in sub-Saharan Africa motivate our attempt to explore new specifications of the HCCMPP. Efforts to this end will be useful in helping to identify useful sources of variation in the risk of infection, which will in turn help to formulate successful plans for interventions and treatment.

3. Methods & data

3.1 Model

The HCCMPP is a multistate projection model, where the duration of HIV infection serves as the state variable. It is a simple case in that individuals are only able to move from shorter duration states to longer durations states. More general multistate models allow individuals to make transitions between states in either direction, e.g., from married to divorced and from divorced to married. Multistate models are used to study various demographic processes, and there is a large body of research on the properties and application of multistate models in demography, as well as other fields such as ecology and economics (for more details, see Schoen 1975; Palloni 2001; Keyfitz and Caswell 2005). A key feature of the multistate approach in the present context is that the vital demographic rates depend on the state that the individual currently occupies. In other words, this model allows us to model the association between HIV and fertility, and HIV and mortality.

The standard cohort component model of population projection (see for example Pritchett 1891; Cannan 1895; Pearl and Reed 1920; Bowley 1924; Whelpton 1936; Leslie 1945; Dorn 1950) was enhanced by Heuveline (2003) to include five additional states to accommodate the duration-specific stages of HIV infection: (i) uninfected, (ii) duration of infection of 0–4 years, (iii) duration of infection of 5–9 years, (iv) duration of infection of 10–14 years, and (v) duration of infection of 15+ years. A time-sex-age-specific incidence profile moves people from the uninfected to the first infected group (with a duration of infection of 0–4 years). Once people are in the infected groups they face diminished odds of surviving as they move to the next infected group. Infected women also experience slightly reduced fertility rates and consequently produce fewer births. As people move through the HIV infected duration groups, the effects of HIV become more pronounced to reflect the intensifying nature of their infections.

We have created a Leslie matrix representation of this model that allows us to run the model easily and allow some additional formal manipulation (Thomas and Clark 2011). We start with a base population count by sex and age, a set of underlying mortality and fertility rates, all from the United Nations (UN), and a set of parameters for the HIV incidence profile, and we multiply the column vector containing our population by the Leslie matrix. We divide both time and age into five-year periods, so one multiplication moves the population forward in time and age by five years. To go twenty years forward we multiply the population vector times the four Leslie matrices that represent the corresponding four five-year periods. The result is a new column vector for each sex containing the age-and HIV status-specific counts of the population twenty years in the future. From this we can calculate HIV prevalence by dividing the total HIV+ population count in a given sex-age group by the total population count in that same sex-age group.

If the starting population, vital rate schedules and HIV incidence parameters are fixed, the HCCMPP can be used in the traditional way to project an HIV-infected population forward in time. Alternatively, the HCCMPP can be used to estimate the values of unknown parameters. When used to estimate, the general idea is to vary the unknown parameters until a set of values are found that create a population that matches some set of criteria.

To estimate the HIV incidence parameters, we start with a reasonable base population and vital rates for the early 1980s (from the UN) and project the population forward ten to fifteen years until the mid 1990s when HIV prevalence measures began to become available (for small populations within Burundi, Tanzania, and Uganda). We then calculate the predicted HIV prevalence from the model and compare it to what was actually measured, and we adjust the incidence parameters until we have a close match to sex- and age-specific prevalence.

We have two methods for doing this: a maximum likelihood approach analogous to Heuveline (2003) (see also Thomas and Clark 2011) and the new Bayesian melding with IMIS technique described below in Section 3.3. Using either method we identify the most likely set of HIV incidence parameter values that, together with our assumptions about the base population and vital rates, produce the sex-age-specific HIV prevalence observed in the mid 1990s (or something very similar), and, additionally, measures of uncertainty around those point estimates. The Bayesian approach is particularly useful in that the parameters can be directly interpreted in a probabilistic framework.

To project an HIV-infected population forward in time, the model is run with known values for all the parameters. This produces a predicted population corresponding to the base population and the sequence of parameter values used to govern the dynamics of the population over time (it is possible to change parameter values as time goes by to reflect changing vital rates or HIV incidence). We use the model in this way to produce probabilistic forecasts of the populations of Tanzania and Uganda (DHS data with information on HIV prevalence for Burundi are not available at the time of writing). We make predictions using the predictive (posterior) distribution of parameter values from the Bayesian estimation method, which yields a distribution of forecasts of the population at some time in the future, and from this distribution we can make probabilistic statements about how likely a given future population is. The result is that the most likely sets of parameter values translate into the most likely set of populations (net of assumptions about trends in parameter values over the projection period).

Our extensions and assessment of the model are based primarily on HIV infection, and thus we focus our attention on the model parameters related to incidence. Consider HIV-negative women in the five-year age group a at time t₁ in a population located in region r. In the HCCMPP, the proportion of these women who are alive and HIV-positive five years later at time t2 is denoted by if_,a,t_1,r and can be decomposed as

$$i_{f,a,t_1,r}=1-\text{exp}\{-{\mathrm{\Gamma }}_{t_2-t_1}{H}_r{j}_{f,a}\},$$ (1)

where subscript f refers to females, Γ_t2–t1 captures the trend in HIV incidence between times t₁ and t₂, H_r is a population-specific parameter that determines the size of the epidemic in region r, and j_f,a is the age-specific parameter for females that measures incidence relative to women aged 25–29 years for whom the value is fixed at one (hereafter age-specific relative incidence ratio). The corresponding model input for males, i_m,a,t₁,r has the same decomposition, with women aged 25–29 years again serving as the reference group. This decomposition allows the level of HIV incidence to vary by age and sex, as well as across populations in different locations, but the general shape of the trend through time will be the same. The value for the trend in HIV incidence between times t₁ and t2 is calculated from the gamma distribution as follows

$${\mathrm{\Gamma }}_{t_2-t_1}={\int }_{t_1}^{t_2}\frac{x^{\alpha -1}{e}^{-x/\beta }}{(\alpha -1)!{\beta }^{\alpha }}dx,$$ (2)

where α and β are parameters taking only positive values. The parameters j_f,a, j_m,a, and H_r are estimated using data compiled by Heuveline (2003), but the time trend is fixed and determined by Equation 2 with α =5 and β =3. It should also be noted that an initial year t0 needs to be chosen for when the country-specific epidemic began. This year is assumed to be the date when HIV prevalence reached 1% in the general population, and the corresponding values for the countries in our analysis are taken from the United Nations (1998).

We extend the work of Heuveline (2003) by exploring several different specifications for the trend in HIV incidence Γ_t2-_t1 using two basic approaches. The first approach simply involves estimating the parameters of the gamma curve, α and β, along with the other HCCMPP parameters. This approach is then extended by estimating separate gamma curves for men and women, with sex-specific reference groups aged 25–29 (i.e. j_f,25–29 = 1 and j_m,25–29 = 1 ). The second strategy is to include an additional parameter for each of the first four projection periods and to estimate them in conjunction with the other HCCMPP parameters. Again, we explore two specifications that include a single trend shared by women and men as well as sex-specific trends.

Forecasts of HIV prevalence are made using each of these specifications for incidence, and the corresponding predictive performance is assessed by comparing the forecasts to the observed levels of HIV prevalence in the HIV/AIDS Indicator and Demographic and Health Surveys for Tanzania and Uganda.

3.2 Data

Three compilations of data are used in this analysis, the first of which is taken from Heuveline (2003) who reviewed the epidemiological literature and compiled data on HIV-related outcomes from populations located in East Africa.⁷ For the current analysis, we use only those data from Burundi, Tanzania, and Uganda to limit the geographic heterogeneity across the local epidemics. The types of outcomes include: HIV test results in a general-population sample; HIV test results in an antenatal clinic (ANC) patient sample; HIV test results in all or a sample of births from HIV+ mothers; HIV test results during a follow-up of an HIV- sample; and survival during a follow-up of HIV+ individuals. These data, which are used to estimate the HCCMPP parameters, were all collected before 1998 with the majority collected during the 1990s and a few from the late 1980s. The outcomes are differentiated by age and sex, and were collected in rural, semi-urban or urban locations. After calibrating the model with the data collected before 1998, we then use the HCCMPP to make forecasts of sex-age-specific HIV prevalence in Tanzania and Uganda, and compare the forecasts to the levels observed in the HIV/AIDS Indicator Surveys and Demographic and Health Surveys collected in 2004 and 2007 for Tanzania, and in 2004 for Uganda (neither source of data is available for Burundi). The third compilation of data is taken from the United Nations global demographic estimates (2007), which provides the basic model inputs needed to make the forecasts. The HCCMPP requires an initial age distribution for women and men as well as sex-age-specific rates of fertility and mortality for the uninfected populations in each country over time. All of these model inputs are treated as fixed (i.e. not estimated) in our analysis.

3.3 Estimation

Maximum Likelihood

We implement a standard maximum likelihood estimation procedure described in full elsewhere (Thomas and Clark 2011). This procedure produces point estimates for each of the model parameters and standard 95% confidence intervals, but does not provide a statistically sound method for making probabilistic projections.

Bayesian Melding

In the Bayesian framework, parameters are treated as random variables. Prior beliefs about the parameters are quantified in the form of a joint probability density p(θ), where θ is a vector of parameters for which we will make inference. The data y are brought in by specifying a likelihood ℒ(y|θ), which is the probability of the observed data for a given value of the parameters. Using Bayes’ Theorem and the marginal density of the datap(y), we can update our prior beliefs to obtain the posterior distribution

$$p(\theta |\mathbf{y})=\frac{ℒ(\mathbf{y}|\theta )p(\theta )}{p(\mathbf{y})}\propto ℒ(\mathbf{y}|\theta )p(\theta ),$$ (3)

which is used to make inferences about θ.⁸

Bayesian melding (Poole and Raftery 2000) was designed for problems in which a deterministic model, such as HCCMPP, is used in the likelihood function. Let M represent the model which transforms a set of parameter inputs θ into a set of model outputs φ = M(θ). As described above, the Bayesian approach requires a prior density for the model inputs p(θ) and a likelihood for the outputs and the data L(M(θ)). These two sources of information are combined to produce the following posterior distribution for the model inputs

$$p(\theta |\mathbf{y})\propto ℒ(\mathbf{y}|M(\theta ))p(\theta ).$$

Inference is performed by sampling from p(θ|y) and summarizing the resulting posterior sample. Furthermore, we can run HCCMPP for each set of inputs in the posterior sample to obtain a posterior sample of the model outputs p(φ|y). Sex-age-specific HIV prevalence is the model output that interests us because we can use it to assess forecasts. Note that the posterior sample reflects the distribution of model outputs, and thus the quantiles of the posterior sample can be used to make probabilistic statements about the values of the model outputs. This feature of the Bayesian framework is used to assess probabilistic forecasts of HIV prevalence by comparing these predictive intervals to observed data.

Bayesian Melding Estimation

In our implementation of Bayesian melding with the HCCMPP we specify independent uniform priors that are relatively uninformative and thereby place most of the influence with the observed data. We use a beta-binomial likelihood to allow for heterogeneity across the different types of data and geographic regions from which they are collected. The beta-binomial distribution is a mixture of binomial distributions n ~ binomial(N, π), with the mean of the binomials following a beta distribution Nπ ~ beta(a, b). We adopt the re-parameterization π ~ beta(µ, M) of the beta distribution used by Grassly et al. (2004), where µ = a/(a + b) and M = a + b. The extra variation in the beta-binomial distribution (relative to the binomial) is determined by M, and the mean and variance of n are Nπ and {1 + (1 + N)/(M + 1)}π(1 − π)/N, respectively. In our application the M parameter is estimated along with the other HCCMPP parameters. The likelihoods for each age, sex, and location are treated as independent and multiplied together to produce a total likelihood.

With the HCCMPP it is effectively impossible to derive the analytic form of the posterior distribution because of the complexity of the model. We address this in the standard way by drawing a sample from the posterior distribution and carrying out inference for the model parameters by summarizing the posterior sample. The posterior distribution is estimated by resampling from an initial sample drawn from the importance sampling distribution using weights that identify sample members that have relatively high posterior probabilities. A transparent way to implement this approach is the sampling importance resampling (SIR) algorithm suggested by Rubin (1987, 1988) which uses the likelihood function to form the resampling weights. In this case the prior distribution serves as the importance sampling distribution. Bayesian melding has been successfully implemented with the SIR algorithm in the past (see for example Poole and Raftery 2000; Alkema, Raftery, and Clark 2007), but with HCCMPP the SIR approach did not work. Because the HCCMPP has so many parameters, samples from the prior distribution failed to cover important regions of the posterior distribution, resulting in a poor approximation. A similar problem often occurs if the posterior distribution is multimodal or concentrated in curved manifolds (Raftery and Bao 2010).

A more efficient approach is incremental mixture importance sampling (IMIS) which was originally introduced by Steele, Raftery, and Emond (2003); Steele, Raftery, and Edmonds (2006) and further developed for posterior distributions of continuous parameters by Raftery and Bao (2010). IMIS is an iterative technique that builds up an importance sampling distribution by adding new points in areas of high posterior probability at each step, based on the idea of defensive mixture distributions developed by Hesterberg (1995). This feature of IMIS ensures that the target distribution (the posterior in our case) is adequately covered by the importance sampling distribution, resulting in much greater efficiency than SIR. The following steps outline the IMIS algorithm we use to implement Bayesian melding. We refer to this version of the algorithm as IMIS-opt because it includes steps that require the use of a function optimizer.⁹

1. Begin by drawing B0 = d* 1, 000 inputs θ₁,…, θ _b0 from the prior distribution p(θ), where d is the dimension of θ. Calculate the importance weights

   $$w_i^{(0)}\propto \frac{{ℒ}_i}{{\sum }_{i=1}^{B_0}{ℒ}_i}$$

   where L_i is the likelihood for the i^th input.

2. Use the input with the maximum weight as the starting value for an optimization routine that maximizes the log likelihood using 100 function evaluations. If the local optimum has a likelihood larger than any other input from the prior, then save the local optimum, ${\theta }_1^{\mathit{\text{opt}}}$, and calculate the inverse of the Hessian matrix, ${\sum }_1^{\mathit{\text{opt}}}$. If the Hessian does not yield a positive definite covariance matrix, then use the matrix of first derivatives of the likelihood times the prior (evaluated at the local optimum) to create a new information matrix by adding it to the precision matrix of the prior distribution, and using the inverse of this new matrix as the covariance matrix.

3. For i = 2:D exclude the starting points and the fraction of inputs $\frac{1}{D}$ that have the smallest Mahalonobis distance to ${\theta }_{(i-1)}^{\mathit{\text{opt}}}$. Of the remaining inputs, choose the one with the largest weight as the new starting point for obtaining ${\theta }_i^{\mathit{\text{opt}}}$. The extent to which the parameter space is searched is partially determined by the parameter D. Larger values of D indicate a more thorough search of different areas of the parameter space for local maxima. In our work, we use a value of 10 for the parameter D.

4. For each saved local optimum, indexed by s, sample B = 400 new inputs, H_s, from a multivariate Gaussian distribution with center ${\theta }_s^{\mathit{\text{opt}}}$ and covariance matrix ${\sum }_s^{\mathit{\text{opt}}}$. This step is included to help ensure that new areas of the parameter space are explored for points with high posterior probabilities.

5. For k= 1, 2,… repeat the following steps until a stopping criterion is satisfied.

   1. Form the posterior sampling weights

      $$w_i^{(k)}\propto \frac{{ℒ}_{i}p({\theta }_i)}{q^{(k)}({\theta }_i)}$$

      where $q^{(k)}(\theta )=\frac{B_0}{N_k}p+\frac{B}{N_k}{\sum }_{s=1}^{D^{*}+k-1}{H}_s$, N_k is the total number of inputs at stage k, and D* is the number of saved local optima.
   2. Take the input with the maximum weight, θ^k, as the center of a multivariate Gaussian distribution, H_D*+k. Use the d * 100 inputs with the smallest distance, with respect to the covariance of the prior distribution, from the mean to calculate the weighted covariance matrix, ∑^(k), with weights that are proportional to the average of the importance weights and $\frac{1}{N_k}$. Sample B new inputs from H_D*+k.
   3. If the expected number of unique points

      $$\widehat{Q}(w)=\sum _{i=1}^{N_k}(1-{(1-w_i)}^M)$$

      is greater than $M*(1-\frac{1}{e})$, then stop iterating and re-sample M inputs with replacement from θ₁,…, θ_Nk with weights w₁,…, w_Nk. In our application to HCCMPP, we set M= 3,000 which requires the expected number of unique points to be 1,896.

The first step in the IMIS-opt algorithm is essentially the same as the SIR algorithm, except that with the latter approach the resampling is done with weights proportional to $w_i^{(0)}$. The additional optimization steps (2 – 4) in the IMIS-opt algorithm seek to cover areas in the posterior sampling space that have high posterior probability (relative to the prior). Given several local optima, the algorithm then proceeds by adding new components to the sampling function that are centered around the inputs with the largest weights, with the local neighborhoods providing the covariance information.

3.4 Calibration & validation

Our assessment of the HCCMPP is based on an attempt to accurately forecast sex-age-specific HIV prevalence in Tanzania, as measured in the 2004 and 2007 DHS. The first step in this assessment involves calibrating the model to adequately reproduce the first twenty years of the HIV epidemic in this country. We use data collected before 2000 from urban and rural areas located in Burundi, Tanzania, and Uganda to estimate the HCCMPP parameters. Observations from these other countries were included to increase the stability and precision of our parameter estimates, and seemed reasonable given the close proximity of these countries. After calibrating the model to the local epidemic in East Africa, these estimates are then used to make HCCMPP forecasts of the levels of HIV prevalence observed in the 2004 and 2007 DHS in Tanzania. The Bayesian melding framework which we employ for parameter estimation and forecasting yields a posterior distribution of HIV prevalence by age and sex. These distributions allow us to assess the accuracy of the HCCMPP forecasts by comparing the observed coverage of the predictions with the nominal coverage. For example, we expect half of the observed levels of HIV prevalence to fall within the 50% prediction intervals, and similarly for the 80% and 95% prediction intervals reported here. Because our forecasts take into account uncertainty in HIV incidence but not the vital rates, our forecasts understate the amount of uncertainty around future levels of HIV prevalence – i.e. the coverage of our forecasts will be slightly too low.

4. Results

4.1 Parameter estimates: Maximum likelihood and Bayesian Melding

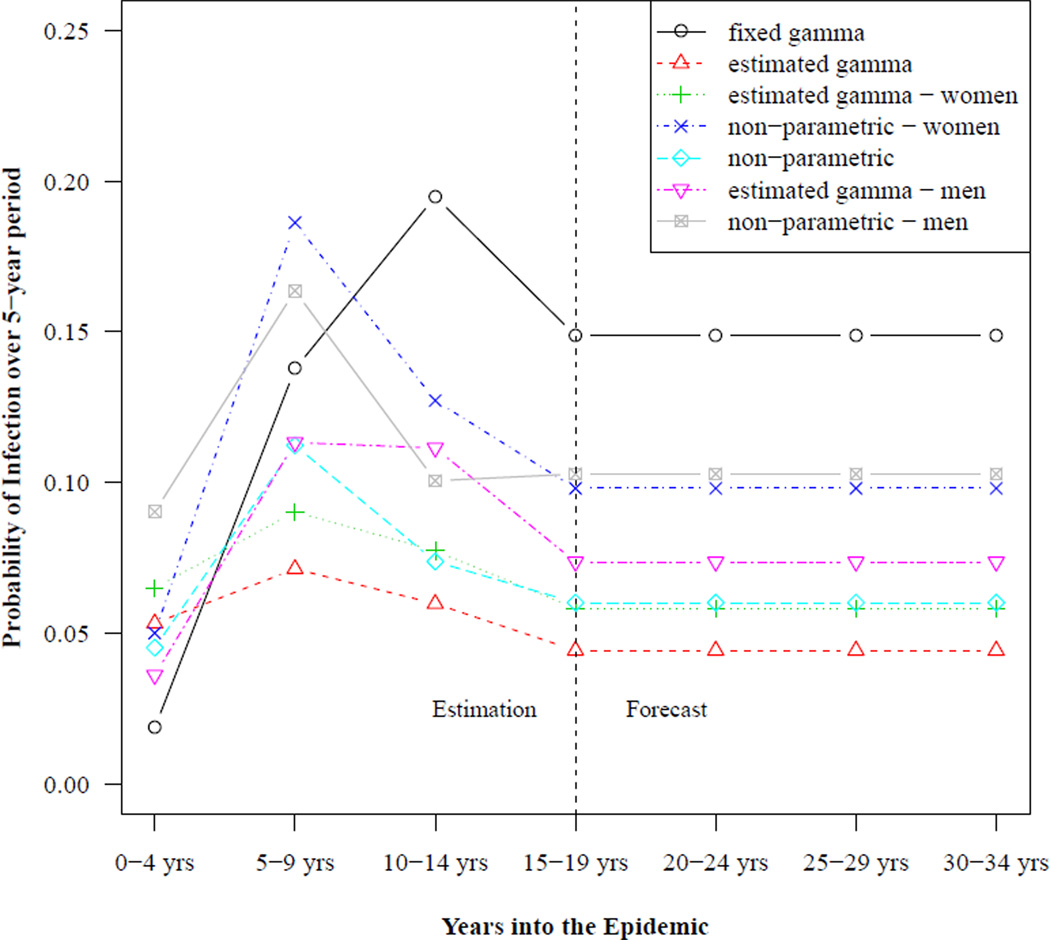
The different trends in HIV incidence used with the HCCMPP to forecast HIV prevalence are shown in Figure 1. Each trend in the plot shows the estimated probabilities of infection over a five-year period for the reference group in Rakai, Uganda (only the posterior means are shown for the estimated trends). For the models where the incidence trend is the same for women and men, only the estimated probabilities for women aged 25–29 are shown.¹⁰ In our specifications where the trend is sex-specific, separate trends are shown in the plot corresponding to the sex-specific reference group aged 25–29. The vertical line indicates the last period for which we use data to estimate the model parameters. HIV incidence is assumed to stabilize during this time period, 15–19 years into the epidemic, and the corresponding level of incidence is used to forecast subsequent levels of HIV prevalence.

Figure 1. Example HIV incidence trends: Rakai, Uganda.

Notes: The level of incidence corresponds to the sex-specific age group 25–29 years when separate trends are used for women and men, and for women aged 25–29 years when a single trend is used for both groups. Values to the left of the vertical line are used to estimate the HCCMPP parameters, and values to the right are used to make forecasts to compare with data from the DHS surveys.

The most striking feature in Figure 1 is how the trend from the fixed gamma curve, which was used in the original analysis (Heuveline 2003), reaches a level that is much higher than the estimated trends during the period 15–19 years into the epidemic. Conversely, when the trend in HIV incidence is estimated, the level of incidence is higher during the initial period of the epidemic and the peak occurs earlier than the trend from the fixed gamma curve. A second finding is that when separate curves are estimated for men and women, the trends appear to be different, for both the gamma and non-parametric specifications. Among those aged 25–29, estimated incidence based on the non-parametric trend is higher for men during the first five years of the epidemic, with a cross-over in the subsequent projection period, and convergence during the period 15–19 years into the epidemic. This cross-over of the incidence trends for men and women is consistent with the HIV-1 hypothesis described by Gregson et al. (1997), which posits a pattern of HIV transmission in rural areas where men are typically infected first, perhaps while working in an urban center or town, and then infect their female partners at a later point in time. The sex-specific trends estimated using gamma curves, however, suggest that the trend for men and women follow the same pattern and that only the levels are different. A final note is that these differences and cross-overs are only suggestive since there is uncertainty around the point estimates shown in Figure 1.

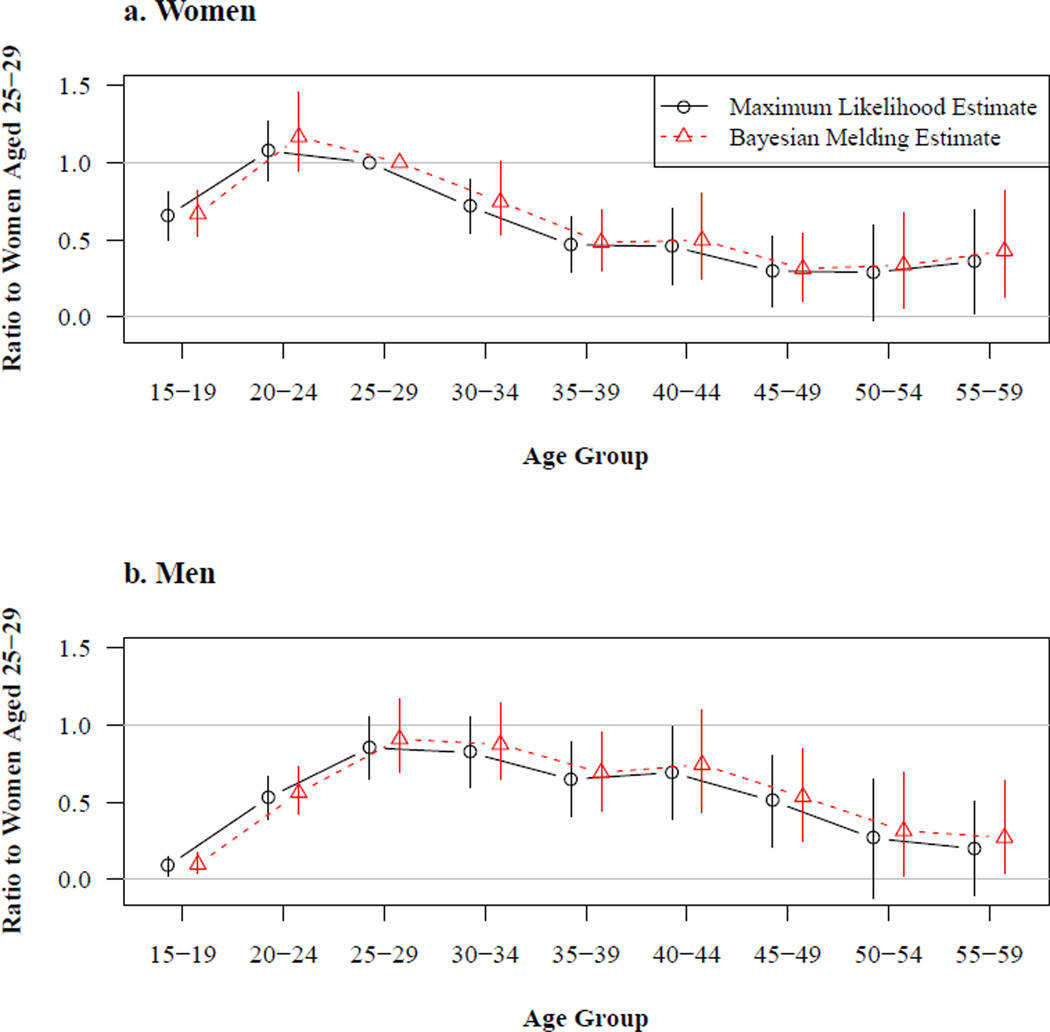
Figure 2 displays the estimated sex-age-specific relative HIV incidence rate ratios obtained using the fixed gamma curve incidence trend. These describe how the risk of acquiring HIV changes with sex and age. This set of incidence profiles is estimated jointly using all of the populations in the estimation procedure. Results from the maximum likelihood (ML) and Bayesian melding (BM) estimation methods are very similar to each other and to Heuveline’s (2003) estimates. Both sets of estimates for women, top panel of Figure 2, show that the risk of infection increases significantly from the 15–19 age group to the 20–24 age group, with the latter experiencing the highest level of incidence. The risk of infection then declines until reaching a fairly stable level after age 35. There are also very few differences between the ML and BM estimates for men, shown in the bottom panel of Figure 2. With either approach, the estimated risk of infection for men is relatively low among those aged 15–19 and clearly increases among the next two older age groups. Uncertainty makes it difficult to identify differences in the risk of infection among men between the ages of 25 and 49, but the ML and BM results seem to suggest that men in their fifties experience a lower risk of infection than men aged 25–34. For both women and men, the ML and BM intervals around the point estimates increase with age, which is expected given the increasingly smaller number of observations at older ages.

Figure 2. Estimated age schedules of HIV incidence.

Notes: These estimates are obtained using the fixed gamma curve incidence trend. The incidence of women aged 25–29 is given by the value of the incidence trend multiplied by a population-specific scale factor. All other sex-age categories in this figure are referenced to women aged 25–29 in a straightforward multiplicative sense, i.e. men aged 20–24 experience HIV incidence a little over 50% as great as women aged 25–29. Consequently this figure displays ‘relative’ HIV incidence by sex and age. The vertical lines running through the point estimates cover the 95% confidence intervals for the results and the 95% credible intervals for the Bayesian results.

Bayesian melding (BM) has been used in previous analyses involving deterministic models of population dynamics and HIV/AIDS that include less than five parameter inputs (Poole and Raftery 2000; Alkema, Raftery, and Clark 2007). A key finding in this paper is the successful implementation of BM in a relatively high dimensional parameter space using the incremental mixture importance sampling (IMIS) algorithm introduced by Raftery and Bao (2010). We are able to perform statistical inference and to make probabilistic projections using models that range from the simplest with 29 parameters up to the most complicated with 36 parameters. The IMIS algorithm proved to be much more efficient than the sampling importance resampling (SIR) technique (Rubin 1987, 1988) that has been used in previous work to implement BM (e.g., Poole and Raftery 2000; Alkema, Raftery, and Clark 2007).¹¹

4.2 Model fit

Having been able to successfully implement BM with various specifications of the model, we are left with the task of choosing among the different models that are distinguished by the trend in HIV incidence. Palloni (1996) pointed out that in a demographic model with HIV/AIDS the force of infection that produces the current level of prevalence should depend on the past level of prevalence, and thus the trend in HIV incidence is endogenous. To make this problem tractable with HCCMPP, Heuveline (2003) assumes an incidence trend based on a gamma curve, a strategy also used in previous models of HIV/AIDS epidemics (e.g., Chin and Lwanga 1991; Salomon and Murray 2001), and treats it as a fixed model input. While the gamma curve may yield a plausible trend, there is at least some uncertainty around this part of the model. In our analysis, we relax the assumption of a fixed gamma curve by estimating the trend in HIV incidence and allowing it to vary by sex and in functional form (see Section 3 for more details about the implementation and estimation). The estimated trends are discussed in the previous section, and here we focus on the comparison of the following five models included in the analysis: (i) fixed gamma curve, (ii) estimated gamma curve, (iii) sex-specific estimated gamma curves, (iv) non-parametric curve, and (v) sex-specific non-parametric curves. Given the seemingly large differences between the trends shown in Figure 1, it is natural to be concerned with the relative merit of each model. One standard criterion is how closely each model fits the data. A simple metric for assessing model fit is the sum of squared residuals. According to this measure, there are only slight differences across all of the models with the values ranging from a high of 0.225 for the HCCMPP with the fixed gamma curve to a low of 0.201 for the model with the sex-specific non-parametric trends. An alternative measure for comparing models is Bayes factor (Jeffreys 1939; Kass and Raftery 1995), which is easily calculated from the IMIS approach taken here (Raftery and Bao 2010). The model comparisons based on Bayes factor, with equal prior probabilities given to each model, favor the HCCMPP with the fixed gamma curve over all of the other models, but the evidence is fairly weak since all of the values for the Bayes factors are less than 1.1 – generally, values greater than 3 indicate important differences between the models being compared (Raftery 1995). Although the evidence is weak, it is interesting to note that the Bayesian model comparison favors the simplest model with the fixed gamma curve, which is also the model that is the best at predicting future observations – another important criterion for evaluating the relative merit of different models.

4.3 Model validation: Calibration and predictive performance for Tanzania

We validate our model by examining its predictive performance in Tanzania. We estimate the model using high quality data collected by small community-based studies in Tanzania, Uganda and Burundi in the mid 1990s. There was little change in the prevalence of HIV in Tanzania from the mid 1990s until the mid 2000s (Asamoah-Odei, Calleja, and Boerma 2004; UNAIDS 2009a), and consequently, if we use our estimated parameter values from the mid 1990s, we should be able to forecast the sex-age distribution of HIV prevalence in the mid 2000s accurately and with reasonable confidence.

Sex-age-specific HIV prevalence measured by the HIV/AIDS Indicator and Demographic and Health Surveys in Tanzania in 2004 and 2007 serve as the targets for our forecast. To produce the forecast we use the best-fitting fixed gamma trend in overall HIV incidence (see Figure 1 for the gamma trends in HIV incidence) and hold it constant from year fifteen of each projection (roughly the year 2000 in calendar time). We use our estimated distributions of HIV incidence by sex and age with no modifications for the duration of the forecast. The distribution of forecasted values of HIV prevalence is generated by making multiple draws from the estimated joint parameter distribution and projecting the population forward for each of those with a constant overall incidence trend; see Figure 1. The result is a sex-age-specific distribution of HIV prevalence values at various times in the 2000s that we can use to compare with the empirical values measured by the surveys.

To assess the accuracy and calibration of the forecast, we take the predicted distributions for sex-age-specific HIV prevalence for Tanzania¹² and calculate the quantiles of the 50%, 80%, and 95% credible intervals and compare these to the corresponding observations from the HIV/AIDS Indicator and Demographic and Health Surveys. Table 1 displays these ‘coverage’ results. There is one row for each of the overall HIV incidence trends that we tried and three sets of columns for the 50%, 80% and 95% credible intervals. Each of these contains the percent of the empirical observations that fall below the lower limit, within the central interval and above the upper limit. Reading the first row of the table, we find that 11% of the observations fall below the 25^th percentile, 43% fall between the 25^th and 75^th percentiles and 46% above the 75^th percentile, etc.

Table 1.

Empirical coverage of the Bayesian prediction intervals for HIV prevalence

	50% Prediction Interval			80% Prediction Interval			95% Prediction Interval
HIV Incidence Trend	<25%	[25%, 75%]	75%<	<10%	[10%,90%]	90%<	<2.5%	[2.5%, 97.5%]	97.5%<
fixed gamma curve   % of Observations	10.7%	42.9% (2.6)	46.4%	3.6%	75.0% (4.9)	21.4%	3.6%	92.9% (7.5)	3.6%
estimated gamma curve   % of Observations	10.7%	10.7% (1.7)	78.6%	3.6%	25.0% (3.0)	71.4%	3.6%	50.0% (4.2)	46.4%
estimated sex-specific gamma curves   % of Observations	10.7%	10.7% (1.8)	78.6%	3.6%	28.6% (3.3)	67.9%	3.6%	53.6% (4.8)	42.9%
non-parametric trend   % of Observations	10.7%	10.7% (2.0)	78.6%	3.6%	39.3% (3.7)	57.1%	3.6%	57.1% (5.4)	39.3%
sex-specific non-parametric trends   % of Observations	10.7%	25.0% (3.1)	64.3%	3.6%	67.9% (5.7)	28.6%	3.6%	89.3% (8.4)	7.1%

Notes: Results for Tanzania for various specifications of the HIV incidence trend. Numbers in parentheses are mean interval widths measured in percentage points. There are 28 observations.

The forecast using the fixed gamma for the overall trend in HIV incidence clearly produces the best calibrated results (the observed coverage comes closest to what we expect), and the calibration is acceptable. 92.9% of observations fall within the 95% credible interval with an even 3.6% below and above. Calibration deteriorates slightly as the credible intervals shrink, and there is a slight tendency to understate prevalence, as indicated by the fact that more observations fall above the prediction intervals than expected. Altogether the calibration results for Tanzania indicate that the model is reasonably accurate and represents uncertainty in a way that corresponds to empirical observation.

Figure 3 displays the the forecast errors for Tanzania 2004 and 2007 and Uganda 2004, again using the best-fit fixed gamma trend in overall HIV prevalence with a constant value for years after 2000. Each plot contains the distribution of forecast errors by age group summarized with a boxplot. If the forecasts were well-calibrated these boxplots would describe compact distributions centered at zero. Each forecast error is the residual between the observed and forecast values (observed – forecast). The distributions arise because there is a distribution of predicted values for each sex-age category. Our forecasts take into account uncertainty in HIV incidence but not underlying vital rates, and consequently we expect that uncertainty will be slightly underestimated.

Figure 3. HIV prevalence forecast error distributions.

Tanzania

Our earlier assessment suggests that the forecasts of the observed levels of HIV prevalence in Tanzania are reasonable. This is reflected in the left two columns of plots in Figure 3, in which the boxplot for every age group is centered near zero with comparatively short tails. The only systematic deviations from zero are in the age range 30–44 for women and ages 40–44 (2004) and 35–39 (2007) for men. For those ages the forecast appears to be slightly too low. Overall the forecast errors for Tanzania are small – a few percentage points – and the error distributions contain small variation and are centered close to zero.

Uganda

The forecast errors for Uganda (rightmost column of plots in Figure 3) clearly reveal the extent and age-pattern of the decline in HIV incidence over the intervening decade. Compared to Tanzania, the forecast error distributions are much more variable and deviate from zero in a systematic age-dependent way. The greater variability likely corresponds to the greater geographic variability in the Ugandan data sources used to estimate the model parameters, including four different sites (Fort Portal, Gulu, Masaka, and Rakai) in both rural and urban areas. For women the 99^th percentile of the error distributions does not include zero until age 30. For younger ages the forecast errors are very significantly negative (the forecast overstates prevalence) with a clear trough in the 25–29 age group at a median error of about –22%. This trough relaxes slowly through the older age groups toward a constant median error of about –5% in the age range 45–59. This striking age-pattern indicates that HIV incidence fell most dramatically in the 15–24 age group (reflected in the later and older drop in prevalence in the 25–34 age group) by perhaps more than 20%. Further, there must have been significant reductions in incidence at all other ages, particularly at 25–34 years old.

For Ugandan men the situation is similar, but the magnitude of the errors is slightly less and the age-pattern is different. The trough for men is wider covering about ages 30– 44, but not quite as low, reaching a minimum of approximately –19%. The trough also begins to develop at older ages, only showing strong deviation from zero in the 20–24 age group. Similar to women, the 99^th percentile of the error distributions does not include zero until age 35. The age-pattern of deviations in the male errors indicate a reduction in incidence over a broad range of ages from roughly 20–29 to 40–49, with the largest reductions over roughly ages 20–44.

4.4 Conclusions

Using some of the early measures of HIV prevalence from community-based studies in Tanzania, Uganda and Burundi during the early to mid 1990s, we estimate the age profile of HIV incidence that is consistent with underlying vital rates and the observed age pattern of HIV prevalence. We apply the new Bayesian melding with IMIS estimation procedure to ‘fit’ the HIV enabled cohort component model of population projection created by Heuveline (2003). Our results corroborate both his and our own earlier work using a maximum likelihood estimation procedure. The age profile of incidence is younger and more focused for women with peaks in the 20–24 year age group for women and 25–29 year age group for men.

The Bayesian estimation framework provides an advantage compared to maximum likelihood techniques because it enables us to quantify uncertainty in estimated parameter values in a statistically valid way that can be interpreted and manipulated in a fully probabilistic framework. Most important to us, however, is the opportunity to produce probabilistic projections – true forecasts – of the HIV-affected populations. This allows us to validate our model in one more way by comparing (probabilistic) forecasts of HIV prevalence with empirical measures of prevalence in Tanzania. There was little change in HIV incidence in Tanzania between the mid 1990s and early 2000s, and we are able to predict, with reasonably calibrated accuracy, age-specific HIV prevalence in Tanzania in the early 2000s by forecasting forward with no change in our estimated HIV incidence pattern.

We use one further advantage of the Bayesian framework to compare models with different specifications of the trend in HIV incidence. The Bayesian framework allows us to use Bayes factors to compare the models and determine that the simple fixed gamma curve originally specified by Heuveline produces better forecasts compared to a variety of more flexible specifications with more parameters – the Bayes factor takes into account the number of parameters, effectively penalizing models with larger numbers of parameters (degrees of freedom).

Finally, we use the probabilistic forecast of HIV prevalence for Uganda to characterize the age-pattern of reductions in prevalence resulting from the well-documented declines in HIV incidence that took place in Uganda between the early 1990s and mid 2000s. This age pattern of change in HIV prevalence reflects the earlier and younger changes in HIV incidence that were required to reduce the HIV+ fraction of the population.

5. Discussion

5.1 Summary

This paper makes two main contributions, the first is to validate the HCCMPP developed by Heuveline (2003). We find that the model can produce accurate forecasts of age- and sex-specific HIV prevalence in Tanzania, and that an assumption of a stabilized trend in HIV incidence provides estimates of the extent of the decline in the risk of HIV infection in Uganda. In order to produce accurate forecasts with the HCCMPP for other countries in sub-Saharan Africa, the model may require new modifications to capture the geographic heterogeneity in the HIV epidemics across this region. Other potential sources of variability not captured by the model are the uncertainty around the start date of the epidemic and around vital rates. Including these as estimated model inputs may be useful in terms of improving the predictive performance of HCCMPP and applying it to other countries. Despite these issues, it is impressive how well the model does when considering the differences between the data used to calibrate it (i.e. estimate the HCCMPP parameters) and the data used to validate the model forecasts. The former were collected from relatively small community-based studies while the latter were collected from nationally representative samples.

The second contribution is to use a new Bayesian estimation technique designed for deterministic models. We have shown that the IMIS algorithm (Raftery and Bao 2010) can be used successfully to implement the Bayesian melding estimation approach with the 30+ parameter HCCMPP model. This suggests that the approach could be used more generally to enable demographers to quantify, in a statistically rigorous way, the uncertainty around both parameter estimates and model outputs in many of the deterministic models they use. With respect to the CCMPP (HIV-enabled or not), the ability to quantify uncertainty around demographic projections is useful in a fundamental sense. This allows decision-makers to define the probability of extreme outcomes, with respect to the levels of HIV prevalence and incidence, and make informed cost-benefit and risk tolerance decisions in a valid probabilistic framework. Furthermore, probabilistic projections produced using a CCMPP-type model and Bayesian melding with IMIS can be used to validate the model by comparing forecasts to observed values. The Bayesian framework can also be used to compare competing model specifications using Bayes factors.

Finally, we attempt to shed some light on the likely pathways that epidemics follow as they mature by using data to estimate the trends in HIV incidence. Our results suggest that the gamma curve used by Heuveline (2003) in the original work with HCCMPP provides the best predictive performance of sex-age-specific HIV prevalence in Tanzania.

5.2 Recommendations

1. Because HIV incidence is such an important indicator of an HIV epidemic, and because it is so difficult to measure HIV incidence empirically, epidemiologists, demographers and statisticians should prioritize further development of mathematical models and statistical procedures that allow us to estimate HIV incidence with uncertainty. To be of practical use to decision makers in the small areas where interventions are implemented and evaluated, these techniques should attempt to provide estimates of incidence by time, sex and age.

2. Given the success of Bayesian melding with IMIS applied to the 30+ parameter HCCMPP and the inherent advantages of the Bayesian framework, epidemiologists and demographers should consider applying this and similar procedures to other models and estimation procedures common to their disciplines.

3. We have successfully produced probabilistic forecasts of HIV epidemics taking into account uncertainty in HIV incidence. Using a similar Bayesian framework, future work on both HCCMPP and regular non-HIV CCMPP should incorporate uncertainty in vital rates and migration to produce probabilistic forecasts that take into account all major sources of uncertainty.

4. The Bayesian framework gives us the ability to conduct Bayesian model comparison using Bayes factors. This ability should be used to investigate the effects of interventions by comparing models that do and do not model the intervention. Bayesian model comparison will tell us if the intervention model fits the data better than the non-intervention model, and if so, the parameter estimates and model outputs will tell us what the effects are and how effective the intervention is.

5.3 Ideas for future work

While the HCCMPP appears to be a useful tool for helping to monitor and study HIV epidemics, there are several areas in which the model could be improved. For example, while the fixed gamma curve used to represent the trend in HIV incidence is simple and easy to work with, it does not acknowledge the fundamental endogeneity of HIV incidence identified by Palloni (1996). Future work with the HCCMPP should modify the model so that HIV incidence depends on the current and past levels of prevalence. Another obvious area of improvement is the need to account for the increases in the coverage of antiretroviral therapies (ART). Given an estimate of ART coverage for a particular population, this share of the infected population should experience improved survival and fertility prospects, and a diminished likelihood of infecting others, relative to those who are HIV+ but not receiving ART. Additional modifications could include the ability to model potential interventions related to male circumcision and microbicides (McNeil Jr. 2010). Building in these features would make the HCCMPP more realistic, and potentially improve the model’s prospects for successfully monitoring and forecasting HIV epidemics. However, in order to add these new features, the overall model would have to be made simpler to require fewer parameters, in order to ensure that the whole thing remains identifiable and tractable enough to estimate. This could be done by modeling existing parameters and defining (a smaller number of) new hyper parameters to govern those models and/or by collapsing across age groups in which there is little meaningful variation.

6. Attributions & acknowledgements

Jason R. Thomas conducted the bulk of the analysis for this project, wrote and ran all of the R code and wrote the first draft of the manuscript. Samuel Clark conceived and supervised this project and wrote the final manuscript. With Adrian Raftery, Le Bao refined the IMIS method and wrote the original IMIS code that was adapted for use in this project, and Le Bao contributed significantly to the adaptation of his IMIS code for use in this project. All authors have read and approved this manuscript.

This project was supported by a seed grant from the Center for Statistics and the Social Sciences (CSSS), University of Washington and by grants K01 HD057246, R01 HD054511, and R24 HD047873 from the National Institute of Child Health and Human Development (NICHD) of the National Institutes of Health (NIH), as well as grant numbers T32 AG00129 and P30 AG17266 from the National Institute of Aging. The content of the work presented here is solely the responsibility of the authors and does not necessarily represent the official views of the the NIH. The authors are very grateful to Patrick Heuveline for his correspondence and for making his work available. We also thank Adrian Raftery, Leontine Alkema, Jennifer Chunn, Greg Mathews, David Sharrow, and Mark Wheldon for invaluable discussion during the preparation of this work. The second author would also like to thank colleagues at the Africa Centre for Health and Population Studies, University of KwaZulu-Natal, South Africa for their hospitality and useful comments on an early version of this work.

This project was entirely conducted using open source software. The methods described above are implemented in the R programming language and run in the R statistical software package (R Foundation for Statistical Computing 2010).