Abstract
The current protocol for image guidance in open abdominal liver tumor removal surgeries involves a rigid registration between the patient's operating room space and the pre-operative diagnostic image-space. Systematic studies have shown that the liver can deform up to 2 cm during surgeries in a non-rigid fashion thereby compromising the accuracy of these surgical navigation systems. Compensating for intra-operative deformations using mathematical models has shown promising results. In this work, we follow up the initial rigid registration with a computational approach that is geared towards minimizing the residual closest point distances between the un-deformed pre-operative surface and the rigidly registered intra-operative surface. We also use a surface Laplacian equation based filter that generates a realistic deformation field. Preliminary validation of the proposed computational framework was performed using phantom experiments and clinical trials. The proposed framework improved the rigid registration errors for the phantom experiments on average by 43%, and 74% using partial and full surface data, respectively. With respect to clinical data, it improved the closest point residual error associated with rigid registration by 54% on average for the clinical cases. These results are highly encouraging and suggest that computational models can be used to increase the accuracy of image-guided open abdominal liver tumor removal surgeries.
Keywords: Image-guided liver surgeries, Finite element analysis/methods, Linear elastic model, Intra-operative deformation, Image registration, Partial hepatectomies
1. Introduction
Image-guided surgery has been used with success in the treatment of brain tumors (Jolesz et al., 2001; Nabavi et al., 2001), breast cancer (Dowlatshahi et al., 2001; Gould et al., 1998) and more recently in deep brain stimulations (D'Haese et al., 2005; Lunsford et al., 1983). These advancements in medical imaging have only been recently translated to open abdominal liver tumor removal surgeries and partial hepatectomies (Cash et al., 2007; Marescaux et al., 1998). As in other image-guided surgical applications, image guidance in open abdominal liver tumor removal surgeries relies on the establishment of an accurate relationship between the patient's pre-operative image-space and the intra-operative organ space/physical-space. This process of establishing a relationship between the image-space and the physical-space is known as registration and the current protocol for registration in partial hepatectomies involves an initial pose estimation provided by a point-based registration of anatomical landmarks which is then improved by using rigid surface registration algorithms that use the pre-operative surface segmented from the diagnostic images and the exposed intra-operative surface (Clements et al., 2008; Herline et al., 2000). While these image-to-physical-space alignments are relatively straight-forward, non-rigid tissue deformation (also known as intra-operative shift) during hepatectomies compounds the procedure and compromises the accuracy of guidance systems that rely on the aforementioned rigid registration techniques.
The existing methods for intra-operative shift compensation can be classified into two main categories: (i) intra-operative imaging techniques such as intra-operative magnetic resonance (iMR) and intra-operative computed tomography (iCT) imaging, intra-operative ultra-sound (iUS) and (ii) computational model compensation using sparse intra-operative data. While iMR techniques have shown promise for complex hepatic surgeries (Bathe et al., 2006) so far it has been limited to research institutions. Lange et al. (2004) reported a combined rigid and non-rigid framework to match iUS images of liver vasculature to the segmented vessel trees from pre-operative diagnostic images. Nakamoto et al. (2007) reported a non-rigid registration algorithm within the context of a freehand three-dimensional laparoscopic iUS system to compensate for respiratory motion and deformation. A majority of the proposed methods for deformation compensation during liver surgeries (open abdominal and minimally invasive) utilize non-rigid registration algorithms that rely on statistical models or voxel-based intensity methods and do not account for the underlying biomechanics that cause intra-operative shift/non-rigid deformations. Computational models can translate complex surgical events into accurate estimates of tissue response and thereby compensate for intra-operative shift.
Researchers have demonstrated reasonable success in compensating for intra-operative deformations during brain tumor resection therapies using computational models. Paulsen et al. (1999) and Miga et al. (1999) used a linear elastic biphasic model to simulate gravitational forces and other surgical loads (such as retraction) during brain tumor resection therapies. Lunn et al. (2003) and Dumpuri et al. (2007) used a weighted combination of finite element model (FEM) solutions to predict intra-operative brain deformations. Ferrant et al. (2000) used FEM in a more interpolative sense to match iMR images to pre-operative diagnostic images. Whilst promising in a neurosurgical setting, these computational models cannot be easily translated to open abdominal liver tumor removal surgeries and partial hepatectomies for the following reason: In neurosurgeries, the brain is confined by the cranium and there is little manipulation of the exposed cortical surface by the surgeon during the initial stages of surgery. In open abdominal liver tumor removal surgeries, a significant amount of tissue deformation occurs at the beginning of surgery. In qualitative observations of common surgical approaches to liver surgery, procedures to decouple the liver from the surrounding supporting ligamenture to better visualize and inspect the organ for the removal of tumors are evident. In addition, the liver is routinely adjusted before the hepatectomy, i.e., “packed and mobilized” for better access to the tumor resulting in significant organ deformation when compared to its pre-operative diagnostic images. Therefore computational models for open abdominal liver tumor removal surgeries call for a strategy to compensate for these initial deformations. Although limited, the use of computational models to compensate for these intra-operative deformations using finite element models has some precedent.
Cash et al. (2005) reported a two step algorithm to compensate for intra-operative liver deformations. In the first step, they used a deformation identifying rigid registration (DIRR) algorithm to establish an initial rigid alignment between the intra-operative liver surface and the pre-operative images. For the DIRR algorithm, they assumed that the intra-operative deformations are concentrated in the central region of the liver. This allowed them to visually identify minimally deformed regions and they used those regions to rigidly align the exposed intra-operative liver surface to the pre-operative liver surface (obtained by segmenting the liver tissue from the pre-operative diagnostic scans and extracting the surface from the segmented images using a marching cubes algorithm). In the second step, they used an incremental FEM approach to accurately align the intra-operative liver surface to the pre-operative images. Cash et al. computed the closest point distances between the intra-operative liver surface and the pre-operative liver surface after rigid alignment, and applied these distances to a linear elastic FEM. They applied these distances as displacement boundary conditions in an incremental fashion by applying a fraction of the computed closest point distances. In each successive solution, they re-computed the closest point distances and applied them to the finite element model. In a series of phantom experiments using this combined DIRR/FEM approach, Cash et al. demonstrated that the sub-surface target errors improved by at least 68%. While encouraging, the algorithm proposed by Cash et al. assumes that the intra-operative deformation is localized to the central portion of the liver and there are minimally deforming regions in the exposed intra-operative surface that can be easily identified. These assumptions work well for phantom experiments in a laboratory setting but they cannot be easily translated to an intra-operative environment for the following reasons: (i) The surgeon manipulates the exposed liver in a random manner to gain better access to the tumor. This induces deformations in the periphery regions of the liver belying the assumption by Cash et al. that the intra-operative deformations are concentrated to the central portion of the liver.
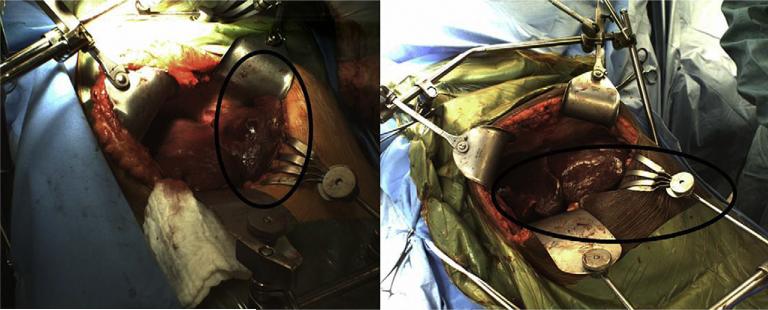
Fig. 1 shows manipulations by the surgeon to the periphery regions of the liver using surgical retractors and clamps for two different patients who underwent open abdominal liver surgery at the University of Florida, Gainesville Medical Center (ii) Visually identifying the minimally deformed regions (defined by Cash et al. as regions that undergo deformation no greater than a few millimeters) on the exposed intra-operative surface is a daunting task as it requires a priori knowledge of the forces that cause the liver to deform intra-operatively and based on our observations in the operating room (OR) it is difficult to ascertain these forces. Also, the exposed intra-operative liver surfaces are spatially sparse in nature thereby making it difficult to distinguish between the deformed and the minimally deformed regions. The sparse coverage of the exposed intra-operative liver combined with incorrect identification of minimally deformed regions could lead to an erroneous registration and therefore an inaccurate alignment using the DIRR algorithm (a limitation addressed by Cash et al., 2005). Cash et al. also used an incremental FEM approach to improve on the rigid alignment and to accurately align the exposed intra-operative surface to the pre-operative liver images. While this incremental approach takes care of the geometric nonlinearities associated with the large deformations experienced by the liver, it also increases the computational demand in the OR. Given the time sensitive nature in the OR and the significant costs that can be associated with running the finite element model numerous times, the incremental approach proposed by Cash et al. is not a practical solution. Another limitation of this approach is that the manner in which the closest point distances are applied to the finite element model. The sparse nature of the intra-operative liver surfaces mean that the closest point distances between the rigidly registered intra-operative surface and the pre-operative liver surface are obtained just for a few points on the pre-operative liver surface and this often results in unrealistic deformations.
Fig. 1.
Exposed intra-operative liver surfaces for two patients who underwent partial hepatectomies at the University of Florida, Gainesville, Medical Center. The two figures show the manipulations to the inferior ridges and the periphery regions of the liver using surgical retractors and clamps (highlighted in the oval regions). These manipulations belie the assumptions by Cash et al. (2005) that the intra-operative deformations are confined to the central portions of the liver.
Clements et al. (2007) also reported a framework to account for intra-operative deformations during open abdominal liver tumor removal surgeries. Clements et al. proposed a framework that combined an atlas of pre-computed FEM solutions with a robust rigid surface registration technique to account for intra-operative deformations. Based on a priori information about the surgical procedure, they assumed a range of driving forces that cause intra-operative deformations and solved a linear elastic FEM for each of these forces thereby assembling a matrix/atlas of deformed surfaces. They used a linear inverse model to match the intraoperatively acquired data to this pre-operatively computed atlas. Additionally, they implemented an iterative approach to update point correspondences between the intra-operative data and pre-operative images. Similar to Cash et al. (2005), Clements et al. demonstrated the success of this algorithm in a series of phantom experiments and reported an improvement of at least 71% in the sub-surface target errors. Given that the atlas of deformed solutions is computed pre-operatively, this approach is better than (Cash et al., 2005) in terms of computational demand in the OR. Also, the iterative procedure adapted by Clements et al. in their algorithm addressed the issue of the initial deformations and therefore the lack of initial correspondences observed during open abdominal liver tumor removal surgeries. However this algorithm requires a priori knowledge of the typical forces that cause intra-operative liver deformations which is a challenging task. This could also lead to a large number of solutions in the deformation atlas thereby increasing the time taken to solve the iterative algorithm in the OR. Also, as noted by the authors in Clements et al. (2007), this approach requires that one generate procedural and surgeon specific deformation atlases to account for all possible sources of intra-operative deformations.
In this work we propose a “direct” approach that involves an initial rigid registration followed by a FEM solution that applies realistic deformations to the liver surface. Although we report a two step based framework, the similarities to that reported in Cash et al. (2005) end there. In this work, we use a robust rigid surface registration algorithm to align the intra-operative surface to the pre-operative images. Unlike the rigid registration algorithm reported in (Cash et al., 2005), the algorithm used here does not require a priori knowledge of the deformation sources in the OR. Also, unlike (Cash et al., 2005) where the authors apply the closest point distances computed after rigid registration in an incremental fashion to the FEM, we solve the FEM in a direct manner. We also use a surface Laplacian equation based extrapolation filter to extrapolate the sparse closest point distances computed after rigid registration to produce a realistic deformation field that is applied to the FEM. Unlike Cash et al. (2005) and Clements et al. (2007) we also demonstrate the success of the proposed framework in a series of clinical experiments. The proposed framework relies on the acquisition of a three-dimensional representation of the exposed intra-operative surface. In that context, we use a commercially available laser range scanner and we have demonstrated in the past that this scanner can be used to acquire intra-operative surfaces during brain tumor resection therapies (Sinha et al., 2005) and partial hepatectomies (Cash et al., 2003). We also demonstrate that intra-operative surface descriptions acquired using a computed tomography (CT) scanner can be used in the framework. The proposed framework has been evaluated in a series of phantom experiments and eight patients who underwent partial hepatectomies (via open abdominal liver tumor removal surgeries) at three different clinical sites. Quantitative and qualitative results have been presented in Section 4.
2. Methods
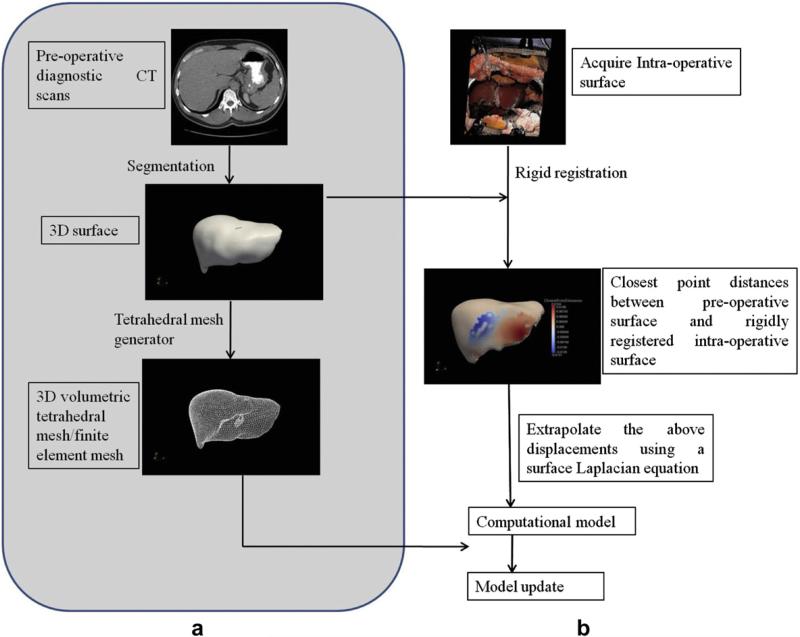
Fig. 2 shows a graphical overview of the proposed computational framework. Fig. 2a shows the overall procedure and Fig. 2b shows the iterative processes involved in the proposed computational framework.
Fig. 2.
a: Graphical overview of the proposed computational framework. All the steps highlighted in grey are performed pre-operatively. b: Computational framework performed intra-operatively.
The steps highlighted in grey in Fig. 2a (segmentation and generation of three-dimensional surface and finite element mesh) are performed pre-operatively. All the other steps are performed intra-operatively. These steps have been described in detail below.
2.1. Generation of a three-dimensional surface and a volumetric tetrahedral mesh
The first step is to segment the liver from the patient's abdominal scans either manually or using a semi-automatic method (Pan and Dawant, 2001). Pathfinder Therapeutics Inc. adopted the algorithm reported in (Nabavi et al., 2001) and performed an accuracy study of that algorithm and reported their findings in Li et al. (2008). In Li et al. (2008) they found a 94.6% overlap percentage of their liver segmentation when they compared it those obtained using MeVis (Breman, Germany). As noted in Li et al. (2008) the segmentation step takes less than 10 min. A marching cubes algorithm (Lorensen and Cline, 1987) is used on the segmented liver data to generate an initial approximation of the surface. FastRBF Toolbox (Farfield Technologies, http://www.farfieldtechnology.com) is then used to define a parametric version of the marching cubes surface. This step provides a smoother description of the liver surface. A tetrahedral mesh generator (Sullivan et al., 1997) is then used to create a volu-metric tetrahedral mesh using the surface obtained from the FastRBF toolbox. These steps are performed pre-operatively and it should be noted that both the three-dimensional surface and the volumetric mesh represent the un-deformed state of the organ. For the phantom experiments and clinical cases reported herein, we used the segmentation tool developed by Pathfinder Therapeutics Inc. and the volumetric tetrahedral meshes contained about 20,000 nodes and 100,000 elements.
2.2. Intra-operative surface acquisition
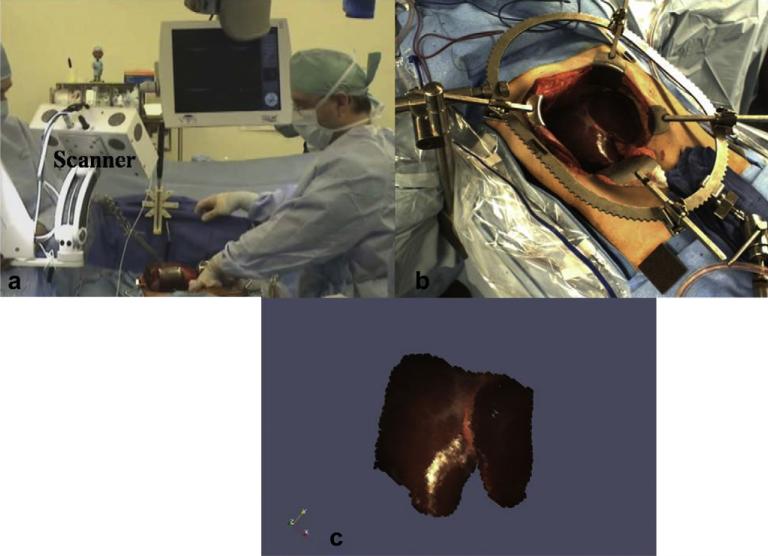
The proposed computational framework relies on the acquisition of a three-dimensional surface representing the deformed state of the organ. For the phantom experiments, surface descriptions of the deformed surface were acquired using a CT scanner and a commercially available laser range scanner, LRS (RealScan 200C; 3-D Digital Corp., Sandy Hook, CT, USA). In addition to collecting three-dimensional surface data the scanner also captures two-dimensional texture information and this texture information was used to obtain the salient anatomical features on the surface of the phantom. However surfaces acquired by the LRS are sparse (lesser number of points) and are not volumetric datasets when compared to those acquired by the CT scanner. For the clinical trials, we used surfaces that were acquired by Pathfinder Therapeutics Inc. using a similar LRS. Fig. 2 shows an example surface acquired in the OR. Fig. 3a shows the scanner used by Pathfinder Therapeutics Inc., in the OR. Fig. 3b shows the exposed intra-operative surface of the liver from the scanner's perspective and Fig. 3c shows the texture-mapped three-dimensional surface acquired by the scanner. As seen in Fig. 3c, the surface is spatially sparse in nature and is limited based on the scanner's field of view.
Fig. 3.
Three-dimensional surfaces of the exposed intra-operative liver surface acquired by Pathfinder Therapeutics Inc., in the OR. a: Laser range scanner (marked as Scanner) in operation in the OR. b: Exposed intra-operative surface of the liver from the scanner's perspective. c: Texture-mapped three-dimensional surface of the exposed liver surface.
2.3. Rigid registration between the pre-operative surface and intra-operative surface
The determination of an accurate initial relationship between the physical-space (as defined by the patient's operating room space) and image-space (as defined by the patient's pre-operative image-space) is an important step in our framework and in this work we use a point-based registration algorithm followed by a robust surface based rigid registration to establish that relationship.
2.3.1. Point-based rigid registration algorithm (PBReg)
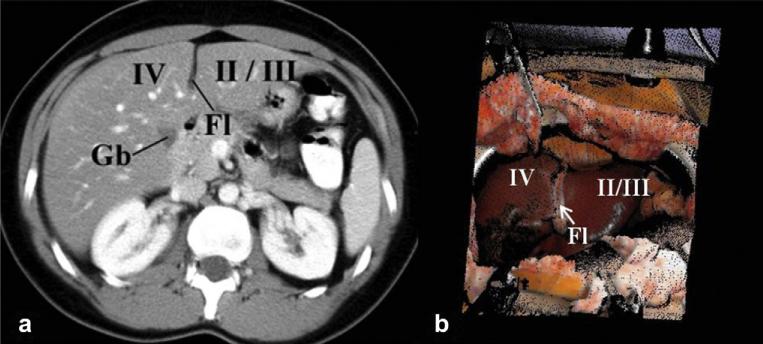
Anatomical landmarks on the liver are identified on the patient's pre-operative diagnostic images before surgery and corresponding landmarks are obtained in the physical-space (in other words on the exposed intra-operative liver surface) using an optically tracked pen probe. Typical landmarks include the tip of segment III, inferior tip of the liver, end points on the falciform ligament, lateral tip of the right lobe and have been shown in Fig. 4. Normally at least four such landmarks are obtained and a point-based registration algorithm (Arun et al., 1987) is used to establish a relationship between the physical-space and image-space.
Fig. 4.
Examples of anatomical landmarks used for point-based registration include end points of falciform ligament (marked as Fl in the figure), tip of segment III and lateral tip of the left lobe. a: Anatomical landmarks marked on the patient's pre-operative diagnostic images before surgery. b: Corresponding anatomical landmarks marked on the exposed intra-operative surface of the liver. These points are marked by the surgeon using an optically tracked pen probe.
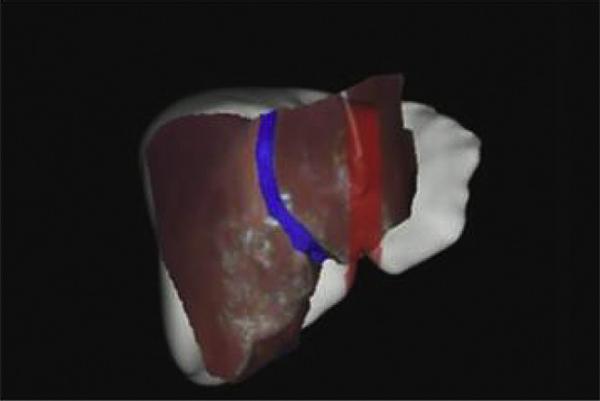
Errors in localizing the anatomical landmarks often lead to misalignment thereby compromising the accuracy of image guidance. Therefore, to improve the accuracy of image-guided open abdominal liver tumor removal surgeries traditional iterative closest point algorithm (ICP) (Besl and McKay, 1992) was introduced to register the exposed intra-operative liver surface to the liver surface derived from pre-operative diagnostic images. Herline et al. (2000) established an initial alignment using a point-based registration algorithm and then used traditional ICP to improve the accuracy of physical-space to image-space registration. While they demonstrated reasonable success in a series of phantom experiments, we observed that the accuracy of the traditional ICP algorithm is often compromised by (i) poor initial alignment and (ii) non-rigid deformations that occur during the beginning of open abdominal liver tumor removal surgeries. Clements et al. (2008) showed that a poor initial alignment resulted in ICP registering the anterior surface of the intra-operative liver to the posterior part of the pre-operative liver surface. Fig. 5 shows an example of misalignment from ICP due to non-rigid deformations. Fig. 5 shows the intra-operative liver surface registered using ICP overlaid on the pre-operative liver surface. As seen in the figure, there is a gross misalignment between falciform ligament delineated from the intra-operative surface (shown as a blue patch) and the falciform ligament obtained from the pre-operative surface (shown as a red patch).
Fig. 5.
Example of misalignment in a clinical case when using the traditional ICP. Exposed intra-operative surface of the liver (red surface) was registered to the liver surface derived from the patient's pre-operative diagnostic images (white surface) using traditional ICP. Note the gross misalignment in falciform ligament (blue patch: falciform ligament delineated from intra-operative surface, red patch: falciform ligament obtained from pre-operative surface).
2.3.2. Weighted patch iterative closest point algorithm (wICP)
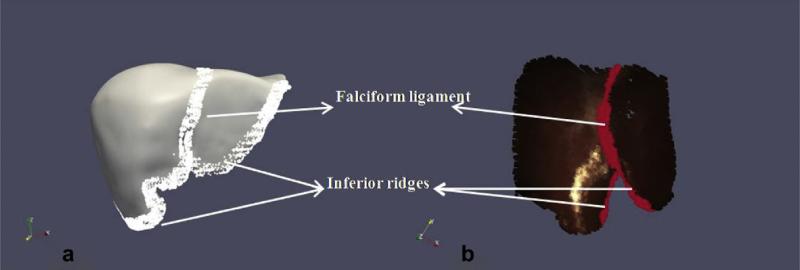
Clements et al. (2008) reported an approach using weighted salient anatomical features to improve the accuracy of rigid registrations and to increase robustness of the rigid surface registrations. They used salient anatomical features that were easily identifiable in both the pre-operative surface (constructed as described in Section 2.1) and the intra-operative surface acquired using the laser range scanner. Fig. 6 shows examples of the salient anatomical features used by Clements et al. in their work. They used these features to bias the point correspondence estimation and also employed them to play a more significant role in the point-based registration performed at every iteration of the algorithm. They showed that the wICP algorithm was robust to poor initial alignments thereby demonstrating the robustness of the wICP algorithm. They also demonstrated the success of the algorithm in a series of clinical cases and showed that it performed better than the point-based registration algorithm and the traditional ICP algorithm.
Fig. 6.
Salient anatomical features used for weighted patch ICP algorithm. Examples of such features include the falciform ligament, left and right inferior ridges and they are easily identifiable on the pre-operative surface (depicted in a) and intra-operative surface acquired using a laser range scanner (shown in b).
2.4. Improving the rigid registration alignment using a computational framework
After establishing an initial alignment between the pre-operative and intra-operative surfaces using rigid registration, the next step is to improve that alignment by accounting for the non-rigid deformation. In this work, we use a computational model to predict the intra-operative deformations and to improve the rigid registration alignment. We assume the liver to be an isotropic solid with a linear stress-strain relationship, governed by the following equation:
| (1) |
where σ represents the stress tensor and B the external forces acting on the object. Since we assume the liver to have a linear relationship between stress (σ) and strain (ε), ε = Cε where C represents the material stiffness matrix and is dependent on Young's modulus (E) and Poissons ratio (ν). Substituting for C, ε, and σ Equation (1) can be represented in terms of the displacement vector (u) by
| (2) |
Using Gallerkin weighted residuals and linear basis functions to solve the above equation, the system of equations to solve the three-dimensional Cartesian displacements {u} at every node in the tetrahedral mesh can be represented as
| (3) |
It should be noted that {u} represents the three-dimensional displacement vector for every node including the sub-surface nodes in the tetrahedral mesh. One way to predict soft-tissue deformations using the above equation is to obtain known displacement values {u} for a few nodes (located either on the surface or in the sub-surface of the un-deformed tetrahedral mesh) and to solve for the remainder of the displacements. In such situations, it is common practice to transform the three Cartesian displacements to a co-ordinate system that is relative to the shape of the organ, i.e., a co-ordinate system described by directions that are normal and approximately tangential to the organ surface.
Rigid registration performed using sparse intra-operative data such as those acquired by the LRS, results in a displacement value {u} along the surface normal for a few surface nodes on the tetrahedral mesh. Fig. 7 shows an example of the closest point distances between the intra-operative surface and the patient's pre-operative surface after rigid alignment. It should be noted that the two surfaces shown in the figure were aligned using the weighted patch ICP algorithm. Since displacement is a vector, the direction of the vector is indicated by the sign of the closest point distances. Positive values in the figure indicate the weighted patch ICP algorithm places the intra-operative surface to be on top of the pre-operative surface and negative values indicate that the algorithm positions the intra-operative surface underneath the pre-operative surface. Though these closest point distances range from –12.6 mm to 17.4 mm it should be noted that these distances are zero at every node outside the oval region highlighted in Fig. 7a.
Fig. 7.
Example result of closest point distances (in mm) between the rigidly registered intra-operative surface and the pre-operative surface. Two views of the liver have been shown (anterior view in (a) and posterior view in (b)). Though the closest point distances range from –12.6 mm to 17.4 mm note how they are zero at every node outside the oval region highlighted in (a). Registration was performed using the wICP algorithm reported in Clements et al. (2008). Positive values mean that the intra-operative surface is on top of the pre-operative surface and negative values indicate that the intra-operative surface is underneath the pre-operative surface.
As mentioned before these closest point distances are sparse in nature. In other words these signed distances are available just for a few nodes on the un-deformed surface of the finite element mesh. In reality, the entire liver deforms during surgery and therefore using these sparse closest point distances to predict intra-operative deformations will decrease the accuracy of predictions and might also result in an unrealistic deformation field. Without access to intra-operative images obtaining a displacement field for the entire liver is impossible. Therefore in this work we extrapolate the sparse closest point distances (obtained after rigid registration) to the entire liver surface by solving a Laplace equation on the surface of the un-deformed finite element mesh. Originally reported in the context of non-rigid registration for breast elastographic techniques, Ou et al. (2008) used a surface based Laplacian equation to find point correspondences between deformed and un-deformed surfaces. We adopted their approach to extrapolate the closest point distances obtained after rigid registration to the entire un-deformed surface of the liver. Fig. 8 shows the results of the extrapolation. As seen in Fig. 8, after solving the Laplacian equation on the surface of the un-deformed finite element mesh, closest point distances now exist for every node in the un-deformed tetrahedral mesh. These closest point distances are applied as type I/displacement boundary conditions in a co-ordinate system that is described by the normal and tangential directions to the un-deformed surface. We also flip the sign of the distance for nodes in the un-deformed tetrahedral mesh that correspond to the posterior part of the pre-operative surface. This computational framework was tested in a series of phantom experiments and eight patients undergoing partial hepatectomies and results have been presented in Section 4.
Fig. 8.
Example result of closest point distances (in mm) after the using the surface Laplacian equation based extrapolation filter. Two views of the liver have been shown (anterior view in (a) and posterior view in (b)). Every node now has a signed closest point distance value assigned to it. It should be noted that the sign of the closest point distances have been flipped for nodes in the posterior surface (shown in b). These signed closest point distances are assigned as displacement boundary conditions to the finite element model in a co-ordinate system that is represented by the normal and two tangential directions to the surface.
3. Datasets used for validation
3.1. Phantom experiments
A series of phantom experiments were performed using a liver phantom created using Smooth-On Ecoex 00-10 (Smooth-On, Easton, PA). The phantom was rigidly attached to a plexiglass base using a Teflon screw. Seven Teflon spheres surrounding the phantom were affixed at varying heights to the plexiglass base. Forty-three stainless steel beads were distributed randomly in the phantom to serve as sub-surface targets for error computation. A stripe of white paint was placed on the phantom in the falciform ligament region to facilitate the delineation of this salient anatomical feature. Computed tomography (CT) scans of the phantom were obtained in the un-deformed state. These scans were used to generate (a) the pre-operative surface for rigid alignment and (b) the volumetric tetrahedral mesh used for the computational model. Two deformations were then imposed on the phantom using a surgical towel underneath the: (i) inferior ridge of right lobe and (ii) left lobe. Surfaces of the deformed state were acquired using a CT scan and a laser range scanner (LRS) from RealScan 200C, 3-D Digital Corporation, Bethel, CT Surfaces. It should be noted that the LRS provided us with a partial description of the anterior surface of the deformed phantom. Fig. 9 shows the experimental set-up. Fig. 9a shows the deformation applied to the left lobe of the phantom and Fig. 9b shows the distribution of forty-three sub-surface stainless beads. Deformed and un-deformed surfaces were obtained by manually segmenting the liver from the CT and LRS scans.
Fig. 9.
(a) Experimental set-up for the phantom datasets. Deformation was applied using a surgical towel placed underneath the left lobe. Seven Teflon spheres that surround the phantom were used as landmarks for point-based registration. A white stripe was painted in the falciform region to facilitate the delineation of that salient anatomical feature. (b) Distribution of the 43 stainless beads that serve as sub-surface targets for error computation.
Seven Teflon spheres that surround the phantom were localized in the CT and LRS datasets and served as landmarks for point-based registration. This point-based registration was used to establish an initial alignment between the deformed surfaces (both CT and LRS) and their un-deformed counterparts. Falciform ligament (designated using the white stripe in the phantom) was used as the salient anatomical feature for the wICP algorithm and the algorithm was used to improve the initial alignment. The computational algorithm described in Section 2.4 was then used to improve all three rigid alignments. Sub-surface target errors were computed for the point-based registration, wICP and the computational model and results have been presented in the following section.
3.2. Clinical cases
Eight patients undergoing partial hepatectomies were selected randomly from a 75 patient clinical conducted by Pathfinder Therapeutics Inc. Patients 1 and 2 underwent partial hepatectomy at University of Pittsburgh Medical Center, Patients 3,4,5 and 6 at Memorial Sloan Kettering Cancer Center and Patients 7 and 8 at University of Florida, Gainesville, Medical Center. Surface and volumetric tetrahedral mesh were generated from the un-deformed pre-operative diagnostic images and four salient anatomical features (falciform, left and right inferior ridges and round ligament) were marked by the surgeons on the pre-operative surfaces using a planning software developed by Pathfinder Therapeutics Inc. After removing the suspending ligaments and packing and mobilizing the liver, the four aforementioned salient anatomical features were marked on the exposed intra-operative liver surface using an optically tracked pen probe. Surface descriptions of the exposed intra-operative surface were acquired using LRS. The LRS unit was optically tracked (in a manner similar to the one described in Cash et al. (2007) and Sinha et al. (2005) and this allowed Pathfinder Therapeutics Inc. to acquire the intra-operative surface description and the salient anatomical features in the same reference co-ordinate system. Centroids of these salient anatomical features served as landmarks for point-based registration and initial alignment of physical-space to the image-space. Pathfinder Therapeutics Inc., acquired the intra-operative datasets (surfaces acquired by the LRS and salient anatomical features acquired by the optically tracked pen probe) during the same apneic period (end expiration point of the respiratory cycles) to minimize the deformation effects due to liver respiratory motion. Intra-operative surfaces acquired by the LRS were then registered to their un-deformed counterparts using the wICP algorithm. The computational algorithm was then used to improve the rigid alignment. It should be noted that full surface descriptions using iCT scanners were not acquired for the clinical cases. Since sub-surface targets were not available for the clinical cases, closest point distances between the un-deformed and rigidly registered surfaces were compared to the closest point distances between the un-deformed surface and the model predictions and have been reported in the following section.
4. Results
4.1. Results for phantom experiments
Table 1 reports the errors at sub-surface targets. Column 1 in the table refers to the mode of deformation, left indicating that the surgical towel was placed underneath the left lobe and right indicating that the surgical towel was placed underneath the inferior ridge of the right lobe. Column 2 in the table reports the target registration error (TRE) for the point-based registration using the Teflon spheres. TRE generated using the wICP algorithm was used as the “ground truth” for the proposed computational approach. Full surface description acquired by the CT scanner was used for the wICP and the computational algorithm and target errors using the CT scanner have been reported under “Full Surface” in the Table. “Partial Surface” in Table 1 refers to using the partial surface description acquired by the LRS to drive the wICP algorithm and the computational framework. Averaging over both modes of deformation the proposed computational framework outperformed the rigid registration algorithm by 74% when the entire deformed surface was used to drive it and it outperformed the rigid registration algorithm by 43% when the partial surface description from the LRS was used.
Table 1.
Target registration errors (TRE) for the left and right modes of deformation. It should be noted that 43 sub-surface targets were used to compute TRE. Post-PBReg: TRE using the point-based rigid registration algorithm. Post-wICP: TRE using the wICP algorithm. TRE computed using the wICP algorithm was used as “ground truth” for the proposed computational approach. Post-Model: Target errors generated using the proposed computational approach. “Full Surface”: Deformed surface description acquired by the CT scanner. “Partial surface”: Deformed surface description acquired by the laser range scanner. Mean ± Standard deviation (maximum) of the values has reported in ‘mm’ units.
| Post-PBReg | Full Surface |
Partial Surface |
|||
|---|---|---|---|---|---|
| Post-wICP | Post-Model | Post-wICP | Post-Model | ||
| Left | 14.8 ± 8.5 (31.0) | 3.2 ± 1.6 (6.8) | 1.2 ± 0.9 (3.8) | 4.1 ± 2.3 (11.3) | 2.3 ± 2.1 (8.6) |
| Right | 22.8 ± 8.8 (42.3) | 2.7 ± 1.6 (6.7) | 1.0 ± 0.8 (3.7) | 4.5 ± 2.1 (10.0) | 2.6 ± 1.9 (8.1) |
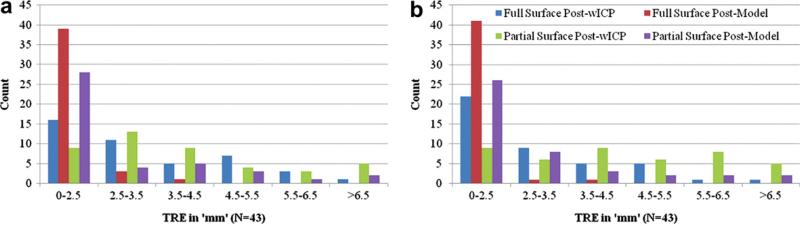
Fig. 10 shows the distribution of target errors in a histogram format for the left (Fig. 10a) and the right (Fig. 10b) modes of deformation. Averaging over both modes of deformation when using partial surface descriptions obtained using LRS, the rigid registration algorithm (wICP) resulted in 43% of the sub-surface targets with TRE less than or equal to 3.5 mm while the computational algorithm resulted in 77% of the sub-surface targets with errors less than or equal to 3.5 mm. As implied by the figures, the proposed computational framework produces a tighter distribution of error when compared to the rigid registration algorithm.
Fig. 10.
Error distribution in a histogram format for the sub-surface targets (N = 43) using the wICP and computational algorithm (reported as model in the figure). a: Error distribution for the left mode of deformation. b: Error distribution for the right mode of deformation.
4.2. Results for the clinical trials
Table 2 reports closest point distances for the clinical cases reported herein. Row 1 reports the closest point distances between the un-deformed pre-operative liver surface and the rigidly registered intra-operative surface while Row 2 reports the closest point distances between the liver surface deformed using model predictions and the rigidly registered intra-operative surface.
Table 2.
Closest point distances for the six clinical cases reported herein. Patients 1 and 2 underwent partial hepatectomies at University of Pittsburgh Medical Center, Patients 3, 4, 5 and 6 at Memorial Sloan Kettering Cancer center and Patients 7 and 8 at University of Florida, Gainesville Medical Center. Column 1 reports the closest point distances between the un-deformed pre-operative surface and the rigidly registered intra-operative surface and Column 2 reports the closest point distances between the surface deformed using model predictions and the rigidly registered intra-operative surface. Mean ± Standard deviation (maximum) of the values have been reported in ‘mm’ units.
| Post-wICP | Post-Model | |
|---|---|---|
| Patient 1 | 7.2 ± 5.2 (19.2) | 3.1 ± 1.8 (11.0) |
| Patient 2 | 3.9 ± 2.6 (11.4) | 3.0 ± 3.2 (23.1) |
| Patient 3 | 6.2 ± 4.2 (17.4) | 2.5 ± 1.3 (7.5) |
| Patient 4 | 5.0 ± 2.7 (9.8) | 1.9 ± 0.8 (4.0) |
| Patient 5 | 3.6 ± 1.8 (8.2) | 1.8 ± 0.7 (5.0) |
| Patient 6 | 8.8 ± 4.4 (14.2) | 3.6 ± 2.0 (10.1) |
| Patient 7 | 4.2 ± 2.5 (11.8) | 2.8 ± 2.5 (12.3) |
| Patient 8 | 5.0 ± 3.1 (11.7) | 1.8 ± 1.0 (5.6) |
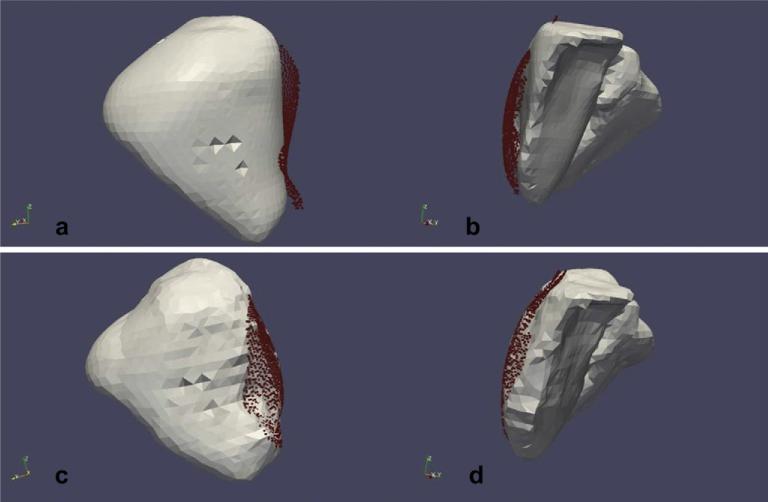
Averaging overall eight cases, the proposed computational approach improves the closest point distances after rigid registration by 54%. Qualitative results for Patient 4 are shown in Fig. 11. As mentioned before LRS was used to acquire the exposed intra-operative surface as a three-dimensional point-cloud. Fig. 11a and b shows the rigidly registered intra-operative surface overlaid on the un-deformed pre-operative surface and Fig. 11c and d shows the rigidly registered intra-operative surface overlaid on the surface deformed using model predictions. In other words, Fig. 11a and b shows the rigid registration results and Fig. 11c and d depicts the results of the proposed computational approach. These qualitative results demonstrate that the surface deformed using displacements predicted by the proposed computational approach fits the intra-operative surface better than the rigid registration.
Fig. 11.
Qualitative results for Patient 5 reported in this study. a and b: Results of rigid registration using the wICP algorithm. Exposed intra-operative surface acquired as a three-dimensional point-cloud (shown in red) was rigidly registered to the pre-operative liver surface using wICP. Notice the misalignment between the two surfaces. c and d: Results of the proposed computational approach. Pre-operative liver surface was deformed using displacements predicted by the computational approach and the rigidly registered intra-operative surface has been overlaid on top of it. Notice the improvement in alignment between the surfaces when compared to the top row.
5. Discussion
In contrast to brain tumor resection therapies, intra-operative deformation occurs at the beginning of open abdominal liver tumor removal surgeries thereby compromising the accuracy of initial physical-space to image-space registration achieved using rigid registration algorithms. This work focuses on improving the accuracy of the initial rigid registrations by incorporating a computational model and the preliminary results presented here from both the phantom experiments and the clinical studies show that the proposed computational framework significantly improves the accuracy of current registration techniques being used for image-guided open abdominal liver tumor removal surgeries.
It is worth noting that the rigid registration approach and the surface Laplacian equation based extrapolation filter described in this work distinguishes it from other studies that use closest point distances between surfaces to guide computational models. The rigid registration approach is robust to poor initial alignments and does not rely on the a priori knowledge of the sources of intra-operative deformation. The extrapolation filter allows us to approximate boundary conditions for regions where intra-operative surface data is not acquired thereby preventing unrealistic deformations. We also use a direct approach to solve the finite element model. Given that computational time is a limiting factor for model-updated image-guided surgeries, this direct approach is a practical solution when compared to methods that call for an incremental (Cash et al., 2005) or iterative approach (Clements et al., 2007).
The proposed framework relies on closest point distances between the un-deformed liver surface and the rigidly registered intra-operative surface and therefore it is reasonable to assume that increasing the accuracy of the rigid registration algorithm will affect the outcome of the computational approach. Though Clements et al. demonstrated improved accuracy of wICP algorithm when compared to the traditional ICP algorithm (Clements et al., 2008), the following surfaces of error can compromise the accuracy of wICP registration: (i) respiratory motion artifacts if the LRS surface and salient features are not obtained using breath-holding protocols (ii) noise and outlier points arising from scanner artifacts (iii) localization errors when acquiring salient features (iv) inexperience of the surgeon while marking salient anatomical features using a tracked pen probe. FastRBF toolkit can be used to fit a surface to the three-dimensional point-cloud acquired using the LRS and this could eliminate noise and outlier points in the surface data. The respiratory motion artifacts were minimized by acquiring the intra-operative datasets at the same apneic period (end expiration point in the respiratory cycle). We do acknowledge that this will not completely eliminate the artifacts due to respiratory motion and we also acknowledge that in certain situations it might be difficult to obtain the salient anatomical features at the same apneic period as the surface descriptions. In such situations, we propose using the texture maps generated by the LRS to segment the salient anatomical features. This not removes the respiratory motion artifacts but it also eliminates localization errors associated with delineating the anatomical features using an optically tracked pen probe.
Previous studies have demonstrated reasonable success using closest point distances to predict intra-operative deformations during brain tumor resection therapies (Ferrant et al., 2001). Integrating dense intra-operative data such as the iMR datasets used in Ferrant et al. (2001) into computational models is relatively straight-forward as closest point distances are available for every node in the finite element mesh. It is clearly evident from the results presented for the phantom experiments in Table 1 that full surface descriptions significantly increase the accuracy of the proposed framework. However, obtaining dense intra-operative datasets using iCT or iMR is not a trivial task. This work integrates sparse intra-operative datasets into a computational framework. While there is no doubt that accuracy is sacrificed using sparse intra-operative datasets, the ease of acquiring such datasets combined with its low operating costs make it worth investigating. Sparse intra-operative datasets can also be acquired using iUS. iUS dataset can be used in a manner similar to the LRS surfaces: establish a rigid registration between the iUS datasets and the pre-operatives images, obtain closest point distance measurements between the two rigidly registered datasets and apply these distances as displacement boundary conditions to the finite element model. It should be noted that if LRS is used in conjunction with iUS, then these two sparse imaging techniques will cover a larger portion of the exposed intra-operative liver thereby increasing the number of measurement points for the sparse closest point distance computation. Such a scenario will increase the accuracy of the proposed computational framework. While we chose to use a closest point operator to find the distances between the rigidly registered pre-operative and intra-operative surfaces and to guide the computational framework, we acknowledge the limitations of closest point operators especially given the differing densities (i.e., total number of points) between the un-deformed pre-operative surface and the rigidly registered intra-operative surface. Other researchers have proposed modifications to the closest point operator (Chui and Rangarajan, 2003; Sharp et al., 2002) in order to achieve a more accurate correspondence and we are currently investigating on incorporating a more robust and accurate closest point operator into our computational framework.
Computational time is an important factor for using computational models in the context of surgeries. We have identified four bottlenecks in the proposed algorithm: (i) acquiring intra-operative surface descriptions using LRS (ii) acquiring salient features for use in wICP algorithm (iii) rigid registration using wICP (iv) computational framework. Based on our anecdotal observations in the OR, it takes less than a minute to acquire scans of the exposed intra-operative surface using LRS. Obtaining salient features using an optically tracked pen probe is heavily dependent on the surgeon's experience and skill level and takes anywhere between 1 and 3 min. It takes about 30 s for rigid registration using the wICP algorithm on a PC running Windows. Preliminary results indicate that it takes about 1 min to extrapolate the sparse closest point distances using the surface Laplacian equation based filter and about 2 min to solve the finite element model on a dual core machine running Linux. Though more detailed studies about computational times are pending, the proposed computational framework takes about 6 min to provide “real time” updates to the surgeon. While this might seem unreasonable based on surgical constraints, we are encouraged by the improvements in accuracy and are currently investigating on decreasing the total time required to provide updates to the surgeon using the proposed computational framework. In this work, liver was assumed to be an isotropic three-dimensional solid with a linear relationship between stress and strain. While this assumption might not be true, preliminary results suggest that a linear elastic model is sufficiently accurate and incorporating non-linearity might increase the computational time required for the framework.
Qualitative results from Fig. 11 demonstrate that the proposed computational approach significantly improves the surface alignment when compared to rigid registration and we believe that this improvement in surface alignment will also translate to the sub-surface features and vasculature. It should however be noted that sub-surface targets were not available for the clinical cases reported here and therefore closest point distances between the un-deformed and deformed surfaces were used to measure accuracy of the proposed approach. Since surgeons are more concerned with the sub-surface vasculature, closest point distances between the surfaces are not a reliable and robust metric to assess the accuracy of the proposed framework. We have started acquiring post-operative scans and are currently investigating the appropriateness of using sub-surface vessels as targets for the proposed approach.
6. Conclusions
Preliminary results reported here indicate that a rigid registration algorithm followed by the proposed computational approach improves the accuracy of guidance during open abdominal liver tumor removal surgeries. And, once we establish the fidelity of the proposed approach in more clinical cases, we plan to update the guidance display using the deformation field predicted by the computational approach.
Acknowledgements
This work has been supported by National Institute of Health, Grant # R21 EB007694-01. We would like to acknowledge that data was provided by Pathfinder Therapeutics Inc., Nashville, TN and is associated with National Cancer Institute Grant # CA119502. The authors would like to thank Dr. Robert L. Galloway, Vanderbilt University for his valuable inputs. Most of the visualization work and algorithms used in this work were developed using the Visualization Toolkit (http://www.vtk.org). For disclosure, Drs. Miga and Dawant are co-founders and hold equity in Pathfinder Therapeutics Inc., Nashville, TN.
References
- Arun KS, Huang TS, Blostein SD. Least-squares fitting of 2 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987 Sep;9(5):699–700. doi: 10.1109/tpami.1987.4767965. [DOI] [PubMed] [Google Scholar]
- Bathe OF, Mahallati H, Sutherland F, Dixon E, Pasieka J, Sutherland G. Complex hepatic surgery aided by a 1.5-tesla moveable magnetic resonance imaging system. Am. J. Surg. 2006 May;191(5):598–603. doi: 10.1016/j.amjsurg.2006.02.008. [DOI] [PubMed] [Google Scholar]
- Besl PJ, McKay ND. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992;14(2):239–256. [Google Scholar]
- Cash DM, Sinha TK, Chapman WC, Terawaki H, Dawant BM, Galloway RL, Miga MI. Incorporation of a laser range scanner into image-guided liver surgery: surface acquisition, registration, and tracking. Med. Phys. 2003 Jun;30(7):1671–1682. doi: 10.1118/1.1578911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cash DM, Miga MI, Sinha TK, Galloway RL, Chapman WC. Compensating for intraoperative soft-tissue deformations using incomplete surface data and finite elements. IEEE Trans. Med. Imag. 2005 Nov.24(11):1479–1491. doi: 10.1109/TMI.2005.855434. [DOI] [PubMed] [Google Scholar]
- Cash DM, Miga MI, Glasgow SC, Dawant BM, Clements LW, Cao Z, Galloway RL, Chapman WC. Concepts and preliminary data toward the realization of image-guided liver surgery. J. Gastrointest. Surg. 2007;11(7):844–859. doi: 10.1007/s11605-007-0090-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Understand. 2003;89:114–141. [Google Scholar]
- Clements LW, Dumpuri P, Chapman WC, Jr., Galloway RL, Miga MI. Atlas-based method for model updating in image-guided liver surgery. Medical Imaging 2007: Visualization and Image-guided Procedures. 2007;6509 [Google Scholar]
- Clements LW, Chapman WC, Dawant BM, Galloway RL, Miga MI. Robust surface registration using salient anatomical features for image-guided liver surgery: algorithm and validation. Med. Phys. 2008 Jun;35(6):2528–2540. doi: 10.1118/1.2911920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D'Haese P-F, Cetinkaya E, Konrad PE, Kao C, Dawant BM. Computer-aided placement of deep brain stimulators: from planning to intra-operative guidance. IEEE Trans. Med. Imag. 2005 Nov;24(11):1469–1478. doi: 10.1109/TMI.2005.856752. [DOI] [PubMed] [Google Scholar]
- Dowlatshahi K, Francescatti DS, Bloom KJ, Jewell WR, Schwartzberg BS, Singletary SE, Robinson D. Image-guided surgery of small breast cancers. Amer. J. Surg. 2001;182(4):419–425. doi: 10.1016/s0002-9610(01)00730-9. JournalOCT495TPAMER J SURG. [DOI] [PubMed] [Google Scholar]
- Dumpuri P, Thompson RC, Dawant BM, Cao A, Miga MI. An atlas-based method to compensate for brain shift: preliminary results. Med. Image Anal. 2007;11(2):128–145. doi: 10.1016/j.media.2006.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrant M, Warfield SK, Nabavi A, Jolesz FA, Kikinis R. LNCS: Medical Image Computing and Computer-assisted Intervention: MICCAI '00. Vol. 1935. Springer Verlag; 2000. Registration of 3D intraoperative mr images of the brain using a finite element biomechanical model. pp. 19–28. [Google Scholar]
- Ferrant M, Nabavi A, Macq B, Jolesz FA, Kikinis R, Warfield SK. Registration of 3-D intraoperative MR images of the brain using a finite-element biomechanical model. IEEE Trans. Med. Imag. 2001;20(12):1384–1397. doi: 10.1109/42.974933. [DOI] [PubMed] [Google Scholar]
- Gould SWT, Lamb G, Lomax D, Gedroyc W, Darzi A. Interventional MR-guided excisional biopsy of breast lesions. JMRI e J. Magn. Reson. Imag. 1998;8(1):26–30. doi: 10.1002/jmri.1880080110. JANeFEB JMRI-J MAGN RESON IMAGING. [DOI] [PubMed] [Google Scholar]
- Herline AJ, Herring JL, Stefansic JD, Chapman WC, Galloway RL, Jr., Dawant BM. Surface registration for use in interactive, image-guided liver surgery. Comput. Aided Surg. 2000;5(1):11–17. doi: 10.1002/(SICI)1097-0150(2000)5:1<11::AID-IGS2>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- Jolesz FA, Nabavi A, Kikinis R. Integration of interventional MRI with computer-assisted surgery. J. Magnet. Reson. Imag. 2001;13(1):69–77. doi: 10.1002/1522-2586(200101)13:1<69::aid-jmri1011>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Lange T, Eulenstein S, Hunerbein M, Lamecker H, Schlag PM. Medical Image Computing and Computer-assisted Intervention. Lecture Notes in Computer Science. Vol. 3217. Springer-Verlag; 2004. Augmenting intraoperative 3D ultrasound with preoperative models for navigation in liver surgery. pp. 534–541. [Google Scholar]
- Li S, Waite JM, Lennon BT, Stefansic JD, Li R, Dawant BM. Development of preoperative liver and vascular system segmentation and modeling tool for image-guided surgery and surgical planning. Medical Imaging 2008: Visualization, Image-guided Procedures, and Display: Proc. of the SPIE. 2008 [Google Scholar]
- Lorensen WE, Cline HE. Marching cubes: a high resolution 3D surface construction algorithm. ACM Comput. Graphics. 1987 Jul;21(4):163–169. [Google Scholar]
- Lunn KE, Paulsen KD, Roberts DW, Kennedy FE, Hartov A, West JD. Displacement estimation with co-registered ultrasound for image guided neurosurgery: a quantitative in vivo porcine study. IEEE Trans. Med. Imag. 2003 Nov.22(11):1358–1368. doi: 10.1109/TMI.2003.819293. [DOI] [PubMed] [Google Scholar]
- Lunsford LD, Latchaw RE, Vries JK. Stereotactic implantation of deep brain electrodes using computed tomography. Neurosurgery. 1983;13(3):280–286. doi: 10.1227/00006123-198309000-00012. [DOI] [PubMed] [Google Scholar]
- Marescaux J, Clement JM, Tassetti V, Koehl C, Cotin S, Russier Y, Mutter D, Delingette H, Ayache N. Virtual reality applied to hepatic surgery simulation: the next revolution. Ann. Surg. 1998 Nov;228(5):627–634. doi: 10.1097/00000658-199811000-00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miga MI, Paulsen KD, Lemery JM, Eisner SD, Hartov A, Kennedy FE, Roberts DW. Model-updated image guidance: initial clinical experiences with gravity-induced brain deformation. IEEE Trans. Med. Imag. 1999 Oct;18(10):866–874. doi: 10.1109/42.811265. [DOI] [PubMed] [Google Scholar]
- Nabavi A, Black PM, Gering DT, Westin CF, Mehta V, Pergolizzi RS, Ferrant M, Warfield SK, Hata N, Schwartz RB, Wells WM, Kikinis R, Jolesz FA. Serial intraoperative magnetic resonance imaging of brain shift. Neurosurgery. 2001;48(4):787–797. doi: 10.1097/00006123-200104000-00019. [DOI] [PubMed] [Google Scholar]
- Nakamoto M, Hirayama H, Sato Y, Konishi K, Kakeji Y, Hashizume M, Tamura S. Recovery of respiratory motion and deformation of the liver using laparoscopic freehand 3D ultrasound system. Med. Image Anal. 2007 Oct;11(5):429–442. doi: 10.1016/j.media.2007.07.009. [DOI] [PubMed] [Google Scholar]
- Ou JJ, Ong RE, Yankeelov TE, Miga MI. Evaluation of 3D modality independent elastography for breast imaging: a simulation study. Phys. Med. Biol. 2008;53(1):147–163. doi: 10.1088/0031-9155/53/1/010. [DOI] [PubMed] [Google Scholar]
- Pan S, Dawant BM. Sonka M, Hanson KM, editors. Automatic 3D segmentation of the liver from abdominal CT images: a level-set approach. Proceedings of SPIE. Medical Imaging 2001: Image Processing. 2001;4322:128–138. [Google Scholar]
- Paulsen KD, Miga MI, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery. IEEE Trans. Biomed. Eng. 1999 Feb;46(2):213–225. doi: 10.1109/10.740884. [DOI] [PubMed] [Google Scholar]
- Sharp GC, Lee SW, Wehe DK. Icp registration using invariant features. IEEE Trans. Pattern Anal. Mach. Intell. 2002;24(1):90–102. [Google Scholar]
- Sinha TK, Dawant BM, Duay V, Cash DM, Weil RJ, Thompson RC, Weaver KD, Miga MI. A method to track cortical surface deformations using a laser range scanner. IEEE Trans. Med. Imag. 2005 Jun;24(6):767–781. doi: 10.1109/TMI.2005.848373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan JM, Charron G, Paulsen KD. A three-dimensional mesh generator for arbitrary multiple material domains. Finite Elem. Anal. Design. 1997;25(3-4):219–241. [Google Scholar]