Nonrigid Point Registration for 2D Curves and 3D Surfaces and its Applications in Small Animal Imaging

Abstract

A nonrigid B-spline based point-matching method (BPM) is proposed to match dense surface points. The method solves both the point correspondence and nonrigid transformation without features extraction. The registration method integrates a motion model, which combines a global transformation and a B-spline based local deformation, into a robust point-matching framework. The point correspondence and deformable transformation are estimated simultaneously by fuzzy correspondence and by a deterministic annealing technique. Prior information about global translation, rotation and scaling is incorporated into the optimization. A local B-spline motion model decreases the degrees of freedom for optimization and thus enables the registration of a larger number of feature points. The performance of the BPM method has been demonstrated and validated using synthesized 2D and 3D data, mouse MRI, and micro-CT images. The proposed B-spline point-matching method can be used to register feature point sets, 2D curves, 3D surfaces, and various image data.

1. Introduction

Surface registration is extensively studied and applied in machine vision and medical imaging. Its applications include object detection and tracking (Dufour et al., 2002; Malassiotis and Strintzis, 2007), aligning medical images with atlases for analysis and quantification (Chui et al., 2003; Liu et al., 2004), and multimodality image integration for diagnosis or surgery planning (Betke et al., 2003; Li et al., 2008). The objective of registration is to determine a spatial transformation between floating and reference surfaces that, semantically, have spatial correspondence. The transformation can be seperated as rigid and nonrigid motions based on the assumption about motion between surfaces (Audette et al., 2000). Because of shape change, nonrigid matching is required in many applications such as recognition of human faces, tracking cardiac motion from serial cardiac images (Wierzbicki et al., 2004), and registration of brain images between different subjects (Ganser et al., 2004; Gee et al., 1993).

Surface registration can be implemented by representing surfaces as points or features (Maurer et al., 1996), or by physical modelling (Ferrant et al., 2001; Stammberger et al., 2000), in which surfaces are aligned based on relatively dense points which could be points in both surfaces or subset points extracted from the surfaces. The surface-points based methods require no extra processing such as feature extraction or definition of a physical motion model, and can provide a solution of free-form matching without determining feature correspondence before registration. For point based surface registration, there are two problems that need be resolved, the point correspondence and the transformation. Registration could be solved by determining the right correspondence, where high level information of the points like lines or shapes (Felmar and Ayache, 1996), where spatial relationships was used as attributes of points to locate point correspondence (Cross and Hancock, 1998). These methods usually were restricted to affine or projective transformation and are not well suited to handling outliers. Other popular methods solve the correspondence and transformation problems iteratively. Most point based registration methods fall into a similar framework that iterates between two steps: seek correspondence and solve transformation. These methods are distinguished by the types of transformation to be recovered, by the way to define the correspondence, and by the approach to solve the transformation.

Various point registrations have been reported in the literature. Besl and Mckay (Besl and McKay, 1992) proposed an iterative closest point (ICP) method to find the rigid transformation between two point sets (Stewart et al., 2003; Zhang, 1994). These methods are guaranteed to converge to a local minimum for a rigid transformation. In order to achieve a global result, the two surfaces are assumed to be relatively close or have sufficient numbers of initial guesses for registration. However, relatively large nonrigid motion invalidates the assumption, and point correspondence established by the closest points generates local minima and usually fails to reach a global nonrigid result. The one-to-one correspondence of the ICP method hinders solving a global nonrigid transformation between point sets. An alternative strategy is to relax the binary correspondence to fuzzy matching where a point in one set is partially corresponding to each point in the other set with fuzzy ratios. One class of the methods models the point alignment as matching of probability density distribution using statistical modeling of point sets (Roy et al., 2007; Wells, 1997). Because of probabilistic modeling of point sets, one-to-one correspondence cannot be enforced. A robust point-matching framework (RPM) was proposed to enforce the correspondence using a soft-assign technique without the strict one-to-one correspondence and by joint estimation of the transformation and correspondence using deterministic annealing (Gold et al., 1998). Chui (Chui and Rangarajan, 2003) extended the framework into thin plate spline (TPS) based nonrigid registration.

In this paper, we extend the robust point-matching method by using a volumetric B-spline motion model. The proposed B-spline-based point mathcing (BPM) method allows efficient registration of surfaces with a large number of points for various applications. Specifically, we applied the method for image registration in small animal imaging. Small animal imaging is increasingly used as a pre-clinical tool to identify new imaging agents or to assess therapeutic efficacy. This involves scanning a cohort of small rodents e.g. mice and rats at different time points and spatially evaluating the animal response in the course. One challenging step in the image analysis is the registration of mouse images at different time points. As a mouse body is quite small and flexible, it is difficult to maintain the animal at the same position in each imaging session. The registration becomes more difficult when there is large respiratory motion. Skeletons and skins are easily idenfiable and are robust anatomical features presented in micro-CT images. Registration of mouse skeletons using a point-based surface matching technique can correct the deformation of a mouse whole body between two time points and allows subsequent refinement of image alignment by intensity-based registration. In this article, we evaluate the proposed BPM method for registration of mouse skeletons and alignment of mouse tumors.

2. Method and materials

2.1. Transformation model

Suppose two point sets R: {r_i, i=1,2, …P} and V: {v_a, a=1,2, …,N} are sampled from reference and floating images, respectively. The term r_i or v_a represents a vector of the coordinates of the point in the 2D image or 3D volume. We define f as a spatial transformation that deforms the point set V to match with R, and f(v_a) is the absolute position resulting from the transformation.

As rigid or affine global transformation alone may not be sufficient to describe the deformation, the transformation is modeled as a combination of a global transformation f_global(v_a) and a local deformation f_local(v_a) described as

$$f(v_a)=f_{\mathit{\text{global}}}(v_a)+f_{\mathit{\text{local}}}(v_a)$$ (1)

where the global motion f_glocal describes the overall position change. We select a transformation which consists of a rigid transformation and scaling along each axis. For points in a 3D volume, the global tranformation is described by 3 rotations (θ), 3 translations (t), and 3 scalings (s), and is wrriten in matrix format. Nine parameters thus determines the global transformation.

The local deformation f_local describes the local shape change between surfaces. We use the B-spline free-form deformation model. The model deforms a volume by manipulating a mesh of control points equally distributed across the volume space. The control point grid produces a smooth and continous non-linear transformation. If the volume domain is spaced by a n_x × n_y × n_z uniform grid of control points, the local deformation for v_a=(x,y,z) is described as the following:

$$f_{\mathit{\text{local}}}(v_a)=\sum _{\delta =0}^3\sum _{\vartheta =0}^3\sum _{o=0}^3{B}_l(u)B_m(\upsilon )B_n(w){\varphi }_{\xi +\delta ,\psi +\vartheta ,\varsigma +o}$$ (2)

where $\xi =\left[\frac{x}{n_x}\right]-1,\psi =\left[\frac{y}{n_y}\right]-1,\varsigma =\left[\frac{z}{n_z}\right]-1,\text{and}u=\frac{x}{n_x}-\left[\frac{x}{n_x}\right],\upsilon =\frac{y}{n_y}-\left[\frac{y}{n_y}\right],w=\frac{z}{n_z}-\left[\frac{z}{n_z}\right]$, [] is the nearest integer operation, Ø is the B-spline coefficient that is defined at the grid points, and B represents the cubic B-spline basis function (Rueckert et al., 1999).

In order to discourage unrealistic shape deformation, the local deformation is regularized by a smoothness penalty that is the second order spatial derivatives of the motion over all the N points in point set V:

$${\mathit{\text{Lf}}}_{\mathit{\text{local}}}=\sum _{a=1}^N[{(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial x^2})}^2+{(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial y^2})}^2+{(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial z^2})}^2+2{(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial x\partial y})}^2{+2(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial x\partial z})}^2{+2(\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial y\partial z})}^2]$$ (3)

The second spatial derivatives in the penalty can be computed as

$$\frac{{\partial }^2{f}_{\mathit{\text{local}}}(v_a)}{\partial x^2}=\sum _{\delta =0}^3\sum _{\vartheta =0}^3\sum _{o=0}^3\frac{d^2{B}_l(u)}{d{u}^2}{B}_m(\upsilon )B_n(w){\varphi }_{\xi +\delta ,\psi +\vartheta ,\varsigma +o}$$ (4)

The other two derivative entries along y and z have a similar format.

2.2. Cost function for surface point matching

In general, object surfaces are extracted from 3D volume segmentation and surface point sets are obtained by down-sampling the surfaces. It is difficult to extract the exact corresponding point sets from two surfaces. The existence of point correspondence for some points cannot be ensured. We incorporate our motion model into the robust point-matching framework that does not require one-to-one point correspondence and is robust to noise and outliers. In the robust point-matching framework, point registration is modeled as a least square problem of linear assignment. The point correspondence is constructed using a fuzzy logic method and is enforced to be one-to-one correspondence using the soft-assignment and deterministic annealing techniques.

For registering two point sets with unknown point correspondence, we would like to map the two point sets as closely as possible while removing the impact of outlier points that do not have corresponding partners. Based on the RPM framework, a point v_a relates to all the points in R with a fuzzy ratio m_ai $(v_a\to \sum _{i=1}^P{m}_{ai}{r}_i)$. Therefore, two point sets are brought into correspondence by a matrix M={m_ai}. In order to handle an outlier situation where a point in V does not correspond to any point in R or vice versa, the RPM method added an extra row and column to the correspondence matrix M. Once a point is identified as an outlier, the points that correspond to this extra row or column are ignored in the transformation computation.

As M gives the point correspondence between two point sets, we minimize the following cost function

$$E=\sum _{a=1}^N\sum _{i=1}^P{m}_{ai}{\parallel r_i-f(v_a)\parallel }^2+\beta {\Vert {\mathit{\text{Lf}}}_{\mathit{\text{local}}}\Vert }^2+\alpha \sum _{a=1}^N{\Vert f_{\mathit{\text{local}}}(v_a)\Vert }^2+\kappa \sum _{a=1}^N\sum _{i=1}^P{m}_{ai}log{m}_{ai}$$ (5)

with the normalization requirement of

$${\sum }_{a=1}^{N+1}{m}_{ai}=1\text{for}i=1,2,\dots P,\text{and}{\sum }_{i=1}^{P+1}{m}_{ai}=1\text{for}a=1,2,\dots ,N$$

The explicit bound constraints [lb, ub] are included for each of the rotation, shift and scaling transformations.

The optimization first evaluates the point set distance weighted by the fuzzy matrix M, then applies the constraints to the motion, and finally makes the point correspondence to be as binary (one-to-one correspondence) as possible. We provide the range for each parameter in the global transformation (scaling, rotation and translation) according to the prior information. The local transformation is constrained by the second order derivatives as described in Equation (3). However, even with this smoothness restraint, the transformed surface could lose its main structure when M is significantly fuzzy at the beginning of the optimization processing. Therefore, we constrain the absolute local deformation $\sum _{a=1}^N{\Vert f_{\mathit{\text{local}}}(v_a)\Vert }^2$ to ensure the predominance of the global transformation. According to the entropy theory (Yao, 2003), the entropy of the matrix M increases as the matrix becomes less fuzzy and the matrix entropy reaches its maximum when M becomes a permutation matrix, meaning either 1 or 0 for each entry. At the final matching step, point sets from both surfaces are expected to be aligned as close as possible so that M should be as binary as possible, therefore minimizing the negative entropy of M, that is,. $(\sum _{a=1}^N\sum _{i=1}^P{m}_{ai}log{m}_{ai})$ will reach a one-to-one correspondence.

The cost function consists of the terms for optimizing both the point correspondence and the transformation. Similar to the expectation maximization method used in the RPM method, we minimize the cost function by iterating the two interlocking optimizations for the correspondence matrix M and the nonrigid transformation f.

2.3. Iteration and updating of the fuzzy correspondence matrix M

The matrix M is updated by evaluating the first derivatives of the cost function (5) with the current transformation f, and each element of the matrix is described below.

$$m_{ai}=e^{-\frac{{\Vert r_i-f(v_a)\Vert }^2}{\kappa }}$$ (6)

for i=1,2, …P, and a=1,2,…,N. Same to the RPM method, we also assume that each point has a small probability to be an outlier point. We define a point as an outlier when the distance of the point to any point in the other surface is more than 3√κ, which means m_ai=exp(-9) for the extra row and column (i=P+1, a=N+1) of matrix M. The parameter κ is a temperature parameter which weights the fuzziness of M with respect to the distance in the cost function. Equation (6) indicates that κ provides a distance range in which two points from both sets have a significant corresponding ratio. When κ has a higher value, M is fuzzier and the objective function becomes more convex for optimization. As κ gradually decreases, points very close to each other can have a significant m_ai, and M becomes less fuzzy, in other words, the points are more close to one-to-one correspondence. This phenomenon was employed to construct a deterministic annealing minimization in the RPM method, which will also be used in this B-spline based registration.

2.4. Solving the transformation parameters

Once M is determined, v_a is considered to correspond to a point ${\overline{r}}_a=\sum _{i=1}^P{m}_{ai}{r}_i/\sum _{i=1}^P{m}_{ai}$. As the two point sets achieve one-to-one correspondence, the problem becomes a constrained least-square fitting of Equation (5) for the transformation f.

Transformation f is resolved in two consecutive steps. First, the global transformation is solved by a constrained linear least square fitting between v and r̄ using the preconditioned conjugate gradient method (Horn and Johnson, 1985). Each unknown variable of the 9-parameter transformation is bounded by [lb, ub] according to the prior information of the global motion between the point sets. Second, the next step is to solve the B-spline coefficients at each control point by fitting the square distances after the removal of the global motion, which is written as the minimization of the following function

$$E=\sum _{a=1}^N{\parallel ({\overline{r}}_a-f_{\mathit{\text{global}}}(v_a))-f_{\mathit{\text{local}}}(v_a)\parallel }^2+\beta {\Vert L{f}_{\mathit{\text{local}}}\Vert }^2+\alpha \sum _{a=1}^N{\Vert f_{\mathit{\text{local}}}(v_a)\Vert }^2$$ (7)

where Lf_local and f_local are defined in Equations (3) and (2), respectively. The function E is quadratic for the B-spline coefficients, and the minimum occurs when all the first-order partial derivatives are zero. Setting the partial derivatives equal to zero leads to the linear equations AØ = b. The local B-spline deformation can be directly solved using the Cholesky decomposition (Barrett et al., 1994).

2.5. Optimization using deterministic annealing

Iterations of the optimization for M and transformation f depend on a given κ that specifies the weight of the correspondence fuzziness. At the initial stage, a wider search range or more fuzzy correspondence is expected for more convex optimization which means a higher κ. At the end, a one-to-one correspondence is desired for surface registration, which requires a low κ. This is analogous to a deterministic annealing scheme where a global solution is gradually reached as the temperature decreases. Therefore, the energy function is minimized in a deterministic annealing schedule. The temperature is linearly decreased according to κ^new = 0.90 · κ^old. At each temperature of κ, the interlocking optimizations are performed until convergence is achieved. We terminate the annealing procedure when there is no correspondence change if decreasing κ.

2.6. Framework of the BPM algorithm

Figure 1 shows the pseudo code for our B-spline robust point-matching algorithm. Minimization of the cost function (5) becomes two interlocking optimizations consisting of the estimation of correspondence matrix M and a least-square fitting for the transformation under the deterministic annealing scheme. Before registration, surface points will be extracted from both surfaces and the coordinates of both point sets are scaled into [0, 1].

Figure 1. Pseudo-code of B-spline nonrigid robust point-matching algorithm.

We initialize the transformation as a unit matrix indicating no transformation initially. We start the annealing scheme with κ₀ = 0.1. The parameters β and α weight the point-matching and the transformation constraint, respectively. When the matrix M is fuzzy at a high κ, the transformation needs to be more rigid for a global matching and also maintains the surface geometry, so the local motion constraints are expected to be greater. As κ becomes smaller, a flexible B-spline transformation is desired for a nonrigid alignment. Therefore, the parameters are set to adaptively decrease following the temperature annealing processing as α=5κ and β=10κ. Our following experiments on simulation and small animal data show that the design can be used for 2D and 3D surfaces without significant influence on the final outcome.

2.7. Registration evaluations

2.7.1. 3D data registration

To test the performance of the method for 3D surface registration in the presence of noise and outliers, we simulated a sphere in a 64 × 64 × 64 volume with a diameter of 40 voxels. We created a mesh for the surface using commercial software (AMIRA, Visage Imaging GmbH, Berlin, Germany). The 1501 triangle mesh vertices were sampled as the surface points for registration. We also down-sampled the surface to obtain 400 vertices as the boundary points. The volume and point set were first artificially transformed by an affine transformation and were then deformed with a smooth nonrigid motion. In order to simulate a realistic motion, the nonrigid motion was generated from a B-spline interpolation with 12 × 12 × 12 control points over the volume. The coefficients of the control points were sampled from a Gaussian distribution with a standard deviation of 8 voxels. The motion at the 400 boundary points was interpolated from the nonrigid B-spline motion. These point displacements form the boundary condition for a finite-element based elastic deformation of the sphere. The displacement at the 400 boundary vertices were the force that drives the deformation, which was modeled as linear isotopic elastic material with Young's modulus of 60 kPa and Poisson's ratio of 0.45 (Fei et al., 2006). The deformation was computed using the finite element analysis software FEMLAB (COMSOL, Inc., Burlington, MA). In this way, we generated two 3D surfaces and obtained 1501 surface points from both surfaces with exactly known deformation. Although the initial 400 boundary points were sampled from a B-spline interpolation, the 1501 surface points are generated from the finite-element modeling of the volumetric deformation. We performed the surface registration with a B-spline of 8 × 8 × 8 control points. The distance between the corresponding point pairs were used to evaluate the BPM registration method for recovering the synthesized motion.

2.7.2. Small animal image registration

We applied the BPM method to MR images of tumor-bearing mice that were treated using photodynamic therapy. Registration of tumor images before and after therapy allows voxelwise assessment of tumor response to therapy (Fei et al., 2007; Fei et al., 2010), which could provide imaging biomarkers for early measure of treatment outcome using various methods such as the Parametric Response Map (PRM) technique (Galban et al., 2009). We conducted MR imaging of the mice before and 24 hour after the treatment for monitoring the therapeutic effect (Fei et al., 2007; Fei et al., 2010; Wang and Fei, 2010). The whole-body mouse MR images were first registered using our rigid-body registration method (Fei et al., 2003a; Fei et al., 2003b; Fei et al., 2004; Fei et al., 2005). Significant global and local deformation was observed. We manually segmented the tumors from MR images and then aligned the surfaces using the proposed method. We applied the volumetric transformation to warp the tumor MR images. Twenty four tumor MR data sets from 24 mice have been examined. The registration was evaluated using the tumor volume overlapping ratio. The overlapping ratio was defined as the intersection of a tumor in the reference and registered images over the union of the tumor volumes in both images.

We also applied the BPM method to register mouse micro-CT images. The significant nonrigid bone motion in micro-CT images makes intensity-based registration difficult. The mouse micro-CT volumes were acquired at three different positions. The CT volumes (resolution: 0.1 × 0.1 × 0.1 mm³) were re-sampled to have a resolution of 0.2 × 0.2 × 0.2 mm³. The images were cropped into a size of 120 × 100 × 200. The mouse bone surfaces were extracted from the volumes using a thresholding method and were finally down-sampled to obtain a point set with 4500∼5000 points. The downsampling was implemented by keeping one surface point within a 3 × 3 × 3 window centered at the point and removing all other surface points within the window. Six mouse micro-CT volumes were registered to each other by the proposed BPM method with one B-spline grid point per 20 voxels in any direction. The micro-CT volumes were also registered using the intensity-based B-spline registration method (Rueckert et al., 1999) in the 3D Slicer software. The method registers two image volumes using B-spline transformation and minimization of mutual information. In order to quantitatively evaluate the bone surface registration, five anatomical landmarks were manually selected from the original and transformed bone skeletons. The distance between corresponding landmarks were computed to compare the BPM method with the intensity-based B-spline method.

3. Results

3.1. 3D registration results

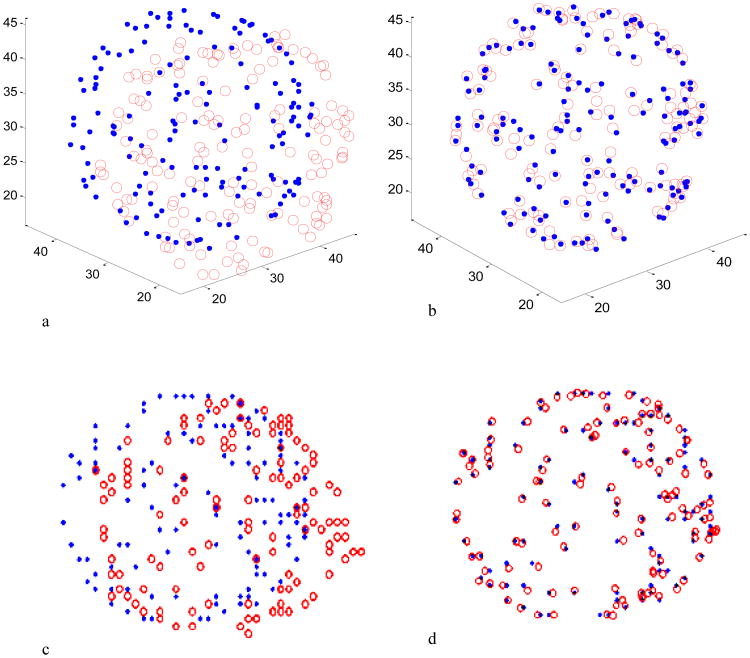
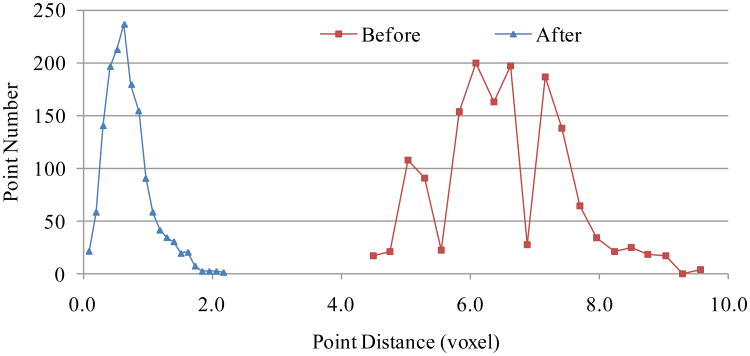
The BPM method was evaluated by the synthesized 3D point datasets (Figure 2). The two point sets were sampled from the surface of a synthesized sphere and from the elastically deformed volume. Only equally sampled 150 points from both point sets are displayed in the figure for better visualization. The 3D and 2D points overlapping clearly demonstrate that the registration successfully restores the simulated motion. Figure 3 plots the histogram of the distances between corresponding point pairs before and after registration, where the distance decreases from 6.5 ± 0.9 voxels before registration to 0.7 ± 0.3 voxels after registration.

Figure 2.

Registration of 3D synthesized point sets. (a) The two point sets with known simulated motion before registration. The transformed point set is labeled with empty circles. The reference point set is labeled with solid dot points. (b) The overlapping of the two point sets after registration. The 3D points in (a) and (b) are projected to the X-Y plane and the results are shown in (c) and (d), respectively. The points are matched after registration (b, d).

Figure 3.

Histogram of the mean distances between corresponding point pairs before and after registration. The distance of 1501 point pairs before registration is 6.5 ± 0.9 voxel and becomes 0.7 ± 0.3 voxel after registration.

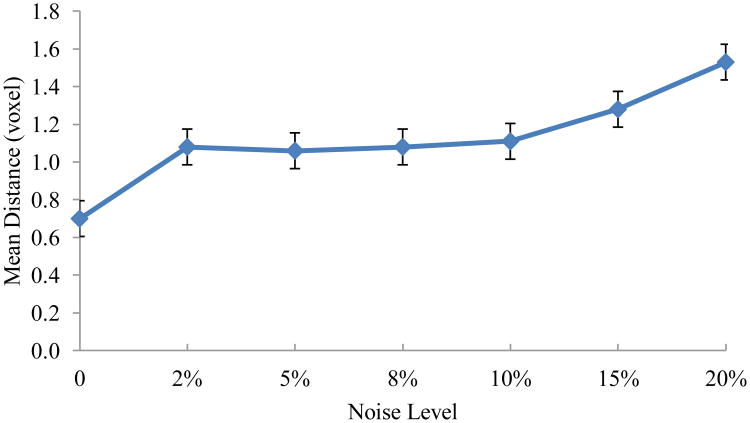
The BPM method was tested with pairs of point sets with motion noise. We added motion noise to perturb the displacement between each point pair. The noisy motion was sampled from a Gaussian distribution whose standard deviation was 2%, 5%, 8%, 10%, 15% and 20% of the maximal synthesized local motion. Figure 4 plots the average distance of the corresponding point pairs after registration, which suggests the registration method is not sensitive to motion noise if the noise level is less than 10%.

Figure 4.

Effect of motion noise on the performance of the BPM method. Y axis shows the mean distances of the point pairs after registration. X asis is the level of motion noise. Motion noise is sampled from a Gaussian distribution whose standard deviation is the percentage noise level of the maximal simulated motion.

3.2. Results of small animal image registration

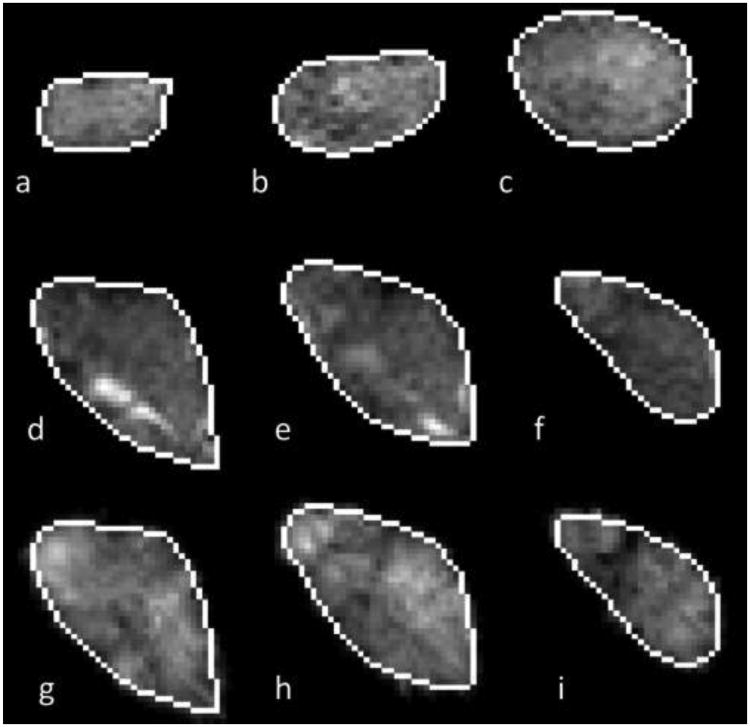
The BPM method was evaluated using mouse images. Figure 5 shows the alignment of a tumor surface before and 24 hours after therapy. There is significant global and local misalignment between the two surfaces after whole-body rigid registration (Figure 5c). After the BPM registration, the two surfaces are well aligned (Figure 5e), indicating the effectiveness of the registration method. We applied the resultant volumetric transformation to transform the tumor MRI volume and computed the overlapping ratio between the reference and deformation tumor. The average overlapping ratio for 24 tumors are 94% ± 5%. Figure 6 shows that the proposed registration method is able to match the tumor boundaries on 24 h MRI image slices to those before treatment.

Figure 5.

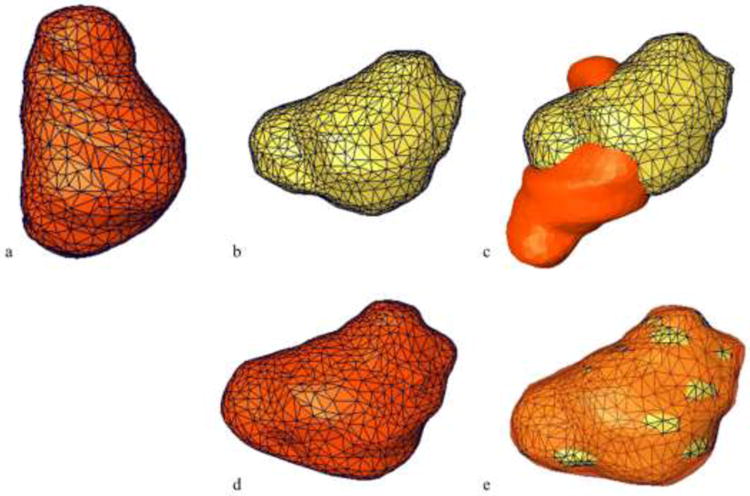
Registration of 3D tumor surfaces from MR images. (a) The floating surface with the triangle surface elements, (b) The reference surface, (c) The global and local difference between the reference and floating surfaces. (d) The transformed surface from (a) by using the BPM method. The overlap of the transformed and reference surfaces is shown in (e), indicating the alignment of the two surfaces after registration.

Figure 6.

Registration of 3D tumor volumes. (a, b, c) are 3 slices from a tumor MRI volume 24 h after treatment, (d, e, f) are the slices from the tumor MRI before treatment. (g, h, i) are the slices from the transformed 24 h MRI volume which has been registered to the volume before treatment by using the proposed BPM method. White contours are the 3D points for the tumor surface matching. The tumor shape from (g, h, i) match with those from (d, e, f).

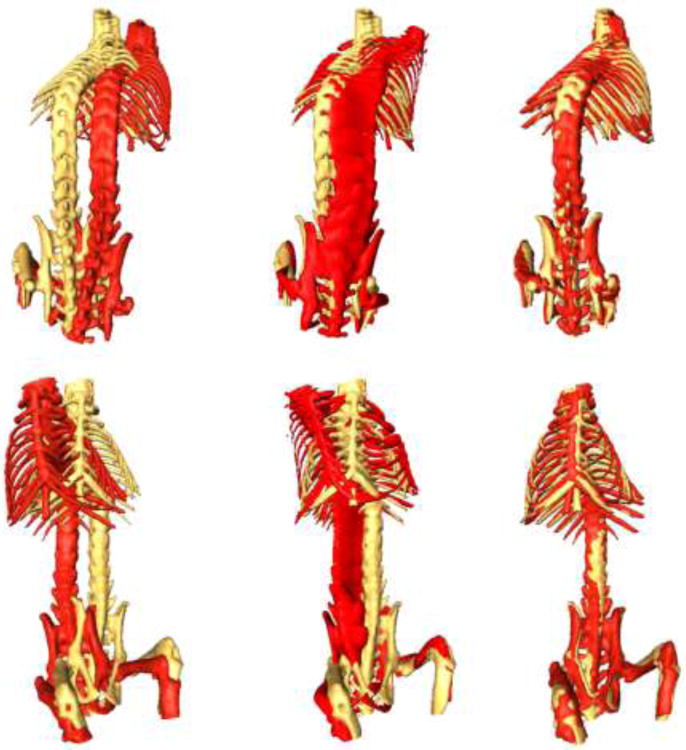
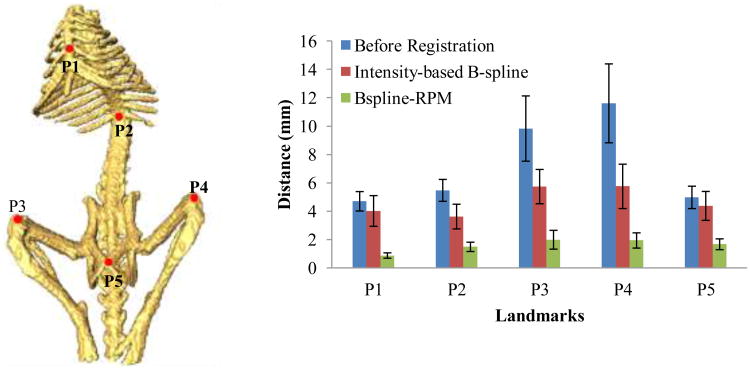
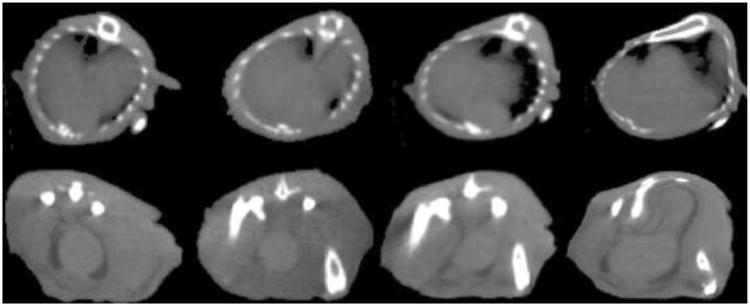
Our BPM method successfully registered the bone surfaces for six mouse micro-CT volumes. Figure 7 compares bone surface registration between the intensity-based B-spline method and our BPM method. Our method can correctly detect the point correspondence between two surfaces and is able to nonrigidly register the floating surface to the reference. However, the intensity-based B-spline method has difficulty to maintain the rigidity of bony structure. We manually selected 5 anatomic landmarks (Figure 8) for registration evaluation. The Euclidean distance between corresponding point pair was computed before and after registration. We averaged the distance of each landmark for all the registration experiments. Figure 8 shows the mean and standard deviation of each point pair distance. The average distance of the five landmarks decreased from 7.3 ± 4.9 mm before registration to 4.7 ± 2.8 mm after the intensity-based B-spline registration. The distances decreased to 1.6 ± 1.1 mm after the BPM method. Figure 9 shows two slices in the registered micro-CT volumes. Compared with the intensity-based B-spline registration method, our BPM method achieves better alignment between the registered and reference volumes.

Figure 7.

Comparison of the BPM and intensity-based B-spline methods. Left: The reference surface (yellow) and the floating surface (red) of a mouse bone skeleton before registration. Center: The reference surface (yellow) and the transformed surface (red) after intensity-based B-spline registration. Right: The two surfaces after BPM.

Figure 8.

Evaluation and quantitative comparison between intensity-based B-spline and BPM methods. Left: Five anatomical landmarks are identified on both surfaces for registration evaluation. Right: The average distances of the landmark pairs before and after registration using the two methods.

Figure 9.

Comparison between intensity-based B-spline and BPM methods for micro-CT image registration. First column: Floating images. Second column: Reference images at the same slice number with respective to the volume. Third column: Registered images after BPM. Fourth column: Registered images after intensity-based B-spline registration.

4. Discussion and conclusions

We proposed and evaluated a BPM method for nonrigid registration using dense sample points. The registration method can be applied to feature point sets, 2D curves, 3D surfaces, or surfaces consisting of multiple objects with outliers. The algorithm solves both the point correspondence and transformation without landmark portraying or features extraction. Fuzzy correspondence and deterministic annealing techniques are employed to achieve global optimization and outlier rejection. We modified the robust point-matching framework by integrating a motion model with a global transformation and a B-spline local deformation. Prior information about translation, rotation and scaling can be incorporated into the optimization and can be used to constrain the local deformation.

We used the deterministic annealing scheme for the optimization during registration, which has been shown to enable more robust registration than the classic ICP approach. We have observed that the global structures are registered at the high temperature κ, and that nonrigid local structures are aligned at low temperature because of more binary correspondence and because of the synchronized decreasing of the local motion constraint. Our motion model enables straightforward restriction of the global motion and dynamic control of the local transformation. The classic rigid ICP approach seeks a local optimal solution and assumes the rough alignment of two surfaces. Therefore, the significant global motion might not be solved by the rigid ICP approach before nonrigid registration. We emphasize the global motion at the high temperature. Therefore, the method is robust to local minima, especially when the correspondence is fuzzy at a high temperature.

Our BPM method is robust to motion noise and outliers that often affect the performance of point-based registration. Point noise and outliers can be from image acquisition and rendering. In our method, temperature κ weights the fuzziness of point correspondence and gives a search distance range for point correspondence. We assume that each point has a small prior probability to be an outlier point and add one row and column for outliers in the correspondence matrix. Therefore, if a point is far away from each reference point, for example, greater than 3√κ the normalization of the row or column of the correspondence matrix M makes the outlier row or column dominates the correspondence. Hence, by thresholding the outlier entry in M, the outlier point can be recognized and removed from the transformation. This outlier registration approach is consistent with the strategy proposed by (Feldmar and Ayache, 1996) where those points with a distance of greater than 3 times of the standard deviation of a Gaussian distribution were rejected as outliers. Our experiments on the 3D data set demonstrated the reliability of the BPM method for point sets in the presence of motion noise and outliers.

Longitudinal comparisons between subject's baseline and follow-up images have been widely performed in small animal imaging studies in order to assess drug or treatment efficacies. A challenge in this broad application is the presence of large whole-body deformation which creates convergence problems for intensity-based registration methods as illustrated in our results of mouse volume registration. Generally, the intensity-based deformable registration methods have a limited range of seeking transformation and thus typically require a rigid transformation in order to get two images roughly aligned in the preprocessing step (Hill et al., 2001; Pluim et al., 2003). Li et al. (Li et al., 2008) has used the TPS-RPM method with two sets of points from bone and body surfaces to provide an initial condition for intensity-based registration. Compared to the TPS-based method, our BPM method decreases the degrees of freedom from thousands parameters to a small number of B-spline coefficients and thus it is able to achieve high computational efficacy for surfaces with larger number of points. Our BPM method has demonstrated the ability to register whole-body mouse micro-CT images that were represented by thousands of dense points. We implemented the proposed method on a computer with 2.67GHz Intel Xeon CPU X5650 using Matlab 2010a. For the mouse skeleton registration, the average runtime of the BPM algorithm was 45 minutes for both the reference and floating surfaces with approximate 4,500 points. The speed can be improved with a high performance computer and C++ implementation.

In summary, we developed and evaluated a B-spline based robust point-matching method. The registration method avoids identification of point correspondence but solves both point correspondence and nonrigid transformation at the same time. The BPM approach can reduce the degrees of freedom, improve computation efficiency, and can be used for various imaging applications.