Comparison Study of Intraoperative Surface Acquisition Methods for Surgical Navigation

Abstract

Soft-tissue image-guided interventions often require the digitization of organ surfaces for providing correspondence from medical images to the physical patient in the operating room. In this paper, the effect of several inexpensive surface acquisition techniques on target registration error and surface registration error (SRE) for soft tissue is investigated. A systematic approach is provided to compare image-to-physical registrations using three different methods of organ spatial digitization: 1) a tracked laser-range scanner (LRS), 2) a tracked pointer, and 3) a tracked conoscopic holography sensor (called a conoprobe). For each digitization method, surfaces of phantoms and biological tissues were acquired and registered to CT image volume counterparts. A comparison among these alignments demonstrated that registration errors were statistically smaller with the conoprobe than the tracked pointer and LRS (p < 0.01). In all acquisitions, the conoprobe outperformed the LRS and tracked pointer: for example, the arithmetic means of the SRE over all data acquisitions with a porcine liver were 1.73 ± 0.77 mm, 3.25 ± 0.78 mm, and 4.44 ± 1.19 mm for the conoprobe, LRS, and tracked pointer, respectively. In a cadaveric kidney specimen, the arithmetic means of the SRE over all trials of the conoprobe and tracked pointer were 1.50 ± 0.50 mm and 3.51 ± 0.82 mm, respectively. Our results suggest that tissue displacements due to contact force and attempts to maintain contact with tissue, compromise registrations that are dependent on data acquired from a tracked surgical instrument and we provide an alternative method (tracked conoscopic holography) of digitizing surfaces for clinical usage. The tracked conoscopic holography device outperforms LRS acquisitions with respect to registration accuracy.

I. Introduction

The acquisition of dense point measurements of anatomic surfaces is a fundamental task in image-guided surgical procedures that require registration of the anatomy to medical images or models derived from medical images. Our interest in using surface measurements for registration purposes is to initialize an automated deformation correction pipeline for soft-tissue interventions [5], [8]–[10].

One simple method of collecting intraoperative surface data is to use a tracked pointer. Such devices are readily available in commercial image-guided surgery systems and clinicians are familiar with their use. Acquiring surface data in this way is particularly useful for orthopedic applications, where surgical access is limited and registrations can be refined from points taken percutaneously [18]. In commercial neurosurgical systems, a tracked pointer is used for providing the initial rigid transformation by matching points acquired from naso-orbital landmarks in the preoperative volume. Fig. 1 demonstrates the intraoperative acquisition of points from the surface of the naso-orbital regions of a patient undergoing tumor resection therapy at Vanderbilt University Medical Center (Nashville, TN), where this method of acquisition has become standard of care. An optically tracked tool is pictured in Fig. 2(a).

Fig. 1.

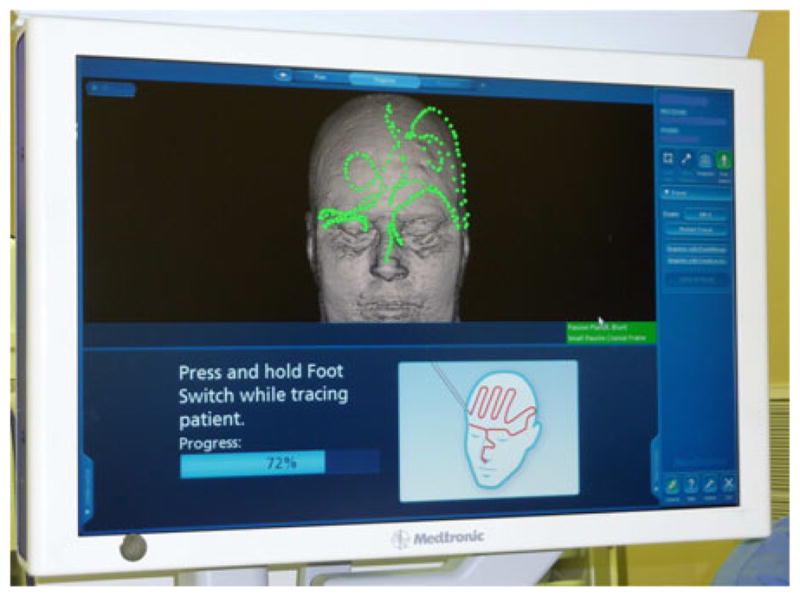
Standard display from the StealthStation (Medtronic Inc., Minneapolis, MN) neurosurgical guidance system. The green points represent the data acquired from a tracked pointer, superimposed on the patient’s skull generated from preoperative images. The red points demonstrate point selection for the user.

Fig. 2.

Surface acquisition devices in experiments: (a) sharp-tipped tracked pointer, (b) LRS, and (c) conoprobe. The tracked pointer and conoprobe are hand-held devices.

Measuring surface data with a tracked pointer is appropriate for rigid structures that do not deform; however, in soft-tissue applications, registration accuracy can be compromised if the pointer loses contact with the surface or displacements of the tissue occur due to contact forces [6], [20]. Furthermore, surgeons are apprehensive with regard to touching delicate anatomical structures such as the surface of the brain, with an inflexible instrument due to the possibility of tissue damage.

Alternatively, intraoperative registration can be achieved by acquiring a laser-range scan (LRS) of the exposed organ surface. Briefly described, an LRS passes a stripe of laser light over a surface and uses the principle of triangulation to determine 3-D points in space. When the reflected light is received by the charge-coupled device (CCD) camera, the reflected light and the known trigonometric relationship between the camera and the laser are used to compute the 3-D location [1]. The CCD also records color information which can be applied to the point cloud and used for identification of landmarks on the surface and segmentation of structures of interest [28]. The LRS is usually fitted with optical tracking targets so that the position and orientation of the device can be determined relative to the patient so that subsequent scans of the patient are in alignment [5], [28]. An optically tracked LRS is pictured in Fig. 2(b). The LRS is designed as a multiface passive tool with three passive targets affixed to it. For each pose of the LRS, a single face of the LRS is tracked. We evaluated the accuracy of LRS tracking in other work [22].

Methods of rigidly aligning preoperative images with the physical patient have been investigated for LRS. In [4]–[6], a traditional iterative closest point (ICP) algorithm [2] was used for alignment of preoperative CT and intraoperative LRS. The accuracy was compromised by sensitivity to errors in the initial alignment and organ deformation resulting from mobilizing and preparing the liver for resection. A weighted ICP [19] variant was proposed that weighs anatomical features for registration in other work [7]. The algorithm performed better than traditional ICP in all phantom and clinical trials. Explorer Liver (Pathfinder Therapeutics Inc., Nashville, TN) is a commercial surgical navigation system that has an LRS (as an optional component) and uses the weighted ICP scheme. In related work, a novel registration using both surface geometry and intensity data for cortical brain surfaces was proposed [21]. This work was expanded upon in a comprehensive comparison of registration study using skin markers and an LRS of the patient’s face for initial alignment in neurosurgical applications yielding similar results [3]. Others have conducted similar studies with similar results [26].

Central to the above rigid/nonrigid registration approaches is the acquisition of intraoperative geometric organ data. While we have previously reported on the use of LRSs and tracked pointers, conoscopic holography has been a recent endeavor. As such, we have not reported our experiences with the use of conoscopic holography. Briefly, conoscopic holography is a noncontact distance measurement method based on polarized light interference originally reported by Sirat and Psaltis [30] for industrial quality control applications. Constructive and destructive interference patterns between emitted and reflected laser light are analyzed. The send and receive paths are collinear, and distances measurements are derived from a solid angle (cone of light) [30] rather than the single ray approach used by triangulation-based technologies resulting in a more precise and robust measurement than triangulation systems [29]. Recently, techniques have been developed which apply the principles of conoscopic holography to image-guided surgery [16]. In that preliminary study, the ConoProbe Mark 3 (Optimet Metrology Ltd., Jerusalem, Israel) was used. The conoprobe reports a distance of the laser source to a surface, and once it is fitted with an optical tracking rigid body, a calibration procedure establishes the conoprobe measurements in optical tracking coordinates such that a tracked 3-D surface of an object could be generated. In this preliminary study reported, the tracked conoprobe was shown to be a promising surface acquisition device in the operating room [16]. An optically tracked conoprobe is pictured in Fig. 2(c).

The z-touch (BrainLab Inc., Feldkirchen, Germany) is a commercially available noncontact digitizer that emits a single laser light that is visible to the optical tracking cameras [23]. The optical tracking camera determines the position of the 3-D point. Direct line-of-sight of the tracking system to the laser point is required. In a study of surface scanning using the z-touch, the mean accuracy (mean measured deviation) was reported as 2.4 ± 1.7 mm [15], [23]. In another study, registration error with the z-touch was higher than fiducial-based registration; 2.77 ± 1.64 mm with z-touch and 1.31 ± 0.87 mm with markers [25]. The Fazer (Medtronic Inc., Minneapolis, MN) is an optically noncontact digitizer. In a similar study to the z-touch study, the root mean square error ranged from 1.3 to 3.2 mm with the Fazer and 0.3 to 1.8 mm with markers [24].

Given this backdrop, we present two contributions in this paper. The primary contribution is the comparison of registrations obtained with three different surface acquisition modalities of phantom and cadaver specimens. We study the effect of acquiring data with a tracked pointer, LRS, and conoprobe on registration accuracy. The subject of our study is not the best theoretically achievable registration accuracy but rather the accuracy attainable in a clinical setting. The secondary contribution is the systematic investigation of conoscopic holography for surface characterization for image-guided surgery. This paper demonstrates the detrimental effect of surface acquisition using a tracked pointer (as used in commercial systems) on accuracy and provides an alternative approach that is noncontact and handheld for use clinically.

II. Methods

A. Surface Acquisition

A Polaris Spectra passive optical tracking system (Northern Digital Inc., Waterloo, ON, Canada) tracked the position and orientation (pose) of all rigid bodies in this study. In all data collections, a rigid body was securely fixed relative to the specimen such that all acquisitions were measured relative to this rigid body and all successive datasets were in the same coordinate frame (analogous to the intraoperative image-guided surgical environment). Great care was taken to ensure that a specimen did not move relative to its rigid body during the experiments (see Sections II-D–II-F for details). The rigid body was attached in close proximity to the object under evaluation to reduce the influence of rotational errors on TRE as much as reasonably possible. Horn’s method [14] was used for all fiducial registrations and for registrations where corresponding points were assumed (e.g., when finding an initial estimate for ground truth registrations). The surfaces of all specimens were acquired using the three optically tracked devices: pointer, LRS, and conoprobe (see Fig. 2). We attempted to cover as much of the visible surface as possible during collections. When using the tracked pointer and the conoprobe, we varied the pattern of collection. The LRS was moved between LRS acquisitions. We collected all tracked pointer datasets after the LRS and conoprobe collections to prevent damage to the specimen due to contact. The tracked pointer (Northern Digital Inc., Waterloo, ON, Canada) was calibrated with a standard sphere-fit procedure provided by the manufacturer such that the tip of the tool was known with respect to the tool’s rigid body (which is measured in the tracking camera frame). The LRS (Pathfinder Therapeutics Inc., Nashville, TN) was calibrated by the manufacturer using a method described in previous work [6] such that the LRS surface could be obtained in the coordinate frame of the camera. The LRS has a reported 3-D root mean square error of 0.47 mm [22]. Finally, a rigid body was fixed to a ConoProbe Mark 3 (Optimet Metrology Ltd., Jerusalem, Israel) and calibrated such that the location of the measured laser point was known in the camera frame. The conoprobe has a reported distance measurement error of ≤ 100 μm. The tracked conoprobe is shown in use in Fig. 3.

Fig. 3.

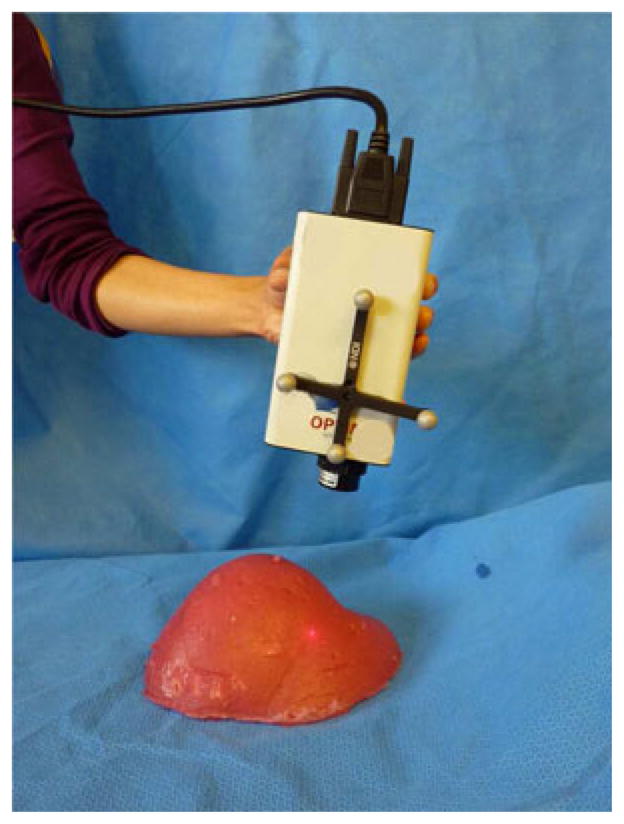
Optically tracked ConoProbe Mark 3 used in our experiments.

B. Calculating Registration Error

Let T_true be an estimate of the ground truth registration transformation, and let T_other be an experimentally obtained registration transformation, where both transformations are represented using 4 × 4 homogeneous matrices that map points from the CT frame to points in the reference rigid body frame.

Given a 3-D model having n points on an anatomic surface computed from a medical image, we define the surface registration error (SRE) of a point, p_i, as the magnitude of the vector difference

$${\text{SRE}}_i=\Vert {\mathbf{T}}_{\text{true}}{\mathbf{p}}_i-{\mathbf{T}}_{\text{other}}{\mathbf{p}}_i\Vert .$$ (1)

We also computed target registration errors (TRE) for sub-surface target points r_i defined in the CT images. Fitzpatrick et al. [11] defined TRE as being the error in position of a target point after registration has been performed; we computed TRE for a target r_i as

$${\text{TRE}}_i=\Vert {\mathbf{T}}_{\text{true}}{\mathbf{r}}_i-{\mathbf{T}}_{\text{other}}{\mathbf{r}}_i\Vert .$$ (2)

We should note that in the traditional formulation of TRE [11], corresponding points are localized in two different modalities (in image space and physical space, for example), the registration is applied, and the displacement is measured. In the formulation used here, we have a ground truth transformation; hence, there is no measurement error (in measuring in CT and in physical space) so the measured TREs are not directly comparable to results computed with traditional TRE. We make the distinction between SRE and TRE because TRE is defined as the error in points not used in the registration, and there is no way to guarantee that a surface point p_i is not used in the registration.

C. Significance Testing With TRE Values

To establish that one acquisition modality is statistically better (with respect to TRE) than another, significance testing was employed. The data were analyzed using the Wilcoxon signed-rank test which is a nonparametric test that ranks difference scores and assumes the distribution of the differences are symmetric about the mean with no normality assumption [27] (a t-test assumes a normal distribution which is not an appropriate assumption for TRE values). The data were also analyzed using a sign test which is a nonparametric test that makes no assumption with regard to the distribution of differences, but carries less statistical power than the Wilcoxon test [12]. If both tests are in agreement, then our conclusion is very credible.

With a sufficiently large data collection, it may be the case that the tests for significance indicate differences in populations that are very small, yet statistically significant though not clinically relevant. To address this, we chose a clinically relevant difference for our application of 0.2 mm and added this value to the TREs produced by the method that we want to show is better. These data were analyzed with the Wilcoxon signed-rank test and sign test.

D. Phantom Experiments

Two anthropomorphic phantoms were cast for use in the study: a liver phantom of silicon rubber (Dragon Skin, Smooth-On Inc., Easton, PA) and a brain phantom of stiff silicon rubber. Even though the optical characteristics and tissue properties are different from human organs, we chose to use plastic phantoms as an idealized baseline comparison with our other experiments. The phantoms were fixated to a pegboard having an array of holes, and then CT scanned [see Fig. 4(a)]. The board was chosen such that the holes would be visible in both LRS and CT data for gold standard calculations. The phantoms were segmented from the CT scan using a standard thresholding method, and 3-D models were constructed using the marching cubes algorithm [17]. The LRS of the board and the 3-D model of the board is shown in Fig. 5 before and after registration.

Fig. 4.

Tissues and phantoms used in experiments: (a) silicon rubber brain (white) and liver (red) phantoms mounted on pegboard, (b) porcine liver with radiographic markers, and (c) cadaver kidney covered in perirenal fat with rigid body in a bowl inside of biplane fluoroscope (biplane not pictured).

Fig. 5.

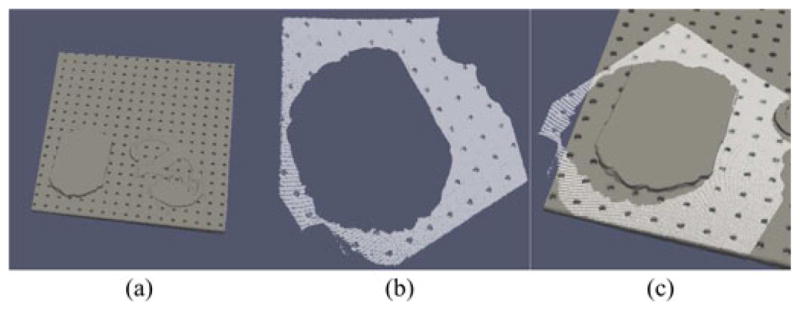
Data used in ground truth determination for brain phantom experiment: (a) 3-D model of board, (b) LRS of board prior to registration, and (c) LRS superimposed on board, after registration.

Surface acquisitions of both phantoms were acquired using the pointer, LRS, and conoprobe five times each, for a total of 15 datasets for each phantom. The optical camera was moved between each acquisition, and the conoprobe and pointer datasets were collected by different individuals. In order to establish correspondence from physical space to CT space, an initial registration estimate was computed from corresponding points picked on the LRS and CT model. This estimate was used to initialize all registrations for all datasets. The final registration transformation was computed using an iteratively reweighted least-squares modification of ICP that is insensitive to spurious points [18] that we call robust ICP.

To establish a gold standard registration for accuracy analysis, the board was segmented from CT, a 3-D model was generated of the board, an LRS of the board was acquired, and the board was segmented from the LRS scan. The gold standard registration estimate was produced by seeding robust ICP with a transformation obtained by manually aligning the LRS with the 3-D model.

We investigated the sensitivity of the SRE to variations in the number of points collected by each acquisition method by downsampling the points and performing a registration with these points. For each of the original 15 datasets, 10–100% of the points were randomly sampled at 10% increments. We registered the points to the model with the same initial estimate used in our other phantom trials and computed the SRE as in (1) for each point in the surface model.

We tested the sensitivity of the SRE to the initial registration estimate by perturbing the initial estimate and rerunning the registration algorithm with the new initial estimate. Specifically, we generated 500 estimates perturbed by up to 5° and 5 mm (selected at random) and repeated the pointer, LRS, and conoprobe registrations.

E. Ex Vivo Porcine Liver Experiments

A fresh porcine liver was provided by the Section of Surgical Sciences at Vanderbilt University Medical Center for the study in accordance with the Institutional Animal Care and Use Committee. The excised organ was placed on a board, similar to the one used in the phantom experiment, and six adhesive radiographic markers (Izi Medical Products Inc., Baltimore, MD) were adhered to the surface of the organ [see Fig. 4(b)]. The liver was imaged in a CT scanner. The pointer, LRS, and conoprobe were used to acquire five surface scans each for a total of 15 datasets. An initial physical-to-CT space registration was obtained by touching the center of the radiographic markers with the pointer, localizing the center of the markers in CT, and finding correspondence. The gold standard registration estimate was established in the same way as the phantom data collections, by aligning an LRS of the board with a CT of the board using robust ICP.

The accuracy of points acquired by a device that uses conoscopic holography technology depend on the absorption properties of the tissue being scanned. The conoprobe software reports the signal-to-noise ratio (SNR) as a percentage for each conoprobe point collected. We tested the effect of the points with a low SNR percentage on TRE. For all five porcine liver data collections with the conoprobe, we performed the registration using 1) only points with SNR < 30%, 2) all points, 3) all points with SNR > 30% (the threshold suggested by the manufacturer), and 4) all points with SNR > 60%. Since the robust ICP registration algorithm used in the study is resistant to spurious points, we repeated our SNR analysis with traditional ICP.

F. Ex Vivo Cadaver Kidney Experiments

One fresh cadaveric kidney was used in this study. The specimen was obtained from an individual that voluntarily provided their organs to the School of Medicine at Vanderbilt University Medical Center [see Fig. 4(c)]. The LRS was not available for this data collection; hence, only pointer and conoprobe data were acquired. Instead of CT, the kidney was imaged using an Allura Xper FD20/20 biplane fluoroscope (Philips Healthcare Inc., Best, The Netherlands) capable of 3-D image reconstruction. The pointer and conoprobe were used to collect five datasets each. Since this experiment was performed inside of the imaging unit, a gold standard registration from physical-to-image space was computed based on the presence of the tracked rigid body in the reconstructed 3-D image. The passive tracking target, attached to the apparatus containing the kidney, is shown in Fig. 4(c). The centers of the passive tracking retroreflective spheres were manually localized from the image. CT slices containing the spheres are shown in Fig. 6. The positions of the individual spheres were extracted from the specifications of the rigid body provided by the manufacturer. Point-based registration was used to establish correspondence between physical and image space.

Fig. 6.

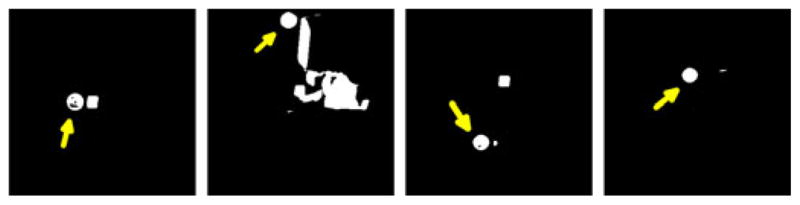
Passive tracking retroreflective spheres visible in CT used to compute ground truth in cadaver kidney experiment.

III. Results

A. Phantom Experiments

1) SRE Results

Figs. 7 and 8 show the SRE computed using (1) for each point in the surface model. Interestingly, the datasets acquired using the tracked pointer contain mostly translational error, evident in the solid red color of the liver in the top row of Fig. 8. To investigate this, we computed the vector TRE, Δr_i − r_i, for ten targets scattered throughout the phantom liver. The directional component of the TRE for each of the five tracked pointer (blue) and five conoprobe (red) trials is shown in Fig. 9. The narrow spread of the arrows (i.e., arrows pointing in one direction) represents small rotational error and (in this case) large translational error. Arrows pointing in diverging directions indicate the presence of rotational errors. In our data collections, it appears that the data collected with the conoprobe contain both translational and rotational errors, whereas the data collected with the pointer contain mostly translational error.

Fig. 7.

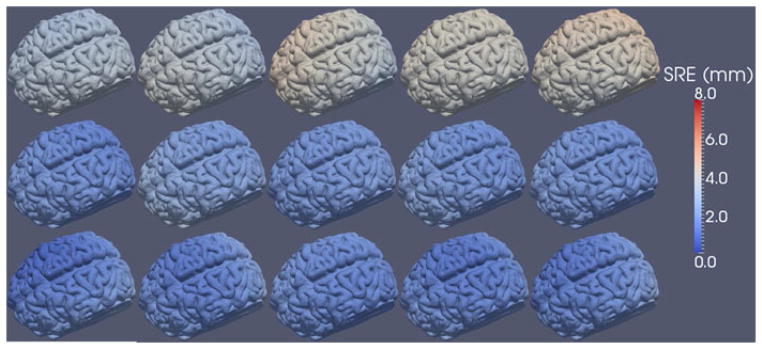
SRE computed for each point in the surface model for the five tracked pointer (top row), five LRS (middle row), and five conoprobe (bottom row) datasets of the brain phantom. Registration error increases from blue to white to red.

Fig. 8.

SRE computed for each point in the surface model for the five tracked pointer (top row), five LRS (middle row), and five conoprobe (bottom row) datasets of the liver phantom. Registration error increases from blue to white to red.

Fig. 9.

Displacements of targets for five tracked pointer (blue) and tracked conoprobe (red) trials. If the translational component of TRE is large, and the rotational component small, the arrows point in largely the same direction. If the rotational component is large, the arrows diverge. In our datasets, the conoprobe acquisitions contain rotational and translational error, while the pointer acquisitions contain largely translational errors.

For the brain phantom, the mean SRE and standard deviation over all five datasets for the tracked pointer, LRS, and conoprobe were 3.69 ± 0.10 mm, 2.14 ± 0.08 mm, and 1.88 ± 0.11 mm, respectively, as summarized in Table I.

Table I.

Anthropomorphic Brain Phantom SRE Results

Pointer SRE (mm)					LRS SRE (mm)					Conoprobe SRE (mm)
trial	mean	sdev	min	max	trial	mean	sdev	min	max	trial	mean	sdev	min	max
1 (n = 2204)	3.28	0.20	2.97	3.69	1 (n = 87903)	1.87	0.24	1.46	2.40	1 (n = 2154)	1.76	0.51	0.81	2.86
2 (n = 2468)	3.36	0.27	2.88	3.85	2 (n = 87729)	2.52	0.33	1.93	3.20	2 (n = 1185)	2.02	0.44	1.23	2.96
3 (n = 2029)	3.77	0.33	3.07	4.33	3 (n = 88378)	2.07	0.12	1.85	2.33	3 (n = 1363)	1.90	0.21	1.51	2.27
4 (n = 2185)	3.92	0.07	3.80	4.04	4 (n = 86414)	2.18	0.28	1.71	2.75	4 (n = 1572)	1.85	0.37	1.14	2.53
5 (n = 2113)	4.12	0.21	3.78	4.56	5 (n = 86005)	2.05	0.17	1.77	2.42	5 (n = 1412)	1.88	0.41	1.13	2.79
total	3.69	0.21	3.30	4.10	total	2.14	0.23	1.75	2.62	total	1.88	0.39	1.16	2.68

The mean SRE and standard deviation for the liver phantom over all five datasets for the tracked pointer, LRS, and conoprobe were 5.15 ± 0.29 mm, 3.22 ± 0.33 mm, and 2.49 ± 0.14 mm, respectively, as summarized in Table II.

Table II.

Anthropomorphic Liver Phantom SRE Results

Pointer SRE (mm)					LRS SRE (mm)					Conoprobe SRE (mm)
trial	mean	sdev	min	max	trial	mean	sdev	min	max	trial	mean	sdev	min	max
1 (n = 1220)	4.71	0.44	4.18	6.00	1 (n = 93277)	3.39	0.89	1.69	5.01	1 (n = 1542)	2.81	0.62	1.85	4.52
2 (n = 910)	5.34	0.53	4.27	6.23	2 (n = 80033)	3.38	1.48	0.51	6.33	2 (n = 1151)	2.83	0.67	1.87	4.57
3 (n = 812)	5.12	0.89	3.31	6.55	3 (n = 111694)	3.39	1.52	0.33	6.42	3 (n = 1311)	2.61	0.90	1.19	4.90
4 (n = 687)	4.99	0.10	4.86	5.26	4 (n = 73001)	2.93	0.79	1.53	4.59	4 (n = 994)	2.20	0.71	1.04	3.72
5 (n = 808)	5.53	0.39	4.86	6.22	5 (n = 88419)	3.03	1.12	1.31	5.63	5 (n = 1624)	2.02	0.52	1.29	3.40
total	5.15	0.47	4.30	6.05	total	3.22	1.16	1.07	5.60	total	2.49	0.68	1.45	4.22

2) Subsurface TRE Results

Ten virtual targets were evenly placed in the subsurface of the brain and liver phantom surface models in locations characteristic of tumors. TRE results computed using (2) for each of the five tracked pointer, five LRS, and five conoprobe data collections are shown in Fig. 10(a) and (b). A Wilcoxon signed-rank test and sign test (described in Section II-C) checked for significant differences in TRE across all data collection methods for both phantoms. The test found significant differences between the tracked pointer, LRS, and conoprobe datasets (p < 0.0001): the conoprobe collections were statistically better than the tracked pointer and LRS collections, and the LRS collections were statistically better than the tracked pointer collections for the brain and liver phantoms. Further application of the Wilcoxon and sign tests established that statistical significance was achieved for a clinically important difference of 0.2 mm (p < 0.01).

Fig. 10.

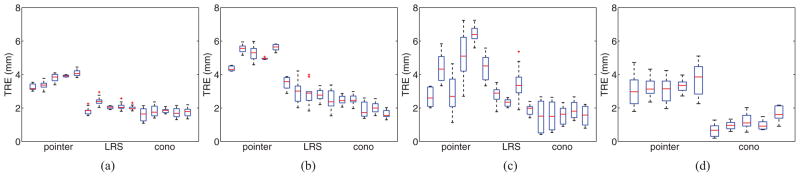
TRE computed for ten subsurface targets for the brain phantom, liver phantom, porcine liver, and cadaver kidney experiments. Each experiment consisted of five surface datasets for each acquisition type. (a) Brain phantom. (b) Liver phantom. (c) Porcine liver. (d) Cadaver kidney.

3) Sensitivity to the Number of Points Collected

The number of points in each point set is listed in the first column of Table II. In results not presented here, the percentage of points that were randomly sampled did not have a significant effect on SRE.

4) Sensitivity to Initial Registration Estimate

In results not reported here, we found that variations in the initial registration estimate did not significantly affect SRE.

B. Ex Vivo Porcine Liver Experiments

1) SRE Results

Fig. 11 shows the SRE computed using (1) for each point in the surface model. The mean and standard deviations of SRE for all five trials of each of the pointer, LRS, and conoscope acquisitions were 4.44 ± 1.19 mm, 3.25 ± 0.78 mm, and 1.73 ± 0.77 mm, respectively, as summarized in Table III.

Fig. 11.

SRE computed for each point in the surface model for the five tracked pointer (top row), five LRS (middle row), and five conoprobe (bottom row) datasets of the porcine liver. Registration error increases from blue to white to red.

Table III.

Porcine Liver SRE Results

Pointer SRE (mm)					LRS SRE (mm)					Conoprobe SRE (mm)
trial	mean	sdev	min	max	trial	mean	sdev	min	max	trial	mean	sdev	min	max
1	2.87	0.85	1.20	4.75	1	4.57	0.97	3.21	6.80	1	1.59	0.95	0.22	3.98
2	4.76	1.09	3.14	7.19	2	3.13	0.73	1.68	4.72	2	1.62	0.90	0.30	3.98
3	3.07	1.39	0.99	6.19	3	2.70	0.41	1.86	3.75	3	1.63	0.65	0.71	3.12
4	5.12	1.86	1.47	8.84	4	3.44	1.21	0.62	5.86	4	2.04	0.74	0.50	3.58
5	6.38	0.77	4.54	7.79	5	2.40	0.56	1.23	3.89	5	1.77	0.62	0.77	3.32
total	4.44	1.19	2.27	6.95	total	3.25	0.78	1.72	5.00	total	1.73	0.77	0.50	3.60

2) Subsurface TRE Results

Ten virtual targets were evenly placed in the surface model of the porcine liver. The TRE results computed using (2) for the ten targets for the registrations using the pointer, LRS, and pointer datasets are shown in Fig. 10(c). Wilcoxon signed-rank test and sign test found significant differences between the tracked pointer, LRS, and conoprobe datasets (p < 0.01): the conoprobe collections were statistically better than the tracked pointer and LRS collections, and the LRS collections were statistically better than the tracked pointer collections for the porcine liver. Further application of the Wilcoxon and sign tests established that statistical significance was achieved for a clinically important difference of 0.2 mm (p < 0.01) with the porcine data.

3) SNR Sensitivity

The TRE for registrations with robust ICP was stable across all trials at all SNR levels. The TRE for registration with traditional ICP were stable across 1) all SNR values, 2) SNR values greater than 30%, and 3) all combined SNR values greater than 60%. For SNR < 30%, TRE was significantly higher using traditional ICP than the robust ICP scheme. For example, for mean TRE for the five collections ranged from 1.74 to 13.25 mm with ICP and 1.08 to 2.92 mm with robust ICP.

C. Ex Vivo Cadaver Kidney Experiment

1) SRE Results

In this experiment with the cadaver kidney, SRE was computed in keeping with the phantom and porcine tissue experiments described earlier. Fig. 12 shows the SRE rendered for each point in the surface model, where the top row represents the pointer datasets and the bottom row represents the conoprobe datasets. In these collections, the mean and standard deviations of the pointer and conoprobe datasets were 3.51 ± 0.82 mm and 1.50 ± 0.50 mm, respectively. The results are summarized in Table IV. Note that the cadaver kidney was covered in perirenal fat so the surface of the kidney was not smooth.

Fig. 12.

SRE computed for each point in the surface model for the five tracked pointer (top row) and five conoprobe (bottom row) datasets of the cadaver kidney. The LRS was unavailable for this experiment. Registration error increases from blue to white to red. The kidney was covered in perirenal fat, so it was not smooth.

Table IV.

Cadaver Kidney SRE Results

Pointer SRE (mm)					Conoprobe SRE (mm)
trial	mean	sdev	min	max	trial	mean	sdev	min	max
1	3.41	1.10	1.30	6.31	1	1.14	0.46	0.05	2.47
2	3.40	0.78	1.75	5.40	2	1.42	0.49	0.53	2.74
3	3.21	0.78	1.52	5.26	3	1.51	0.49	0.39	2.85
4	3.51	0.45	2.40	4.46	4	1.16	0.29	0.66	2.10
5	4.00	0.96	1.48	5.98	5	2.25	0.74	0.69	4.10
total	3.51	0.82	1.69	5.48	total	1.50	0.50	0.47	2.85

2) Subsurface TRE Results

Ten virtual targets were placed in the subsurface of the cadaver surface model. The targets were placed in locations where tumors are typically found. TRE computed using (2) for each of the five tracked pointer and five conoprobe data collections is shown in Fig. 10(d). Wilcoxon signed-rank test and sign test found significant differences between the tracked pointer and conoprobe datasets (p < 0.0001): the conoprobe collections were statistically better than the tracked pointer collections with the cadaver kidney. Further application of the Wilcoxon and sign tests established that statistical significance was achieved for a clinically important difference of 0.2 mm (p < 0.0001).

IV. Discussion

In all experiments, the mean SREs and subsurface TREs computed based on registrations achieved with the conoprobe were smaller than those using the tracked pointer and LRS; the tracked pointer registrations were the least accurate of all (see Tables I–IV and Fig. 10). For example, in porcine tissue, the surface TRE of the five tracked pointer, five LRS, and five conoprobe collections ranged from 2.87 to 6.38 mm, 2.40 to 4.57 mm, and 2.02 to 2.81 mm, respectively. As discussed in Section II-B, our formulation of TRE is not the traditional one by Fitzpatrick et al. [11]; hence, it is difficult to compare our specific numbers with other authors. However, our LRS results are in line with those reported by Shamir et al. for face registration using an LRS [26].

The Wilcoxon signed-rank test and sign test established that (with respect to TRE) in all trials for all phantoms and biological tissue, 1) the registrations with the LRS were significantly better than those achieved with the tracked pointer, and 2) registrations with the conoprobe were significantly better than those with the LRS and tracked pointer (p < 0.01). The accuracy differences between LRS and the conoprobe are likely due to the reliance of the LRS on triangulation, rather than the more accurate solid-angle approach of conoscopic holography. Triangulation measures the angle of a single ray, whereas in conoscopic holography, the reflected beam disperses light in all directions (a solid angle). For a typical conoprobe, a single measurement consists of 1400 angles [29].

It is possible to collect reasonable surfaces with the tracked pointer (see trial 1 in Table III); however, the consistency of these acquisitions is subject to operator error. The obvious difference between the pointer and the other noncontact methods of acquiring surface measurements of soft tissue is that the pointer will cause some inwards deformation of the tissue surface (as evident in the high-translational component in Fig. 9), leading to a bias in the measurement errors (i.e., measurement errors will not be zero-mean in magnitude). Furthermore, the measurement errors will likely differ in magnitude and direction depending on the orientation of the surface being swabbed and variations in the force applied to the pointer (i.e., measurement errors will be heteroscedastic). Bias and heteroscedasticity in measurement errors both violate the usual noise assumptions inherent to least-squares registration algorithms such as ICP, thus leading to reduced accuracy of the pointer registrations. Compromised registration accuracy caused by displacements due to contact force and attempts to maintain contact with the tissue has been reported by other researchers [6], [20].

Registration accuracy was found to be insensitive to the number of points acquired (evaluated in Section III-A3), likely because of the large number of points collected by each of the acquisition methods. The conoprobe can collect points at a frequency of up to 3 kHz (700 Hz was used in our collections). The measurement frequency of the Polaris Spectra is 30 Hz; hence, the rate of tracked pointer and conoprobe collections is determined by the Polaris Spectra. As in any registration, the accuracy of the registration is contingent on the quality of points as well as the quantity [18]. The speed at which the user characterizes the surface with the pointer and conoprobe can effect accuracy and is dependent on the ability of the tracking system to localize these devices; care must be taken so that acquisitions are not faster than the tracking system allows.

Each registration was compared to a gold standard transformation due to the absence of ground truth. The TRE and SRE presented do not reflect measures of absolute accuracy (i.e., absolute spatial positions). In a study of absolute accuracy, one would acquire surface data from regularly shaped objects, and SRE and TRE would be established from a coordinate measurement machine, Cartesian robot, or from the precision of the object. In our experiments, obtaining absolute accuracy is challenging because the objects are not regularly shaped. In this sense, our method for establishing ground truth is a gold standard. However, as each measurement is made under the same conditions and the standard is a good approximation to ground truth, the findings is this study represent a best comparison within the context of soft-tissue registration under a realistic guidance environment.

Several research groups have compared fiducial-based neurosurgical registration methods using skin fiducials or skull-implanted fiducials with the Fazer and z-touch, commercial noncontact acquisition devices [13], [24], [25]. In a previous study from our research group, face LRS and skin markers localized with a contact pointer were found to perform the same with respect to TRE [3], which is contrary to our current results comparing noncontact and contact surface acquisition. This can be explained by the fact that the displacement of a skin marker on the face caused by contact with the pointer is typically small because there is little soft tissue between the skin and skull, whereas in our current experiments, there was no rigid tissue to physically limit the amount of displacement. Also, point correspondences are known in marker-based registration and must be estimated in surface-based registration. A potential avenue of research is the use of the conoprobe for acquisition of points from the face for establishing image-to-physical space registration in neurosurgical systems.

It would be interesting to compare the conoprobe to other non-contact surface measurement devices such as the commercially available Fazer or z-touch. In terms of being able to localize a surface point, we expect such devices would be less accurate due to their reliance on triangulation, rather than the more accurate solid angle approach of conoscopic holography. However, the z-touch device is itself untracked, as the tracking system is able to directly localize the surface point intersected by the emitted laser beam; this means that such devices do not require a calibration procedure. The conoscope produces distance measurements in its own frame of reference; thus, it requires instrumentation with a rigid tracking body and a calibration procedure to produce 3-D measurements in the tracking system coordinate frame. Conoscope calibration methods and understanding calibration error and calibration drift are all potential directions for further investigation.

The quality of conoprobe points is largely dependent on the absorption of the laser into the target tissue. Tissue absorption is a function of the components of the tissue: hemoglobin, water, melanin, and fat [31]. These quantities will change depending on whether the tissue is, for example, living or dead, or prepared in a solution. The manufacturer suggests that points with an SNR of greater than 30% can be used reliably, which was supported in our study of the effect of SNR on registration accuracy (see Section III-B3). Understanding the effect of tissue absorption on LRS, Fazer, and z-touch surface acquisitions is a potential avenue of research.

We addressed sources of error specific to acquisition devices used in the study; however, in general, tracking and registration error are contingent on other factors not addressed here. For example, tracking accuracy varies based on the geometry of the rigid body. A full evaluation of conoscopic holography for surface registration is needed with analysis of the specific effects of tracking error and distance measurements on registration accuracy using both clinical data and objects of known size. In this type of experiment, initial registration estimates could be established using the conoprobe. For example, for the neurosurgery application, the conoprobe could be used to acquire points on the face for initializing image-to-physical space registrations and compared to traditional skin fiducial registrations.

V. Conclusion

We found in our experiments that the conoprobe consistently produced registrations statistically better (p < 0.0001) than those produced by either a tracked surgical tool or LRS for both phantom models and biological tissue. While the conoprobe does not provide color texture information like an LRS, it is a reliable tool for collecting surface points from soft tissue for the purposes of image-to-physical space registration. The accuracy of registrations based on data acquired from a tracked surgical instrument are substantially less accurate than registration achieved from noncontact acquisition techniques; as such, their use should be limited. The tracked pointer used in commercial surgical navigation systems compromises registration accuracy and could lead to surgical error.

Biographies

Amber L. Simpson received the B.Sc. degree from Trent University, Peterborough, ON, Canada, in 2000, and the M.Sc. and Ph.D. degrees from Queens University, Kingston, ON, Canada, in 2002 and 2010, respectively, all in computer science.

She joined the faculty at Vanderbilt University, Nashville, TN, in November 2009, where she is currently a Research Assistant Professor in the Department of Biomedical Engineering. She is a member of the Vanderbilt Initiative in Surgery and Engineering. Her research interests include evaluation and validation methodologies for surgical navigation and the computation and visualization of measurement uncertainty in surgery.

Jessica Burgner (M’08) received the Diplom (Dipl.-Inform.) degree from the University of Karlsruhe (TH), Karlsruhe, Germany, in 2006, and the Doctorate degree (Dr.-Ing.) from the Karlsruhe Institute of Technology, Karlsruhe, in 2010, both in computer science.

Since 2010, she has been a Postdoctoral Research Scholar in the Medical and Electromechanical Design Laboratory, Department of Mechanical Engineering, Vanderbilt University, Nashville, TN. Her current research interests are surgical robotics, image-guided interventions, and patient registration.

Courtenay L. Glisson, photograph and biography not available at the time of publication.

S. Duke Herrell, photograph and biography not available at the time of publication.

Burton Ma received the Ph.D. degree in computer science from Queens University, Kingston, ON, Canada, in 2005.

He joined the faculty at York University, Toronto, ON, Canada, in February 2009, where he is currently an Assistant Professor in the Department of Computer Science and Engineering.

Thomas S. Pheiffer received the B.S. degree in biosystems engineering from Clemson University, Clemson, SC, in 2007, and the M.S. degree in biomedical engineering from Vanderbilt University, Nashville, TN, in 2010, where he is currently working toward the Ph.D. degree in the Department of Biomedical Engineering, with research interests include image-guided surgery and ultrasound strain imaging.

Robert J. Webster III (S’97–M’08) received the B.S. degree in electrical engineering from Clemson University, Clemson, SC, in 2002, and the M.S. and Ph.D. degrees in mechanical engineering from the Johns Hopkins University, Baltimore, MD, in 2004 and 2007, respectively.

In 2008, he joined the faculty of Vanderbilt University, Nashville, TN, as an Assistant Professor of mechanical engineering, where he currently directs the Medical and Electromechanical Design Laboratory. His current research interests include medical robotics, image-guided surgery, and continuum robotics.

Dr. Webster received the IEEE Volz Award for Ph.D. thesis impact as well as the National Science Foundation CAREER Award in 2011.

Michael I. Miga (M’98) received the B.S. and M.S. degrees in mechanical engineering from the University of Rhode Island, Kingston, in 1992 and 1994, respectively, and the Ph.D. degree in biomedical engineering from Dartmouth College, Hanover, NH, in 1998.

He joined the faculty at Vanderbilt University, Nashville, TN, in November 2000, where he is currently an Associate Professor of Biomedical Engineering, Radiology and Radiological Sciences, and Neurological Surgery. He is the Director of the Biomedical Modeling Laboratory, co-founder of the Vanderbilt initiative in Surgery and Engineering, and co-founder of Pathfinder Therapeutics, Inc. His research interests include image-guided surgery, computational modeling for therapeutic applications, and inverse problems in therapeutics and imaging.