Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Dec 1.
Published in final edited form as: Cardiovasc Eng Technol. 2013 Dec;4(4):10.1007/s13239-013-0165-3. doi: 10.1007/s13239-013-0165-3

Computational Fluid Dynamics Simulations of Hemodynamics in Plaque Erosion

Ian C Campbell a,*, Lucas H Timmins a,b, Don P Giddens a, Renu Virmani c, Alessandro Veneziani a,d, S Tanveer Rab b, Habib Samady b, Michael C McDaniel b, Aloke V Finn b, W Robert Taylor a,b,e, John N Oshinski a,f
PMCID: PMC3819207  NIHMSID: NIHMS522014  PMID: 24223678

Abstract

Purpose

We investigated whether local hemodynamics were associated with sites of plaque erosion and hypothesized that patients with plaque erosion have locally elevated WSS magnitude in regions where erosion has occurred.

Methods

We generated 3D, patient-specific models of coronary arteries from biplane angiographic images in 3 human patients with plaque erosion diagnosed by optical coherence tomography (OCT). Using computational fluid dynamics, we simulated pulsatile blood flow and calculated both wall shear stress (WSS) and oscillatory shear index (OSI). We also investigated anatomic features of plaque erosion sites by examining branching and local curvature in x-ray angiograms of barium-perfused autopsy hearts.

Results

Neither high nor low magnitudes of mean WSS were associated with sites of plaque erosion. OSI and local curvature were also not associated with erosion. Anatomically, 8 of 13 hearts had a nearby bifurcation upstream of the site of plaque erosion.

Conclusions

This study provides preliminary evidence that neither hemodynamics nor anatomy are predictors of plaque erosion, based upon a very unique dataset. Our sample sizes are small, but this dataset suggests that high magnitudes of wall shear stress, one potential mechanism for inducing plaque erosion, are not necessary for erosion to occur.

Keywords: Computational fluid dynamics, atherosclerosis, plaque erosion, endothelium, wall shear stress

Introduction

The role of biomechanics in plaque disruption has been widely studied. Solid mechanics help explain how a pressurized vessel wall experiencing a local maximum of stress leads to plaque rupture [1]. Pressurized blood isn’t static, however, and fluid flow may play a role in plaque disruption as well. Although a direct link between rupture and fluid mechanics parameters such as wall shear stress has not been clearly demonstrated, the role of shear stress in atherogenesis is well established, and plaque rupture is known to occur preferentially downstream of bifurcations [2–5]. Low magnitude and oscillatory wall shear stress (WSS) patterns tend to be present in regions where plaques form, whereas higher magnitudes of wall shear stress are typically atheroprotective, as long as the magnitude is below the threshold to cause endothelial damage (typically > 70 dynes/cm2) or acute denudation (around 400 dynes/cm2) [6–10].

In addition to modulating the progression of atherosclerosis, flow also affects thrombosis. High shear activates von Willebrand factor and results in platelet adhesion [11]. Given these relationships and the fact that solid mechanics alone has not yet explained why certain vulnerable plaques suddenly rupture, a role for fluid mechanics in both plaque rupture and plaque erosion deserves consideration. Initial case reports have shown a correlation between shear and site of plaque rupture, but to date no study has considered the role of shear in the localization of plaque erosion [12–14].

Plaque erosion is the formation of a thrombus over an atherosclerotic plaque without rupture of the fibrous cap over a lipid-rich necrotic core. It tends to occur mostly in women and young men, especially smokers, and it is thought to be the cause of approximately 25–40% of coronary occlusions and 20% of all cases of sudden death from coronary thrombi [15, 16]. Despite identification that plaque erosion exists, the exact mechanism responsible for thrombus formation is not known. It has been noted in histological studies that endothelial cells tend to be apoptotic or absent at the site of erosion, suggesting that denudation has occurred [17, 18].

One possible mechanism by which flow patterns might result in erosion is through extremely high magnitudes of shear in stenotic flow. High shear could forcefully detach endothelium, especially if the endothelium is already apoptotic. Mural thrombus formation would also be aided in this high-shear environment. Given that plaque erosion frequently occurs in women and that women, on average, have narrower coronary arteries than men, local elevation of shear stress in patients with plaque erosion is possible [19, 16, 20]. In this two-part study, we used a unique dataset to study the role of flow and anatomy in plaque erosion. First, we employed patient-specific geometric models based upon in vivo angiographic data in patients with plaque erosion to perform computational fluid dynamics simulations of blood flow through coronary arteries. We hypothesized that patients with plaque erosion experience locally elevated WSS magnitude in regions where erosion has occurred. Second, we examined hearts obtained at autopsy to investigate the role of local curvature and branching of human coronary arteries in plaque erosion. We hypothesized that the curvature and branching of the vasculature is associated with erosion location.

Methods

Computational Fluid Dynamics of In Vivo Angiograms

We obtained coronary biplane angiograms from three patients who presented to cardiac catheterization labs in the Emory Healthcare system (Figure 1) and received a diagnosis of plaque erosion using optical coherence tomography (OCT, Figure 2). Diagnosis of plaque erosion requires evidence of thrombus such as an uneven lumen surface and no evidence of rupture in adjacent OCT frames [15, 21, 22]. After thrombus extraction or lysis, minimal disease was identifiable by angiography, a feature consistent with plaque erosion as opposed to plaque rupture [23]. All patient research was performed under the approval of the Emory University Institutional Review Board.

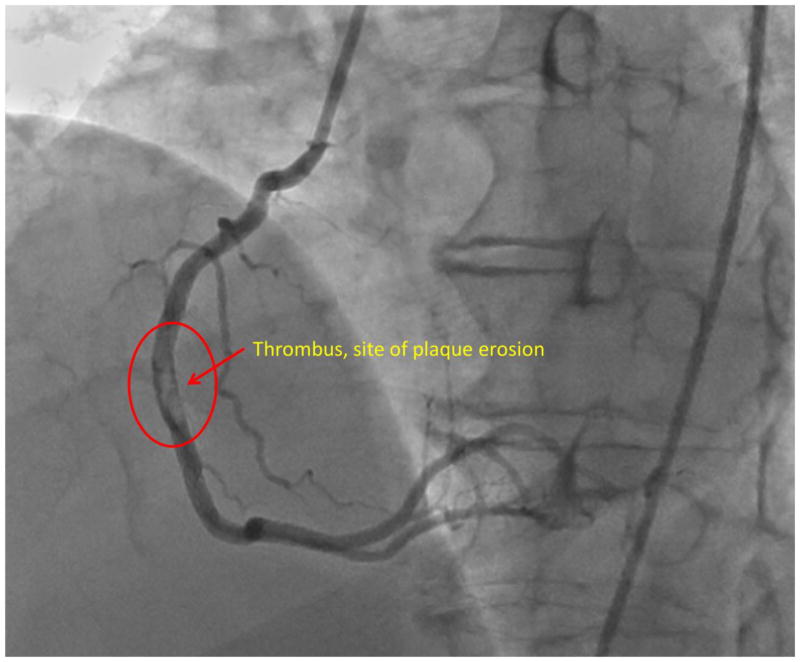
Figure 1. Plaque erosion in right coronary artery.

Figure 1

Open in a new tab

Images from an angiogram in a patient who presented to Emory University Hospital and underwent cardiac catheterization. A filling defect from a large thrombus was identified in the right coronary artery, (circled region). Subsequent OCT imaging identified the source of the thrombus as an eroded plaque.

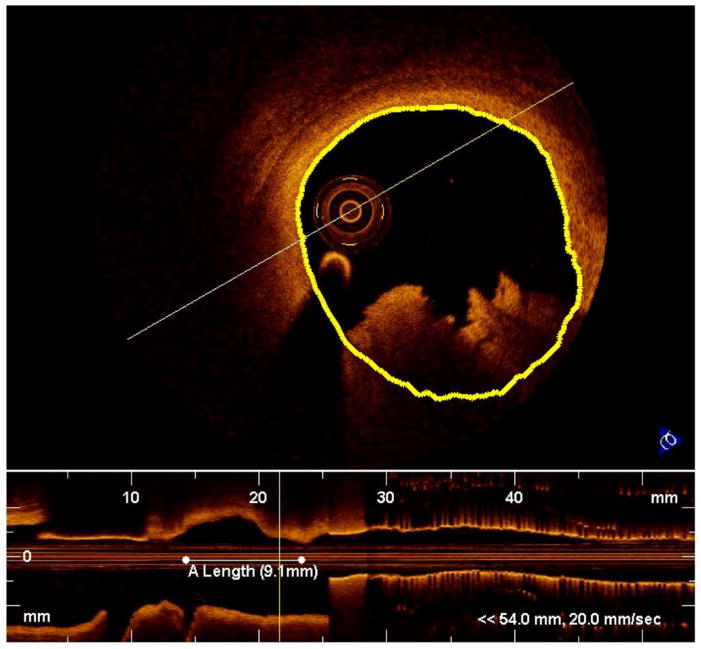
Figure 2. Optical coherence tomography identification of plaque erosion.

Figure 2

Open in a new tab

Intravascular OCT reveals the cross-sectional anatomy of a coronary artery (top) and a longitudinal view of the vessel (bottom). Thrombus appears at the bottom of the cross-section as positive signal with jagged edges. We approximated the vessel boundary (yellow line) although underneath the thrombus, exact segmentation is impossible. In the longitudinal view, extent of the thrombus is marked with a horizontal white line.

3D Vessel Reconstruction

We reconstructed the anatomy of culprit arteries using Paieon CardioOp-B software (Paieon, Inc., New York City, sold as CV-3D by Toshiba Medical Systems, Inc., Tustin, CA). This commercial software allowed us to segment the borders of angiograms at diastole. We selected angiograms performed immediately after thrombectomy for two patients and at 12-day follow up catheterization after thrombectomy for one other patient in order to reconstruct anatomy without influence of the erosion’s thrombus (Figure 3). Paieon produced coordinates of centerlines and corresponding radii for the culprit vessel and any nearby branches with a spatial resolution of approximately 0.2 mm in the axial direction. Centerlines and radii were imported into custom Matlab software (R2011b, Natick, MA) to generate a 3D point cloud representing vessel borders, which was then imported into Geomagic Studio 2012 (Morrisville, NC) in order to generate a smooth 3D surface.

Figure 3. Segmentation of culprit vessels in Paieon software.

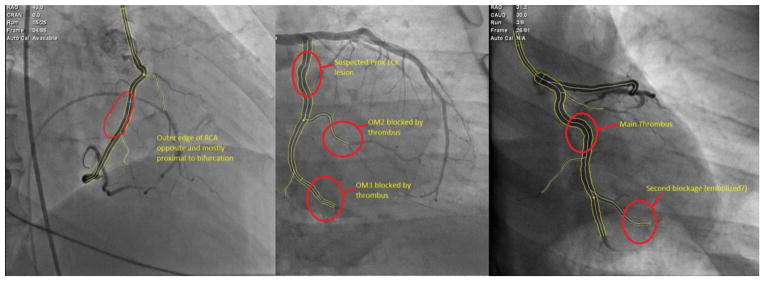
Figure 3

Open in a new tab

We semi-automatically identified the silhouette of vessels in biplane angiograms for each of three patients using Paieon software. Filling defects and blockage sites are circled.

Meshing and Flow Extensions

We then imported the 3D geometry from Geomagic into Ansys ICEM meshing software (Canonsburg, PA) to generate a 3D finite element mesh for computational fluid dynamics. Models were generated with between 1.2 and 1.9 million tetrahedral elements, as well as a prism boundary layer (8 layers deep, with a linear element size growth factor of 1.1 sized such that the innermost element was the same volume as the adjacent tetrahedral element). We added flow extensions to all inlets and outlets by projecting the edge contour of the inlet or outlet outward parallel to the vessel path. Inlet flow extensions were one diameter long, and outlet flow extensions were 7 diameters long. Each model included one inlet and either four or six outlet branches, depending on patient-specific geometry.

Computational Fluid Dynamics

We performed patient-specific computational fluid dynamics (CFD) simulations using Fluent 14.0 software (Ansys, Inc., Canonsburg, PA) [24]. Because patient-specific flow or pressure waveforms were not available, we simulated pulsatile blood flow through rigid walls by prescribing a generic coronary flow waveform (Figure 4) as a blunt velocity inlet into our flow extension. This yielded a plug-shaped velocity distribution entering our model geometry. We simulated three continuous cardiac cycles and discarded the first two in order to remove transient artifacts from our model. We simulated 300 time steps per cardiac cycle (for a total of 900 time steps) for a heart rate of 75 beats per minute (0.0027 seconds per time step). Outlets were traction-free pressure outlets. Blood was modeled as a Newtonian fluid with density 1060 kg/m3 and dynamic viscosity 0.0035 Pa·s [25]. We used the SIMPLE algorithm for pressure-velocity coupling and second-order Green-Gauss node based spatial discretization for both momentum and pressure equations. We used a second-order implicit time advancing scheme. At each time step, convergence was achieved when the residual of momentum and continuity equations fell below 10−6.

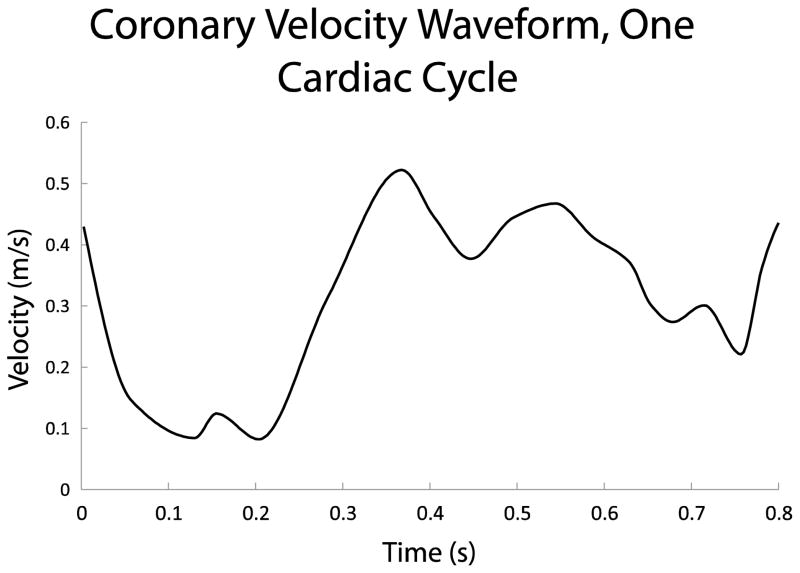
Figure 4. Coronary velocity waveform.

Figure 4

Open in a new tab

We prescribed a blunt velocity profile through an inlet flow extension into each CFD model. This waveform was derived from a typical patient, as patient-specific velocity data were not available.

To investigate the inlet velocities that would be required to reach WSS magnitudes sufficient to damage (>70 dynes/cm2) or denude endothelium (400 dynes/cm2), we performed additional CFD simulations for each patient. All aspects of these simulations were identical to baseline simulations except that the pulsatile inlet velocity waveform was multiplied by a constant value of 1.25, 1.5, 2, 3, 4, or 8.

Rendering and Postprocessing

We exported results from Fluent in Ensight Gold format. Using custom Matlab code, we calculated the temporal mean of WSS and oscillatory shear index (using the algorithm of Moore et al. with an oscillation threshold of π/6) [26]. We then rendered all data in Paraview (Kitware, Inc., Clifton Park, NY). We generated images of WSS and OSI distributions, as well as instantaneous streamlines and particle paths. To assess that we had achieved mesh convergence, we re-meshed the same geometries at half resolution and confirmed that neither the distribution of mean WSS nor OSI changed. The site of plaque erosion (circled in Figure 3) where OCT and intervention were performed was manually located on our 3D reconstructions for analysis of WSS and OSI at the site.

Anatomical Location of Thrombi in Autopsy Hearts

In the second part of the study, we used hearts from the Maryland Medical Examiner’s Office that were perfused with barium gelatin and then x-rayed onto film, which was subsequently digitized with a flatbed scanner. Angiographic data were collected from two viewing angles for each heart, and we used these images to estimate the effects of through-plane curvature in each image. Prior histological analysis of the hearts resulted in identification of plaque erosion in 13 hearts and plaque rupture in 6. Although a lack of precise relevant position information in film x-rays prohibited 3D reconstruction of these vessels for CFD, qualitative analysis of vessel anatomy was possible.

We identified the site of plaque erosion or rupture in single-plane x-ray angiograms from 19 explanted autopsy hearts [18]based on the site of greatest stenosis as well as histological images acquired at this site of thrombosis. Next, we identified geometric features of the coronary anatomy for each patient, tallying whether each was in a section of vessel that was nearly straight, gradually curved, or highly serpentine by visually examining the local path of the vessel and quantifying the number of inflection points (Figure 5). Straight vessels had no inflection, gradually curved arteries had one inflection point, and serpentine vessels had 2 or more inflection points locally around the stenosis. We also tallied whether bifurcations or trifurcations existed within 2.5 diameters length upstream, downstream, or immediately across from the site of thrombosis.

Figure 5. Identification of local curvature.

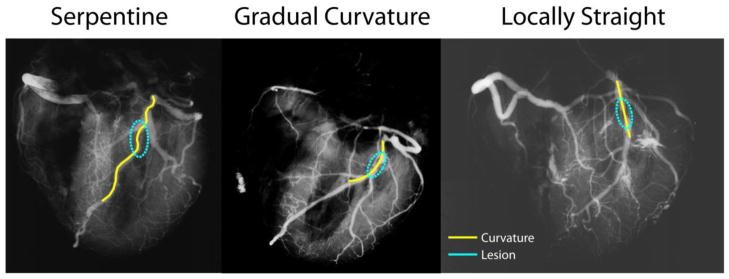
Figure 5

Open in a new tab

For each lesion identified in x-ray angiograms (circled), we tallied whether the local region was serpentine (left), gradually curving (middle), or locally straight (right) based on the number of inflection points near the lesion.

Results

Patient Characteristics

Three patients were identified by retrospective chart review who had both biplane angiography and a diagnosis of plaque erosion by OCT. Follow-up angiography revealed clearance of the thrombus. Summary characteristics are listed in Table 1.

Table 1.

Characteristics of patients with plaque erosion diagnosed by OCT and with biplane angiograms.

Patient # Gender Age (yrs) Location of Lesion Method of Thrombus Removal
1 M 57 Mid. RCA Extraction
2 M 34 Prox. LCx Extraction
3 M 38 Mid. LCx Lysis
Open in a new tab

Computational Fluid Dynamics

We simulated blood flow in all culprit vessels: two in the left circumflex (LCx) and one in the right coronary artery (RCA). In all three, thrombus location coincided with relatively low magnitudes (< 3 Pa) of mean WSS (Figure 6), but these regions were neither the lowest WSS in the vessel nor the only region with mean WSS < 3 Pa (Figure 7). The spatial distribution of peak WSS at any point across the cardiac cycle was nearly identical to that for mean WSS. Again, maximum WSS magnitude at sites of erosion was neither the highest for the vessel nor was it unique. Maximum WSS magnitude at sites of erosion was < 12 Pa.

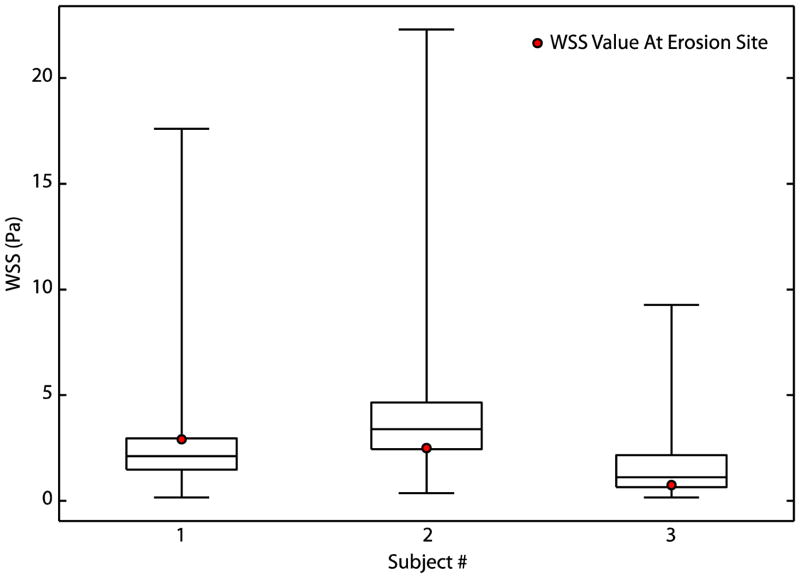
Figure 6. Wall Shear Stress at Sites of Plaque Erosion is Neither High Nor Low.

Figure 6

Open in a new tab

Box plots of temporal mean WSS over the cardiac cycle with superimposed WSS magnitude at site of thrombus formation revealed that extreme magnitudes of WSS were not associated with plaque erosion in these patients. Whiskers represent minimum and maximum WSS of all elements, the box represents the 25th/75th percentile of elements, and the middle line represents median WSS.

Figure 7. Mean Wall Shear Stress.

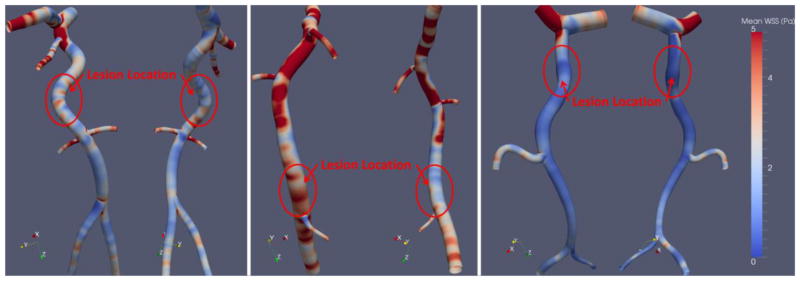
Figure 7

Open in a new tab

We computed the temporal mean WSS for all three patients. All patients’ erosions were at sites containing low magnitudes of WSS, but this is not a unique feature to the erosion sites.

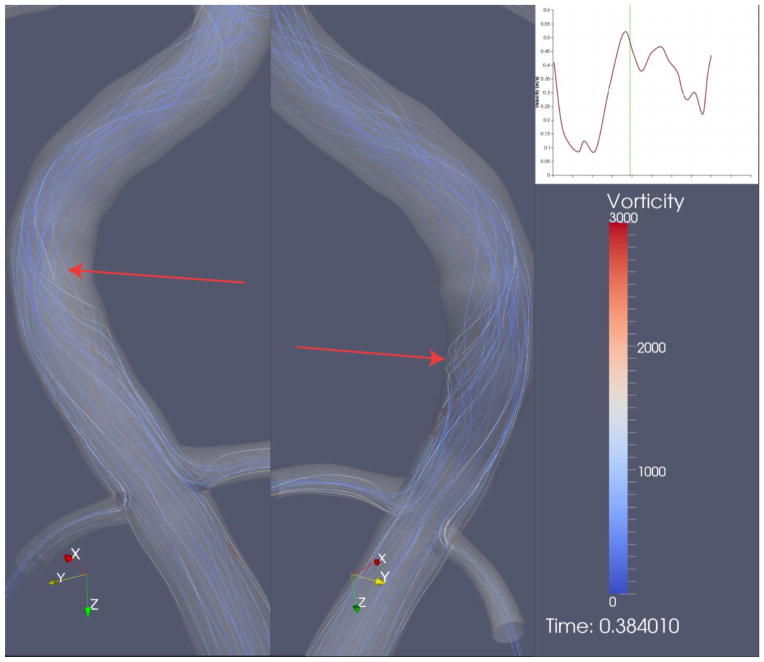
We found no association between thrombus location and OSI (Figure 8). Streamline analysis revealed some helical flow patterns within the region of erosion for part of the cardiac cycle (Figure 9), but this too was not unique to the site of thrombus formation. Our simulations revealed essentially no reversal of flow in the region of the thrombus, although one lesion (LCx) was distal to a bifurcation and some reversal was observed upstream at the site of bifurcation.

Figure 8. Oscillatory shear index.

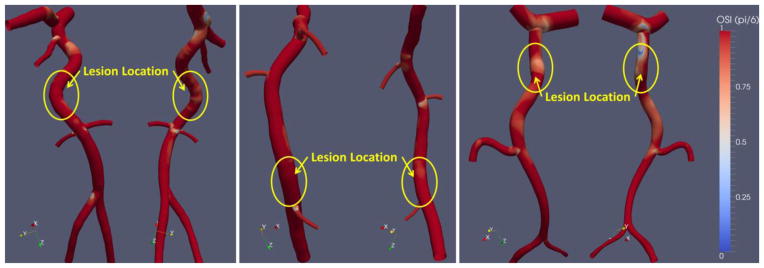
Figure 8

Open in a new tab

We calculated oscillatory shear index, a measure of the duration of the cardiac cycle when flow deviates from its mean direction by more than π/6 radians. No remarkable patterns in OSI related to plaque erosion location were identified.

Figure 9. Transient helical flow structures.

Figure 9

Open in a new tab

Occasional helical flow structures (arrows) appeared at the site of plaque erosion when visualized by streamline analysis. The zoomed region encompasses the site of erosion where the filling defect was observed in the angiogram. Other regions of the same coronary artery (not shown) also exhibited transient helical flow structures.

For all patients, instantaneous WSS at the site of thrombus formation reached 70 dynes/cm2 for at least one time-step of the cardiac cycle, but inlet velocity magnitude had to be multiplied by at least 3 for instantaneous WSS to reach 400 dynes/cm2 at the site of erosion. For mean WSS throughout the entire cardiac cycle to reach 70 dynes/cm2 at the sites of interest, inlet velocity had to be multiplied by at least 1.5, and to reach 400 dynes/cm2 it had to be multiplied by 8.

Anatomical Location of Thrombi

Local curvature and downstream bifurcation were not associated with site of plaque erosion in explanted hearts, but an upstream bifurcation or trifurcation existed in 8/13 erosions. Among biplane angiograms from the in vivo study (n=3), sites of erosion were again evenly distributed among all three categories of local curvature based upon number of inflection points. One patient had nearby upstream bifurcation, and one had adjacent downstream bifurcation. Of rupture specimens, two-thirds were in gradually curving regions, one-third had a bifurcation at the site of rupture, and one specimen had a nearby downstream trifurcation. Data are tallied in Tables 2 and 3.

Table 2.

Tallies of local curvature at sites of plaque erosion and plaque rupture.

Lesion Type Serpentine Gradually Curving Straight Total
Erosion (autopsy heart) 4 (30.8%) 4 (30.8%) 5 (38.4%) 13
Erosion (cath lab) 1 (33.3%) 1 (33.3%) 1 (33.3%) 3
Rupture (autopsy heart) 1 (16.7%) 4 (66.7%) 1 (16.7%) 6
Open in a new tab

Table 3.

Tallies of nearby branching (within 2.5 diameters) at sites of plaque erosion and plaque rupture.

Lesion Type Upstream Branch Branch at Site Downstream Branch Total
Erosion (autopsy heart) 8 (61.5%) 0 (0%) 3 (23.1%) 13
Erosion (cath lab) 0 (0%) 0 (0%) 1 (33.3%) 3
Rupture (autopsy heart) 1 (16.7%) 2 (33.3%) 1 (33.3%) 6
Open in a new tab

Discussion

This initial modeling study suggests that flow is not a major factor in the localization of plaque erosion. In all cases, neither the local flow environment nor the surrounding geometry at the site of plaque erosion were particularly remarkable. High wall shear stress, which we hypothesized would induce plaque erosion by damaging endothelium via shear, was not present in any of these patients at the site of thrombus formation. Instead, WSS tended to be moderate at these sites (Figure 6). Although we cannot rule out that very high WSS is sufficient to induce plaque erosion, we can conclude that it is not necessary.

We formulated this hypothesis because of the possibility for high WSS directly to cause endothelial denudation. Current understanding of the mechanism of plaque erosion is that the loss of endothelial cells results in presentation of a thrombogenic surface to the blood pool [15]. The initiating event for this spontaneous denudation is not known, although very high magnitudes of WSS arising from either geometric features or from vessel spasm have been proposed as possible mechanisms [8, 27]. This desquamation has also been replicated in animal models by inducing apoptosis, and both apoptosis and endothelial dysfunction may be induced by flow patterns [28–30]. Disturbed flow patterns have been shown to induce an erosion-like phenotype of apoptotic and detached endothelial cells in rabbits, although no animal model of spontaneous erosion exists [29].

Low magnitudes of WSS and oscillating shear are known to be associated with increased apoptosis. However, this relationship is complex [31–33]. There were numerous other sites in each culprit vessel that also experienced low mean WSS, and yet no erosion occurred at those sites. Helical flow patterns were also present in the eroded regions during part of the cardiac cycle, but these too were present in segments without erosion. Thus, the relationship between plaque erosion and fluid mechanics is complex and possibly multifactorial, if one exists at all. Another mechanistic hypothesis for plaque erosion, that erosion is at least in part a blood clotting disorder that results in thrombus formation, has also been proposed [34, 35].

A major obstacle in most clinical plaque disruption research is the lack of data from before initiation of thrombosis. In plaque erosion, a mural thrombus accumulates over a period of weeks, and during this time vascular remodeling may occur [36]. If vasospasm induces plaque erosion, as has been hypothesized, fluid mechanics could well play a role, as vasospasm would lead to very high magnitudes of WSS, potentially resulting in endothelial denudation [7, 8, 17]. However, vasospasm is a transient phenomenon [37], and no evidence of stenosis from such an event was observed in our angiograms. Ideal computation fluid dynamics modeling would simulate coronary flow based upon anatomies prior to the occurrence of plaque erosion, but such a dataset will continue to be nonexistent without prospective diagnostic criteria for erosion.

Other challenges when generating relevant vascular geometry include the possibility of thrombus in the angiogram. We used angiograms from the end of the procedure (or in one patient’s case, a follow-up angiogram from several days later) when the thrombus had resolved or been removed. Because angiograms only image the lumen of vessels where flow is occurring, any residual mural thrombus would create a geometric artifact, artificially narrowing the lumen. We saw no such evidence of stenosis in any of the images after thrombectomy, and if it would have occurred, our estimates of WSS should overestimate the true magnitude. Given that we computed relatively low WSS in regions of erosion, this possibility seems unlikely.

Geometric modeling assumptions could have affected our results as well. We simulated coronary vessels as rigid structures. In reality, arteries can both distend under pulsatile pressure as well as deform as the myocardium contracts and expands. Coronary deformation has been hypothesized as direct cause of plaque rupture, and although moving walls alter WSS magnitudes, they do not appear to change the overall relative distributions [38, 39]. Furthermore, solid mechanical stresses from repeated bending do not appear to be a critical factor in plaque erosion [1, 40]. Still, future modeling using fluid-structure interaction (FSI) would alleviate some of these artifacts.

Additionally, the software we used to generate 3D geometries from angiography data yields circular cross-sections for all vessels. In reality, vessel cross-sections are not perfectly symmetric and sometimes are rather elliptical, especially in the presence of atherosclerosis. Although more accurate geometry reconstructions could be produced by considering vessel diameter in both views of biplane angiograms, previous research has shown that patterns of WSS are not significantly altered by assuming a circular cross section [41, 42].

Paieon software exports vessel centerline points with corresponding lumen diameters at a resolution of approximately 0.2 mm resolution along the vessel centerline. This resolution is much greater than other image-based reconstruction techniques that we perform in the lab, as IVUS-based reconstructions have a resolution around 0.5 mm [43, 44]. Typically, minimal smoothing is necessary to prepare the final geometry for CFD simulations. The accuracy of the biplane angiographic image reconstruction and resulting WSS distributions has been validated in clinical and phantom studies [45–47].

In this retrospective study, we prescribed a non-patient-specific set of boundary conditions. As each patient had entered the catheterization laboratory on an emergency basis, no patient-specific coronary pressure or velocity waveform was recorded. Therefore, we were forced to model a non-patient-specific velocity waveform. Previous studies have investigated the effects of missing boundary condition data in computational hemodynamics [48–50], since availability of a complete set of patient-specific measures is, in general, an exceptional situation. Numerical models have been devised for finding rigorous and reliable ways of filling the gap between the data required by the mathematical model and the ones actually available. We have previously shown that although WSS and OSI magnitudes are affected by choice of waveform, patient geometry is the greatest driving factor in both the magnitude and distribution of waveform [24].

Here, we prescribed traction-free pressure outlets for each branch of the coronary arteries. This approach has been recommended as being less mathematically invasive in the sense that non-patient-specific pressure boundary data are expected to have less effect on the numerical solution than velocity or flow rate data [51]. In addition, flow extensions added to the geometrical domain limit the effect of non-patient-specific boundary data outside the region of interest. For these reasons, we have selected these boundary conditions over other possibilities (each one carrying its own set of assumptions and limitations). In this study, we have shown that a radical increase in flow (outside the physiological range) is necessary to reach the WSS magnitudes necessary for endothelial damage such that minor changes in outflow conditions are unlikely to change our overall conclusions.

The opportunity to acquire both pre- and post-procedure biplane angiograms in conjunction with OCT in a case of plaque erosion is indeed very rare. Although our sample size of three patients is small, these are very unique data. Indeed, our combined clinical service performs over 7,000 heart catheterizations annually, and these were the only cases to be identified. This study is exploratory in nature but does rule out a very obvious flow-related etiology as being necessary for plaque erosion.

Our data also indicate that anatomic features related to flow patterns do not appear associated with plaque erosion or rupture, although this initial work involves a small sample size and has not been evaluated statistically. We see the same trends in plaque erosion in both patient and autopsy heart angiograms. Local curvature of the vessel segment is not associated with erosion, although this could alter flow patterns. The relationship between WSS and atherogenesis is especially apparent on the inner edge of curvatures and bifurcations, where low and oscillatory WSS occurs [52]. We do observe that many plaque erosions happen shortly downstream of vessel branching, but just the same, many erosions occur in regions without unusual geometry.

In this exploratory study, we have modeled flow patterns in the coronary arteries of human patients confirmed to have experienced plaque erosion. Although we hypothesized that high WSS would occur at the site of erosive thrombus formation, we did not observe any extreme magnitudes of WSS or OSI in these regions. Analysis of a different cohort of patients with plaque erosion and rupture revealed that erosions were not predominantly located at sites of significant coronary branching, a geometric feature that could cause flow disturbance. For these reasons together, we suggest that flow is not a direct modulator of plaque erosion and that biological or solid mechanical explanations may offer more promise for elucidating the exact mechanism of plaque erosion.

Acknowledgments

This material is based upon work supported by an American Heart Association Predoctoral Fellowship (11PRE7040000, Campbell) and an American Heart Association Postdoctoral Fellowship (11POST7210012, Timmins), by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-0644493, and by the National Institutes of Health Bioengineering Research Partnership Grant No. R01 HL70531. The Robert M. Nerem International Travel Award supported training for the execution of this study.

References

  • 1.Loree HM, Kamm RD, Stringfellow RG, Lee RT. Effects of fibrous cap thickness on peak circumferential stress in model atherosclerotic vessels. Circulation research. 1992;71(4):850–8. doi: 10.1161/01.res.71.4.850. [DOI] [PubMed] [Google Scholar]
  • 2.Ku DN. Blood flow in arteries. Annu Rev Fluid Mech. 1997;29:399–434. doi: 10.1146/annurev.fluid.29.1.399. [DOI] [Google Scholar]
  • 3.Ku DN, Giddens DP, Zarins CK, Glagov S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis. 1985;5(3):293–302. doi: 10.1161/01.atv.5.3.293. [DOI] [PubMed] [Google Scholar]
  • 4.McDaniel MC, Galbraith EM, Jeroudi AM, Kashlan OR, Eshtehardi P, Suo J, et al. Localization of culprit lesions in coronary arteries of patients with ST-segment elevation myocardial infarctions: relation to bifurcations and curvatures. American heart journal. 2011;161(3):508–15. doi: 10.1016/j.ahj.2010.11.005. [DOI] [PubMed] [Google Scholar]
  • 5.Fujii K, Kawasaki D, Masutani M, Okumura T, Akagami T, Sakoda T, et al. OCT assessment of thin-cap fibroatheroma distribution in native coronary arteries. JACC Cardiovascular imaging. 2010;3(2):168–75. doi: 10.1016/j.jcmg.2009.11.004. [DOI] [PubMed] [Google Scholar]
  • 6.Feldman CL, Stone PH. Intravascular hemodynamic factors responsible for progression of coronary atherosclerosis and development of vulnerable plaque. Current opinion in cardiology. 2000;15(6):430–40. doi: 10.1097/00001573-200011000-00010. [DOI] [PubMed] [Google Scholar]
  • 7.Fry DL. Acute vascular endothelial changes associated with increased blood velocity gradients. Circulation research. 1968;22(2):165–97. doi: 10.1161/01.res.22.2.165. [DOI] [PubMed] [Google Scholar]
  • 8.Gertz SD, Uretsky G, Wajnberg RS, Navot N, Gotsman MS. Endothelial cell damage and thrombus formation after partial arterial constriction: relevance to the role of coronary artery spasm in the pathogenesis of myocardial infarction. Circulation. 1981;63(3):476–86. doi: 10.1161/01.cir.63.3.476. [DOI] [PubMed] [Google Scholar]
  • 9.Chatzizisis YS, Jonas M, Coskun AU, Beigel R, Stone BV, Maynard C, et al. Prediction of the localization of high-risk coronary atherosclerotic plaques on the basis of low endothelial shear stress: an intravascular ultrasound and histopathology natural history study. Circulation. 2008;117(8):993–1002. doi: 10.1161/CIRCULATIONAHA.107.695254. [DOI] [PubMed] [Google Scholar]
  • 10.Koskinas KC, Feldman CL, Chatzizisis YS, Coskun AU, Jonas M, Maynard C, et al. Natural history of experimental coronary atherosclerosis and vascular remodeling in relation to endothelial shear stress: a serial, in vivo intravascular ultrasound study. Circulation. 2010;121(19):2092–101. doi: 10.1161/CIRCULATIONAHA.109.901678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Para A, Bark D, Lin A, Ku D. Rapid platelet accumulation leading to thrombotic occlusion. Annals of biomedical engineering. 2011;39(7):1961–71. doi: 10.1007/s10439-011-0296-3. [DOI] [PubMed] [Google Scholar]
  • 12.Fukumoto Y, Hiro T, Fujii T, Hashimoto G, Fujimura T, Yamada J, et al. Localized elevation of shear stress is related to coronary plaque rupture: a 3-dimensional intravascular ultrasound study with in-vivo color mapping of shear stress distribution. Journal of the American College of Cardiology. 2008;51(6):645–50. doi: 10.1016/j.jacc.2007.10.030. [DOI] [PubMed] [Google Scholar]
  • 13.Groen HC, Gijsen FJ, van der Lugt A, Ferguson MS, Hatsukami TS, van der Steen AF, et al. Plaque rupture in the carotid artery is localized at the high shear stress region: a case report. Stroke; a journal of cerebral circulation. 2007;38(8):2379–81. doi: 10.1161/STROKEAHA.107.484766. [DOI] [PubMed] [Google Scholar]
  • 14.Lovett JK, Rothwell PM. Site of carotid plaque ulceration in relation to direction of blood flow: an angiographic and pathological study. Cerebrovascular diseases. 2003;16(4):369–75. doi: 10.1159/000072559. 72559. [DOI] [PubMed] [Google Scholar]
  • 15.Prati F, Uemura S, Souteyrand G, Virmani R, Motreff P, Di Vito L, et al. OCT-Based Diagnosis and Management of STEMI Associated With Intact Fibrous Cap. JACC Cardiovascular imaging. 2013;6(3):283–7. doi: 10.1016/j.jcmg.2012.12.007. [DOI] [PubMed] [Google Scholar]
  • 16.Virmani R, Burke AP, Farb A, Kolodgie FD. Pathology of the vulnerable plaque. Journal of the American College of Cardiology. 2006;47(8 Suppl):C13–8. doi: 10.1016/j.jacc.2005.10.065. [DOI] [PubMed] [Google Scholar]
  • 17.van der Wal AC, Becker AE, van der Loos CM, Das PK. Site of intimal rupture or erosion of thrombosed coronary atherosclerotic plaques is characterized by an inflammatory process irrespective of the dominant plaque morphology. Circulation. 1994;89(1):36–44. doi: 10.1161/01.cir.89.1.36. [DOI] [PubMed] [Google Scholar]
  • 18.Farb A, Burke AP, Tang AL, Liang TY, Mannan P, Smialek J, et al. Coronary plaque erosion without rupture into a lipid core. A frequent cause of coronary thrombosis in sudden coronary death. Circulation. 1996;93(7):1354–63. doi: 10.1161/01.cir.93.7.1354. [DOI] [PubMed] [Google Scholar]
  • 19.Knot HJ, Lounsbury KM, Brayden JE, Nelson MT. Gender differences in coronary artery diameter reflect changes in both endothelial Ca2+ and ecNOS activity. The American journal of physiology. 1999;276(3 Pt 2):H961–9. doi: 10.1152/ajpheart.1999.276.3.H961. [DOI] [PubMed] [Google Scholar]
  • 20.Yang F, Minutello RM, Bhagan S, Sharma A, Wong SC. The impact of gender on vessel size in patients with angiographically normal coronary arteries. Journal of interventional cardiology. 2006;19(4):340–4. doi: 10.1111/j.1540-8183.2006.00157.x. [DOI] [PubMed] [Google Scholar]
  • 21.Rathore S, Terashima M, Matsuo H, Kinoshita Y, Kimura M, Tsuchikane E, et al. Association of coronary plaque composition and arterial remodelling: a optical coherence tomography study. Atherosclerosis. 2012;221(2):405–15. doi: 10.1016/j.atherosclerosis.2011.10.018. [DOI] [PubMed] [Google Scholar]
  • 22.Tearney GJ, Regar E, Akasaka T, Adriaenssens T, Barlis P, Bezerra HG, et al. Consensus standards for acquisition, measurement, and reporting of intravascular optical coherence tomography studies: a report from the International Working Group for Intravascular Optical Coherence Tomography Standardization and Validation. Journal of the American College of Cardiology. 2012;59(12):1058–72. doi: 10.1016/j.jacc.2011.09.079. [DOI] [PubMed] [Google Scholar]
  • 23.Kolodgie FD, Burke AP, Wight TN, Virmani R. The accumulation of specific types of proteoglycans in eroded plaques: a role in coronary thrombosis in the absence of rupture. Current opinion in lipidology. 2004;15(5):575–82. doi: 10.1097/00041433-200410000-00012. [DOI] [PubMed] [Google Scholar]
  • 24.Campbell IC, Ries J, Dhawan SS, Quyyumi AA, Taylor WR, Oshinski JN. Effect of inlet velocity profiles on patient-specific computational fluid dynamics simulations of the carotid bifurcation. Journal of biomechanical engineering. 2012;134(5):051001. doi: 10.1115/1.4006681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Wootton DM, Markou CP, Hanson SR, Ku DN. A mechanistic model of acute platelet accumulation in thrombogenic stenoses. Annals of biomedical engineering. 2001;29(4):321–9. doi: 10.1114/1.1359449. [DOI] [PubMed] [Google Scholar]
  • 26.Moore JA, Steinman DA, Prakash S, Johnston KW, Ethier CR. A numerical study of blood flow patterns in anatomically realistic and simplified end-to-side anastomoses. Journal of biomechanical engineering. 1999;121(3):265–72. doi: 10.1115/1.2798319. [DOI] [PubMed] [Google Scholar]
  • 27.Malek AM, Alper SL, Izumo S. Hemodynamic shear stress and its role in atherosclerosis. JAMA : the journal of the American Medical Association. 1999;282(21):2035–42. doi: 10.1001/jama.282.21.2035. [DOI] [PubMed] [Google Scholar]
  • 28.Durand E, Scoazec A, Lafont A, Boddaert J, Al Hajzen A, Addad F, et al. In vivo induction of endothelial apoptosis leads to vessel thrombosis and endothelial denudation: a clue to the understanding of the mechanisms of thrombotic plaque erosion. Circulation. 2004;109(21):2503–6. doi: 10.1161/01.CIR.0000130172.62481.90. [DOI] [PubMed] [Google Scholar]
  • 29.Sumi T, Yamashita A, Matsuda S, Goto S, Nishihira K, Furukoji E, et al. Disturbed blood flow induces erosive injury to smooth muscle cell-rich neointima and promotes thrombus formation in rabbit femoral arteries. Journal of thrombosis and haemostasis : JTH. 2010;8(6):1394–402. doi: 10.1111/j.1538-7836.2010.03843.x. [DOI] [PubMed] [Google Scholar]
  • 30.Mallat Z, Tedgui A. Current perspective on the role of apoptosis in atherothrombotic disease. Circulation research. 2001;88(10):998–1003. doi: 10.1161/hh1001.090571. [DOI] [PubMed] [Google Scholar]
  • 31.Brooks AR, Lelkes PI, Rubanyi GM. Gene expression profiling of vascular endothelial cells exposed to fluid mechanical forces: relevance for focal susceptibility to atherosclerosis. Endothelium : journal of endothelial cell research. 2004;11(1):45–57. doi: 10.1080/10623320490432470. [DOI] [PubMed] [Google Scholar]
  • 32.Tricot O, Mallat Z, Heymes C, Belmin J, Leseche G, Tedgui A. Relation between endothelial cell apoptosis and blood flow direction in human atherosclerotic plaques. Circulation. 2000;101(21):2450–3. doi: 10.1161/01.cir.101.21.2450. [DOI] [PubMed] [Google Scholar]
  • 33.Yoshizumi M, Abe J, Tsuchiya K, Berk BC, Tamaki T. Stress and vascular responses: atheroprotective effect of laminar fluid shear stress in endothelial cells: possible role of mitogen-activated protein kinases. Journal of pharmacological sciences. 2003;91(3):172–6. doi: 10.1254/jphs.91.172. [DOI] [PubMed] [Google Scholar]
  • 34.Shah PK. Inflammation and plaque vulnerability. Cardiovascular drugs and therapy / sponsored by the International Society of Cardiovascular Pharmacotherapy. 2009;23(1):31–40. doi: 10.1007/s10557-008-6147-2. [DOI] [PubMed] [Google Scholar]
  • 35.Shah PK. Mechanisms of plaque vulnerability and rupture. Journal of the American College of Cardiology. 2003;41(4 Suppl S):15S–22S. doi: 10.1016/s0735-1097(02)02834-6. [DOI] [PubMed] [Google Scholar]
  • 36.Kramer MC, Rittersma SZ, de Winter RJ, Ladich ER, Fowler DR, Liang YH, et al. Relationship of thrombus healing to underlying plaque morphology in sudden coronary death. Journal of the American College of Cardiology. 2010;55(2):122–32. doi: 10.1016/j.jacc.2009.09.007. [DOI] [PubMed] [Google Scholar]
  • 37.Fuster V, Chesebro JH. Atherosclerosis - A. Pathogenesis: initiation, progression, acute coronary syndromes, and regression. In: Giuliani E, Gersh B, McGoon M, Hayes D, Schaff H, editors. Mayo Clinic Practice of Cardiology. 3. St. Louis: Mosby; 1996. pp. 1056–81. [Google Scholar]
  • 38.Zeng D, Ding Z, Friedman MH, Ethier CR. Effects of cardiac motion on right coronary artery hemodynamics. Annals of biomedical engineering. 2003;31(4):420–9. doi: 10.1114/1.1560631. [DOI] [PubMed] [Google Scholar]
  • 39.Santamarina A, Weydahl E, Siegel JM, Jr, Moore JE., Jr Computational analysis of flow in a curved tube model of the coronary arteries: effects of time-varying curvature. Annals of biomedical engineering. 1998;26(6):944–54. doi: 10.1114/1.113. [DOI] [PubMed] [Google Scholar]
  • 40.McCord BN. Fatigue of Atherosclerotic Plaque. Georgia Institute of Technology; 1992. [Google Scholar]
  • 41.Timmins LH, Suo J, Eshtehardi P, Dhawan SS, McDaniel MC, Oshinski JN, et al. Geometric and Hemodynamic Evaluation of 3-Dimensional Reconstruction Techniques for the Assessment of Coronary Artery Wall Shear Stress in the Setting of Clinical Disease Progression. Farmington, PA: ASME; 2011. [Google Scholar]
  • 42.Wellnhofer E, Goubergrits L, Kertzscher U, Affeld K. In-vivo coronary flow profiling based on biplane angiograms: influence of geometric simplifications on the three-dimensional reconstruction and wall shear stress calculation. Biomedical engineering online. 2006;5:39. doi: 10.1186/1475-925X-5-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Eshtehardi P, Luke J, McDaniel MC, Samady H. Intravascular imaging tools in the cardiac catheterization laboratory: comprehensive assessment of anatomy and physiology. Journal of cardiovascular translational research. 2011;4(4):393–403. doi: 10.1007/s12265-011-9272-4. [DOI] [PubMed] [Google Scholar]
  • 44.Samady H, Eshtehardi P, McDaniel MC, Suo J, Dhawan SS, Maynard C, et al. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation. 2011;124(7):779–88. doi: 10.1161/CIRCULATIONAHA.111.021824. [DOI] [PubMed] [Google Scholar]
  • 45.Girasis C, Schuurbiers JC, Muramatsu T, Aben JP, Onuma Y, Soekhradj S, et al. Advanced three-dimensional quantitative coronary angiographic assessment of bifurcation lesions: methodology and phantom validation. EuroIntervention : journal of EuroPCR in collaboration with the Working Group on Interventional Cardiology of the European Society of Cardiology. 2013;8(12):1451–60. doi: 10.4244/EIJV8I12A219. [DOI] [PubMed] [Google Scholar]
  • 46.Goubergrits L, Wellnhofer E, Kertzscher U, Affeld K, Petz C, Hege HC. Coronary artery WSS profiling using a geometry reconstruction based on biplane angiography. Annals of biomedical engineering. 2009;37(4):682–91. doi: 10.1007/s10439-009-9656-7. [DOI] [PubMed] [Google Scholar]
  • 47.Schuurbiers JC, Lopez NG, Ligthart J, Gijsen FJ, Dijkstra J, Serruys PW, et al. In vivo validation of CAAS QCA-3D coronary reconstruction using fusion of angiography and intravascular ultrasound (ANGUS) Catheterization and cardiovascular interventions : official journal of the Society for Cardiac Angiography & Interventions. 2009;73(5):620–6. doi: 10.1002/ccd.21872. [DOI] [PubMed] [Google Scholar]
  • 48.Formaggia L, Nobile F, Quarteroni A, Veneziani A. Multiscale modelling of the circulatory system: a preliminary analysis. Computing and visualization in science. 1999;2(2):75–83. [Google Scholar]
  • 49.Formaggia L, Quarteroni A, Veneziani A. Multiscale models of the vascular system. In: Formaggia L, Quarteroni A, Veneziani A, editors. Cardiovascular Mathematics. Milan: Springer; 2009. [Google Scholar]
  • 50.Vignon-Clementel IE, Alberto Figueroa C, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Computer Methods in Applied Mechanics and Engineering. 2006;195(29–32):3776–96. http://dx.doi.org/10.1016/j.cma.2005.04.014. [Google Scholar]
  • 51.Heywood JG, Rannacher R, Turek S. Artificial Boundaries and Flux and Pressure Conditions for the Incompressible Navier-Stokes Equations. International Journal for Numerical Methods in Fluids. 1996;22(5):325–52. doi: 10.1002/(sici)1097-0363(19960315)22:5&#x0003c;325::aid-fld307&#x0003e;3.0.co;2-y. [DOI] [Google Scholar]
  • 52.Ku DN, Giddens DP. Pulsatile flow in a model carotid bifurcation. Arteriosclerosis. 1983;3(1):31–9. doi: 10.1161/01.atv.3.1.31. [DOI] [PubMed] [Google Scholar]

RESOURCES