Abstract
Folded graphene has exhibited novel electrical and mechanical properties unmatched by pristine graphene, which implies that morphology of graphene adds the dimensionality of design space to tailor its properties. However, how to overcome the energy barrier of the folding process to fold the graphene with the specific morphology remains unexplored. Here we propose a programmable chemical functionalization by doping a pristine graphene sheet in a certain pattern with hydrogen atoms to precisely control its folding morphology. Molecular dynamics simulation has been performed to create a cross-shaped cubic graphene nanocage encapsulating a biomolecule by warping the top graphene layer downward and the bottom graphene layer upward to mimic the drug delivery vehicle. Such a paradigm, programmable enabled graphene nanocage, opens up a new avenue to control the 3D architecture of folded graphene and therefore provides a feasible way to exploit and fabricate the graphene-based unconventional nanomaterials and nanodevices for drug delivery.
The nature of unique and unprecedented functional properties of graphene, such as electronic1,2, magnetic3, mechanical4, and thermal conductivity5, is determined to a large extent by its unique two dimensional graphene morphology. In recent years, tremendous efforts have been devoted to manipulate the graphene morphology, such as graphene folding by growth and transfer from patterned surfaces6, ion radiation7, capillary forces8, mechanical strain9,10,11 and chemical functionalization12,13, to controllably design 3D architectures of graphene. The chemical functionalization of pristine graphene sheet by absorbing hydrogen atoms attracts extensive attentions for controlling graphene physical properties as the hydrogenation creates a local geometric distortion by changing the hybridization from sp2 to sp3. Significant progresses and methodologies have been made on the precisely controlled hydrogenation of graphene from the perspective of hydrogenation style and size. For instance, double sides hydrogenation bonded to the single atomic plane of graphite on an alternating manner forms the hexagonal network and transforms the chemically inert semimetal into an insulator14,15. One side half of hydrogenation on the single layer of graphite (graphone) becomes a ferromagnetic semiconductor with a small indirect gap by breaking down the delocalized π bonding network of graphene16. Double sides half of hydrogenation along the zigzag chain leads to lower thermal conductivity5. By changing the size of hydrogenation area, patterned graphone domain arrays embedded in a graphene sheet could serve as the template to precisely position and pack molecules17. A proper size of single-side hydrogenation can completely scroll up into a stable carbon nanoscroll under the room temperature18. However, the effect of hydrogenation related to the chirality of graphene and how the assigned interatomic potential components quantitatively affect the graphene folding remain excessively unexplored. Novel functionalization patterns have the potential to lead to astounding new capabilities, and should be intensively studied in order to maximize the capabilities of graphene-based devices. In this paper, we will perform molecular mechanics simulations to study the effect of doping patterns on the graphene folding and comprehensively investigate the fundamental mechanism that govern the formation of graphene folding with precise control from the energetic viewpoint.
Tethering drug particles to nano/micro-structures or encapsulating them into programmable nano/micro-devices is a widespread strategy to serve as drug delivery vehicles to precisely target the diseased cells without compromising the rest of the body, creating unprecedented opportunities for a wide range of application in nanomedicine. For example, DNA origami possess immense potential as an efficient, biocompatible drug carrier by attaching the doxorubicin as well as inhabiting lysosomal acidification in the treatment of cancer19. A rigid tetrahedral cage made of DNA is utilized to encapsulate a single molecule of cytochrome c20. Carbon nanotube in the nanomaterials family has also emerged as an efficient carrier, by attaching drug molecule to it via covalent functionalization or non-covalent coating21,22,23, to translocate the molecule such as peptide, nucleic acid, cells etc. owing to its isolated physicochemical architecture and inert properties24,25,26. Two dimensional graphene and its oxidized form (NGO) with outstanding solution stability have recently been exploited to bind specific molecule and transport to the target cells for the biomedical applications27,28. Structural DNA nanotechnology has matured to the stage that finite-sized fully addressable molecular pegboards or DNA origami can now be readily constructed in both two- and three-dimensions for nano-scale drug delivery. However it is still a formidable challenging to fabricate the graphene-based 3D nano-architectures for capsuling drug molecules for nano-medicine. Here from the modelling and simulation viewpoint, we will provide the proof-of-concept of graphene nanocage generated by chemical functionalization to contain an amino acid as antiviral agent to mimic the drug delivery system.
Results
Effect of doping pattern on graphene folding
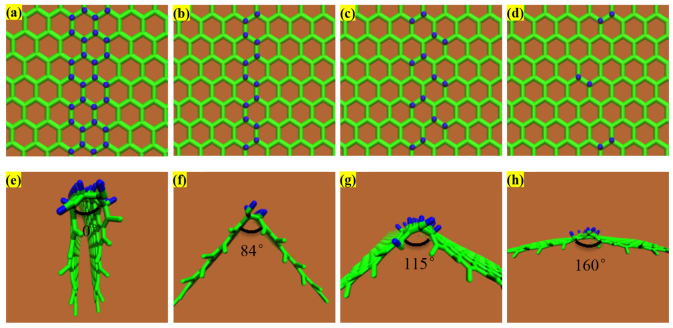
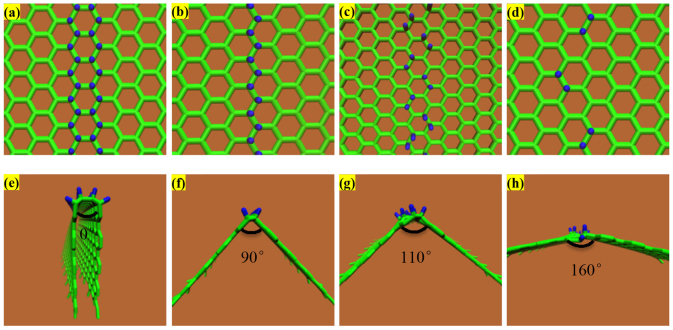
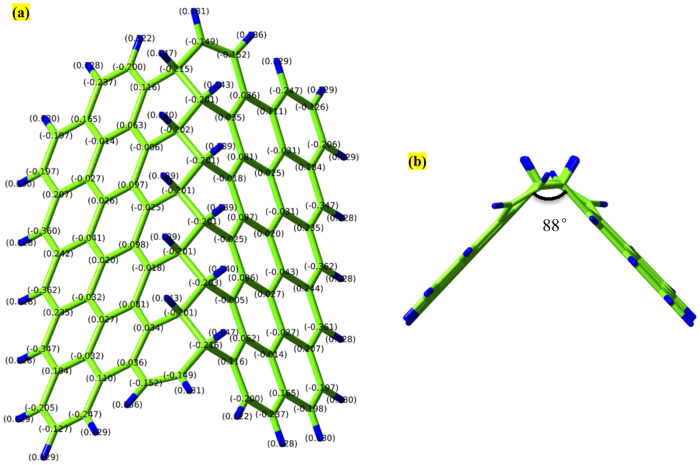
From an energetic perspective, folding a sheet of graphene requires a sufficiently large driving force to overcome the strain energy barrier due to the bending process. The reaction of atomic hydrogen with a graphene sheet converting its hybridization from sp2 to sp3 with a geometric distortion provides huge driving force to tackle the energy barrier. When the carbon atoms are doped, two main factors cause the graphene to fold in the manner it does: (i) the hybridization of the carbon bonds and the resultant geometry, and (ii) the van der Waals forces between the dopants and the graphene. In the pristine graphene, carbon atoms in graphene have sp2 hybridization, forming three equidistant co-planar bonds with their neighbour carbon atoms. Upon forming a fourth bond, the hybridization changes to sp3, and the doped carbon atoms seek an energetically preferential state wherein all formed bonds seek to be as far from each other as possible. This leads to a nearly tetrahedral arrangement locally which, as the other three bonds are constrained by surrounding carbon atoms, pushes the graphene on either side of the newly created bond away from where the bond is formed. For the graphene to fold towards the dopants, all of the bonds on the sp3 hybridized carbons would be in a single hemisphere of the carbon atoms which would generate instability in the doped system. As for the van der Waals interactions between the graphene and the dopants, it is true that the London dispersion component of the van der Waals force is weakly attractive, but it is overpowered by the effect of the hybridization force. The Keesom interaction component of the van der Waals force is non-existent, as there are no dipole-dipole interactions. The final component of the van der Waals force is the Debye interaction, where a dipole exerts a force on an uncharged molecule due to a charge from the dipole preferentially moving the electrons of the uncharged molecule. This effect is reflected by the tendency for dopants which form strong dipoles to cause a slightly smaller deflection in the graphene than those which are more neutral. In our study, to what extent the density of doped hydrogen atoms affects the graphene folding and the differences between the doped hydrogen along the zigzag direction and armchair direction of pristine graphene sheet remains unexplored. In this research, we perform simulation tests to demonstrate the role of doping pattern and doping density on the graphene folding (see Methods). The hydrogen atoms are covalently bonded at a distance of 1.09 Å above the carbon atoms along the armchair and zigzag direction with a co-linear pattern, initiating the folding mechanism to bend the graphene sheet. Figure 1(a–d) show zoomed-in profiles with two different doping patterns of hydrogen atoms on the pristine graphene along the armchair direction; each doping pattern has two types of doping density, termed as AH, AL, BH, and BL respectively. Pattern A(H,L) means the graphene sheet doping hydrogen atoms continuously with (high, low) density; pattern B(H,L) means the graphene sheet doping hydrogen atoms discretely with (high, low) density. After energy minimization is initiated, the graphene sheet near the functionalization reconfigures quickly followed by the adjustment of the further sections of the sheet. Figure 1(e–h) show the folding angle of each pattern, with the value as 0°, 84°, 115° and 160°, respectively, implying that the folding angle decrease as the density of hydrogenation increases. This intriguing result indicates that high density of doped hydrogen atoms produces a more pronounced driving force to overcome the energy barrier of bending graphene sheet and represents a prominent signature of graphene folding. Similarly, Figure 2 shows that the four different doping patterns CH, CL, DH and DL with folding angles as 0°, 90°, 110°, and 160°, respectively. Meanwhile, to demonstrate the credibility of our molecular simulation, we perform the density functional theory (DFT) calculations of the pattern (b) in Figure 2 to make a comparison. The optimized results DFT calculation showed in the Figure 3 are in good agreement with the result from the CHARMM27 force field we adopted. Just as we discussed above, the hydrogenated graphene forms a V-Shape with two molecular planes joining at the hydrogenation line with a dihedral angle of around 88°, close to our MD result with the bending angle 90°, and with a hydrogen-carbon bond length 1.085Å, close to the value of 1.09Å from the MD simulations. The hydrogenated benzene rings attain a skewed structure in which the saturated carbon atoms extrude from the six-membered ring plane. The numerical values depicted on the atoms in the figure here are the calculated Mullicken partial charges which indicate the electronegativity of the hydrogenated graphene. The hydrogenated carbon atoms are saturated with four σ single bonds. The initial π bond over the graphene plane is converted into two separate π conjugation on two intersected plane. DFT calculation provides a compelling evidence to demonstrate the feasibility of graphene folding patterns from our MD calculations. Therefore, molecular simulation offers an invaluable and feasible way to form programmable three-dimensional graphene structure by hydrogen chemical functionalization.
Figure 1. Four different hydrogen doping pattern along armchair direction on the pristine graphene and its corresponding folding results.
Figure 2. Four different hydrogen doping pattern along the zigzag direction on the pristine graphene and its corresponding folding results.
Figure 3. Optimized configuration of hydrogenated graphene via density functional theory calculations: (a) top view with charge value; (b) side view.
Carbon atoms are in green color while hydrogen atoms are in blue color.
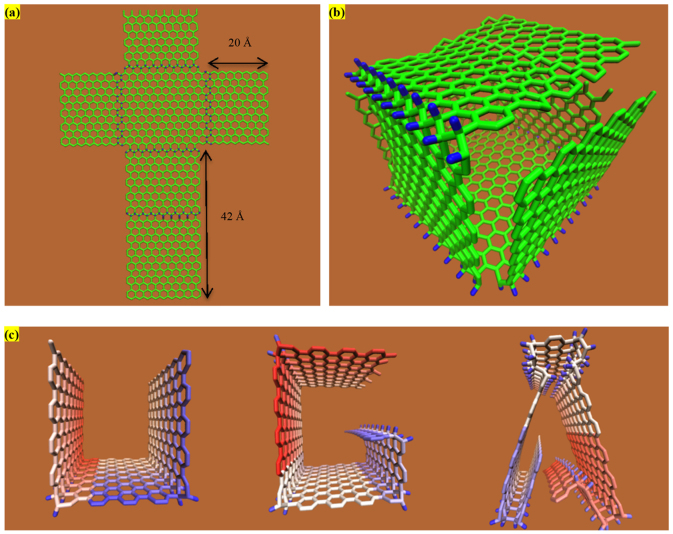
To further demonstrate this promising idea and appreciate the full benefit from chemical hybridization, here we present a single layer graphene containing 752 carbon atoms with single-side hydrogenated with only one row along the armchair and zigzag lines on the inner edge of each petals as depicted in Figure 4(a). Each petal has identical size except for one petal is two size larger than other ones. During the molecular mechanics minimization, the combination of the forces between the dopants and the graphene and the sp3 hybridization geometry significantly contributes to bend the large petal to fold up to seal the simple cubic box eventually as shown in Figure 4(b). The folding process is terminated when the outside edges of the largest petal reaches to the edge of the opposite petal on the graphene sheet due to the repulsive force acting on them.
Figure 4. Programmable graphene folding with designed morphology: (a) and (b) represent the initial and final configuration of graphene nanocage, respectively; (c) a UGA logo from a simple and plain graphene nanoribbon.
Following the identical technique by decorating a graphene nanoribbon with varying densification of hydrogen atom at specific sites, we device the elegant but complex UGA logo from a plain but simple graphene nanoribbon as shown in Figure 4(c). Combining these novel ways to tailor the natural folding angle of a pristine graphene sheet results in programmable and unique origami-like folded structures, holding great promise to design and eventually fabricate novel graphene-based unconventional nanomaterials and nanodevices.
Effect of interatomic potential on graphene folding
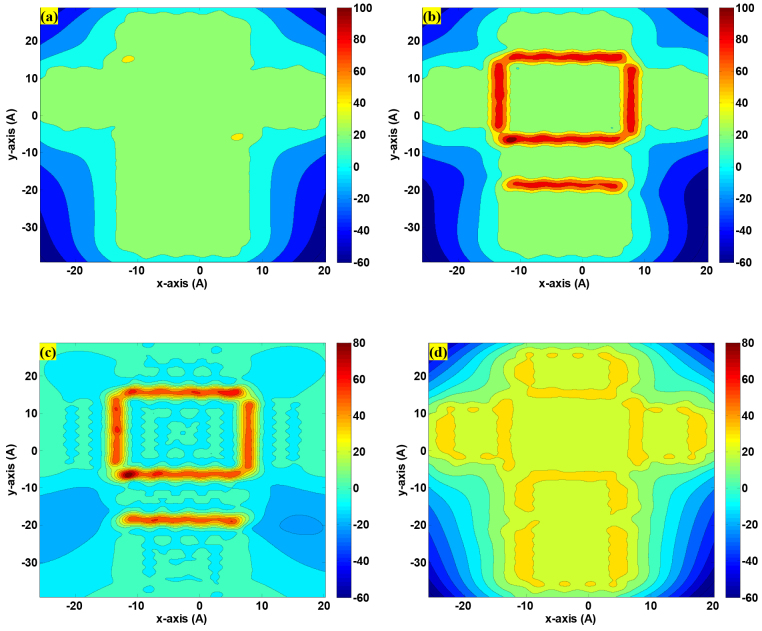
We have unveiled the fundamental concept of folding a graphene sheet with programmable morphology by controlling the doping pattern in previous section. The interesting question is what the fundamental driving force is to fulfill the specific folding process. To tackle this riveting question, here we devote our efforts to explore how the interatomic potential components in equation (1) (see Methods) affect the graphene folding process. Firstly we explore how the hydrogenation affects the total energy distribution on the cross-shaped graphene. Figure 5(a–b) show contour profiles of the total energy of the cross-shape graphene sheet before and after hydrogenation. The total energy of the simulated system is in the range with positive values. For the purpose of illustration, the negative value of total energy in blue color is adopted to achieve a better representation of the contour plot without real physical meanings. In the pristine graphene as shown in Figure 5(a), the total energy of almost any carbon atom is identically 27.15 kcal/mol except for the carbon atoms on the edge of the graphene, which have weaker interactions with other carbon atoms than the interior carbon atoms. After the hydrogenation, the distortion of the local carbon atoms at the doped area triggers drastic bond bending and reshape the average energy maps from 27.15 kcal/mol to 83.36 kcal/mol as shown in red color in Figure 5(b). The total energy on the carbon atoms outside of the hydrogenation area are slimly affected by the hydrogenation, which therefore provides the possibility for the precise programmable and controllable graphene folding. To uncover the dominant factor of these components of potential energy during the graphene folding process, we distinguish these components one by one from the rest of interatomic potential to produce the contour plots for a better interpretation. Figure 5(c) depicts the contour profile of the angle bending energy on each carbon atom while Figure 5(d) depicts the sum of the rest energy components described in equation (1). The average of angle bending energy on the carbon atoms in the hydrogenation regions changes profoundly from 0.3329 kcal/mol before the hydrogenation to 52.91 kcal/mol after the hydrogenation. Intriguingly all the rest energy components remain almost unaffected from 26.81 kcal/mol before the hydrogenation to 29.88 kcal/mol after the hydrogenation. This plot demonstrates that the accumulated angle bending energy by hydrogenation makes a prominent contribution to shape the doped graphene to a preferable geometric morphology.
Figure 5. Contour plot of energy distribution of the system with cross-shaped structure as depicted in Figure 3(a): (a) and (b) represent the total energy contour profile of the simulated graphene sheet before and after hydrogenation, respectively; (c) and (d) show the angle bending potential energy and the rest of total potential energy of the system of interest, respectively.
Graphene nanocage as a potential drug delivery vehicle
An efficient drug delivery system is of fundamental importance to improve the development of pharmacological issues. The fullerene cage, in another way, bulkyball, has particular stable cage-like shape which is extremely useful for the drug delivery. However, the encapsulating structure becomes constraint as the drug is loaded and released. Besides, the radius of the bulkyball seriously depends on the size of the drug. CNT is also used for drug delivery due to its unusual high ratio cavity. Filling in CNT with appropriate drug and binding the drug interior or exterior of the CNT are the most popular ways to implement the drug delivery with CNT. However, the drug can be released from the unsealed end without covalent bonding before it reaches the desired location. To make the delivery efficient, large doses than required should be used, thereby resulting in a lot of unexpected peripheral damage to healthy cells or immune reactions. The drug releasing will be difficult with chemical binding and the properties of the drug are also affected by the chemical reaction of binding. Other concerns for researchers are the fact that CNT or bulkyball could be hazardous and toxic to human cells. Therefore, the toxicity of CNT needs to be alleviated to a certain level before applying them for drug delivery. Functional graphene, stable in the physiological environment, allows binding specified molecule and transport to the target cells. The graphene-based 3D nano-architectures for capsuling drug molecules for nano-medicine remain an open issue to be explored. Here a proof-of-concept of graphene nanocage for a drug delivery vehicle is contrived by chemical hydrogenation to encapsulate an amino acid as virtual antiviral agent which is allowed to be transferred to the target cell in the drug delivery system. In what follows, by performing molecular dynamics simulation, we demonstrate the novel concept by devising a graphene nanocage through combining two hydrogenated cross-shaped graphene sheets to seal them together. The carbon-based nanocage is also demonstrated as a stable 3D structure in the solution which means it can be inserted into the human cells after the delicate functionalized coating29. The graphene-based nanocage has three advantages: (1) the size of cage is easy to tailor by modifying the hydrogenated area on the original graphene sheet; (2) bulkyball as well as carbon nanotubes are required to be functionalized with appropriate molecule on the surface to make them less toxic. The graphene-based nanocage in this manuscript is functionalized by the hydrogen, which can be easily replaced by other alien atoms or chemical groups such as peptides and proteins30 and thereby make it biocompatible and less toxic without loss of its other functionalities; (3) the graphene-based nanocage is formed by two hydrogenated half box which provides a feasible way to open and release the drug while retaining drug structures intact.
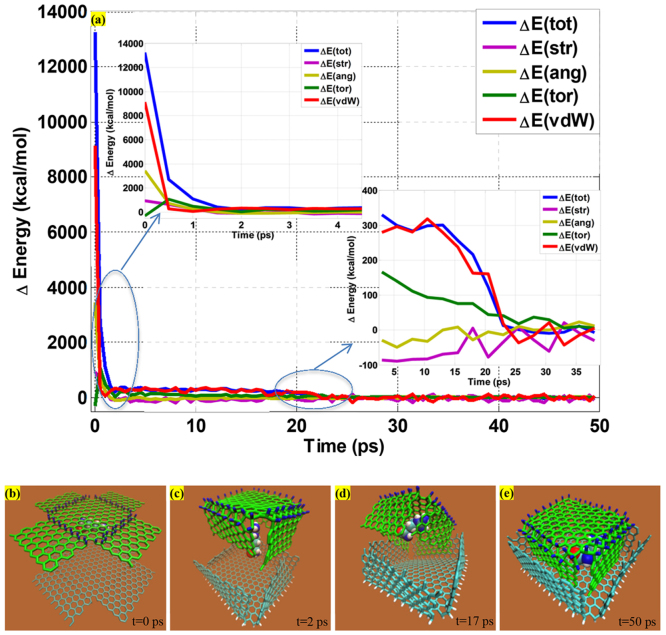
The system is composed of two cross-shaped graphene with specific hydrogenation region with total 1378 atoms. Molecular dynamics simulations are carried out with NVT canonical ensemble at temperature 300 K. The variation of total energy of system as well as each potential energy component as simulation time is depicted in Figure 6(a). Initially the total energy of the pristine graphene sheet is minimized by applying conjugate gradient algorithm until the total energy change between two successive iterations divided by the energy magnitude is less than or equal to 10−8. Figure 6(b) shows the initial state of two separate hydrogenated graphene sheet. The upward and downward graphene sheets are single-sided hydrogenated identically as shown in Figure 4(a). To guarantee the two sheets seal together with one inside and the other outside of the nanocage, the edge length of the petal for the upward graphene sheet is 1.237 nm while the petal length for the downward graphene sheet is 1.193 nm. The distance between two graphene sheets is 2.1 nm which is extremely larger than the empirical graphene-graphene distance value 0.34 nm. The distance between two hydrogenated graphene sheet is smaller than the sum of petal length of two graphene sheets 2.43 nm which act as the maximum distance of two graphene sheets, otherwise, the interactions between two graphene sheets is too weak to fold together. The small organic molecule inside the box, represented by the arginine amino acid in the simulation, is situated at random position between two hydrogenated graphene sheets to mimic the antiviral agent.
Figure 6. Evolution of energy variation of the graphene nanocage as simulation time and four key configurations during the folding process.
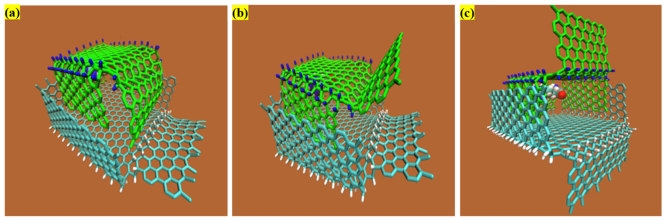
Figure 6(c) shows that the upward and downward hydrogenated graphene sheets fold simultaneously at t = 2ps. The total energy drops spontaneously from 2.729 × 104 kcal/mol to 1.445 × 104 kcal/mol as the folding process goes on. The accumulated angle bending energy easily overcome the energy barrier of graphene bending, then fold the upward and downward graphene sheets to capture the small molecule inside which can't flee away easily in any directions. Figure 6(a-1) shows that during the first 2ps, both the angle bending energy and vdW interaction contributed to the folding of two graphene sheets. For one graphene sheet, the influence of the vdW interaction can be neglected as discussed in section (3.2), however for two graphene sheets in the effective range, the vdW interaction between two graphene sheets favourably facilitate and accelerate the graphene folding (Figure 6(a-2)). As simulation continues, the upward graphene sheet pushes the molecule down to the interior cubic of downward folded graphene sheet. At t = 17ps, as shown in Figure 6(d), when the upward folded graphene sheets enter slowly inside the downward folded graphene, the total energy of the system starts to decrease obviously from 1.428 × 104 kcal/mol. To further illustrate from perspective of energy, Figure 6(a-2) shows that the dramatic pitch of the upload graphene sheets is mainly caused by the vdW interaction between two folded boxes. At t = 50ps, the nanocage is basically formed and the amino acid rotates freely to attain the preferable configuration as non-covalent attachment with total energy of 1.403 × 104 kcal/mol. Meanwhile, the whole system reaches the equilibrium state, and due to the vdW interaction the small molecule eventually lies in the plane parallel with the graphene sheet in Figure 6(e), which indicates the structure and functionality of molecule remain unaltered in the nanocage. With respect to how to control or modulate the kinetics of release, surprisingly, by alternating the doped hydrogen to the opposite side of two petals on the face of nanocage, the nanocage is forcedly opened and the amino acid can be released from the nanocage, shown in Figure 7(a–c). The hydrogenated graphene with four petals has been realized to encapsulate the biomolecule by forming a proof-of-concept nanocage and holds a bright future for the drug delivery system in the medical field.
Figure 7. Evolution of opening graphene nanocage as simulation time by reversing the direction of doped hydrogen on the gate sides.
Discussion
In conclusion, we have performed molecular mechanics and dynamics simulations to investigate the effect of chemical hydrogenation doping pattern on the graphene morphology and presented an intriguing concept for designing of promising drug delivery vehicle termed as graphene nanocage by folding a single piece or two pieces of graphene sheet via chemical hydrogenation. It has been observed that graphene folding with chemical hydrogenation is strongly dependent on the chirality and density of doped patterns. The hydrogenation on the zigzag direction generates a better outcome than the armchair direction does. By tailoring the doping pattern and doping density of hydrogen atoms to contrive programmable but unique ‘origami-like’ folded graphene structures, the research findings from this study provide a promising concept for quantitatively controlling the folding process of the graphene and can also serve as a guideline to design novel graphene-based unconventional nanomaterials and nanodevices in the near future.
No research, however, provides a perfect answer, with this work being no exception to the rule. Based on current assumptions employed in implementing the drug delivery vehicle with graphene nanocage, more work remains to be done. Specifically, how to control and release the drug from the nanocage poses a great challenge. We will further study the drug release based on the electric or magnetic field as an ongoing research, which could provide sufficient driving force to overcome the van der Waals interaction of the upward and downward box to release the drug out of the cage. The authors hope that this work can catalyze further work in the drug delivery system with graphene-based nanodevices.
Methods
Our home-brewed molecular dynamics (MD) simulations package are employed to perform the simulations and the simulation results are visualized and analysed by using the visualization program VMD. Meanwhile, we perform the density functional theory (DFT) calculation based on Gaussian03 based on the B3LYP/6-31G* package31 to provide the credence for our molecular simulation. In the MD simulation, we adopt the powerful CHARMM27 force field32,33 to describe the bonded and non-bonded interactions between organic chemical elements such as C, O, S, N and P. The CHARMM27 force field has been perceived to give a quantitatively accurate description of bond-bond interaction between organic chemical elements as well as covalent bond formations during the graphene folding due to doped foreign atoms or groups, thus rendering the drug delivery vehicle computationally accessible. The potential components described in the CHARMM27 force field with specific parameters34 are defined as
 |
where the first five terms account for the intramolecular interactions (bond stretch, bond angle, dihedral angle, improper angle, Urey-Bradley) characterizing the short-range bonding while the last two terms are associated with intermolecular interactions describing the long-range van der Waals (vdW) interactions and electrostatic interactions. Typically, 12–6 Lennard-Jones potential is adopted to describe the vdW interaction based on the Lorentz-Berhelot mixing rule. To terminate the unphysical high bond force arising from improper cutoff functions, we set the cutoff as 8Å, and periodic boundary conditions are also applied in the simulation. To achieve the most favourable structures of graphene after doping foreign atoms, the conjugate gradient algorithm has been employed to perform the energy minimization until the total energy change between two successive iterations divided by the energy magnitude is less than or equal to 10−8. After the equilibrium state is achieved, NVT ensemble simulations with constant temperature 300 K are carried out based on the Berendsen thermostat35. The velocity Verlet time stepping method is utilized with the integration time step 0.5fs.
Initially a pristine rectangular graphene with dimension 40Å × 35Å is constructed. The hydrogen atoms are chemically bonded to the carbon atoms on the graphene sheet along the zigzag and armchair direction as shown in Figure 1(a–d) and Figure 2(a–d), respectively. For DFT calculation, we choose the pattern (b) in Figure 2 to be optimized by the Gaussian03 based on the B3LYP/6-31G* package. The B3LYP function is a semi-empirical density functional while the 6-31G* is a split-valence basis. The combination of these two bases is generally used as a universal basis in the DFT study on the small molecules. The hydrogenated structure has 82 carbon atoms 34 hydrogen atoms in which 10 hydrogen atoms is on the zigzag direction of edge of third and fourth rows of aromatic rings of pristine graphene. The configuration optimization process based on Gaussion03 will be terminated until the force acting on each atom is less than 10−10 eV/Å. To better illustrate the graphene folding under different doping patterns, a folding angle is define by the two bended pieces of graphene sheets as depicted in Figure 1(e). Due to the transition from sp2 to sp3 bonding of hydrogenated carbon atoms, the hybridization deforms the local hexagonal carbon structures by creating a geometric distortion. To further explore the feasibility and programmability of graphene folding with varying but unique morphologies, a proof-of-concept drug delivery vehicle comprising of a nanoscale cubic box is constructed by a single hydrogenated cross-shaped graphene layer as shown in Figure 2(a). Also, two hydrogenated graphene sheets are applied to convert a graphene nanocage for capturing an amino acid inside with the molecular dynamics simulation.
Author Contributions
L.Z. and X.W. wrote the main manuscript text. X.Z. revised the manuscripts. L.Z. performed all the calculations. All authors discussed the results and commented on the manuscript.
Acknowledgments
The authors acknowledge support from the University of Georgia (UGA) Research Foundation. Calculations are performed at the UGA Advanced Computing Resource Centre. The authors also would like to thank Jiawang Hong for his helpful discussions.
References
- Matis B. R. et al. Surface doping and band gap tunability in hydrogenated graphene. ACS Nano 6, 17–22 (2011). [DOI] [PubMed] [Google Scholar]
- Zhou J., Wu M. M., Zhou X. & Sun Q. Tuning electronic and magnetic properties of graphene by surface modification. Appl. Phys. Lett. 95, 103108 (2009). [Google Scholar]
- Wu M., Wu X., Gao Y. & Zeng X. C. Patterned hydrogenation of graphene: magnetic quantum dot array. J. Phys. Chem. C 114, 139–142 (2010). [Google Scholar]
- Zheng Y., Wei N., Fan Z., Xu L. & Huang Z. Mechanical properties of grafold: a demonstration of strengthened graphene. Nanotechnology 22, 405701 (2011). [DOI] [PubMed] [Google Scholar]
- Liu B. et al. Morphology and in-plane thermal conductivity of hybrid graphene sheets. Appl. Phys. Lett. 101, 211909 (2012). [Google Scholar]
- Kim K. et al. Multiply folded graphene. Phys. Rev. B 83, 245433 (2011). [Google Scholar]
- Terdalkar S. S., Zhang S., Rencis J. J. & Hsia K. J. Molecular dynamics simulations of ion-irradiation induced deflection of 2D graphene films. Int. J. Solids Struct. 45, 3908–3917 (2008). [Google Scholar]
- Patra N., Wang B. Y. & Kral P. Nanodroplet Activated and Guided Folding of Graphene Nanostructures. Nano Lett. 9, 3766–3771 (2009). [DOI] [PubMed] [Google Scholar]
- Pang A. L. J., Sorkin V., Zhang Y. W. & Srolovitz D. J. Self-assembly of free-standing graphene nano-ribbons. Phys. Lett. A 376, 973–977 (2012). [Google Scholar]
- Zhang J. et al. Free folding of suspended graphene sheets by random mechanical stimulation. Phys. Rev. Lett. 104, 166805 (2010). [DOI] [PubMed] [Google Scholar]
- Zhou Z., Qian D., Vasudevan V. K. & Ruoff R. S. Folding mechanics of bi-layer graphene sheet. Nano LIFE 02, 1240007 (2012). [Google Scholar]
- Johns J. E. & Hersam M. C. Atomic covalent functionalization of graphene. Acc. Chem. Res. 46, 77–86 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boukhvalov D. W. & Son Y. W. Covalent functionalization of strained graphene. Chemphyschem 13, 1463–1469 (2012). [DOI] [PubMed] [Google Scholar]
- Elias D. C. et al. Control of graphene's properties by reversible hydrogenation: evidence for graphane. Science 323, 610–613 (2009). [DOI] [PubMed] [Google Scholar]
- Sofo J. O., Chaudhari A. S. & Barber G. D. Graphane: A two-dimensional hydrocarbon. Phys. Rev. B 75, 153401 (2007). [Google Scholar]
- Zhou J. et al. Ferromagnetism in semihydrogenated graphene sheet. Nano Lett. 9, 3867–3870 (2009). [DOI] [PubMed] [Google Scholar]
- Reddy C. D., Zhang Y. W. & Shenoy V. B. Patterned graphone—a novel template for molecular packing. Nanotechnology 23, 165303 (2012). [DOI] [PubMed] [Google Scholar]
- Zhu S. & Li T. Hydrogenation enabled scrolling of graphene. J. Phys. D: Appl. Phys. 46, 075301 (2013). [Google Scholar]
- Jiang Q. et al. DNA origami as a carrier for circumvention of drug resistance. J. Am. Chem. Soc. 134, 13396–13403 (2012). [DOI] [PubMed] [Google Scholar]
- Erben C. M., Goodman R. P. & Turberfield A. J. Single-molecule protein encapsulation in a rigid DNA cage. Angew. Chem. 45, 7414–7417 (2006). [DOI] [PubMed] [Google Scholar]
- Peretz S. & Regev O. Carbon nanotubes as nanocarriers in medicine. Current Opinion in Colloid & Interface Science 17, 360–368 (2012). [Google Scholar]
- Prato M., Kostarelos K. & Bianco A. Functionalized carbon nanotubes in drug design and discovery. Acc. Chem. Res. 41, 60–68 (2007). [DOI] [PubMed] [Google Scholar]
- Hilder T. A. & Hill J. M. Modeling the Loading and Unloading of Drugs into Nanotubes. Small 5, 300–308 (2009). [DOI] [PubMed] [Google Scholar]
- Ajima K. et al. Carbon nanohorns as anticancer drug carriers. Mol. Pharm. 2, 475–480 (2005). [DOI] [PubMed] [Google Scholar]
- Bianco A., Kostarelos K. & Prato M. Applications of carbon nanotubes in drug delivery. Current Opinion in Chemical Biology 9, 674–679 (2005). [DOI] [PubMed] [Google Scholar]
- Mendes R. G., Bachmatiuk A., Buchner B., Cuniberti G. & Rummeli M. H. Carbon nanostructures as multi-functional drug delivery platforms. J. Mater. Chem. B 1, 401–428 (2013). [DOI] [PubMed] [Google Scholar]
- Liu Z., Robinson J. T., Sun X. & Dai H. PEGylated nanographene oxide for delivery of water-insoluble cancer drugs. J. Am. Chem. Soc. 130, 10876–10877 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Xia J., Zhao Q., Liu L. & Zhang Z. Functional graphene oxide as a nanocarrier for controlled loading and targeted delivery of mixed anticancer drugs. Small 6, 537–544 (2010). [DOI] [PubMed] [Google Scholar]
- Chen J. et al. Functionalized single-walled carbon nanotubes as rationally designed vehicles for tumor-targeted drug delivery. J. Am. Chem. Soc. 130, 16778–16785 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becton M., Zhang L. & Wang X. Effects of surface dopants on graphene folding by molecular simulations. Chem. Phys. Lett. 584, 135–141 (2013). [Google Scholar]
- Frisch M. J. et al. Gaussian 03, Revision C.02. Gaussian, Inc., Wallingford CT, (2004), http://www.gaussian.com/g_misc/g03/citation_g03.htm, September 10, 2013. [Google Scholar]
- Brooks B. R. et al. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comp. Chem. 4, 187–217 (1983). [Google Scholar]
- MacKerell A. D. et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616 (1998). [DOI] [PubMed] [Google Scholar]
- Mackerell A. D., Feig M. & Brooks C. L. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 25, 1400–1415 (2004). [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A. & Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690 (1984). [Google Scholar]