Abstract
Magnetic nanoparticles have attracted much research interest in the past decades due to their potential applications in microwave devices. Here, we adopted a novel technique to tune cut-off frequency exceeding the natural resonance frequency limit of monodisperse Fe3O4 nanoparticles via superparamagnetic relaxation. We observed that the cut-off frequency can be enhanced from 5.3 GHz for Fe3O4 to 6.9 GHz forFe3O4@SiO2 core-shell structure superparamagnetic nanoparticles, which are much higher than the natural resonance frequency of 1.3 GHz for Fe3O4 bulk material. This finding not only provides us a new approach to enhance the resonance frequency beyond the Snoek's limit, but also extend the application for superparamagnetic nanoparticles to microwave devices.
The frequency response of magnetic moment to an alternating magnetic field plays a vital role in designing the microwave, and even terahertz devices1,2,3. The miniaturization and rapid increase in frequencies of electric devices require that magnetic materials possess high resonance frequency, large permeability, and low magnetic loss. The natural resonance frequency, fr, originated from the magnetocrystalline anisotropy field, HK, is generally regarded as the upper limit frequency, i.e. cut-off frequency, of magnetic materials. For traditional spinel ferrites, their natural resonance frequencies typically fall near or below 1 GHz4. Although the resonance frequency can be enhanced by introducing additional magnetic anisotropies, including shape anisotropy, strain-induced anisotropy, as well as exchange anisotropy5,6,7,8,9, it is a great challenge to increase both resonance frequency and permeability simultaneously due to the Snoek's limit10, i.e. the product of the susceptibility and the resonance frequency is proportional to the saturation magnetization.
Magnetic nanoparticles have attracted much research interest in the past decades due to their potential applications in ultrahigh density magnetic storage11, biomagnetism12,13, and microwave absorption14. When the nanoparticle volume, VP, is reduced to a certain extent that magnetic anisotropy energy, KVP, is comparable to the thermal energy, kBT, there exists a finite probability that the magnetization vector will reverse its direction by thermal fluctuation at certain temperature T. Both theoretical and experimental data indicated that the frequency dependence of the susceptibility for a single domain particle depended on the ratio of the magnetic anisotropy energy to the thermal energy (α = KVP/kBT)15,16. In the case of  , the real part of the complex susceptibility x′(f) decreases monotonically with increasing f, whilst the imaginary component, χ"(f), has a maximum at a frequency fb = 1/τ. τ is relaxation time is introduced to describe how rapidly this superparamagnetic/ferromagnetic relaxation takes place17.
, the real part of the complex susceptibility x′(f) decreases monotonically with increasing f, whilst the imaginary component, χ"(f), has a maximum at a frequency fb = 1/τ. τ is relaxation time is introduced to describe how rapidly this superparamagnetic/ferromagnetic relaxation takes place17.
 |
where τ0 is determined by the intrinsic precession rate of the spin moment in the equivalent field for magnetic anisotropy.
The frequency, 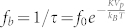 , which superparamagnetic state transits to ferromagnetic one in frequency domain, will increase with decreasing the nanoparticle volume. Therefore, the superparamagnetic dynamics in GHz range, which is governed by both natural resonance frequency (fr) and superparamagnetic/ferromagnetic relaxation rate (fb), should be attractive and challenging issue. The great challenge is whether fb can be tuned to surpass fr or not.
, which superparamagnetic state transits to ferromagnetic one in frequency domain, will increase with decreasing the nanoparticle volume. Therefore, the superparamagnetic dynamics in GHz range, which is governed by both natural resonance frequency (fr) and superparamagnetic/ferromagnetic relaxation rate (fb), should be attractive and challenging issue. The great challenge is whether fb can be tuned to surpass fr or not.
In contrast to conventional bulk microwave ferrites, the magnetic properties of superparamagnetic nanoparticles can be easily tuned by controlling the volume, shape, anisotropy, dipolar interaction between particles, and by applying exchange bias and electric field18,19,20,21. However, the effect of superparamagnetism on high frequency properties is not well understood. Here, we adopted a novel technique to tune the cut-off frequency exceeding the natural resonance frequency limit of monodisperse Fe3O4 nanoparticles via superparamagnetic/ferromagnetic relaxation. We observed that the cut-off frequency can be enhanced from 5.3 GHz for Fe3O4 to 6.9 GHz for Fe3O4@SiO2 core-shell structure superparamagnetic nanoparticles, which are much higher than the natural resonance frequency of 1.3 GHz for Fe3O4 bulk material. In addition to the enhancement of cut-off frequency, the magnetic loss is significantly reduced via SiO2 coating. This finding in superparamagnetic nanoparticles not only provides us a new approach to enhance the resonance frequency beyond the Snoek's limit, but also opens a new avenue for exploring superparamagnetic nanoparticles in microwave devices.
Results
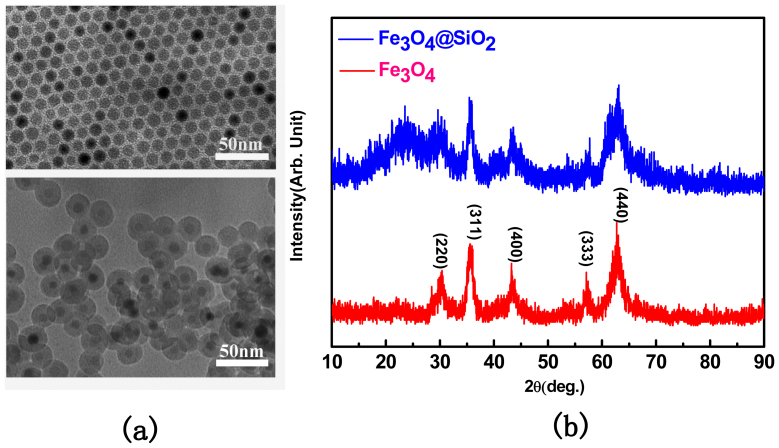
Figures 1(a) and 1(b) illustrate the Transmission electron microscopy (TEM) micrographs and X-ray diffraction (XRD) patterns for as-prepared Fe3O4 nanoparticles and Fe3O4@SiO2 core-shell composites, respectively. Fe3O4 nanoparticles have a regularly spherical morphology and an average size of 9.0 ± 0.5 nm with a narrow size distribution of (σ = 5%). Every Fe3O4 particle was coated by the SiO2 shell after the magnetic collection process. For SiO2 thickness of 8.0 nm, nearly every Fe3O4 core was located at the center of the core-shell structures, and the Fe3O4/SiO2 core-shell nanoparticles became well-dispersed in ethanol, which provide an indirect evidence of the decrease of interparticle interaction. Although the particle size of Fe3O4 does not change obviously, the interspacing of nanoparticles increases via SiO2-shell coating. XRD patterns of the samples indicate that all the highly crystalline peaks match well with the standard crystal phase of magnetite (JCPDS No. 894319, 19-0629). The broad peak around 15° to 35° presents the existence of amorphous-SiO2.
Figure 1.
(a) TEM micrographs; and (b) XRD patterns for as-prepared Fe3O4 nanoparticles and Fe3O4@SiO2 core-shell composites.
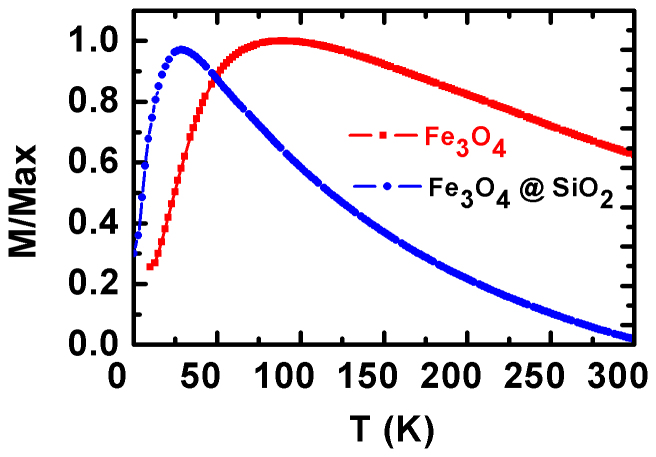
In order to determine the effect of interparticle spacing on the collective magnetic behavior of the Fe3O4 nanoparticles, the temperature-dependent zero-field-cooled (ZFC) magnetization of the as-prepared Fe3O4 and Fe3O4@SiO2 core-shell structure nanoparticles is measured at a low magnetic field of 100 Oe and shown in Fig. 2. The maxima of the ZFC curves related to the blocking temperatures, TB, of superparamagnetic behavior shift from 86 K for as-prepared Fe3O4 nanoparticles to 37 K for Fe3O4@SiO2. A similar trend was previously observed in dilute dispersed magnetic nanoparticles and by Monte Carlo simulations21,22. The dipole-dipole interaction results in an additional energy barrier for the thermal fluctuations, and consequently increases the blocking temperature.
Figure 2. Temperature-dependent zero-field-cooled (ZFC) magnetization of the as-prepared Fe3O4 and Fe3O4@SiO2 nanoparticles.
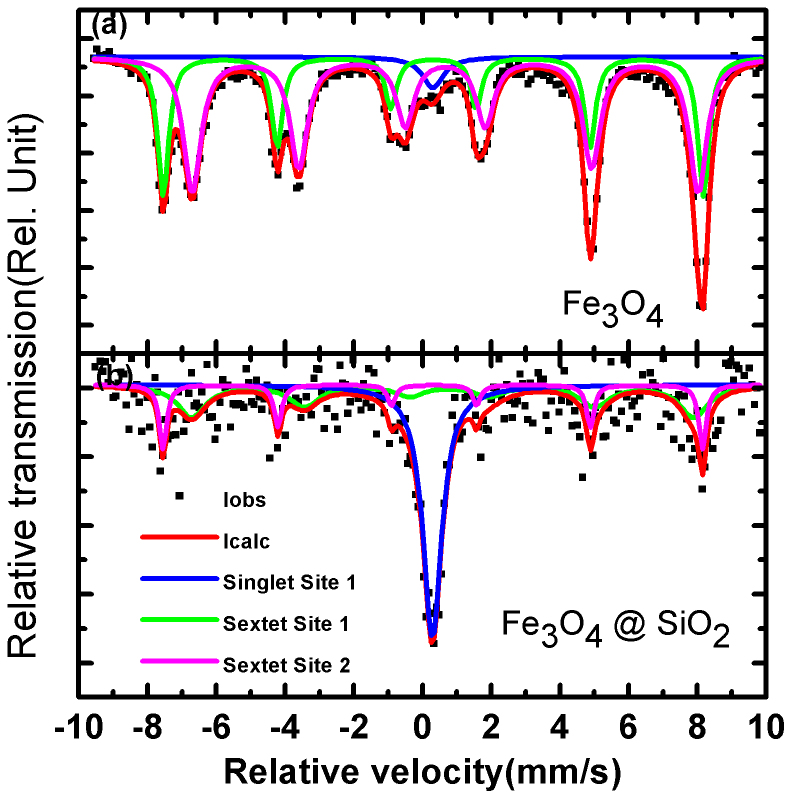
Since the value of the blocking temperature for a given particle is dependent upon the observation time, which is determined by the instrument used, it will be useful to collect information using various techniques with observation times different over a large range. Figures 3(a) and 3(b) illustrate the 57Fe Mössbauer spectra collected at room temperature for as-prepared Fe3O4 nanoparticles and Fe3O4@SiO2 core-shell nanoparticles, respectively. Although DC magnetization measurement indicates that a superparamagnetic behavior, the Mössbauer spectrum of as-prepared Fe3O4 nanoparticles shows clearly two strong sextets and a weak doublet (5%) at room temperature, suggesting that a ferromagnetic behavior is dominated in this sample. The concentration of ferromagnetic phase deceases to 54% for Fe3O4 coated with SiO2 shell (Fig. 3(b)). The two sextets with hyperfine fields (Hhf), and center shift (CS) of one (487.55 kOe and 0.32 mm/s) and the other (456.5 kOe and 0.66 mm/s) suggest the Fe3+ ions on the tetrahedral sites and Fe2.5+ (Fe2+Fe3+) ions on the octahedral sites, respectively. The results are consistent with the room-temperature results observed for magnetite nanoparticles23. The hyperfine fields are lower than those of the bulk material and the resonance lines are broadened. The change in the Mössbauer spectra is due to the finite size effect, which can cause a higher percentage of surface atoms, additional stresses between atoms, and superparamagnetic behavior24. The stoichiometry of nanoparticles is extracted by comparing the relative areas of the TetFe3+ and the OctFe2.5+ using the following equation x = Fe2+/Fe3+ = (1/2OctFe2.5+)/(1/2OctFe2.5+ + TetFe3+). According to the ratio of Fe2+ and Fe3+ of about 46.7%, one can deduce that the stoichiometry of nanoparticles is Fe3+2 + 0.066Fe2+1-0.066O4. The possible reason for the slightly shift of Fe3+:Fe2+ = 2:1 is partly oxidation of Fe2+ ions on the surface layer or slight presence of vacancies in tetrahedral sites.
Figure 3. Room-temperature 57Fe Mössbauer spectra collected at for (a) as-prepared Fe3O4 nanoparticles, and (b) Fe3O4@SiO2.
The different results obtained from Mössbauer spectra with those from DC magnetization measurements can be explained by the relationship between relaxation time τ and the experimental observation time, τobs. It is well known that the magnetic behavior of a particle is dependent on the experimental observation time, τobs. For 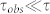 , the particle shows ferromagnetic behavior, while for
, the particle shows ferromagnetic behavior, while for 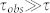 , the particle is superparamagnetic behavior. Since the experimental observation time for Mössbauer measurements (τobs ~ 10 ns) is significantly shorter than that for DC magnetization measurements (τobs ~ 10 ns), a superparamagnetic behavior obtained DC magnetization measurements can behaves as ferromagnetism in shorter observation time scale, such as Mössbauer measurements. In other word, we can expect the superparamagnetic behavior can transit to ferromagnetic one in higher frequency regime.
, the particle is superparamagnetic behavior. Since the experimental observation time for Mössbauer measurements (τobs ~ 10 ns) is significantly shorter than that for DC magnetization measurements (τobs ~ 10 ns), a superparamagnetic behavior obtained DC magnetization measurements can behaves as ferromagnetism in shorter observation time scale, such as Mössbauer measurements. In other word, we can expect the superparamagnetic behavior can transit to ferromagnetic one in higher frequency regime.
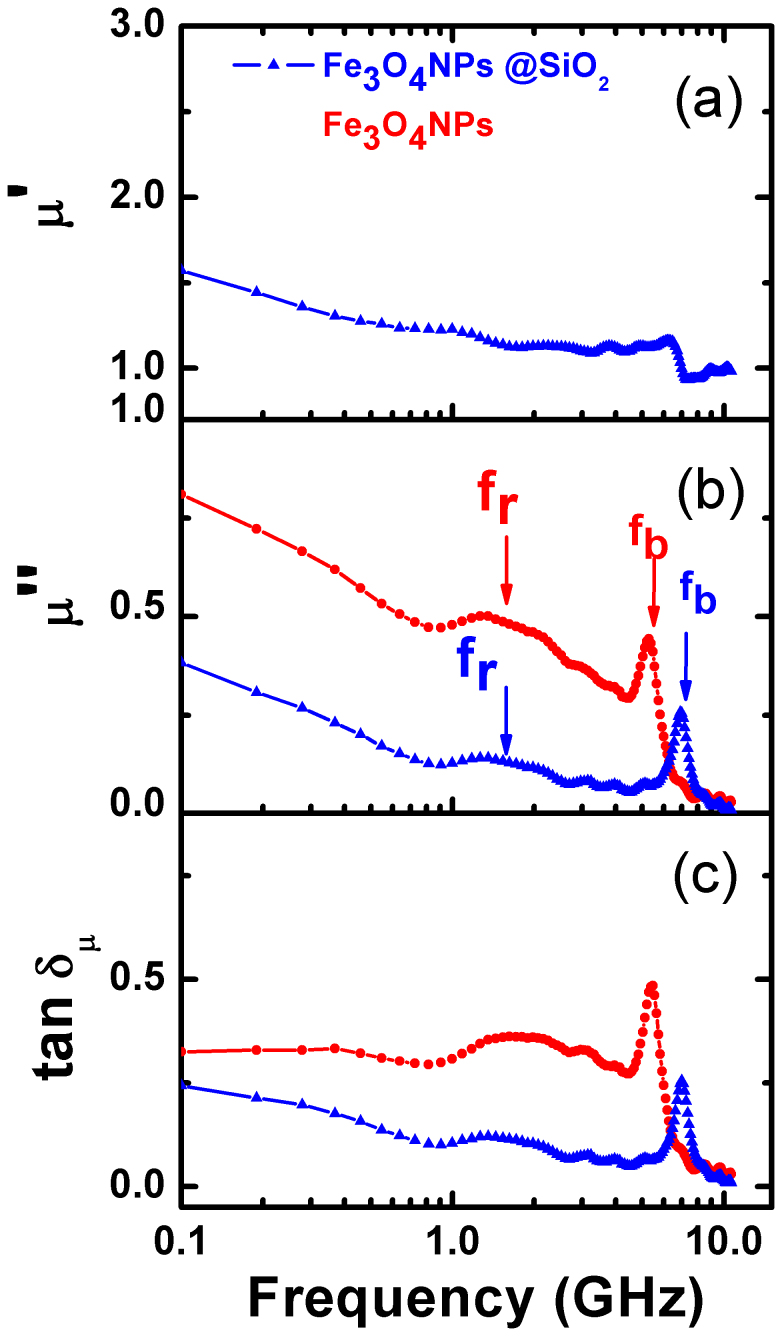
In order to confirm our expectation, the frequency dependence of relative complex permeability, μr = μ′ − jμ", is measured in the frequency range of 0.1–10.0 GHz. It reveals that the real part, μ′ exhibit a relaxation behavior and decreases with increasing from 0.1 GHz to 2.0 GHz, and keeps a constant with further increasing frequency(Fig. 4(a)). An abrupt decrease to less than 1.0 was observed at 5.3 GHz and 6.9 GHz for the as-prepared Fe3O4 nanoparticles and Fe3O4/SiO2 core-shell particles. The negative excursion in the real part of the susceptibility(χ′ = μ′ − 1) implies a resonant behavior. The resonant behavior was more evident by the two peaks in the curves of the frequency dependence of imaginary part, μ" (Fig. 4(b)).
Figure 4.
(a) Frequency dependence of real part μ′; (b) imaginary part μ" and (c) magnetic loss tangent tanδμ = μ"/μ′ of the Fe3O4/paraffin wax and Fe3O4@SiO2/paraffin wax.
According to the Kittel equation, the natural resonance frequency of a sphere-shaped magnetic particle is25
 |
where γ is the gyro-magnetic ratio. For cubic symmetric system, the magnetocrystalline anisotropy field, 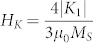 . Using the magnetocrystalline anisotropy constant K1 = −1.2 × 104 J/m3 and saturation magnetization MS = 4.6 × 105 A/m for single crystal Fe3O426, the theoretical calculation of the natural resonance frequency should be 1.5 GHz. Therefore, the first peak around at 1.3 GHz was assigned to the natural resonance frequency. The lower resonance frequency is related to the slightly smaller magnetocrystalline anisotropy for nonstoichiometric magnetite nanoparticles26.
. Using the magnetocrystalline anisotropy constant K1 = −1.2 × 104 J/m3 and saturation magnetization MS = 4.6 × 105 A/m for single crystal Fe3O426, the theoretical calculation of the natural resonance frequency should be 1.5 GHz. Therefore, the first peak around at 1.3 GHz was assigned to the natural resonance frequency. The lower resonance frequency is related to the slightly smaller magnetocrystalline anisotropy for nonstoichiometric magnetite nanoparticles26.
The second peak at 5.3 GHz and 6.9 GHz for the two samples is attributed to the superparamagnetism/ferromagnetic transition relaxation rate, fb, respectively. In addition to the relaxation behavior, a resonance behavior was also predicted and observed at a frequency in the range of 30–60 MHz in a number of ferrofluids15,16. In the case of a single particle, the results calculated by Raikher and Shliomus demonstrated that the transition between the region of the relaxation and resonance behaviors was depended on the ratio of the magnetic anisotropy energy to the thermal energy (α = KVP/kBT) and occurred for α ≈ 0.715. By using the magnetic anisotropy constant and the grain size of Fe3O4 nanoparticles, α ≈ 0.85 can be derived. Therefore, the dispersion of μr(f) for our samples has both relaxation and resonance characteristics.
The calculated magnetic phase diagram against frequency for nanoparticle assembly by Haesegawa et al. demonstrates that the transition from superparamagnetic state to no response state is strongly dependent upon the ratio of the effectively thermal field of Ht = kBT/VPμ0MS to effectively magnetic anisotropy field HK27. In the case of Ht < HK, with increasing frequency, nanoparticle assembly undergoes from superparamagnetic state into no response state through ferromagnetic state. In this case, fb can be written as27,
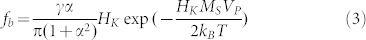 |
where α is the Gilbert damping constant.
Eq.(3) suggests that fb corresponds to a relaxation time for the Gillbert damping of the moment under HK. Hence, fb can not exceeds fr and decreases drastically with increasing the particle size.
In the case of our samples, however, 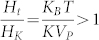 , nanoparticle assembly undergoes from superparamagnetic state to no response state directly, and fb can be written as27,
, nanoparticle assembly undergoes from superparamagnetic state to no response state directly, and fb can be written as27,
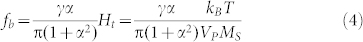 |
Eq. (4) suggests that the fb can be interpreted as a resonance frequency originating from the Gilbert damping under thermal field. Thus, fb can be increased by decreasing VP, and consequently the relaxation loss peak is higher than the natural resonance frequency of 1.3 GHz for Fe3O4 bulk material.
Since the nanoparticle sizes between Fe3O4 and Fe3O4@SiO2 core-shell nanoparticles are almost same, the enhancement of the relaxation rate in Fe3O4/SiO2 core-shell nanoparticles is resulted from the reduction of dipole-dipole interaction. In our previous work20,21, we found the blocking temperature increases with the strength of dipolar interaction. Therefore, the relaxation rate will increase by SiO2 coating, at which the dipolar interaction is weakened.
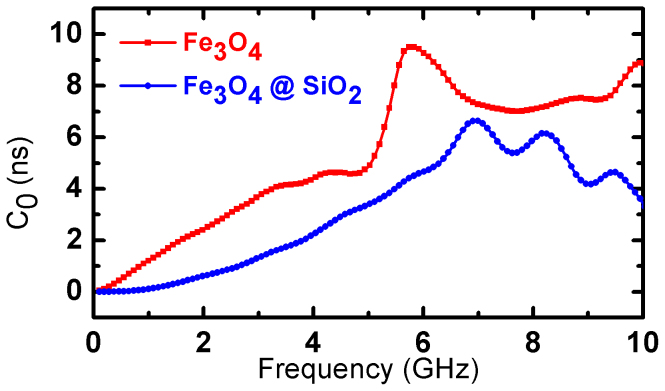
The magnetic loss tangent tanδμ varies smoothly in the frequency range from 0.1 GHz to 5 GHz, reaches a maximum value at the blocking frequency (Figure 4(c)). It was known that the microwave magnetic loss of magnetic materials originates mainly from hysteresis, domain wall resonance, eddy current effect and the natural ferromagnetic resonance. The hysteresis loss comes from irreversible magnetization and is negligible in a weak applied field. The domain wall resonance occurs only in multidomain materials and usually in the 1–100 MHz range. In this study the permeabilities were measured at a low microwave power and over a frequency range of 0.1–10.0 GHz, so neither hysteresis loss nor domain wall resonance is the main contributor to magnetic loss. The eddy current loss is related to the diameter of nanoparticles d and the electric conductivity σ, which can be expressed by μ" ≈ 2πμ0(μ′)2σd2f/3, where μ0 is the permeability of vacuum. If the magnetic loss only results from eddy current loss, the value of C0 (C0 = μ"/(μ′)2 f = 2πμ0σd2/3) should be a constant when the frequency is varied28. As shown in Fig. 5, the values markedly decrease with increasing frequency at 0.1–10.0 GHz, suggesting the magnetic loss is not related to eddy current. Therefore, it can be explained that the peak of magnetic loss at 5.3 and 6.9 GHz is caused by the blocking resonance between superparamagnetism and ferromagnetism. Moreover, the SiO2 coating also results in the reduction of magnetic loss.
Figure 5. The value of C0 (C0 = μ"/(μ′)2 f = 2πμ0σd2/3) as a function of frequency tanδμ = μ"/μ′of the Fe3O4/paraffin wax and Fe3O4@SiO2/paraffin wax.
Discussion
According to the transmission line theory, for a single layer absorber with a backed metal plate, the reflection loss (RL) curves were simulated from the electromagnetic parameters at various sample thicknesses by means of the following expressions29:
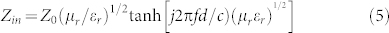 |
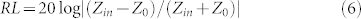 |
where f is the frequency of the electromagnetic wave, d is the thickness of the sample, c is the velocity of light, Z0 is the impedance of air, and Zin is the input impedance of the sample.
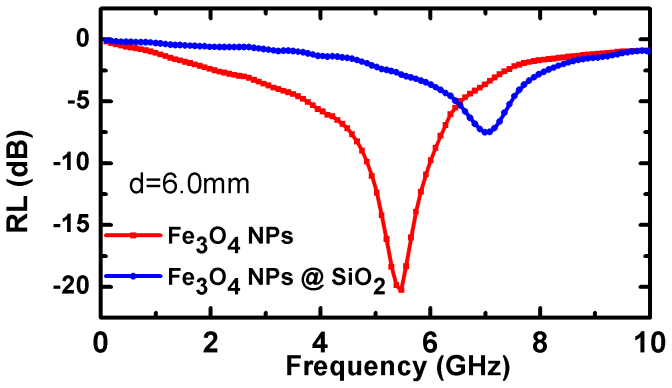
Figure 6 illustrates the frequency dependence of RL for these two samples with thickness of 6.0 mm. It was observed the magnitude of absolute value of reflection loss of 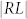 decrease from 20.3 dB for as-prepared Fe3O4 to 7.5 dB for Fe3O4 coated with SiO2 shell. In addition, a considerable reduction of RL can be obtained by SiO2-coating in whole frequency range of 0.1–10.0 GHz. The higher resonance frequency and lower magnetic loss make the Fe3O4@SiO2 core-shell nanoparticles suitable for high frequency application.
decrease from 20.3 dB for as-prepared Fe3O4 to 7.5 dB for Fe3O4 coated with SiO2 shell. In addition, a considerable reduction of RL can be obtained by SiO2-coating in whole frequency range of 0.1–10.0 GHz. The higher resonance frequency and lower magnetic loss make the Fe3O4@SiO2 core-shell nanoparticles suitable for high frequency application.
Figure 6. Frequency dependence of calculated RL for of the Fe3O4/paraffin wax and Fe3O4@SiO2/paraffin wax.
In conclusion, we have demonstrated that the high frequency properties of core-shell Fe3O4/SiO2 superparamgnetic nanoparticles can be tuned via dipolar interaction. The cut-off frequency can exceed the natural resonance frequency by superparamagnetic/ferromagnetism transition. In addition, the magnetic loss is significantly reduced via SiO2 coating. The finding of non-gyromagnetic resonance mechanism in superparamagnetic nanoparticles not only provides us a new approach to enhance the resonance frequency beyond the Snoek's limit, but also opens a new application field for superparamagnetic nanoparticles.
Methods
Monodisperse Fe3O4 nanoparticles with 9.0 ± 0.5 nm diameter were synthesized in octadecene, instead of the dioctyl ether used in a synthesis procedure reported in Refs. 30 and 31. SiO2 coating onto the Fe3O4 nanoparticles was carried out in reverse micelles by the hydrolysis of tetraethyl orthosilicate19,29. Transmission electron microscopy (TEM) was performed on HITACHI H8100 at 120 kV to determine particle shape and size distribution. X-ray diffraction (XRD) patterns were used to characterize the crystal structure of the samples using a step-scanning with 0.02° step and 5 s integration time. 57Fe Mössbauer spectra at room temperature were recorded by a Wissel system constant acceleration Mössbauer spectroscopy system with a 57Co (Rh) source. The values of CS given here are relative to the room temperature value of α-Fe. DC magnetization measurements were performed on a Superconducting Quantum Design (SQUID) magnetometer (MPMS-XL). Zero-field-cooled (ZFC) DC magnetization measurements were carried from room temperature to 10 K at a field of 100 Oe. For magnetic and dielectric spectra measurements, the Fe3O4/paraffin wax mixtures were prepared by homogenously mixing Fe3O4 and Fe3O4@SiO2 nanoparticles with paraffin wax with a mass ratio of 7:3 and then pressed into the toroidal-shaped samples of 7.00 mm outer diameter and 3.04 mm inner diameter. The scattering parameters (S11 and S21) were measured by a vector network analyzer (Agilent N5224A) using a coaxial transmission–reflection method in the frequency range of 0.1–10 GHz. The complex permeability, μr, and permittivity, εr, were determined from the scattering parameters using the Nicolson models32.
Author Contributions
Z.H.C. and H.T.Y. planned the experiments. N.N.S. prepared the samples and carried out the microwave experiments. H.L.L. performed Monte Carlo calculations; R.X., H.F.D. and X.Q.Z. contributed to the analysis and discussion for the results. Z.H.C. wrote the paper and all authors comment on it.
Acknowledgments
This work was supported by the National Basic Research Program of China (973 program, Grant Nos. 2012CB933102, 2011CB921801 and 2010CB93420) and the National Natural Sciences Foundation of China (11174351, 11034004, and 51021061).
References
- Yen T. J. et al. Terahertz magnetic response from artificial materials. Science 303, 1494–1496 (2004). [DOI] [PubMed] [Google Scholar]
- Kobljanskyj Y. et al. Nano-structured magnetic metamaterial with enhanced nonlinear properties. Sci. Rep. 2, 478 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kampfrath T. et al. Terahertz spin current pulses controlled by magnetic heterostructures. Nature Nanotech. 8, 256–260 (2013). [DOI] [PubMed] [Google Scholar]
- Harris V. G. Modern Microwave Ferrites. IEEE Trans on Magn. 48, 1075–1104 (2012). [Google Scholar]
- Wang S. X. et al. Properties of a new soft magnetic material. Nature 407, 150–151 (2000). [DOI] [PubMed] [Google Scholar]
- Greve H. et al. Nanostructure magnetic Fe-Ni-Co/Teflon multilayers for high-frequency applications in gigahertz range. Appl. Phys. Lett. 89, 242501 (2006). [Google Scholar]
- Sohn J. et al. Tunable electromagnetic noise suppressor integrated with a magnetic thin film. Appl. Phys. Lett. 89, 103501 (2006). [Google Scholar]
- Fan X. L. et al. In situ fabrication of Co90Nb10 soft magnetic thin films with adjustable resonance frequency from 1.3 to 4.9 GHz. Appl. Phys. Lett. 92, 222505 (2008). [Google Scholar]
- Chai G. Z. et al. Adjust the resonance frequency of (Co90Nb10/Ta)n multilayers from 1.4 to 6.5 GHz by controlling the thickness of Ta interlayers. Appl. Phys. Lett. 96, 012505 (2010). [Google Scholar]
- Snoek J. L. Gyromagnetic resonance in ferrites. Nature 160, 90 (1947). [DOI] [PubMed] [Google Scholar]
- Zeng H. et al. Exchange-coupled nanocomposite magnets by nanoparticle self-assembly. Nature 420, 395–398 (2002). [DOI] [PubMed] [Google Scholar]
- Nam J. M., Thaxton C. S. & Mirkin C. A. Nanoparticle-Based Bio–Bar Codes for the Ultrasensitive Detection of Proteins. Science 301, 1884–1886 (2003). [DOI] [PubMed] [Google Scholar]
- Hoffmann C. et al. Spatiotemporal control of microtubule nucleation and assembly using magnetic nanoparticles. Nature Nanotech. 8, 199–205 (2013). [DOI] [PubMed] [Google Scholar]
- Liu J. W. et al. Microwave Absorption Enhancement of Multifunctional Composite Microspheres with Spinel Fe3O4 Cores and Anatase TiO2 Shells. Small 8, 1214–1221 (2012). [DOI] [PubMed] [Google Scholar]
- Raikher Y. L. & Shliomis M. I. Dispersion theory of magnetic-susceptibility of small ferromagnetic particles. Zhrunal Eksperimentalnoi Teoreticheskoifiziki. 67, 1060–1073 (1974). [Google Scholar]
- Fannin P. C., Scaife B. K. P. & Charles S. W. Relaxation and resonance in ferrofluids. J. Magn. Magn. Mater. 122, 159–162 (1993). [Google Scholar]
- Brown W. F. Thermal fluctuations of a single-domain particle. Phys. Rev. 130, 1677–1686 (1963). [Google Scholar]
- Skumryev V. et al. Beating the superparamagnetic limit with exchange bias. Nature 423, 850–853 (2003). [DOI] [PubMed] [Google Scholar]
- Kim H. K. D. et al. Magnetoelectric control of superparamagnetism. Nano. Lett. dx.doi.org/10.1021/nl3034637 (2013). [DOI] [PubMed] [Google Scholar]
- Yang H. T. et al. Achieving a noninteracting magnetic nanoparticle system through direct control of interparticle spacing. Appl. Phys. Lett. 94, 013103 (2009). [Google Scholar]
- Yang H. T. et al. Determination of the critical interspacing for the noninteracting magnetic nanoparticle system. Appl. Phys. Lett. 98, 153112 (2011). [Google Scholar]
- García-Otero J., Porto M., Rivas J. & Bunde A. Influence of dipolar interaction on magnetic properties of ultrafine ferromagnetic particles. Phys. Rev. Lett. 84, 167 (2000) [DOI] [PubMed] [Google Scholar]
- Lima Jr E. et al. Surface effects in the magnetic properties of crystalline 3 nm ferrite nanoparticles chemically synthesized. J. Appl. Phys. 108, 103919 (2010). [Google Scholar]
- Gorski C. A. & Scherer M. M. Determination of nanoparticulate magnetite stoichiometry by Mossbauer spectroscopy, acidic dissolution, and powder X-ray diffraction: A critical review. Am. Mineral. 95, 1017–1026 (2010). [Google Scholar]
- Kittel C. On the theory of ferromagnetic resonance absorption. Phys. Rev. 73, 155–161 (1948). [Google Scholar]
- Aragon R. Cubic magnetic anisotropy of nonstoichiometric magnetite. Phys. Rev. B. 46, 5334–5338 (1992). [DOI] [PubMed] [Google Scholar]
- Hasegawa D., Yang H. T., Ogawa T. & Takahashi M. Challenge of ultra high frequency limit of permeability for magnetic nanoparticle assembly with organic polymer-Application of superparamgnetism. J Magn. Magn. Mater. 321, 746–749 (2009). [Google Scholar]
- Wu M. Z. et al. Microwave magnetic properties of Co50/(SiO2)50 nanoparticles. Appl. Phys. Lett. 80, 4404–4406 (2002). [Google Scholar]
- Davalos A. L. & Zanette A. Fundamentals of Electromagnetism (Springer Verlag, Berlin 1999). [Google Scholar]
- Sun S. & Zeng H. Size-controlled synthesis of magnetite nanoparticles. J. Am. Chem. Soc. 124, 8204–8205 (2002). [DOI] [PubMed] [Google Scholar]
- Song N. N. et al. Non-monotonic Size Change of Monodisperse Fe3O4 Nanoparticles in the Scale-up Synthesis. Nanoscale 5, 2804–2808 (2013). [DOI] [PubMed] [Google Scholar]
- Nicolson A. M. & Ross G. F. Measurement of intrinsic properties of materials by time-domain techniques. IEEE Transactions on Instrumentation and Measurement. IM19, 377–382 (1970). [Google Scholar]