Cortical Surface Registration for Image-Guided Neurosurgery Using Laser-Range Scanning

Abstract

In this paper, a method of acquiring intraoperative data using a laser range scanner (LRS) is presented within the context of model-updated image-guided surgery. Registering textured point clouds generated by the LRS to tomographic data is explored using established point-based and surface techniques as well as a novel method that incorporates geometry and intensity information via mutual information (SurfaceMI). Phantom registration studies were performed to examine accuracy and robustness for each framework. In addition, an in vivo registration is performed to demonstrate feasibility of the data acquisition system in the operating room. Results indicate that SurfaceMI performed better in many cases than point-based (PBR) and iterative closest point (ICP) methods for registration of textured point clouds. Mean target registration error (TRE) for simulated deep tissue targets in a phantom were 1.0 ± 0.2, 2.0 ± 0.3, and 1.2 ± 0.3 mm for PBR, ICP, and SurfaceMI, respectively. With regard to in vivo registration, the mean TRE of vessel contour points for each framework was 1.9 ± 1.0, 0 9 ± 0.6, and 1.3 ± 0.5 for PBR, ICP, and SurfaceMI, respectively. The methods discussed in this paper in conjunction with the quantitative data provide impetus for using LRS technology within the model-updated image-guided surgery framework.

I. Introduction

Image-guided neurosurgery (IGS) requires the accurate alignment of the preoperatively acquired diagnostic image series to a coordinate system that is specific to the intraoperative patient’s neuroanatomy, a process often referred to as registration. Once the registration has been provided, all preoperative planning and acquired data relevant to the patient’s neuroanatomy can be displayed to the neurosurgeon intraoperatively and used for assistance in guidance and treatment. This process to a large extent has become routine within medical centers across the country. Additionally, the methods of localization within image space (establishment of coordinate system within the diagnostic image series) and physical space (coordinate system relevant to patient features) have been investigated to a great extent. For example, the necessary shape and volume of synthetic image landmarks, i.e., fiducials, has been rigorously analyzed and has resulted in design constraints that optimize localization within conventional imaging modalities [1], [2]. Regarding localization in physical space, various optical, acoustic, electromagnetic, and mechanical devices have been developed to characterize the intraoperative environment for the registration process.

With respect to mathematical aspects of image-to-patient alignment, the most common approach used is a point-based registration (PBR) whereby landmarks, either natural or synthetic, are localized in the patient’s image series and aligned with corresponding landmarks digitized in physical space intraoperatively. The geometric transformation is generated based on the minimization of the squared distance error between corresponding points [3]. Further analysis on the configuration of fiducial markers, the optimum number, and the effects on target localization error have also been forthcoming [2]. Apart from the point-based approach, another common technique for registration is the use of matching geometric surfaces. The ability to acquire surface data using optical/electromagnetic/ultrasound probes and lasers [4]–[8] in conjunction with surface extraction algorithms applied to imaging data have led to new robust methods of registration [9]. Surface-based alignment techniques have two distinct advantages: 1) point correspondence is not required and 2) an averaging effect serves to reduce uncorrelated localization error generated during the acquisition of spatially well-resolved surface data. However, some disadvantages are present in that the scalp in general lacks geometric specificity, and the skin surface may deform due to intraoperative drugs or procedural retraction [10]. A third registration technique, less commonly used for IGS purposes, is the intensity-based or volume registration approach [2]. Usually applied for the alignment of image volumes, the predominant use for these techniques in IGS has been within the intraoperative magnetic resonance (iMR) environment where serial image volumes are acquired during surgery.

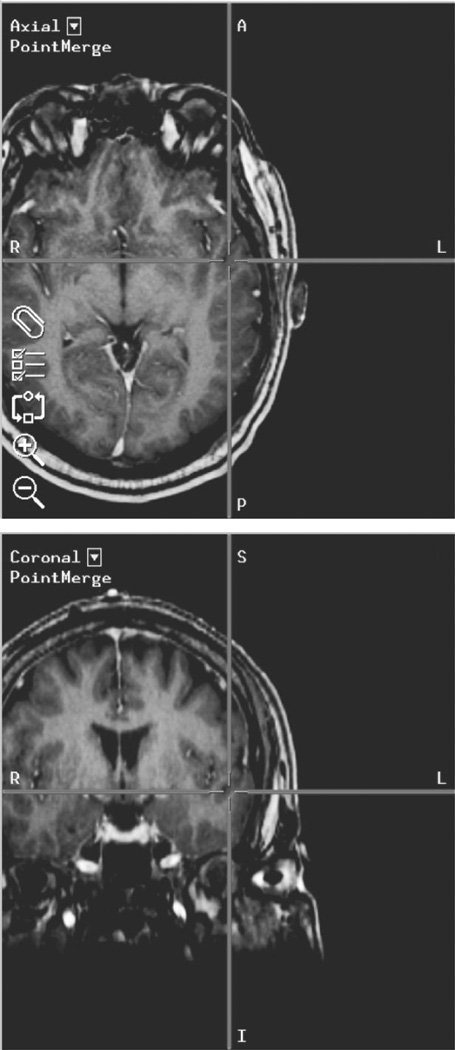
One common assumption in all of the above methods is that the skull and brain can be characterized by rigid body mechanics and, in general, many of these techniques have achieved accuracy measures that are clinically useful. However, with the growing experience in applying these enhancements in surgical navigation, design characteristics for the next generation of surgical guidance systems are slowly emerging. More specifically, one of the most challenging problems to IGS development is the realization that rigid body assumptions are in many cases inadequate. Identified as early as 1986 by Kelly et al. [11], the potential problem of “brain shift,” i.e., deformation, during surgery has given rise to concerns regarding the fidelity of current IGS systems. The earliest assessments of error from brain shift using IGS were on the order of 5 mm [12]. Subsequent investigations measuring intraoperative brain surface movements have reported an average deformation of 1 cm. An example of intraoperative brain shift experienced by our group can be seen in Fig. 1

Fig. 1.

Example of brain shift seen using an intraoperative image-guided surgery system. The crosshairs indicate the location of the surgical probe in image space, in this case inside the brain. In reality, the probe is touching the surface of the brain near the superior temporal gyrus.

Insightful relationships regarding the predisposition for brain movement in the direction of gravity have also been reported [13], [14]. In addition, with the advent and use of iMR sys systems, more detailed studies measuring both surface and subsurface shift have been performed [15], [16]. The general conclusion from these studies is that brain deformation during surgery needs to be accounted for to maximize the effectiveness of IGS systems.

The approaches to accounting for brain shift can be generally placed into two categories: 1) intraoperative imaging and 2) intraoperative nonrigid registration frameworks. Intraoperative imaging would include the use of computed tomography (iCT), magnetic resonance (iMR), and/or ultrasound (iUS) imaging. In the 1980s, there was a significant effort to introduce iCT, but concerns regarding patient radiation, the need for radiological staffing of the operating room (OR), and the cumbersome lead protection seemed to adversely affect the adoption of this technique [17]. Several medical centers are now deploying iMR imaging capabilities [18], [19] and have developed elegant and sophisticated methods for visualization in the OR [4], [20], [21]. Although conceptually appealing, the exorbitant cost and cumbersome nature of such systems (e.g., need for an MR-compatible OR) have left their widespread adoption unclear at this time. In addition to these logistical concerns, recent reports have illustrated potential problems related to surgically induced contrast enhancement which can be often confused with contrast-enhancing residual tumor [22]. Other reports have illustrated “image distortions from susceptibility and/or eddy current artifacts” related to the presence of MRI-compatible Yasargil clips for aneurysm clipping procedures [23]. Although this did not compromise this particular procedure, the question regarding the degree of distortion from other MR compatible instruments (e.g., retractors) must be studied further. It should be noted, however, that researchers have also shown significant benefits with iMR by increasing patient survival times and decreasing patient complications [24]. Appropriately, investigators are still determining the efficacy of iMR in order to identify its most important uses. An interesting alternative to iCT and iMR also under consideration is coregistered intraoperative ultrasound (iUS) [25]–[28]. Although not capable of whole-brain imaging, many advocate that the locally reconstructed volumes provided by iUS can provide real-time guidance feedback. However, the clarity of iUS images is limited and using this technique as the sole source of feedback may not be the best approach. Often the images become less valuable as the procedure continues since the contrast between tumor and normal brain begins to diminish. This is not to say that iUS does not have a role in image-guided neurosurgery, but rather that its role could be as one source of data within the mechanics of building an intraoperative updating system.

The second category of solutions to intraoperative brain shift represent a more minimally invasive approach to the OR environment whereby nonrigid registration methods would be used to register preoperative data to the intraoperative environment. This strategy as highlighted by Roberts et al. [29] uses computational models in conjunction with nonintrusive intraoperative data acquisition as a means for deforming high-resolution pre-operative-based images to reflect intrasurgical conditions. Detailed work regarding the fidelity of such computations within animal and human systems has been reported [30], [31]. One advantage of this framework is that all forms of preoperative data can be simultaneously updated (i.e., positron emission tomography, electroencephalography data, functional MR imaging, and MR spectroscopy) whereas iMR/iCT/iUS systems will still require a nonrigid registration method for the effective utilization of all preoperatively acquired data. In addition, computational techniques to nonrigidly register image data via modeling methods have a long precedent in the neurosurgical community. Elastic matching has been a technique employed by many to register multimodality images [32], [33]. Deformable templates for large deformation warping of images has also been utilized [34]. With respect to the model-updating paradigm, other investigators have also been pursuing variants of this approach [35]–[37]. Although computational models may not be able to predict the extent of tumor margins as well as iMR or iCT, it must be recognized that alternative localized imaging techniques are rapidly being developed for this task (e.g., such as optical spectroscopy [38], [39]).Within this vision of IGS, neurosurgeons will have a collection of minimally invasive tools to aid in navigation, visualization, and demarcation of diseased tissue. The work reported in this paper subscribes to this shift compensation strategy.

Rapidly acquiring minimally invasive data that describes changes in brain geometry during surgery is necessary to develop a computational approach that accounts for brain deformations. In this paper, preliminary work using a laser range scanner (LRS) is presented within the context of a new image-to-patient registration framework that is inherently sensitive to the brain shift problem. The registration method employs both geometric and intensity data acquired from the LRS to align the patient’s intraoperative cortical surface to the MR image counterpart. Since the LRS captures both geometric and color-intensity information from the intraoperative brain surface, a feature-rich source of data is provided for registration and the eventual tracking of deformation. In this work, a detailed set of phantom experiments was performed to illustrate the method. This paper concludes with a clinical example. To our knowledge, these results represent the first clinical illustration of an image-to-patient registration between an MR tomogram and a laser range scanned cortical surface. It should be noted that using features from the cortical surface to register images does have some precedent. Nakajima et al. demonstrated an average of 2.3 ± 1.3 mm fiducial registration error using cortical vessels for registration [40]. Also, some preliminary work using a scanning based system for cortical surface geometric registration has been reported but a systematic evaluation has not been performed to date [6]. In addition to LRS work, efforts by Skrinjar et al. have been reported for the use of a stereo-pair camera systems to capture and characterize the brain surface during surgery [41], [42]. The work presented here represents an initial step in developing OR-compatible equipment designed to capture brain shift systematically for the eventual use in a model-updating paradigm.

II. Methods

A. Laser Range Scanner

One critical component in developing a model-updating strategy for compensating for shift is the rapid acquisition of geometric data that describes the deforming nature of the brain during surgery. For this task, we have employed an LRS (RealScan 3D, 3D Digital Corporation, Bedford Hills, NY) that is capable of capturing three-dimensional (3-D) topography as well surface texture mapping to submillimeter accuracy [Fig. 2(a)].

Fig. 2.

The 3-D Digital RealScan USB and its use in the operating room. (a) Close up of the scanner showing the laser emit window in the middle and the CCD and laser received cameras on the right. (b) LRS in the operating room covered with sterile isolation bag and mounted on custom built vibration damping monopod (shown here in collapsed state). (c) LRS in the OR, covered in sterile bag and mounted to overhead swing arm.

The LRS is lightweight, compact, and has a standard tripod mount (L9.5" × W12.5"× H3.25", 4.5 lbs). For clinical use, the LRS has been equipped with a customized vibration-damping monopod [Fig. 2(b)], or it can be attached to a surgical arm within the operating room [Fig. 2(c)]. The scanning field consists of 512 horizontal by 500 vertical points per scan and is accomplished in approximately 5–7 s. The laser used is a Class-I “eye-safe” 6.7–mW visible laser. The laser stripe generator has an adjustable fan-out angle (maximum fan-out is 30°) and acquires each stripe at approximately 60 Hz. The scanner accuracy is 300 µm at 30 cm from the object of interest and approximately 1000 µm at 80 cm.

For the experimental and clinical data reported herein, the scanner was brought to between 30–45 cm of the target. The complete process of moving the scanner into the field of view (FOV), acquiring a scan, and exiting from the FOV takes approximately 1–1.5 min (this includes laser light adjustments and LRS fan-out angle). In general, the surgical staff has considered the impact of the LRS in the OR to be negligible. Also, the Institutional Review Board at the Vanderbilt University Medical Center, Nashville, TN, has approved the LRS for use on human patients, and patient consent was acquired for all clinical data.

B. Registration

With respect to the alignment of image space to patient space, several standard registration methodologies have been used with the addition of a novel registration strategy custom-developed for the unique data acquired by the scanner. The distinction between this last approach and the more traditional methods is that the feature-rich intraoperative brain surface as acquired by an LRS and the MR grayscale encoded brain surface derived from the image volume are used for patient registration. One advantage of cortical surface registration over rigid cranium-based techniques is that the method is inherently sensitive to brain shifts occurring in the early stages of surgery. For example, often during clinical cases involving tumor resection, the brain will swell upon opening of the cranium and dura. By registering with respect to the shifted brain surface, one could argue that a more accurate and spatially consistent registration can be achieved (even when using rigid body assumptions). In addition, the surface of the brain could be registered dynamically during surgery to account for some portion of shift or be used to track nonrigid deformations for use in a model-updating shift compensation strategy.

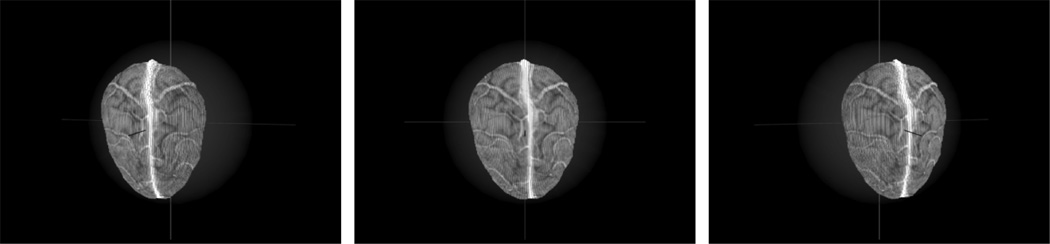
The new registration approach (SurfaceMI) begins with the segmentation of the region of interest, i.e., brain, from the MR image volume. From this segmented volume, a point cloud representation of the brain surface geometry is extracted. Using the preoperative plan, the location of the resection surface is identified on the CT/MR images and positioned orthogonal to a ray-casting source. A ray-casting algorithm combined with voxel intensity averaging (averages 3–5 voxel intensities along ray) is employed to grayscale encode the point cloud. At the conclusion of this process, the patient’s cortical image surface is rendered into a textured point cloud that contains intensity patterns representing sulcal-gyrus differences as well as contrast- enhanced vasculature (Fig. 3). These unique tissue patterns of intensity will be central to the alignment process. For the point clouds used in this paper generated via ray casting, the mean and median point-to-point distances were 0.7 and 0.6 mm, respectively. With respect to the intraoperative acquisition of data, a calibration object is routinely scanned prior to registration to ensure operational fidelity of the laser scanner. At select times during the surgery, after durotomy, the LRS is positioned over the exposed brain surface and a range scan is acquired. Triangulating between the laser light source and the captured laser light pattern on a charge-coupled device (CCD) digital camera, the 3-D location of each illuminated point can be determined. In addition, each 3-D point is color encoded by a second digital camera on the scanner that captures an image of the surgical field of view. The mean and median point-to-point distances for the range-scan point clouds used in this paper were 0.65 and 0.6 mm, respectively.

Fig. 3.

Three views of the surface extracted from a patient-specific gadolinium enhanced MR volume.

The intensity and geometric data acquired by the laser scanner coupled with the image processing of the segmented brain surface provides a novel avenue for developing a new registration framework. The process begins with an initial guess based on aligning natural fiducials using a traditional point-based framework. Following this process, an iterative closest point (ICP) algorithm is used to further align the LRS point cloud to the CT/MR counterpart. The disparity function d used within this minimization algorithm is

$$d=\frac{1}{N}\sum _j^N{\Vert y_j-T(x_j)\Vert }_2$$ (1)

where T(x_j) represents a rigid transformation of N points on the source surface to corresponding points on the target surface, y_j. Given that one-to-one point correspondence does not exist with surface-based registrations, correspondence is established by pairing points according to a closest distance metric. Following the determination of correspondence, a point-based registration can be executed and subsequently followed by an update to the closest point operator. This sequence of steps proceeds iteratively until the disparity function shown in (1) satisfies a specified tolerance. Although excellent at aligning geometrically unique surfaces, ICP in general may have difficulty with the intraoperative environment if relied upon solely. In our experience, not all regions of the brain surface express a unique geometry with respect to visible sulcal/fissure features of the intraoperatively exposed brain. Pathology, such as a tumor, can also influence the initial shape of the brain surface dramatically. In addition, the fidelity of image segmentation can also become a potential source of misalignment. There is some research that addresses these problems and relates to our work. Specifically, the work of Feldmar et al. [43] and Johnson et al. [44] attempt to register using both geometry and intensity, by adding intensity differences to the disparity function in (1). These methods, although effective, are not applicable to our LRS/MR data due to the contrasting colormaps of the two point clouds. Thus, we employ an optimization of normalized mutual information, as reported by Studholme et al. [45] between the two textured point clouds. Normalized mutual information is written here as

$$\mathrm{N}\mathrm{M}\mathrm{I}(x,y)=\frac{H(x)+H(y)}{H(x,y)}$$ (2)

where H(x) and H(x,y) are the marginal and joint entropies of the point clouds, respectively. Although extensively used within image-to-image alignment [46]–[48], there are no readily apparent means for calculating mutual information in this context. The difficulty arises in determining correspondence among point cloud intensity distributions. For this initial work, the closest point metric determined from the initial geometric registration is used to determine proper intensity correspondence among source and target surfaces. To further constrain the approach, a spherical geometry was fitted to the target surface and was used to reduce the registration degrees of freedom from six to three angular references in spherical coordinates about the fitted center and radius. The method of optimization employed for the mutual information-based registration was Powell’s iterative method [49]. Results regarding the implementation of SurfaceMI on intramodal and simulated intermodal phantom data are presented in [50].

In addition to this new registration approach, more traditional methods of cortical surface registration were performed for the purposes of comparison and feasibility. The second method used for registration was based on the approach by Nakajima et al. where cortical features such as vessel bifurcations were localized in both MR and scanner image space and a rigid PBR was performed between the two. A third registration framework based on iterative closest point transforms (ICP) was used where the registration targets became vessel and sulcal contours visible on the MR and laser-scanned cortical surface. This suite of registration approaches provides multiple avenues to pursue for determining an optimal cortical surface alignment under varying surgical conditions.

C. Experimental Setup

A set of experiments using a watermelon phantom was utilized to test the algorithm’s ability to register intermodality surfaces. In this experiment, Omnipaque (Amersham Health plc.) soaked twine was laid into the watermelon surface to simulate the appearance of contrast-enhanced vasculature on the brain surface [Fig. 4(a)] in CT.

Fig. 4.

The watermelon phantom used in this paper for registration accuracy experiments. (a) Watermelon with Omnipaque soaked twine laid into carved vessel grooves. (b) Acustar imaging marker filled with CT/MR contrast enhancement fluid. (c) Acustar divot caps for localization using Optotrak.

In addition, CT/MR visible rigid markers (Acustar^®, Z-Kat, inc.) were also implanted into the watermelon surface for use as an alternate digitization technology [Fig. 4(b)]. The phantom was imaged in the CT imager (Mx8000, Philips Medical Systems), scanned by the laser scanner and digitized by a Northern Digital Optotrak^® 3020 (rms accuracy of 0.1 mm)¹ [Fig. 4(c)].

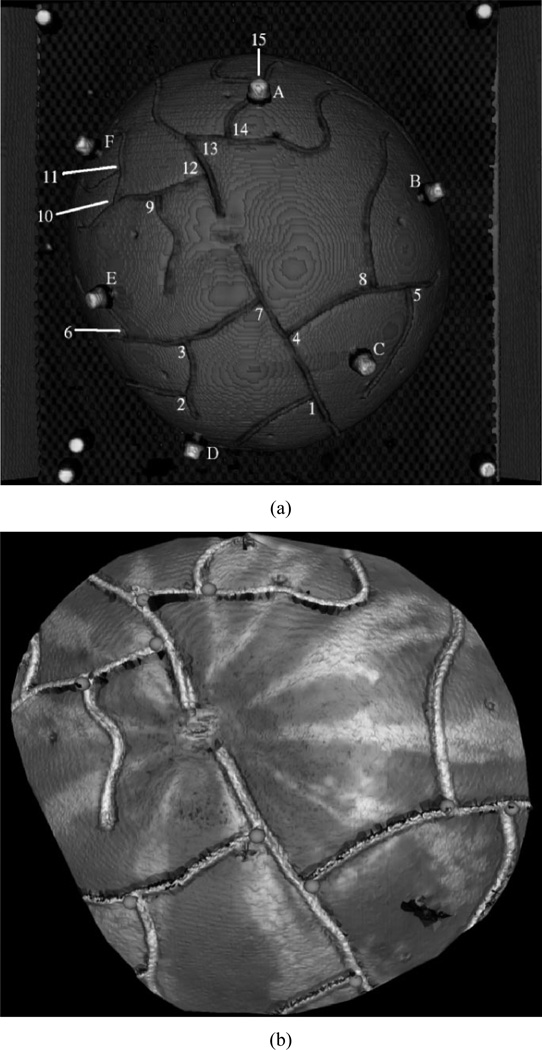
Several registrations were performed and fiducial registration and target localization errors were reported. The first registration aligned the image space coordinate system, img, to the Optotrak coordinate system, opto, using the Acustar markers in each modality, i.e., find T_img→opto. Fiducial registration errors (FRE) and target registration errors (TRE), as defined by Mandava and Fitzpatrick [51], [52], were calculated for this registration to provide the optimal registration for physical space to image space. Fig. 5(a) shows the location of the six fiducial markers (letters) and 15 manually identified points (numbers).

Fig. 5.

Localized points in img, opto, and lrs. (a) Volume rendering of image data showing markers (letters) and manually localized landmarks (numbers) in opto and img. (b) Landmarks localized in lrs space.

Having established this registration optimum, corresponding sets of manually identified points at vessel bifurcations in img and opto were registered to provide quantitative validation of Nakajima’s method of using cortical features for registering physical space to image space. Additionally, ten visible bifurcation points in LRS space, lrs, corresponding to those in img and opto, were localized [Fig. 5(b)] and used for PBR registration as a verification of Nakajima’s method applied to the LRS data. FRE was calculated and reported for all registrations (i.e.,T_img→opto, T_{img→ lrs}, and T_opto→lrs). The manually identified points in each space were localized three times and averaged to minimize localization error.

The other candidates for intraoperative registration were also examined within the context of phantom experiments. ICP registrations were performed using phantom vessel contours extracted (using simple thresholding) from the LRS and CT data. In addition, the segmented surface was aligned using the SurfaceMI framework. For each registration, a reduced region of the watermelon LRS surface was extracted to simulate the approximate size of the surgical FOV. For both registration methods (ICP and SurfaceMI), initial alignment of the surfaces was provided by using three manually localized targets visible in the segmented surface. TRE was calculated in both registration frameworks using seven novel surface targets (i.e., those landmarks that were not in the surgical FOV) and was compared to the TRE provided by the PBR alignment of vessel landmarks.

Robustness studies for the registration frameworks were carried out by perturbing initial landmarks uniformly along the surface of a sphere fitted to the target point cloud, i.e., perturbing the landmarks in spherical coordinates ϕ, θ, and ψ at the fitted radius r. The perturbations were independently and uniformly sampled from –2.5° to 2.5° (simulates approximately 1-cm fiducial localization error, i.e., perturbation arc length rΘ = 9.29 mm) in each spherical axis for each trial, and each framework was subject to 500 perturbation trials. The results of this experiment provide insight as to the efficacy of the registration frameworks given suboptimal initial conditions.

Accuracy of the registration frameworks with regard to deep tissue targets was also investigated. For this experiment, deep tissue targets were sampled within a 5-cm radius of the centroid of the manually localized surface points. The sampling was constrained to only deep tissue targets, i.e., sample points which lie within both the sphere and melon (Fig. 6). “True” positions of the deep tissue targets were found in LRS space by transforming targets from image space using the rigid-body transformation T_img→lrs (based on identifying vessel points in both modalities). These same tissue targets within image space were also registered to LRS using transformations based on SurfaceMI which when compared served as an estimate of TRE.

Fig. 6.

Simulated deep tissue sampling. The larger sphere demonstrates the geometric sphere fit of the point cloud. The smaller sphere represents a sampling region with radius of 50 mm, centered about the centroid of the localized fiducials. The volume of overlap demonstrates the deep tissue sampling region.

D. Clinical Setup

In addition to phantom experiments, a preliminary clinical example has been achieved. The patient was a 37-year-old man with a six-week history of focal motor seizures. MR imaging revealed a hypointense nonenhancing mass in the posterior, superior left frontal lobe, abutting the motor strip. He underwent awake resection, with motor and speech mapping. Intraoperatively, he was placed in the supine position, with the vertex of the head elevated 15° and the head turned 30° to the right. A fronto-temporal-parietal craniotomy was performed and the tumor was localized using ultrasound and frameless stereotaxy. The vein of Trolard coursed superiorly to the superior sagittal sinus, immediately behind the posterior extent of the tumor and directly in front of the motor gyrus. After mapping of the speech and motor regions of the face and arm, gross total resection of the tumor was accomplished. The patient tolerated the procedure without neurological sequelae. Intraoperatively, following durotomy, the scanner was moved into position via the customized monopod [Fig. 2(b)] above the craniotomy site at approximately 30–45 cm from the brain’s surface. The scanner was activated and acquired approximately 20 000 points in 5–7 s. Following retrieval of the scanner data, registration between the patient’s intraoperative data and the MR tomogram were performed retrospectively. Fig. 7 shows the surgical FOV as well as the textured range scan of the FOV acquired during surgery.

Fig. 7.

Intraoperative FOV. (a) Digital photograph with the surgeon highlighting the vein of Trolard, a significant vessel in the area of therapy. (b) Textured point cloud generated intraoperatively using our LRS.

III. Results

The registration results achieved with implantable markers were comparable to previously published data [1]. Using the Acustar marker system, a mean FRE of 0.3 ± 0.1 mm was attained using six markers. The mean TRE for this registration was 1.7 ± 0.3 mm using 15 target landmarks. These results demonstrate the accuracy associated with implantable fiducial markers and provide a baseline for comparison with subsequent registrations.

The registration results for studies concerned with the alignment of the cortical surface using vessel-based landmarks show excellent correlation with the previously published studies of Nakajima et al. [40]. FRE using ten manually localized landmarks in all three spaces (i.e., opto, img, and lrs) were 1.3 ± 0.5 mm and 1.7±0.6 mm for T_img→optoand T_img→lrs, respectively. In addition, a second PBR was calculated using a subset of the vessel markers within a focal cortical region (to simulate vessel fiducials within a craniotomy). The remaining vessel bifurcations outside the simulated surgical FOV were used as targets. The TRE is reported in Table I.

TABLE I.

TRE for the Three Registration Protocols in Melon Experiment: PBR, ICP, and SurfaceMI, on an LRS Surface That Approximates a Surgical FOV. Three Landmarks Were Used as Fiducials and Seven Targets Were Used to Calculate TRE

Registration Method	Mean TRE (mm)
PBR	2.6 ± 0.7
ICP	2.4 ± 0.8
SurfaceMI	2.5 ± 0.7

As an aside, a measure of localization precision was calculated since each set of landmarks (i.e., in img, opto, and lrs) was identified three times. Precision was measured as the mean standard deviation for each measurement (x, y, z) in corresponding landmarks across the three trials. For the landmarks selected in img, the mean standard deviations in x, y, and z were 0.27, 0.28, and 0.31 mm, respectively. In opto, the mean standard deviation in x, y, and z are 0.35, 0.22, and 0.13 mm, respectively. For the ten landmarks chosen in lrs, the mean standard deviations in x, y, and z were 0.71, 0.58, and 1.14 mm.

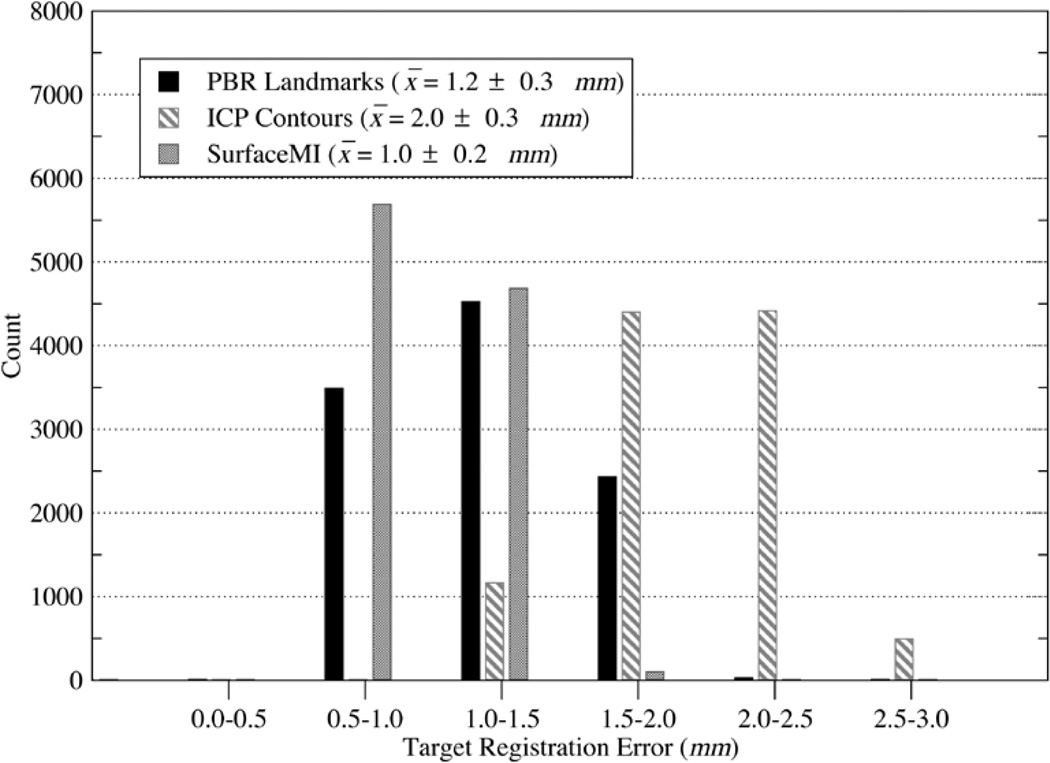
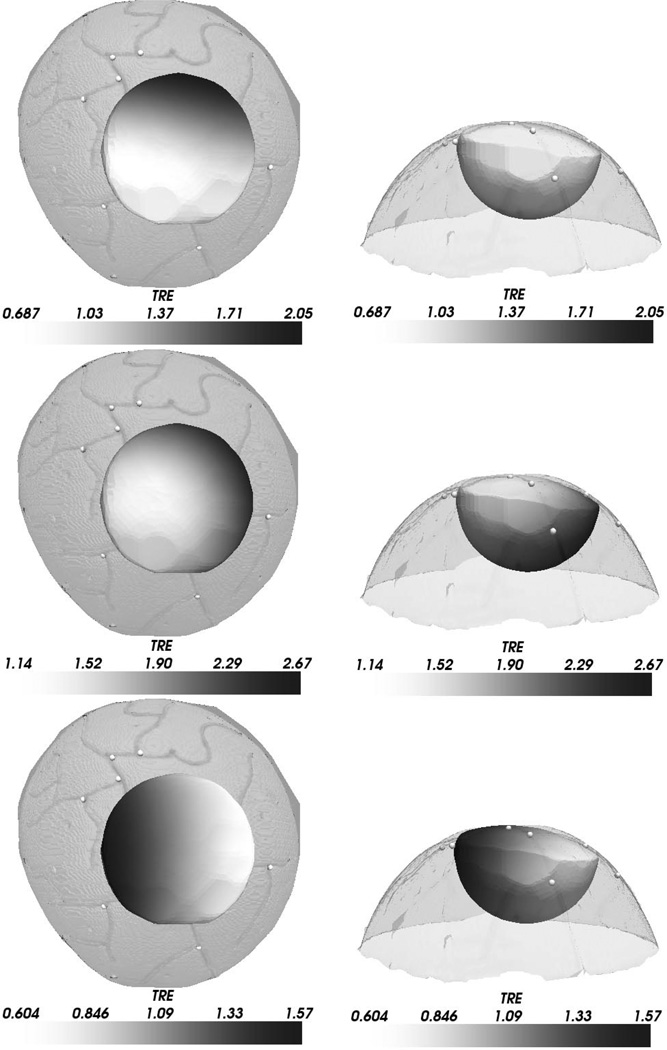
In addition to FRE studies, the histogram and mean TRE for simulated deep tissue targets is provided in Fig. 8 with a spatial distribution of TRE overlaying the melon image volume shown in Fig. 9. The results suggest that SurfaceMI may predict deep tissue targets more accurately then the PBR and ICP registration methods. Also, the 3-D distribution of TRE demonstrates that SurfaceMI predicts deeper targets more accurately than either PBR or ICP for this registration case.

Fig. 8.

TRE histogram for deep tissue targets using PBR-based registration on surface landmarks, ICP-based registration on surface contours, and SurfaceMI on textured surfaces.

Fig. 9.

Three-dimensional distribution of TRE for deep tissue targets. The left column shows a top-down view of the watermelon surface with the TRE distribution shown for PBR (top), ICP (middle), and SurfaceMI (bottom). The right column shows the respective front views of the TRE distribution. Each deep tissue sample of TRE is grayscale encoded on the hemispheric surface shown. The range of scalar values is shown in the color bar associated with each figure.

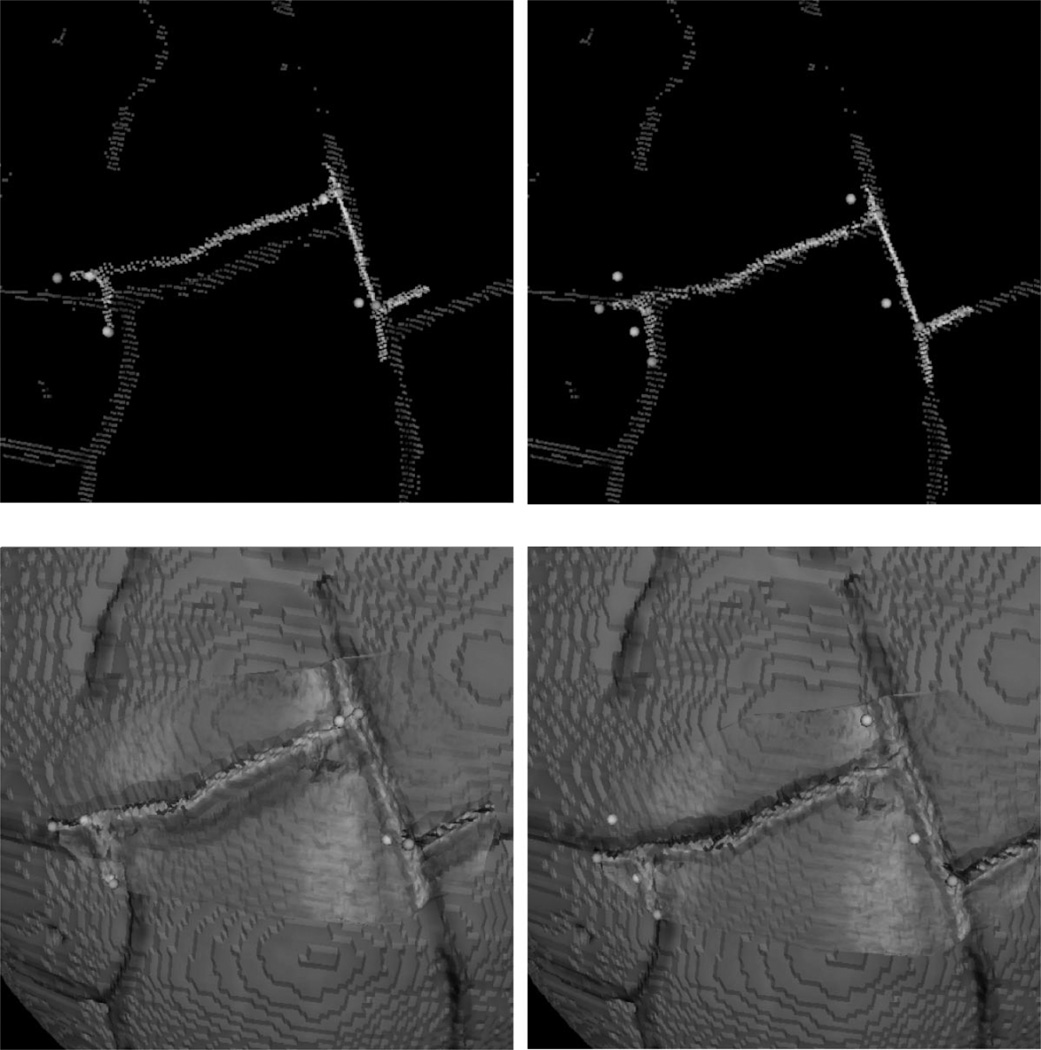
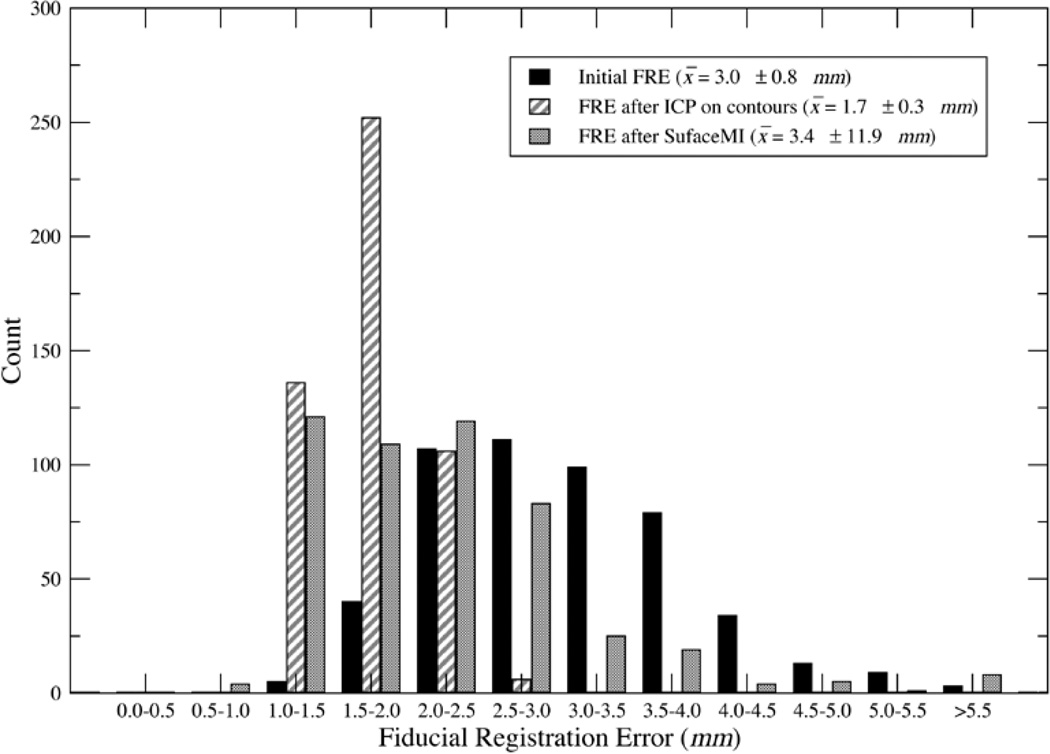
In addition to reporting registration results based on a routine application of each alignment framework, a series of robustness studies was performed to investigate the effects of varied initial guesses (i.e., approximate 1–6-mm fiducial localization error with individual fiducial error as large as 9.3 mm). Examples of the registration provided by ICP and SurfaceMI with a given initial landmark perturbation are shown in Fig. 10. FRE results from these perturbation studies for PBR, ICP, and SurfaceMI on the same cortical subregion used for the TRE studies of Table I are given in Fig. 11 over 500 trials. The distribution of fiducial registration error ranged from 1.0 to 5.8 mm for the three landmarks used in initialization of the ICP and SurfaceMI registrations. ICP on the surface contours performed well and reduced FRE by approximately 43%. SurfaceMI also performed well, but produced some outliers. Using the extreme studentized deviate (ESD) [53], eight outliers were detected with >99.95% confidence. Removing these outliers from the SurfaceMI trials produced a mean FRE of 2.2 ± 0.8 mm, reducing FRE by approximately 27%.

Fig. 10.

Results of ICP and SurfaceMI on intermodality registration of two textured surfaces. ICP registration conditions are shown in the top row with perturbed initial condition shown left and ICP registered shown right. SurfaceMI registration conditions are shown in the bottom row with perturbed initial condition shown left and SurfaceMI registered shown right. It should be noted that there is a texture projected on the surface of the watermelon that is an artifact of the rendering process, i.e., this texture did not affect the registration process. A gross-scale representation of the texture, which is a result of the slice-to-slice spacing in the CT image, can be seen in Fig. 5(a) for comparison.

Fig. 11.

Fiducial registration error distribution given initial landmark perturbation. The landmarks in the FOV were perturbed up to ±2.5° in each spherical coordinate (ϕ, ψ, θ) in img.

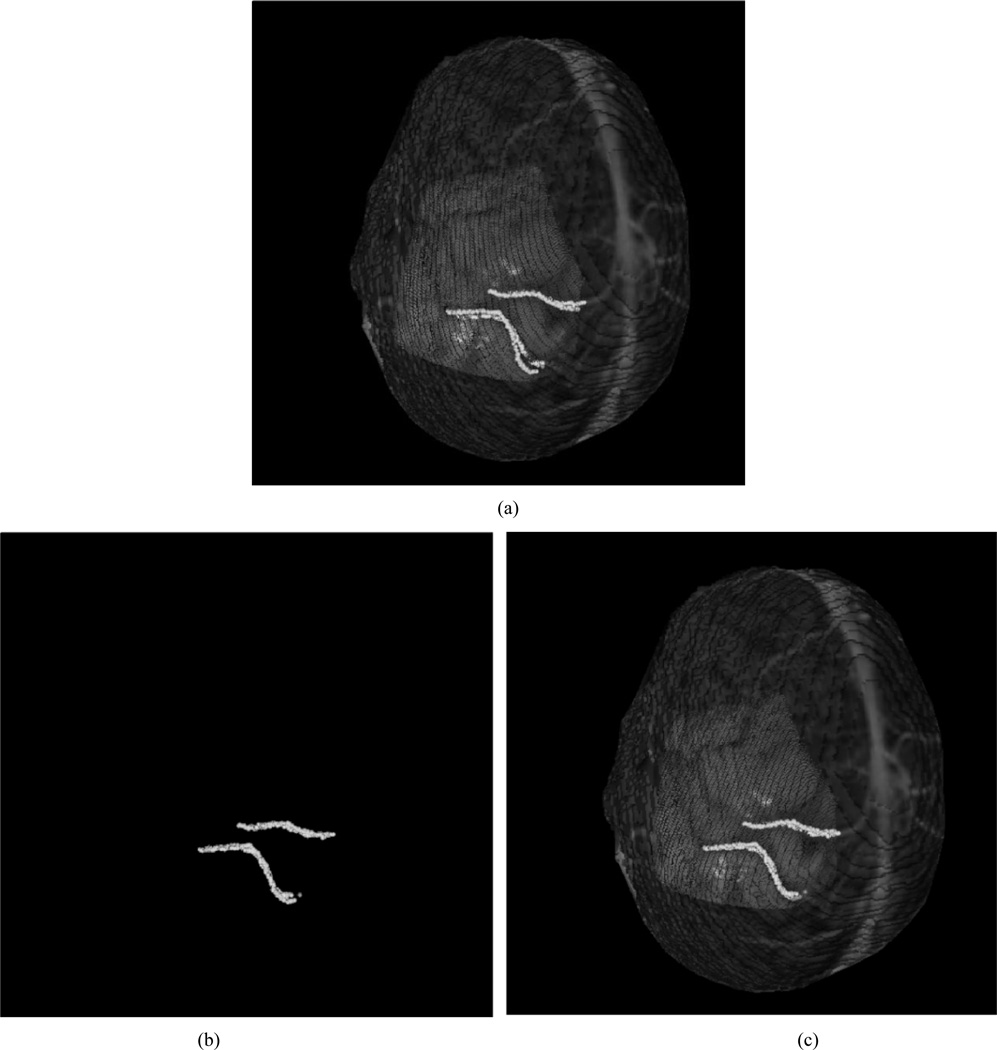
Central to using the LRS within the clinic is to demonstrate in vivo registration results. A clinical example is shown in Fig. 12 with corresponding measures of registration error reported in Table II. The first column in Table II represents the mean registration error associated with the cortical surface points used in PBR. The second column in Table II represents the mean closest point residual between contours. Although PBR performs better with respect to fiducial error, the results in Fig. 12 suggest that the registration error reported for the contour points may be the better metric as to the quality of alignment.

Fig. 12.

Registration results from intraoperative data. (a) The result of PBR-based registration using manually localized landmarks in img and lrs. (b) ICP registration using highlighted contours in img and lrs. (c) SurfaceMI registration given the initial alignment provided by the PBR method. The highlighted contours are prominent sulcal and vessel patterns visible in both spaces.

TABLE II.

Registration Errors For In Vivo Alignment Using PBR, ICP, And Surfacemi Frameworks

Registration Type	Mean Error Measure(mm) Fiducial Points (n = 3)	Mean Error Measure(mm) Contour Points (n = 468)
PBR	2.4 ± 1.0	1.9 ± 1.0
ICP	3.4 ± 1.4	0.9 ± 0.6
SurfaceMI	3.5 ± 1.7	1.3 ± 0.5

IV. Discussion

Several methods to register images to the exposed intraoperative cortical surface have been utilized within the context of phantom and clinical experiments. The methods include traditional approaches (PBR and ICP) and highlight the development of a novel technique that takes advantage of unique data provided by an LRS. More specifically, the LRS captures the geometric complexity of the brain surface and maps the feature-rich texture as acquired by a color CCD to this geometric data. The new approach presented (called SurfaceMI) uses both forms of data to align the LRS-acquired surface to its image counterpart.

Initial studies using rigid markers were performed to provide a baseline registration accuracy with respect to unknown errors associated with the phantom and/or imaging method; results reflected comparable accuracies reported in the literature [1]. The next set of studies used vessel bifurcations localized in all modalities as the basis for registration. Reassuringly, the FRE between img and opto using the manually localized vessel bifurcations were comparable to values reported by Nakajima et al. Similar values were also determined when registering vessel bifurcations using LRS data within the context of PBR, ICP, and SurfaceMI. This would indicate that using techniques similar to Nakajima et al. should be achievable using LRS data. In addition to reporting error within the simulated craniotomy region, targets outside the focal region were also used to assess alignment quality. Overall, the difference between results among all three methods was negligible. The increased magnitude of TRE over FRE agrees with an accepted understanding regarding the effects of fiducial placement on target registration error; that is, even with a low FRE, a sparse number of fiducials localized within a concentrated area can precipitate a “lever-arm” effect in areas remote to the registration region. Interestingly, a different result is seen with respect to targets in close proximity to the subregion of interest on the melon surface. Fig. 8 reports the distribution of TRE data compared among all three registration approaches. With respect to the mean TRE error for the entire region, SurfaceMI performed the best with an average TRE of 1.0 mm. When comparing deep tissue results between the PBR and SurfaceMI methods (see Fig. 9), PBR has a greater range of TRE error than SurfaceMI, which may be due to the difficulty in localizing bifurcations upon the LRS data for PBR methods. The ICP registration performed considerably worse, and this may be due to the contour thresholding process. More specifically, any spatial noise contained within the thresholded vessel structure is not averaged out as well within the ICP framework when compared to using a denser point cloud. This possible source of error would not be present within the SurfaceMI approach since the dense geometric data are maintained and the fine adjustments to alignment are provided by an intensity-based registration. SurfaceMI and PBR produced comparable results although the TRE spatial distribution for deep tissue targets was greater for the PBR method. This may suggest that the effects of a combined surface and intensity approach produce a lower error due to the averaging effects associated with the registration metrics used in SurfaceMI. When comparing SurfaceMI to ICP, the results suggest that vessel contours alone may not be the best approach to cortical surface registration, but rather, the addition of the intensity data provides significant refinement to the alignment.

The results from the perturbation studies highlight that ICP is more robust with respect to poor initial alignment guesses (i.e., fiducial localization errors up to 9.3 mm). Fig. 11 demonstrates that ICP maintains a better FRE on average with tighter standard deviation. SurfaceMI was not as robust and produced eight outliers over 500 trials. In results not presented here, the function space has been characterized and has been shown to be populated with local extrema. More specifically, the areas of local extrema are found near the global extrema and result in frustrating numerical optimization methods. It should be noted, however, that these outliers represent a less than 2% failure rate. Furthermore, if the outliers are eliminated from the trial set, the FRE is sharply reduced from mean error of 3.4–2.2 mm. It is clear that investigation into a more sophisticated optimization strategy is needed and/or extending the registration to a multiresolution approach might be helpful [54]–[56].

The results from the clinical experiment demonstrate the feasibility of cortical surface registration within the OR environment as well as provide a limited quantitative assessment to the approach’s accuracy. Table II demonstrates that a PBR approach similar to Nakajima et al. (except using LRS data in lieu of optical digitization) produces a mean registration error for vessel fiducials that is 1-mm less on average than that provided by ICP or SurfaceMI. However, in the region of the contours, the method did not fare as well. Fig. 12 demonstrates a qualitatively better alignment in the area of the contours when using either ICP or SurfaceMI. Table II also quantifies this improved closest point residual for ICP and SurfaceMI over the PBR method. One likely reason for this discrepancy is that brain deformation may have occurred upon opening the cranium and may be distributed nonuniformly over the brain surface. This would be consistent with the results in Table II since the PBR method relies on the selection of the vessel fiducials as the basis for registration while ICP and SurfaceMI only use these for initialization. Hence, if the brain surface is nonuniformly deformed, it would logically follow that methods which base their registration on the vessel fiducials (PBR) would be better within the fiducial region, while methods that use contour information (SurfaceMI and ICP) would be better within the contour region.

The clinical results also demonstrate that the registration protocol used within this work may be a viable approach for surgeries where minimal brain shift is encountered. In addition, the visual results shown in Fig. 12 may provide new anatomical cues to surgeons by correlating the FOV observed in the OR to the MR tomogram volume studied prior to surgery for preoperative planning. Furthermore, although not developed within this work, deformable registration coupled with serial range scans may allow for the detailed tracking of brain shift during surgery. We are currently exploring methods to allow deformable registration of intermodal textured surfaces for the measurement and characterization of brain shift.

Another important aspect of the SurfaceMI results presented in this paper is its ability to perform multimodal registration. Within the phantom and clinical experiments, SurfaceMI represents a multimodal registration between CT data and CCD color texture, and MR data and CCD color texture, respectively. This result is quite remarkable and adds impetus for the use of laser-range scanning within the neurosurgical OR environment.

V. Conclusion

In this paper, a unique intraoperative approach to registering patient images to the patient’s cortical surface during brain surgery has been presented. The multiregistration platform under development is capable of aligning the brain surface to its intraoperative counterpart using traditional as well as novel alignment methods within the context of LRS data. To our knowledge, this paper represents the first quantitative evaluation of laser-range scanning used within the context of intraoperative cortical surface registration. Phantom experiments are presented that compare traditional point-based (Procrustes alignment) and surface-based (ICP) registration methods to a novel registration approach which uses a combined geometric and intensity-based metric (SurfaceMI). The registration approach is a 3-D surface alignment technique that begins with an ICP-based initialization followed by a constrained mutual information-based refinement. The algorithm has demonstrated better accuracy with respect to deep tissue targets within the simulated craniotomy region. However, some limitations did appear within the robustness studies whereby a 2% failure rate occurred during phantom registration experiments. In results not presented here, the objective function space with the melon has been characterized and indicates that the multiextrema exist and can confound the current method of optimization. Alternative optimization and multiresolution methods need to be investigated further to decrease this failure rate. The SurfaceMI algorithm was capable of multimodal registration in both phantom and clinical data. The data presented from the clinical case demonstrates the approach’s feasibility within the OR as well as semi-quantitative estimates of registration accuracy.

The methods discussed in this paper in conjunction with the quantitative results provide substantial motivation for using LRS technology within the neurosurgical operating theater. More specifically, LRS methods provide rapid detailed characterization of the cortical surface during surgery and can be used as a tool for registration and the eventual measurement of deformation. This versatility will make LRS technology advantageous in pursuing model-updating strategies [29] for the compensation of brain shift during image-guided neurosurgery.