An atlas-based method to compensate for brain shift: Preliminary results

Abstract

Compensating for intraoperative brain shift using computational models has shown promising results. Since computational time is an important factor during neurosurgery, a priori knowledge of the possible sources of deformation can increase the accuracy of model-updated image-guided systems. In this paper, a strategy to compensate for distributed loading conditions in the brain such as brain sag, volume changes due to drug reactions, and brain swelling due to edema is presented. An atlas of model deformations based on these complex loading conditions is computed preoperatively and used with a constrained linear inverse model to predict the intraoperative distributed brain shift. This relatively simple inverse finite-element approach is investigated within the context of a series of phantom experiments, two in vivo cases, and a simulation study. Preliminary results indicate that the approach recaptured on average 93% of surface shift for the simulation, phantom, and in vivo experiments. With respect to subsurface shift, comparisons were only made with simulation and phantom experiments and demonstrated an ability to recapture 85% of the shift. This translates to a remaining surface and subsurface shift error of 0.7 ± 0.3 mm, and 1.0 ± 0.4 mm, respectively, for deformations on the order of 1 cm.

1. Introduction

Ever since its advent, medical imaging has played a significant role in surgical planning and treatment because it provides valuable information about anatomical structures and function. This has been particularly helpful for neurosurgical procedures where often the surgeon has to remove a tumor without damaging the healthy brain tissue surrounding it. In order to take advantage of image guidance during a neurosurgical procedure (also known as image-guided neurosurgery, IGNS), preoperative tomograms of the patient must be registered to the patient’s anatomy in physical space. While image-to-patient rigid alignment is relatively straight-forward, clinical studies in IGNS have exposed limitations to this approach. Systematic studies have reported that the brain is capable of deforming during surgery for a variety of reasons, including pharmacologic responses, gravity, edema, surgical manipulation and respiration (Roberts et al., 1998; Nimsky et al., 2001; Nabavi et al., 2001) and that the brain can shift a centimeter or more in a non-rigid fashion (Hartkens et al., 2003).

To correct for deformations, various imaging techniques such as computed tomography (CT) (Butler et al., 1998), magnetic resonance imaging (MRI) (Nabavi et al., 2001), and ultrasound (US) (Letteboer et al., 2005) have been investigated for intraoperative image-guided surgery. CT procedures have been questioned for their dose exposure, while MR procedures are considered cumbersome and have been questioned for their cost-effectiveness. Current US systems suffer from low soft-tissue contrast and lack image clarity as compared to CT and MR imaging methods. Therefore, in their current state intraoperative imaging systems do not present a complete solution for guidance correction of the brain shift phenomenon.

As a cost-effective and efficient method, computational modeling is a procedure that can translate complex surgical events into accurate estimates of tissue response and thereby compensate for intraoperative brain shift. In model-updated image-guided neurosurgery (MUIGNS), a biomechanical model of brain shift is driven with sparse data¹ to accurately deform preoperative images to their current intra-operative position. Several groups have investigated the potential value of physical/biomechanical models underpinned by various biomechanical concepts (Miga, 1998; Wittek et al., 2005; Miller, 1999; Skrinjar et al., 2002; Edwards et al., 1998; Hagemann et al., 1999; Ferrant et al., 2001). Towards this end, Paulsen et al. (1999) reported a 3-D biomechanical model governed by consolidation mechanics. Additional development of the equations and their solutions can be found elsewhere (Paulsen et al., 1999; Miga, 1998). In this work, a patient-specific mesh is created and case-specific boundary data such as tumor resection and/or tissue retraction is imposed to generate updates of the preoperative images over the entire course of surgery. Despite previous success with the model approach (Miga et al., 1999; Platenik et al., 2002; Miga et al., 1998, 2000, 2001), there are several remaining challenges discussed below that need addressing in order to attain the goal of MUIGNS.

One of the greatest challenges presented by MUIGNS is that the computational time associated with the model does not meet the real-time constraints of neurosurgery. For a 23,000 node, 123,500 element mesh with four degrees of freedom (DOF) at each node on a single central processing unit (CPU) Silicon Graphics Indigo workstation, Miga et al. (2001) reported a run time of 8.5 min to simulate gravity-induced deformations, 6.5 min to simulate retraction, 5.5 min to simulate excision and 6.0 min to simulate unretraction for the first time step, and 5.75–7.0 min for every subsequent time step. These run times can be significantly improved with use of parallel processing and more powerful computers, as demonstrated by Warfield et al. (2002). Using a Sun Microsystems Sun Fire 6800 with 12 750 MHz UltraSPARC-III CPUs, for a 43,584 nodes, 214,035 element mesh with three DOF at each node, Warfield et al. reported a run time of 15 s. These performance improvements are encouraging and will only add to the impetus to bring complex models to the operating room.

Another critical component of MUIGNS is the accurate translation of boundary conditions during the course of surgery. For example, the amount of cerebrospinal fluid (CSF) loss during surgery and the head orientation of the patient in the operating room (OR) may be two important factors in determining the degree of shift from gravitational forces (Miga et al., 1999). Although the preoperative surgical plan can provide an estimate of the patient’s orientation a priori, estimates for the degree of change in buoyancy forces acting on the brain are somewhat more elusive. Related to the hydrated nature of the brain, intracranial pressure from the edematous tissue surround tumors can cause the brain to swell within the craniotomy region. Models that are biphasic in nature may be better suited to capture these brain shift effects. In addition, deformations from retractor blades and internal strain energy changes that occur during tumor exposure and resection can also contribute to brain shift during surgery. Each of these factors present a challenge with respect to prescribing boundary and internal forcing conditions. While nonguided prediction is desirable, there is little doubt that the accuracy of brain shift models can be increased by integrating feedback from sparse intraoperative data (Roberts et al., 1999). These sparse displacement measurements can be obtained from a number of sources (Nauta, 1994; Hartkens et al., 2003; Lunn et al., 2001; Sun et al., 2003, 2005; Sinha et al., 2005). Sparse intraoperative data is typically used as displacement or stress boundary conditions to constrain the computational model. Using the measured sparse displacements, Ferrant et al. (2002) and Skrinjar et al. (2002) rigidly constrained their computational model to exactly match the measured displacements, as if they were known boundary conditions. Though this method is relatively easy to implement, it faces the potential limitation that since boundary displacements are constrained to match measured surface displacements, artificial forces can be introduced at the measured points which by observation are stress-free. More specifically, in this framework, all deformations result from the application of contact forces when the force environment is considerably more complex and could involve a myriad of contact and distributed loading conditions. Given this, it is worth exploring alternative approaches for integrating sparse intraoperative data with computational modeling. Also, it should be noted that time taken to compute the displacements using the computational model and the time taken to integrate the sparse data with the computational model, must meet the real-time constraints of neurosurgery. Thus the incorporation of sparse measurements must not only improve accuracy, but also significantly reduce the time required to update the preoperative images.

In recent developments, Lunn et al. (2005) presented a novel method that corrects brain shift by combining a best prior estimate (BPE) with a force perturbation correction technique to better match sparse data to model output. The reported method casts the model correction with a nonlinear optimization framework which uses the method of Lagrange multipliers to rapidly correct their BPE of brain deformations. They call the method the adjoint equation method (AEM) and have had encouraging preliminary results. While the mathematical approach is quite elegant, it still represents a challenging optimization framework that is significantly under-determined. Also in addition to the computational cost, the AEM reduces modeling efforts to solve for the optimal distribution of forcing functions rather than concentrating on generating a more deterministic model. For the sole purpose of shift correction, this is quite appropriate but it focuses the framework at using models to regularize data rather than model deformation events.

In the work presented here, a constrained linear inverse model is combined with a biomechanical tissue model to best fit the measured sparse intraoperative data. Initially presented in Dumpuri et al. (2003), the method reported here extends the earlier framework by incorporating a smoothing constraint to improve the efficiency and accuracy of solution. In order to account for the degree of uncertainty associated with all the sources of deformation, the computational model is run multiple times and these multiple model solutions are combined with the help of a inverse model to predict the intraoperative brain shift. It should also be noted that a considerable amount of the framework can be pre-computed and that at this time the inverse approach is a direct solution. With this technique, the model solutions act as training samples for the inverse model and the sparse intraoperative data act as control points, thereby removing the degree of uncertainty associated with MUIGNS. The framework proposed herein has some specific distinctions from the work of others: (1) the atlas of deformations is constructed from simulations based on physiological events, therefore the framework moves beyond the role of image interpolator to one that provides quantitative estimates of deformation-related properties (e.g. stresses, interstitial pressure dynamics, etc.), (2) the atlas of solutions generated is of more considerable breadth and attempts to include all the forces causing intraoperative brain shift and the varying surgical presentations of the patient (e.g. mannitol induced deformations, gravity-induced sag, and resection), (3) the inverse model is linear, and takes advantage of pre-processing, (4) the framework introduces a simple weighting scheme to constrain the atlas, and (5) presents a semi-automatic boundary condition generator to translate the boundary conditions encountered in the OR and should allow for the easy reproduction by others.

In this study, the fidelity of a constrained linear inverse model approach is demonstrated in a phantom experiment, two in vivo cases and a simulation study. It should be noted that though the sparse intraoperative data can include both pressure and displacement measurements, displacement data was chosen to test the accuracy of the proposed inverse model. In this study a laser-range scanner (LRS) is used to acquire sparse data measurements (Sinha et al., 2005, 2006). The laser-range scanner used in Sinha et al. (2005) is capable of generating a three-dimensional point cloud corresponding to (x, y, z) cartesian coordinates and two-dimensional texture co-ordinates (u, υ). In Sinha et al. (2005, 2006) the LRS was modified by the attachment of 12 infrared light emitting diode (IRED) markers, allowing for the scanner to be tracked in physical-space. The approach to measuring brain shift using LRS is as follows: LRS is used to scan the cortical surface, the initial scan is registered to the patient’s preoperative images thereby establishing a correspondence between image-space and physical-space (Miga et al., 2003), the brain then deforms during surgery, and LRS is used to acquire a serial scanning dataset of the cortical surface after deformation. The shift acquired is then transformed to physical-space coordinates with the aid of a calibration phantom. The shift-tracking protocol using LRS has been described in detail in Sinha et al. (2005). These sparse intraoperative measurements are used to constrain the linear inverse model. Also to meet the real-time demands of neurosurgery a parallel implementation of the computational model on a multiprocessor architecture is considered.

2. Methods

2.1. Computational model

Eqs. (1) and (2) were originally developed by Biot (1941) to represent biphasic soil consolidation, but were later used by Nagashima et al. (1990) and Paulsen et al. (1999) to model the deformation behavior of brain tissue.

$$\nabla ·G\nabla \overrightarrow{u}+\nabla \frac{G}{1-2\nu }(\nabla ·\overrightarrow{u})-a\nabla p=-({\rho }_{\mathrm{t}}-{\rho }_{\mathrm{f}})g$$ (1)

$$a\frac{\partial }{\partial t}(\nabla ·\overrightarrow{u})+\frac{1}{S}\frac{\partial p}{\partial t}+k_{\mathrm{c}}(p-p_{\mathrm{c}})=\nabla ·k\nabla p$$ (2)

where u⃗ is the displacement vector, p the interstitial pressure, G the shear modulus, ν the poisson’s ratio, a the ratio of fluid volume extracted to volume change of the tissue under compression, ρ_t the tissue density, ρ_f the fluid density, g the gravitational unit vector, 1/S the amount of fluid which can be forced into the tissue under constant volume, t the time, k_c the capillary permeability, p_c the intracapillary pressure, k the hydraulic conductivity.

Eq. (1) reflects the equations of mechanical equilibrium. Within this description, deformations can be caused from surface forces and displacements, the existence of interstitial fluid pressure gradients, and changes to tissue buoyancy forces. Additionally, this expression assumes that the continuum consists of a porous solid tissue matrix infused with an interstitial fluid whereby the matrix deforms as a linear elastic solid while the fluid flows according to Darcy’s law. Eq. (2) relates the time rate of change of volumetric strain to changes in interstitial hydration.

First reported within the context of gravity-induced brain shift by Miga et al. (1999), the right-hand-side of Eq. (1) is used to represent the effect of gravitational forces acting on the brain. The effect of gravitational forces on the brain can be modeled as a difference in density between tissue and surrounding fluid. Intraoperative CSF drainage reduces the buoyancy forces which serve to counteract gravity forces thus causing the brain to sag.

The last term on the left-hand-side of Eq. (2) represents the hydrodynamic forces that act on the brain due to fluid capillary exchange. The term k_c(p − p_c) represents the fluid exchange between capillary and interstitial spaces and can be used to simulate the effects of hyperosmotic drugs or swelling on the brain. Hyperosmotic drugs such as mannitol are administered to decrease the effect of elevated intracranial pressure due to edema. These drugs have the effect of reversing the blood–brain osmotic barrier, drawing water from the extracellular brain space, thereby decreasing brain volume. This decreased capillary pressure pulls interstitial fluid from the extracellular brain space causing a decrease in tissue volume. Conversely, elevated capillary pressures increase local tissue volume, resulting in tissue stress and distortion. A pressure elevation of 20–30 mmHg has been measured in experimental brain edema and shown to be capable of driving edema fluid through the brain (Reulen et al., 1977) (for this work, a value of 27 mmHg was used). The term k_c(p − p_c) is intended to model these fluid exchanges. It should be noted that the effects of mannitol are modeled as a volumetric force with decreased pressures acting on the whole brain, whereas tissue swelling is modeled as a local force with elevated pressures acting in the edematous region alone. Material properties reported in Appendix A.2 are based on values in the literature as well as those deduced through optimization in experiments by Miga (1998). As reported in appendix, a heterogenous distribution of k_c is assumed to account for the different structural and biomechanical characteristics of the gray and white matter, tumor and edema.

Eqs. (1) and (2) are solved numerically using the Galerkin weighted residual method. Finite element treatment of these equations coupled with a weighted time-stepping scheme results in an equation of the form [A]U_n+1 = [B]U_n + C_n+1 where [A] and [B] represent the stiffness matrices for the n + 1 and nth time step, respectively, C represents boundary condition information and known force distributions, and U represents the solution vector (3 displacements and pressure) at the node. The detailed development of these equations can be found in previous publications (Paulsen et al., 1999; Miga, 1998).

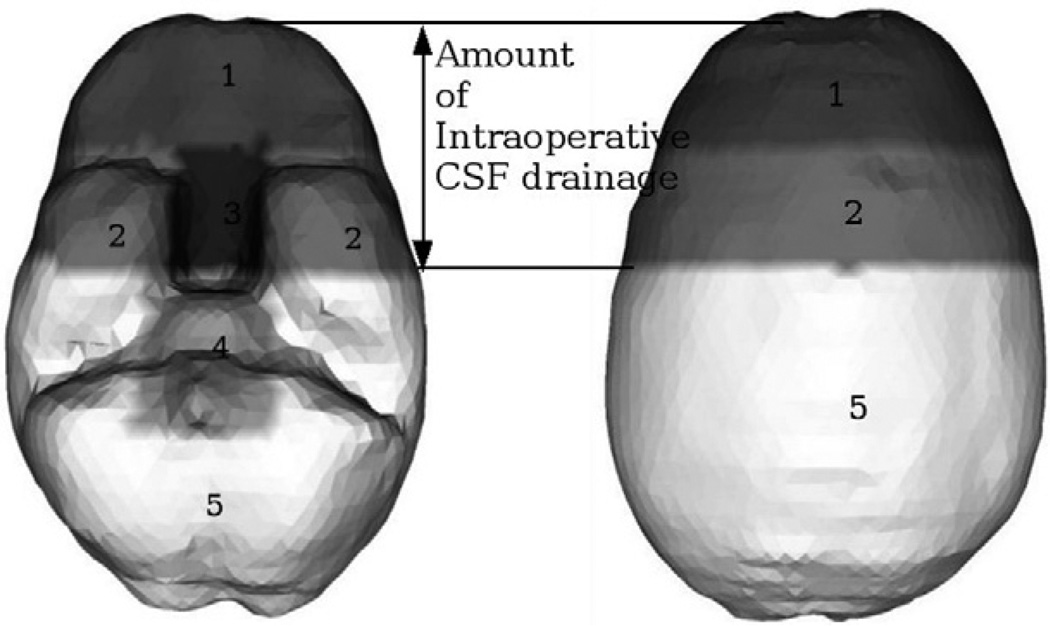
The boundary conditions used in the model are illustrated in Fig. 1 and was first reported in Miga et al. (1998). Although the actual boundary conditions are patient specific, the highest elevations in the brain are stress-free, the mid-elevations are permitted to move along the cranial wall, while the brain stem is fixed. The amount of intraoperative CSF drainage determines the fluid drainage boundary condition for each of these elevations. Elements and hence the corresponding nodes in the mesh lying above the assumed level of intraoperative CSF drainage are assumed to reside at atmospheric pressure, while elements lying below the CSF drainage level do not allow fluid drainage. These boundary conditions were used to validate the accuracy of the computational model in Miga et al. (1998, 1999, 2000). The results reported suggest that these boundary conditions compare well to those encountered in the OR.

Fig. 1.

BC set for a supine patient with neutral head orientation in the OR. Displacement BCs: Surface 1 is stress-free at atmospheric pressure. Surfaces 2 and 5 are permitted to move along the cranial wall but not along the normal direction. Surfaces 3 and 4 are fixed for displacements. Interstitial pressure. BCs: Surfaces 1, 2 and 3 lie above the assumed level of intraoperative CSF drainage and therefore reside at atmospheric pressure. Surfaces 4 and 5 lie below the assumed level of intraoperative CSF drainage and therefore allow no fluid drainage.

2.2. Parallel computation of the finite element model

As described earlier, the volumetric deformation of the brain is determined by solving the three displacements (x, y and z) and pressure (p) at each node of the finite element mesh. Each node thus gives rise to four degrees of freedom. The elements in the finite element mesh matrix are divided equally amongst the processors available for computation. The boundary conditions are then applied in a similar manner (divided amongst available processors). It should be noted that though the rows of the matrix and the boundary condition nodes are divided equally amongst the processors, some processors do more work than others due to the irregular connectivity of the mesh. The Portable, Extensible Toolkit for Scientific Computation (PETSc) package (Balay et al., 1997, 2001, 2004) is used to assemble the stiffness matrix and to solve the biphasic brain model.

2.3. Inverse model

As discussed above, computation time is an important factor in MUIGNS. By incorporating a priori knowledge about the sources of deformation, it may be possible to improve efficiency of a MUIGNS system by decreasing the computational time and it may also be possible to increase the accuracy of a MUIGNS system. With respect to the accuracy, certain aspects of the brain shift problem can be difficult to predict within the OR environment regardless of available data acquisition. For example, in the practical OR setting, it is very difficult to differentiate shift due to changes in CSF volume and from fluid-depleting drugs such as mannitol. Even something as simple as knowing the patient orientation in the OR, i.e., the direction of gravity with respect to the brain can be challenging. For example, in frameless stereotactic procedures, the reference emitter is commonly attached to the patient’s fixation. This allows tracked instruments to be directly related to the patient’s image volume once the patient has been registered. This has the advantage that as the patient’s bed is lowered and/or rotated, the reference frame is rotated with the patient. However, in so doing, the absolute reference to the OR (the reference frame of gravity) can be lost unless a second reference emitter is attached to OR space (not commonly done). Without a second reference emitter, the direction of gravity relative to the patient is lost. One approach to addressing this uncertainty is to generate an atlas of deformation solutions based on a range of possible surgical presentations. This has the added benefit to efficiency by allowing for precomputation of the deformation atlas.

In this paper, a realization to the brain shift compensation problem is proposed using a precomputed deformation atlas. Operationally, Eqs. (1) and (2) are solved for a range of possible factors causing brain shift. Let the deformation atlas, E, be the matrix obtained by assembling these model solutions whereby E is of size (n × 3) × m, where n is the number of nodes in the finite element mesh, 3 is the number of Cartesian displacement components at each node, and m the number of model solutions. In general, n × 3 is significantly larger than m, so E is a rectangular matrix. The model-data misfit error between a linear combination of precomputed displacement solutions and the actual displacements can be written as

$${\epsilon }_{\text{volume}}=[\mathbf{E}]\{\alpha \}-\{U\}$$ (3)

where U is the measured volumetric intraoperative shift, i.e., shift at all nodes and is (n × 3) × 1 vector, and α is the m × 1 vector of regression coefficients. This can then be expressed as the least squared error objective function,

$$G_{\text{volume}}(\alpha )={([\mathbf{E}]\{\alpha \}-\{U\})}^{\mathrm{T}}([\mathbf{E}]\{\alpha \}-\{U\})$$ (4)

As noted above, the measurements U are often incomplete or sparse. As a result, model solutions within E are interpolated to the specific measured intraoperative data points and these interpolated solutions are assembled in an intraoperative sparse deformation atlas, M. Thus M is of size (n_s × 3) × m, where n_s is the number of points for which sparse intraoperative data has been measured. The displacement data sets in M serve as the training samples for the inverse model and reduce the model-data misfit error, and objective function to

$${\epsilon }_{\text{sparse}}=[\mathbf{M}]\{\alpha \}-\{u\}$$ (5)

$$G_{\text{sparse}}(\alpha )={([\mathbf{M}]\{\alpha \}-\{u\})}^{\mathrm{T}}([\mathbf{M}]\{\alpha \}-\{u\}),$$ (6)

respectively. Here, u is the sparse intraoperative shift measured at n_s points in the brain. This, however, can transform the problem into an undetermined system because there are usually more regression coefficients than measurement points (i.e. m > n_s). While minimum norm solutions can produce perfect fitting of the data they are often unsatisfying with respect to volumetric shift prediction due to the measurements being confined to a small spatial region (e.g. craniotomy in this case). This is addressed by introducing an extra constraint, which has the effect of encouraging a spatially smooth displacement field that is confined within the cranial extents. The modified objective function can be written as,

$$G_{\text{sparse}}(\alpha )={([\mathbf{M}]\{\alpha \}-\{u\})}^{\mathrm{T}}([\mathbf{M}]\{\alpha \}-\{u\})+\varphi {[W]}^{\mathrm{T}}\{\Upsilon \}\{\alpha \}$$ (7)

The second term in this expression is a function of the mechanical strain energy at each point within the model and serves to constrain the regression coefficients to values that would also minimize the elastic energy across the deformation atlas. In this expression, the term ϒ refers to the linear elastic strain energy matrix, described by ϒ_i,j = 1/2{ε_i,j}^t[S_i,j]{ε_i,j}, where S_i,j, ε_i,j is the elastic stiffness tensor, and Cartesian strain tensor in vector form, respectively, for the ith node of the jth solution from the atlas (material properties are in Appendix A.2). With the development of any multi-term objective function (Eq. (7)), care must be taken to allow proper scaling of terms such that the data is matched optimally while also retaining the beneficial effects of constraints. This process of regularization is often problem specific. With this in mind, a distance based weighting factor vector W^T = [W₁, W₂, W₃, … ] is introduced that is similar to that in Lynch (2004), and is used with the strain energy matrix described above. The weighting vector is constructed as,

$$W_i=\frac{1}{(1+r_i/l)e^{-r_i/l}}$$ (8)

where r_i is the distance between the centroid of the measurement nodes and the ith node in the brain volume. The l is a characteristic length that specifies the domain over which measurement nodes should have influence. With that, the form of Eq. (8) reduces the strain energy constrain within the region of measurements nodes, i.e. the craniotomy in this case. While displacements tend to be small in areas remote from the craniotomy, they will have increased strain energy and increased weighting. When Eq. (7) is optimized for the regression coefficients, the net effect of the constraint term is to enforce a minimal elastic energy state on remote regions of the domain while selecting coefficients that best match the shift in the cranial and tumor regions. ϕ in Eq. (7) provides a scaling role such that the solution is not biased by the strain energy constraint term. The values for l and ϕ were found empirically and are 0.125 and 1/2700, respectively.

Finally, setting the partial derivative to zero, the optimum for Eq. (7) has a direct solution for {α}. Once the regression coefficients are determined, these are used to calculate the full volume displacements using

$$\{U^{*}\}=E\alpha$$ (9)

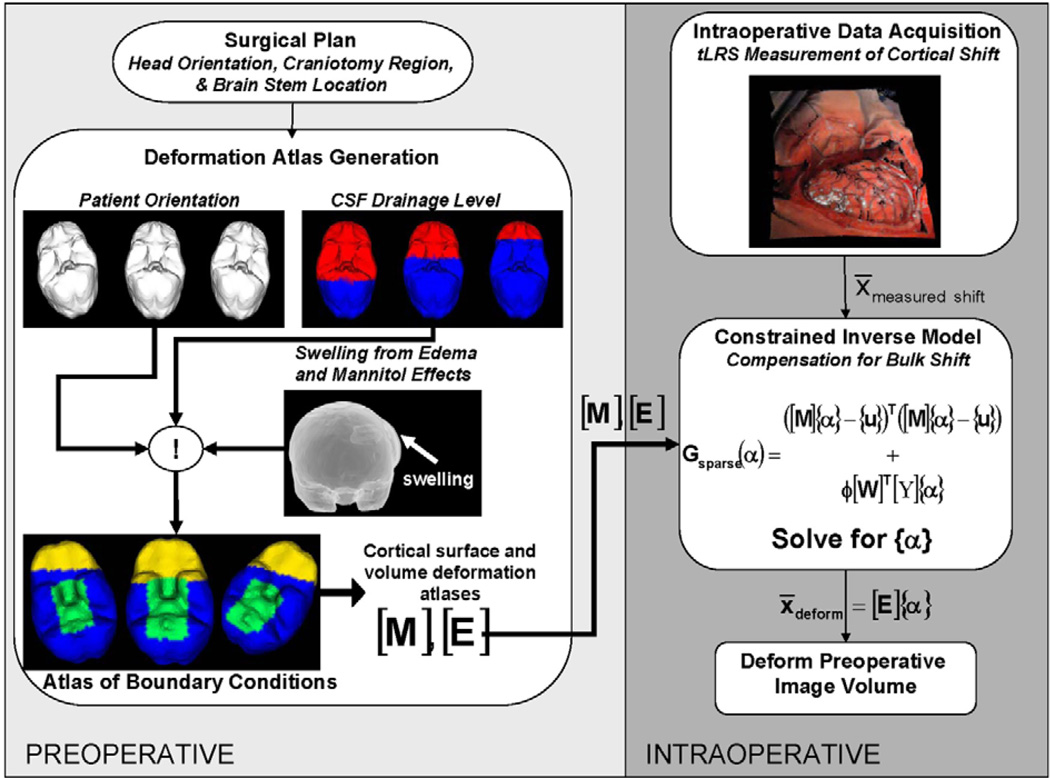
where {U*} is the predicted volumetric brain shift. Fig. 2 shows a schematic of the MUIGNS system using the inverse finite-element model approach.

Fig. 2.

Framework for MUIGNS using the constrained linear inverse model.

2.4. Automatic boundary condition generator and atlas formation

In order to predict intraoperative brain shift using the inverse model based on a pre-computed deformation atlas, a number of training samples/displacement data sets are required. Additionally, for increased accuracy, it is important that the model represent the degree of uncertainty associated with all the sources of deformation. For example, a deformation atlas for predicting gravity-induced brain deformations should contain displacement data sets for a range of possible patient orientations in the OR and varying degree of buoyancy force changes for each patient orientation. The surgeon’s preoperative plan can be used to approximate the patient’s orientation in the OR and subsequently used to generate multiple boundary condition sets (BCs), to sample all possible patient orientations. This underscores the need for a template BC that is accurate so as to facilitate automatic BC generation.

Based on the BC representation shown in Fig. 1, a patient-specific automatic boundary condition generator has been developed. The only necessary inputs are the approximate patient orientation in the OR as predicted by the neurosurgeon’s preoperative surgical plan, an anticipated region/size for the craniotomy, the computational mesh based on the preoperative image volume, and the location of the patient’s brain stem in the preoperative image study. Based on this information, all possible patient orientations in the OR are assumed and BCs for the patient-specific mesh domain are generated. The automatic BC generator algorithm is as follows:

1. For a given preoperative patient-orientation estimate (PPoE), the node normals for all nodes on the boundary are calculated and the following operation is performed over all boundary nodes: e⃗_g · e⃗_ni ≤ ξ, i = 1, 2, 3, …, n boundary nodes, where e⃗_g is the gravitational unit vector, e⃗_ni is the unit vector associated with the nodal normal to the brain surface for the ith boundary node and ξ is a scalar tolerance specified by the user.² Boundary nodes that satisfy this condition are assigned stress-free boundary conditions (Neumann condition), while those that do not are allowed to slide along the cranial cavity but not in the direction of the surface normal. However in cases where tissue swelling, due to elevated intracranial pressure, is to be taken into account, the nodes in craniotomy region are identified and assigned stress-free boundary conditions while other boundary nodes are allowed to slide along the cranial cavity but not in the direction of the surface normal.

2. The brainstem is identified from the patient’s preoperative images and nodes within a given radius are classified as fixed (Dirichlet condition), which overrides the conditions determined in Step 1.

3. The interstitial pressure BCs are determined by: d⃗_i · (−e⃗_g) ≥ h_j; h_min ≤ h_j ≤ h_max, j = 1, 2, 3, …, m elevations, where d⃗_i is the Cartesian coordinate of the ith boundary node and h_j is an elevation distribution. Based on previous experience in the OR, it has been determined that the upper (h_max) and lower bound (h_min) for the elevation distribution is 65% and 15% of the total elevation, respectively. Boundary nodes that satisfy the above expression are considered to be at atmospheric conditions (Dirichlet condition in pressure), while those that do not are the non-draining regions of the brain (Neumann condition in pressure).

4. Elements in the domain with reduced buoyancy forces are identified based on the following expression: D⃗_k · (−e⃗_g) ≥ h_j; h_min ≤ h_j ≤ h_max, j =1, 2, 3, …, M elevations, where D⃗_k is the Cartesian position of the kth tetrahedral element centroid. Elements satisfying this condition are considered to have a complete reduction in their buoyancy forces and are assumed to have a surrounding fluid density equal to that of air (ρ_f as shown in Eq. (1)). Elements that do not satisfy the above condition are assumed to have a surrounding fluid density equal to that of the tissue density (ρ_t as shown in Eq. (1)).

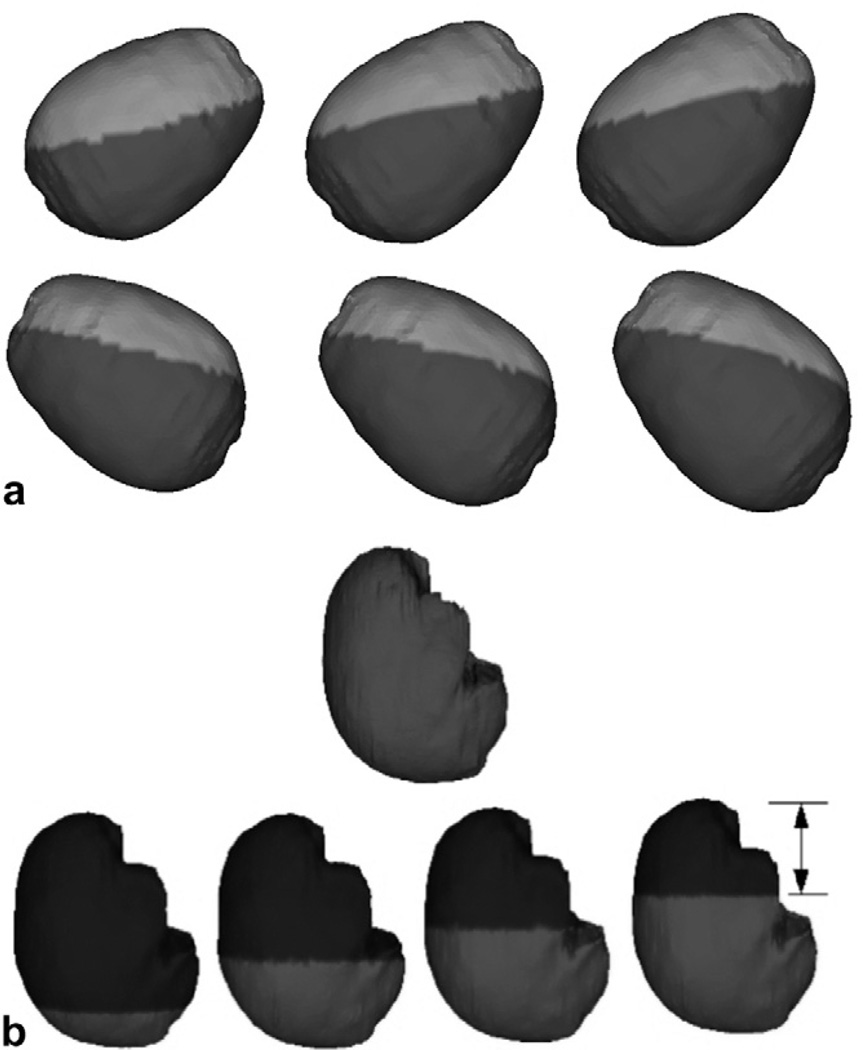
Fig. 3a shows a sampling of the BC atlas as generated by the automatic BC generator algorithm for the displacement/stress BCs. Fig. 3b shows a sampling of the BC atlas for the interstitial pressure BCs.

Fig. 3.

BC atlas developed using the automatic BC generator algorithm. (a) Displacement BCs generated for varying patient orientations based on PPoE. Nodes in the light gray regions of the figure are assigned stress-free BCs and those in the dark gray regions are allowed to slide along the cranial cavity but not in the direction of the surface normal. (b) Pressure BCs for varying levels of intraoperative CSF drainage, for a given patient orientation. Nodes above the CSF drainage level (black region) are assumed to be at atmospheric conditions and nodes below the CSF drainage level (gray region) are assumed to be the non-draining regions of the brain. Also, elements in gray are submerged in CSF and are assumed to have a surrounding fluid density equal to that of the tissue density and elements in blue are assumed to have a surrounding fluid density equal to that of air. For brevity and clarity, only a few BC sets are shown here.

3. Experiments

3.1. Phantom studies

Phantom experiments were conducted to quantify the fidelity of the constrained linear inverse model and to simulate gravity-induced brain shift. Fig. 4 shows the experiment set up.

Fig. 4.

Phantom experiment set up used to simulate gravity induced deformations and assess the accuracy of the proposed constrained linear inverse model. For picture clarity, the tank is shown with no water in it.

The phantom was made of polyvinyl alcohol(PVA) (Flinn Scientific, Inc., Batavia IL). A 7% solution of PVA with one freeze–thaw cycle was used to construct the brain phantom. The phantom was fixed on an incline and submerged in a water-filled tank and a baseline CT scan was acquired. To simulate the loss of CSF drainage during neurosurgery, water was drained to two different levels and CT scans were acquired for each drainage level. Twelve 1 mm diameter stainless steel bearings (http://www.bocabearings.com) were fixed on the surface of the phantom and used to track the motion of the phantom surface during all CT scans. It is worth noting the following two limitations of these phantom experiments: (i) in surgery, the brain is confined within the skull thereby constraining the brain shift, whereas no such confinements existed for the phantom, (ii) the brainstem is assumed not to shift in this framework whereas in these experiments the entire bottom surface of the brain phantom was fixed to the incline. While the phantom experiment is not exactly analogous to surgical conditions, the goal was to simulate the scale of gravity-induced deformations in an experimental setup and validate the fidelity of the constrained linear inverse model. The CT images were acquired in a fixed experimental setup so that any discrepancies between image sets after drainage were solely due to deformation. Examples of phantom deformations can be seen in Fig. 5.

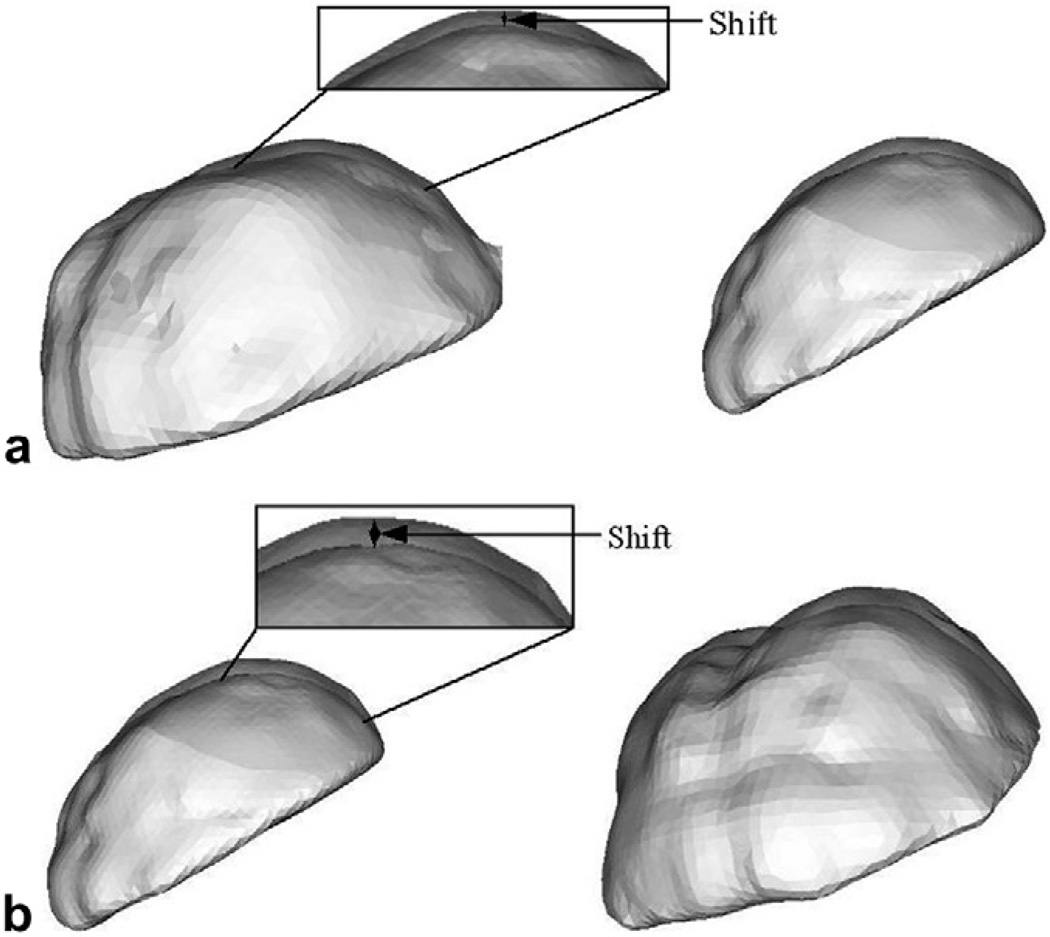
Fig. 5.

Phantom deformation results of the RBF surfaces of the segmented brain phantom from CT image volumes. Two different views have been shown for each water drainage level to assist in depth perception. (a) Resulting shift when water in the tank was drained to half the original level. (b) Resulting shift when water in the tank was drained to about 90% of the original level. Regions have been highlighted and zoomed in to show the shifts at a finer scale.

The starting point for the framework begins with the generation of the subject-specific model in the “preoperative” state in this case, a geometric model of the phantom in its fully submerged state. From the imaging data, a marching cubes algorithm (Lorensen and Cline, 1987) was used on the segmented CT data to generate an initial approximation of the surface of the brain phantom. FastRBF Toolbox (Farfield Technologies, http://www.farfieldtechnology.com) was then used to define a parametric version of the marching cubes surface. A tetrahedral mesh generator (Sullivan et al., 1997) was then used to create a volumetric tetrahedral mesh using the patch description obtained from the FastRBF toolbox. The angle of inclination was used for the phantom PPoE. Twenty-seven different orientations with three different drainage levels were used to create the displacement data sets/training samples using a 3D linear elastic model. Material properties used in the computational model have been reported in Appendix A.1. Also, the model was reduced to an isotropic elastic material model and hence Eq. (1) was used with a = 0. Displacements obtained using the stainless-steel bearings were used to constrain and to assess the accuracy of the constrained linear inverse model. To estimate the accuracy of the constrained linear inverse model in predicting full volume displacements, six 1 mm stainless steel bearings implanted at a depth of 1–2 cm inside the phantom were used as targets and the magnitude of target registration errors (TRE)³ of the sub-surface bearings were examined. Additionally, displacements of the surface and the sub-surface bearings were predicted using the forward model in an open-loop manner to determine its accuracy with respect to modeling sag. In this case, boundary conditions i.e., drainage levels, and the inclination of the phantom were known a priori and therefore the gravity forces causing shift were ascertained. These forces were then applied to the computational model and the displacements were compared to those estimated using the constrained linear inverse model. Results have been presented in Section 4.2.

3.2. Clinical studies

Two patients undergoing tumor resection (Sinha, 2005; Sinha et al., 2005) were used to validate the constrained linear inverse model. In both cases, an optically tracked LRS system was used to track the cortical surfaces during neurosurgery. Upon opening the dura, the tracked LRS unit was used to capture the brain surface. After tumor resection, the process was repeated. Corresponding cortical features were identified in both scans and used as measures of displacement. Previous work has shown that serial brain shift measurements using a tracked LRS were in agreement with those measured independently by an optically tracked stylus (i.e. a gold standard in measurement).

Patient 1 was a 65 year old male with a history of esophageal cancer and had an associated 3 cm area abnormal enhancement in the left frontal lobe. He underwent a stereotactic left frontal craniotomy for microsurgical resection of the tumor.

Patient 2 was a 36 year old male with a 6 × 8 cm tumor mass originating in the left frontal lobe and crossing across the midline in the corpus collosum to the collateral frontal lobe.

In each case, mannitol was administered and no initial shift was observed after opening the durage. It is important to note that the absence of initial shift post dura opening is not necessarily commonplace. Findings by Dorward et al. (1998), Nimsky et al. (2000), and Sun et al. (2005) have reported post dura opening shift in many cases. Intraoperative cortical surfaces (after dura opening but before tissue resection, and after tumor resection) of each patient were acquired by the tracked LRS unit. Fig. 6 shows the LRS surfaces overlaid on the textured preoperative MR volume.

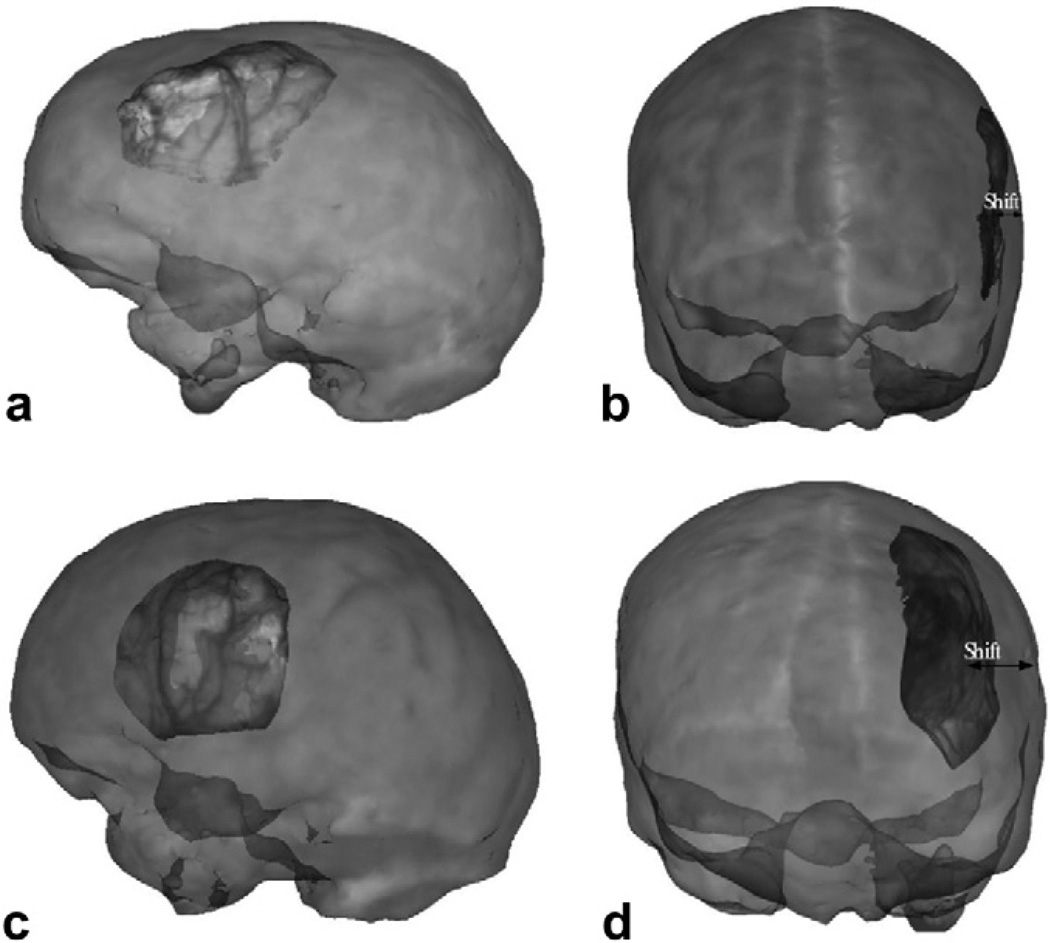
Fig. 6.

Pre- and post-resection LRS surfaces overlaid on the preoperative MR volume. (a) and (b) respectively show the pre- and post-LRS surfaces overlaid on Patient 1’s preoperative MR volume. (c) and (d) respectively show the pre- and post-LRS surfaces overlaid on Patient 2’s preoperative MR volume. See Sinha (2005) and Sinha et al. (2005).

A patient-specific model was generated for each patient. The brain, falx cerebri, tumor and edema were segmented from the patient’s preoperative MR data set and the tetrahedral mesh was generated in a manner similar to the brain phantom. Tissue mechanical properties were based on previous experiences and have been reported in Appendix A.2. For each patient, brain shift was simulated with five different atlases that reflected different assumptions about the surgical presentations of the patient: (I) tumor was assumed to be stiffer than the brain tissue (Miga et al., 2001) and was not resected from the brain volume. Mannitol was not administered and gravity was the solitary factor causing shift, (II) tumor was resected from the volume. As in the previous atlas, mannitol was not administered and gravity was the solitary factor causing shift, (III) tumor was assumed to be stiffer than the brain tissue. Mannitol was administered and was the solitary factor causing shift, and (IV) tumor was resected from the brain volume. As in the previous atlas, mannitol was the solitary factor causing brain shift (V) all four aforementioned atlases were concatenated into one large deformation atlas. Atlas I and II employed 64 different orientations with five different CSF drainage levels for each orientation, resulting in 320 displacement data sets/training samples for each deformation atlas for a total of 640 among Atlas I and II. Atlas III and IV used three different capillary permeability values for each of the 64 patient orientations, thus resulting in 192 displacement data sets for each atlas for a total of 384 among Atlas III and IV. Atlas V thus consisted of 1024 deformation data sets. Tissue resection was simulated by identifying the model elements that coincide with the preoperative tumor volume and decoupling the corresponding nodes (Miga et al., 2001) Fig. 7.

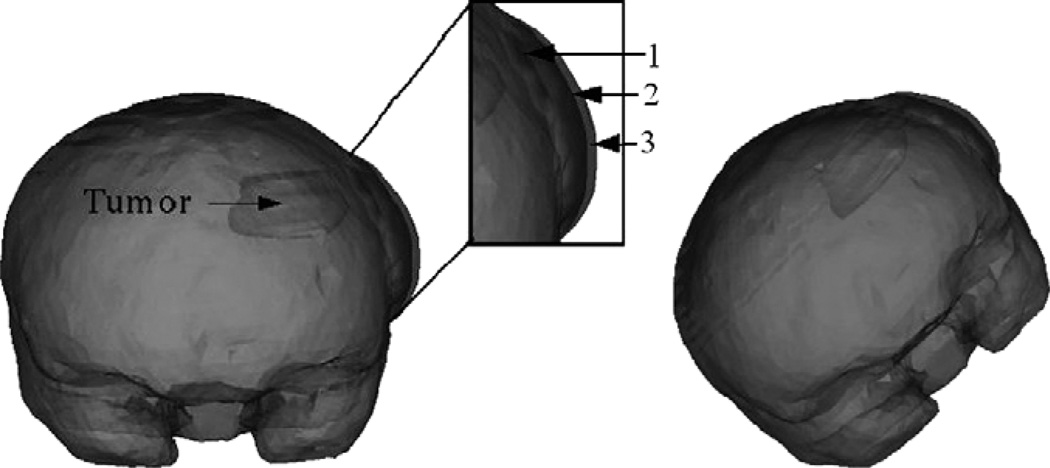
Fig. 7.

Two frontal views of the volume rendered brain with an increase in tissue volume simulated at the craniotomy region, simulated using two different k_c values. The craniotomy region is highlighted and zoomed in to show the increase in tissue volume on a finer scale. 1 in the figure refers to the undeformed mesh. 2 refers to the increase in tissue volume simulated using k_c1. 3 refers to the increase in tissue volume simulated using k_c2. k_c1 and k_c2 values have been reported in Appendix A.2. Though the falx cerebri was modeled, it has not been shown in the figure.

With respect to the driving sparse data, 12 corresponding points between the serial LRS scans were identified manually by an experienced user. These points are transferred to physical-space coordinates as described in Section 1 and (Sinha et al., 2005). The registration results reported in Sinha (2005) and Sinha et al. (2005) are used to establish correspondence between the initial LRS scan (physical-space) and the finite element mesh (image-space). Nodes on the brain surface closest to the twelve corresponding points identified on the initial LRS scan are then identified using a closest-point algorithm and these nodes are used to compute the intraoperative deformation Atlas [M] described in Section 2.3. Also, the difference in position between the twelve corresponding points in physical space, i.e., the difference in physical-space coordinates between the twelve points identified on the initial LRS scan and post-resection scan, was used to constrain and validate the accuracy of the five deformation atlases using the inverse approach. Sub-surface measurements were not available for the clinical studies. Therefore, a “leave one out” technique was employed for the surface points to validate the accuracy of the constrained linear inverse model. In other words, the inverse model is challenged 12 times, each time leaving out one of the corresponding points from the intraoperative deformation Atlas [M] and the measured shift u. Error is then computed using only the omitted point, thereby resulting in 12 error measurements for each deformation atlas. Mean, standard deviation and maximum values across these 12 error samples have been reported in the following section.

3.3. Simulation studies

To test the fidelity of the approach in a controlled manner and to validate sub-surface shifts predicted by the inverse model, brain shift was compensated for using two different deformation atlases that reflected different assumptions about the surgical presentations of the patient. A finite element mesh representative of a human brain was generated in a manner similar to the one described in Section 3.2. Twelve nodes on the brain surface closest to the tumor were picked to simulate the sparse intraoperative measurement points. Nodes belonging to the brain stem are fixed and in cases where tumor is resected, nodes corresponding to the tumor volume are decoupled when assembling the stiffness matrix. As a result, brain stem, tumor and measurement nodes were excluded when assessing the accuracy of the proposed framework. Shift error for all the other surface and sub-surface nodes served as unbiased error estimates and results have been presented in the following section.

Atlas I is a concatenated deformation atlas reflecting brain shift due to gravity, mannitol and tumor resection, while Atlas II additionally included shift caused by tissue swelling. It should be noted that Atlas I as defined here is analogous to Atlas V used in Section 3.2. In order to account for the brain shift due to increased intracranial pressure from the edematous tissue, brain shift was simulated due to increased intracranial pressure using the k_c(p − p_c) in Eq. (2). Three different craniotomy sizes (2 cm radius, 2.5 cm radius and 3 cm radius) were assumed and for each craniotomy size, three different edematous tissue regions were assumed. The edematous tissue was subjected to an elevated intracranial pressure of 27 mmHg and three different k_c values were assumed, thus resulting in a total of 27 different scenarios. The displacement data sets resulting from these 27 scenarios were used to build the aforementioned deformation Atlas II. Atlas II the concatenated deformation atlas, thus consisted of 1051 deformation data sets.

Six different displacement data sets, not part of the atlases mentioned above, were used to validate the accuracy of two aforementioned atlases using the constrained linear inverse model. The forces causing shift in these different displacement sets are as follows: (A) Gravity-induced deformations with tumor not being resected from the tissue volume. (B) Mannitol-induced shift with tumor being resected from the tissue volume. (C) Brain shift resulting from tissue swelling being the solitary factor causing shift. (D) Brain shift resulting from tissue swelling with mannitol being administered. (E) Brain shift from tissue swelling with gravity-induced deformations and (F) Gravity and mannitol-induced deformations with tumor resected from the tissue volume. It should be noted that although mannitol and gravity-induced sag were used to neutralize the effect of tissue swelling in (D), and (E), respectively, the net displacements on the surface still reflected a swelled brain within the craniotomy region. Also the robustness of the constrained linear inverse model was tested by adding random noise to displacement vectors contained in Atlases I and II. The random noise level was assigned to have a maximum of 3% of a given displacement magnitude and incurred a maximum random angular error of 4°. This ensured that the perturbed displacement data sets was still contained within the atlases.

4. Results

4.1. Parallel implementation of the finite element model

Table 1 illustrates the computational time necessary to solve the biphasic model on a finite element mesh containing 19,468 nodes and 104,596 elements, using 16 processors (2.8 GHz, Intel Pentium4, 1GB RAM).

Table 1.

Computational times associated with parallel implementation of the finite element model

Number of processors	Total time (s)	Precondition + iterative solution for first time step (s)	Successive time steps (#5) (s)
2	853.7	154.3	623.4
4	392.2	51.7	212.5
6	202.6	32.2	117.0
8	140.0	23.9	86.0
10	138.3	23.3	85.1
12	117.5	19.0	70.5
14	130.2	16.6	81.8
16	116.7	20.7	67.5

With four degrees of freedom this requires the solving of a total of 77,872 equations. Also the biphasic model is time dependent and a total of five time-steps were used to solve the system reported here. The second column in the table is the total computational time taken to solve the system and includes file I/O, communication across processors, stiffness matrix assembly, application of boundary conditions, and solution of the matrix system for all the five time steps. The total times reported assume the patient-specific finite element mesh has already been prepared. The third column in the table reports the time taken to precondition the matrix of equations and solve for the first time increment. The fourth column in the table reports the time required to complete all subsequent time-step calculations. The table shows that using two processors the total computational time required to solve the system takes 853.7 s and using all 16 processors it takes 116.7 s to solve the system.

4.2. Phantom studies

Fig. 8 shows the mean error between the measured and predicted shift for the phantom experiments using the constrained linear inverse model. Measured shift is defined as the displacement of the bearings as measured during subsequent CT scans.

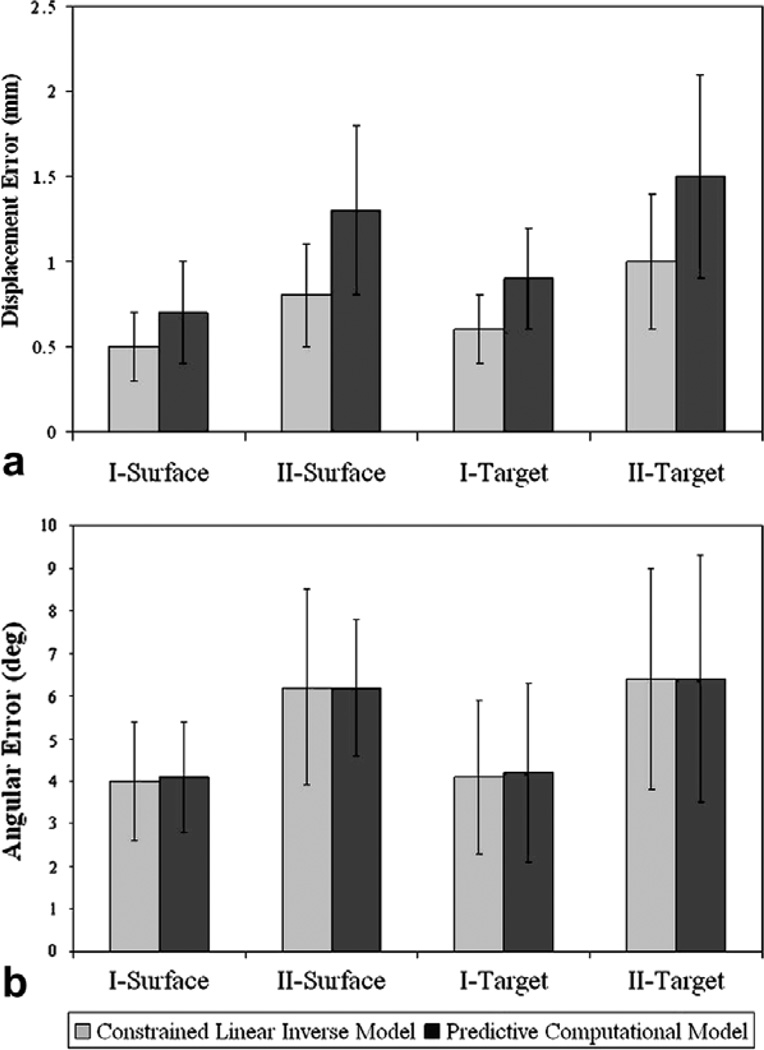
Fig. 8.

Phantom Experiment Results. (a) Mean Shift error in mm, between the measured and predicted shift. Measured shift is defined as the displacement of the bearings as measured during subsequent CT scans. (b) Mean angular (θ) error in degrees between the measured and predicted shift. I and II represent water drainage levels of 50% and 90% respectively. Surface represents displacements of the bearings fixed on the phantom surface and were used to constrain the inverse model whereas Target represents the displacements of bearings implanted inside the phantom and were used as unbiased error estimators. The average measured surface shift of the phantom was 10.1 ± 4.5 mm, and 21.2 ± 9.3 mm for drainage conditions I and II, respectively. The average measured target shift of the phantom was 5.6 ± 2.1 mm, and 11.3 ± 4.3 mm for drainage conditions I and II, respectively.

In addition, simulation results using the model in a purely predictive mode are presented. I and II in the figure represent water drainage levels of 50% and 90%, respectively. Surface represents the beads on the phantom surface and were used to constrain the inverse model, while Target is associated with the sub-surface beads that represent novel points for assessing unbiased prediction errors. Shift error refers to the magnitude error between the measured and predicted shifted positions of the bearings. Fig. 8 shows the angular error θ, which represents the directional accuracy between the measured and the predicted shift. Averaging over both the drainage levels, the constrained linear inverse model recaptured 95.9% of the mean deformation on the surface and 88.5% of the average shift at subsurface targets while the purely predictive computational model recaptured 92% of the mean deformation on the surface and 85.3% of the average shift at subsurface targets. The formula for % shift recapture has been reported in Appendix A.3.

4.3. Clinical studies

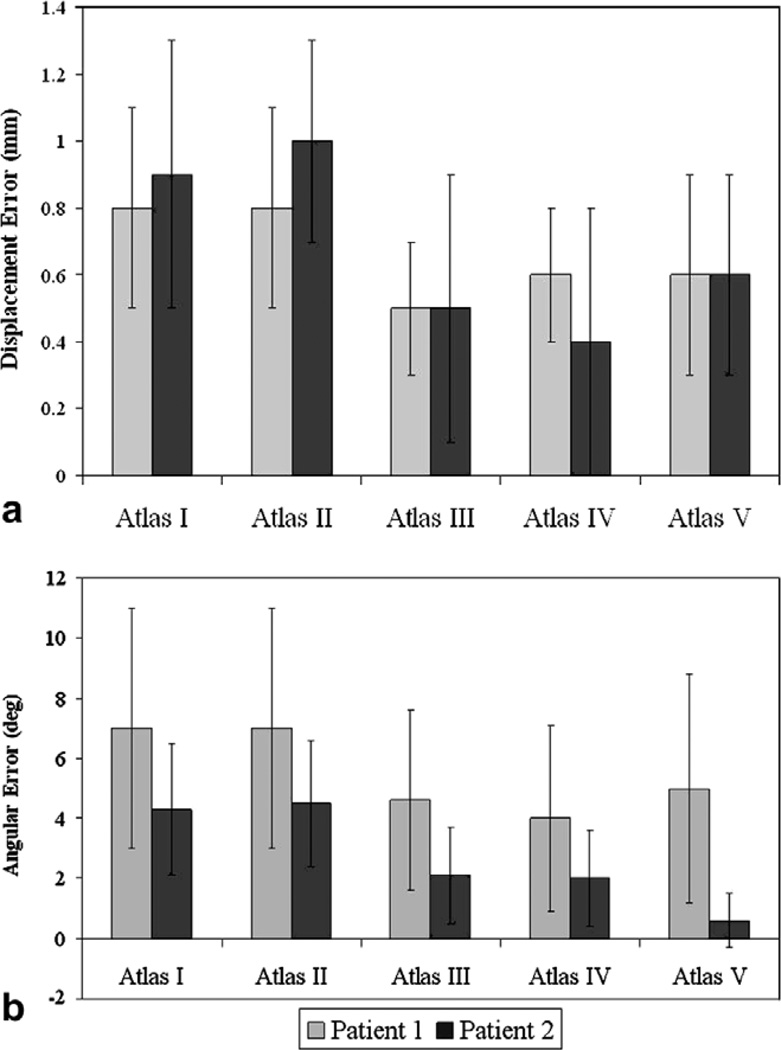
Fig. 9a shows the mean shift error and the mean angular error between the predicted and the measured intraoperative brain shift for Patient 1 and Patient 2 reported in Section 3.2 computed using the constrained linear inverse model. As in Fig. 9b, predicted shift error in the figure refers to the error in the magnitude between the measured and the predicted intraoperative brain shift, while angular error, θ, represents the inaccuracies in the direction of propagation. The deformation atlases used to simulate the predicted shift have been described in detail in Section 3.2.

Fig. 9.

Patient 1 and 2 results. (a) Mean shift error between the measured and predicted shift. Measured Shift for Patient 1: 6.1 ± 2.4 mm with a maximum displacement of 10.3 mm. Measured Shift for Patient 2: 10.8 ± 3.7 mm with a maximum displacement of 16.3 mm. (b) Mean angular (θ) error in degrees between the measured and predicted shift. Atlas I: Tumor was not resected from the brain volume and gravity was the solitary shift-causing factor. Atlas II: Tumor was resected from the brain volume and gravity was the solitary shift-causing factor. Atlas III: Tumor was not resected from the brain volume and mannitol was the solitary shift-causing factor. Atlas IV: Tumor was resected from the brain volume and mannitol was the solitary shift-causing factor. Atlas V: All four aforementioned atlases were concatenated into one deformation atlas.

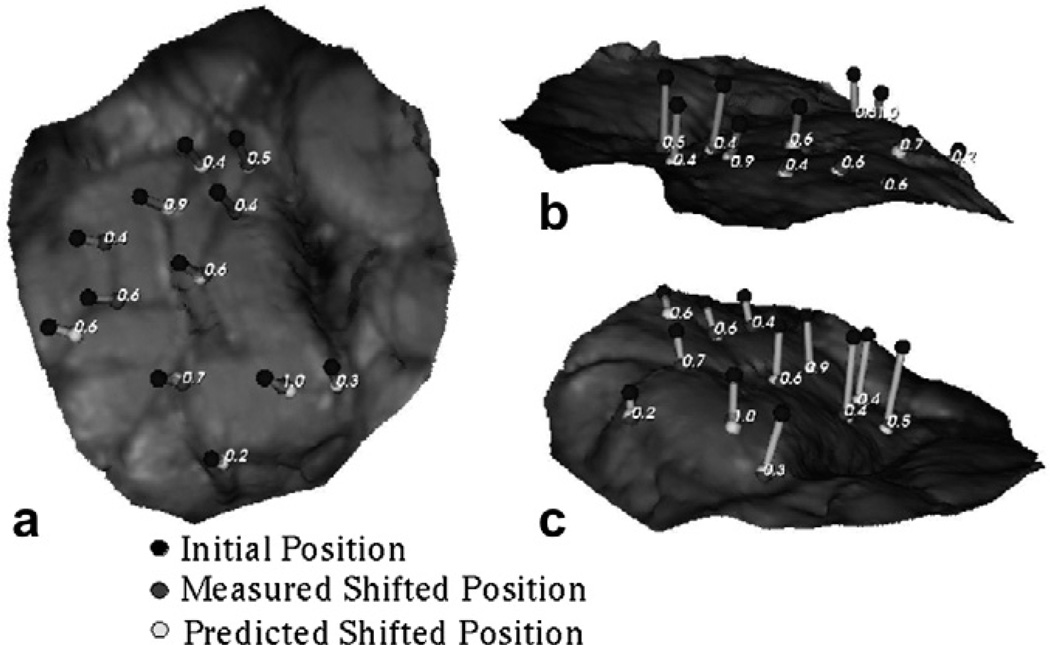
In order to visualize the shift vectors predicted using the constrained linear inverse model for Patient 1, (shown in Fig. 10), the measured and predicted shifts of the corresponding points were added to their respective initial positions and were projected on to the LRS surface acquired after resection. Shift vectors predicted using displacement data sets in Atlas IV were used to generate the figure shown.

Fig. 10.

Measured and shift vectors predicted using the constrained linear inverse model (shown as line segments) overlaid on the post-resection LRS surface for Patient 1. Shift predicted using Atlas IV (mannitol being the solitary shift causing factor, tumor resected from the tissue volume) has been shown here. The numbers in the figures represent the absolute error between the measured and predicted shift. Each figure, (a), (b) and (c) demonstrates the overlay from a different camera angle to assist with depth perception.

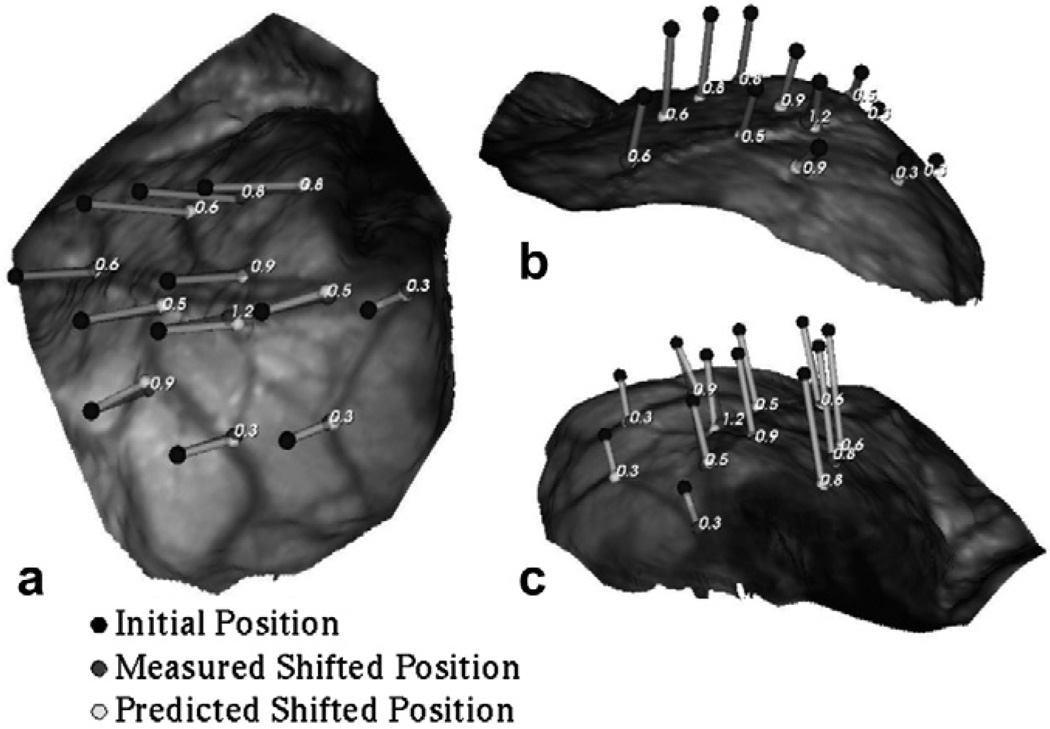
Similarly for Patient 2, Fig. 11 shows the measured and predicted shift vectors projected onto the LRS surface acquired after resection. Shift vectors predicted using displacement data sets in Atlas V were used to generate the figure shown.

Fig. 11.

Measured and shift vectors predicted using the constrained linear inverse model (shown as line segments) overlaid on the post-resection LRS surface for Patient 2. Shift predicted using Atlas V (concatenated deformation atlas) has been shown here. The numbers in the figures represent the absolute error between the measured and predicted shift. Each figure (a), (b) and (c), demonstrates the overlay from a different camera angle to assist with depth perception.

Averaging over all five atlases for Patient 1, the constrained linear inverse model produces a mean displacement error of 0.7 mm ± 0.3 mm and a mean angular error of 5.8° ± 3.6° with respect to a mean cortical shift of 6.1 ± 2.4 mm. Similarly for Patient 2, the constrained linear inverse model produces a mean displacement error of 0.7 mm ± 0.4 mm and a mean angular error of 3.2° ± 0.4° with respect to a mean cortical shift of 10.8 ± 3.7 mm.

4.4. Simulation studies

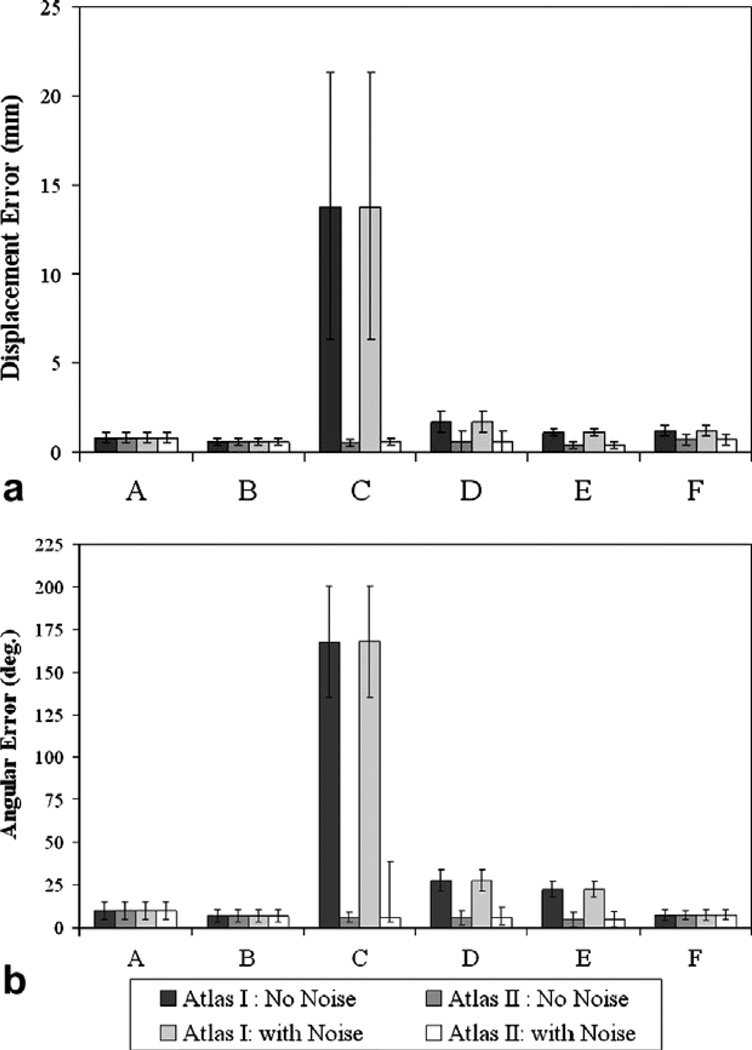
As stated earlier, in the simulation studies, the constrained linear inverse model was challenged by using a deformation field that was novel to the training atlas. The six different displacement sets that were used to validate the accuracy have been presented in detail in Section 3.3. Also noise was added to the displacement data sets in the atlas to test the robustness of the constrained linear inverse model. Fig. 12 shows the mean error between the predicted and the total shift using the constrained linear inverse model for the atlases with and without the noise added to them.

Fig. 12.

Simulation study results. (a) Mean shift error between the total and predicted shift. (b) Angular error between measured and predicted shift. Atlas I is a concatenated deformation atlas reflecting brain shift due to gravity, mannitol and tumor resection, while Atlas II additionally included shift caused by tissue swelling. (A) Gravity-induced deformations with tumor not being resected from the tissue volume. (B) Mannitol-induced shift with tumor being resected from the tissue volume. (C) Brain shift resulting from tissue swelling being the solitary factor causing shift. (D) Brain shift resulting from tissue swelling with mannitol being administered. (E) Brain shift from tissue swelling with gravity-induced deformations and no mannitol being administered, and (F) Gravity and mannitol-induced deformations with tumor being resected from the tissue volume. The average total shift for A, B, C, D, E, and F in the simulation cases was 11.7 ± 3.4 mm, 8.8 ± 2.4 mm, 5.5 ± 1.3 mm, 6.5 ± 1.2 mm, 3.3 ± 0.6 mm, and 14.3 ± 3.7 mm, respectively.

Atlas I did not include tissue swelling and hence behaved poorly when challenged with displacements resulting solely due to tissue swelling, i.e., displacement data set C. It is worth noting that though the accuracy of Atlas I improved when presented with displacements resulting from a combination of tissue-swelling and gravity and mannitol-induced deformations, i.e., displacement data sets D and E, Atlas II which included the displacement data sets due to tissue swelling, significantly outperformed Atlas I. The figure also demonstrates that the constrained linear inverse model is relatively insensitive to the noise added to the displacement data sets contained in the Atlases.

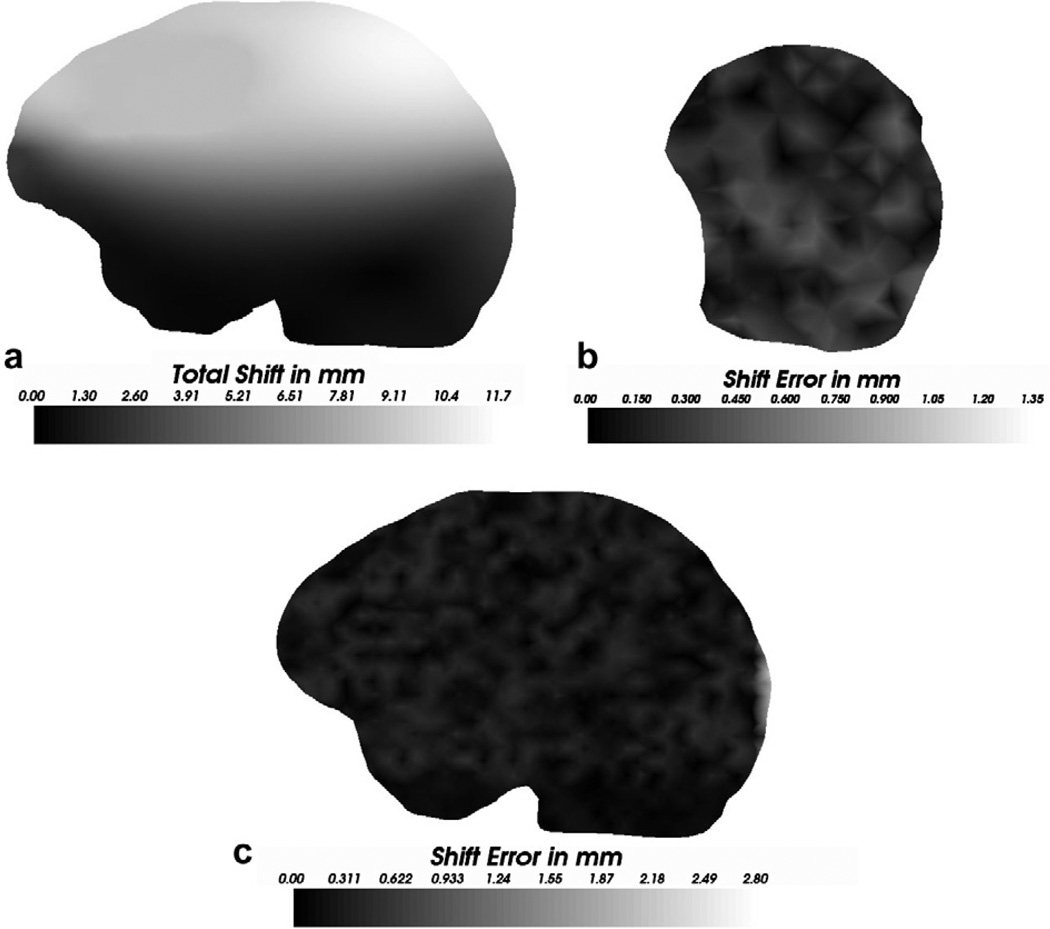
As stated earlier, nodes other than the measurement nodes and the zero displacement nodes were used as targets to quantify the accuracy of the constrained linear inverse model and the shift error of these targets across the volume of the brain is shown in Fig. 13. Shift predicted by Atlas II when challenged with displacement data set A was used to calculate the shift error shown in the figure. Fig. 13a presents the total shift at a slice passing through the tumor and Fig. 13c shows the shift error at approximately the same slice through the brain volume, while Fig. 13b shows the error distribution on the surface in the vicinity of the measurement nodes. As seen in the figures, though the error increases as one moves farther away from the measurement nodes, the inverse approach performs well in the vicinity of the tumor, producing a mean shift error of 1.3 ± 0.7 mm, a mean angular error of 9.7 ± 2.3° and a maximum shift error of 2.8 mm with respect to a mean shift of 5.9 ± 2.8 mm and a maximum shift of 11.7 mm. It should be noted that the tumor was being modeled as not being resected from the tissue volume. Though the figure depicts error distribution for a single displacement data set, similar error distributions were observed for all the displacement data sets that were used to validate the inverse model.

Fig. 13.

Shift error computed using Atlas II when challenged with the displacement data set A. (a) Magnitudes of the shift in mm, for a slice passing through the tumor (b) Shift (magnitude) error at the surface in the vicinity of the measurement nodes (c) Shift (magnitude) error at approximately the same slice as (a). It should be noted that tumor was modeled as not being resected from the tissue volume for the displacement data set A. The nodes corresponding to the tumor region were not used to calculate the shift error reported herein.

4.5. Summary of results

To summarize the performance of the constrained linear inverse model for all the experiments reported herein, the % shift recaptured and shift error and directional error (angular error) of the constrained linear inverse model for all experiments is reported in Table 2. For a given water drainage level in the phantom experiments, the predicted surface and sub-surface deformations were averaged and was used to calculate the % recapture and the shift and angular error reported in the Table. For the in vivo cases, shift predicted using Atlas V, the concatenated deformation atlas was used to calculate the amount of shift that was recaptured and the error characteristics reported here. For the simulation study, shift recapture, directional accuracy and shift error was calculated from the results of the averaged over all six distributed loading condition simulations using Atlas II.

Table 2.

% shift recaptured, angular error and the mean ± standard deviation (max.) shift error using the deformations predicted by the constrained linear inverse model

	Measured/total shift, mm	% Shift recaptured		Angular error, degrees	Shift error, mm
		Min.	Mean
Phantom
Level I	7.9 ± 3.3(17.3)	91.4	91.8	4.2 ± 2.4(6.9)	0.6 ± 0.4(1.5)
Level II	16.3 ± 6.8(32.3)	81.9	92.6	6.9 ± 2.9(12.5)	1.2 ± 0.6(5.8)
Clinical
Patient 1	6.1 ± 2.4(10.3)	84.4	89.4	6.0 ± 3.8(12.6)	0.6 ± 0.5(1.6)
Patient 2	10.8 ± 3.7(16.3)	88.9	96.3	2.9 ± 1.5(5.7)	0.6 ± 0.5(1.8)
Simulation
Atlas II	8.4 ± 2.1(15.6 ± 7.2)a	76.8	85.9	2.8 ± 0.7(4.4)	1.2 ± 0.4(3.7)

Mean ± standard deviation (maximum) of the measured/total shift have been reported.

^aSix different displacement sets were used to constrain and test the fidelity of constrained linear inverse model. Therefore average maximum total shift and the standard deviation of the shift over the six different displacement sets has been reported.

5. Discussion

The integration of sparse intraoperative data into MUIGNS is not a trivial task. As stated in Miga et al. (2001), sparse intraoperative data applied in an interpolative/extrapolative sense cannot capture the entire range of deformation. They also note that the sparse intraoperative displacement data must be applied in a manner that is consistent with the forces causing those displacements. The constrained linear inverse modeling approach proposed here achieves this integration in an efficient manner. Although it may seem time consuming to build an atlas of deformations, results from Section 4.1 indicate that using a multiprocessor environment significantly reduces the amount of time taken to generate atlases. As stated in Section 4.1, using 16 processors it takes approximately 117 s to calculate one basis solution/training sample in the deformation atlas. Therefore for a deformation atlas with 320 basis solutions, using 16 processors it required approximately 10 h to build each atlas reported in Section 3.2. It should be noted that a sensitivity analysis has not been performed which may indicate that the level of detail in the atlases presented here may not be necessary to achieve meaningful shift corrections during surgery. The results here are encouraging given this relatively modest atlas; and perhaps similar results may be achieved with sparser training sets. This awaits further study.

The in vivo cases reported in this work were treated as unknown systems, i.e. the surgeon did not generate the PPoE but rather retrospective estimates based on operation notes were used. Ultimately, the PPoE will be provided by the surgeon using an ordinary graphical user interface (GUI) one day prior to the surgery. The information provided will reflect the anticipated patient orientation, craniotomy size, and location of the brain stem in reference to the preoperative image volume. Once these have been designated, the automatic BC generation is performed to sample the possible deviations from the PPoE. This boundary condition atlas and the model is then submitted to the multi-processor cluster which returns a deformation atlas several hours later. This strategy has several distinct advantages: (1) it accounts for the uncertainty in distributed surgical loads, such as the gravitational sag and the physiological parameters like the amount of mannitol that will be administered, in a real-time sense (2) the method relies on relatively inexpensive small-scale computer clusters, (3) the time-consuming calculations are performed preoperatively, and (4) all forms of data (e.g. fMR, PET, SPECT, etc.) can be mapped within each solution and either combined through the inverse model or they can be actively computed based on the displacement fields predicted using the constrained linear inverse model. It should also be noted that the compensation for distributed loading conditions is only the first stage in this compensation strategy. The second stage is to monitor the more direct interactions such as retraction, and resection. These actions are more representative of surface loading conditions as opposed to distributed ones. We hypothesize that direct predictive modeling approaches with these should deliver the required accuracy. Previous experience with animal systems supports this tenet (Platenik et al., 2002; Miga et al., 2000). Surface loadings resulting from tissue retraction and the resulting deformations can be modeled as a multistep process (Miga et al., 2001) and this has been demonstrated previously (Platenik et al., 2002; Miga et al., 2000, 2001). This paper represents an approach to the more difficult distributed loading conditions.

The results from the Phantom experiments are important on two distinct levels. The first level is in validating the model approximation reported by Miga et al. for modeling brain sag (Miga et al., 1999), i.e. using the (ρ_t − ρ_f)g term in Eq. (1). In Miga et al. (1999), gravitational sag in four clinical cases was compensated for using this term and encouraging results were presented. The data reported in Miga et al. (1999) used the same mechanism for simulating sag but only represent surface measurements. In the work presented here, surface and subsurface beads were tracked in a phantom under controlled gravitational loading conditions. As stated in Section 4.2, the computational model recaptured approximately 88.7% of the surface and subsurface shift. The second level of significance for the phantom experiments is in validating the proposed constrained linear inverse model approach for distributed surgical loads. Table 2 indicates an approximate 92% compensation capability when only using sparse surface data to guide the inverse model. One interesting aspect to observe in the phantom results is that the constrained linear inverse model outperformed the forward-based computational model that used the known boundary conditions. Undoubtedly the inaccuracies in the forward model are from inappropriate small-strain approximations, nonlinear material effects. Despite these inaccuracies and the lack of explicit drainage/incline information, the constrained linear inverse model delivered a modest improvement over the open-loop predictive model synthesizing a better match through the combination of the pre-computed basis solutions.

For the clinical studies, it was interesting to note that in both the patient cases, the atlas with mannitol-induced deformations recaptured most of the measured shift. Atlas III, mannitol-induced deformations with non-resected tumor recaptured most of the shift for Patient 1, while for Patient 2, Atlas IV, mannitol-induced deformations with resected tumor recaptured most of the measured shift. While no statistical significance can be inferred, it is interesting that mannitol was administered in both patients and that when comparing the results among the atlas’, the predictions by mannitol induced shift are better than the gravity-induced shift. Although anecdotal, this may suggest that mannitol-induced shift may have a more prominent role in compensation strategies than previously reported. While these thoughts are intriguing, unfortunately, more detailed validation with subsurface measurements in a bigger patient population will be required to assert any conclusions. Nevertheless, the results among the experiments are markedly consistent and indicate that the constrained linear inverse modeling approach is a viable method for the compensation of distributed loading conditions.

The simulation results concerned with brain swelling were of comparable accuracy to the phantom and clinical experiments. In addition, the reported swelling shift magnitudes were comparable to those found in the literature (Dorward et al., 1998; Nimsky et al., 2000; Sun et al., 2005). One common criticism of the MUIGNS systems is that tissue swelling cannot be accounted for. Initial results of the sensitivity of the inverse model to noise (as shown in Fig. 12) shows that the model is relatively insensitive to noise, as long as the displacement data are still contained by the atlas. The results shown here suggest that swelling conditions encountered in the OR can be simulated using computer models. Fig. 13c shows the distribution of the shift error recaptured in the tumor region. Though the error increased when compared to the error distributions on the surface containing the measurement nodes (shown in Fig. 13b), the constrained linear inverse model still recaptured 83.6% of the mean shift in the vicinity of the tumor. These results combined with the target/sub-surface validations from the phantom experiments suggest that the constrained linear inverse model is a good framework for predicting sub-surface displacements using sparse intraoperative measurements.

While the work presented here is encouraging, the following issues need to be addressed before implementing this approach in a MUIGNS system: (i) more detailed validations with intraoperative imaging modalities such that the accuracy of the technique in predicting full volume displacements can be achieved; though validating the accuracy of the model has been reserved for a future study, the phantom results shown here and the simulation study results reported in Dumpuri et al. (2003) suggest that the model will behave in a similar fashion when predicting full volume displacement fields from sparse intraoperative data; (ii) sensitivity analysis of the inverse model to the particular selection of the boundary conditions and the consistency of the atlas; (iii) more detailed understanding of the internal structures affecting brain shift, e.g. the falx cerebri has been shown to inhibit cross-hemisphere movement; (iv) new studies focused on the improvement from subsurface data such as from co-registered ultrasound; and, (v) more studies regarding the sensitivity of the methods to the number and spatial distribution of sparse intraoperative data points. With respect to this last point, the results presented here have yielded a potentially important finding. In both the phantom and clinical experiments, the constrained linear inverse model was guided with a relatively modest number of points (12–15 points) spatially distributed on the area of observation. The level of model-fit in these cases is remarkable and makes it evident that assumptions regarding the extent, i.e. amount of data necessary for model-updating can and should be challenged as these new systems are developed.

Previous work has demonstrated that modeling can predict deformations induced by surface loading conditions such as tissue retraction (Platenik et al., 2002; Miga et al., 2001). Although detailed clinical studies have not been presented, the results suggest that the inverse model has the capability to predict intraoperative brain shift resulting from distributed loading conditions. These preliminary results indicate that the inverse model when combined with the approach reported in Platenik et al. (2002) and Miga et al. (2001) has the ability to predict introperative brain shift resulting from surface loads and distributed loads, thereby completing the MUIGNS framework.

6. Conclusions

In is interesting to note early reports dismissing methodologies to correct for intraoperative shift that did not involve traditional intraoperative imaging (specifically, iMR, and iCT) (Rubino et al., 2000). These early reports believed that conditions such as swelling and brain volume changes due to hyperosmotic drugs could not be predicted or practically modeled. In the experiences shown here and by others, these conclusions continue to be challenged and the potential for computer modeling within the OR environment is only now being realized. There is a growing acceptance that predicting brain shift at scales relevant to surgical interventions through computer models is very possible when proper approximations to forcing conditions are understood and when sufficient data is present to guide predictions. Albeit for surface displacements, the results presented in this work show that with a good set of basis-solutions/training-samples, the constrained linear inverse model can be used to predict cortical shift. In future work, the accuracy of this approach in predicting full volume displacement fields from sparse intraoperative data sets will be achieved using a comprehensive digitization approach. Further approach enhancements are being pursued and will include more anatomical constraint information and possibly a non-linear optimization framework.

Appendix A

The symbols used for the material properties have been described in Section 2.1.

A.1. Material properties used for the phantom experiments

Symbol	Value	(units)
E	1875	N/m2
ν	0.45	(no units)
$G=\frac{E}{2(1+\gamma )}$

A.2. Material properties used for the in vivo and simulation studies

Symbol	Value	(units)
E, white and gray	2100	(N/m2)
E, tumor	100,000	(N/m2)
E, falx	210,000	(N/m2)
ν	0.45	(no units)
ρt	1000	(kg/m3)
ρf	1000	(kg/m3)
g	9.81	(m/s2)
a	1.0	(no units)
1/S	0.0	(no units)
kwhite	1 × 10−10	(m3s/kg)
kgray	5 × 10−12	(m3s/kg)
kc1, white*	9.2 × 10−9	(Pa/s)
kc2, white*	4.6 × 10−9	(Pa/s)
kc3, white*	2.3 × 10−9	(Pa/s)
kc1, gray*	45.9 × 10−9	(Pa/s)
kc2, gray*	22.9 × 10−9	(Pa/s)
kc3, gray*	11.5 × 10−9	(Pa/s)
pc, mannitol	−3633	(Pa)
pc, swelling	3633	(Pa)

^*Three different values used in Section 3.3 to simulate tissue swelling due to elevated intracranial pressures.

A.3. Shift recapture

$$\%\text{shift recapture}=(1-\frac{\text{shift error}}{\text{total shift}})*100$$