Towards a More Universal Approach in Health Valuation

Abstract

By polling individual responses to hypothetical scenarios, valuation studies estimate population preferences toward health on a quality-adjusted life year (QALY) scale. The scenarios typically involve trade-offs in time (time trade-off [TTO]), risk (standard gamble [SG]), or number of persons affected (person trade-off [PTO]). This paper revisits the QALY assumptions and provides a coherent health econometric approach that unites TTO, SG, and PTO techniques under a common estimator. The proposed approach avoids the use of ratio statistics in QALY estimation and the common convention of arbitrarily changing trade-off responses. As an example, 34% of the TTO responses from the seminal Measurement and Valuation of Health (MVH) study were changed in the original UK analysis, which led to substantially lower QALY estimates. As a general rule, if the original estimate is less than 0.5 QALYs, add 0.25 QALYs to get the new estimates.

Decisions between alternative health scenarios typically require trade-offs in time (time trade-off [TTO]), risk (standard gamble [SG]) or number of persons affected (person trade-off [PTO]). For example, 10 years with a disease can be preferred over 9 years without disease. By polling individual responses using trade-off techniques (e.g., TTO, SG, and PTO), health valuation studies summarize the relative value of these scenarios. In this paper, we introduce a more universal approach to health valuation that builds from utility theory and unifies the various trade-off techniques (TTO, SG, and PTO) under a common estimator.

To illustrate this approach, we examined the TTO responses from the seminal UK Measurement and Valuation of Health (MVH) study of EQ-5D states (Williams, 1995). The EQ-5D descriptive system characterizes general health using five domains (mobility, self-care, usual activities, pain/discomfort, and anxiety/depression), each with three levels. The original MVH analysis predicted the value of the 243 EQ-5D states on a quality adjusted life year (QALY) scale, anchored by optimal health (1) and dead (0) (Dolan, 1997). Prior to estimation, 34% of the TTO responses were changed to improve the face validity of its QALY estimates. For example, the MVH study collected 838 TTO responses for the EQ-5D state with level two on all five domains (EQ-5D 22222), and the original estimation predicts its value to be 0.5 QALYs after changing 109 (13%) TTO responses.

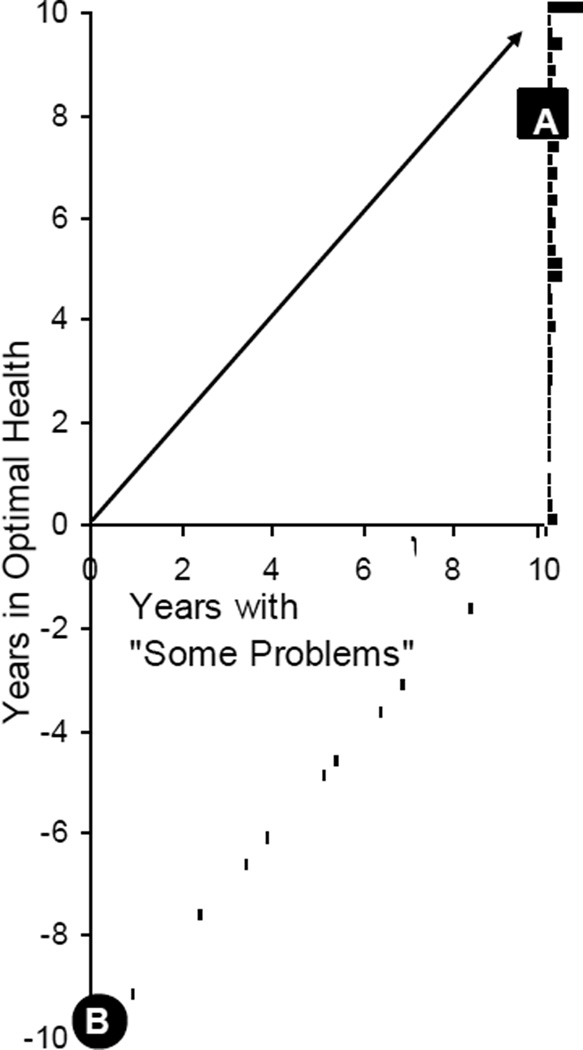
Figure 1 illustrates a customary TTO protocol popular among the EuroQol Group (Gudex, 1994). In this case, the x-axis represents time with “some problems” (EQ-5D 22222) and the y-axis is the amount of time in optimal health that is of equivalent value. The histogram (bars) is based on the frequency of MVH TTO response (Williams, 1995). For example, 15 of the 838 MVH respondents (Point A) equate 10 years with “some problems” (22222) to 8 years in optimal health (11111). At Point B, 8 respondents equate “immediate death” to the scenario of 9.75 years in optimal health followed by 0.25 years with “some problems” (22222). On a QALY scale, “immediate death” has a value of 0 and optimal health for 1 year has a value of 1. Therefore, the worse than dead (WTD) responses (Point B) suggest that 0.25 years in the state (22222) equates to a loss of 9.75 years in optimal health. The units traded in this figure are years (i.e., TTO); however, a similar figure can be constructed in risk or person units using SG or PTO responses.

Figure 1.

Time Trade-off Responses *

* Histogram is based on 838 TTO responses for the “some problems” EQ-5D state (22222) taken from the Measurement and Value of Health (MVH) study in the United Kingdom (Dolan, 1997).

All trade-offs in time, risk, or number of persons affected can be described by Cartesian coordinates (x, y), where x is units of disease and y is units without disease of equivalent value. This pair is known as an equivalence statement, where the responder is ambivalent between receiving x and y. In TTO, respondents report the value of disease time (x) in units of disease-free time (y). In standard gamble, the unit is risk. For example, a respondent at point A equates the “some problems” state (22222) to a gamble with 80% chance of optimal health (11111) and 20% chance of “immediate death.” If, instead, the respondent were at point B, he or she would be indifferent between “immediate death” and a gamble with 97.5% chance of optimal health and 2.5% chance of the state (22222). Using trade-off responses (x,y), health valuation studies can summarize population-specific values on a QALY scale.

Multiple statistical procedures have been applied to QALY estimation using TTO, SG, and PTO responses (x,y). The original MVH estimation initially applied ratio statistics (i.e., mean of y/x), but mean ratios were not found to be robust, particularly as x approaches 0. To make the mean ratios more robust, the original study changed the data specifically time in the EQ-5D state, x, was changed to 10 years, when x was less than 10 years. This change affected the lower tertile of the sample (34%) and bounds the ratios (y/x) above −0.975 creating a more symmetrical range around dead (0) from 1 to −0.975. The assumption that all QALYs are greater than −0.975 has no theoretical basis, yet the practice was replicated in nearly all subsequent QALY estimations and has become the conventional approach to TTO, SG, and PTO responses. One of the more blatant examples is the United States EQ-5D QALY estimation, where the lowest quartile of ratios were arbitrarily divided by 39, instead of replacing × with 10 (Shaw et al., 2005). In this paper, we begin afresh by describing the theoretical assumptions of QALYs and follow their econometric implications. To demonstrate the resulting estimator, we predict the values for 242 EQ-5D health states using the original MVH responses and compare this new value set to published values.

THEORY

Health utility refers to preferences over health-related qualities of life. Before characterizing such qualities, life itself can be described along three numeraire domains: time, risk, and number of persons affected. Let y represent a positive amount of a numeraire: time, risk, or number of persons affected. Each health scenario can be described by (h, y), where h is health and y is a selected numeraire characterizing life. For example, if time is the numeraire (i.e., TTO), a person living in optimal health for 10 years can be represented by optimal, 10 years.

To value a health scenario, U(h,y), the QALY framework imposes three conditions. First, numeraire (i.e., y>0) is required for life. This implies that if the numeraire is 0, the person is dead and the value of an immediate, certain death is 0. It further implies the value of dead for 1 day is equal to the value of dead for a millennium. Second, the QALY value of a health scenario at each numeraire amount has an upper bound expressed by the function U(optimal, y) = y. This upper bound is more controversial: while dead is considered terminal, objective, and verifiable, the definition of optimal health can be variable, normative, and difficult to measure (e.g., athleticism). Still, most valuation studies express values anchored on the value of optimal health (i.e., U(optimal,y) = y) and dead (i.e., U(dead,y) = 0). Because these two states anchor the QALY scale, their values have no variance, an attribute that becomes important in ordinal analyses (Craig et al., 2009a, Craig et al., 2009b).

Lastly, the QALY framework assumes increasing life in a particular health scenario is either always good or always bad. While the beneficence of life can seem more natural, a person can consider a scenario worse than immediate death; therefore, increasing its duration, risk, or persons lowers the scenario’s value. This assumption of monotonic preferences in the numeraire (i.e., either $\frac{\partial U}{\partial y}>0$ for all y, or $\frac{\partial U}{\partial y}<0$ for all y) implies that there is a one-to-one correspondence between utility and the numeraire, y. In their structural assumptions, Doctor and Miyamoto provide an axiomatic definition of monotonic preferences with respect to time, which we extend to other numeraire for a more universal approach to trade-off responses (e.g., risk and persons) (Doctor and Miyamoto, 2003). In the absence of this extension, a health scenario, h, can have two numeraire amounts, y₁ and y₂, such that U(h,y₁) = U(h,y₂), which complicates the interpretation of trade-off responses.

METHODS

Imagine two separate health scenarios: (h₂,x) and (h₁,y). A valuation survey can ask a respondent which scenario they prefer (e.g., U(h₁,y)>U(h₂,x)?). Based on the response, the interviewer can increase or decrease y, and repeat the question. Under the assumption of monotonic preference, a series of discrete choice leads to an amount of y such that the respondent is indifferent (i.e., U(h₁,y) = U(h₂,x)). The final response, y|x, can have some measurement error, but should reflect the respondent’s indifference. Health valuation studies using trade-off responses collect information about the relative value of health scenarios as expressed in terms of numeraire amounts (x,y). The TTO and SG involve trade-offs in a person’s health scenario, and the PTO typically involves trade-offs in health improvements for multiple persons.

Each valuation technique (i.e., TTO, SG, and PTO) involves a similar process: asking the respondents to make a series of discrete choices that result in an amount of optimal numeraire, y, that compensate for the difference in value between dead and a nonoptimal scenario. If the nonoptimal scenario is better than dead (BTD, U(h,1) > U(dead,∞)), the amount of numeraire, y₁, is positive and the respondent completes a series of choices with different y₁ until:

$$U\mathit{(}h,\mathit{1}\mathit{)}=U\mathit{(}\mathit{\text{optimal}},y_{\mathit{1}}\mathit{)}+U\mathit{(}\mathit{\text{dead}},\mathit{1}-y_{\mathit{1}}\mathit{)}$$ (1)

This equivalence statement (i.e., tie in rank) implies that the nonoptimal scenario equates to a bundle of an optimal health scenario and a dead scenario at a balancing amount of optimal numeraire, y₁. For the SG, the numeraire, y₁, is probability; the TTO numeraire, y₁, is measured in decades of time (e.g., U(h, 10 years)); and the PTO numeraire, y₁, is typically measured in number of persons. If the nonoptimal scenario is worse than dead (WTD, U(h,1) < U(dead,∞)), balancing equation 1 requires negative optimal numeraire, y₁<0, representing losses in time, risk, or persons in optimal health.

Instead of expressing the value of WTD scenarios in terms of losses of optimal numeraire (e.g., lost years in optimal health), the conventional approach is to switch dead and nonoptimal health in the equivalence statement:

$$U\mathit{(}\mathit{\text{dead}},\mathit{1}\mathit{)}=\mathit{U}\mathit{(}\mathit{\text{optimal}},y_{\mathit{2}}\mathit{)}+U\mathit{(}h,\mathit{1}-y_{\mathit{2}}\mathit{)}$$ (2)

In this second equation, the dead scenario is compared to a bundle of an optimal health scenario and a nonoptimal health scenario, and the optimal numeraire that balances this equation is again positive by construction.

On the QALY scale, U(dead,1) = 0 and U(optimal,y) = y; therefore, equations 1 and 2 are simplified: U(h,1) = y₁ and U(h,1-y₂) = −y₂. By definition, y is QALYs and x is nonoptimal numeraire; therefore, each response is the number of QALYs equal to an amount of nonoptimal numeraire, QALY_i|disease time (See Figure 1). Although the concept of QALYs (e.g., time in optimal health) can seem esoteric, such trade-offs are commonplace, such as currency exchanges (e.g., dollars for a 10 euros), parking (e.g., location|likelihood of getting a ticket) or vacation planning (e.g., value of a pleasure cruise|length of voyage). In the valuation of nonoptimal numeraire (e.g., time in disease, 10 Euros, risk of a ticket, or length of vacation), responses can vary.

ESTIMATION

Under a random utility model, the utility of a nonoptimal scenario, U_i(h, x), is random and its expected value is related to the nonoptimal numeraire x:

$$U_i(h,x)={\beta }_{h}x+{\epsilon }_i\mathit{\text{or}}{y}_i={\beta }_{h}x+{\epsilon }_i\mathit{\text{where}}{y}_i\in \{y_{i,1},y_{i,2}\}$$ (3)

In this specification (equation 3), the coefficient on the nonoptimal numeraire, β_h, is constant; however, constant proportionality can be relaxed by including a squared term in the model (e.g., δ_hx²). Constant proportionality is a central assumption in most QALY applications and relaxed in future studies (i.e., duration effects) (Craig, 2009). The randomness term, ε_i, has an expected value of 0 and finite variance, which can be attributable to measurement error or differences between respondents or variation in a person’s preference. The nonoptimal numeraire, x, equals 1 or 1-y₂ and has no measurement error because this variable is determined by the interviewer.

The purpose of this paper is to present an unbiased estimation of a random utility model (equation 3) using trade-off responses, y_i|x. If the randomness term, ε, is uncorrelated and has an expected value of 0 and finite variance, the minimum variance estimator of the coefficient is the ordinary least squares estimator:

$${\widehat{\beta }}_{OLS}=\underset{\beta }{\mathit{\text{Min}}}\sum _{i=1}^N{{\epsilon }_i}^2=\underset{\beta }{\mathit{\text{Min}}}\sum _{i=1}^N{(y_i{\beta }_h{x}_i)}^2=\sum _{i=1}^N{x}_i{y}_i/\sum _{i=1}^N{x_i}^2=\overline{xy}/\overline{x^2}$$ (4)

Conventionally, the coefficient estimator is considered BLUE (i.e., the best linear unbiased estimator) (Goldberger, 1964). For example, using the data in Figure 1, the mean of xy is 54.38 years and the mean of x² is 90.76 years; therefore, the estimated value for the state 22222 is 0.60 QALYs (or 54.38/90.76). Under the original MVH analysis, the mean of y/x for EQ-5D 22222 is −0.003 and the mean of y/10 is 0.50, which is a tenth QALY lower than the coefficient estimate. Over all MVH TTO responses, the mean of y/x is −2 QALYs, the mean of y/10 is 0.23 QALYs, and the mean of xy over mean of x² is 0.50 QALYs. To assess normality, we examine for extreme outliers (residuals 3 inter-quartile ranges above or below the 1^st and 3^rd quartiles) and perform a Shapiro-Francia W test and tests for skewness and kurtosis (Shapiro and Francia, 1972, D’Agostino et al., 1990). Future analyses can impose more complex, parametric approaches, which can reduce standard error in the points estimate; however, the estimate is unlikely to change with further assumptions.

State-specific Utility Model

Valuation studies that examine a single health state only estimate one coefficient (e.g., Figure 1). However, most studies examine multiple health states. For example, a valuation study can examine the “some problems” state (EQ-5D 22222) and the “pits” state (EQ-5D 33333). The constant proportional random utility model accommodates both states by adding a second nonoptimal numeraire:

$$y_i={\beta }_{22222}{x}_{22222}+{\beta }_{33333}{x}_{33333}+{\epsilon }_i\mathit{\text{where}}{y}_i\in \{y_{i,1},y_{i,2}\}$$ (5)

For the TTO, the first numeraire, x₂₂₂₂₂, is years in the “some problems” state (EQ-5D 22222) and the second, x₃₃₃₃₃, is years in the “pits” state (EQ-5D 33333). Equation 5 would require the addition of a third dimension to Figure 1. Typically, only one numeraire is non-zero for each trade-off response, y_i, but future valuation studies can include a mixture scenario, such as 5 years in “some problems” followed by 5 years in “pits.”

State-specific coefficients can be estimated using ordinary least squares (equation 4) after considering potential correlation. In valuation studies, respondents typically provide responses for multiple health states; therefore, the randomness terms are likely correlated. To relax the independence assumption and correct the estimated standard errors for this potential correlation, responses can be clustered within the OLS estimation. Controlling for clustering generally increases standard errors, but does not affect the coefficient estimates. More conservative approaches for robust variance calculation were applied and produced nearly identical p-values, standard error, and confidence interval estimates (MacKinnon and White, 1985).

Multi-attribute Utility Model and the EQ-5D Descriptive System

Descriptive systems, like the EQ-5D, describe numerous health states. Instead of collecting trade-off responses on all potential states (e.g., 242), valuation studies typically collect responses on a subset of states and predict the values of excluded states with common attributes. For the estimation of a multi-attribute utility model, the amount of nonoptimal time, x, is interacted with a series of attribute variables, known as a multi-attribute utility (MAU) regression. For a simple example (equation 5), nonoptimal time, x, can be interacted with a MAU regression including two state-specific dummy variables (i.e., I₂₂₂₂₂ and I₃₃₃₃₃).

Choice of multi-attribute regression model depends on the descriptive system. In the MVH study, health is characterized using the EQ-5D descriptive system, which comprises a set of scores on five dimensions (mobility, self-care, usual activities, pain/discomfort, and anxiety/depression) each with three possible levels. A vector of these five scores can be used as shorthand. For instance, the abbreviation 21122 represents the health of a person with some problems in walking, no problems with self-care or performing usual activities, moderate pain, and moderate anxiety.

To predict the value of each EQ-5D state, we interact nonoptimal time with a MAU regression model including 12 indicator variables: five for second level domains, five for third level domains, one for any second or third level domains (i.e., constant); and one for any third level domains (i.e., N3). This MAU model is identical to the original MAU model proposed by Dolan (Dolan, 1997). Coefficients are shown in terms of decrements from optimal health (1.00) to facilitate interpretation (Table 1).

Table 1.

Coefficients Estimates^*

N = 3,355 respondents with 39,673 responses
State Attributes	Coefficient	Robust Standard Errors	95% Confidence Interval
Mobility, 2	−0.038	0.004	−0.046	−0.030
Self-Care, 2	−0.076	0.004	−0.084	−0.068
Usual Activity, 2	−0.032	0.004	−0.040	−0.024
Pain/Discomfort, 2	−0.083	0.004	−0.091	−0.075
Anxiety/Depression, 2	−0.072	0.004	−0.080	−0.063
Mobility, 3	−0.268	0.008	−0.285	−0.252
Self-Care, 3	−0.189	0.007	−0.202	−0.176
Usual Activity, 3	−0.100	0.007	−0.114	−0.086
Pain/Discomfort, 3	−0.313	0.008	−0.328	−0.298
Anxiety/Depression, 3	−0.227	0.007	−0.241	−0.212
Any 2’s or 3’s	−0.094	0.004	−0.102	−0.086
Any 3’s	−0.107	0.008	−0.122	−0.092
R-squared	0.525

^*For example, the value for 21111 is 0.868 QALYs (i.e., 1.0 − 0.094 − 0.038).

With the aid of model estimates, the values of all 242 states within the EQ-5D descriptive system are predicted. We apply the percentile method with 1,000 iterations of cluster bootstrap resampling to assess the 95% percent confidence interval around the predicted values (Appendix) (Efron and Tibshirani, 1993).

Measurement and Valuation of Health study

In 1993, the University of York administered 3,395 interviews with a response rate of 64% and collected values of 42 EQ-5D health states, as well as the state of unconsciousness (Dolan, 1997, Gudex, 1994, Kind et al., 1998). The MVH protocol developed for the aforementioned study, describes a face-to-face interview that can be separated into several sections. First, the respondents are asked to describe their health using the EQ-5D descriptive system. Then, the respondents rank 15 cards each representing a different health state. After the ranking exercise, the subjects are asked to place each card on the EQ-VAS, often referred to as the EuroQol “thermometer.” Once the EQ-VAS valuation section is complete, the deck of health state cards is reshuffled and 13 health states are valued using the TTO method. The two missing states are 11111 and “immediate death” as these states cannot be valued directly using the standard TTO because they anchor the scale. The TTO-interview is complemented by a visual aid, a TTO-probe board that graphically displays the difference in life years between health states.

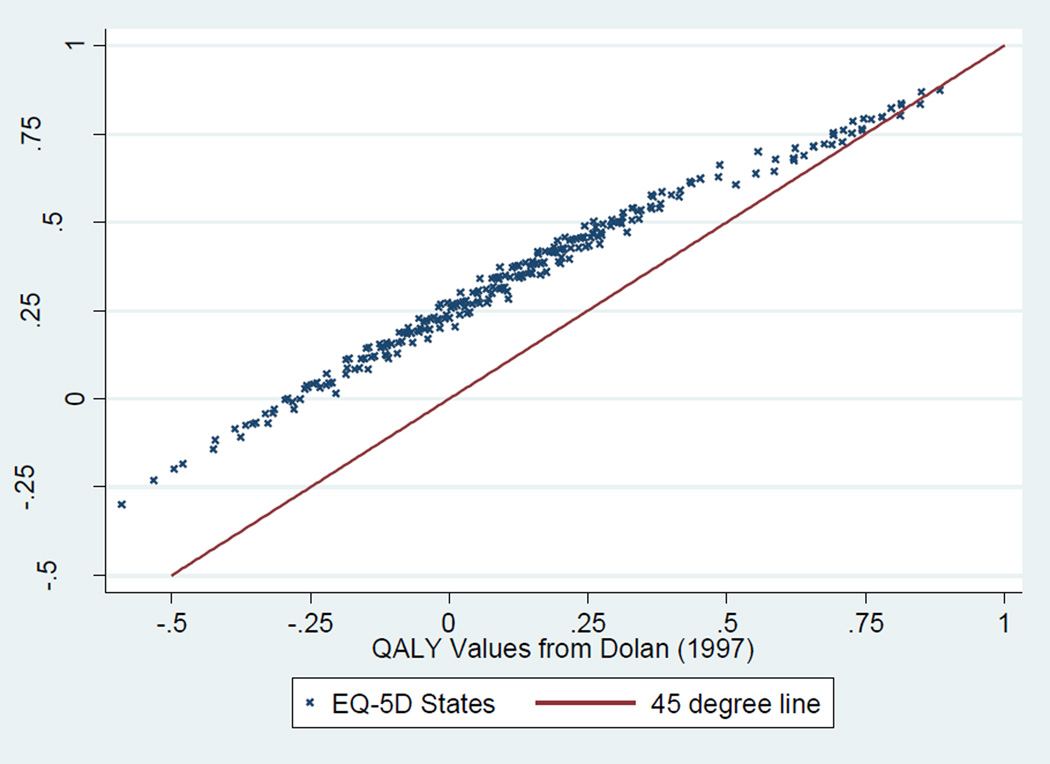
For the TTO analytical sample (N = 3,355), respondents were excluded (1) if only 1 or 2 health states were valued (other than 11111, “immediate death,” and “unconscious”); (2) if all states were given the same value; or (3) if all states were valued worse than “immediate death.” These 3 criteria motivated the exclusion of 1.2% of the TTO respondents. Compared to the original study, we examined the same data and applied an identical multi-attribute regression. The predictions for the 242 nonoptimal EQ-5D states were compared to the published UK value set (Figure 2) to aid policy discussion.

Figure 2.

Comparison of New QALY Estimates and Published Estimates from Dolan (1997)

RESULTS

Multi-attribute Utility Model

Table 1 provides the twelve coefficient estimates for the multi-attribute utility model. Each coefficient represents a statistically significant decrement in value on the QALY scale. To assess face validity, we compared the estimates using Wald tests. As expected, all second level coefficients are significantly smaller than their third level counterparts. Among the second level coefficients, some problems in mobility and usual activities resulted in small decrements compared to some problems on the remaining three domains. The third level coefficients are ranked statistically from worst to best: pain/discomfort, mobility, anxiety/depression, self-care, and usual activities.

The coefficient for any second or third level measures the nonoptimal gap, predicting that the highest value for a nonoptimal health state is 0.906 QALYs (95% CI: 0.898, 0.914). The third level modifier, also known as N3, captures the magnification of any severe problems. If a state has severe problems on any domain, its value significantly decreases by more than a tenth of a QALY (−0.107; 95% CI: −0.122, −0.092).

Examining the residual distribution, the Shapiro-Francia test failed to reject normality at 0.05 significance level and no extreme outliers were identified. However, tests for skewness and excess kurtosis rejected normality (−0.175 and −0.78, respectively), suggesting a more platykurtic distribution over the positive range.

Comparing Predictions with and without Transformation of Worse than Dead Responses

In Figure 2, we compared the predicted values with the previously published estimates to better discuss how the QALY estimates might change guidance over alternative interventions. Near the top end of the QALY scale, the original and new estimates are similar, but this difference is substantially larger for nonmild states. A simple rule of thumb is that:

If the original estimate is less than 0.5, add 0.25 to get the new estimates

For example, the original estimate of 33222 is −0.104 with a new estimate of 0.155. Overall, the original estimates are downward biased by 0.25 for the majority of EQ-5D states (210 out of 243; 86%). The appendix provides the predictions for the 242 EQ-5D states, 95% confidence intervals, and Dolan estimates for comparison. Dead and optimal health (EQ-5D 11111) are excluded from the appendix because these states anchor the QALY scale at 0 and 1, respectively.

DISCUSSION

In this paper, we introduce a general approach to estimating QALY values using trade-off responses. We demonstrate the approach by producing a UK value set for the 242 EQ-5D health states. These estimates can be used in cost-utility analyses for National Institue for Health and Clinical Excellence (NICE) guidance, replacing previous estimates (Brazier et al., 2004). If so, regulating agencies like NICE can find that life saving interventions and interventions in patients with relatively mild health states are given higher priority than previously under the original parameters. To better understand the source of difference requires a review of the original estimation procedure.

Paul Dolan conducted the original statistical analysis of the UK MVH TTO responses (Dolan, 1997). Largely, the original analysis is identical to this one, except that the worse-than-dead (WTD) responses were originally changed from (x_i,y_i) to (10, y_i). At the time of the Dolan analysis, the convention within health valuation was to transform trade-off responses into fractions (y/x) (Patrick et al., 1994, Torrance, 1986). For better-than-dead (BTD) responses, fractions ranged from 0 and 1, but WTD fractions ranged from 0 to −39. To force the range of WTD fractions to be similar to the range of BTD fractions, the WTD nonoptimal numeraire values, x_i, were replaced with 10. After this arbitrary replacement, the WTD fractions ranged from 0 to −0.975, which is more similar to the range of BTD fractions. Although making the ranges above and below dead more equal is appealing, this practice has no basis in economic theory or psychometrics. Our paper takes a fresh look at the analysis of then UK TTO responses using a more universal approach and applies a common OLS estimator to produce a value set for EQ-5D states on a QALY scale.

The implications of this paper go beyond the revision of the UK value set and associate cost-utility analyses, as many valuation studies have repeated Dolan’s transformation of WTD responses (Szende et al., 2007). For their estimation of US value set, Shaw et al. applied a slightly different replacement: from (x_i,y_i) to (39, y_i/x_i). Under the Shaw transformation, the resulting fractions range from 1 to −1, not −0.975 like Dolan’s transformation (Shaw et al., 2005, Torrance et al., 1982). Both transformations are well known and have been debated with great scrutiny since their introduction, but more important is that they continue to be applied, because no study has offered an alternative TTO estimator.

In addition to implications for other TTO analyses, studies of SG responses also adopted the Dolan transformation. Brazier and colleagues exclude dead from most SG scenarios, minimizing WTD responses (Brazier et al., 2002, Brazier and Roberts, 2004). Instead, they describe gambles between optimal health (11111) and the “pits” (33333). At the end of their SG valuation task, respondents are asked to choose between the “pits” state (33333) and a gamble between optimal health (11111) and dead. If the “pits” (33333) is considered WTD, the SG WTD response is transformed similar to Dolan’s transformation, from (x_i,y_i) to (10, y_i).

In most PTO protocols, WTD responses are not allowed. Nevertheless, some respondents attempting to report WTD responses for moderate and severe health states report large ratios of the equivalent numbers of patient in the different scenarios (Green, 2001). To accommodate this compression, many researchers estimated median ratio, which is less sensitive than mean ratio to truncation in the tail of a distribution. Again, the method presented here incorporates extreme responses, removing the central impetus to motivate the prohibition of WTD responses and the median as a measure of central tendency.

The assumption of constant proportionality is a limitation of all valuation techniques. As described in the theory section, the value of a health state is measured by varying a numeraire representing quantity of life (i.e., time, risk, persons). For example, the value of a 5-year episode in a health state can be worth more than half the value of a 10-year episode in the same state (i.e., fair innings hypotheses) (Williams, 1997). Researchers have shown the nonproportional effects of duration on the value of an episode (Craig, 2009, Bleichrodt, 2002). In terms of risk, the Allais paradox is common behavioral phenomenon where the attributable value of a health state can not be proportional to its likelihood (Allais, 1953). Furthermore, some respondents can overly favor certainty, such as choosing not to gamble for religious reasons or belief in the rule of rescue (Craig and Ramachandran, 2006, Cookson et al., 2008). In PTOs, issues of fairness and equity raise further challenges to constant proportionality. Because each valuation technique uses a different numeraire and each numeraire can uniquely violate the constant proportionality assumption, the estimated value of a health state can vary by trade-off technique (i.e., TTO, SG, PTO).

The normality assumption is not necessary for the OLS estimation to be unbiased, but it is quite relevant for the efficiency of the OLS estimates. In particular, if the errors are non-normally distributed, the OLS estimates will be efficient only if the homoskedasticity and independence assumptions are met and the sample is large. At this time, little is known about the distribution of health preference at the population level, and more research is required in this area of health econometrics.

Two further conventions in model specification also merit scrutiny for future UK valuation studies. Shaw and colleagues applied sampling weights to improve the generalizability of their US EQ-5D QALY estimates (Shaw et al., 2005). Yet, selection weight variables, uncertainty in the weight estimates, and measurement error of the responses needed for weight assignment were not accounted for or justified in their analysis. An updated UK study may consider incorporating such weights. A second questionable convention is the use of random and fixed effects at the respondent levels (Brazier et al., 2002). Some respondents can value all states higher than others and the inclusion of individual effects can control for such eccentricities. However, controlling for deviant responses seems to contradict the societal intent of valuation studies. Population-specific studies may examine subpopulation differences (e.g., do patients value health states higher than providers); however, it seems inappropriate to apply a model specification that intentionally marginalizes fringe respondents.

Summary

This paper proposes a more universal approach to health valuation using trade-off responses and introduces an alternative estimator that addresses long-standing issues in conventional practice (i.e., transformation of WTD responses). To demonstrate, we estimated UK health state values for EQ-5D states on a QALY scale and show that these values are substantially different from the published estimates (i.e., if the original estimate is less than 0.5, add 0.25 to get the new estimates). Future work can entail a re-estimation of value sets for other countries, further comparison of values by trade-off techniques, and expansions upon constant proportional random utility model (i.e., duration effects, Allias paradox, and fairness). Implications of the results arise for future NICE evaluations and the whether past NICE evaluations should be revisited due to the sizable differences in QALY estimates.