Evidence-based recommendations for PISA measurements in mitral regurgitation: systematic review, clinical and in-vitro study

Abstract

Background

Guidelines for quantifying mitral regurgitation (MR) using “proximal isovelocity surface area” (PISA) instruct operators to measure the PISA radius from valve orifice to Doppler flow convergence “hemisphere”. Using clinical data and a physically-constructed MR model we (A) analyse the actually-observed colour Doppler PISA shape and (B) test whether instructions to measure a “hemisphere” are helpful.

Methods and results

In part A, the true shape of PISA shells was investigated using three separate approaches. First, a systematic review of published examples consistently showed non-hemispherical, “urchinoid” shapes. Second, our clinical data confirmed that the Doppler-visualized surface is non-hemispherical. Third, in-vitro experiments showed that round orifices never produce a colour Doppler hemisphere.

In part B, six observers were instructed to measure hemisphere radius r_h and (on a second viewing) urchinoid distance (d_u) in 11 clinical PISA datasets; 6 established experts also measured PISA distance as the gold standard. r_h measurements, generated using the hemisphere instruction significantly underestimated expert values (− 28%, p < 0.0005), meaning r_h² was underestimated by approximately 2-fold. d_u measurements, generated using the non-hemisphere instruction were less biased (+ 7%, p = 0.03).

Finally, frame-to-frame variability in PISA distance was found to have a coefficient of variation (CV) of 25% in patients and 9% in in-vitro data. Beat-to-beat variability had a CV of 15% in patients.

Conclusions

Doppler-visualized PISA shells are not hemispherical: we should avoid advising observers to measure a hemispherical radius because it encourages underestimation of orifice area by approximately two-fold. If precision is needed (e.g. to detect changes reliably) multi-frame averaging is essential.

1. Introduction

The PISA method is highly recommended in current guidelines for the quantification of the effective regurgitant orifice area (EROA) in mitral regurgitation [1]. It is generally accepted that the major practical difficulty with the technique lies in the measurement of the distance from the valve orifice to the flow convergence colour Doppler aliasing point (PISA distance).

Operators are instructed that this surface is a hemisphere and to measure its “radius”. Whether this is good advice does not appear to have been formally tested under scientific conditions before becoming established in guidelines and repeated in the literature.

Doppler visualizations are not of speed, which is a quantity independent of direction, but rather of the velocity component in the particular direction towards the probe. This prevents echocardiographic colour Doppler-visualized isovelocity contours from being hemispheres even when the flow is hemispherical. From mathematical first principles the Doppler isovelocity contour is expected to be not a hemisphere, but a distinct ‘flattened sphere’ shape, whose surface shape resembles a sea-urchin, or an “urchinoid” [2–5] (Figs. 1 and 2). Whether this distinction between two abstract mathematical shapes is relevant depends on whether it affects measurements made by operators who are following guideline instructions.

Fig. 1.

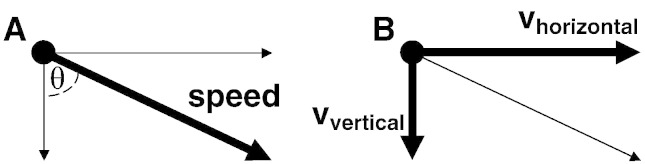
Difference between speed and velocity. The motion of an object can be described in two exactly equivalent ways: speed-and-direction or velocity components. The left panel (A) shows speed and direction. The right panel (B) shows the same motion decomposed into horizontal velocity (v_horizontal) and vertical velocity (v_vertical). For movement in a plane, speed² = v_horizontal² + v_vertical². Doppler shows only movement towards/away from the probe, which in this figure is approximately vertical.

Fig. 2.

Isospeed hemisphere (outer curve) versus isovelocity urchinoid (inner curve). The consequence of the difference between speed (Fig. 1A) and vertical Doppler velocity component (Fig. 1B) is that when flow convergences hemispherically, Doppler imaging correctly shows not a hemisphere but a more completely round shape. For blood moving directly away from the ultrasound probe, i.e. vertically on this figure, (a), speed and velocity are practically synonymous, so the isospeed hemisphere (grey) is at the same position as the Doppler isovelocity surface (blue). For blood moving at 45° (b) the vertical velocity is reduced to cos 45° × speed, i.e. is substantially smaller. Therefore only closer to the orifice (label b on right), where the speed is even higher, is the Doppler velocity component high enough to match its value at (a). For blood moving almost perpendicularly to the ultrasound beam (c), the vertical Doppler velocity component is very much smaller than the speed for example by a factor of ~ 10 at 84° (cos 84° ≈ 0.10). Therefore the Doppler isovelocity surface is ~ 10 times closer to the orifice at that angle.

Guidelines imply that PISA EROA should be measured on a single beat without giving a reason, or specifying what level of precision should be expected, or even that the level of precision obtained would be considered adequate by real world clinicians.

In this study first we established the realistic Doppler shape of the PISA flow convergence zone through (i) a systematic review of text descriptions and their corresponding PISA images in published guidelines and research, (ii) clinical Doppler echocardiographic data from patients in our hospital and (iii) a purpose-constructed physical model of mitral regurgitation.

Second, in a controlled experiment in human behaviour we assessed the effect on the measured PISA distance of instructing the operators to measure the “hemisphere radius” r_h, or the “urchinoid distance” d_u without mentioning a hemisphere (Fig. 3).

Fig. 3.

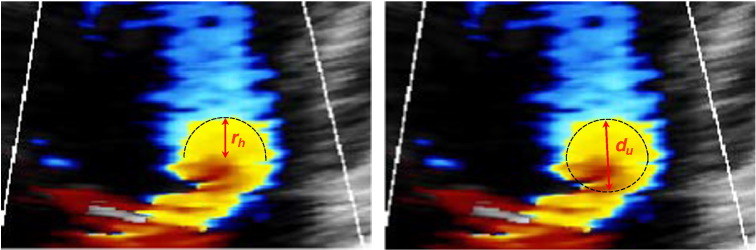
Two possible measurements of PISA from the same frame of a 2D colour Doppler image. On the left the operator has measured the radius of a hemisphere, denoted as distance r_h. On the right the operator has measured the distance from the valve orifice to the aliasing point of the Doppler signal, in the direction of the probe beam, denoted as distance d_u (urchinoid distance, when we assume the PISA shape to be a flattened sphere or urchinoid).

Third we established quantitatively the beat-to-beat and frame-to-frame variability of PISA distance in clinical data. Since some of this variability might be due to genuine biological fluctuation in orifice area [6–9], we also measured the frame-to-frame variability in the data obtained from the in-vitro model, acquired in ideal conditions of absolute stillness.

2. Methods

2.1. Systematic review

We searched PubMed using the search terms ‘PISA mitral regurgitation’, and ‘European Society of cardiology guidelines valvular’ and ‘ACC/AHA guidelines valvular’. A total of 157 studies were found.

We searched the publications for figures that displayed example images of PISA colour flow Doppler and noted from the text the corresponding description of the shape of the PISA flow convergence zone, and the term used to describe the measured PISA distance.

2.2. Clinical data

2.2.1. Clinical subjects

11 subjects with mitral regurgitation (MR), identified from the clinical echocardiography laboratory of Imperial College Healthcare NHS Trust, underwent transthoracic echocardiography. Inclusion criteria were the presence of mild, moderate or severe MR as judged from a conventional clinical echocardiogram. Patients were excluded who had atrial fibrillation or functional valve disease of another valve of greater than moderate severity. The study protocol conforms to the ethical guidelines of the 1975 Declaration of Helsinki as reflected in a priori approval by the institution's human research committee. Written informed consent was obtained.

2.2.2. Clinical echocardiography

Echocardiographic data were acquired with the patient lying in the left lateral decubitus position using an iE33 Philips Medical echocardiography system (Andover, Massachusetts, USA). Continuous wave (CW) Doppler images and colour Doppler video loops were acquired with simultaneous ECG monitoring using a S5-1, 3.5 MHz transducer. Images were acquired in the apical 4 chamber view, using a 30° colour Doppler sector with image optimization performed as per current guidelines [1,10]. For acquisition of 2D colour Doppler maps of the PISA shells, the aliasing velocity was set at 31.9 cm/s, the depth and zoom were adjusted for optimal measurement precision and to optimize the frame rate.

Consecutive cardiac cycles were stored as digital video loops, and each frame was separately converted to an image in bmp format. Still images were stored as DICOM images and then converted to bmp format for subsequent offline analysis.

2.3. Physical model of mitral regurgitation

A physical model simulating mitral regurgitation through a fixed orifice was built to observe the PISA flow convergence zone. A continuous flow pump with an adjustable flow rate circulated a Doppler Test Fluid (Model 707, ATS laboratories, Inc.) in the closed circuit. Two different shapes of orifices were tested (round shape orifice, EROA = 0.30 cm² and slit-like orifice, EROA = 0.31 cm²). The same iE33 Philips Medical echocardiography system (Andover, Massachusetts, USA) and S5-1, 3.5 MHz transducer described above were used for the in-vitro acquisition.

2D colour Doppler video loops each containing 30 separate consecutive frames were acquired and stored digitally. The aliasing velocity used was changed between 12 values in the range 7.7 to 31.9 cm/s, to assess the effect of this on the PISA flow convergence zone shape.

Digital loops were stored and then converted to high quality (uncompressed) AVI files for subsequent analysis offline.

To minimise the effect of noise we ensemble averaged multiple frames. We constructed a single image from each video loop to show the shape of the Doppler flow convergence zone using the average velocity values at each pixel locations from 30 consecutive raw data frames.

2.4. Analysis of the effect of the instructions given for measuring the PISA distance

We asked 6 mutually blinded observers to follow 2 specific instructions to measure the PISA distance on a series of 11 still images, each one taken from a different clinical subject with MR.

• •Under the “hemispherical” instruction, the observers were instructed to measure r_h, the distance of the radius of a hemisphere (Fig. 3)
• •Under the “non-hemispherical” instruction, they were instructed to measure d_u, the urchinoid distance (Fig. 3), from the valve orifice to the aliasing point in the direction of the probe beam

These 11 still frames were then shown to 6 different blinded experts, all of whom were teachers of echocardiography, and all of whom were either specialist imaging cardiologists or cardiac physiologists accredited for performing and interpreting transthoracic echocardiography by the British Society of Echocardiography. These experts were told to measure the PISA distance as they would normally measure it in clinical practice.

The variability of the distance measured using r_h and d_u was compared with the “gold standard” of expert operators measuring the PISA distance according to guideline practice. The groups were compared using ANOVA techniques, with group differences and confidence intervals calculated using Tukey's Honest Significant Differences post-hoc tests. The interobserver variability between the two different instructions was compared using an F-test. The data were log-transformed as graphical analysis revealed that the variances and group differences were proportional to the measured radius. “R” version 2.14.1 was used for analysis [11].

2.5. Measurement of variability of the PISA distance

For the clinical data, the PISA distance was measured for each frame with a single cardiac cycle and then repeated with consecutive cycles using one single trained sonographer performing all studies. The sonographer was instructed to measure the PISA distance using the same technique that would be used in standard clinical practice.

For the data acquired using the physical model, the same sonographer measured the PISA distance in each of the 30 frames of the round orifice. To eliminate operator bias, we also analysed the variability of this model data using custom software written in Matlab that automatedly measured the distance from a fixed orifice location to the aliasing point of the PISA.

Frame-to-frame variability was measured using the coefficient of variation (CV) which was calculated as the standard deviation divided by the mean of the measured PISA distance of all of the frames from the cardiac cycles (for the clinical data) or for the 30 frames (for the physical model data, which had continuous flow).

Beat-to-beat variability was calculated from the clinical data, using 2 different (guideline-recommended) methods for PISA frame selection, for each beat. First, we used the PISA distance for each beat measured from the mid-systolic frame, and then we used the largest PISA distance measured for each beat [1,10,12–14]. From this data, we calculated the coefficients of variation from the means and standard deviation PISA distances across all beats in each individual patient, using the 2 different methods.

To calculate an unbiased estimate of the coefficients of variation across the whole patient group for both frame-to-frame variability and the 2 methods used to determine beat-to-beat variability, we used $\sqrt{\frac{{\displaystyle \sum _1^n\left(C{V_i}^2\right)}}{n}}$, where n is the number of patients and CV_i is the CV of the i^th patient.

2.6. Scientific integrity

All authors confirm that the study was designed to make measurements without bias, to be held jointly and severally responsible for procedural deficiency, and to retract the paper if any is suspected. We are aware of no reason why the study if reproduced in independent hands by these described methods should give different results. Patients were recruited only by the method described. Measurements were made blinded and uniformly. No data were deleted, nor re-measured to favour one result over another [15]. The authors are committed to conducting and presenting research reliably and without precondition welcome workers seeking to confirm, develop, or contradict these findings.

3. Results

3.1. Qualitative description of PISA shape

3.1.1. Systematic review of published literature

The terms used to describe the PISA distance, the descriptions and the images of PISA Doppler flow convergence zone identified from the systematic review of all publications found on PubMed are shown in Fig. 4.

Fig. 4.

Examples taken from the systematic review of the published literature showing the terms used to describe the shape and measurement distance of the PISA flow convergence zone and the published images. Specific examples manifesting controversy (A, B and C).

Amongst these publications, in 9 cases the shape of the surface was given as a hemisphere and in one case it was given as “spherical or non-spherical”, in 1 case it was described as hemispheroid, in 1 case as hemiellipsoid, and in 3 cases no short description was given. Amongst these publications, in 9 cases the PISA distance was described as a radius and in 4 as the diameter, and in 2 there was no description of what was being measured.

In 5 out of those describing a hemisphere, the accompanying image selected was not of a hemisphere, but was of a different shape with a much narrower base.

Even these selected ideal examples manifested controversy, perhaps unwittingly. In example A, the authors have drawn a radius in a way that suggests that neither the top nor the bottom markers are appropriate fiducial points for measuring the PISA distance. In example B the authors of the publication draw a PISA distance appropriately to where the orifice appears to be, but the colour profile is distinctly not a hemisphere, despite their description of a ‘hemisphere’ in the text. In example C, the original operator (white cross circled) and paper authors (black double arrow) are in very serious conflict regarding the PISA measurement, with enough discrepancy in their measurements to generate almost 100% disagreement in assessing EROA.

In order not to be wrongly perceived as criticising any particular authors who are tackling an extremely challenging area in which there is currently no consensus, we have not associated individual images with individual publications [1,5–7,12,16–23].

3.1.2. Clinical data

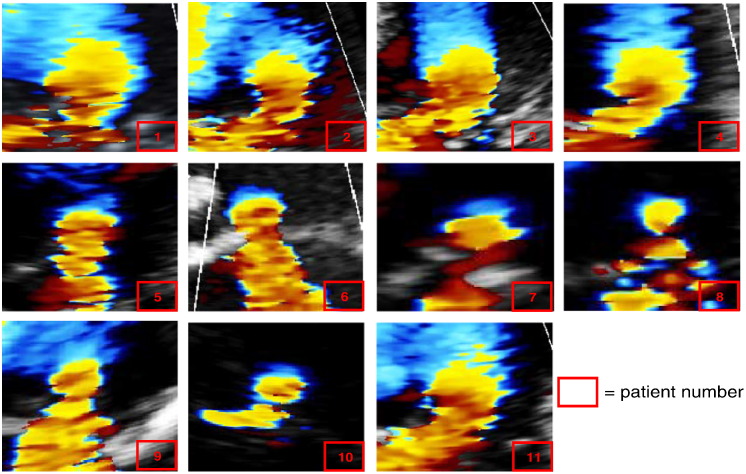
Echocardiographic colour Doppler data suitable for analysis using the PISA technique was obtained from all 11 subjects. Fig. 5 shows the shapes of the flow convergence zones on the colour Doppler images from each subject.

Fig. 5.

Clinical data used to assess the shape of the PISA flow convergence zone and for measurement of PISA distance. Individual frames from colour Doppler loops visualizing PISA flow convergence zone in 11 patients with MR. In most of the frames the shape of PISA is more similar to an urchinoid rather than a hemisphere.

3.1.3. Physical model of mitral regurgitation

30-Frame loops of colour Doppler data were acquired using the physical model with both the slit and round orifices, across a range of 12 aliasing velocities. Figs. 6 and 7 show the average of the 30 frames from each loop of the PISA colour Doppler flow convergence zones, with 3 of the 12 different aliasing velocities (the full dataset showing the PISA shapes at all 12 different aliasing velocities is shown in the Online Appendix 1).

Fig. 6.

Physical model data showing PISA flow convergence zones obtained by averaging 30 frames of 2D colour Doppler video loops of the round orifice sample using Matlab software, to minimise ambiguity. Each image shows the PISA shell obtained in experimental in-vitro condition of stillness at a different aliasing velocity. The shape of the PISA shell is closer to an urchinoid or flattened sphere than a true hemisphere in all frames.

Fig. 7.

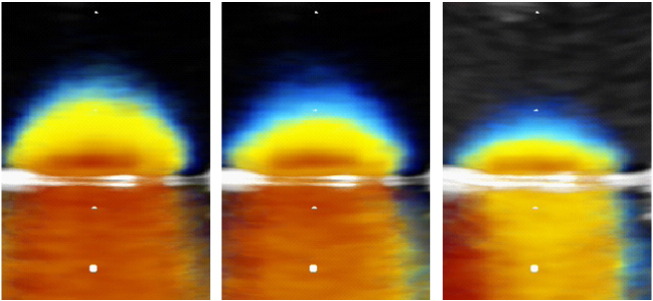
Physical model data showing PISA flow convergence zones obtained by averaging 30 frames of 2D colour Doppler video loops of the slit-like orifice sample using Matlab software, to minimise ambiguity. Each image shows the PISA shell obtained in experimental in-vitro condition of stillness at a different aliasing velocity. In all the frames it is possible to visualize a hemispherical or a hemiellipsoidal shape of PISA shell.

With the round shaped orifice, the Doppler flow convergence zone was urchinoid in shape rather than hemispherical (Fig. 6). When the orifice was slit-like, the Doppler flow convergence zone was closer to being a hemisphere (Fig. 7).

3.2. Comparison of the measured PISA distance with different operator instructions

3.2.1. Clinical data

Analysis of variance showed that the effect of instruction, or experience, had a significant effect on the distance measured (F = 120), Fig. 8. Post-hoc analysis using Tukey's HSD demonstrated that observers, when instructed to measure the PISA distance as the radius of a hemisphere reported a significantly smaller value (mean value 28% smaller, 95% CI 24 to 33%, p < 0.0001) than the experts. In contrast, when given the non-hemispherical instructions, the urchinoid distances d_u measured were instead marginally higher than those obtained by the experts (mean values 7% greater, 95% CI 1 to 14%, p = 0.03).

Fig. 8.

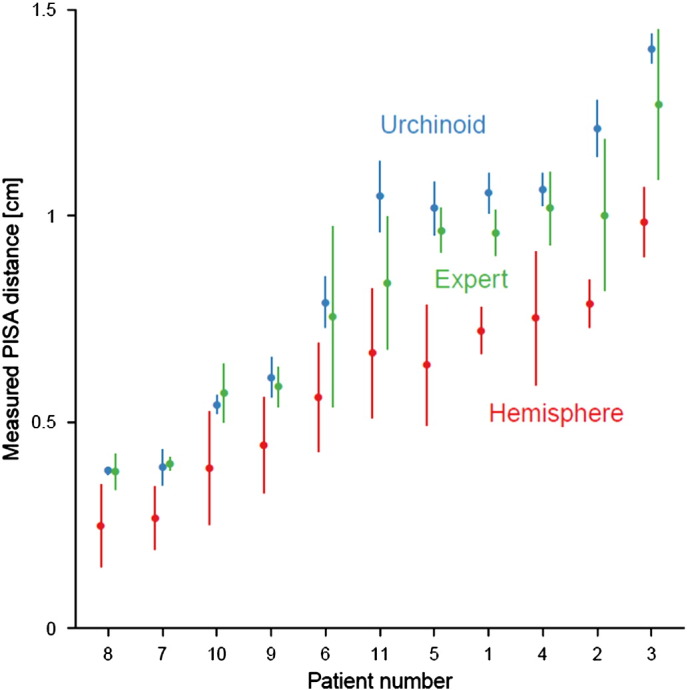
Measured PISA distance for the 11 clinical patients, as measured by experts and observers instructed to measure either the radius of a hemisphere, r_h, or the urchinoid distance, d_u. The distance was consistently smaller when operators were measuring r_h than either when they measured d_u or when experts measured PISA distance according to their usual clinical practice. In addition the spread of values for each individual patient for each of the measurement techniques was smaller when observers measured d_u than for the other groups. Lines represent 95% confidence intervals.

The instruction to measure a hemisphere radius produced not only a smaller value but also a larger spread of values between observers. The standard deviation of the measurement error when measuring PISA distance as the radius of a hemisphere was double that than with non-hemispherical instructions (0.11 vs 0.05 cm; p < 0.0001).

3.3. Measurement of variability of the PISA distance

For each individual clinical data set and for the round orifice physical model data, the variability of PISA measurement distance was calculated using the coefficient of variation (CV).

3.3.1. Within patient variability

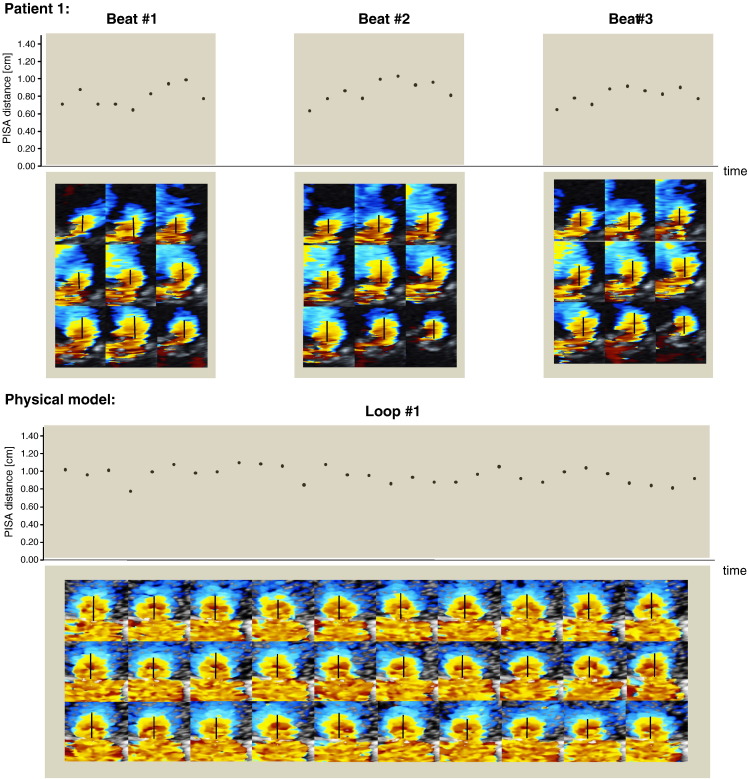
Frame-to-frame variability of PISA measurements across the entire group of patients using each individual CV was 25% (range across individual patients 14–37%). Beat-to-beat variability was narrower. Using the “mid-systolic frame” definition, beat-to-beat variability was 15.5% (range across individual patients 2–29%). Using the “largest PISA distance” definition, beat-to-beat variability was 14.6% (range across individual patients 3–28%). Fig. 9 (top panel) shows the colour Doppler data and corresponding PISA distance measurements for each systolic frame for three consecutive beats in patient 1. The images of all patients are displayed in the Online Appendix 2 in the same format.

Fig. 9.

Frame-to-frame and beat-to-beat data for assessing the variability of PISA shape and PISA distance. Top panel: example data from patient 1. Nine systolic frames for each of the 3 beats of colour Doppler PISA data showing the inter and intra beat variability in measuring PISA distance. Bottom panel: variability of measuring PISA distance using the in-vitro model. 30 frames of a 2D colour Doppler video loop showing intraobserver variability in measuring the distance of the flow convergence zone of the round orifice.

3.3.2. In-vitro variability

Using the in-vitro static model with continuous flow through a round orifice we were aiming to minimise the variability of PISA measurement distance. Despite these conditions, the calculated CV for the PISA distance measurements of the 30 colour Doppler frames was found to be 9% (Fig. 9, bottom panel).

The measurements of the PISA distance made by the sonographer were not significantly different from the ones made by the automated analysis software (p = 0.3).

4. Discussion

Real-life published images, our local clinical echocardiograms, and images from the physical model, all indicate that the true shape of the PISA Doppler flow convergence zone is an “urchinoid” or a sphere flattened at the base, rather than a hemisphere. This distinction is not academic: observers instructed to measure a hemisphere consistently underestimate PISA distance, resulting in an EROA that is underestimated by a factor of ~ 2 because the measured radius is squared for the area calculation.

Beat-to-beat variability in PISA distance from single measurements is large. This study calculates how many beats must be measured and averaged in order to obtain any required level of precision. Simply calling for “more training” cannot help because the variability is present even under the artificially idealised perfectly-still, stable-flow conditions of the physical model.

4.1. The “hemisphere radius” instruction — helpful or not?

Current guidelines instruct echocardiographers when measuring the PISA distance to measure a hemisphere radius. Although the underlying mathematical concept is a series of concentric hemispherical shells of blood moving at progressively increasing speed towards the orifice there is no reason to expect Doppler visualization to show this pattern, because Doppler shows only the vector velocity component (towards or away from the probe) and not speed. Simple guidance is good, but guidance that biases operators away from correct measurement is not. Our study suggests that an instruction to measure “hemisphere radius” encourages the operator to look for a semicircle of colour, and use the base of that semicircle as the starting point of measurement of the “radius”. In fact, the colour profile of the flow convergence zone is more like a complete round ball, with a flattened base, i.e. if there is a visible semicircle the orifice location is well below the lowest point of the semicircle. Instructions should avoid the words “hemisphere radius”.

The “hemisphere” instruction reduced the measured PISA distance to 72% of the value measured by experts. This reduction results in an even more drastic underestimation of the orifice area, to 52% of its true value, i.e. by a factor of 2, because the radius is squared (0.72 × 0.72 = 0.52).

In practice how often this underestimation of EROA affects the categorisation of MR severity in patients depends on the distribution of EROA values. Guidelines recommend severe mitral regurgitation to be diagnosed at an EROA > 0.4 cm². Any patients with measured values in the moderate range of 0.20 to 0.40 cm² using the “hemisphere” instruction would otherwise have measurements of 0.40 to 0.80 cm², i.e. severe when measured correctly: the word “hemisphere” would have caused those patients to have their MR severity miscategorised as non-severe.

4.2. Why does the PISA vary between beats?

When measurements vary between beats, this can be because of genuine physiological beat-to-beat variability or measurement error. Examining clinical data alone does not easily allow these two possibilities to be distinguished. In this study we also made measurements with the same scanner in a physically constructed simplified model of mitral regurgitation in which there was deliberately no pulsatility and the entire structure was free of the translational movement that is inherent in clinical measurements. Even in this artificially idealised setting, there was substantial frame-to-frame variability in the measured PISA distances. From this we conclude that the limits to the resolution of ultrasound physics of a standard widely-used clinical scanner, in combination with any natural perturbations in flow in a model that is artificially designed to have steady flow, are enough to produce this frame-to-frame variability of 9%. 9% is therefore a floor below which clinical variability can never fall under any circumstances using this equipment and protocol. Only the increment from 9% to our clinically-observed frame-to-frame variability of 25% could ever be discussed as a target for improvement.

Some of the measurement variability (that between 15% and 25%) comes from the variation in the PISA distance during the cardiac cycle. We know this because when we implement a policy of measuring PISA distance at a fixed predetermined time, such as midsystole or the frame with the largest PISA distance, the variability in the PISA distance falls to 15%.

The residual difference between the theoretical minimal variability of 9%, and the observed 15% arises from a combination of factors including movement of the heart and biological beat-to-beat variability with resultant nonequality of between beat cardiac flows. In clinical practice, the relevant variability is between one complete examination and the next, which will be wider than this because the probe position cannot be guaranteed to be the same. If the patient has atrial fibrillation, beat-to-beat variability becomes much greater, and even sinus rhythm with frequent ectopy causes functional changes in blood flow that last beyond the ectopic beats themselves. Different valve shapes, regurgitant orifice shapes and other valve disease do not themselves cause beat-to-beat variability, but do change blood flow patterns preventing the true orifice area from being assessed using blood flow analysis: it is for this reason that PISA, and similar algorithms, always indicate effective regurgitant orifice area (EROA) rather than orifice area.

4.3. How many measurements of PISA distance should be made to give a clinically adequate result?

Our data augment current guidelines by making it possible for any clinician to design a protocol to measure PISA EROA to any precision clinically desired. Knowing the error in single measurements of PISA distance permits calculation of the number of beats that must be averaged to obtain any desired measurement precision.

For example, if clinicians require EROA with a confidence interval of ± 10% then the standard error of the EROA must be ~ 10/1.96 = 5.1%, meaning that the standard error of the PISA distance must be ~ 2.55% (assuming there is no error in the peak CW velocity). Our data indicate that a single measurement of PISA distance has a standard deviation of 15%. To reduce this to 2.55% requires averaging of (15/2.55)^2 beats, i.e. 35 beats. With this number of measurements an EROA might be presented for one patient as “0.45 cm², 95% confidence interval 0.41 to 0.49 cm²” so the clinician could be confident that the underlying measurement is > 0.40 cm². Clearly if clinicians require greater measurement precision, or there is the possibility of variation between measurements in CW peak velocity, then more beats must be averaged. For departments conducting serial follow-up of patients with mitral regurgitation to detect changes in EROA, such as sometimes occurs in trials of intervention, the confidence interval of interest is not that of a measurement at one time-point but that of the difference between EROA at two time-points: this confidence interval is √2 times larger, and therefore twice as many beats, 70, must be measured at each time point.

In Table 1 we show how many beats must be averaged for any clinically desired precision of the EROA and in Table 2 how many beats must be averaged for any clinically desired precision of ∆EROA between visits. Referrers unaware of these values may overinterpret random variation as a genuine change or, worse, require a very large change (> 200 or 300%) before taking action. Guidelines advising on the quantification of valve disease could usefully be augmented with tables such as this, devised using measures in human patients with mitral regurgitation, so that operators can measure sufficient beats for their local purposes. If operators are not made aware of the need to measure multiple beats they may lose confidence in echocardiographic methods or lose trust in the guidelines.

Table 1.

Number of beats to be averaged for different levels of clinically desired precision of EROA calculation using PISA method, assuming 0% and 3% error in measuring peak CW velocity.

Desired size of 95% confidence interval of EROA	Coefficient of variation CW Doppler	No. of beats needed at visit
20%	0%	9
10%	0%	35
5%	0%	138
20%	3%	12
10%	3%	71
5%	3%	864

Table 2.

Number of beats to be averaged for different levels of clinically desired precision of ΔEROA calculation using PISA method in the follow-up of patients with mitral regurgitation, assuming 0% and 3% error in measuring peak CW velocity. The confidence interval of interest is not that of a measurement at one time-point but that of the difference between EROA at two time-points: this confidence interval is √2 times larger. Therefore double the number of beats is needed to achieve the same level of precision in the difference between two visits as compared to the absolute value from a single visit.

Desired size of 95% confidence interval of ∆EROA	Coefficient of variation CW Doppler	No. of beats needed at visit
20%	0%	17
10%	0%	69
5%	0%	277
20%	3%	24
10%	3%	141
5%	3%	1729

Another undesirable approach that may be taken by referrers unaware of beat to beat variability is to require a large number of follow-up visits, each measuring a few (or just one) beats in order to observe the sequence of EROAs thus obtained. This analysis shows that there is no possibility of consistent gradual trends with time unless sufficient beats are measured and averaged. Costs for a health care system are considerably smaller to measure 34 extra beats during one visit than to make 34 extra visits, to gain the same quantitative information.

4.4. 35 (or 70) beats is too much to ask for

This number of beats is 10 or 20 times the number described in protocols (typically 3) and may appear inconvenient. However if the scan is intended to measure an EROA “within ± 10%”, then this is the minimal amount of clinical data that can provide this. Reluctance to measure enough beats is unlikely to arise from reluctance to spend the necessary time acquiring Doppler data since 35 to 70 beats totals only 0.5–1 minute at a heart rate of 70 bpm. Reluctance arises from the impossibility of fully automatic image analysis, and the resultant requirement for 0.5–1 minute of analysis time per beat, thus totalling 15 minutes–1 hour of analysis alone.

This could be resolved in 3 ways: 1) develop a fully automated analysis system [24]; 2) allocate enough time to acquire and analyse enough beats to make measurements of the precision requested by local clinicians (Tables 1 and 2); and 3) abandon attempts to quantify EROA and revert to qualitative judgements that have been shown to be unreliable [25]. Option 3 may seem extreme but continuing to measure EROA in an unreliable manner, while rejecting the steps necessary to reduce the random variability to acceptable levels, potentially exposes patients to harm. A conceivable final option, to measure several values and pick the one which best matches the value from previous sessions or the overall echocardiographic and/or clinical picture, is not acceptable because in clinical practice it is self-deception and in research practice it is the first step to fraud.

4.5. Slit-like orifice

The physical model allows assessment of different geometric shapes of orifice although we have deliberately kept the spectrum simple. It is known [5,26,27] that the PISA shape differs between shapes of mitral valve orifice, and may differ with the aetiology of the MR. The orifice in functional MR is generally more elongated or slit-like than organic MR, and our physical model data suggest that measurement of PISA distance may be less valid with slit-like orifices. Our data and previous observations suggest that in functional MR, PISA-derived assessments of valve severity may be less useful.

4.6. Study limitations

The physical model was intentionally designed to eliminate variability arising from movement from the orifice which inevitably occurs in the beating heart. The narrow scatter seen in the physical model should not been taken as a target of what should be achievable in clinical practice. Instead it is a limit beyond which claims in clinical practice are not believable. The model has a simplistic design of flat walls and a fixed orifice of regular shape. Real life walls are more complex, and all real life orifices are much more complex in their 3 dimensional structure. While these extra complexities in real life make it harder to truly assess orifice area, they should not themselves cause additional beat-to-beat variability which is the target of this study.

Assessment of variability between beats (or frames) does not need a large number of patients but does need meticulously unbiased measurement of several beats in each patient. Our study covered only 11 subjects but carefully presented their data to 6 experts and to 6 mutually blinded observers under two forms of instruction, to provide previously unavailable information.

This study was not designed to classify the severity of the mitral regurgitation, nor to monitor progression of the disease, but rather only to investigate the shape of the PISA shell and the suitability of commonly-given instruction for its measurement, and also to support anyone planning to use PISA for purposes requiring any degree of precision.

4.6.1. Linear versus sector transducer

With a linear transducer the Doppler velocity component being visualized is almost exactly vertical over a wide region. With a sector transducer the Doppler velocity component being visualized is averaged vertically, so that it is not exactly the vertical component that is being assessed, for points away from the centreline. However, at the distances from the probe that are typical for PISA assessment, the rays even from a sector probe are almost parallel, so that the dominant contribution to inequality between Doppler velocity and speed in a clinical PISA evaluation is the angle of blood flow, and not the spread of the ultrasound beam.

4.6.2. All data, all the time

Like any science, our study may be in error. We encourage readers to recheck, confirm or refute these findings using the online dataset. The online supplement exposes all images acquired in this study so that if image quality is considered inadequate against local standards routine practice, this study can be discredited. Readers may alternatively prefer to check with locally-acquired clinical data, and if they wish to re-run the physical model we are ready to give any assistance necessary.

5. Conclusion

The shape of the Doppler-visualized PISA surface is not a hemisphere, but rather an “urchinoid” or a sphere flattened at the base. Advising observers to measure hemisphere-radius encourages underestimation of orifice area by approximately two-fold. Moreover, the variability in PISA distance is sizeable, even under the “optimal” conditions of a physical model. Operators and clinicians should be aware of this variability and resultant ceiling of measurement precision that is possible, especially in the serial follow-up of patients in whom they are attempting to detect small changes in EROA. Guiding operators to seek an “urchinoid” (or at least not mentioning “hemisphere”) would minimise bias, and using multi-frame averaging would maximise reproducibility.

Appendix A. Supplementary data

Supplementary material 1.

Supplementary material 2.

Supplementary material 3.