Superimposed topographic and chemical cues synergistically guide neurite outgrowth

Abstract

Guidance of neuronal extensions is a complex process essential for linking neurons into complex functional networks underlying the workings of the neural system. Decades of research have suggested the ability of neuronal growth cones to integrate multiple types of cues during the extension process, but also have raised numerous still unanswered questions about synergy or antagonism between the superimposed chemical and mechanical signaling inputs. In this study, using a novel microfabricated analysis platform, we investigate the response of primary mouse embryonic hippocampal neurons to superimposed topographic and soluble chemical cues. We find that an optimal spatial frequency of topographic cues exists, maximizing the precision of the neurite extension. This optimal frequency can help the extending neurites navigate a topographically complex environment, providing pronounced directional selectivity. We also demonstrate that this cue can synergistically enhance attractive and suppress repulsive guidance by the bi-functional soluble cue Netrin-1, and eliminate the repulsive guidance by a chemorepellent Semaphorin3A (Sema3A). These results suggest that topographic cues can provide optimal periodic input into the guidance signaling processes involved in growth cone chemoattraction and can synergistically interact with chemical gradients of soluble guidance cues, shedding light on complex events accompanying the development of the functional nervous system.

INTRODUCTION

Complex, spatially resolved re-organization of constituent cells is a hallmark of tissue development, emphasized by the intricate nature of the resulting tissue architectures. This is especially prominent in development and re-organization of nervous tissue, particularly the brain. Neurons can send projections, or neurites, over considerable distances, far exceeding the size of the cell body^1,2. The neurites can follow convoluted trajectories to ultimately link with other cells, taking their cues from both mechanical and chemical environmental features^3–6. Successful cell connections of extending neurites can lead to formation of full-fledged axons and dendrites, and synaptic junctions. Whereas chemotactic tropism of extending neurites has been explored at a substantial level of detail^7–12, both in terms of the underlying signaling networks and the quantitative characteristics of the migration processes, understanding mechanical cues and their influence on neurite guidance has lagged far behind. However, with the advent of new technologies allowing for more precise, reproducible and high-throughput analysis¹³, one can hope to explore not only the influence of mechanical and chemical cues, but also their interplay at a level of quantification not previously possible. In this report, we illustrate how the response of migrating neurites to complex mechanical and chemical cues can be analyzed within the context of novel integrated micro-fabricated devices, permitting simultaneous control of the texture of the cell adhesion substratum and of the gradients of soluble chemical cues.

The micro-texture or micro-topography of the immediate physical environment of an extending neurite can constitute a powerful cue defining the directionality and extent of the chemotropic growth and migration^14,15. In vivo, these mechanical cues can arise from the complex preexisting features of the extracellular matrix and cellular organization within the field of neurite migration, leading to such phenomena as contact guidance and fasciculation^16–18. Recent in vitro studies of neurite guidance in the presence of well-controlled micro-texture or micro-topography of the cell adhesion substrata also suggest that the immediate environment of an extending neurite can be a powerful, perhaps dominant cue defining its directionality^15,19–22. For instance, extending neurites were shown to exhibit a high degree of fidelity in orientation and migration on surfaces with arrays of micro-ridges^23,24. Furthermore, neurites extending from hippocampal neurons can also exhibit mostly linear orientations when cultured on arrays of micro-pillars arranged in parallel rows and columns of equal inter-pillar spacing^25,26. The precision of following straight lines of equally spaced pillars within regular 2D arrays with 'square' pillar arrangements was shown to be a function of the pillar density, for reasons not yet understood²⁶. These and other studies have raised a series of questions that remain unanswered. First, it is not clear whether the guidance by micro-pillars within large 2D arrays can occur in different pillar arrangements (e.g., hexagonal vs. 'square' geometry); whether there is an optimal spacing between the pillars leading to maximal guidance fidelity that decreases for either higher or lower pillar densities; and whether neurite extension can be sensitive to an anisotropic pillar arrangement, e.g., with density varying in one but not the other of two orthogonal directions. Most importantly, we still do not know how neurite extension can be controlled by a combination of chemical and topography-dependent cues. We begin to address these questions in this report.

An important advantage of micro-fabrication technologies is the high degree of control that can be exercised over multiple aspects of the extracellular environment, thus permitting one to examine cell responses to a combinatorial presentation of multiple cues^22,27–33. Recent experiments with the simultaneous presentation of multiple types of signaling inputs that can affect neurite navigation yielded surprising results, suggesting that our understanding of the biological processes underlying the control of neurite migration is still very incomplete, even for purely chemical cues^22,34,35. For instance, combinations of soluble and substratum-bound ligand gradients, capable of separately guiding neurite extension, yielded cues whose effect was in some cases consistent and some opposite of what was expected based on the presentation of each cue alone³⁵. It is therefore instructive to investigate neurite responses to combinatorial chemical and mechanical cues, under precise and quantifiable conditions enabled by current microfabrication technologies. Here we explored the responses of neurites extending from embryonic hippocampal neurons cultured on substrata of different local micro-topographies and geometric organizations, combined with attractive and repulsive soluble chemical cues. The results suggested the potential for powerful synergies between distinct guidance cues that could be relevant for our understanding of complex in vivo guidance control, both in development and regeneration, as well as for the efforts to create model neuronal networks interfaced with artificial growth substrata and in drug screening applications.

MATERIALS AND METHODS

Cell isolation and culture

Primary neurons were isolated from hippocampi of mouse embryos at the age of embryonic day 16.5 (E16.5). Mice were housed in the Johns Hopkins University vivarium and colonies were maintained in accordance with institutional guidelines. Isolation of primary hippocampal neurons was conducted using a protocol approved by the Johns Hopkins University Animal Care and Use Committee. The hippocampi were dissociated using 0.25% trypsin (Life Technologies) and filtered through 35 µm filter to create a single-cell suspension. For studies involving the guidance of neurites by topographic signals in isolation, the cells were seeded on silicon substrata with pillar arrays pre-coated with poly-L-lysine (Sigma) and cultured for 22 h. For studies involving the combined influence of chemical signals and topographic signals, the cells were introduced into the cell chamber of a polydimethylsiloxane (PDMS) (RTV615, R.S. Hughes) microfluidic device integrated with a silicon substrata with pillar arrays. The cell chamber was coated with poly-L-lysine prior to introduction of neurons. The culture was allowed to attach on the substrata for 4 h prior to exposure to stimuli for 18 h.

All cultures of primary hippocampal neurons were conducted in Neurobasal medium supplemented with B27, Glutamax, sodium pyruvate and glucose (all from Life Technologies). Human Netrin-1 and human Semaphorin-3A used for generating soluble linear gradients were procured from R&D systems. For experiments with a netrin-1 gradient, the concentration of netrin-1 was varied from 500ng/ml to 0ng/ml across the width of the cell chamber. For Sema3A gradients, the concentration decreased linearly from 250ng/ml to 0ng/ml. For both sets of experiments, a fluorescent dye was used to visualize the gradient and a stable linear gradient was observed after 1 h of starting flow.

Immunostaining

The microfluidic device was detached from the silicon substrata at the end-point of the experiment and the cells were fixed using 4% paraformaldehyde solution (Sigma). The cell bodies and neurites were visualized using immunostaining with mouse monoclonal antibody against neuron specific β-III- tubulin (Covance, 1:5000). The nuclei were counter-stained using Hoechst 33342 (Life Technologies, 1:500). The cells were imaged using confocal microscopy (Zeiss Meta 510).

Image analysis and definition of metrics

Images were analyzed using a custom-designed software in MATLAB (The Mathworks Inc.) capable of segmenting cell bodies and neurites. An algorithm was developed to automatically compute the length, initial angle, final angle, turning angle, overall angle, and the overall trajectory of each neurite. The initial angle was the angle for the first 10 µm at the base of the neurite adjacent to the cell body. The final angle was defined as the angle for the last 10 µm farthest from the cell body. The turning angle was defined as the difference between the final angle and the initial angle. The overall angle was defined as the angle of the line joining the base of the neurite to the growing tip. For all images, the horizontal axis to the right was defined as 0° and all counter-clockwise angles were assigned positive values and clockwise angles were assigned negative values.

To compare the propensity of different signals to guide neurites, we introduced a metric called the guidance index. The guidance index was defined for a specific angle by taking a sector of width 10° around the angle of consideration. The number of neurites whose final angles were within this sector was computed and normalized to the number of neurites that would have been expected to have final angles in that sector in a uniform distribution of neurite final angles. This ratio was termed ‘the guidance index’ and was an indicator of the fold-change of the number of neurites growing in a specific direction over what would be expected in the absence of any guidance signals. When expressed quantitatively,

$$\text{Guidance Index for angle}\alpha =\frac{\text{Number of neurites with final angles between}(\alpha -5)\text{and}(\alpha +5)}{\text{Number of neurites expected to have final angles between}(\alpha -5)\text{and}(\alpha +5)\text{in a uniform distribution}}$$

To further understand the degree of anisotropy of neurite guidance introduced by topographic signals or chemical signals, we introduced a metric for quantifying the bias in the system. The bias metric was defined as the ratio of the average of the guidance indices along the 3 preferred topographical directions towards the right (i.e. 0°, 60° and −60°) to the average of the guidance indices along the 3 preferred topographical directions towards the left (i.e. 180°, 120° and −120°).

$$\text{Bias Metric}=\frac{\text{Average of guidance indices for}0°,-60°\text{and}60°}{\text{Average of guidance indices for}180°,-120°\text{and}120°}$$

RESULTS

Construction of a device combining defined substratum micro-topography with imposition of gradients of soluble chemical cues

Our goal was to design and fabricate a device that would facilitate the simultaneous exposure of neurons to soluble chemical signals from the medium surrounding the cell and to topographically-defined signals from the cell adhesion substratum. For the precise control of the chemical micro-environment, we designed a microfluidic device capable of generating a linear concentration gradient of a soluble molecule (Fig. 1a). We designed a cell chamber into which neurons were seeded using cell seeding ports. The cell chamber was flanked on either side by channels containing media with and without the molecule of interest. Diffusion across the cell chamber created a linear concentration gradient as previously described³⁶. The PDMS microfluidic devices were fabricated using soft lithography, following standard protocols^37,38.

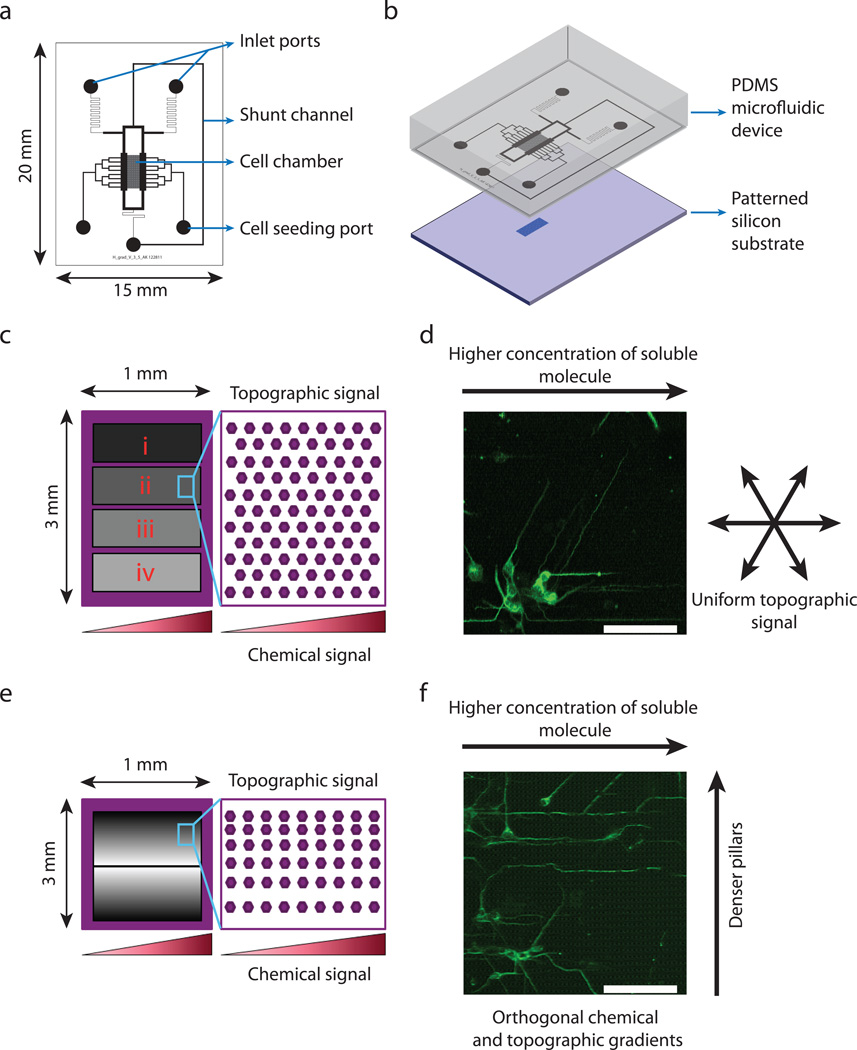
Fig. 1.

Combined microfluidically imposed graded cues and patterned silicon cell adhesion substrata allow simultaneous chemical and topographic guidance of neurites. (a) Schematic representation of the gradient-generating microfluidic device showing cell chamber, cell seeding port, inlet ports, and the shunt channel. (b) Integration of the microfluidic device with the patterned silicon substrate to create a combined platform for simultaneous chemical and topographic guidance of neurites. (c) Schematic representation of patterned substrata with spatially uniform topography. Each substratum contains four distinct pillar arrays, indicated i, ii, iii, and iv, having spacing of 4.0 µm, 1.8 µm,1.4 µm, and 0.6 µm, respectively. (d) Representative image of E16.5 hippocampal neurons cultured for 22h in a Netrin-1 gradient over a substratum with uniform topography. Cells have been immunostained for β-III tubulin. (e) Schematic representation of a patterned substratum with a topographic gradient. The spacing in the x-direction is uniform while the spacing in the y-direction is linearly decreasing from the center to the edges of the pillar array. (f) Representative image of E16.5 mouse hippocampal neurons cultured for 22h on a substratum with combined orthogonal Netrin-1 and topographic gradients. Scale bar is 50 µm.

The topographic micro-environment was controlled by micro-fabricating pillar arrays on silicon substrata, which were then coated with poly-L-lysine by adsorption. For our studies we used two different geometries of pillar arrays (Fig. 1c,e). In the first type of substrata, we designed and fabricated hexagonal pillar arrays that were topographically isotropic in all directions (Fig. 1c). Each substratum was covered with 4 different pillar arrays as indicated by i, ii, iii, and iv in Fig. 1c. For all arrays, the pillar width and height were kept constant (1.6 µm and 3 µm, respectively). The spacing between the pillars was uniform within each pillar array but varied between the different arrays. Arrays i, ii, iii, and iv had 4.0 µm, 1.8 µm, 1.4 µm, and 0.6 µm inter-pillar spacings, respectively. The second type of substrata was designed to present a topographically anisotropic signal to neurons (Fig. 1e). In this substratum, we fabricated rectangular pillar arrays in which the pillar widths and heights were kept constant and the same as the isotropic substratum described above. The inter-pillar spacing was kept constant at 1.6 µm in the x-direction (horizontal), while the inter-pillar spacing in the y-direction (vertical) was linearly increased from 0.6 µm at the edges of the substratum to 5.6 µm in the center with a step size of 50 nm. Thus by design, this substratum had a different degree of topographic anisotropy at different positions along the y-direction.

The silicon substrata were integrated with the microfluidic device manually by aligning the pillar arrays directly under the cell chamber using a stereo microscope (Zeiss Stemi DV4) and incubating the devices overnight at 85°C (Fig. 1b). This allowed us to expose the cells inside the cell chamber to chemical and topographical neurite guidance signals simultaneously. We designed two different experimental paradigms (Fig. 1d,f). In the first, neurons were seeded into the cell chambers of devices integrated with the substrata containing isotropic hexagonal pillar arrays that were then exposed to a concentration gradient across the cell chamber (Fig. 1d). In the second, neurons were seeded onto the topographically anisotropic substrates with a similar concentration gradient. In these experiments we designed the gradient of pillar spacing to be in a direction orthogonal to the chemical gradient (Fig. 1f). These two experimental designs allowed us to study two different cases where topography and chemical signals would interplay in different ways to guide neurite extension. In the first, the substrata alone did not impose any directional bias on axon guidance; only the superimposed soluble chemical gradient was capable of inducing a bias. In the second, the substrata could impose a bias in a direction orthogonal to the bias induced by gradients of chemical signals.

Strength of topographic guidance optimally depends on separation between topographic features

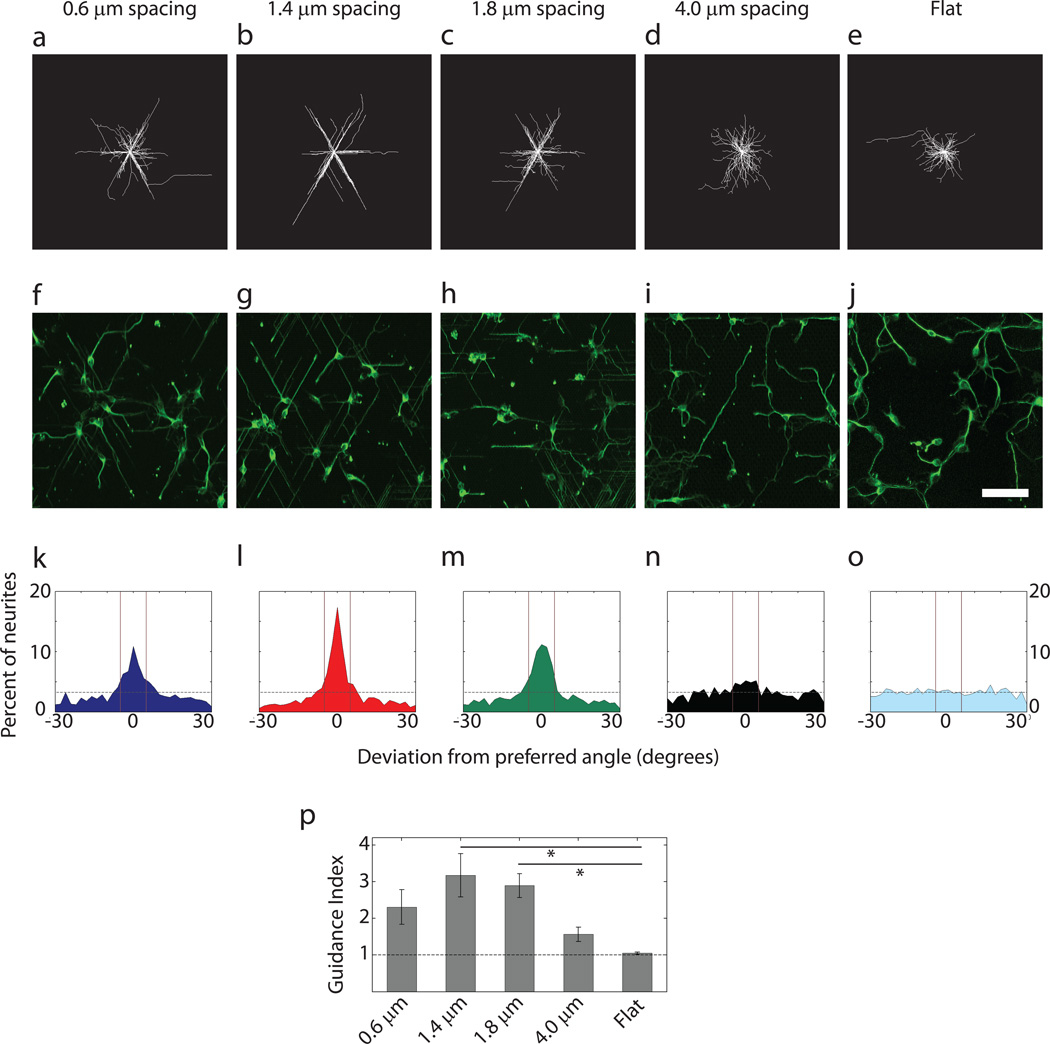
To characterize cell behavior in the device, we first explored whether the cells would be able to display guided neurite extension in response to hexagonal arrays of different spatial frequency (density). Prior analysis suggested that, in square pillar arrays, reducing inter-pillar spacing progressively improves the guidance effect, resulting in an increased probability of straight neurite extension along individual rows of pillars²⁴. We investigated neurite guidance in pillar arrays displaying a different symmetry inherent to the hexagonal pillar arrangements. Primary neurons isolated from the embryonic day 16.5 (E16.5) mouse hippocampus and cultured for 22 h on the isotropic substrata, were fixed and immunostained for β-III tubulin. Analysis of the neurite trajectories for the 4 different isotropic pillar arrays is shown in Fig. 2a–d, f–i. Trajectories on flat surfaces were used as a control (Fig. 2e,j). We found that the hexagonal pattern of the pillars had a strong influence on the direction of neurite growth, resulting in 6 preferred directions along 3 directional axes, sectioning the 360° of available direction angle space into 6 sectors defined by 60° angles. Furthermore, we found that there was indeed an optimal value of inter-pillar separation, corresponding to 1.4 µm spacing (Fig. 2b,g), below and above which the precision of topographic guidance was severely reduced. A weaker but significant guidance by topography was observed for the pillars with 0.6 µm and 1.8 µm spacing (Fig. 2a,f,c,h), whereas pillars with a spacing of 4.0 µm failed to guide neurites along the preferred angles of the hexagonal array (Fig. 2d,i). These results suggested that neurite outgrowth could be strongly guided by the substratum topography, being particularly sensitive to this mechanical cue at an optimal spacing between the topographic features.

Fig. 2.

Guidance of neurites by surface topography displays an optimal regime as a function of the spacing between pillars. (a–e) Overlay of neurites of E16.5 mouse hippocampal neurons cultured for 22h on substrata with spatially uniform topography. (f–j) Representative images of cultures on different substrata immunostained for β-III tubulin to visualize neurites. Scale bar is 50 µm. (k–o) Distribution of the direction of neurite growth around the preferred angles of the substrate topography. The dashed horizontal line represents the expected deviation from the preferred angles in a uniform distribution. The solid vertical lines represent the small angle range of ±5° surrounding the preferred angles. This range was used to calculate the guidance indices. (a),(f) and (k), (b),(g) and (l), (c),(h) and (m), (d),(i) and (n), (e),(j) and (o) correspond to pillar arrays with 0.6 µm, 1.4 µm, 1.8 µm, and 4.0 µm spacings and flat substratum, respectively. Number of neurites for panels (f) through (j) are 423, 428, 366, 439 and 485 respectively. (p) Guidance index of neurites cultured on pillar arrays with different uniform spacings. The dashed line indicates the expected value of guidance index in a uniform distribution. n=3 experimental replicates with 300–500 neurites for each pillar array in each replicate. One-way ANOVA showed that varying pillar density had a statistically significant effect on guidance index (p<0.05). This was followed by pair-wise comparison using Tukey's HSD and * indicates statistical significance at p<0.05 between a pair.

We quantified the deviation of the direction of neurite growth from the preferred topographic angles (i.e. 0°, 60°, 120°, 180°, −60° and −120°). For each neurite, we found the final angle (defined above) and calculated the deviation of that direction from the closest topographically preferred direction. When done for all neurites in a culture, we were able to obtain a distribution of deviation from preferred angles for each topographic condition. This distribution for the arrays with 1.4 µm spacing again showed the strongest peak centered around 0, indicating that a large fraction of neurites do not deviate from topographically dictated angles (Fig. 2l). Pillars with 0.6 µm spacing (Fig. 2k) and 1.8 µm spacing (Fig. 2m) showed wider peaks indicating greater variability in neurite guidance by the topographic signals. The distribution at 4.0 µm inter-pillar separation was essentially random (Fig. 2n) and comparable to the distribution on a flat surface (Fig. 2o). These distribution characteristics prompted us to quantitatively investigate the effectiveness of the pillar arrays to align neurites. More specifically, we examined the number of neurites with final angles within a small range around each preferred direction (±5° around 0°, 60°, 120°, 180°, −60° and −120°) and took the ratio of this value to the number of neurites expected to be within those ranges in a uniform distribution of neurite directions. This metric was defined as the guidance index. As shown in Fig. 2p, this analysis confirmed our observation that guidance is dependent on inter-pillar spacing. Neurites incubated over pillars separated by 1.4 µm had the highest guidance index of 3.17 ± 0.59 (mean ± standard error of mean). An increase or decrease in inter-pillar spacing resulted in a decrease in neurite guidance, with guidance indices of 2.89 ± 0.33 and 2.31 ± 0.47 for spacings of 1.8 µm and 0.6 µm, respectively. Pillar arrays with 4.0 µm spacing had a guidance index of 1.56 ± 0.19, which was not significantly different from a random distribution (1.05 ± 0.03 for the Flat surface) (mean ± standard error of mean for all). These results suggest that topographic guidance is sensitive to the geometry of the underlying pillar arrangements, and displays maximal sensitivity at an optimal inter-pillar spacing.

Guidance by graded topographic signals favors extension along directions with optimal inter-pillar spacing

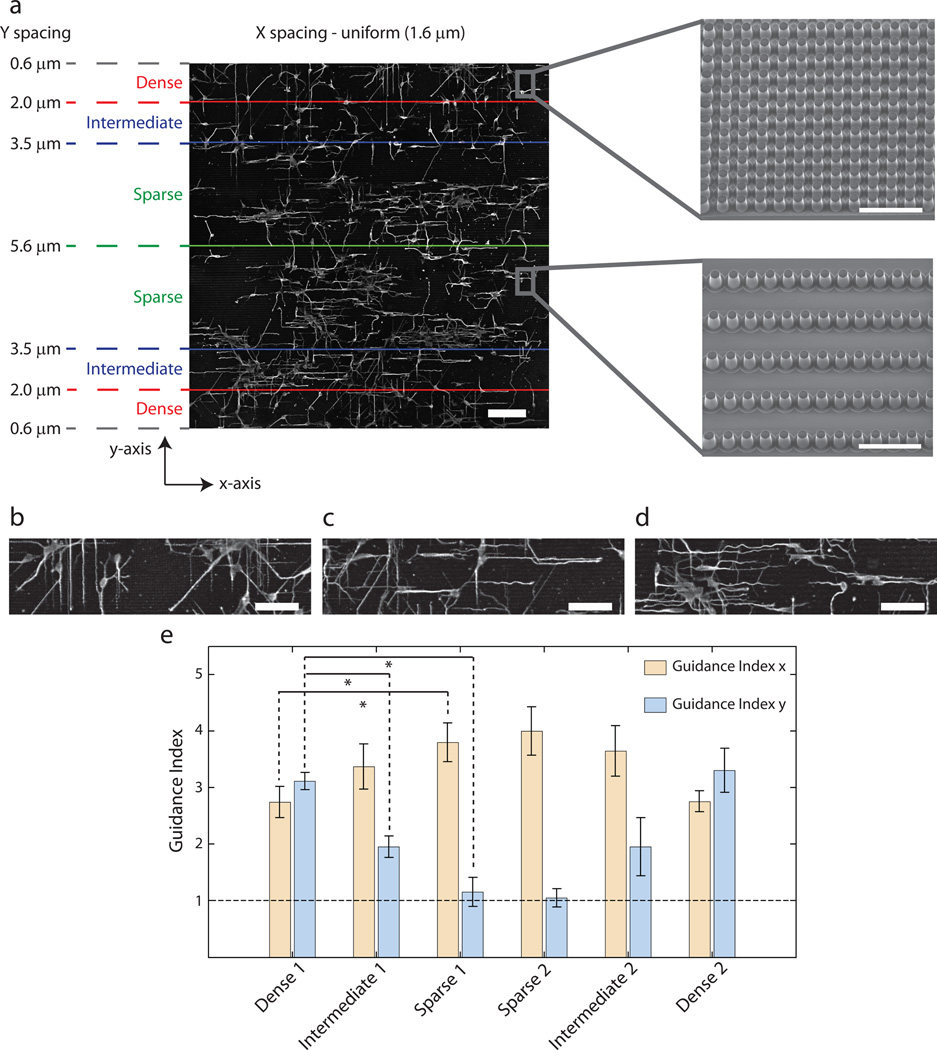
The hexagonal pillar arrays explored so far were each of constant density. It was thus not clear if anisotropic pillar density distribution might affect the directionality of response. More specifically, it is of interest to explore whether the extension of neurites is sensitive to different pillar density values in orthogonal directions. To address this question we switched the geometry of the pillar distribution to rectangular arrays of pillars, arranged such that the pillar density was variable in one direction (y-axis in Fig. 3a) but not in the other (x-axis in Fig. 3a). We further segmented the entire pillar array into 6 zones as shown in Fig. 3a to investigate neurite responses in areas of distinct pillar densities in the y-axis direction. The top and bottom segments (labeled "Dense") had inter-pillar spacing in the y-axis direction varying from 0.6–2 µm. The adjacent segments were classified as "Intermediate" with the corresponding y-axis inter-pillar spacing varying between 2–3.5 µm. The 2 remaining segments were classified as "Sparse", with the y-axis inter-pillar spacing ranging between 3.5–5.6 µm. The pillar spacing in the x-direction was 1.6 µm and constant throughout the substratum.

Fig. 3.

Guidance of neurites by topographic gradient shows distinct domains of guidance. (a) Representative montage image of E16.5 hippocampal neurons on a substrate with topographic gradient having uniform spacing in x-direction (1.6 µm) and linearly varying spacing in the ydirection (0.6 µm at the upper and lower edges and 5.6 µm at the center). Scale bar is 100 µm. The entire pillar array is segmented into 6 domains based on the spacing in the y-direction - two Dense domains (spacing 0.6–2.0 µ m), two Intermediate domains (spacing 2.0–3.5 µm) and two Sparse domains (spacing 3.5–5.6 µm). Electron micrographs of the dense and sparse regions are shown. Scale bar is 10 µm. (b–d) Higher resolution image of cells in the Dense (b), Intermediate (c) and Sparse (d) domains indicate stronger guidance of neurites in the y-direction in Dense domain and in the x-direction in the Sparse domain. Scale bars are 50 µm. (e) Guidance index in the x- and y-directions show dependence on the spacing between pillars in the y-direction. n=5 experimental replicates with 450–800 neurites for each replicate. One-way ANOVA showed that varying pillar density (Dense, Intermediate and Sparse) had statistically significant effects on guidance indices in both x- and y-directions (p<0.05). This was followed by pair-wise comparison using Tukey's HSD and * indicates statistical significance at p<0.05 between a pair. The dashed line represents the guidance index expected for a uniform distribution.

The optimal inter-pillar spacing in the y-axis direction was in the Dense zone. Hence, as expected in this zone, there was a strong preference for neurite extension along the y-axis (Fig. 3b). However, in the Intermediate segments, the neurites exhibited a higher propensity to orient themselves in the direction of the x-axis (Fig. 3c). This result suggested that neurites preferentially extend along pillars equally spaced at 1.6 µm as compared to pillars with spacing between 2–3.5 µm, in general agreement with the results on the hexagonal arrays. In the Sparse segments, the topographic signal in the y-axis direction was even weaker and the neurites were primarily exposed to one strong topographic signal in the x-axis direction which dominated their guidance (Fig. 3d).

We quantified the results of neurite extension in the different density segments of the substratum by calculating the corresponding guidance indices of the x- and y-axis directions (Fig. 3e). We found that, as a function of the local inter-pillar spacing in the y-direction, the guidance index values in the orthogonal directions changed reciprocally, with the maximum discrepancy (highest guidance along the x-axis and lowest along the y-axis) occurring in the Sparse segments. This discrepancy was based on the moderate increase in the x-axis directed guidance and a strong decrease (to the values expected based on random neurite orientation) in the y-axis directed guidance. These results, in combination with the analysis of the neurite extension on hexagonal patterns, suggested that substratum topography can provide neurites with strong guidance cues, which can reflect the geometry of the local topographic pattern organization. In particular, the guidance directionality reflects the local symmetry of the topographic features and the degree of anisotropy in the density of these features, favoring the direction most consistent with an optimal feature density.

Attraction of neurites by a Netrin-1 gradient is synergistically enhanced in the presence of a co-directional topographic signal

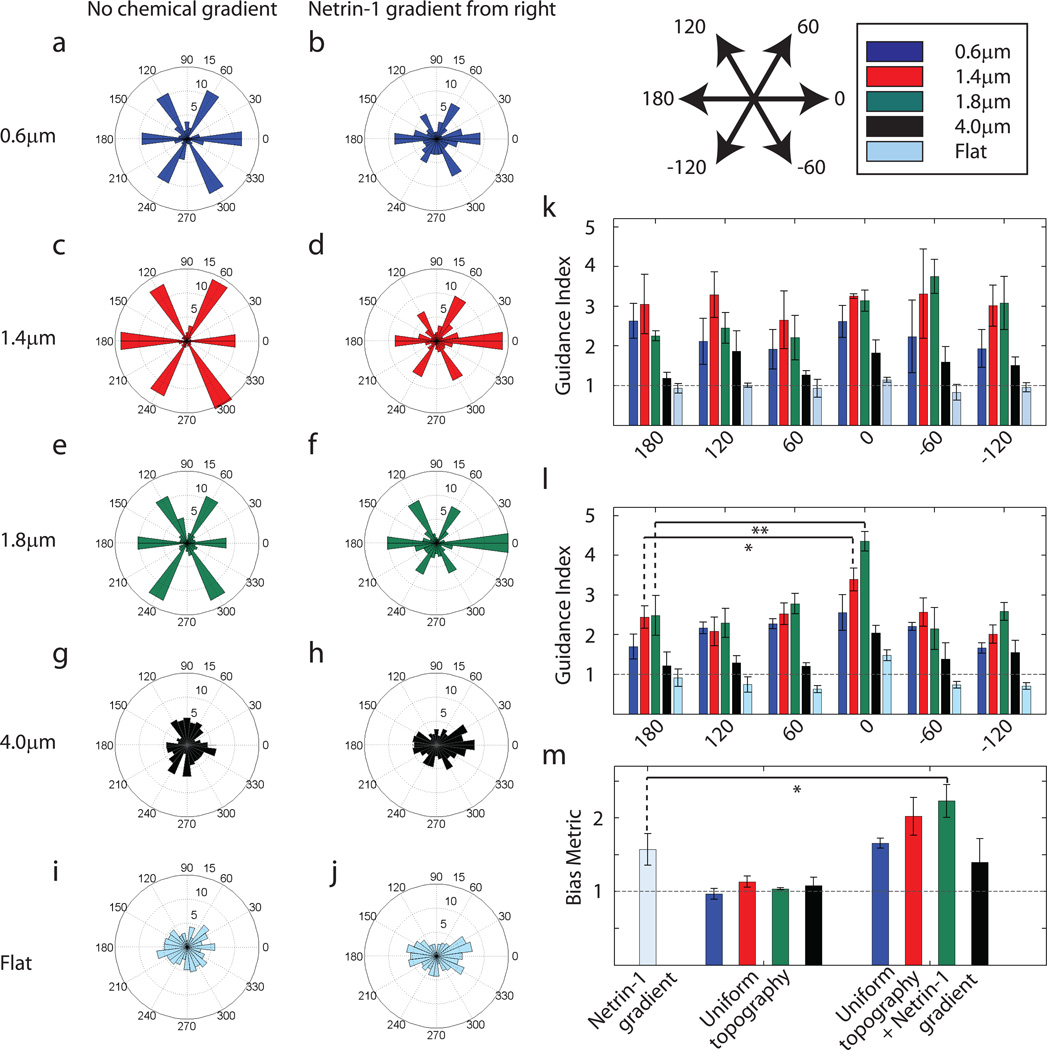
We next studied the effect of the simultaneous guidance of neurites by soluble chemical cues and topographic signals. In the first set of experiments, hippocampal neurons were cultured on hexagonal pillar arrays with spatially uniform topographies, with a simultaneous addition of a linear gradient of Netrin-1, a bi-functional cue that can trigger both attraction (in most cases under the conditions used) and repulsion (Fig. 4b,d,f,h). As a control, neurite responses to the same topographies without a Netrin-1 gradient were analyzed (Fig. 4a,c,e,g). We also isolated the effect of the chemical signal alone by imposing a linear Netrin-1 gradient over cells cultured on a flat surface (Fig. 4i,j).

Fig. 4.

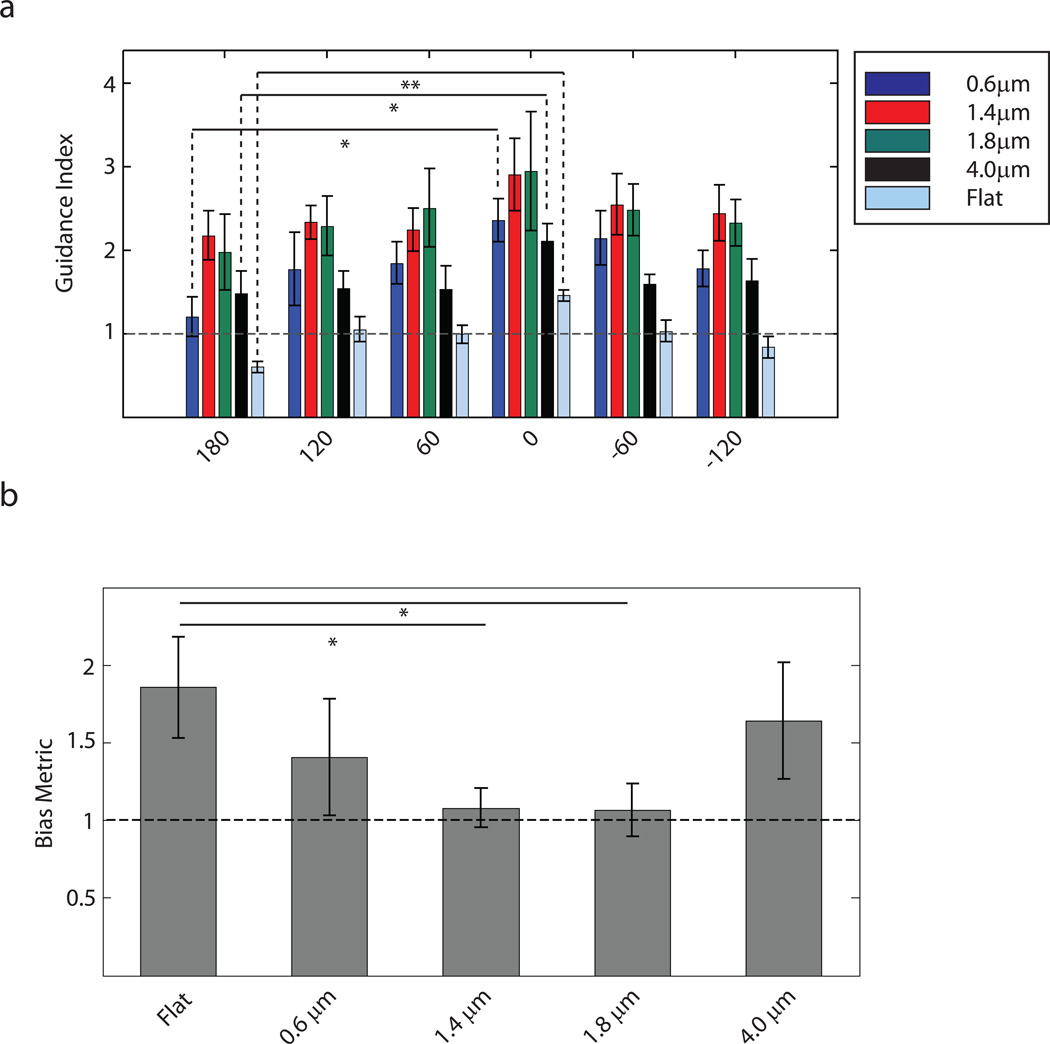
Co-directional Netrin-1 gradient and optimal topographic signals have a synergistic effect on neurite guidance. (a,c,e,g,i) Distribution of the final angles of neurites in a representative experiment in the absence of any chemical gradient. (b,d,f,h,j) Distribution of direction of neurite growth in a representative experiment with the presence of a simultaneous Netrin-1 gradient from the right. (a) and (b), (c) and (d), (e) and (f), (g) and (h), (i) and (j) correspond to pillar arrays with 0.6µm, 1.4 µm, 1.8 µm, and 4.0 µm spacings, and flat substratum, respectively. The radial axis represents the percent of neurites in each sector. Number of neurites for panels (a) through (j) are 404, 516, 405, 423, 406, 441, 261, 390, 481 and 299 respectively. (k,l) Guidance index on pillar arrays of 0.6 µm (blue), 1.4 µm (red), 1.8 µm (green), and 4.0µm spacings (black), and flat substratum (cyan) for each of the preferred directions of topography in the absence (k) and presence (l) of a chemical gradient (* indicates p<0.10 and ** indicates p<0.05 using Tukey's HSD pair-wise comparison) (m) The Bias Metric was calculated by taking the ratio of the average guidance index at 0°, 60°, and −60° to the average guidance index at 180°, 120°, and −120°. In the presence of both signals, there is a synergistic increase in bias towards 0° for pillar arrays with 1.4 µm and 1.8 µm spacings when compared to the Netrin-1 gradient only condition (* indicates p<0.10 using Tukey's HSD pairwise comparison). In (k–m), the horizontal line represents the guidance index or Bias Metric expected for a uniform distribution. n=3 experimental replicates with 300–500 neurites for each pillar array in each replicate for (k–m).

Consistent with the results presented above, topographic guidance in the absence of the soluble guidance signal showed equal bias for all 6 preferred angles, especially on substrata with 0.6 µm, 1.4 µm, and 1.8 µm pillar spacing (Fig. 4a,c,e). Also, as expected, in the absence of topographic cues, Netrin-1 exerted a bi-functional chemotropic influence (i.e., having both attractive and repulsive influence), with the attractive cue prevailing for most neurites (Fig. 4j). Combination of Netrin-1 gradient with the optimal topographic guidance cues, so that the gradient was aligned with one of the topographically induced preferred directions, affected neurite extension much stronger than anticipated based on the analysis of the Netrin-1 effect alone (Fig. 4d,f). Analysis using guidance indices showed a significant preference for the direction where topographic and chemical guidance vectors were co-directional (i.e.0°) as compared to the other five preferred directions of topographic guidance (Fig. 4l). As a control, we used the guidance index analysis to verify that topography in the absence of a chemical bias did not show a preference for any of these six directions (Fig. 4k). We further compared the guidance indices towards 0° both in the presence and absence of a Netrin-1 gradient and found an increase in guidance index towards the Netrin-1 source for the pillar array with 1.8 µm spacing but not for the other substrata (Fig s1). Together, these results suggested that, in the presence of optimal topographic cues, there was a powerful and synergistic enhancement of attractive and inhibition of repulsive effects of the Netrin-1 gradient. To quantify this synergistic attractive bias induced by the Netrin-1 gradient, we calculated the Bias Metric which is essentially a ratio of the average of the guidance indices in the directions towards Netrin-1 to the average of the guidance indices in the directions away from it (definition described in the Materials and Methods section). The Netrin-1 gradient alone introduces a bias in neurite directionality with the calculated Bias Metric equal to 1.57± 0.21 (mean ± standard error of mean). The topographic signals acting alone do not induce any appreciable bias. (Bias Metric equal to 0.97 ± 0.07, 1.13 ± 0.08, 1.04 ± 0.01 and 1.08 ± 0.11 for pillar arrays with 0.6 µm, 1.4 µm, 1.8 µm and 4.0 µm spacings, respectively; mean ± standard error of mean for all). However, the Bias Metric in the presence of both the Netrin-1 gradient and optimal topographic cues was greater than 2 (Bias Metric = 2.02 ± 0.26 for pillar array of 1.4 µm spacing and Bias Metric = 2.23 ± 0.22 for 1.8 µm spacing; mean ± standard error of mean for both) (Fig. 4m), supporting the claim that the effect of the topographic cues and the chemical gradient was synergistic in nature.

Netrin-1 gradient modulates guidance by orthogonal topographic signals

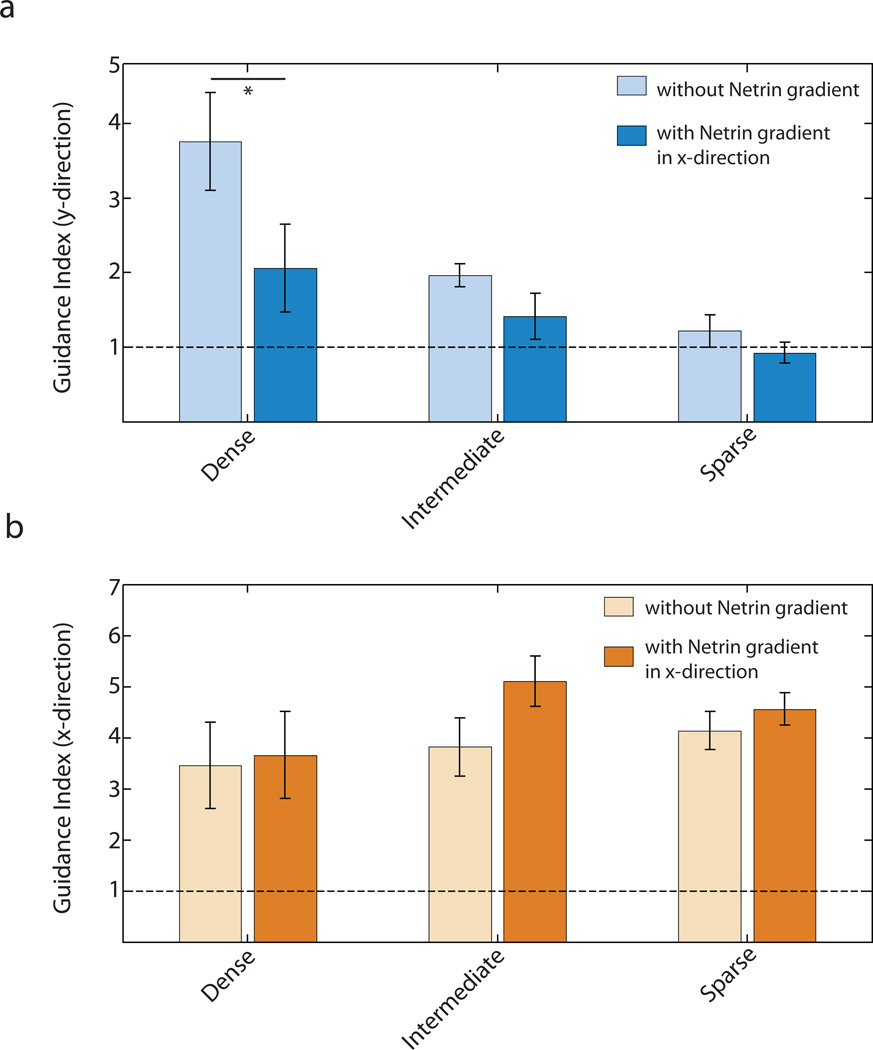
The isotropic hexagonal pillar arrangement alone does not provide a particular bias to neurite extension in any one of the six preferred directions. The anisotropic rectangular pillar arrays, on the other hand, can bias the neurite extension in one of the orthogonal directions, depending on the local anisotropy of the pillar densities (Fig. 3e). Given these findings, we next investigated whether a Netrin-1 gradient on an anisotropic pillar array could modify the pillar density dependent switch in directionality of neurite extension (Fig. 3e), in a manner consistent with the effect of the Netrin-1 gradient on the hexagonal pillar arrays. To explore this possibility, we imposed a linear gradient of Netrin-1 in the orthogonal (x-axis) direction over the substratum with a gradient of pillar spacing in the other (y-axis) direction (Fig. 1e). The neurons cultured on these substrata were thus exposed to three different guidance signals simultaneously - a spatially varying topographic signal in the y-direction, an orthogonal chemical signal in the x-direction and a uniform topographic input in the x-direction. We again segmented the entire substratum into 3 spatial zones, as described above. The results showed that the Netrin-1 gradient is indeed able to modulate neurite extension under these complex conditions. In particular, we observed a decrease in the capability of the topographic signals in the direction orthogonal to the chemical signal to guide neurites, as is reflected in the lower guidance index in the y-direction in the presence of a Netrin-1 gradient over the same segments of substrate (Fig. 5a). This indicates that a competing chemical signal decreases the effectiveness of topography to determine the direction of neurite growth. The effect of this competition was most pronounced in the Dense segments of the substratum where we had previously observed the topographic signal in the y-direction to have the strongest influence in the absence of the soluble cue (Fig. 3e). The guidance index in the x-direction showed only a slight increase in the presence of a Netrin-1 gradient, indicating that there was little enrichment to the strength of the total guidance signal in the x-direction by the Netrin-1 gradient as compared to the topographic signal alone (Fig. 5b).

Fig. 5.

Orthogonal Netrin-1 gradient decreases neurite guidance by surface topography. (a) Guidance index in the y-direction shows weaker guidance by topography in the presence of a Netrin-1 gradient in the x-direction Two-way ANOVA showed that both the Netrin-1 gradient and the density of pillars had significant effects on Guidance Index in the y-direction (p<0.05). Pair-wise comparison using one-way ANOVA for dense segments in the presence and absence of Netrin-1 gradient shows a statistically significant drop in guidance index in y-direction (p<0.10) in the presence of the gradient (indicated by *) (b) Guidance index in the x-direction shows a slightly stronger guidance in the presence of a Netrin-1 gradient in x-direction in the Intermediate domain (p=0.12 using one-way ANOVA). The horizontal line indicates the guidance index expected for a uniform distribution. n=6 experimental replicates with 450–800 neurites for each replicate (for both (a) and (b)).

Optimal topographic signal can overcome chemorepulsion by Semaphorin3A

The interplay between topographic guidance cues and a bi-functional chemoattractant Netrin-1 has demonstrated synergy between these two modalities of guidance under optimal codirectional conditions and competition when applied orthogonally. To explore if this synergy and competition effects were a hallmark of the interaction between topographic guidance and Netrin-1 specifically or whether these properties could be extended to other soluble chemical signals as well, we focused our analysis on cues generating exclusive chemorepulsion response. We used substrata with isotropic hexagonal pillar arrays superposed with a linear gradient of a known chemorepellent, Semaphorin3A (Sema3A). This experimental design, having the source of Sema3A at 180°, allowed us to introduce a possible bias towards the 0°-direction similar to the effect of Netrin-1 investigated above (Fig. 4 a–j).

When Sema3A-mediated repulsion was studied in isolation (i.e. on flat substrates), we observed a significant repulsion of neurites away from the source of Sema3A (Fig. 6a). When studied in combination with isotropic topographic cues, Sema3A was capable of repelling neurites for the pillar arrays with 0.6 µm and 4.0 µm spacing. However, we did not observe any statistically significant repulsion when Sema3A was imposed on pillar arrays with 1.4 µm and 1.8 µm spacings.

Fig. 6.

Optimal topographic cues overcome chemorepulsion by Semaphorin3A (Sema3A) gradient. (a) Guidance index in the preferred directions of the pillar arrays with a superimposed Sema3A gradient from 180°. The pillar arrays with spacings of 0.6 µm, 1.4 µm, 1.8 µm, and 4.0 µm are represented in blue, red, green, and black, respectively. Flat substratum is represented in cyan. Statistically significant repulsion was observed on flat substratum and on pillar arrays with 0.6 µm and 4.0 µm spacings, but not on pillar arrays with 1.4 µm and 1.8 µm spacings (** indicates p<0.05, * indicates p<0.10 using Tukey's HSD pair-wise comparison) . (b) Bias Metric for a Sema3A gradient superimposed over pillar arrays and flat substratum show that the Sema3A-induced bias is overcome on pillar arrays of spacing 1.4 µm and 1.8 µm (* indicates p<0.10 using Tukey's HSD pair-wise comparison). n=3 experimental replicates with 300–400 neurites for each pillar array in each replicate. The horizontal lines indicate the guidance index or Bias Metric expected for a uniform distribution.

We extended our analysis to quantify the bias introduced in the system by the Sema3A gradient. The Bias Metric was quantified as described previously. We observed that the bias introduced when the Sema3A gradient was acting in isolation (Bias Metric equal to 1.86 ± 0.33; mean ± standard error of mean), was completely abrogated by pillar arrays with 1.4 µm and 1.8 µm spacings (Bias Metric equal to 1.08 ± 0.13 and 1.07 ± 0.17 for 1.4 µm and 1.8 µm spacings, respectively; mean ± standard error of mean for both) (Fig. 6b). In combination, these results indicate that optimal topographic signals allows neurites to overcome chemorepulsion by Sema3A.

DISCUSSION

Precise control of neurite extension is critical for correct wiring and, ultimately, functioning of nervous tissues, including the brain. Neurites are guided by diverse combinations of complex, spatially distributed chemical and mechanical cues. Our results strongly suggest that embryonic hippocampal neurons can display complex responses to periodic topographic cues and to combinations of these cues with more commonly studied gradients of chemical guidance molecules.

One of the more surprising findings of this study is the evidence for existence of the optimal density of the micro-pillars mediating the highest fidelity in neurite guidance. The neurite guidance by pillars was maximized at this density, but not at either higher or lower density values. The recognition of the optimal inter-pillar spacing was most obvious in pillar arrays of isotropic arrangement, but was also clearly pronounced in arrays with anisotropically variable pillar density. The preferred direction of neurite extension was thus generally defined by a predilection for traversing the rows of pillars most closely approximating this optimal inter-pillar spacing regardless of the local pillar arrangement, suggesting a surprising level of sensitivity to this periodic cue. The reason for the strong favoring of a particular inter-pillar spacing is not immediately clear, but this finding suggests that neurites experience a periodic input from the ECM enriched environment during each sequential neurite-pillar contact and that an optimal periodicity facilitates maximal re-enforcement of the particular neurite extension direction. Understanding the nature of the processes occurring within the neurites that can be enhanced in a resonant fashion by the periodic extracellular input is an exciting problem suggested by this study, whose analysis is the subject of a separate investigation¹⁵. However, the initial hints at the underlying chemical networks are provided by the nature of interplay between the guidance by micro-pillars and gradients of chemical cues, as described below.

A striking observation detailed in this report is the emergence of synergistic interactions for some but not all combinations of soluble and micro-topographic cues in neurite guidance. A particularly interesting case was the synergistic enhancement of attraction but not repulsion by the bi-functional chemotropic factor Netrin-1, when cells were simultaneously exposed to the optimal micro-pillar pattern for neurite extension. This result strongly suggests that topographic cues interface within a growth cone with the signaling networks triggered by the engagement of the DCC receptors associated with the growth cone attraction, but not the signaling networks activated by chemorepulsion associated DCC/UNC-5 receptor complexes³⁹. In particular, this finding implicates an increased synergistic activation by two different cues of a signaling circuit involving cytosolic Ca²⁺ and RhoA family GTPases, Rac1 and Cdc42⁴⁰. This synergistic activation by both Netrin-1 and topographic cues was only evident when growth cones interfaced with pillars of the optimal density. This conclusion is further strengthened by the observation that the effect of the repulsive cue, Sema3A, observed on the flat substrata was significantly diminished if neurons were cultured on pillar arrays of optimal density. Overall, these results strongly suggest that the cue presented to growth cones by periodic exposure to micro-pillars controls growth cone guidance by activating the Ca²⁺-dependent activation of Rac1/Cdc42 dependent circuit responsible for enhancement in the persistence cell motility, while at the same time inactivating the RhoA-dependent circuit responsible for a decrease in the cell motility persistence associated with repulsive response.

The findings of this study offer a mechanistic explanation for the counter-intuitive observation that neurites often traverse ridge-like nanostructures in a direction perpendicular to the structural features. Such behavior of neurites has been observed in vivo when cortical neurons have been shown to extend their axons perpendicular to the fibers of the radial glia in a developing brain^18,41. This observation has been replicated in vitro when neurons grown on micro-fabricated ridge arrays have been shown to extend their neurites in a direction orthogonal to the direction of the ridges, in contrast to alignment with the ridges more commonly found in various cell types^23,42. Our finding about the existence of an optimal frequency for topographic input substantiates these findings. Traversing topographic features orthogonally can provide the neurites with the optimal signal frequency that is preferred over the higher frequency input when the neurites extend parallel to the topographic features and are hence in constant contact.