A unifying framework for robust association testing, estimation, and genetic model selection using the generalized linear model

Abstract

The analysis of genome-wide genetic association studies generally starts with univariate statistical tests of each single-nucleotide polymorphism. The standard approach is the Cochran-Armitage trend test or its logistic regression equivalent although this approach can lose considerable power if the underlying genetic model is not additive. An alternative is the MAX test, which is robust against the three basic modes of inheritance. Here, the asymptotic distribution of the MAX test is derived using the generalized linear model together with the Delta method and multiple contrasts. The approach is applicable to binary, quantitative, and survival traits. It may be used for unrelated individuals, family-based studies, and matched pairs. The approach provides point and interval effect estimates and allows selecting the most plausible genetic model using the minimum P-value. R code is provided. A Monte-Carlo simulation study shows that the asymptotic MAX test framework meets type I error levels well, has good power, and good model selection properties for minor allele frequencies ≥0.3. Pearson's χ²-test is superior for lower minor allele frequencies with low frequencies for the rare homozygous genotype. In these cases, the model selection procedure should be used with caution. The use of the MAX test is illustrated by reanalyzing findings from seven genome-wide association studies including case–control, matched pairs, and quantitative trait data.

Introduction

Genome-wide association studies (GWAS) are widely used to uncover novel genetic susceptibility loci for complex genetic diseases. If the true genetic model is known, the association test reflecting this model has optimal power. However, in most applications, the true mode of inheritance is unknown, and, unfortunately, there is not one best test statistic for all situations.¹ For the analysis of GWAS data, the standard approach is to assume an additive genetic model and to perform the Cochran-Armitage trend test or a logistic regression using a 1 degree of freedom (df) test following Sasieni's seminal paper.² The power of this approach is, however, reduced if the true genetic model is not additive, and it does not allow identifying the underlying genetic model.

One alternative approach is Pearson's χ²-test with 2 df. It is able to detect any alternative, including additive, dominant, or recessive genetic models,³ but, as a global or omnibus test, it does not allow to identify the underlying mode of inheritance. Instead, specific alternatives need to be investigated subsequently in case of significant association.

Another interesting alternative is the MAX test,⁴ where the three different modes of inheritance (MOI), additive, dominant, and recessive, are simultaneously tested. Although three tests are performed, the number of effective tests is ∼2.2 (González et al⁵). In its original version, P-values for the MAX test were obtained from computer-time intensive permutation testing; for details, see Joo et al⁶ and Zang et al.⁷ More recently, different approaches have been taken to derive the exact and/or asymptotic distribution of the MAX test statistic.^{5, 8, 9, 10} In a similar way, Li et al¹¹ derived an upper bound for P-values.

The approaches taken differ in many ways. While Hothorn and Hothorn analytically derived the correlation between the different test statistics,⁸ González et al⁵ proposed to estimate the correlation coefficients. Neither approach allows to adjust for covariates or for population stratification. In contrast, Li et al¹¹ allowed adjustments for covariates and population stratification by using different logistic regressions for the three genetic models. Using the robst estimator of variance from generalized estimating equations, they estimated the joint covariance matrix from Wald tests and derived the upper bound of the P-value. In all three approaches, only dichotomous endpoints were considered.

Therefore, the work of So and Sham⁹ can be considered an important extension. They derived the asymptotic distribution of the MAX test using a score test in the framework of the generalized linear model (GLM). They thus allow for a wide variety of traits, as well as the adjustment for covariates and population stratification. Finally, Zang and Fung¹⁰ derived the asymptotic null distribution of the MAX test using a robust Mantel-Haenszel test, which can cope with sparse data. However, confidence intervals were provided in neither approach.

For trio data consisting in an affected offspring and both parents (single affected offspring=SAO trio), MAX tests based on score tests have been introduced.^{6, 12, 13} To the best of our knowledge, only Monte-Carlo simulations were proposed for estimation of P-values, and asymptotics have not been used.

For matched pairs, the situation is different, and asymptotic results are available¹⁴ in addition to simulation-based approaches.^{6, 15, 16}

To combine the different approaches in an all-in-one toolbox, we here propose a single model framework. The MAX test approach derived in this work can be used for statistical testing, the calculation of confidence intervals, and the selection of the most plausible genetic model. To this end, we embed the MAX test approach into the GLM and derive its limiting distribution. The approach can handle all common response variables, including binary (disease), count (symptom score), quantitative intermediate phenotypes (metabolite, hormone, protein, and gene expression), and even survival endpoints. It naturally allows for the inclusion of covariates representing environmental factors or adjustments for population stratification. The model will initially be formulated for independent subjects, but we also provide an extension to family-based association studies, including SAO trios, and matched pairs samples.

The core of the new method is to first estimate a GLM with three dummy variables according to the three possible genotypes but without an intercept. Linear contrasts are used in the second step to form the genetic models of interest, and the asymptotic distribution, which is a multivariate normal distribution, is derived by the Delta method. In this way, our approach is similar to the method by González et al.⁵ The MAX test is the maximum over a multivariate normal distribution. Model-specific confidence intervals can be derived using the multivariate normal distribution, and P-values adjusted for the testing of three tests at a single genetic marker are obtained.

Various approaches are available for genetic model selection.^{8, 17, 18, 19, 20} Here, we follow Hothorn and Hothorn and use the minimum of the P-values (min(p)) to decide which genetic model is the most plausible one.⁸ As already noted in 1977 by Cox,²¹ this procedure has useful diagnostic properties.

Only minor modifications of the model are required to extend the approach to family-based and matched pairs studies.^{6, 15, 16} Here, the asymptotic results are derived by making use of the conditional regression approach proposed by Cordell and Clayton.²²

The MAX test can easily be implemented with standard software, and R code for the analysis using independent samples and family-based studies is provided in the Supplementary Material.

To demonstrate the validity of the method and the model selection performance of the min(p) approach, we simulate quantitative and binary phenotypes, vary the minor allele frequency (MAF) and allow for departure from Hardy–Weinberg equilibrium (HWE). For binary responses, we additionally vary the proportion of cases and controls, and we analyze SAO trios. We demonstrate its application to a recent GWAS on malaria.²³ Additionally, we illustrate the method by reanalyzing findings from seven GWAS including case–control studies and a quantitative trait, as well as a matched pairs study.

Materials and methods

The statistical model

Our starting point is a sample of n independent subjects with trait values y₁,…, y_n. The q × 1 vector of covariates of an individual is denoted by z_i. Typical covariates may be environmental variables or adjustments for population stratification. The genetic marker of interest is assumed to be autosomal diallelic, eg, a single-nucleotide polymorphism (SNP), with alleles a and A. Three dummy variables are used to code the three genotypes with x_i,0, x_i,1 and x_i,2 corresponding to the genotypes AA, Aa and aa, respectively, ie, x_i,j=1 if subject i has j (j=0,1,2) a alleles, and 0 otherwise.

We consider the GLM

where g⁻¹ is the link function, β=(β₀, β₁, β₂)′ are the genetic parameters of interest, and γ is the q × 1 parameter vector of covariates. Model (1) does not include a regression constant, but an extension to the model description with a regression constant is provided in the Supplementary Material. For a disease phenotype and a quantitative trait, the logistic link function and the identity link function, respectively, are the natural link functions and, therefore, the standard choices. For survival endpoints, equation (1) is adapted to the Cox model.

All parameters of equation (1) are estimated by maximum likelihood estimation and are jointly asymptotically normally distributed. More specifically, the vector 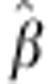is asymptotically normally distributed with mean β and 3 × 3 covariance matrix .

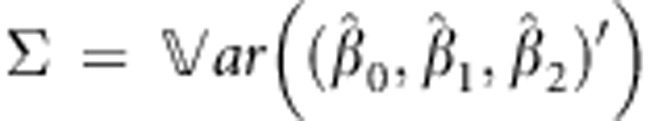The MAX test derived from the Delta method

Specific genetic models can be obtained by introducing restrictions in terms of linear contrasts on the parameter vector β. For a standardized linear contrast, the sum over all coefficients needs to be 0, and the sum of all positive-valued coefficients should be 1. To exemplify the construction of the contrast, we consider the additive genetic model which has penetrances 0, , and 1 for carriers of 0, 1, and 2 a alleles. If is subtracted from the penetrances and if these values are multiplied by 2, the linear contrast (−1, 0, +1) is obtained. The contrast for the recessive genetic model is obtained as 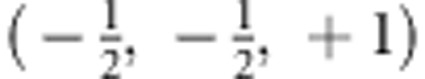, and the contrast for the dominant genetic model is given by 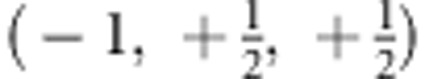. The new parameter vector

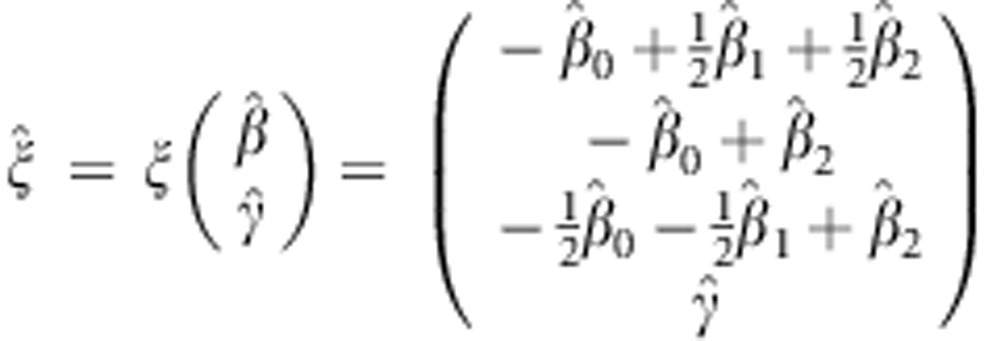is asymptotically normally distributed with mean 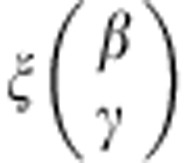. The covariance matrix of ξ can be derived using the Delta method (details provided in the Supplementary Material).²⁴

The MAX test statistic is finally given by

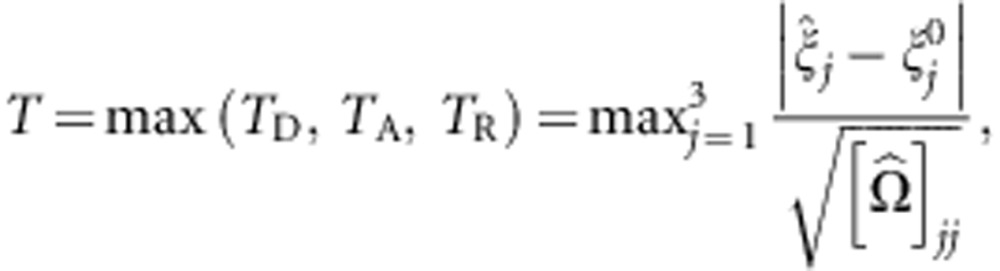where 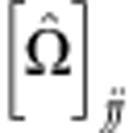denotes the variance estimate of 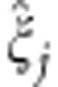. Thus, the MAX test is obtained by taking the maximum of the first three components, or, phrased differently, by taking the maximum of the contrast tests for T_D, T_A, and T_R, which are the test statistics corresponding to the dominant, additive, and recessive MOI, respectively. The null hypothesis tested here is 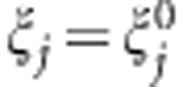, for j=1,2,3, and the general choice i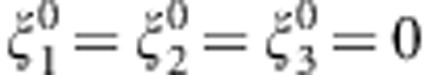s . As 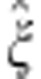is asymptotically normal, P-values of the MAX test statistic T, which consists of three components, can be obtained from a three-dimensional normal distribution. Specifically, we calculate

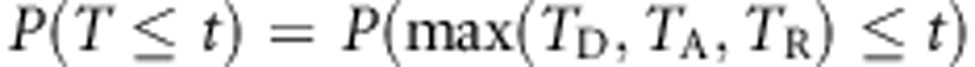using the results of Strasser and Weber.²⁵ A worked-out example for these calculations is provided in Ziegler and König¹⁸, pp. 284–286.

The three-dimensional normal distribution can also be used for the calculation of confidence intervals with or without adjustment for the joint analysis of three different MOI. Details are provided in the Supplementary Material.

In itself, the MAX test does not inform on the underlying MOI. However, the minimum multiplicity adjusted P-value, termed min(p), for each test indicates, which MOI is the most plausible one.⁸ This procedure has useful diagnostic properties and allows for model selection.²¹

The MAX test approach using the GLM framework can be extended to family-based and matched case–control association studies. Technical details are provided in the Supplementary Material.

Simulation study

The performance of the asymptotic MAX test with respect to type I error level and power, and its ability to select the true MOI was evaluated in a Monte-Carlo simulation study. To this end, we compared it with standard tests used in (1) case–control studies of unrelated individuals, (2) SAO trio studies, and (3) the analysis of quantitative traits using 10 000 replicates for every constellation.

For a sample of 3000 subjects, we simulated genotypes using varying genotype relative risks GRR₁ and GRR₂ for dominant, additive, and recessive MOI. To allow for deviation from HWE, we simulated samples of r cases and s independent controls by drawing random numbers from two multinomial distributions with three categories representing the three genotypes.²⁶ Departure from HWE was measured by the disequilibrium coefficient,¹⁸ and the disease prevalence was set to 0.1. We used the logistic link function and varied the ratio of cases and controls, as well as the MAF of the SNP; a summary of the various simulation parameters is provided in Supplementary Table 1. We compared the MAX test to allele- and genotyped-based χ²-tests with 1 and 2 df, respectively. We also fitted three logistic regression models for additive, dominant, and recessive MOI. The score test of the Cochran-Armitage trend test is asymptotically equivalent to the additive genetic test using the Wald statistic in the logistic regression,²⁷ and we, therefore, display only the results from the logistic regression model.

We also validated the approach by simulating SAO trio data and quantitative trait data. Details of this simulation study are provided in the Supplementary Material.

Model selection

To assess the performance of the model selection procedure described above, we estimated the selection probabilities for dominant, additive, and recessive MOI, given the true MOI. Additionally, we estimated the positive predictive values (ppV) of all three genetic models which is the probability that the true MOI is dominant (additive, recessive) if the dominant (additive, recessive) MOI has been selected (see Supplementary Material for detailed information on the estimation of the ppV).

Example data

Recently, we applied the model selection approach to a GWA on severe falciparum malaria.²³ For a sample of 1325 severe malaria cases and 828 unaffected controls from Ghana, a logistic regression was fitted with adjustment for age, gender, and population stratification. We identified 102 SNPs located in 41 distinct genomic regions using thresholds of P<5 × 10⁻⁵. The most likely MOI was identified using the MAX test model selection approach. Using the most likely MOI, replication was performed in an additional 1320 severe malaria cases and 2222 controls from the same population and in 958 severe malaria cases among Gambian children and 1382 Gambian controls, provided by the MalariaGEN Network.²⁸

Additionally, we reanalyzed case–control studies for Type II diabetes (T2D),²⁹ age-related macular degeneration,³⁰ prostate cancer,³⁰ breast cancer,³⁰ and hypertension from GWAS with significant association findings. For a matched pair case–control design, we reanalyzed the African American data from an etiologic study of sarcoidosis.¹⁶ As an example for a quantitative trait, we reanalyzed data on the body mass index from a sample of the 1958 British Birth Cohort.³¹ Details of the analyses and the results are given in the Supplementary Material.

Results

Simulation study: Type I error levels

Nominal type I error levels are kept well for all models (Supplementary Table 3), except for the allele-based χ²-test if HWE was violated (results not displayed). The test for the recessive model and the MAX test were slightly conservative for the disease trait at the low risk allele frequency of 0.1, and they had slightly inflated type I error levels for the log-normally distributed trait, again at the low MAF.

Simulation study: Power

The statistical test assuming the true MOI had the highest statistical power in all simulation scenarios (Figure 1 (case–control data); Supplementary Figure 1 (trio data); Supplementary Figure 2 (quantitative trait with normal distribution); Supplementary Figure 3 (quantitative trait with log-normal distribution)). The allele-based χ²-test with 1 df, used for independent case–control data and requiring the assumption of HWE, and the TDT, used for SAO trio data, implicitly assumed an additive MOI, and results of these tests were, therefore, similar to the logistic regression test adapted to an additive MOI.

Figure 1.

Power results for independent case–control data. Abscise: homozygous relative risk; ordinate: power of test statistics. T_all: allele-based χ²-test with 1 df; T_gen: Pearson's χ²-test with 2 df; T_dom: dominant mode of inheritance (MOI); T_add: additive MOI; T_rec: recessive MOI; T_max: Max test. True mode of inheritance and MAF given in headings.

The power of the MAX test was depending on the MAF of the investigated SNP. For a MAF of 0.5, the MAX test was the second most powerful under all genetic models. In contrast, tests adapted to an additive MOI had higher power at MAF=0.3 than the MAX test if the true MOI was dominant. For low MAF, the MAX test lost considerable power under both additive and dominant MOI. For independent case–control data and MAF smaller than 0.3, the genotype-based χ² with 2 df had greater power than MAX and, therefore, seems to be preferable in these scenarios. Results obtained under departure from HWE were very similar (results not shown). The dependency of the performance of the MAX test on the allele frequency has been reported before, and alternatives have been suggested.³²

Simulation study: Model selection

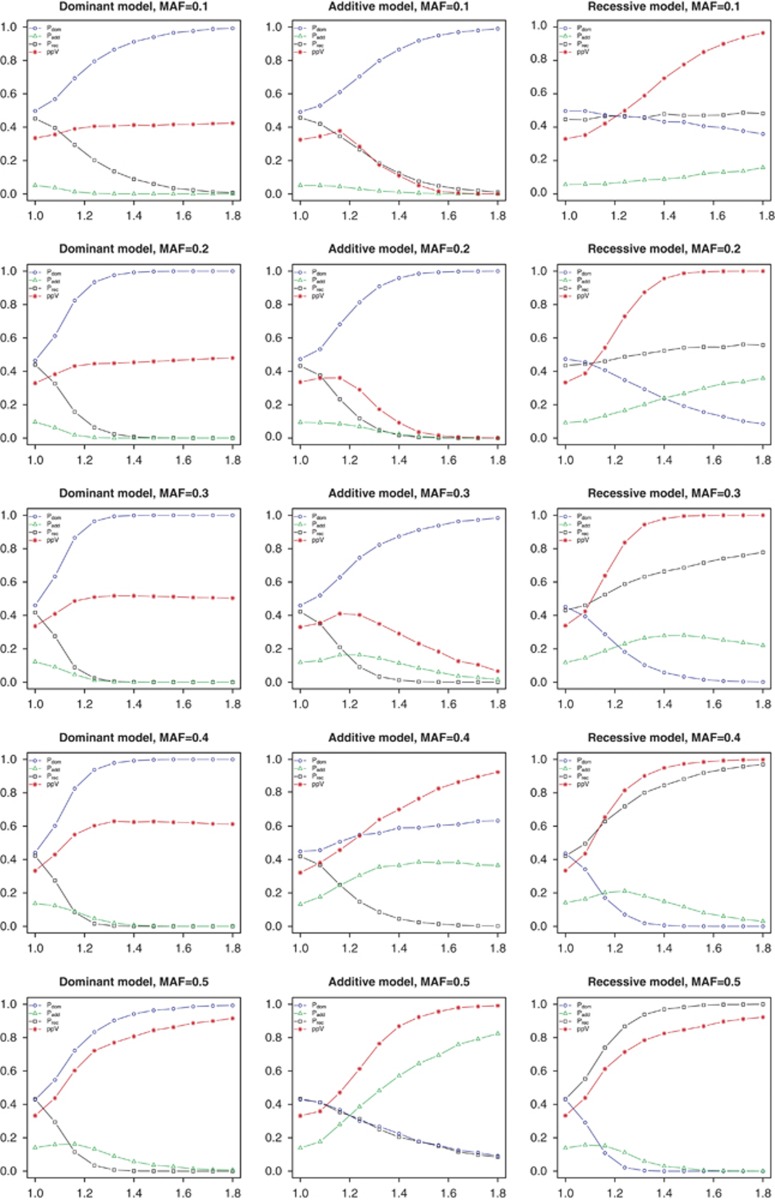
Figure 2 and Supplementary Figures 4–6 summarize the performance of selecting the true genetic MOI using the MAX test approach for dominant, additive, and recessive genetic models depending on the effect size. The true underlying model and MAF are specified in the heading, and the ppV is additionally plotted for the genetic models.

Figure 2.

Model selection for independent case–control data. Abscise: homozygous relative risk; ordinate: probability of choosing the dominant (P_dom), additive (P_add), recessive (P_rec) model and the ppV.True mode of inheritance and MAF given in headings.

For a high MAF of around 0.5, the true genetic model was identified correctly with high probability, and, therefore, the ppV of each model approached 1 as effect sizes increased. However, the probability to identify the true MOI decreased with the MAF. Specifically, if the true MOI was additive, the MAX test was most likely to indicate a dominant model instead of the additive one, if the MAF was around 0.3 and lower. Therefore, the ppV for the dominant model did not obtain values larger than about 0.5, and the ppV of the additive model even decreased with increasing effect sizes.

Only for the matched case–control data (Supplementary Figure 4), the ppV of the additive model still increased with effect size for a MAF of 0.3. However, the same unfortunate behavior was observed for the additive genetic model and MAFs ≤0.2. The recessive model was likely to be identified correctly for medium MAF, and the ppV increased with effect size to values close to 1. Interestingly, for a MAF of around 0.1, the probability to correctly select a recessive model also remained at around 0.5, although the ppV for this model still approached 1.

Conclusions are similar under departure from HWE (results not displayed). Similarly, the choice of SD σ for the normally distributed or corresponding log-normally distributed traits had only minor influence (results not displayed). Different ratios of cases to controls did not alter the results substantially (results not displayed).

Real data analysis

In the malaria study,²³ two novel loci were genome-wide significant (P<5 × 10⁻⁸), and the first has lead SNP rs10900589 on chromosome 1q32.1 within the ATPase, Ca⁺⁺ transporting, plasma membrane 4 (ATP2B4) gene. The most likely MOI for the initial Ghanaian GWA sample and the combined Ghanaian samples is a recessive one (Table 1, genotype counts given in Supplementary Table 4) with an effect of the risk allele of 0.58 with a MAF of 0.36. The ppV for this choice is almost 100%. Replication in The Gambia was successful only for the recessive model.

Table 1. Case–control study of severe falciparum malaria for association with the SNP rs10900589 of the ATPase, Ca⁺⁺ transporting, plasma membrane 4 (ATP2B4) gene.

	MAF	n	Pdom	Padd	Prec	Pmax	OR01 (95% CI)a	OR02 (95% CI)b	Modelc
Ghanaian GWAS group	0.35	2147	1.0E-01	6.8E-04	9.5E-06	2.1E-05	0.96 (0.80;1.16)	0.53 (0.41;0.70)	REC
Ghanaian replication group	0.37	3474	2.3E-03	7.4E-05	3.8E-04	1.3E-04	0.85 (0.73;0.98)	0.61 (0.49:0.77)	ADD
Ghanaian groups combined	0.36	5621	6.7E-04	1.8E-07	3.4E-08	2.1E-08	0.89 (0.79;0.99)	0.58 (0.49;0.69)	REC
Gambian GWAS group	0.28	2209	5.7E-01	4.1E-01	2.8E-03	4.6E-03	1.06 (0.89;1.26)	0.69 (0.49;0.96)	REC
Combined analysis of all three groups	0.34	7830	2.9E-02	9.9E-06	8.1E-09	2.0E-08	0.95 (0.87;1.05)	0.63 (0.54;0.73)	REC

Abbreviations: CI, confidence interval; MAF, minor allele frequency; n, sample size; OR, odds ratio; P_dom, P-value for dominant mode of inheritance (MOI); P_add, P-value for additive MOI; P_rec, P-value for recessive MOI; P_max, P-value of MAX test.

^aGenotypic OR and 95% CI for one compared with zero risk alleles.

^bGenotypic OR and 95% CI for two compared with zero risk alleles.

^cModel selected by MAX test procedure: DOM, dominant, ADD, additive, REC, recessive.

A hint at whether model selection was done correctly can be obtained by investigating the genotypic odds ratio (OR), ie, the increase in risk for carriers of 1 and 2 risk alleles as compared with 0 risk alleles, denoted by OR₀₁ and OR₀₂, respectively (Table 1). If OR₀₁≈OR₀₂, a dominant MOI would be most plausible, if 1<OR₀₁<OR₀₂ an additive MOI is more plausible, and if OR₀₁≈1 and OR₀₂>1 a recessive MOI is most plausible. The last column of Table 1 provides the MOI selected by the MAX test using the minimum P-value, and, in general, the model selection by the MAX test seemed to be plausible.

Results of the reanalysis of other case–control data are provided in Supplementary Table 5 (genotype counts provided in Supplementary Table 6). Here, the MAX test showed to be robust under various genetic models, mostly having P-values comparable to those of Pearson's χ²-test. Supplementary Tables 7 and 8 report the results for matched case–control data, and these were similar to those obtained by Zang and Fung.¹⁶ A detailed description of the GWAS results on BMI is provided in the Supplementary Material.

Discussion

Previous work has shown that there is no single best association test for all genetic models.¹ Although the Cochran-Armitage trend test or the logistic regression model assuming an additive genetic model are both widely used in GWAS, they can lose considerable power if the model is not additive. Alternatives include Pearson's test for genotypes and the MAX test. In this paper, we have used the GLM as unifying framework for the MAX test. The MAX test keeps the nominal type I error level well and shows good performance for a MAF of 0.3 and higher. However, neither power nor model selection ability are high for low MAFs, ie, MAF≤0.2 because of the low frequencies of the rare homozygous group. For example, for a MAF of 0.1 and a sample of 3000 subjects, only 30 individuals are expected in the homozygous rare genotype group. Therefore, the estimate of the parameter β₂ is expected to show a high standard error which reduces the ability to distinguish the different genetic models and the power to detect an association. If much larger samples can be investigated, the parameter estimates will be very precise and the true genetic model can be deduced more reliably.

The dependence of the MAX test on the allele frequency of the marker of interest has been observed before.³² One alternative test, which does not depend on the marker allele frequencies, is MIN2. MIN2 has been considered by the Wellcome Trust Case Control Consortium,³³ and it combines the χ²-test for an additive genetic model and the Pearson's χ²-test. Interestingly, Zheng et al³⁴ showed that the MAX test is identical to Pearson's test under the assumption that no overdominance is present. In other words, the MAX test captures all the information in Pearson's χ²-test in case there is no advantage or disadvantage for heterozygotes. However, Pearson's χ²-test may be more powerful than the MAX test when the family of genetic models includes the overdominant (underdominant) model. It would be interesting to see whether Pearson's test can be linearized and formulated in terms of linear contrasts so that formal differences between Pearson's test and the MAX test are possible.

The computational burden for calculating the MAX test is about twice that of estimating a standard logistic regression. The reason is the extra calculation of the linear contrast and its variance, but most importantly the evaluation of the multivariate normal distribution. If users choose a fast and precise implementation for calculating probabilities from multivariate normal distributions,³⁵ the calculation of the MAX test for a GWA can be easily done on a standard computer.

The all-in-one approach derived here allows the identification of the most plausible genetic model. The usefulness of the model selection performance is limited given today's GWAS sample sizes, and it would be interesting to see a comparison with other model selection procedures.^{19, 20, 36}

The importance of the MAX test or other robust association tests is likely to increase in the next few years. With standard GWAS, which have been conducted in the past 7 years, the concept of indirect mapping has been used, which means that the functional loci were not part of the GWA marker panel. Instead, we have expected to detect regions that are in linkage disequilibrium with the functional loci. Kuo and Feingold¹ have shown that even if the functional locus is purely recessive or purely dominant, the marker locus near it may not be. Only an additive functional locus will always give an additive marker locus. Even more, the larger the difference in allele frequencies between the trait and marker loci, the more additive the marker locus looks, even if the trait locus is dominant or recessive.¹ It is, therefore, unlikely that truly recessive and dominant loci appear recessive and dominant, respectively, in GWAS. However, the number of SNPs on commercially available chips has increased substantially over the past years. Furthermore, the new high throughput sequencing approaches enable direct genotyping of the functional variant. Direct mapping, therefore, has already increased in importance, and it is very likely that several non-additive genetic model associations will be identified.

Nonetheless, the application of the MAX test considered here will be restricted to common variants given the sample sizes used in recent studies. The statistical analysis of rare variants will, therefore, remain challenging, unless we can work with substantially larger sample sizes. As a result, sample sizes of 50 000 and higher are considered in large consortia to investigate SNPs with a MAF of 0.01 and lower.

Future research should focus on increasing the power of the MAX test in case of low MAFs. Furthermore, the MAX test provided here has been constructed for autosomal SNPs only. To test for association on X-chromosomal markers, modified tests are needed, which can account for the different data structure of males and females and for the phenomenon of the inactivation of one female X-chromosome.³⁷ Therefore, an extension to the analysis of X-chromosomal data is needed.

The authors declare no conflict of interest.