Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2013 Oct 21;40(11):111914. doi: 10.1118/1.4824926

CONRAD—A software framework for cone-beam imaging in radiology

Andreas Maier 1,a), Hannes G Hofmann 2, Martin Berger 2, Peter Fischer 3, Chris Schwemmer 3, Haibo Wu 3, Kerstin Müller 3, Joachim Hornegger 3, Jang-Hwan Choi 4, Christian Riess 4, Andreas Keil 4, Rebecca Fahrig 4
PMCID: PMC3820625  PMID: 24320447

Abstract

Purpose: In the community of x-ray imaging, there is a multitude of tools and applications that are used in scientific practice. Many of these tools are proprietary and can only be used within a certain lab. Often the same algorithm is implemented multiple times by different groups in order to enable comparison. In an effort to tackle this problem, the authors created CONRAD, a software framework that provides many of the tools that are required to simulate basic processes in x-ray imaging and perform image reconstruction with consideration of nonlinear physical effects.

Methods: CONRAD is a Java-based state-of-the-art software platform with extensive documentation. It is based on platform-independent technologies. Special libraries offer access to hardware acceleration such as OpenCL. There is an easy-to-use interface for parallel processing. The software package includes different simulation tools that are able to generate up to 4D projection and volume data and respective vector motion fields. Well known reconstruction algorithms such as FBP, DBP, and ART are included. All algorithms in the package are referenced to a scientific source.

Results: A total of 13 different phantoms and 30 processing steps have already been integrated into the platform at the time of writing. The platform comprises 74.000 nonblank lines of code out of which 19% are used for documentation. The software package is available for download at http://conrad.stanford.edu. To demonstrate the use of the package, the authors reconstructed images from two different scanners, a table top system and a clinical C-arm system. Runtimes were evaluated using the RabbitCT platform and demonstrate state-of-the-art runtimes with 2.5 s for the 256 problem size and 12.4 s for the 512 problem size.

Conclusions: As a common software framework, CONRAD enables the medical physics community to share algorithms and develop new ideas. In particular this offers new opportunities for scientific collaboration and quantitative performance comparison between the methods of different groups.

Keywords: C-arm computed tomography (CT), hardware acceleration, GPU, software frameworks, open-source, cone-beam

INTRODUCTION

Good common software frameworks bring the great benefit that they simplify scientific collaborations and support the reuse of previous work. Such commonly used software packages are found in many research fields, such as ImageJ (Ref. 1) in the biomedical image analysis community, Plastimatch (http://plastimatch.org/) and ITK (Ref. 2) in the segmentation and registration community, Geant4 (Ref. 3) in the physical simulation community, and Weka4 in the machine learning domain. All of these platforms have in common that they are based on an open infrastructure. Implementations within these platforms can be used by everyone. This fosters collaborations between groups in the same field and the overall scientific progress. Additionally, some of the frameworks provide mechanisms that facilitate correct accreditation of the algorithms to the original authors.

In the medical reconstruction domain, the prevalent software is MATLAB (Mathworks, Natick, MA). However, MATLAB has the problem that expensive licenses exclude parts of the scientific community and that MATLAB code has more of a rapid prototype character rather than sustainable software development. On the other hand, MATLAB code is reasonably straightforward to understand and modify. In this context, several MATLAB frameworks exist [such as OSCaR (http://www.cs.toronto.edu/~nrezvani/OSCaR.html) and ASTRA (https://code.google.com/p/astra-toolbox/)], with a growing userbase within the community. This observation is an indicator for the need for openly accessible reconstruction and simulation software. At present, there are already platforms available in other languages than MATLAB, but their functionality focuses mostly on reconstruction only, and does not include necessary correction steps to be able to reconstruct data acquired with a real system [such as NiftyRec (http://niftyrec.scienceontheweb.net/wordpress/) and RTK (http://www.openrtk.org/rtkindex.html)].

However, a hurdle toward this goal is that many labs are hesitant to share their software: as written and tested code represents a significant investment of person-hours, informal code sharing raises sometimes fears of the loss of intellectual property and therewith the control over their own ideas.

As a result many labs have developed software tools that solve similar tasks, but are often incompatible with each other (even within the same lab). Thus, the wheel has been reinvented over and over again. However, reimplementations of algorithms end up performing slightly differently in most cases. This renders scientific comparisons between different methods difficult.

To avoid such reimplementaions and to propose a standard base, we started working on the software framework CONRAD (CONe-beam in RADiology) in which we address many of these issues. From our point of view such a software package must satisfy at least the following goals:

  • Integration into the scientific workflow: While good software can have a significant impact on the scientific community, it is often not credited in a scientific manner. One major outcome parameter of scientific work is a strong publication. Often the importance of a publication is measured in the number of citations. Software is sometimes difficult to cite and only the creators of the first version receive the scientific credit. Deployment of an algorithm within the framework should also bring scientific recognition. Thus, a strong software package should support the use of scientific citations. Algorithms in it should be able to be cited.

  • Collaboration and reusable software: It is not easy to transfer software between different labs or even PhD students within one lab. If the main person that developed the software package leaves the lab, the software is often orphaned. Open-source projects have the potential to alleviate this problem.

The design of our framework reflects these high level goals. Furthermore, it implements many state-of-the-art algorithms. However, there are also technical requirements that are important for the success of a software platform. In contrast to existing frameworks, our package offers the following unique combination of features:

  • Platform portability: The framework is implemented in Java and has users on Linux and Windows.

  • Use of hardware acceleration: All compute-intensive algorithms are implemented in two versions: CPU only and OpenCL.

  • Interfaces to existing software packages and integration of commonly used software packages.

  • Streaming pipeline: The framework may be used to stream data and is thus able to reconstruct even if the projection data do not fit the host computer's main memory. Furthermore, algorithms can be configured interchangeably along the processing chain.

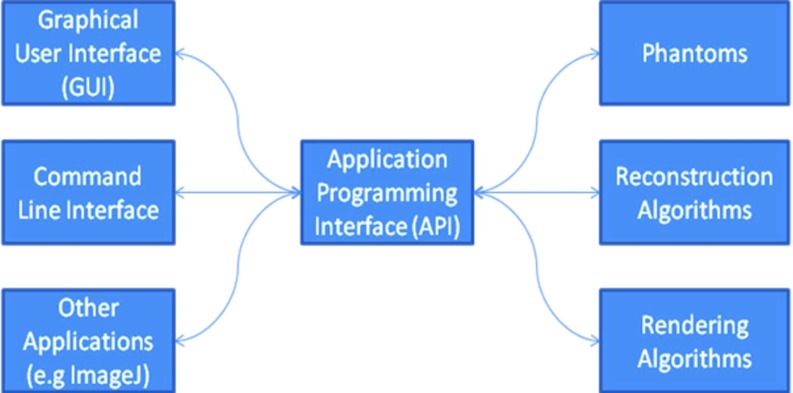
  • Separation of logic and UI: The software framework should not mix functionality with a graphical user interface (GUI), i.e., it should have a clear boundary between user interaction and the actual processing pipeline. Any algorithm must provide an application programming interface (API) such that it can be used/executed without the user interface.

METHODS

CONRAD offers the basic functionality needed to generate cone-beam x-ray projections and reconstruct them back to the image domain. For accurate simulations, one major point in the package is the availability of simple physical models in these processes. Additionally, the current state of the framework is the result of principled development which also yields a clear direction for the future development—a software rationale.

Software rationale

The rationale of CONRAD can be divided into three parts. The fundamental design describes the basic concepts that are realized within the CONRAD package and how the package is intended to be used. Additionally, many applications in the medical imaging community are closely related to industry. Hence, intellectual property is explicitly considered in the framework. The last part of the rationale deals with the integration of CONRAD and how compatibility with other frameworks is achieved.

CONRAD makes use of two important design concepts that are commonly used in many programming environments: Object orientation and streaming. As streaming implies a sequence, the imaging process is modeled as a sequence of processing steps that are performed after each other (as in ITK) or in parallel. The streamed objects are slabs of raster images that represent either projection sequences or volumes.

Another major concept is the use of projection matrices to describe the imaging process. Let x denote the coordinate of a 3D point in homogeneous coordinates, the homogeneous 2D point u can then be computed using a projection matrix P:

u=Px=K[Rt]x.

The projection is composed of a camera matrix K, a rotation matrix R, and a translation vector t. The 3 × 4 matrix P describes the system geometry up to a scaling factor. A similar concept is also found in OpenGL. In contrast to OpenGL, however, CONRAD includes all of the tools that are required to decompose projection matrices to various other representations such as the KRt decomposition. The code allows the extraction of source and detectors position and their respective coordinate axes. Doing so, the software also supports the integration of many analytic reconstruction formulae.

The integration of the software into the scientific workflow is key in CONRAD. The software documentation is based on intrinsic documentation features and supports typesetting formulae in LaTeX format directly in the source code. In the main classes of the system, elaborate documentation is found that is also suitable for users that are new to the subject. This alone, however, is not enough to put an emphasis on scientific work within the framework. Similar to Weka, we wanted to integrate the scientific workflow into the system. In Weka, a reference to the literature is found at the top of every processing module within its source code. In CONRAD, we went one step further: Every module or processing step has an API interface that references the correct scientific article describing the module's functionality. Doing so, this information is not only available in the source code but directly to the user over a graphical user interface. On the one hand this implies that if functions are embedded into CONRAD, the credit goes directly to the authors that published the method. On the other hand, we also encourage that new processing steps that are going to be embedded into the system are published within the scientific community. Figure 1 shows a screenshot of the current GUI.

Figure 1.

Figure 1

Open in a new tab

Screenshot of an implementation of a GUI using CONRAD. All algorithms that are used are reported with the respective citation. Supported formats are the Medline and BibTeX citations styles.

In medical imaging, intellectual property is an important issue. No contributor to CONRAD would like to bear the risk of being sued for patent infringement. Thus, one requirement for algorithms which are integrated into CONRAD is that they are published. This aspect is in exact agreement with the integration of scientific workflow in CONRAD.

Furthermore, CONRAD is released under the GNU General Public License (GPL) that allows anybody to use the software. Modifications are only allowed, if they are shared. Use in a commercial system would only be possible if all source code using CONRAD would be made publicly available. As most commercial users in the medical software engineering community will not agree to these terms, CONRAD is a framework designed for the use in teaching and research.

CONRAD promotes a separation of logic and GUI. Any algorithm that is integrated into the system has to be operational without GUI. Hence, any processing step can also be used via an API call from a different application (cf. Fig. 2).

Figure 2.

Figure 2

Open in a new tab

General structure of CONRAD. All algorithms and functions are separated from the user interface. This allows first algorithm design close to a GUI while large scale experiments can be executed on a cluster via command line interface. Of course other applications can also access CONRAD. Many of its algorithms are embedded into ImageJ plugins as an example of the API use.

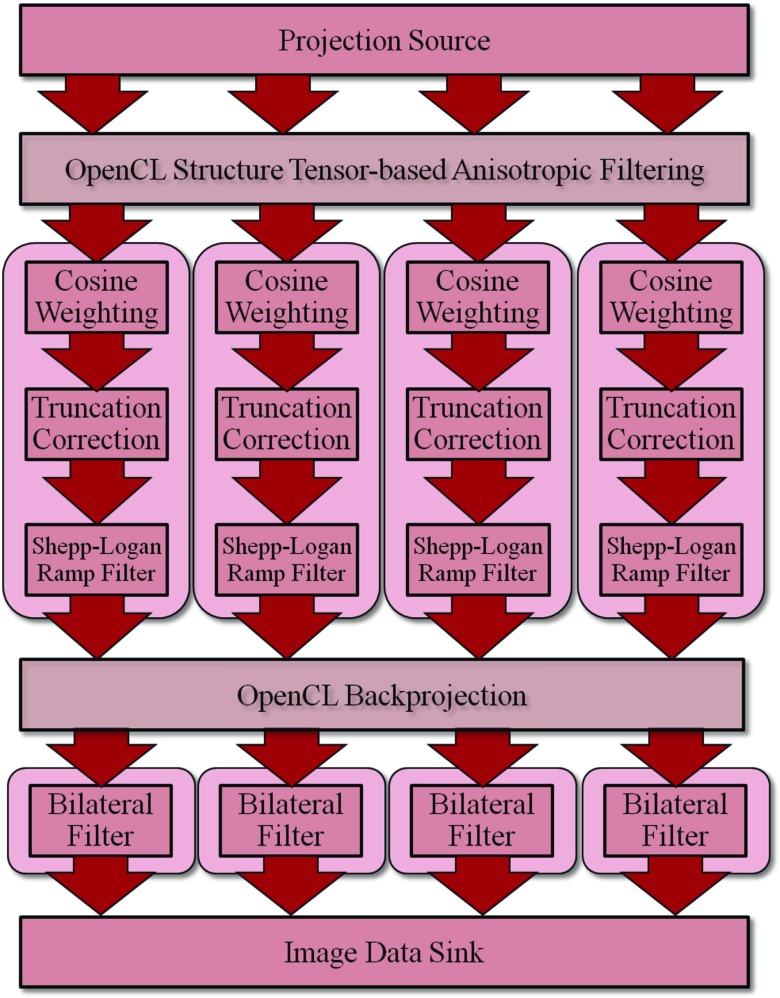
Integration of efficient processing techniques is also important in CONRAD, as many image processing steps are computationally expensive. Thus, CONRAD brings functional structures that facilitate parallelism. In fact, the programmer does not have to have significant knowledge of parallel design as CONRAD can—depending on the degree of parallelism that is suitable for the data—detect which resources have to be allocated to which processing step (as displayed in Fig. 3). The actual processing is planed prior to the execution and the resources are derived accordingly.

Figure 3.

Figure 3

Open in a new tab

Graphical representation of the parallel processing scheme on multiple resources. For the user and the developer of CONRAD parallelizing algorithms is a minor concern: CONRAD plans and distributes a parallel algorithm automatically on the available hardware. The streaming concept in CONRAD allows the use of parallel streams. Here, the processing pipeline for a 3D reconstruction is shown. All data are streamed from a projection source, that is, either a scanner or an offline file through the pipeline. After the projection domain filter, the next three steps can be performed in parallel (here: on four parallel CPUs). This is followed by a step that uses the graphics card exclusively again. Hence, the data have to be buffered and the step cannot be performed in parallel, as there is only 1 GPU in the system. The next step can be performed in parallel again followed by the last step, which collects the data in an image data sink, e.g., a file container.

Today, graphics hardware is often used for reconstruction, thus CONRAD also offers integration of OpenCL to execute massively parallel processes. As CONRAD is completely based on Java technology it is platform-independent, can be run on clusters at no additional license cost, is suited for 64 bit, and can easily interoperate with both Java-based projects such as ImageJ and Weka and native applications. Being compatible with ImageJ, there are also bindings for ITK and other image processing libraries.

Simulation

One of the two main fields of application of CONRAD is the simulation of x-ray projection images and volume data. Geometric phantom modeling is possible using simple geometric shapes and their intersections. More complex descriptors such as surface splines and NURBS are also supported. Motion models are defined as an interface that allows various implementations. Any physical shape in CONRAD consists of both a geometric description and a material. This allows for physically correct absorption modeling. Imaging of projection images and volumetric representation is based on a priority model and ray casting. However, due to CONRAD's modular design, other methods may also be implemented.

Geometric modeling

CONRAD brings powerful tools to describe geometric shapes. The basic shapes are boxes, cones, planes, spheres, etc. that can be combined by intersections. Therefore, CONRAD is able to render any phantom defined by the FORBILD phantom group (http://www.imp.uni-erlangen.de/forbild). Furthermore, CONRAD supports more complex shape descriptors such as surface splines and NURBS like those used in XCAT.5 In order to speed up the rendering process, the spline-based surfaces can be decomposed into triangles.

If users want to define a new phantom they can either use the FORBILD phantom language, describe the scene using the API, or mix both. In order to resolve occlusions, a linear scene graph is used that employs priorities. If the user chooses not to use explicit priorities, they are assigned implicitly by the order in which the objects were added. In the source code, this is shown in an example for the Shepp-Logan phantom.6

Motion modeling

The basic motion model M that is used in CONRAD is a point based interface. Given position x at time t, and the target time t′ it returns the new position x′:

x′=M(x,t,t′).

As repeated calls of this method may result in a weak computational performance, the interface also supports a second method to access the motion model M. Its third parameter is a vector of target times t′ and it returns a vector of positions X′ using the following matrix notation:

X′=M(x,t,t′).

The actual motion model does not have to be defined by the interface. This is done in the respective implementation. Examples using 4D surface splines7 or affine transforms8 are found in the source code.

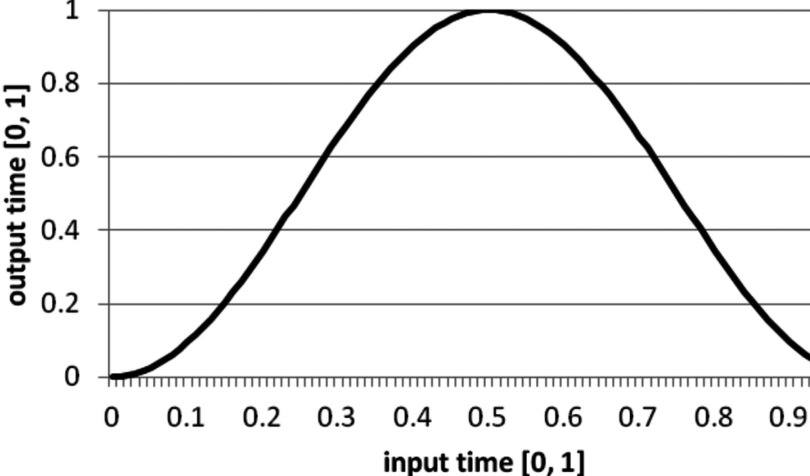
Another general concept that is found in CONRAD is the use of time warpers W(t) to describe nonlinear and periodic motion.8 The idea is to define the time within a motion as a number in the interval t ∈ [0, 1]. Based on this, the time can be internally warped to a new time t* by application of the time warper:

t*=W(t).

For example, any motion can be transformed into a periodic motion by use of a cosine-like time warper Wcos(t):

Wcost=12−12· cos (t·2·π). (1)

Figure 4 displays a cosine time warper.

Figure 4.

Figure 4

Open in a new tab

Plot of the cosine-based time warper from Eq. 1. Input and output time are displayed on the y-axis in the interval [0,1].

In this manner, we can decompose the actual physical change in position and its velocity. Acceleration, linear, and constant motion can be easily modeled using exactly the same movement while using different time warpers. Additionally, shivering motion can be easily integrated with a time warper consisting of a general movement pattern and added random noise.

Physical modeling

At present two different absorption models are supported, namely monochromatic and polychromatic x-ray absorption. In order to facilitate the use of the latter, the user can supply a source spectrum E(b) with b ∈ [1, B] being an index of a single energy bin. Parameter B is the number of energies modeled. Energy-dependent attenuation coefficients μ(η, E(b)) can be either interpolated for different compounds and mixtures depending on their atomic structure or directly downloaded from the X-COM element and compound database from NIST (Ref. 9) via an interface to the website (http://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html).

If photon statistics are known or generated, a Poisson-distributed noise model10 can also be added to the projection data.

Imaging process

The generation of projection data are based on ray casting. For each pixel, a ray S is cast through the scene. Along the ray all intersections with geometric objects are determined. The path segments through the different materials of the scene are determined and the absorption model is evaluated according to Lambert-Beer's Law,10

N=∑b=1BNb·e−∫Sμη,E(b)dη,

where N is the number of detected photons in the respective detector cell, Nb is the number of initial photons emitted from the source at Energy E(b), and η is the position along ray S.

As CONRAD is built as a modular framework, it is straight-forward to extend to a detector model that is specific to a particular detector, e.g., by incorporation of additional absorption by a CsI scintillator.

A similar process can be applied to generate rasterized volumetric data. Instead of casting a ray from the source to a detector pixel, a ray is cast along the x direction of the raster volume in the (y, z)-plane. Then all intersections with the scene are determined. Note that this process is the same as for the generation of projection images. However, instead of evaluation of the absorption model, the actual ray segments can be drawn into a rasterized 3D volume.

Furthermore, CONRAD also includes fast routines for projection image simulation as described in Ref. 11. This allows the simulation of projection data of various phantoms.12, 13, 14, 15, 16, 17

Image reconstruction

The second large application domain of CONRAD is cone-beam image reconstruction. In a similar spirit as for the simulation component, one important feature is the ability to compensate for nonlinear physical effects. However, the reconstruction component is not limited to simulations, and aims to also be applicable to real cone-beam data. To date, the system has already been used with raw data from different vendors.

Many of the currently implemented algorithms concentrate on analytical reconstruction methods. In particular, the geometric correction algorithms tackle analytical reconstruction problems. However, the available physical correction and the noise reduction algorithms are independent of the reconstruction method.

Physical correction algorithms

At the time of writing, CONRAD comprises a beam hardening correction that requires at least two reconstructions.18 In a first pass, the area containing the “hard” material is identified, whereas in a second pass a reconstruction is performed on corrected absorption values.

For scatter compensation, CONRAD offers a simple correction method based on unsharp masking.19 Basically unsharp masking is equivalent to a scatter correction with a single Water-Equivalent-Thickness in the projection.20 As most C-arm CT data are truncated, this approximation yields a simple scatter correction approximation. Note that this step has to be performed in intensity domain, not in line-integral domain. Further scatter correction approaches are subject of future work.

Geometric correction algorithms

Cosine weighting—as described in Ref. 21—weights each pixel in the projection data with its actual distance to the x-ray source to correct for fan- and cone-beam artifacts.

An approximate truncation correction is implemented according to Ohnesorge et al.22 The method virtually extends the detector by mirroring the detector edge. Within the mirrored data a cosine-like roll-off is applied to reduce truncation artifacts and enforce an end of the object.

In order to support (super) short scans, several redundancy weights are found in CONRAD. Implementations follow Parker et al.,23 Wesarg et al.,24 Silver et al.,25 Noo et al.,26 and Riess et al.27

Noise reduction algorithms

There are several methods to reduce noise in CONRAD starting from simple mean filtering28 to more sophisticated methods such as 2D and 3D bilateral filtering.29 An interesting noise reduction method that is performed in the projection domain is also found in the package.30 The method computes different direction-dependent 3D high-pass filters and a 3D isotropic low-pass filter which are then combined into an anisotropic filtered image. The combination of the different filters is controlled by a structure tensor.31

Reconstruction algorithms

CONRAD provides several methods for analytic reconstruction. For filtered back projection,21 different ramp filters (Ram-Lak, Shepp-Logan, Shepp-Logan with roll-off, Cosine, Hamming, Hanning, and custom double precision windows) are provided. Additionally, CONRAD contains Hilbert filtering32 and differentiation as required, e.g., for differentiated back projection, super short scans,33 and the simplest implementation of back projection according to the RabbitCT project.34 In addition, an algorithm that separates the reconstruction volume into sub-volumes which are then reconstructed in parallel in order to support multi-core CPUs (Ref. 35) is also available in OpenCL. Hence, the implementation can also be executed on graphics cards which cannot hold the entire reconstruction volume in their device memory.

RESULTS

An evaluation measure for a software framework is its growth and its use. Since November 2009, 30 filter modules and 13 phantoms have been implemented within the framework. To date, the framework comprises 60.000 lines of code plus 14 000 lines of comments, i.e., 19% of the code lines are used for documentation. Currently, there are two groups (one at Stanford University and one at the Friedrich-Alexander University of Erlangen-Nuremberg) that are using the framework. The software package is available for download at http://conrad.stanford.edu.

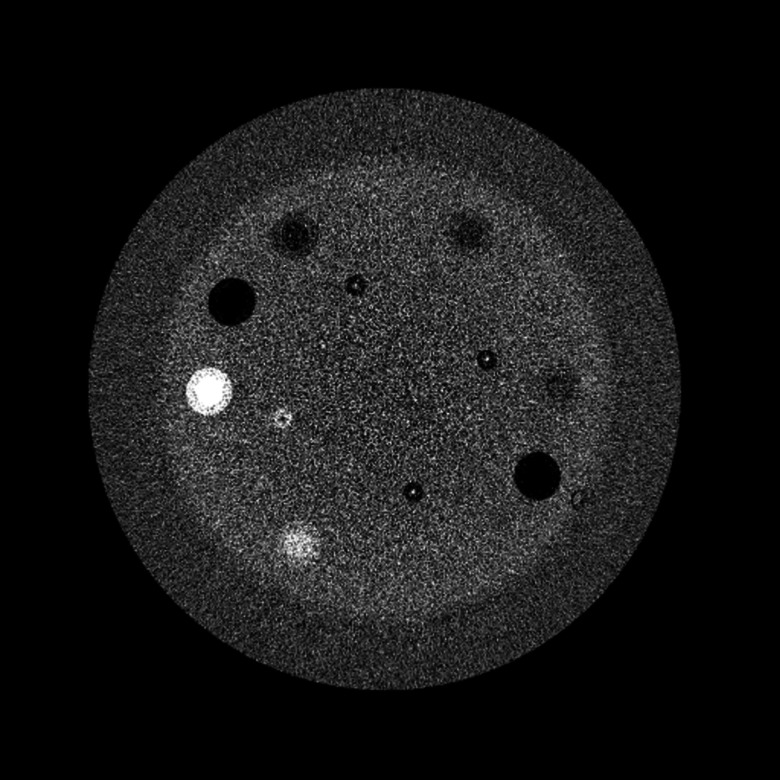
In order to show that the software is also able to reconstruct images from real systems (cf. Fig. 5), we present two reconstructions using real data. In the first case, we show a reconstruction of a Catphan 500. The data were acquired with 360° of rotation with an angular increment of 1° with a Varian detector (Detector Model 4030CB, Varian Systems, Palo Alto, CA), narrow collimation, detector image size 1024 × 768 with an isotropic pixel size of 0.388 mm. The source detector distance was 1404.4 mm and the source to center of rotation distance was 879.1 mm. The system was laser aligned and a perfect circular trajectory was assumed for reconstruction. The reconstruction slice matrix was 512 × 512 × 50 voxels with a voxel size of 0.4 × 0.4 × 0.5 mm. The reconstructed image is shown in Fig. 6.

Figure 5.

Figure 5

Open in a new tab

CONRAD offers the possibility to reconstruct data from various systems. We show reconstructions using the table top system on the left and a Siemens zeego system shown on the right. Both systems are installed at the Stanford University.

Figure 6.

Figure 6

Open in a new tab

Reconstruction from the table top system.

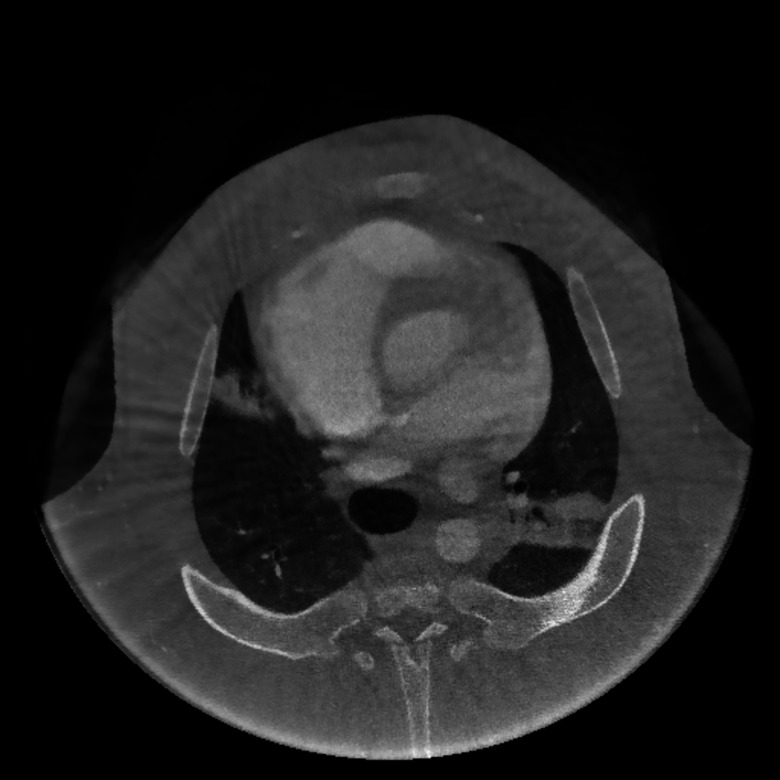
In addition, we have reconstructed data from a clinical C-arm system, an Artis zeego (Siemens AG, Forchheim, Germany). The detector matrix was read in a 2 × 2 binning with 1240 × 960 pixels at an isotropic pixel size of 0.308 mm. Source detector distance was 1200 mm and source to center of rotation distance was 750 mm. In total, 661 projections were acquired. We used a prototype software from Siemens that is able to extract line integral data and calibrated projection matrices. Both can be supplied to CONRAD and reconstructed as displayed in Fig. 7. The size of the reconstruction matrix was 512 × 512 × 512 with a voxel size of 0.5 × 0.5 × 0.5 mm.

Figure 7.

Figure 7

Open in a new tab

Reconstruction of a pig from a clinical C-arm system.

The runtime of our OpenCL back-projector was evaluated using RabbitCT.34 RabbitCT offers a standardized reconstruction problem with 496 projections of a resolution of 1280 × 960 pixels. We achieved a runtime of 2.5 s for the 2563 voxel problem and 12.4 s for the 5123 voxel problem using an Intel Xeon 5160 with 3 GHz and 4 Processors with a NVIDIA Quadro FX5800 graphics card. The execution hardware and the runtime are comparable to a CUDA implementation that is already published with RabbitCT (SpeedyGonzales) with 4.8 s for the 2563 problem and 14.7 s for the 5123 problem. Note that the measurement procedure was slightly changed due to bugfixes in RabbitCT when comparing the two numbers.

DISCUSSION

We believe that none of the currently existing frameworks for reconstruction are able to reconstruct data from a real clinical scanner. Most of the required physical correction steps are neglected. However, we see the trend in science that more and more physical aspects are integrated into the reconstruction process. Thus, this should also be modeled in the reconstruction software package. With CONRAD, we provide tools for physical modeling as well as tools for reconstruction.

The presented software framework will contribute to the scientific community. To do so, we will also set up collaborative tools in order to facilitate collaboration between researchers. A mailing list and tutorials how to use the software are provided on the project's website. Contributions by other researches can either be published by themselves on their own websites or they can send us the software for integration into the package. We will review the code and integrate it into the software framework in a timely manner. The same also holds for bugfixes by other researchers which will be made available by nightly builds.

As CONRAD's core is written in Java and OpenCL only no complex build tools such as cmake or autobuild are required. The complete source tree is loaded into an advanced development environment (e.g., Eclipse) and after adjustment of only few project settings, the project builds automatically. OpenCL integration is handled by the CL driver, such that no other compiler than the Java compiler is required. The compilation of the whole source tree performs in less than 1 min. Furthermore, unit tests are provided to check the functionality of the software.

As CONRAD features both GUI and API, it can be used in two ways: Researchers interested in reconstruction only can use the GUI to create the desired images. Integration into other software frameworks is possible using the API. Based on MATLAB's Java functionality, the CONRAD API can be incorporated as is into the MATLAB environment. A tutorial for the MATLAB integration is available on the website. For integration in C/C++ frameworks, Java Native Interfaces have to be used and wrapper classes have to be designed. This feature is possible and will be scope of future work. Integration of packages that already have ImageJ bindings (such as ITK) is also quite easy, as the same interface can be used by CONRAD.

Regarding performance there is only little difference between CUDA and OpenCL.36 We observed the same for our CONRAD OpenCL backprojector in a publicly available benchmark. With respect to the implementation, there is a big advantage for OpenCL in our case, as the OpenCL driver handles the code compilation. This enables us to use a single compiler integrated into our development environment without the need to use special building tools. This clearly enhances the convenience for the developer.

CONCLUSION AND OUTLOOK

CONRAD is a software framework for cone-beam applications in radiology. The framework delivers tools to simulate x-ray projection data and allows their reconstruction. Intrinsically, CONRAD already supports 4D applications and allows different definitions of motion fields.

One major goal of CONRAD is to support the scientific workflow in terms of collaboration and comparability of results. As CONRAD reports the citations of all employed algorithms, it is also a tool that will promote efficient algorithms in a scientific sense.

We hope that this paper will encourage more research groups to join this community effort, to develop algorithms together, and to increase scientific collaboration. A basis for these goals is now available.

ACKNOWLEDGMENTS

The authors thank Lars Wigström for the contribution of the structure tensor filtering software, Rotimi X. Ojo for the interface to the X-COM database and the FORBILD parser, and Benjamin Keck and Sungwon Yoon for the OpenCL back projector. This work was supported in part by NIH under Grant Nos. R01EB003524 and R01HL087917, and the Lucas Foundation. The authors gratefully acknowledge funding of the Erlangen Graduate School in Advanced Optical Technologies (SAOT) and the Research Training Group Heterogeneous Imaging Systems by the German Research Foundation (DFG) in the framework of the German excellence initiative.

References

  1. Collins T. J., “ImageJ for microscopy,” BioTechniques 43(1 Suppl), S25–S30 (2007). 10.2144/000112517 [DOI] [PubMed] [Google Scholar]
  2. Yoo T. S., Ackerman J., Lorensen W. E., Schroeder W., Chalana V., Aylward S., Metaxes D., and Whitaker R., “Engineering and algorithm design for an image processing API: A Technical Report on ITK - The insight toolkit,” in Proceedings of Medicine Meets Virtual Reality (IOS Press, Amsterdam, 2002), pp. 586–592. [PubMed]
  3. Allison J. et al. , “Geant4 developments and applications,” IEEE Trans. Nucl. Sci. 53(1), 270–278 (2006). 10.1109/TNS.2006.869826 [DOI] [Google Scholar]
  4. Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., and Witten H., “The WEKA data mining software: An update,” SIGKDD Explor. 11(1), 10–18 (2009). 10.1145/1656274.1656278 [DOI] [Google Scholar]
  5. Segars W. P., Mahesh M., Beck T. J., Frey E. C., and Tsui B. M. W., “Realistic CT simulation using the 4D XCAT phantom,” Med. Phys. 35, 3800–3808 (2008). 10.1118/1.2955743 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Shepp L. A. and Logan B. F., “The Fourier reconstruction of a head section,” IEEE Trans. Nucl. Sci. 21, 21–43 (1974). 10.1109/TNS.1974.6499235 [DOI] [Google Scholar]
  7. Segars W. P., Lalush D. S., and Tsui B. M. W., “A realistic spline-based dynamic heart phantom,” IEEE Trans. Nucl. Sci. 46(3), 503–506 (1999). 10.1109/23.775570 [DOI] [Google Scholar]
  8. Segars W. P., Lalush D. S., and Tsui B. W. M., “Modeling respiratory mechanics in the MCAT and spline-based MCAT phantoms,” IEEE Trans. Nucl. Sci. 48(1), 89–97 (2001). 10.1109/23.910837 [DOI] [Google Scholar]
  9. Hubbell J. H. and Seltzer S. M., “Tables of x-ray mass attenuation coefficients and mass energy-absorption coefficients from 1 keV to 20 MeV for elements Z = 1 to 92 and 48 additional substances of dosimetric interest,” NISTIR 5632 (1989). [Google Scholar]
  10. Buzug T., Computed Tomography - From Photon Statistics to Modern Cone-Beam CT, 2nd ed. (Springer, Berlin, Germany, 2008). [Google Scholar]
  11. Maier A., Hofmann H. G., Schwemmer C., Hornegger J., Keil A., and Fahrig R., “Fast simulation of x-ray projections of spline-based surfaces using an append buffer,” Phys. Med. Biol. 57(19), 6193–6210 (2012). 10.1088/0031-9155/57/19/6193 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bögel M., Maier A., Hofmann H. G., Hornegger J., and Fahrig R., “Diaphragm tracking for respiratory motion compensated cardiac C-Arm CT,” in Proceedings of 2nd CT Meeting, Salt Lake City, UT (University of Utah, Salt Lake City, UT, 2012), pp. 13–16.
  13. Choi J. H., Maier A., Keil A., and Fahrig R., “Acquisition of 3D knee geometry under weight-bearing conditions using a C-arm CT scanner,” in Proceedings of RSNA, Chicago, IL, 2011. [DOI] [PubMed]
  14. Mueller K., Zheng Y., Lauritsch G., Rohkohl C., Schwemmer C., Maier A. K., Fahrig R., and Hornegger J., “Evaluation of interpolation methods for motion compensated tomographic reconstruction for cardiac angiographic C-arm data,” in Proceedings of CT Meeting, Salt Lake City, UT (University of Utah, Salt Lake City, UT, 2012), pp. 5–8.
  15. Müller K., Schwemmer C., Hornegger J., Zheng Y., Wang Y., Lauritsch G., Rohkohl C., Maier A., Schultz C., and Fahrig R., “Evaluation of interpolation methods for surface-based motion compensated tomographic reconstruction for cardiac angiographic C-arm data,” Med. Phys. 40(3), 031107 (12pp.) (2013). 10.1118/1.4789593 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Müller K., Schwemmer C., Lauritsch G., Rohkohl C., Maier A., Heidbüchel H., De Buck S., Nuyens D., Kyriakou Y., Köhler C., Fahrig R., and Hornegger J., “Image artifact influence on motion compensated tomographic reconstruction in cardiac C-arm CT,” in Proceedings of the 12th Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, Lake Tahoe, CA (University of California, Davis, CA, 2013), pp. 98–101.
  17. Wu H., Maier A., Hofmann H., Fahrig R., and Hornegger J., “4D-CT reconstrucion using sparsity level constrained compressed sensing,” in Proceedings of 2nd CT Meeting, Salt Lake City, UT (University of Utah, Salt Lake City, UT, 2012), pp. 206–209.
  18. Joseph P. M. and Spital R. D., “A method for correcting bone induced artifacts in computed tomography scanners,” J. Comput. Assist. Tomogr. 2, 100–108 (1978). 10.1097/00004728-197801000-00017 [DOI] [PubMed] [Google Scholar]
  19. Malin D. F., “Unsharp masking,” AAS Photo-Bull. 16(3), 10–13 (1977). [Google Scholar]
  20. Rührnschopf E. P. and Klingenbeck K., “A general framework and review of scatter correction methods in x-ray cone-beam computerized tomography. Part 1: Scatter compensation approaches,” Med. Phys. 38(7), 4296–4311 (2011). 10.1118/1.3599033 [DOI] [PubMed] [Google Scholar]
  21. Kak A. C. and Slaney M., Principles of Computerized Tomographic Imaging (IEEE Service Center, Piscataway, NJ, 1988). [Google Scholar]
  22. Ohnesorge B., Flohr T., Schwarz K., Heiken J. P., and Bae K. T., “Efficient correction for CT image artifacts caused by objects extending outside the scan field of view,” Med. Phys. 27(1), 39–46 (2000). 10.1118/1.598855 [DOI] [PubMed] [Google Scholar]
  23. Parker D. L., “Optimal short scan convolution reconstruction for fanbeam CT,” Med. Phys. 9(2), 254–257 (1982). 10.1118/1.595078 [DOI] [PubMed] [Google Scholar]
  24. Wesarg S., Ebert M., and Bortfeld T., “Parker weights revisited,” Med. Phys. 29(3), 372–378 (2002). 10.1118/1.1450132 [DOI] [PubMed] [Google Scholar]
  25. Silver M. D., “A method for including redundant data in computed tomography,” Med. Phys. 27(4), 773–774 (2000). 10.1118/1.598939 [DOI] [PubMed] [Google Scholar]
  26. Noo F., Defrise M., Clackdoyle R., and Kudo H., “Image reconstruction from fan-beam projections on less than a short scan,” Phys. Med. Biol. 47(14), 2525–2546 (2002). 10.1088/0031-9155/47/14/311 [DOI] [PubMed] [Google Scholar]
  27. Riess C., Berger M., Wu H., Manhart M., Fahrig R., and Maier A., “TV or not TV? That is the question,” in Proceedings Fully3D, Lake Tahoe, CA (University of California, Davis, CA, 2013), pp. 341–344.
  28. Paulus D. W. R. and Hornegger J., Applied Pattern Recognition, 4th ed. (GWV-Vieweg, Wiesbaden, Germany, 2003). [Google Scholar]
  29. Perona P. and Malik J., “Scale space and edge detection using anisotropic diffusion,” IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639 (1990). 10.1109/34.56205 [DOI] [Google Scholar]
  30. Maier A., Wigström L., Hofmann H. G., Hornegger J., Zhu L., Strobel N., and Fahrig R., “Three-dimensional anisotropic adaptive filtering of projection data for noise reduction in cone beam CT,” Med. Phys. 38(11), 5896–5909 (2011). 10.1118/1.3633901 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Knutsson H., Haglund L., Bårman H., and Granlund G. H., “A framework for anisotropic adaptive filtering and analysis of image sequences and volumes,” in Internationcal Conference on Acoustics, Speech, and Signal Processing (ICASSP), San Francisco, CA (IEEE Consortium, 1992), pp. 469–472.
  32. Kak S. C., “The discrete Hilbert transform,” Proc. IEEE 58(4), 585–586 (1970). 10.1109/PROC.1970.7696 [DOI] [Google Scholar]
  33. Yu H. and Wang G., “Feldkamp-type VOI reconstruction from super-short-scan cone-beam data,” Med. Phys. 31(6), 1357–1362 (2004). 10.1118/1.1739298 [DOI] [PubMed] [Google Scholar]
  34. Rohkohl C., Keck B., Hofmann H., and Hornegger J., “RabbitCT - An open platform for benchmarking 3D cone-beam reconstruction algorithms,” Med. Phys. 36(9), 3940–3944 (2009). 10.1118/1.3180956 [DOI] [PubMed] [Google Scholar]
  35. Scherl H., Keck B., Kowarschik M., and Hornegger J., “Fast GPU-based CT reconstruction using the common unified device architecture (CUDA),” in IEEE Nuclear Science Symposium, Medical Imaging Conference Record, Honolulu, HI (IEEE Consortium, 2008), pp. 6:4464–6:4466.
  36. Siegl C., Hofmann H. G., Keck B., Prümmer M., and Hornegger J., “OpenCL, a viable solution for high-performance medical image reconstruction?,” Proc. SPIE 7961, 79612Q (2011). 10.1117/12.878058 [DOI] [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES