Electro-entropic excluded volume effects on DNA looping and relaxation in nanochannels

Abstract

We investigate the fluctuation-relaxation dynamics of entropically restricted DNA molecules in square nanochannels ranging from 0.09 to 19.9 times the persistence length. In nanochannels smaller than the persistence length, the chain relaxation time is found to have cubic dependence on the channel size. It is found that the effective polymer width significantly alter the chain conformation and relaxation time in strong confinement. For thinner chains, looped chain configurations are found in channels with height comparable to the persistence length, with very slow relaxation compared to un-looped chains. Larger effective chain widths inhibit the formation of hairpin loops.

INTRODUCTION

Stiff biological macromolecules such as actin filaments and DNA are restricted in partitions comparable to or much smaller than their longest characteristic length, inside a natural environment such as the cell and a cell nucleus. The strong confinement constraint rearranges the structure of the molecules and also affects the dynamics of processes such as nucleosome folding/unfolding, DNA transcription, and actin polymerization. Advances in nano-fabrication have greatly facilitated studies that directly probe changes to a single polymer structure and dynamics in confinement^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} in well-defined nanoslits and nanochannels. These studies typically adopt double stranded viral phage DNA molecules as model polymers due to its mono-dispersity, long persistence length (P ≈ 50 nm at high ionic strength), and the ease of direct observation. Several recent studies have examined the conformation and relaxation of a semi-flexible chain (SFC) in sub-persistence length quasi-one dimensional (Q1D) square nanochannels and found that these properties are qualitatively different from unconfined SFC.^{5, 19, 20, 21, 22, 23} Due to the strong restriction on coordinated segmental motion in nanochannels, the dominant segmental motions are not yet clear. In this study, measurements of DNA extension and dynamics are compared to predictions for chains in sub-persistence nanochannels and the results from Brownian dynamics simulations (BDs). We investigated how changes in the effective polymer width and the bulk persistence length, which may be controlled by varying solvent ionic strength,^{24, 25} affect the confined polymer properties. The chain relaxation mechanisms are found to depend on both the strong confinement and the effective polymer width.

The physical properties of a SFC can be considered on the length scales of the monomer width σ_m, the persistence length P, the radius of gyration in free solution R_g,bulk, and the contour length L = (N−1)σ_m, where N is the number of monomers. Depending on which length scale one probes a polymer, it can exhibit both flexible rod-like (<P) and coil-like (>R_g,bulk) characteristics. For double stranded λ-phage DNA, P = 50 nm and L = 16 μm are separated by nearly three orders of magnitude. Confinement effects begin to significantly restrict accessible polymer conformations when the channel height H is comparable to R_g,bulk.

A scaling argument can provide some insight to how the chain relaxation time depends on confinement for R_g > H > P. Scaling theory^{26, 27, 28} predicts that the chain size in a channel would increase ∼H^−2/3 for self-avoiding chains (SAW) and ∼H⁻¹ for Gaussian chains (GCs). In small (H < P) channels, the chain extension X is the projection of (L/l) deflection segments stretched along the channel length, with the deflection length l = (H²P)^1/3.¹⁹ For a small deflection angle (H/l ≪ 1), X = L[1−A(H/P)^2/3], with the predicted value of A = 0.17 verified in recent MC studies.^{5, 17, 29, 30}

For unconfined polymers, the longest relaxation time is τ_bulk = (R_g²/D), where D = ⟨(R(t)-R(0))²⟩/(6 t) is the chain diffusivity and R(t) is the chain center-of-mass position at time t. In Q1D confinement, the longest chain relaxation time is the reptation time τ_Q1D ∼ R_g²/D ∼ [N(P/H)^−2/3]²/D ∼ N³. In free solution, if intra-chain hydrodynamic interactions (HIs) were neglected, the bulk solution diffusivity D ∼ N⁻¹ and τ_bulk ∼ NR_g² ∼ N^11/5 (SAW) and ∼N² (GC).³¹ Thus, a scaling law τ/τ_bulk ∼ (R_g,bulk/H)^ν with the exponents v = 4/3 (SAW) and 2 (GC) are found for the intermediate region. With intra-chain HI, D ∼ R_g⁻¹, τ_bulk ∼ N^9/5 (SAW), and N^3/2 (GC) for free polymers.³¹ Following the same argument, the scaling exponents are v = 2 (SAW) and 3 (GC) for the intermediate region. The qualitative dependence is consistent with the idea that chain relaxation slows as the chain becomes more confined. It is also expected that τ depends more strongly on H for the Gaussian chain due to the greater change in the chain fractal dimension.

However, a recent experiment showed that the chain stretch relaxation time has a non-monotonic dependence on the channel height.⁵ In nanochannels, the conformational restriction results in a large separation between the chain and segmental relaxation times. The dominant segmental relaxation process thus depends on the transverse correlation length, with τ ∼ l_⊥²/D_seg ∼ H²/D_seg, where D_seg, is the segment diffusivity. For the channel-deflected segments, one may consider the segments of length H to be rod-like, with the segmental diffusivity D_seg ∼ ln(H/σ_m)/H and τ ∼ H³/ln(H/σ_m).³¹

METHOD

To examine the fluctuation-relaxation process of chain segments in the nanochannel, Brownian dynamics simulations with and without HIs are employed to track the chain trajectory,^{32, 33, 34, 35, 36, 37}

$$-\zeta [v_p-v_f({\mathit{r}}_i)]+{\mathit{f}}_i^R\left(t\right)-\frac{\partial U}{\partial {\mathit{r}}_i}=0.$$ (1)

The friction force is determined from the friction coefficient of a bead ζ, the monomer bead velocity v_p, and the fluid velocity v_p(r_i). f_i^R(t) is a random force that satisfies the fluctuation-dissipation theorem, with a Gaussian distribution with zero mean and a variance 2k_BTζ/dt. Intra-chain hydrodynamic interaction is determined by coupling the polymer to a lattice Boltzmann fluid with thermal fluctuations, where the friction forces acting on the polymer are exchanged to the fluid with full coupling.³³ The bead-wall repulsive interaction is a cubic potential with a range of σ_m.³⁸ The integration time step is dt = 5 × 10⁻³ τ_D, where τ_D = ζσ_m²/k_BT is the bead diffusion time. With the viscosity with of water at 298 K, dt = 0.091 ns for σ_m = 2 nm.

In order to capture how strong confinement affects the chain rigidity in a Q1D channel, two coarse-grained double stranded DNA molecules with 40 and 160 persistence lengths are examined. The total chain lengths are N = 160, 400, 800, and 1000 beads. Hydrodynamic interactions is included only for N = 160 due to the significant computation cost. Each spring has equilibrium length σ_m, which is the chosen unit length. The spring potential energy is

$$U_{\mathit{s}\mathit{p}\mathit{r}\mathit{i}\mathit{n}\mathit{g}}=\frac{k_v{k}_{B}T}{2{\sigma }_m^2}{\displaystyle \sum _i{\left(\left|{\mathit{r}}_i-{\mathit{r}}_{i+1}\right|-{\sigma }_m\right)}^2},$$ (2)

where k_v = 400 for a harmonic spring is chosen to capture the rigidity of the double helix, and k_BT = 1. r_i is the position of the i-th bead. The beads repel each other with a short range repulsive Morse potential with a cutoff distance of 1.5 to coarsely mimic the inter-segmental steric and electrostatic repulsion,

$$U_{M,rep}={\epsilon }_m{k}_{B}T{\displaystyle \sum _{i,j}\exp \left[-{\alpha }_m\left(r_{i,\hspace{0.17em}j}-{\sigma }_m\right)\right]},$$ (3)

with ε_m = 0.2, α_m = 6, such that the monomer core radius is 0.5σ_m. r_i,j is the distance between the i-th and j-th beads. The chain rigidity is defined by a bending potential of the angle between v_i−1 = (r_i−1-r_i) and v_i = (r_i-r_i+1),

$$U_{\mathit{b}\mathit{e}\mathit{n}\mathit{d}}=k_{\mathit{b}\mathit{e}\mathit{n}\mathit{d}}{k}_{B}T{\displaystyle \sum _i\left(1-\frac{{\mathit{v}}_{i-1}\cdot {\mathit{v}}_i}{\left|{\mathit{v}}_{i-1}\right|\left|{\mathit{v}}_i\right|}\right)}.$$ (4)

The persistence length is determined from the exponential decay of the segmental correlation function C(j) = ⟨v_i·v_i+j⟩. k_bend are chosen such that P/σ_m = 4, 5, 10, and 25 for N = 160, 800, 400, and 1000, respectively. By matching P to the measured DNA persistence length, the effect of increasing effective chain widths in a channel of length 2000 × H × H is observed.

DNA persistence length increases as the solution ionic strength decreases due to stronger electrostatic repulsion. The model bead excluded volume diameters correspond to the change of polymer width due to the electrostatic screening length (high ionic strength). P/σ_m = 25 corresponds to the bare DNA with σ_m = 2.0 nm. Based on prior studies, the model chain with P/σ_m = 4, 5, and 10 are matched to effective DNA widths of σ_m = 16.6, 12.2, and 5.1 nm in 0.006, 0.016, and 0.12 M monovalent salt solutions.^{24, 25}

RESULTS AND DISCUSSION

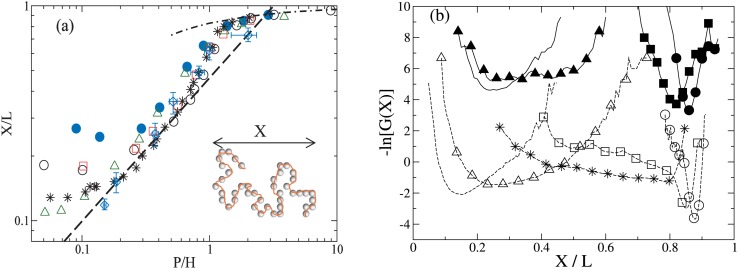
The chain conformation is analyzed from the chain extension, X = max(x_i)–min(x_i), as illustrated in Fig. 1a. Ensemble properties are calculated from more than 100 trials of chain relaxation trajectories, each trial length is at least 5 chain relaxation times. In free solution, R_g,bulk/P = 3.65 ± 0.18, 2.96 ± 0.09, 6.58 ± 0.22, and 3.46 ± 0.12 for N = 160, 400, 800, and 1000, respectively. The extensional relaxation of initially nearly fully stretched chains is captured as each chain relaxes via an individual trajectory. The equilibrium chain stretch ⟨X⟩ is shown in Fig. 1a. As observed in prior studies,^{5, 14, 17, 39} there are multiple regimes of conformation change. for H < R_g,bulk, ⟨X⟩ increases following H^−2/3 as expected for SAW. As H approaches P, it is found that ⟨X⟩ deviates from the expected scaling, possibly due to the depletion of intra-chain loops.^{23, 40} For H < P, Eq. 1 captures the chain extension dependence with A = 0.17.

Figure 1.

(a) Equilibrium chain stretch as a function of P/H for N = 160, P/σ_m = 4 (filled circle), N = 1000, P/σ_m = 25 (circle), N = 400, P/σ_m = 10 (square), N = 800, P/σ_m = 5 (triangle). Data from Refs. ¹⁷ (star) and 5 (diamond with error bars) are also shown. Scaling predictions of (P/H)^2/3 (dashed line), (P/H) (solid line) and Eq. 1 (dotted-dashed line) are also shown. Inset: Illustration of the chain dimension. (b) The configuration free energy for N = 160, P/σ_m = 4 (solid lines) in nanochannels with H/P = 14.5, 3.2 (triangle), 0.95 (square), and 0.7 (circle) and N = 1000, P/σ_m = 25 chains (dashed lines) in nanochannels of H/P = 9.9, 1.9 (triangle), 1.1 (star), 0.9 (square), 0.3 (circle). The data for N = 160 are shifted up by 2 for clarity.

For chains with the same number of persistence lengths (N = 160, 400, and 1000), ⟨X⟩ increases as the effective chain width increases due to the increased equilibrium chain stretch, but the qualitative dependence for H < R_g does not change. The results for N = 1000, P/σ_m = 25 agrees very well with MC results¹⁷ for H < R_g, and also with the experimental results⁵ except for the smallest nanochannel.

Deviation of ⟨X⟩ from the scaling law prediction for H ≈ P nanochannels is investigated by examining the chain configuration free energy -ln(G(X)), with the chain stretch distribution function G(X), as shown in Fig. 1b. The configuration free energy of N = 1000, P/σ_m = 25 exhibits a sharp minimum for H/P = 9.9. As H decreases, the free energy minimum broadens and the curvature flattens as H decreases to 0.9P, which indicates the presence of hairpin configurations with the chain looping on itself in the nanochannel as reported in MC simulations.^{17, 22, 39, 41} For smaller H, the minimum shifts to higher X and finally become a single minimum. The coexistence of looped and extended configurations for H ≈ P is analogous to an intermediate state during the transition from coil to stretch configurations under an external extensional force.

The broad distribution for X is not found for P/σ_m = 4 and 5, which reflects the packing constraints of chain segments inside small channels and the inhibition of chain folding for the larger effective width. This would correspond to stronger electrostatic repulsion between DNA segments and between the segments and the walls at lower ionic strength. The reduction of chain folding at low ionic strength could explain observations of higher-than-expected average DNA extension in low-salt solution in nanoslits^{6, 42} and nanochannels.⁴³

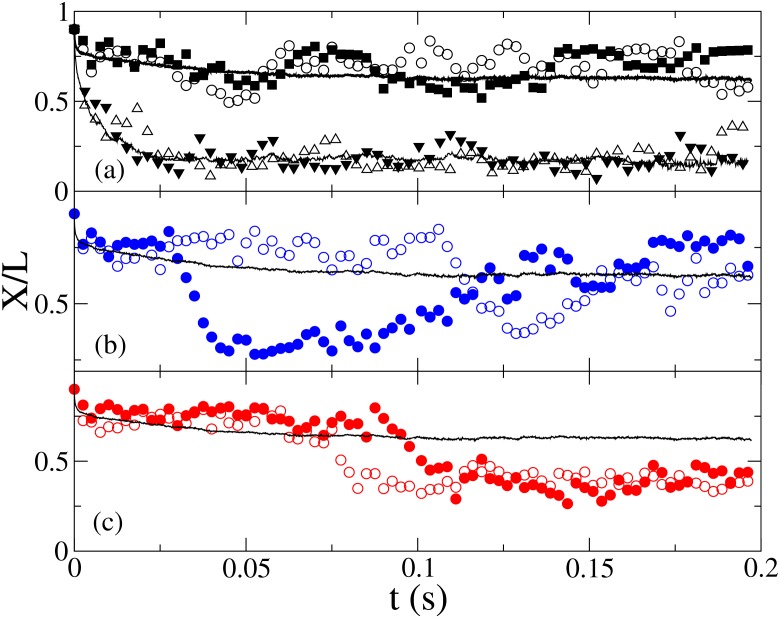
BD allows direct probing of the relationship between chain conformation and relaxation from individual chain relaxation trajectories, as illustrated in Fig. 2. For P/σ_m = 25 and H/P = 9.9, the chains relax to a small equilibrium extension (⟨X/L⟩ = 0.17 ± 0.01, Fig. 2a) following a single fast exponential decay. For H ≪ P, the chains become highly extended with hairpin loops inhibited, and the chain relaxation follow a single exponential decay. However, for H/P ≈ 1, very different relaxation trajectories are found. Fig. 2a shows two fast relaxation trajectories to an extended conformation, with ⟨X/L⟩ = 0.63 ± 0.03. Other trajectories are observed to relax slowly to reduced chain extension conformations due to folding with long lifetimes. The relaxation times of the folded states vary, as some looped states become unfolded (Fig. 2b), while other trajectories enter and remain in the looped state for extended period (Fig. 2c). The ensemble average of 100 trajectories shows both the fast (t < 0.01 s) and the slow relaxation processes.

Figure 2.

Selected chain stretch relaxation trajectories (circles) and ⟨X(t)⟩ (solid line) showing non-looped (a), relaxed loops (b), and un-relaxed loops (c) for N = 1000, P/σ_m = 25, H/P = 1. Trajectories in channels with H/P = 9.9 (triangles) are shown in (a).

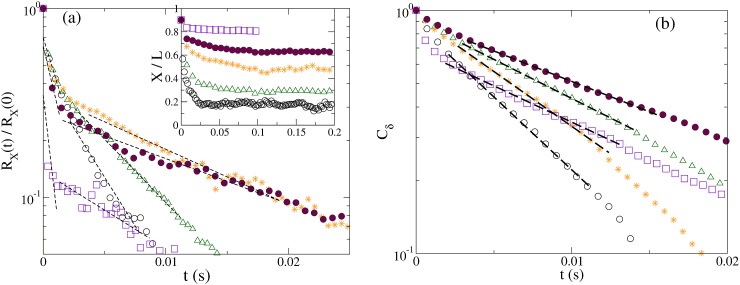
The chain relaxation time (τ_relax) can be directly measured from the stretch-relaxation process and the fluctuation correlation function in H < P nanochannels. For R_g > H > P channels, chain stretch relaxation exhibits exponential decay as expected, as shown in Fig. 3a inset.^{31, 44} Fig. 3a shows the stretch relaxation function R_X(t) = (X(t)−⟨X⟩)² ∼ exp(−2t/τ_X) with the relaxation time τ_X.^{45, 46} With stronger spatial restrictions in the nanochannel, coordinated segmental relaxation processes such as whole chain reorientation become more inhibited. For H ≈ P, fast and slow relaxation regimes are both observed. They correspond to the fast contraction of the chain from the initial stretched configuration to when the segments encounter the channel walls, and the slower relaxation of wall-confined segments. Prior studies of DNA in nanoslits have also found a separation of segmental relaxation and coordinated chain rotation times.¹ In Q1D nanochannels, coordinated chain rotation is strongly inhibited, leading to a large separation between segmental relaxation and chain reptation. For comparison to experiments,⁵ which measured the fluctuation correlation time from the fluctuation correlation C_δ(t) = ⟨δX(0)δX(t)⟩∼exp(−t/τ_δ), δX(t) = X(t)−⟨X⟩, as shown in Fig. 3b. τ_δ is found to agree well with slow stretch relaxation time τ_X.

Figure 3.

(a) The stretch relaxation function R_X(t) for N = 1000, P/σ_m = 25, for H/P = 9.9 (circle), 1.9 (triangle). 1 (star), 0.9 (filled circle), 0.6 (square). The dashed lines indicate the exponential fits to extract the relaxation time. Inset: The relative chain stretch X(t)/L. (b)The fluctuation correlation function C_δ(t) for the same H/P as in (a).

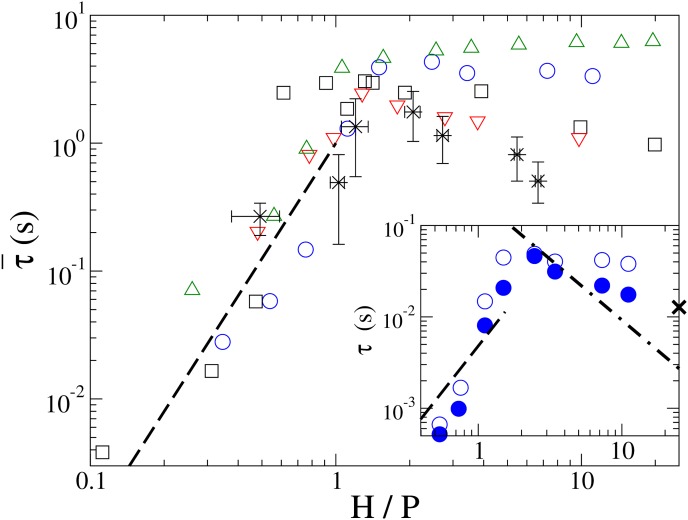
Accounting for HI significant quickens chain relaxation time for R_g > H > P, as observed for P/σ_m = 4 in Fig. 4 inset. With HI, stronger dependence on H is observed. Without accounting for HI, τ does not change significantly for P/σ_m = 4 and 5 as H decreases for R_g > H > P, in contrast to the expected H^−3/4 dependence, due to the limited range between R_g and P. For P/σ_m = 10 and 25, τ increases and reaches a maximum near H/P = 1. The delayed transition and longer relaxation time near H ≈ P for P/σ_m = 25 may be attributed to the slow relaxation of loops.

Figure 4.

The scaled chain relaxation time for N = 1000, P/σ_m = 25 (circles), N = 400, P/σ_m = 10 (squares), and N = 800, P/σ_m = 5 (triangles). Data from Ref. 5 are shown as stars with error bars. Chain relaxation time is rescaled according to its dependence on the chain contour length, $\overline{\tau }={\tau }_{\delta }{(L_{\lambda }/L)}^{11/5}$, L_λ = λ-DNA contour length of 16 μm. The inset shows the relaxation time with (filled circle) and without HI (empty circle) for N = 160, P/σ_m = 4. X marks the estimated τ_bulk for L = 2 μm. The dashed and dotted-dashed lines show H³/ln(H/σ_m) and (H/P)² dependences, respectively. The error estimates are comparable to the symbol size.

For H < P, τ is found to decrease sharply as H decreases, with and without HI. The transition occurs near H = P except for P/σ_m = 25, which may be due to slower loop relaxation for the thinner chain. For P/σ_m = 25, the transition at H ≈ 0.6 P corresponds to the disappearance of the long tail in G(X) at which height the chain cannot fold by looping due to strong segmental repulsion. For P/σ_m = 4 and 5, chain folding is inhibited by the large effective chain width at channel height H ≈ P. For all chains, τ consistently decrease as H³/ln(H/σ_m) if slower loop relaxation is eliminated.

The observed strong dependence on the effective chain width indicates that segmental motions could be strongly influenced by the electrostatic repulsion and the solution ionic strength, corresponding to the lack of chain folding for effectively wider chains in nanochannels. Interestingly, we note that even with the very coarse-grained polymer model for the DNA molecule, the rescaled relaxation time is in reasonable agreement to the experimental data within the error bars.

CONCLUSIONS

In this study, we found that Brownian dynamics simulations of chain properties with a coarse-grained DNA model capture the inhibition of long wave length segmental relaxation in strong confinement, and predictions of the chain relaxation time are in good agreement with a prior experiment. It is also found that the effective DNA width can determine whether DNA can fold inside a nanochannel comparable to its persistence length, and intra-chain repulsive interactions can strongly affect polymer dynamics for polymers under strong confinement. Our study finds that the chain dynamics have qualitatively different behavior depending on whether the molecule is able to form loops in the nanochannel, which suggests that experimental ionic strength for DNA molecules in nanochannels needs to be carefully controlled. Furthermore, reaction mechanisms that depend on loop formation, such as proteins that require two binding sites far apart on the chain backbone, would be strongly affected by the strong confinement and ionic conditions.

Editorial Note: This paper, along with Ref. 47, is part of a coordinated submission of two contributions with different approaches to the same phenomenon.