Abstract
Objective
To demonstrate the clinical feasibility of accurately measuring tricuspid annular area by 3-dimensional (3D) transesophageal echocardiography (TEE) and to assess the geometric differences based on the presence of tricuspid regurgitation (TR). Also, the shape of the tricuspid annulus was compared with previous descriptions in the literature.
Design
Prospective.
Setting
Tertiary care university hospital.
Interventions
Three-dimensional TEE.
Participants
Patients undergoing cardiac surgery.
Measurements and Main Results
Volumetric data sets from 20 patients were acquired by 3D TEE and prospectively analyzed. Comparisons in annular geometry were made between groups based on the presence of TR. The QLab (Philips Medical Systems, Andover, MA) software package was used to calculate tricuspid annular area by both linear elliptical dimensions and planimetry. Further analyses were performed in the 4D Cardio-View (TomTec Corporation GmBH, Munich, Germany) and MATLAB (Natick, MA) software environments to accurately assess annular shape. It was found that patients with greater TR had an eccentrically dilated annulus with a larger annular area. Also, the area as measured by the linear ellipse method was overestimated as compared to the planimetry method. Furthermore, the irregular saddle-shaped geometry of the tricuspid annulus was confirmed through the mathematic model developed by the authors.
Conclusions
Three-dimensional TEE can be used to measure the tricuspid annular area in a clinically feasible fashion, with an eccentric dilation seen in patients with TR. The tricuspid annulus shape is complex, with annular high and low points, and annular area calculation based on linear measurements significantly overestimates 3D planimetered area.
Keywords: tricuspid valve, 3-dimensional transesophageal echocardiography, tricuspid regurgitation, tricuspid annuloplasty, cardiac surgery, right ventricle
In patients with left-sided valvular disease, tricuspid regurgitation (TR) is most often functional, with normal tricuspid valve (TV) morphology, and often is associated with right ventricular (RV) dysfunction.1–3 The favorable prognostic effects of TV annuloplasty, as an adjunct procedure under these circumstances, are well established.4–8 However, prior to the development of clinically significant TR, the annulus undergoes significant remodeling through dilation when RV dysfunction is potentially reversible.9 Therefore, during left-sided valvular surgery, TV annuloplasty often is recommended for annular dilation even in the absence of significant TR.10,11 This decision is based on echocardiographic evidence of the ‘functional’ nature of the TR and demonstration of tricuspid annular dilation. Therefore, in addition to leaflet structure and function and quantification of TR, accurate echocardiographic measurement of tricuspid annular dimensions has important clinical and surgical implications.
Despite its importance, the echocardiographic views and axes to measure the tricuspid annular diameter are not well established.12 In addition, some studies suggest that the actual axis of annular dilation may be different from those routinely measured during echocardiography.13–15 As the tricuspid annulus has a complex and irregular shape, the concept of estimating area from a linear diameter in one axis is flawed intuitively. To better understand the complex tricuspid annular structure, there have been a number of invasive animal studies or in vitro models.16–18 In humans, the volumetric nature of the 3-dimensional (3D) data with transesophageal echocardiography (TEE) has the potential to allow a more comprehensive assessment of the tricuspid annulus. Ready availability of real-time 3D TEE (RT-3D TEE) already has provided a better geometric understanding of similar complex intracardiac structures, such as the mitral annulus.19,20 The 3D data are particularly useful to analyze nonplanar structures and to make accurate linear measurements using the multiplanar reformatting (MPR) method. MPR is a method by which the 3D data set may be manipulated to ensure that planes for measurement are precisely across the structure of interest, ensuring that there is no ambiguity or parallax error in dimensions. The authors, therefore, sought to demonstrate the clinical feasibility of geometric reconstruction of the tricuspid annulus utilizing volumetric data obtained with RT-3D TEE. To compare tricuspid annular shape with what has been described previously, the authors analyzed tricuspid annular area by both the 2D ellipsoid method and planimetry via 3D MPR.
MATERIALS AND METHOD
The study was conducted as a part of an Institutional Review Board–approved protocol with a waiver of informed consent for prospective data collection in cases undergoing routine intraoperative TEE examinations for cardiac surgery. Data from 20 consecutive patients with echocardiographically adequate 3D images were used for analysis (Table 1). All patients had normal RV function and structurally normal TVs.
Table 1.
Preoperative Data
| Group 1 | Group 2 | p Value | |
|---|---|---|---|
| Number of patients | 12 | 8 | |
| Sex | 8M, 4F | 4M, 4F | |
| Age | 69.1 ± 6.5 | 71.3 ± 12.9 | 0.62 |
| Height (in) | 67.2 ± 3.0 | 66.5 ± 2.6 | 0.62 |
| Weight (kg) | 90.6 ± 14.6 | 74.6 ± 10.1 | 0.01 |
All TEE examinations were conducted after induction of general anesthesia and prior to the institution of cardiopulmonary bypass and were conducted with an iE-33 ultrasound system with an X7-2t TEE probe (Philips Medical Systems, Andover MA), capable of RT and R-wave-gated 3D data acquisition. The 3D data were acquired during brief periods of apnea without electric interference or patient movement over 4 to 8 R-wave-gated cycles. Image acquisition was initiated in the midesophageal 4-chamber view, and the TEE probe was positioned to include the entire tricuspid annulus in the sector boundaries. Then, echocardiographic data, which were devoid of artifacts and image dropout, were exported via digital media in Digital Imaging for Communication in Medicine format (the standard echocardiography export format) to a Windows-based workstation (Windows 7, Microsoft Corporation) equipped with Image Arena software (TomTec Corporation GmBH, Munich, Germany) for analysis. The data were accessed by the 4D Cardio-View (version 2.1) module in Image Arena for further processing. All analyses were conducted at end-diastole in the frame immediately prior to initiation of TV closure.
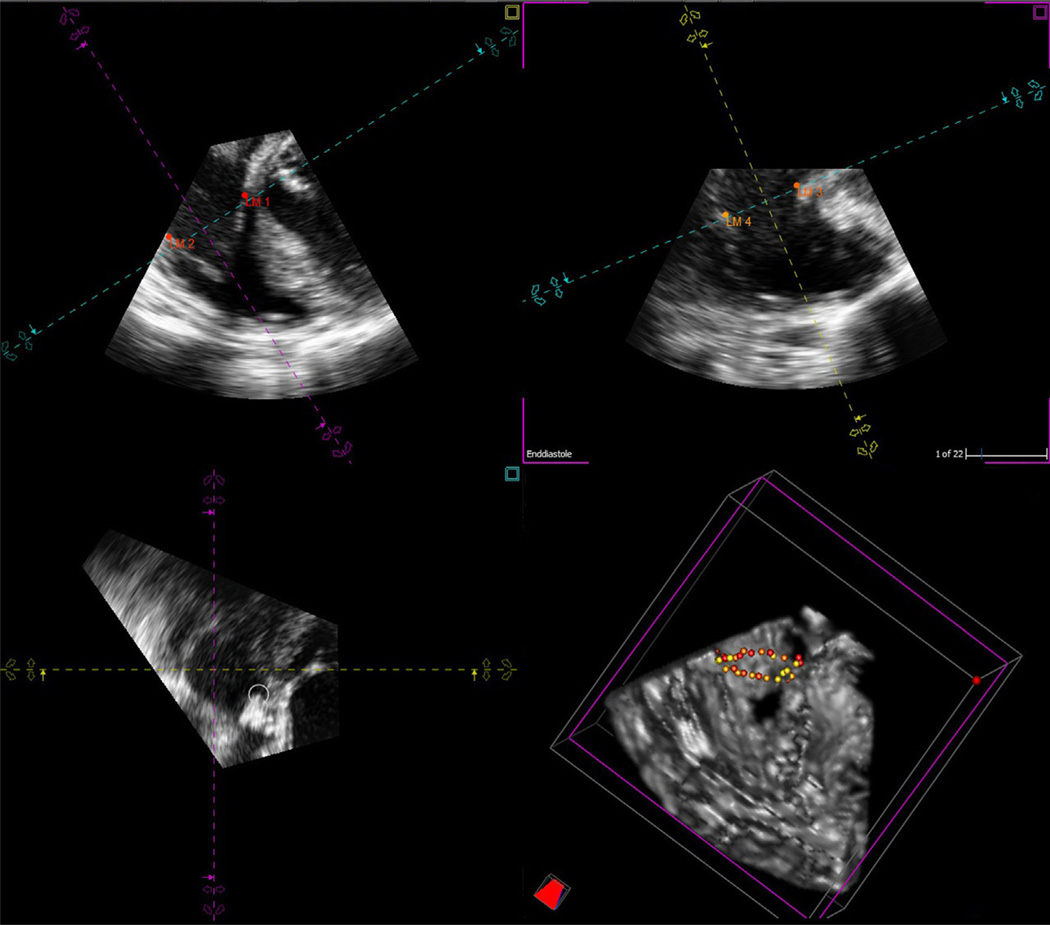
In the 4D Cardio-View interface, the sagittal, coronal, and transverse views were displayed simultaneously, with the rendered 3D image in the lower right quadrant (Fig 1). The TV was identified, and with manipulation of the software controls, the MPR was aligned with the tricuspid annulus in the sagittal and coronal planes. The points of intersection of the MPR planes were manipulated to cross the point of coaptation in the sagittal and coronal planes and through the center of the transverse plane. A digital landmark was added to the point of insertion of the septal leaflet of the tricuspid leaflet in the coronal plane. Next, the transverse plane was rotated and opposing annular points digitally marked in the associated coronal and sagittal planes in a series of 16 paired points (32-point software limit), until the entire annulus was represented. These digital annular points were displayed simultaneously in the 3D rendered image in the lower right quadrant (Fig 1). Then, the 3D data of the spatial orientation of the annular points (x, y, and z coordinates) were exported as a comma-separated version text file.
Fig 1.
Tricuspid annulus recreated with 32 landmark points in the TomTec 4D Cardio-View environment. All points are represented in the 3D representation of the right ventricle at the bottom right corner.
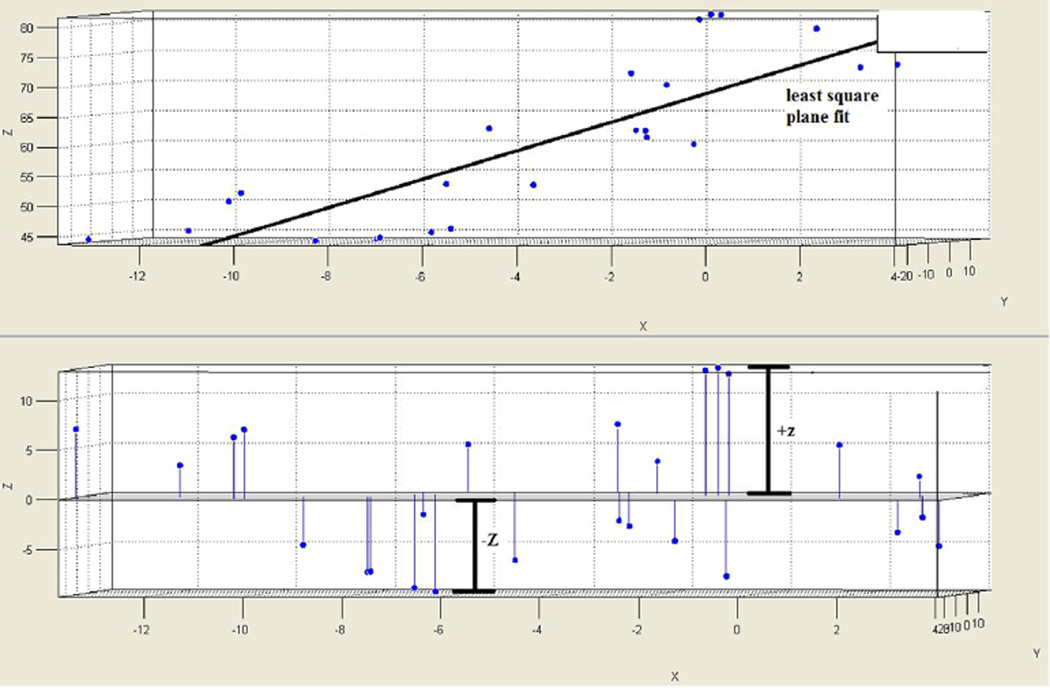
Each comma-separated version file containing the spatial coordinate data was exported to the MATLAB environment where the tricuspid annulus for each patient was to be graphically visualized. Then, the appropriate anterior, posterior, septal, and lateral points corresponding to the coordinates labeled in 4D Cardio-View were identified in the MATLAB environment. The 3D distance was calculated between anterior and posterior points and labeled as the anterior-posterior (AP) diameter. Also, the 3D distance between the septal and lateral points was calculated and labeled as the septal-lateral (SL) diameter. Then, the annular height was calculated by subtracting the maximum z coordinate from the minimum z coordinate for each data set (Fig 2). The 2D area was approximated by calculation with the ellipse formula, using AP and SL diameters as the orthogonal dimensions. The ellipse formula can be described as follows: Area = π × ½AP × ½SL.
Fig 2.
An example of a mathematic reconstruction of the tricuspid annulus in MATLAB following importing of coordinates from TomTec 4D Cardio-View. The upper frame shows a plot of all the coordinates in the 3 dimensions of X, Y, and Z. The least-square plane fit line represents the neutral plane of the annulus, which is used as the baseline in the lower panel. Here, the annular high and low points are indicated as +Z and −Z to reconstruct the 3D annulus.
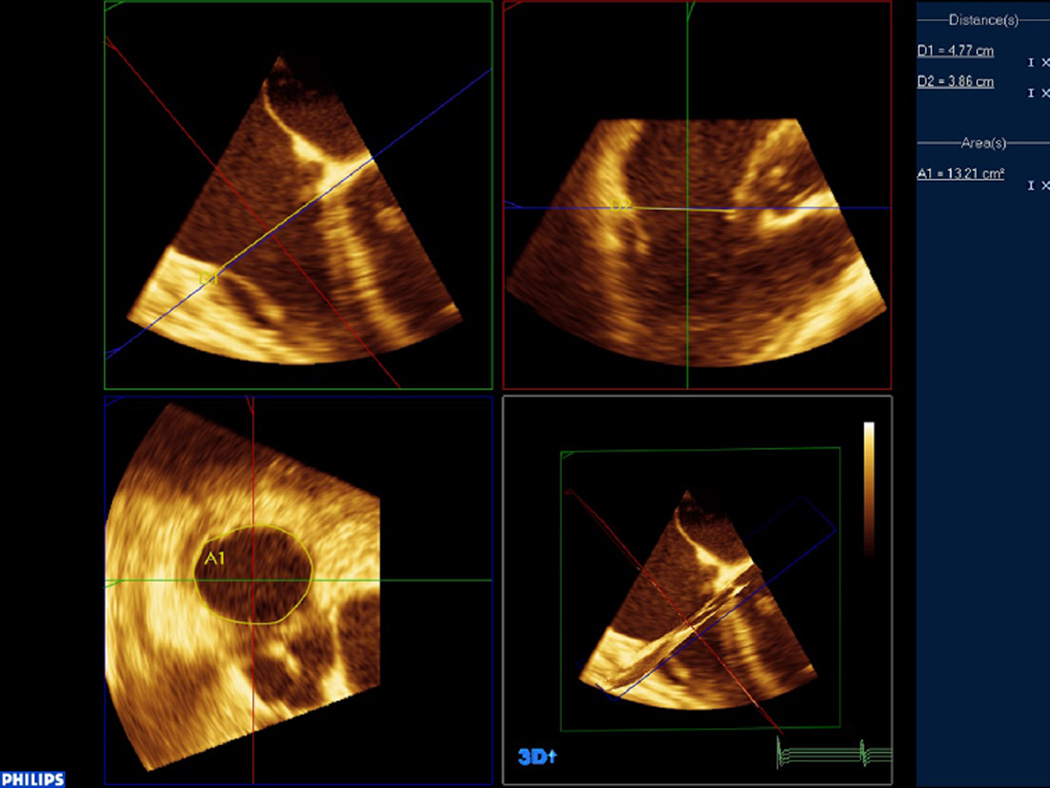
For the second portion of the analysis, the 3D data were then accessed by QLab (version 8.1) to calculate the diameters and area using planimetry. Manipulation of the 3D data sets by MPR was performed to accurately identify the transverse, coronal, and sagittal dimensions of the tricuspid annulus (Fig 3). The SL and AP dimensions were measured in the coronal and sagittal plane, respectively, and then, the tricuspid annulus was planimetered in the transverse plane to obtain a tricuspid annular area directly.
Fig 3.
Tricuspid annular data imported into the QLab MPR environment to accurately measure planimetered annular area in the bottom left corner. Through 3D manipulation of the coronal and sagittal planes, an ideal axial plane for measurement by planimetry can be achieved.
STATISTICAL ANALYSIS
The groups were divided into ‘Group 1’ with none-to-trace TR and ‘Group 2’ with mild or greater TR (Table 2). This grouping was based on TR severity agreed upon by 2 National Board of Echocardiography–certified anesthesiologists. Following this, statistical analysis of geometric variables was conducted by 2-tailed t-tests for unpaired parameters between these groups. The parameters of AP and SL diameters and height were compared between Group 1 and Group 2, as well as the tricuspid annular area calculated by both methods.
Table 2.
Geometric Measurements for Group 1 and Group 2
| MATLAB |
QLab |
||||||
|---|---|---|---|---|---|---|---|
| Amount of TR | SL Diameter | AP Diameter | Formula of Ellipse Area | SL Diameter | AP Diameter | Planimetered Area | |
| Group 1 | |||||||
| 1 | NTR | 3.36 | 3.66 | 9.68 | 2.98 | 3.64 | 9.63 |
| 2 | NTR | 3.25 | 3.01 | 7.70 | 4.47 | 2.9 | 8.25 |
| 3 | NTR | 3.74 | 3.64 | 10.67 | 3.32 | 2.42 | 6.36 |
| 4 | NTR | 2.93 | 3.44 | 7.96 | 3.1 | 2.49 | 4.75 |
| 5 | NTR | 3.68 | 3.08 | 8.96 | 3.32 | 4.11 | 8.76 |
| 6 | NTR | 3.80 | 3.82 | 11.42 | 3.98 | 3.46 | 9.94 |
| 7 | NTR | 2.45 | 4.15 | 8.57 | 2.47 | 3.4 | 7.36 |
| 8 | NTR | 3.27 | 3.46 | 8.90 | 2.7 | 2.52 | 4.83 |
| 9 | NTR | 2.89 | 2.91 | 6.61 | 2.6 | 3.59 | 6.2 |
| 10 | NTR | 2.86 | 3.05 | 6.87 | 2.69 | 3.72 | 7.95 |
| 11 | NTR | 3.49 | 3.31 | 9.06 | 2.8 | 2.38 | 5.89 |
| 12 | NTR | 3.28 | 3.46 | 8.93 | 3.58 | 2.58 | 7.91 |
| Avg | 3.25 | 3.42 | 8.78 | 3.17 | 3.10 | 7.32 | |
| StDev | 0.41 | 0.37 | 1.41 | 0.60 | 0.61 | 1.73 | |
| Group 2 | |||||||
| 1 | Mild | 3.81 | 4.61 | 13.93 | 3.63 | 4.72 | 11.09 |
| 2 | Mild | 3.34 | 2.95 | 7.77 | 3.99 | 2.86 | 10.81 |
| 3 | Mild | 3.59 | 4.41 | 12.56 | 4.51 | 3.49 | 9.76 |
| 4 | Mild | 4.25 | 3.85 | 12.88 | 4.27 | 4.04 | 14.69 |
| 5 | Mild | 3.99 | 3.00 | 9.60 | 3.82 | 3.31 | 9.67 |
| 6 | Moderate | 4.61 | 4.87 | 17.63 | 3.61 | 4.41 | 11.44 |
| 7 | Mild | 3.12 | 3.55 | 8.83 | 2.56 | 2.7 | 4.99 |
| 8 | Moderate | 4.91 | 4.43 | 17.12 | 4.77 | 3.86 | 13.21 |
| Avg | 3.96 | 3.96 | 12.54 | 3.90 | 3.64 | 10.71 | |
| StDev | 0.61 | 0.74 | 3.67 | 0.68 | 0.72 | 2.87 | |
| p Value | 0.0060 | 0.041 | 0.0044 | 0.02 | 0.07 | 0.003 | |
Abbreviation: NTR, none-to-trace tricuspid regurgitation.
After these variables were compared between Group 1 and Group 2, an additional analysis among all the patients was performed to compare the areas as measured by the 2 methods of MATLAB and QLab. Paired t-tests were used to assess whether there was any difference in areas calculated between these methods, as the MATLAB area calculation was based on linear dimensions, whereas the QLab measurement was based on direct planimetry. A scatterplot for linear regression was constructed to assess the correlation of these measurements, and the Bland-Altman analysis was completed to assess their agreement.
RESULTS
Echocardiographic data from 20 consecutive patients were collected, with 3 patients excluded for atrial fibrillation (unable to obtain R-wave-gated acquisitions) and one with inadequate image quality for analysis. No differences in demographics were found among these 20 patients, except for a significant increase in weight in Group 1 (Table 1).
From analysis of the data in MATLAB after importing the coordinates from Image Arena (Table 3), there was a significantly larger diameter in both the SL and AP diameters of the tricuspid annulus in Group 2 (p = 0.0060 and 0.041, respectively). Also, the area as derived from the ellipse formula was significantly larger in Group 2 (p = 0.0045). However, the annular height did not differ between the 2 groups (p = 0.70), nor did the ratios of the height to SL and AP diameters (p = 0.24 and p = 0.34, respectively).
Table 3.
TomTec-acquired Data
| Group 1 | Group 2 | p Value | |
|---|---|---|---|
| SL diameter (cm) | 3.25 ± 0.41 | 3.96 ± 0.61 | 0.0060 |
| AP diameter (cm) | 3.42 ± 0.37 | 3.96 ± 0.74 | 0.041 |
| Annulus height (cm) | 1.87 ± 0.90 | 1.73 ± 0.57 | 0.70 |
| Area by the ellipse formula (cm2) | 8.78 ± 1.41 | 12.54 ± 3.67 | 0.0044 |
| Height-to-SL ratio | 0.59 ± 0.33 | 0.44 ± 0.15 | 0.24 |
| Height-to-AP ratio | 0.56 ± 0.29 | 0.45 ± 0.19 | 0.34 |
From the QLab analysis, similar findings were obtained (Table 4). An increased SL diameter was seen in Group 2 with a p value of 0.02, and the AP diameter was larger but narrowly insignificant with a p value of 0.07. Also, the area as measured by planimetry using MPR in the QLab environment was significantly larger in Group 2 (10.71 ± 2.87 cm2) than Group 1 (7.32 ± 1.73 cm2) with a p value of 0.0039.
Table 4.
QLab-acquired Data
| Group 1 | Group 2 | p Value | |
|---|---|---|---|
| SL diameter (cm) | 3.17 ± 0.60 | 3.90 ± 0.70 | 0.022 |
| AP diameter (cm) | 3.10 ± 0.61 | 3.67 ± 0.72 | 0.072 |
| Area by planimetry (cm2) | 7.32 ± 1.73 | 10.71 ± 2.87 | 0.0039 |
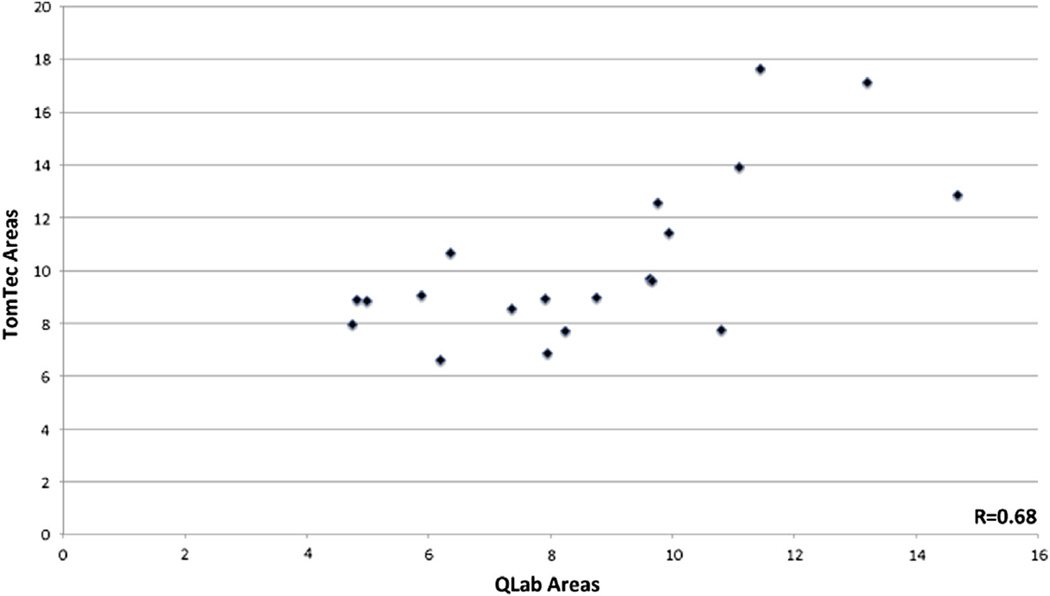
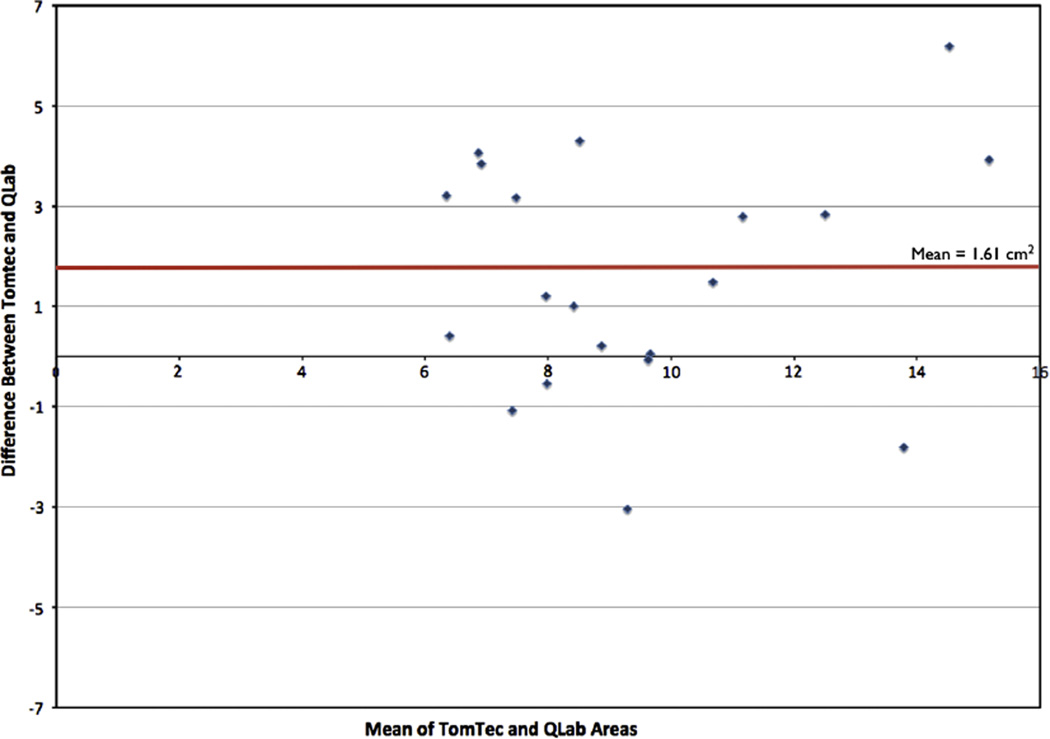
When comparing measurements among all the patients with the 2 modalities of MATLAB and QLab (Table 5), the SL diameter did not differ between techniques, whereas the AP diameter was slightly larger when measured by MATLAB (p = 0.05). The area, however, was much larger when measured by the area of ellipse by MATLAB (10.28 ± 3.11 cm2) when compared to the area measured by direct planimetry in QLab (8.67 ± 2.77 cm2), with a p value of 0.0069. Although the area measurements by these 2 methods had reasonable correlation with r = 0.68 (Fig 4), the distribution displayed by the Bland-Altman analysis indicates that the MATLAB measurements consistently were larger than the areas as measured by QLab (Fig 5). On this analysis, the bias was 1.61 cm2, precision −0.71 cm2 to 3.98 cm2, and limits of agreement −3.13 to 6.35 cm2.
Table 5.
MATLAB versus QLab Data
| MATLAB | QLab | p Value | |
|---|---|---|---|
| SL diameter (cm) | 3.53 ± 0.60 | 3.46 ± 0.72 | 0.55 |
| AP diameter (cm) | 3.63 ± 0.59 | 3.33 ± 0.70 | 0.050 |
| Calculated area (cm2) | 10.28 ± 3.11 | 8.67 ± 2.77 | 0.0069 |
NOTE. Areas calculated by area for ellipse in MATLAB and planimetry in QLab.
Fig 4.
Scatterplot of tricuspid annular area as measured by the ellipse formula in MATLAB versus area as measured by direct planimetry by 3D MPR in QLab.
Fig 5.
The Bland-Altman analysis to compare the agreement of the tricuspid annular area as measured by the ellipse formula in MATLAB versus area as measured by direct planimetry by 3D MPR in QLab. (Color version of figure is available online.)
DISCUSSION
This study has highlighted that it is clinically feasible to geometrically analyze 3D TEE-acquired echocardiographic data of the TV using commercially available software. Furthermore, using the described 3D reconstructive mathematic methodology in MATLAB, the structure of tricuspid annulus outlined in the study conforms to its earlier descriptions in the literature.13–16,21,22 The results demonstrated that the tricuspid annulus has a saddle configuration with annular high and low points, similar to those described in previous models (Table 6). It is also irregular in shape, thus further questioning the concept of using linear measures to describe the dimensions and area. Importantly, the calculated annular area using the 2D ellipsoid method was significantly larger than the 3D planimetered area of the tricuspid annulus (p = 0.0069). Due to the assumptions inherent in area measurements of an irregular annulus based on linear orthogonal dimensions, planimetered area obtained using 3D MPR is likely a more accurate representation of the tricuspid annulus. Also, the authors were able to show differences in multiple anatomic parameters between Group 1 and Group 2. The results showed that both SL and AP diameters were increased in Group 2. However, the degree of dilation in the SL axis was of greater magnitude in Group 2, suggesting an eccentric axis of dilation. Also, the tricuspid annular area was shown to be larger by both ellipsoid calculation and planimetry in Group 2 patients. With this increase in diameters and area, a concomitant reduction in annular height was not seen in Group 2, as has been suggested by previous studies.13,23 Unlike the mitral valve, tricuspid annular height to either AP or SL diameter ratio or the nonplanarity angle significantly did not differentiate the 2 groups,24 implying a more complex saddle shape (Table 3). However, the increase in annular dimensions with no associated change in height implies a relative flattening of the annulus qualitatively.
Table 6.
Previously Described Geometry of the Tricuspid Annulus
| Largest Diameter |
|||||
|---|---|---|---|---|---|
| Author | Normal | FTR | Largest Change in FTR | Shape in FTR | Annular Height |
| Ton-Nu et al13 by 3D rotational coordinates | SL | AP | AP | More circular, flatter (absolute), and dilated. | Reduced in FTR (absolute). Saddle shaped with highest points at AP and lowest at SL. |
| Ring et al14 by MPR through Philips MVQ software | AP | AP | SL | More circular, relatively more planar | No absolute difference in annular height, but annulus to height ratio is reduced. Highest point at septal leaflet attachment. Lowest point is PS near coronary sinus. Saddle shaped. |
| Fukuda et al15 by 3D rotational coordinates | AP, with variation among subjects | PS-AL | Equivalent for all | SL and PS | More severe TR had a more planar annulus. Highest point at AS and lowest point at PS. Complicated 3D structure. |
| Fawzy et al16 by sonomicrometry array in pigs | Changes in segment length described | – | – | – | Highest point at the AS commissure and lowest point at the PS commissure. Multiplanar. |
Abbreviations: FTR, functional tricuspid regurgitation; AP, anterioposterior; PS, posteroseptal; AS, anteroseptal; AL, anterolateral; SL, septolateral; MPR, multiplanar reformatting; MVQ, Mitral Valve Quantification software by Philips.
Tricuspid annular dimensions are used as markers of the chronicity of regurgitation and RV dysfunction.1–3 However, the most suitable 2D TEE view for the measurement of tricuspid annular diameters is not well established.12 Due to the irregular shape and complex geometry, tricuspid annular area calculations derived from linear measures and based on the assumptions of circular shape obviously are incorrect.13–16,21,22 The annular marking methodology used in this study is based on visual tracking in 3D space and devoid of assumptions of geometric shape. Due to the eccentric axis of dilation of the tricuspid annulus, it also is intuitive to assume that planimetry would be a more suitable technique to derive annular area. Many of the prior descriptions of tricuspid annular geometry were based on time-consuming laboratory techniques or customized software.13,15–18 In this study, the authors were able to perform similar reconstruction using 3D echocardiographic data acquired during routine clinical care using commercially available software. Despite being an off-line technique, the results were readily available, making it a clinically applicable technique. With tricuspid annular dimensions gaining significance as the basis of surgical decision making, prompt availability of this information can have a significant clinical influence on patient care and outcome.
This study was significant in that it demonstrated the clinical feasibility of assessment of tricuspid annular geometry and the limitations of tricuspid annular area estimations based on single-axis linear measures. Due to its eccentric axis of dilation, 3D planimetry utilizing MPR should be a more accurate estimate of tricuspid annular area. Therefore, the use of the circumferential tricuspid annular area as a marker for annular dilation is a more logical and accurate option than single-axis linear measures and indirect area calculation. This irregular shape of the tricuspid annulus possibly explains the differences in annular diameters obtained from previous studies (Table 5). By providing an accurate tricuspid annular area, this methodology also has the potential to influence intraoperative surgical decision making and postoperative outcome.
The authors identified certain limitations of the study. Firstly, although the reconstruction and analysis of the tricuspid annulus was based on RT-3D data, it was performed off-line. However, the results of the analysis were available within minutes of data acquisition. The MATLAB portion of the analysis was time consuming, yet this reconstruction was conducted only to confirm annular shape with previous descriptions and not to show its clinical feasibility. Secondly, the study group consisted of patients undergoing cardiac surgery and, therefore, did not represent truly a normal population. Also, when patients were divided based on the quantification of TR, the comparison groups were small. Larger studies to determine the strength of this correlation between geometry and function should be conducted in the future. However, the results of the study indicated that this would be a worthwhile undertaking.
In conclusion, the authors were able to acquire RT-3D TEE data and analyze it to describe the tricuspid annular shape and dimensions in a clinically feasible fashion. The results showed that the tricuspid annulus is irregular in shape; hence, annular area derivation from a single-axis linear measure is not accurate. Also, differences in annulus shape were demonstrated when patients were grouped according to the presence of TR. This information may be helpful during intraoperative surgical decision making to accurately diagnose tricuspid annular dilation and guide annuloplasty procedures.
REFERENCES
- 1.Sagie A, Schwammenthal E, Padial LR, et al. Determinants of functional tricuspid regurgitation in incomplete tricuspid valve closure: Doppler color flow study of 109 patients. J Am Coll Cardiol. 1994;24:446–453. doi: 10.1016/0735-1097(94)90302-6. [DOI] [PubMed] [Google Scholar]
- 2.Matsunaga A, Duran CM. Progression of tricuspid regurgitation after repaired functional ischemic mitral regurgitation. Circulation. 2005;112:I453–I457. doi: 10.1161/CIRCULATIONAHA.104.524421. [DOI] [PubMed] [Google Scholar]
- 3.Rogers JH, Bolling SF. Valve repair for functional tricuspid valve regurgitation: Anatomical and surgical considerations. Semin Thorac Cardiovasc Surg. 2010;22:84–89. doi: 10.1053/j.semtcvs.2010.05.001. [DOI] [PubMed] [Google Scholar]
- 4.Anyanwu AC, Chikwe J, Adams DH. Tricuspid valve repair for treatment and prevention of secondary tricuspid regurgitation in patients undergoing mitral valve surgery. Curr Cardiol Rep. 2008;10:110–117. doi: 10.1007/s11886-008-0020-6. [DOI] [PubMed] [Google Scholar]
- 5.Tang GH, David TE, Singh SK, et al. Tricuspid valve repair with an annuloplasty ring results in improved long-term outcomes. Circulation. 2006;114:I577–I581. doi: 10.1161/CIRCULATIONAHA.105.001263. [DOI] [PubMed] [Google Scholar]
- 6.De Bonis M, Lapenna E, Sorrentino F, et al. Evolution of tricuspid regurgitation after mitral valve repair for functional mitral regurgitation in dilated cardiomyopathy. Eur J Cardiothorac Surg. 2008;33:600–606. doi: 10.1016/j.ejcts.2008.01.011. [DOI] [PubMed] [Google Scholar]
- 7.Calafiore AM, Gallina S, Iaco AL, et al. Mitral valve surgery for functional mitral regurgitation: Should moderate-or-more tricuspid regurgitation be treated? A propensity score analysis. Ann Thorac Surg. 2009;87:698–703. doi: 10.1016/j.athoracsur.2008.11.028. [DOI] [PubMed] [Google Scholar]
- 8.Chikwe J, Anyanwu AC. Surgical strategies for functional tricuspid regurgitation. Semin Thorac Cardiovasc Surg. 2010;22:90–96. doi: 10.1053/j.semtcvs.2010.05.002. [DOI] [PubMed] [Google Scholar]
- 9.Dreyfus GD, Corbi PJ, Chan KM, et al. Secondary tricuspid regurgitation or dilatation: Which should be the criteria for surgical repair? Ann Thorac Surg. 2005;79:127–132. doi: 10.1016/j.athoracsur.2004.06.057. [DOI] [PubMed] [Google Scholar]
- 10.Bonow RO, Carabello BA, Chatterjee K, et al. Focused update incorporated into the ACC/AHA 2006 guidelines for the management of patients with valvular heart disease: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines (writing committee to revise the 1998 Guidelines for the Management of Patients With Valvular Heart Disease): Endorsed by the Society of Cardiovascular Anesthesiologists, Society for Cardiovascular Angiography and Interventions, and Society of Thoracic Surgeons. Circulation. 2008;118:e523–e661. doi: 10.1161/CIRCULATIONAHA.108.190748. [DOI] [PubMed] [Google Scholar]
- 11.Vahanian A, Baumgartner H, Bax J, et al. Guidelines on the management of valvular heart disease: The task force on the management of valvular heart disease of the European Society of Cardiology. Eur Heart J. 2007;28:230–268. doi: 10.1093/eurheartj/ehl428. [DOI] [PubMed] [Google Scholar]
- 12.Anwar AM, Geleijnse ML, Ten Cate FJ, et al. Assessment of tricuspid valve annulus size, shape and function using real-time three-dimensional echocardiography. Interact Cardiovasc Thorac Surg. 2006;5:683–687. doi: 10.1510/icvts.2006.132381. [DOI] [PubMed] [Google Scholar]
- 13.Ton-Nu TT, Levine RA, Handschumacher MD, et al. Geometric determinants of functional tricuspid regurgitation: Insights from 3-dimensional echocardiography. Circulation. 2006;114:143–149. doi: 10.1161/CIRCULATIONAHA.106.611889. [DOI] [PubMed] [Google Scholar]
- 14.Ring L, Rana BS, Kydd A, et al. Dynamics of the tricuspid valve annulus in normal and dilated right hearts: A three-dimensional transo-esophageal echocardiography study. Eur Heart J Cardiovasc Imaging. 2012;13:756–762. doi: 10.1093/ehjci/jes040. [DOI] [PubMed] [Google Scholar]
- 15.Fukuda S, Saracino G, Matsumura Y, et al. Three-dimensional geometry of the tricuspid annulus in healthy subjects and in patients with functional tricuspid regurgitation: A real-time, 3-dimensional echocardiographic study. Circulation. 2006;114:I492–I498. doi: 10.1161/CIRCULATIONAHA.105.000257. [DOI] [PubMed] [Google Scholar]
- 16.Fawzy H, Fukamachi K, Mazer CD, et al. Complete mapping of the tricuspid valve apparatus using three-dimensional sonomicrometry. J Thorac Cardiovasc Surg. 2011;141:1037–1043. doi: 10.1016/j.jtcvs.2010.05.039. [DOI] [PubMed] [Google Scholar]
- 17.Spinner EM, Shannon P, Buice D, et al. In vitro characterization of the mechanisms responsible for functional tricuspid regurgitation. Circulation. 2011;124:920–929. doi: 10.1161/CIRCULATIONAHA.110.003897. [DOI] [PubMed] [Google Scholar]
- 18.Spinner EM, Buice D, Yap CH, et al. The effects of a three-dimensional, saddle-shaped annulus on anterior and posterior leaflet stretch and regurgitation of the tricuspid valve. Ann Biomed Eng. 2012;40:996–1005. doi: 10.1007/s10439-011-0471-6. [DOI] [PubMed] [Google Scholar]
- 19.Valocik G, Kamp O, Visser CA. Three-dimensional echocardiography in mitral valve disease. Eur J Echocardiogr. 2005;6:443–454. doi: 10.1016/j.euje.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 20.Qamruddin S, Naqvi TZ. Advances in 3D echocardiography for mitral valve. Expert Rev Cardiovasc Ther. 2011;9:1431–1443. doi: 10.1586/erc.11.137. [DOI] [PubMed] [Google Scholar]
- 21.Kwan J, Kim GC, Jeon MJ, et al. 3D geometry of a normal tricuspid annulus during systole: A comparison study with the mitral annulus using real-time 3D echocardiography. Eur J Echocardiogr. 2007;8:375–383. doi: 10.1016/j.euje.2006.07.010. [DOI] [PubMed] [Google Scholar]
- 22.Nii M, Guerra V, Roman KS, et al. Three-dimensional tricuspid annular function provides insight into the mechanisms of tricuspid valve regurgitation in classic hypoplastic left heart syndrome. J Am Soc Echocardiogr. 2006;19:391–402. doi: 10.1016/j.echo.2005.10.025. [DOI] [PubMed] [Google Scholar]
- 23.Hung J. The pathogenesis of functional tricuspid regurgitation. Semin Thorac Cardiovasc Surg. 2010;22:76–78. doi: 10.1053/j.semtcvs.2010.05.004. [DOI] [PubMed] [Google Scholar]
- 24.Warraich HJ, Chaudary B, Maslow A, et al. Mitral annular nonplanarity: Correlation between annular height/commissural width ratio and the nonplanarity angle. J Cardiothorac Vasc Anesth. 2012;26:186–190. doi: 10.1053/j.jvca.2011.09.007. [DOI] [PubMed] [Google Scholar]