OK, maybe the title is a little cheeky, but it does accurately and humorously convey a valuable learning experience that I recently had: a large dataset is absolutely critical for statistically significant results with tight confidence intervals. In this case, bigger really is better! Of course, more accurate data is better too.
The Community Structure-Activity Resource (CSAR)1 periodically holds exercises to allow scientists to test their docking and scoring methods. This issue of the Journal of Chemical Information and Modeling presents the papers that resulted from our most recent exercise, one based on blinded data. CSAR was very fortunate to receive large datasets of unpublished protein-ligand binding data from Abbott and Vertex. My concern was that there was too much data to use in an exercise; surely, it would take participants too long to accurately calculate all the possibilities. To make the exercise tractable in a limited period of time, I decided that we should use a smaller subset of data for the exercise and release the full set after it concluded. Unfortunately, reducing the size of the dataset made the error estimates very large, and it was very difficult to compare the results. To quote one of the participants, “Thanks, but no thanks!” To address this issue, we asked that participants submit papers to this issue of the Journal of Chemical Information and Modeling that present both their initial, blinded results and results based on the full dataset.
Guidelines to help you plan ahead
In the medical and social sciences, studies that involve human subjects require a great deal of oversight. This includes approval of the design of the study, number of subjects, and the statistics proposed for analysis before any data are collected. In the field of computational chemistry, statistics are usually considered at the end of the project. The worst do not consider statistics at all, leading to erroneous conclusions. However, papers with rigorous statistical analysis indicate a higher regard for the data and the potential information gained from the research; they include estimated error bars, 95%-confidence intervals, p-values, and maximal information coefficients.
Too frequently, we see papers that compare two computational methods, declaring one to be superior when the size of the dataset is too small to support the conclusions. For instance, a dataset of 200 complexes is too small to support the claim that one approach with a correlation to experiment of Pearson R = 0.7 is superior to another with Pearson R = 0.6. This may sound surprising to many, and it underscores the need to better educate our community. Consider that squaring a Pearson R of 0.7 leads to R2 = 0.49 (in a linear least-squares fit, the coefficient of determination – R – is equal to the square of the Pearson correlation coefficient). This means that the “better” method only captures half of the experimental trend; half of the variance is not explained. A different slice through protein-ligand space with a different set of 200 complexes could easily lead to both methods having the same correlation to experiment.
Below, I outline the linear regression that is typically used to evaluate methods, the simple least-squares analysis used to compare a calculated binding affinity to the actual experimental value. One issue that has received attention recently is the accuracy of experimental data and its influence upon this type of analysis2. Of course, highly accurate data with low error is essential to developing good methods. Here, I describe the influence of many factors on linear regression and highlight the limits that they impose. To improve our field, this information should be considered before initiating any study.
Basics of linear regression
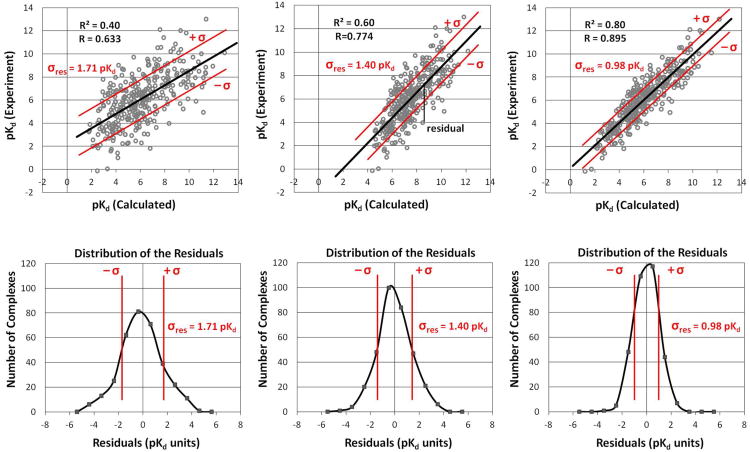
Let us assume that you have a set of calculated affinities kd(calc)i for a given set of N protein-ligand complexes. Those complexes are accompanied by experimentally determined affinities kd(expt)i. The calculated values are predictions, so they are plotted on the X-axis. The experimental values are plotted on the Y-axis. The data is usually normally distributed along the y-axis. A simple, least-squares linear regression, starts with a fit line that must intersect the point (x̄, ȳ, the average calculated and experimental values. The fit is then dictated by finding a slope that minimizes the squared distances in the y-direction between the data points and the fit line (ie, the residuals in Figure 1).3 A tighter correlation means better agreement between the data points and the fit line; therefore, there are smaller residuals and a tighter distribution of those residuals around the value zero. A tighter distribution means that there is a smaller standard deviation of the distribution of the residuals for the data points (ie, smaller σres) and a higher R. As noted above, R2 is the percentage of the total variation that can be fit by the line. While there is an inherent relationship between R and σres, there is no inherent relationship of R and σres to the slope and intercept of the fit line. Weak and tight correlations can be obtained for lines with any slope and intercept, and the scatter plots in Figure 1 are meant to show this variation.
Figure 1.
Approximately 300 data points are presented for three theoretical methods, pKd (Calculated) with differing correlations to the experimental binding affinities. The residuals (top) for all the data points have a normal distribution around zero. The characteristics of the residuals (bottom) are well defined, including the standard deviation (σres in red). Higher correlations lead to larger R2 and smaller σres and weaker correlations lead to lower R2 and larger σres, but the distributions remain Gaussian in shape. When the slope of the fit line is ∼1 and the intercept is ∼0, then σres is equal to RMSE, as in the case of the right-most frames.
A more predictive method will have a tighter correlation to the experimental values, and we typically designate methods with larger R2 as better than methods with lower R2. A perfect method would have R2 = 1.0, slope = 1.0, and intercept = 0. However, a fit with a slope of 1 and intercept of 0 does not necessarily have a high R2; that is dictated by the spread of the points around the line. High R2 can be obtained for any slope and intercept, provided there is a good linear relationship. A method with a high R2 and any slope/intercept is preferable because it is more predictive than a method with low R2 but a slope and intercept near 1 and zero, respectively. The one with high R2 is more predictive because it does a better job at relative ranking. This is further underscored if we consider examples where the fit lines happen to have a slope ∼1 and an intercept of ∼0, but with varying values of R2. In these cases, σres is also the root mean squared error (RMSE) for the method, and clearly, the cases with lower R2 have higher RMSE. In cases where the slopes ≠ 1 and intercepts ≠ 0, σres is a “relative RMSE” or an RMSE of the rescaled values from the predictive method.
Influence of experimental error on linear regression
It is important to recognize that the value of σres is a “relative RMSE” for the scoring method, not a measure of the error in the experimental measurements themselves. The range of affinities in Figure 1 is quite large, much larger than the inherent errors in the methods. This is an important property for linear regression.
Experimental error can be incorporated as error bars in the y-direction if there is a need to address some difference in uncertainty between different data points. This simply calls for a weighted linear regression. The weights bias the fitting to preferentially minimize the residuals of the points with the smallest error. Though straightforward, this is usually not used in scoring function papers because the error of the data points is assumed to be roughly the same across the whole set. If all points have the same error, they all have the same weight, so no bias or weighting is actually necessary. However, we all know that the error in the experiments is a very important factor in developing good scoring functions.
Instead of concentrating on error in each data point, it is important to recognize that the inherent experimental error limits the maximum value that Pearson R can take (Rmax).2,4 Each protein-ligand complex has a binding affinity, but experimental error is always introduced2 in measuring the values: ΔGbind(expt)i = ΔGbind(true)i + err(expt)i. The perfect scoring function would reproduce ΔGbind(true), but even if that were possible, the experimental error would always give some spread to the data (R2 ≠ 1). The RMSE for the perfect scoring function would always be equal to σexpt. Obviously, smaller experimental error would lower the RMSE, improve the agreement between the x and y values, and increases the possible values for R2.
What may be less obvious, especially at the onset of a project, is that the ratio between the experimental error and the range of experimental data imposes the greatest limitation. If you have data distributed over a range that is equal to your experimental error, you will simply have a random circle of points with R2=0. Larger ranges of experimental data make it possible to obtain non-zero values for R2. Brown et al.5 estimated that a reliable experimental assay has an error of ∼0.3 pIC50 or a factor of 2 in IC50. They simulated IC50 data with random error in both experimental and computational values, using bootstrapping to show that at least 50 data points with ≥3 orders of magnitude in affinity were required to obtain a good fit to experimental data (with σexpt=0.3 pIC50). Obviously, the actual values of R were dependent on the simulated error in the proposed prediction method; after all, higher error always leads to smaller R.
Rmax is simply the limit of a perfect scoring function, not an actual value that should be obtained. If a scoring method fits experimental data with R near or in excess of Rmax, the model is clearly over-fit. The only other possibility is dumb luck, the kind that wins the lottery or gets struck by lightning… and lightning won't strike twice when the method is applied to a new set of data!
Recently, Kramer et al.2 have elegantly derived the analytical form for Pearson Rmax:
| (1) |
where Rmax is dictated by the distribution of experimental error and the distribution of all affinity data used in the analysis. The derivation assumes that all err(expt)i are independent and all are distributed with σexpt. This group also did a careful curation of ChEMBL6 to identify protein-ligand complexes that had affinity data measured by more than one independent group. The study involved a heroic effort to identify all unique data (repeated citations of the same data were eliminated), and they removed all straightforward sources of disagreements in the data (unit errors, typos, etc). Their examination of the reproducibility of data allowed them to estimate the inherent experimental uncertainty across multiple data sources. For their filtered set from ChEMBL, σexpt was 0.54 pKi and Rmax2 was 0.81 for an ideal scoring function. (Up to a 3-fold difference in Kd, equal to 0.5 pKd, is considered agreement by experimentalists,4 and the agreement of this anecdotal value with the ChEMBL measurement of σexpt is surprising!)
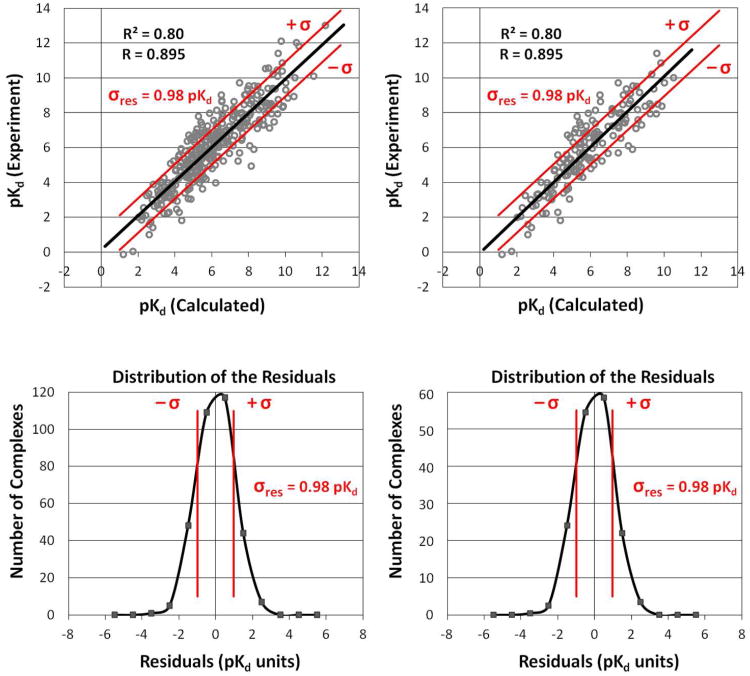
As is appropriate, the analytical form of Rmax in Eqn 1 is independent of the actual values of the data (ie, it doesn't matter if the data is for weak binders or tight binders). If σexpt = σdata, Rmax = 0 as we noted for the example of a random circle of points. The limit Rmax=1 is only possible when either there is no experimental error or σ expt ≪ σ data. The suggested guideline of Brown et al.5 translates to an Rmax2 = 0.89 (σexpt=0.3 and σdata=0.9 for 50 points evenly distributed over 3 pIC50). It should be noted that Kramer et al. have also done a follow-up analysis of ChEMBL's IC50 data which contains important information on comparing IC50s and pKi data.7 What is most important is that Rmax is independent of the number of data points in this analytical form. This is correct because the value of R itself is not impacted by the number of data points (Figure 2).
Figure 2.
Two sets of predictions are compared. The set on the left has ∼300 protein-ligand complexes, and the set on the right has ∼150. The set on the right is simply a random subset of the larger set on the left. The error in the method (RMSE) is still the same, so the value of R is still the same. Technically, σexpt and σdata are still the same, so even Rmax would be unchanged.
Influence of the number of data points
Though the value of R is not influenced by the number of data points, the confidence interval of R is strictly dictated by the size of the dataset and the level of confidence you choose. The most common value used is the 95% confidence interval, but there is nothing magical about that choice. In fact, a 90% confidence interval is probably fine, considering the experimental error inherent to the protein-ligand binding data that is used to train and test docking/scoring methods.
It is important to recognize that the converse is true: the size of the dataset needed can be dictated by R and the level of confidence desired.8 If you want to have a dataset where you are 95% confident in the statistical significance of two methods differing by at least ΔR=0.1 (ie, R=0.85 vs R=0.75 or R2=0.72 vs R2=0.56), you would need to compile a dataset of at least 298 complexes (see Table 1). Of course, lowering the statistical confidence lowers the minimum number of required complexes. The number of complexes increases with requiring a tighter ΔR (ie, R=0.85 vs R=0.80) or evaluating lower Pearson R values (eg, R=0.75 vs R=0.65). The notation in ref 8 is a bit different, but it derives that the minimum number of data points required can be calculated by
Table 1.
The minimum number of data points required to accurately compare models with different Pearson correlation coefficients.
| R | R2 | ΔR ≥ 0.1 95% confidence N | ΔR ≥ 0.1 90% confidence N | ΔR ≥ 0.05 95% confidence N | ΔR ≥ 0.05 90% confidence N |
|---|---|---|---|---|---|
| 0.95 | 0.90 | NA | NA | 62 | 44 |
| 0.90 | 0.81 | 59 | 42 | 225 | 159 |
| 0.85 | 0.72 | 122 | 86 | 477 | 335 |
| 0.80 | 0.64 | 203 | 143 | 800 | 561 |
| 0.75 | 0.56 | 298 | 209 | 1180 | 827 |
| 0.70 | 0.49 | 403 | 283 | 1602 | 1123 |
| 0.65 | 0.42 | 516 | 362 | 2053 | 1439 |
| 0.60 | 0.36 | 633 | 444 | 2521 | 1766 |
| 0.55 | 0.30 | 751 | 527 | 2994 | 2097 |
| 0.50 | 0.25 | 868 | 609 | 3461 | 2424 |
| 0.45 | 0.20 | 981 | 688 | 3913 | 2740 |
| (2) |
where R is the smaller correlation coefficient in the comparisons above and the value of zα/2 is dictated by the statistics of normal distributions: 1.64 for 90% confidence, 1.96 for 95%, and 2.58 for 99%. Values for Pearson N are given in Table 1. Note that zα/2=1.0 is 67% confidence or simply the ±σ that is estimated by experimentalists using measures in triplicate (only n = 3!).
In our first benchmark exercise for the community, we found that the best scoring methods estimated binding affinity with a correlation to experiment of R ≈ 0.75.9 Most of the methods ranged R = 0.55-0.65 and there was no statistical significance in their difference from one another. The reader can see in Table 1 that many hundreds, if not thousands, of structures would have been required to accurately differentiate their performance.
To calculate the confidence interval of R, a Fischer transformation must be used as shown in Eqns 3-6.8 The confidence interval depends upon the number of data points N and the value of zα/2 that is used.
| (3) |
| (4) |
The minimum and maximum of the confidence interval are determined by z'low = z(R) – zα/2.and z'high = z(R) + zα/2, respectively. These are translated back to R values by Eqns 5 and 6.
| (5) |
| (6) |
It is important to remember that the difference in two 95%-confidence intervals is not the same as a 95%-confidence in the difference between two values of R. It is most appropriate to evaluate differences in R through the residuals from the linear regression (see Figure 1). The difference in the distribution of the residuals can be evaluated using Levene's F-test for the equality of variance. In essence, very minor overlap in the confidence intervals does not weaken the statistical significance.
Evaluating methods using non-parametric assessments
There are also the non-parametric measures of correlation which evaluate rank ordering: Spearman ρ and Kendall τ. These values range from −1 to 1, same as Pearson R. Spearman ρ and Kendall τ are classified as non-parametric because they just require monotonic changes in the ranking, but the relationship is not required to be linear like it is for Pearson R. The difference between ρ and τ is the penalty for misranking. Kendall τ simply notes the misrank with a penalty of 1, but Spearman ρ penalizes by how badly misranked a data point is. This makes Spearman ρ more sensitive to misrankings, particularly for systems where a lot of data may be clustered in subregions of the overall distribution. There are a few flavors of Spearman ρ that differ slightly on their treatment of ties in the ranking. The numbers of data points required are dictated by Eqns 7 and 8. Tables 2 and 3 provide the counts of N for different ρ, τ, and confidence intervals. Counts for Kendall τ tau are less than those for Pearson R, but Spearman ρ requires more.
Table 2.
The minimum number of data points required to accurately compare models with different Spearman ρ.
| ρ | Δρ ≥ 0.1 95% confidence N | Δρ ≥ 0.1 90% confidence N | Δρ ≥ 0.05 95% confidence N | Δρ ≥ 0.05 90% confidence N |
|---|---|---|---|---|
| 0.95 | NA | NA | 88 | 63 |
| 0.90 | 81 | 58 | 315 | 222 |
| 0.85 | 165 | 116 | 648 | 455 |
| 0.80 | 266 | 188 | 1055 | 740 |
| 0.75 | 380 | 267 | 1511 | 1059 |
| 0.70 | 501 | 352 | 1994 | 1397 |
| 0.65 | 624 | 438 | 2486 | 1742 |
| 0.60 | 746 | 523 | 2974 | 2083 |
| 0.55 | 864 | 606 | 3446 | 2414 |
| 0.50 | 976 | 684 | 3893 | 2727 |
| 0.45 | 1080 | 757 | 4309 | 3018 |
Table 3.
The minimum number of data points required to accurately compare models with different Kendall τ.
| τ | Δ τ ≥ 0.1 95% confidence N | Δ τ ≥ 0.1 90% confidence N | Δ τ ≥ 0.05 95% confidence N | Δ τ ≥ 0.05 90% confidence N |
|---|---|---|---|---|
| 0.95 | NA | NA | 30 | 22 |
| 0.90 | 29 | 21 | 101 | 72 |
| 0.85 | 56 | 41 | 211 | 149 |
| 0.80 | 92 | 65 | 353 | 248 |
| 0.75 | 133 | 94 | 519 | 364 |
| 0.70 | 179 | 127 | 703 | 494 |
| 0.65 | 228 | 161 | 900 | 632 |
| 0.60 | 280 | 197 | 1105 | 775 |
| 0.55 | 331 | 233 | 1311 | 919 |
| 0.50 | 382 | 269 | 1515 | 1062 |
| 0.45 | 432 | 304 | 1713 | 1201 |
| (7) |
| (8) |
Conclusion
As scientists, we are taught to use linear regression in our undergraduate courses, but it is usually presented in a black-box fashion without information about the caveats and limitations. I believe that our use of “hard” data has created a false sense of security that is not shared by our colleagues in the “soft” sciences. Social and medical scientists who use human subjects have relied very heavily on statistics and careful experimental design to try to reach the most solid conclusions. I hope that the data provided here can help our community to take a step back and carefully analyze their assumptions and limitations.
The issues presented here may help to explain the difference in the success rates for QSAR methods over docking and scoring. Both aim for accuracy over the same affinity ranges (roughly the same σdata), but QSAR methods are typically trained on congeneric series of data for one protein system, often from one data source. QSAR approaches are usually limited in their description of chemical space, but their σexpt is likely low. The distribution of experimental error is minimized with the QSAR approach, definitely in comparison to training a scoring method on affinities for many proteins, diverse ligands, and multiple assays. After all, experimental error bars are underestimates of the true experimental uncertainty, and this is exacerbated in heterogeneous data. In the end, this makes the QSAR ratio of σdata / σexpt, and subsequently Rmax, rather large. It is also possible that this success might come from the larger sets of data used to train QSAR individual models, which leads to greater statistical significance.
Acknowledgments
I would like to whole heartedly thank all of CSAR's pharma collaborators, particularly Abbott and Vertex who donated their blind data to the exercise covered in this issue of JCIM. Additional data has been donated by GlaxoSmithKline, which is coming out soon. Bristol Myers Squibb and Genentech are also very valuable partners in our efforts. I appreciate enthusiastic exchanges about statistics and experimental error with many people, especially Christian Kramer (Novartis), Anthony Nicholls (OpenEye), Paul Labute (Chemical Computing Group), Ajay Jain (UCSF), Alex Tropha (UNC), Richard Smith (Michigan), and Jim Dunbar (Michigan). The CSAR Center is funded by the National Institute of General Medical Sciences (U01 GM086873).
References
- 1.www.CSARdock.org.
- 2.Kramer C, Kalliokoski T, Gedeck P, Vulpetti A. The experimental uncertainty of heterogeneous public Ki data. J Med Chem. 2012;55:5165–5173. doi: 10.1021/jm300131x. [DOI] [PubMed] [Google Scholar]
- 3.Hogg RV, Tanis EA. Probability and Statistical Inference. Prentice Hall College Division; Englewood Cliffs, NJ 07632: 2001. pp. 402–411. [Google Scholar]
- 4.Dunbar JB, Jr, Smith RD, Yang CY, Ung PM, Lexa KW, Khazanov NA, Stuckey JA, Wang S, Carlson HA. CSAR Benchmark Exercise of 2010: Selection of the protein-ligand complexes. J Chem Inf Model. 2011;51:2036–2046. doi: 10.1021/ci200082t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brown SP, Muchmore SW, Hajduk PJ. Healthy skepticism: assessing realistic model performance. Drug Discov Today. 2009;14:420–427. doi: 10.1016/j.drudis.2009.01.012. [DOI] [PubMed] [Google Scholar]
- 6.Gaulton A, Bellis L, Chambers J, Davies M, Hersey A, Light Y, McGlinchey S, Akhtar R, Atkinson F, Bento AP, Al-Lazikani B, Michalovich D, Overington JP. ChEMBL: A large-scale bioactivity database for chemical biology and drug discovery. Nucleic Acids Res. 2012;40:D1100–D1107. doi: 10.1093/nar/gkr777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kalliokoski T, Kramer C, Vulpetti A, Gedeck P. Comparability of mixed IC50 data – A statistical analysis. PLoS ONE. 2013;8:e61007. doi: 10.1371/journal.pone.0061007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bonett DG, Wright TA. Sample size requirements for estimating Pearson, Kendall and Spearman correlatons. Psychometrika. 2000;65:23–28. [Google Scholar]
- 9.Smith RD, Dunbar JB, Jr, Ung PM, Esposito EX, Yang CY, Wang S, Carlson HA. CSAR Benchmark Exercise of 2010: Combined evaluation across all submitted scoring functions. J Chem Inf Model. 2011;51:2115–2131. doi: 10.1021/ci200269q. [DOI] [PMC free article] [PubMed] [Google Scholar]