Post-Reconstruction Non-Local Means Filtering Methods using CT Side Information for Quantitative SPECT

Abstract

Quantitative SPECT techniques are important for many applications including internal emitter therapy dosimetry where accurate estimation of total target activity and activity distribution within targets are both potentially important for dose-response evaluations. We investigated non-local means (NLM) post-reconstruction filtering for accurate I-131 SPECT estimation of both total target activity and the 3D activity distribution.

We first investigated activity estimation versus number of ordered-subsets expectation-maximization (OSEM) iterations. We performed simulations using the XCAT phantom with tumors containing a uniform and a non-uniform activity distribution, and measured the recovery coefficient (RC) and the root mean squared error (RMSE) to quantify total target activity and activity distribution, respectively. We observed that using more OSEM iterations is essential for accurate estimation of RC, but may or may not improve RMSE.

We then investigated various post-reconstruction filtering methods to suppress noise at high iteration while preserving image details so that both RC and RMSE can be improved. Recently, NLM filtering methods have shown promising results for noise reduction. Moreover, NLM methods using high-quality side information can improve image quality further. We investigated several NLM methods with and without CT side information for I-131 SPECT imaging and compared them to conventional Gaussian filtering and to unfiltered methods. We studied four different ways of incorporating CT information in the NLM methods: two known (NLM CT-B and NLM CT-M) and two newly considered (NLM CT-S and NLM CT-H). We also evaluated the robustness of NLM filtering using CT information to erroneous CT.

NLM CT-S and NLM CT-H yielded comparable RC values to unfiltered images while substantially reducing RMSE. NLM CT-S achieved −2.7 to 2.6% increase of RC compared to no filtering and NLM CT-H yielded up to 6% decrease in RC while other methods yielded lower RCs than them: Gaussian filtering (up to 11.8% decrease in RC), NLM method without CT (up to 9.5% decrease in RC), and NLM CT-M and NLM CT-B (up to 19.4% decrease in RC). NLM CT-S and NLM CT-H achieved 8.2 to 33.9% and −0.9 to 36% decreased RMSE on tumors compared to no filtering respectively while other methods yielded less reduced or increased RMSE: Gaussian filtering (up to 7.9% increase in RMSE), NLM method without CT (up to 18.3% increase in RMSE), and NLM CT-M and NLM CT-B (up to 31.5% increase in RMSE). NLM CT-S and NLM CT-H also yielded images with tumor shapes that better-matched the true shapes than other methods. All NLM methods using CT information were robust to small misregistration between SPECT and CT, but NLM CT-S and NLM CT-H were more sensitive than NLM CT-M and NLM CT-B to missing CT information.

1. Introduction

There is much interest in quantitative SPECT techniques for accurate estimation of both total target activity and activity distribution within targets. For example in internal emitter therapy dosimetry, SPECT-derived total target activity is used to determine the mean radiation absorbed dose to tumor and normal organs while the 3D activity distribution is used to determine the dose-volume histogram. In dose-response evaluations, the dose measure of interest is not only the mean absorbed dose to the target, but also other summary measures from dose-volume histogram analysis (Sgouros et al. 2003, Dewaraja, Schipper, Roberson, Wilderman, Amro, Regan, Koral, Kaminski & Avram 2010, Cicone et al. 2013)

Statistical image reconstruction such as the unregularized ordered-subset expectation-maximization (OSEM) (Hudson & Larkin 1994) algorithm has been implemented in many clinical SPECT scanners. Since unregularized image reconstruction is ill-posed, using many iterations usually leads to very noisy images. For visually pleasing low-noise images, one may use early stopping criteria or post-reconstruction filtering. However, these images may not provide accurate quantification. Early stopping rule may not yield detailed images since more iteration is required to recover more image detail. Post-reconstruction filtering such as Gaussian filter may blur images. Thus, filter generally is not recommended for quantifying total target activity, but may be desirable to suppress noise effects when estimating activity distributions to calculate 3D dose metrics (Dewaraja et al. 2012).

Non-local (or non-stationary) information has been very useful for image noise reduction. For example, the image-dependent Metz filter yielded improved quantification for nuclear medicine imaging (Metz & Pizer 1971, King et al. 1988). Recently, non-local means (NLM) filtering has been proposed (Buades et al. 2005) and this filter yielded excellent noise reduction results compared to conventional local filters such as Gaussian filter. NLM filters also have been used as a regularizer in image reconstruction (Zhang et al. 2010). Moreover, using these NLM methods with high-quality side information can improve image quality further (Deledalle et al. 2010, Rousseau 2010, Chan et al. 2010, Vunckx et al. 2012, Nguyen & Lee 2012). Unlike other SPECT image reconstruction methods using CT side information (Fessler et al. 1992, Gindi et al. 1993, Dewaraja, Koral & Fessler 2010), these NLM-based methods using side information do not require CT image segmentation. Multi-modal imaging systems such as PET-CT, PET-MR, or SPECT-CT can potentially benefit from these NLM methods to improve PET or SPECT images. SPECT-based dosimetry in non-Hodgkin lymphoma (NHL) patients undergoing I-131 radioimmunotherapy (RIT) is another natural application for these enhanced NLM methods since a high resolution CT image is available from the SPECT-CT system (Dewaraja, Schipper, Roberson, Wilderman, Amro, Regan, Koral, Kaminski & Avram 2010).

Our objective is accurate SPECT estimation of both total target activity and the 3D activity distribution. We performed simulations using the XCAT phantom (Segars et al. 2008) with uniform and non-uniform tumors, and measured the recovery coefficient (RC) and the root mean squared error (RMSE) to quantify total target activity and activity distribution, respectively. We first investigated activity estimation versus iteration of OSEM reconstruction. We then investigated various post-reconstruction filtering methods to suppress noise at high iteration while preserving image details. We studied several NLM methods with and without CT side information for I-131 SPECT-CT imaging and compared them to conventional Gaussian filtering and to unfiltered methods. We studied two existing methods and two new methods for incorporating CT side information in NLM methods. We also tested the robustness of all NLM methods using CT information by evaluating the methods when there is misregistration between SPECT and CT and when there is missing CT information (e.g., tumors with non-uniform SPECT uptake, but with the non-uniformity not evident on CT).

2. Method

2.1. Statistical image reconstruction for SPECT

Statistical image reconstruction methods for emission tomography can yield better image quality than other non-iterative algorithms. The usual form of statistical image reconstruction is to perform the following constrained optimization with respect to an image f:

$$\widehat{\mathit{f}}\stackrel{\mathrm{\Delta }}{=}\underset{\mathit{f}\ge \mathbf{0}}{\text{argmin}}\mathrm{L}(\mathit{y}|\mathit{f})$$ (1)

where y is a measured sinogram data and L denotes a negative Poisson log-likelihood function. The negative Poisson log-likelihood is defined as follows:

$$\mathrm{L}(\mathit{y}|\mathit{f})=\sum _i{\overline{y}}_i(\mathit{f})-y_i\text{log}{\overline{y}}_i(\mathit{f})$$ (2)

where y_i is the ith element of the measurement y and

$${\overline{y}}_i(\mathit{f})\stackrel{\mathrm{\Delta }}{=}{[\mathit{A}\mathit{f}]}_i+s_i$$

where A denotes the system model and s_i is a scatter component for the ith measurement. Eq. (1) can be solved efficiently using algorithms such as OSEM algorithm (Hudson & Larkin 1994).

For SPECT imaging, we incorporated a non-uniform attenuation map and a depth-dependent point spread function model including penetration tails (Chun, Fessler & Dewaraja 2013) in the system matrix A. In our simulation, we assumed known s_i, but in practice, this scatter component can be obtained by using a triple energy window (TEW) method or by Monte Carlo methods (Dewaraja et al. 2006).

Unregularized image reconstruction in Eq. (1) is ill-posed. So, converged maximum likelihood (ML) images are very noisy. There are usually three approaches to deal with this noise. First of all, one can stop iteration before convergence. However, more iteration may be necessary for recovering image details. Secondly, one can use a post-reconstruction filter (e.g., Gaussian filter) to reduce noise. Lastly, one can add a regularizer to Eq. (1) (e.g., quadratic roughness penalty). However, using non-local regularizers for 3D images is computationally very expensive (Chun, Dewaraja & Fessler 2013). In this paper, we focus on post-reconstruction filters with and without high-quality CT side information.

2.2. Non-local means filtering

Recently, NLM filters have been proposed that yield better image quality than other conventional local filters (Buades et al. 2005). Many post-reconstruction filters are essentially weighted averages of image intensities. For example, the weight of Gaussian filter is determined by the distance between two voxels based on the assumption that images are smooth. In this case, the number of voxels that can be averaged with positive weights is limited and wrong intensities can be averaged around sharp edges. Instead of using the distance between voxels for weight calculation, NLM filters use the similarity measure between two “patches” around two voxels. The assumption of NLM filters is that two voxels will have the same image intensities if the patches around these two voxels are similar. Therefore, unlike conventional local filters, NLM filters can average correct image intensities over many more voxels in principle.

For a given noisy (SPECT) image f̂ from Eq. (1), let us denote N_jf̂ the patch of f̂ centered at the jth voxel. This patch is a vector of image intensities on voxels around the jth voxel. Then, the similarity of two patches can be measured using a function h_f as follows:

$$w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})\stackrel{\mathrm{\Delta }}{=}{h}_{\mathrm{f}}(\Vert {\mathit{N}}_i\widehat{\mathit{f}}-{\mathit{N}}_j\widehat{\mathit{f}}\Vert ),$$ (3)

where $\Vert \mathit{x}\Vert \stackrel{\mathrm{\Delta }}{=}\sqrt{{\sum }_j{x}_j^2}$ for a vector x. One usual choice for h_f(t) can be (Buades et al. 2005)

$$h_{\mathrm{f}}(t)=\text{exp}(-\frac{t^2}{2N_{\mathrm{f}}{\sigma }_{\mathrm{f}}^2})$$ (4)

where σ_f is a design parameter and N_f is the number of voxels in the patch. Another choice can be

$$h_{\mathrm{f}}(t)=\{\begin{array}{c}1,t\le {\sigma }_{\mathrm{f}}\sqrt{N_{\mathrm{f}}}\hfill \\ 0,t>{\sigma }_{\mathrm{f}}\sqrt{N_{\mathrm{f}}}\hfill \end{array}$$ (5)

or a polynomial to approximate Eq. (5) with a finite support (Duval et al. 2011). The parameter σ_f can be varying locally (i.e., σ_f depends on ij). The similarity metric in Eq. (3) will be close to 1 if two patches are similar and will be close to 0 if two are very different.

NLM filtering methods use the similarity measure between two patches for weighted averaging. The NLM filtered image at the ith voxel can be defined as follows:

$${[{\widehat{\mathit{f}}}_{\text{NLM}}]}_i=\sum _{j\in {\mathrm{\Omega }}_i}\frac{w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})}{{\sum }_{j\prime \in {\mathrm{\Omega }}_i}{w}_{\mathrm{f}}(i,j\prime |\widehat{\mathit{f}})}{[\widehat{\mathit{f}}]}_j$$ (6)

where Ω_i is the search neighborhood, i.e., the set of voxels around the ith voxel. Ω_i can be an entire domain.

There are a few factors in Eq. (6) that determine the image quality of f̂_NLM (Duval et al. 2011). Firstly, the size of the patch N_if̂ should be large enough to measure the similarity between two patches in high noise, but patches that are too large could fail to preserve small details. Secondly, the large number of voxels in Ω_i can increase the chance to have more similar patches so that one may reduce noise further, but too large Ω_i will increase computation complexity significantly and it may also introduce more error when one uses Eq. (4) since it still assigns a small but nonzero weight for two very dissimilar patches. This accumulated small error can not be ignored for large Ω_i. Lastly, small σ_f preserves details, but at the same time, it also increases noise. There has been some effort to determine optimal parameters for Eq. (6) for some limited cases (Buades et al. 2005, Duval et al. 2011). For example, one can determine σ_f for Gaussian noise case. However, for SPECT reconstructed image, there is no known method to determine all these parameters. Furthermore, the number of iterations in Eq. (1) for f̂ will also determine the accuracy of Eq. (3) and the quality of Eq. (6). In this paper, we determine these parameters empirically.

2.3. Non-local means filtering with side information

It is important to accurately measure the similarity between two patches to improve the performance of NLM filter in Eq. (6). However, it is challenging to obtain accurate weight in Eq. (3) from a noisy SPECT image. One may be able to measure robust similarity between two patches by using large patches, but but they may not preserve image details.

One may improve the accuracy of this similarity measure further for small patches by using side information that is closely correlated with noisy reconstructed image f̂. Since in SPECT-CT imaging, an anatomical CT image denoted by g is available for attenuation correction and tumor delineation, we can use this additional information to improve image quality. We can define the weight from CT image similar to Eq. (3). Let us denote M_jg the patch of CT image g centered at the jth voxel. Then, the similarity of two CT patches can be measured using a function h_a as follows:

$$w_{\mathrm{a}}(i,j|\mathit{g})\stackrel{\mathrm{\Delta }}{=}{h}_{\mathrm{a}}(\Vert {\mathit{M}}_i\mathit{g}-{\mathit{M}}_j\mathit{g}\Vert )$$ (7)

where

$$h_{\mathrm{a}}(t)=\text{exp}(-\frac{t^2}{2N_{\mathrm{a}}{\sigma }_{\mathrm{a}}^2})$$ (8)

where σ_a is a design parameter and N_a is the number of voxels in the patch M_jg.

There has been some research illustrating that combining the two weights of Eq. (3) and Eq. (7) can improve image quality of NLM filtered image. One usual form of incorporating anatomical side information into NLM filtering is (Deledalle et al. 2010)

$${[{\widehat{\mathit{f}}}_{\text{NLM CT-M}}]}_i=\sum _{j\in {\mathrm{\Omega }}_i}\frac{w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})w_{\mathrm{a}}(i,j|\mathit{g})}{{\sum }_{j\prime \in {\mathrm{\Omega }}_i}{w}_{\mathrm{f}}(i,j\prime |\widehat{\mathit{f}})w_{\mathrm{a}}(i,j\prime |\mathit{g})}{[\widehat{\mathit{f}}]}_j$$ (9)

and we call this NLM CT-M (M for multiplication).

A method similar to Eq. (9) was proposed inspired by Bowsher prior (Bowsher et al. 2004) and it used w_a(i, j|g) = 1 when g_i/g_j is inbetween pre-defined two values and w_a(i, j|g) = 0 otherwise (Chan et al. 2010). Similarly one can also design Bowsher prior-based NLM weights for post-reconstruction filtering as follows:

$$w_{\mathrm{a}}(i,j|\mathit{g})=\{\begin{array}{c}1,\text{first M smallest}\Vert {\mathit{M}}_i\mathit{g}-{\mathit{M}}_j\mathit{g}\Vert \text{for each}i\hfill \\ 0,o.w.\hfill \end{array}$$ (10)

By applying Eq. (10), one can rewrite Eq. (9) as follows:

$${[{\widehat{\mathit{f}}}_{\text{NLM CT-B}}]}_i=\sum _{j\in {\mathrm{\Delta }}_i(\mathit{g})}\frac{w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})}{{\sum }_{j\prime \in {\mathrm{\Delta }}_i(\mathit{g})}{w}_{\mathrm{f}}(i,j\prime |\widehat{\mathit{f}})}{[\widehat{\mathit{f}}]}_j$$ (11)

where Δ_i(g) is the set of the voxels among the first M smallest ‖M_ig − M_jg‖ for the ith voxel. We call this NLM CT-B (B for Bowsher prior).

The NLM weights Eqs. (7) and (10) use CT patch information differently. Eq. (7) preserves similarity information by using a strictly monotone function, but Eq. (10) does not preserve it by using a step function (or thresholding). However, these two weights are used in a similar way in Eqs. (9) and (11) by multiplication.

We consider a different form of incorporating side information, which is to add the two weights of Eq. (3) and Eq. (7). A new NLM filtering using these two weights can be defined as follows (Chun et al. 2012):

$${[{\widehat{\mathit{f}}}_{\text{NLM CT-S}}]}_i=\sum _{j\in {\mathrm{\Omega }}_i}\frac{(1-\tau )w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})+\tau w_{\mathrm{a}}(i,j|\mathit{g})}{{\sum }_{j\prime \in {\mathrm{\Omega }}_i}(1-\tau )w_{\mathrm{f}}(i,j\prime |\widehat{\mathit{f}})+\tau w_{\mathrm{a}}(i,j\prime |\mathit{g})}{[\widehat{\mathit{f}}]}_j$$ (12)

where τ is a design parameter to determine how much we want to rely on anatomical information. For example, we can use τ close to 1 if we can trust the anatomical information more than the emission information (e.g., high correlation between anatomical and emission information, high noise in emission data). In this paper, we set τ to be 0.5 for simplicity, thereby giving equal weight to the emission and anatomical information. We call Eq. (12) NLM CT-S (S for summation).

We can also combine Eq. (12) with the concept of Bowsher prior in Eq. (10) as follows:

$${[{\widehat{\mathit{f}}}_{\text{NLM CT-H}}]}_i=\sum _{j\in {\mathrm{\Delta }}_i(\mathit{g})}\frac{(1-\tau )w_{\mathrm{f}}(i,j|\widehat{\mathit{f}})+\tau w_{\mathrm{a}}(i,j|\mathit{g})}{{\sum }_{j\prime \in {\mathrm{\Delta }}_i(\mathit{g})}(1-\tau )w_{\mathrm{f}}(i,j\prime |\widehat{\mathit{f}})+\tau w_{\mathrm{a}}(i,j\prime |\mathit{g})}{[\widehat{\mathit{f}}]}_j$$ (13)

and we call this method NLM CT-H (H for hybrid).

Using accurate weights for the NLM filter in (6) is important to yield high-quality filtered images. However, these weights can not be accurately calculated from the noisy SPECT image alone. When the associated CT image has high SNR and is highly correlated with the noiseless SPECT image, then it should be possible to improve the accuracy of the NLM weights using CT information. In this case, the weights in Eqs. (9) and (11) may be suboptimal because the weights from CT can be contaminated by the weight from poor-quality SPECT due to the multiplication operation. In contrast, the weights in Eqs. (12) and (13) can be more suitable than the weight in Eqs. (9) and (11) since the weights from CT and SPECT are combined separately by summing. For an extreme example, suppose that we have an extremely noisy SPECT image and a CT image that is correlated perfectly with the noiseless SPECT image. In this case, for two similar patches, the NLM weights between them are w_f ≈ 0 due to high noise in SPECT and w_a ≈ 1 due to high SNR of CT. For NLM CT-M, w_fw_a ≈ 0 so that we may not benefit from the CT information, but for NLM CT-S, 0.5w_f + 0.5w_a ≈ 0.5 for τ = 0.5 so the CT information still has influence even in the midst of high noise in SPECT.

3. Evaluation and Parameter Selection

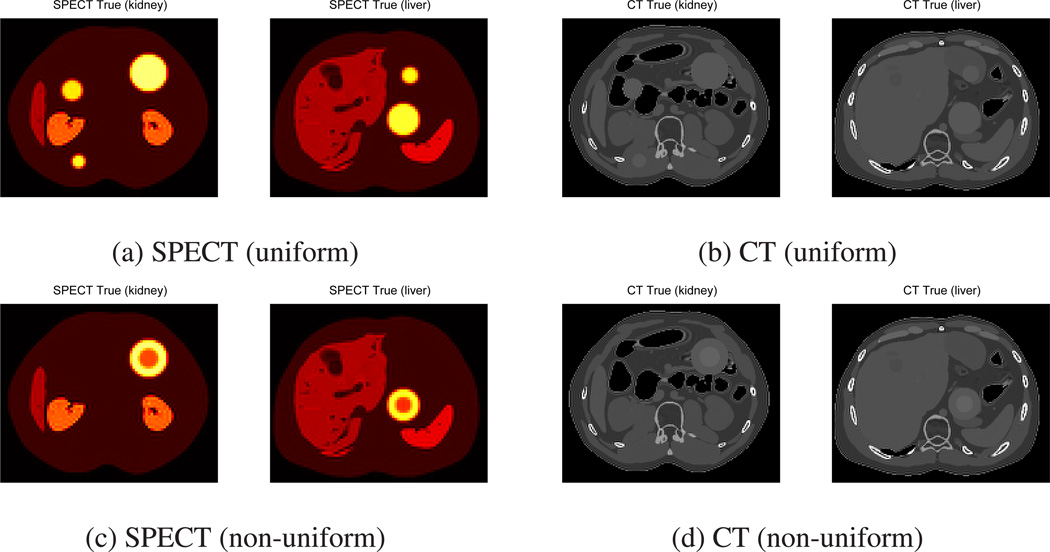
We simulated a 3D SPECT-CT system with attenuation map, collimator-detector response, and scatter fraction. We used the XCAT phantom (Segars et al. 2008) to generate the true activity map and CT images with five uniform spherical tumors as shown in Figure 1 (a), (b) and with two non-uniform tumors (non-uniformity in both activity map and CT) as shown in Figure 1 (c), (d). The uniform tumor sizes were 9, 16, 32, 113, and 177 cc, while the non-uniform tumor sizes were 113 and 177 cc. The activity concentration ratios for the various structures were liver 3 : kidney 6 : uniform tumor and outer shell of non-uniform tumor 8 : inner core of non-uniform tumor 4 : rest of the body 1. These activity concentration ratios and tumor sizes were chosen to reflect typical imaging data of NHL patients following I-131 tositumomab RIT for more realistic simulation (Dewaraja et al. 2005, Dewaraja, Schipper, Roberson, Wilderman, Amro, Regan, Koral, Kaminski & Avram 2010). The dimensions of the SPECT and CT images were 128 × 128 × 128, 4.8³mm³ voxel size and 256 × 256 × 256, 2.4³mm³ voxel size, respectively. We generated SPECT projection data using a system matrix that incorporates the non-uniform attenuation maps and full collimator-detector response including penetration tails (Chun, Fessler & Dewaraja 2013). After adjusting the total number of counts to be similar to the total number of counts in post-therapy SPECT imaging following I-131 tositumomab RIT (about 300K counts per slice for primary and 300K counts per slice for scatter), we added Poisson noise.

Figure 1.

True SPECT and CT images of 3D XCAT phantom (one slice near kidney and one near liver) with five spherical uniform and two non-uniform tumors (non-uniformity in both activity map and CT).

We evaluated the image quality using the root mean squared error (RMSE) between the true and the reconstructed image of the whole field of view (FOV) and the RMSE of five spherical lesions (ROI). RMSE was normalized by the mean value on the FOV and ROI, respectively. We also used the recovery coefficient (RC) for ROI defined as follows:

$$\mathrm{R}\mathrm{C}\stackrel{\mathrm{\Delta }}{=}\frac{\text{Count in ROI}(\text{recon})}{\text{Count in ROI}(\text{true})}$$

and we assume that reconstructed counts are proportional to the image activity.

We set the patch size to be 3 × 3 × 3 voxel, which is the smallest patch size we can use to preserve small details of image. We also set the search neighborhood size to be 7 × 7 × 7 voxel since this was the largest size that the memory in our system could handle.

We determined the other filter parameters experimentally as follows. First of all, we only selected 21 slices of the 3D volume containing three spheres near kidney to reduce computation complexity. Then, we chose parameters to minimize the following modified RMSE using a function p:

$$\text{MRMSE}\stackrel{\mathrm{\Delta }}{=}\text{RMSE}+p(\text{Count in ROI}(\text{recon})/\text{Count in ROI}(\text{true}))$$ (14)

where the count ratio below 85% and above 115% is discouraged by the following function p:

$$p(t)=\{\begin{array}{c}{(t-0.85)}^2,t<0.85,\hfill \\ 0,0.85\le t<1.15,\hfill \\ {(t-1.15)}^2,t\ge 1.15.\hfill \end{array}$$

We chose the smallest tumor as ROI and determined filter parameters to minimize Eq. (14) for all filters. We added the function p to preserve contrast of small spheres since minimum RMSE of FOV can be sometimes achieved by sacrificing contrast of small tumors.

These are design parameters for each filter: the width of Gaussian kernel (Gaussian filter), σ_f (NLM filter), σ_f & σ_a (NLM CT-M and NLM CT-S filters), the size of the set Δ_i(g) (or M) (NLM CT-B filter), and σ_f & σ_a & M (NLM CT-H filter).

4. Simulation Results

4.1. Unregularized OSEM

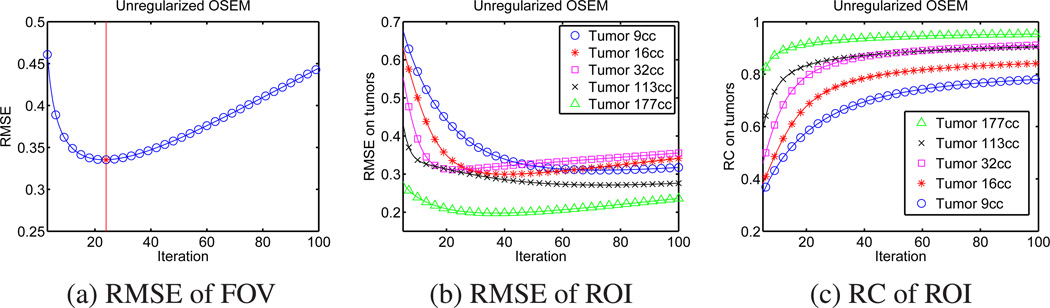
We reconstructed an image with uniform tumors using conventional unregularized OSEM in Eq. (1) with up to 100 iterations (6 subsets). Then, we calculated the RMSE of FOV, the RMSE of ROIs (5 tumors), and the RC of ROIs for each iteration. Figure 2 shows the RMSE of FOV, RMSE of ROIs, and RC of ROIs versus iteration. More iteration in image reconstruction is usually required to recover more details, but also causes increased noise level. Since recovering more details decreases RMSE of FOV and higher noise increases RMSE, the minimum RMSE of FOV was achieved at 24 iteration in our simulation as shown in Figure 2 (a). This “trade-off” can be different for different ROIs, so the minimum RMSE of ROI was achieved at different iteration (usually more than 24 iteration) for each tumor as shown in Figure 2 (b). Unlike RMSE, RC of ROIs is not usually affected by noise, but by recovered details since the definition of RC contains averaging operation over ROI. Thus, the RC of ROI is increasing over iteration for each tumor as shown in Figure 2 (c).

Figure 2.

RMSE of FOV, ROI, and RC of ROI (5 uniform tumors) over iterations for unregularized OSEM images. Minimum RMSE of FOV can be achieved at 24 iteration (6 subsets), but minimum RMSE of ROI can be achieved at various iteration for each tumor. Maximum RC of ROI (each tumor) can be achieved at the highest iteration.

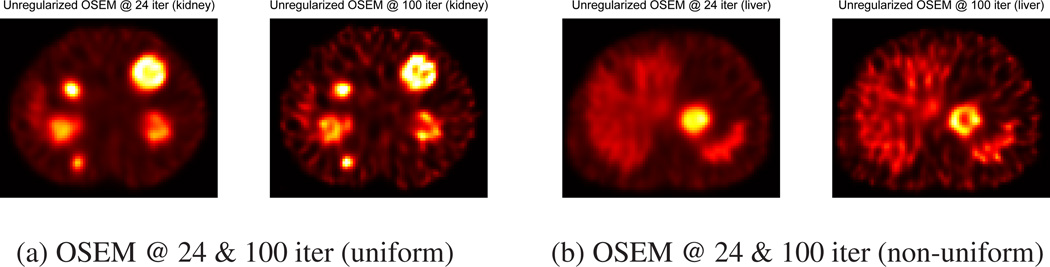
Figure 3 shows unregularized OSEM images of XCAT phantoms with five uniform tumors (a) and with two non-uniform tumors (b) at 24 and 100 iterations. This figure visually shows the noise-detail trade-off shown in Figure 2. Images at 100 iteration contain more noise than images at 24 iteration. In Figure 3 (a), we can observe artifacts on large uniform tumor at 100 iteration (ringing artifact). However, it seems that less details are recovered at lower iteration. For example, we can not observe the inner part of large non-uniform tumor at 24 iteration as shown in Figure 3 (b), but this feature is visible at 100 iterations.

Figure 3.

Unregularized OSEM images of uniform and non-uniform spheres at 24 and 100 iterations (6 subsets). In (a), we can observe artifacts on large uniform tumor at 100 iteration and in (b), we can not observe the inner part of large non-uniform tumor at 24 iteration.

Tables 1, 2, and 3 show the quantification values (RC, RMSE) of unregularized OSEM images at 24 and 100 iterations for the phantoms with uniform and non-uniform tumors. We observed that more iteration is essential for accurate estimation of total target activity. Only 61.3% of RC was achieved for the smallest tumor (9 cc) at low iteration (24 iteration, 6 subsets), but 78.2% of RC was achieved at high iteration (100 iteration, 6 subsets). However, more iteration of OSEM reconstruction may or may not improve activity distribution estimation since RMSE of ROIs may increase or decrease for each tumor.

Table 1.

RCs of different filtering methods for five uniform tumors. The best value is indicated in boldface. Filters are applied to estimated image at 100 iterations if not indicated.

Post-recon. Filter	RC (tumor volume)
	(9 cc)	(16 cc)	(32 cc)	(113 cc)	(177 cc)
None @ 24 iter.	61.3%	71.6%	82.0%	84.7%	92.5%
None @ 100 iter.	78.2%	84.3%	91.3%	90.7%	95.5%
NLM without CT @ 24 iter.	60.7%	71.3%	81.7%	84.4%	92.4%
NLM without CT	70.8%	79.4%	87.1%	87.7%	93.8%
Gaussian	69.0%	76.5%	85.4%	87.4%	91.8%
NLM w. true weight	76.8%	84.6%	93.6%	92.3%	95.4%
NLM CT-B	63.0%	75.4%	84.7%	88.9%	93.8%
NLM CT-M	65.1%	77.2%	90.5%	88.3%	94.5%
NLM CT-S	76.1%	85.0%	91.8%	93.1%	95.0%
NLM CT-H	73.5%	83.1%	89.9%	93.6%	94.0%
NLM CT-B w. 3.4mm misreg. CT	63.0%	75.0%	84.4%	88.6%	93.6%
NLM CT-M w. 3.4mm misreg. CT	64.6%	77.1%	90.4%	88.2%	94.4%
NLM CT-S w. 3.4mm misreg. CT	70.2%	84.6%	91.9%	92.7%	95.2%
NLM CT-H w. 3.4mm misreg. CT	68.4%	82.8%	89.8%	93.3%	94.2%
NLM CT-B w. 6.8mm misreg. CT	62.3%	74.2%	83.5%	88.0%	93.2%
NLM CT-M w. 6.8mm misreg. CT	63.7%	76.7%	89.4%	87.9%	94.2%
NLM CT-S w. 6.8mm misreg. CT	59.9%	80.4%	90.5%	91.7%	96.0%
NLM CT-H w. 6.8mm misreg. CT	58.9%	79.0%	88.2%	92.3%	95.3%

Table 2.

RMSE of different filtering methods on whole image (FOV) and five uniform tumors. The best value is indicated in boldface. Filters are applied to estimated image at 100 iterations if not indicated.

Post-recon. Filter	RMSE (tumor volume)
	FOV	(9 cc)	(16 cc)	(32 cc)	(113 cc)	(177 cc)
None @ 24 iter.	0.335	0.410	0.325	0.312	0.307	0.204
None @ 100 iter.	0.445	0.317	0.342	0.355	0.276	0.236
NLM without CT @ 24 iter.	0.315	0.415	0.327	0.314	0.308	0.202
NLM without CT	0.311	0.375	0.367	0.367	0.264	0.202
Gaussian	0.363	0.342	0.306	0.294	0.249	0.187
NLM w. true weight	0.241	0.297	0.277	0.254	0.197	0.127
NLM CT-B	0.267	0.417	0.366	0.346	0.233	0.167
NLM CT-M	0.288	0.403	0.359	0.321	0.240	0.167
NLM CT-S	0.293	0.291	0.264	0.318	0.191	0.156
NLM CT-H	0.265	0.320	0.280	0.319	0.196	0.151
NLM CT-B w. 3.4mm misreg. CT	0.275	0.416	0.373	0.350	0.238	0.170
NLM CT-M w. 3.4mm misreg. CT	0.290	0.405	0.365	0.322	0.242	0.169
NLM CT-S w. 3.4mm misreg. CT	0.292	0.328	0.279	0.310	0.189	0.155
NLM CT-H w. 3.4mm misreg. CT	0.270	0.347	0.291	0.314	0.192	0.150
NLM CT-B w. 6.8mm misreg. CT	0.290	0.423	0.384	0.362	0.244	0.175
NLM CT-M w. 6.8mm misreg. CT	0.297	0.414	0.375	0.335	0.246	0.176
NLM CT-S w. 6.8mm misreg. CT	0.293	0.443	0.320	0.297	0.191	0.156
NLM CT-H w. 6.8mm misreg. CT	0.282	0.449	0.327	0.305	0.192	0.150

Table 3.

RC and RMSE of different filtering methods for non-uniform tumors. The best value is indicated in boldface. Filters are applied to estimated image at 100 iterations if not indicated.

Post-recon. Filter	RC (tumor volume)		RMSE (tumor volume)
	(113cc)	(177cc)	FOV	(113cc)	(177cc)
None @ 24 iter.	82.9%	92.3%	0.334	0.358	0.211
None @ 100 iter.	90.1%	96.2%	0.438	0.285	0.235
NLM without CT @ 24 iter.	82.4%	92.3%	0.314	0.359	0.210
NLM without CT	87.4%	94.5%	0.307	0.288	0.206
Gaussian	86.4%	92.0%	0.359	0.274	0.185
NLM w. true weight	90.4%	96.8%	0.239	0.213	0.137
NLM CT-B	87.6%	94.1%	0.264	0.261	0.171
NLM CT-M	87.5%	95.1%	0.285	0.264	0.174
NLM CT-S	89.1%	96.2%	0.291	0.222	0.171
NLM CT-H	88.8%	95.6%	0.264	0.227	0.166
NLM CT-B w. miss. CT	87.3%	93.7%	0.264	0.255	0.171
NLM CT-M w. miss. CT	87.4%	94.9%	0.285	0.266	0.174
NLM CT-S w. miss. CT	89.3%	92.1%	0.293	0.235	0.194
NLM CT-H w. miss. CT	88.5%	88.7%	0.265	0.226	0.175

4.2. NLM filtering

Unregularized OSEM images usually contain details and noise together. An ideal filter should suppress noise while preserve details. We applied NLM filter in Eq. (6) and conventional Gaussian filter to unregularized OSEM images. These filters do not use CT information.

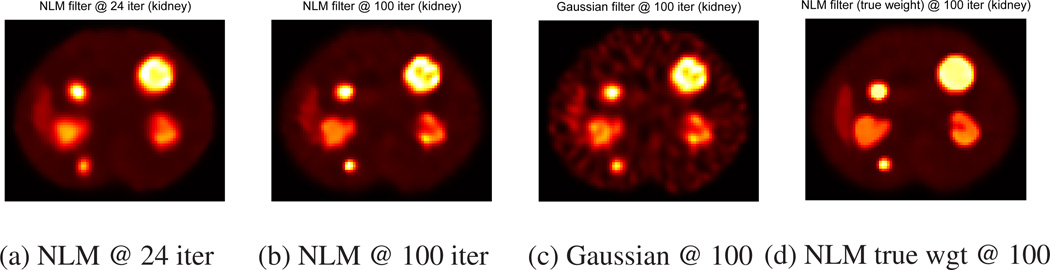
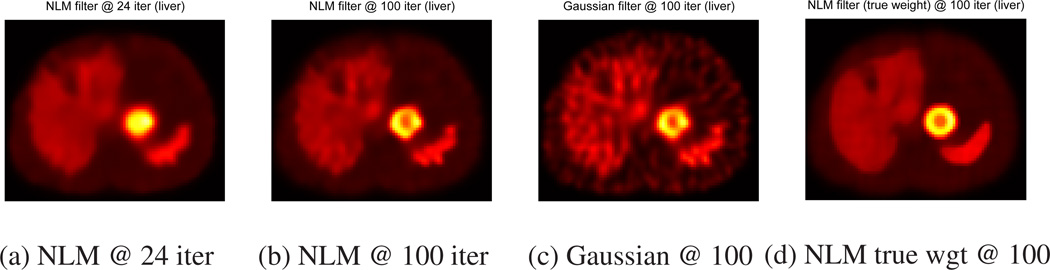
Figures 4 (a) and 5 (a) show NLM filtered images at 24 iteration. However, Tables 1, 2, and 3 show that NLM filtering did not change RMSE and RC values much at low iteration. Similar results were observed for Gaussian filtering.

Figure 4.

NLM filtered images with uniform tumors at 24 (a), 100 (b) iterations, Gaussian filtered images at 100 iteration (c) and NLM filtered images with weights calculated from the true image at 100 iteration (d).

Figure 5.

NLM filtered images with non-uniform tumors at 24 (a), 100 (b) iterations, Gaussian filtered images at 100 iteration (c) and NLM filtered images with weights calculated from the true image at 100 iteration (d).

At 100 iteration, Figures 4 (b–c) and 5 (b–c) show that NLM filtering method yields less noisy images than conventional Gaussian filtering method for both uniform and non-uniform tumors. One may reduce noise further for Gaussian filtering by adjusting parameters, but in that case, it may also blur details more. Tables 1 and 3 show that RCs of NLM filtering are higher than RCs of Gaussian filtering for both uniform and non-uniform tumors. Tables 2 and 3 also show that NLM filtering can achieve better global noise reduction (lower RMSE of FOV) than Gaussian filtering. However, Gaussian filtering yielded better activity distribution estimation within targets (lower RMSE of ROI) than NLM filtering for both uniform and non-uniform tumors.

NLM filtering requires calculating weights in Eq. (3), but NLM filters at 100 iteration obtain their weights from noisy images as shown in Figures 3. In order to study the importance of these NLM weights, we calculated the NLM weights from the true image (true weights) and then performed NLM filtering in Eq. (6) at 100 iteration. Figures 4 (d) and 5 (d) show that NLM filtering methods with true NLM weights yield superior image quality among all NLM and Gaussian filtering methods for both uniform and non-uniform tumors. Tables 1 and 3 show that this ideal NLM filtering does not compromise the accuracy of total target activity estimation. RCs of this NLM filtered image are higher than or comparable to RCs of original unregularized OSEM image whereas other NLM and Gaussian filtering methods lowered RC values. Tables 2 and 3 show that NLM filtering with true weights can achieve minimum RMSE of FOV as well as minimum RMSE of ROIs for both uniform and non-uniform tumors among all post-reconstruction filtering methods without CT information for almost all tumors. This simulation implies that improving the accuracy of NLM weights in Eq. (3) may lead to improved quantification in SPECT imaging.

4.3. NLM filtering with CT side information

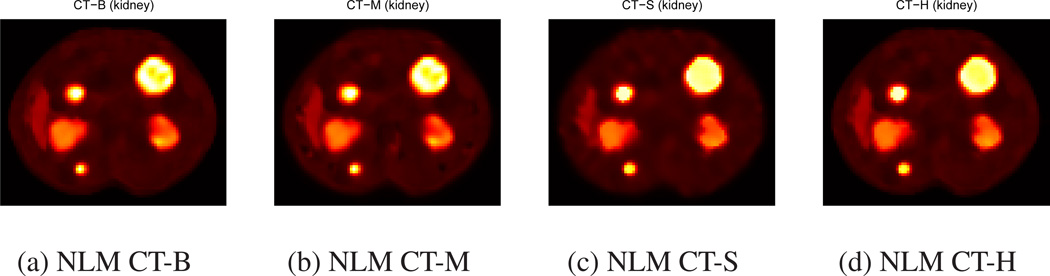
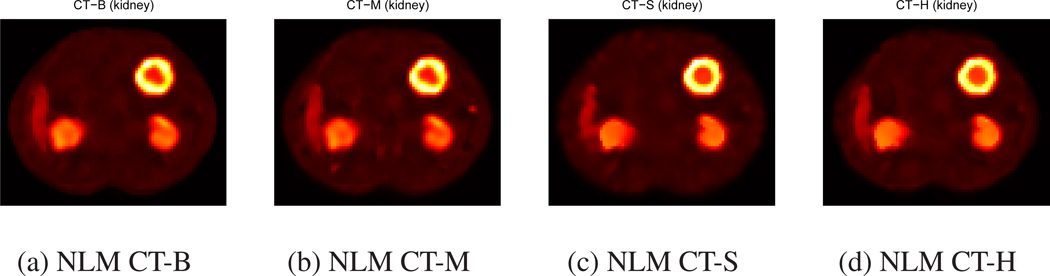
We applied NLM filters using CT side information in Eqs. (9), (11), (12), (13) to unregularized OSEM images at 100 iteration. Figures 6 and 7 show filtered images with uniform and non-uniform tumors using four different methods. The edges in these images are sharper than those in NLM filtered images without CT side information or Gaussian filtered images in Figures 4 and 5. Among four methods using CT information, NLMCT-S and NLMCT-H yielded better boundary shape than NLM CT-B and NLM CT-M for the inner core of non-uniform tumors as shown in Figure 7.

Figure 6.

NLM filtering using CT side information at 100 iteration for uniform tumors.

Figure 7.

NLM filtering using CT side information at 100 iteration for non-uniform tumors.

Quantification results of NLM CT-S and NLM CT-H show substantial improvement in RC and RMSE over other methods. Tables 1 and 3 show that NLM CT-S and NLM CT-H yielded the best RC among all methods and achieved −2.7 to 2.6% and −6 to 3.2% increase of RC compared to no filtering, respectively. However, other methods experienced significant decrease of RC: NLM (1.8 to 19.4% decrease in RC), Gaussian (3.6 to 11.8% decrease in RC), NLM CT-B (2 to 19.4% decrease in RC), and NLM CT-M (1 to 17.4% decrease in RC). NLM filtering with additive CT information (two new: NLM CT-S and NLM CT-H) yielded better total target activity than NLM filtering with multiplicative CT information (two existing: NLM CT-B and NLM CT-M).

Tables 2 and 3 show that NLM filtering with Eq. (10) such as NLM CT-B and NLM C-TH achieved the best RMSE of FOV among all other post-filtering methods. However, those tables show that our new NLM methods using additive CT information yielded the best RMSE of ROIs among all methods. NLM CT-S and NLM CT-H achieved 8.2 to 33.9% decrease and −0.9 to 36% decrease of RMSE of ROI compared to no filtering while other methods achieved the following RMSE of ROI: NLM (−18.3 to 14.4% decrease in RMSE of ROI), Gaussian (−7.9 to 20.8% decrease in RMSE of ROI), NLM CT-B (−31.2 to 28% decrease in RMSE of ROI), and NLM CT-M (−27.8 to 28.4% decrease in RMSE of ROI). Thus, NLM filtering with additive CT information (NLMCT-S and NLM CT-H) yielded better activity distribution estimation within targets than other methods including NLM filtering with multiplicative CT information (NLM CT-B and NLM CT-M).

4.4. Erroneous side information

Erroneous CT side information can be sometimes used due to missing information in CT image or misregistration between CT and SPECT. In here, we investigate how robust NLM filtering methods are for these cases with erroneous side information.

We modified our CT image to have about 3.4 mm and 6.8mm misregistration (in x, y, z directions) with SPECT image and then performed four NLM filtering methods with this misregistered CT side information. Tables 1 and 2 show that NLM CT-S and NLM CT-H are fairly robust to small misregistration (3.4 mm) and achieved better RC and RMSE values than other existing methods. They also yielded the best RC and RMSE results for large misregistration (6.8 mm) for all tumors but the smallest tumor (9 cc).

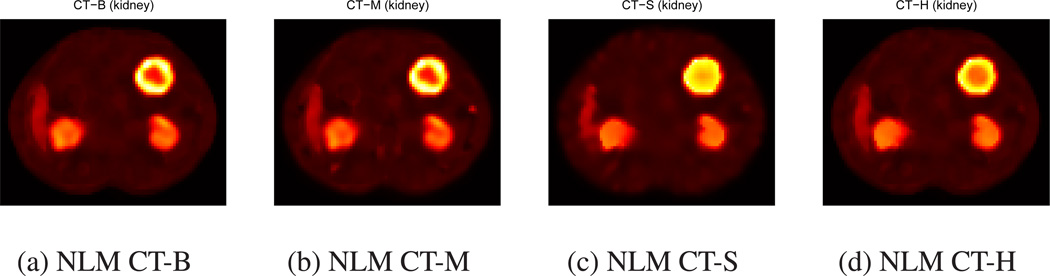
In internal emitter therapy, the volume within which the radionuclide localizes may not be the same as the anatomical tumor volume because of differences between physiology and anatomy. Thus, non-uniform SPECT uptake in a tumor may not have a corresponding non-uniformity in the CT. We therefore simulated the case of missing information in CT: we performed the four NLM filtering methods with CT side information for the phantom with non-uniform tumors using the CT image for uniform tumors (CT of Figure 1 (b) was used instead of CT of Figure 1 (d)). Figure 8 shows that NLM CT-B and NLM CT-M with erroneous CT information yielded similar figures compared to those methods with correct CT image as shown in Figure 7. However, NLM CT-S yielded blurred inner part of non-uniform tumors. NLM CT-H preserved the inner part of tumors better than NLM CT-S. Table 3 shows that RC and RMSE for the large lesion (177 cc) were degraded when there is missing CT information for all methods. In particular, the degradation for NLM CT-S and NLM CT-H was more severe than that for NLM CT-B and NLM CT-M as indicated in Figure 8. However, for the small lesion (113 cc), erroneous CT information caused image degradation on the inner core of the lesion, but yielded better images on the outer rim of the tumor. The degradation on the inner core for NLM CT-S and NLM CT-H was more severe than that for NLM CT-B and NLM CT-M when missing CT information was used. However, the degradation on the outer rim for NLM CT-B and NLM CT-H was more severe than that for NLM CT-M and NLM CT-S when correct non-uniform CT was used. It is because for the voxel on the outer rim, one can find more similar patches with small uniform CT lesion (missing CT information) than with small non-uniform lesion. Therefore, RCs of all methods did not change much with correct and erroneous CT information since the changes on the inner core and on the outer rim compensated each other. However, RMSE for NLM CT-B was worse with correct non-uniform CT information due to severe degradation on the outer rim. RMSE for NLM CT-S was worse with missing CT information due to severe degradation on the inner core. RMSEs for NLM CT-M and NLM CT-H are similar with correct and missing CT information since the changes on the inner core and on the outer rim compensated each other.

Figure 8.

NLM filtering using CT side information at 100 iteration for non-uniform tumors using CT side information for uniform tumors.

5. Discussion

Conventional early stopping criteria of unregularized OSEM methods for I-131 SPECT imaging may yield good RMSE over a FOV, but may not be able to yield good RC of ROIs (total target activity) and RMSE of ROIs (activity distribution within targets). Post-reconstruction filtering methods can be potentially useful for improving SPECT quantification of both total target activity and activity distribution within targets.

We investigated various NLM filtering methods with and without CT side information for uniform and non-uniform tumors. For NLM methods using CT information, we studied four different methods: two existing methods with multiplicative CT information and two new methods with additive CT information. We showed that using CT information for NLM filtering can achieve substantially better RC and RMSE compared to NLM filtering without CT. We also showed that our NLM methods using additive CT information (NLM CT-S and NLM CT-H) usually yielded better RC and RMSE of ROI than those using multiplicative CT information (NLM CT-B and NLM CT-M). This suggests that the CT weights are contaminated when multiplied by the lower quality SPECT weights operation in Eqs. (9) and (11), while the CT weights in Eqs. (12) and (13) are less contaminated because of its separate summation operation. Note that using CT information sometimes yielded better quantification results than using noiseless true SPECT image. Our optimal parameters do not guarantee the optimal RMSE and RC since they were obtained by optimizing (14), which is the combination of RMSE and RC. In the present study for our new methods, we gave equal weight to the emission and anatomical data by setting the design parameter τ to 0.5, but in the future we will investigate adjusting this weight under different conditions such as more or less noisy emission data.

We also investigated the noise reduction performance of NLM methods for the case of erroneous CT information. For misregistration between SPECT and CT, we observed that RC and RMSE of ROI did not change much for large tumors but were degraded for small tumors. However, NLM CT-S using misregistered CT image still achieved the best RCs and RMSEs of ROI for these small tumors among all NLM methods using CT information. For the missing CT information (non-uniform SPECT uptake in tumor, but with uniform CT), NLM CT-S and NLM CT-H experienced performance degradation in terms of RC and RMSE of ROI. However, they still achieved comparable RC and RMSE results compared to other existing methods.

When evaluating the effects of misregistration in this paper, we assumed that the ‘true’ ROI segmentation was available for calculating RC and local RMSE. Thus, we are only evaluating the effects of misregistration on filter performance. However, in practice, ROI segmentation is obtained from CT and will be erroneous when there is misregistration. Misregistration between SPECT and CT can severely degrade the quantification results for small ROIs even when there is no filtering applied to the original image. Therefore, it seems critical to have well-aligned SPECT and CT images for better quantification regardless of the filtering. In well aligned cases, NLM CT-S and NLM CT-H had better RC and lower RMSE than other existing methods.

The missing CT information condition that we tested represents the possible mismatch between anatomical and physiological information in clinical studies. For example, a tumor with uniform CT information may have highly non-uniformactivity uptake evident on SPECT. An extreme case of such non-uniformity is a tumor with a highly metabolic surface and a necrotic core with no uptake. However, in non-Hodgkin lymphoma this level of non-uniformity is rare as tumors are generally well perfused with relatively uniform uptake (Du et al. 2007). When necrosis is evident on SPECT, it is sometimes also evident on CT as a low attenuation dark region. Thus, we expect that NLM CT-S and NLM CT-H can improve quantification results in most of our cases in non-Hodgkins lymphoma. For tumor with a high level of anatomical and physiological mismatch, which can be observed easily before applying the NLM filter, we can always revert to other existing methods that are more robust to this mismatch.

In this phantom simulation study, our additive CT information incorporation for NLM filtering yielded better total target activity estimation and activity distribution estimation within targets than other NLM methods using CT information. The edge-preserving property of NLM methods depends on NLM parameters such as patch size and search window size (Duval et al. 2011). Researchers usually choose NLM parameters so that NLM-based methods are ‘almost’ edge-preserving. In prior studies, they outperformed other edge-preserving methods for noise reduction and contrast preservation (Chan et al. 2010, Wang & Qi 2012).