Abstract
In traditional schedule or dose-schedule finding designs, patients are assumed to receive their assigned dose-schedule combination throughout the trial even though the combination may be found to have an undesirable toxicity profile, which contradicts actual clinical practice. Since no systematic approach exists to optimize intra-patient dose-schedule assignment, we propose a Phase I clinical trial design that extends existing approaches to optimize dose and schedule solely between patients by incorporating adaptive variations to dose-schedule assignments within patients as the study proceeds. Our design is based on a Bayesian non-mixture cure rate model that incorporates multiple administrations each patient receives with the per-administration dose included as a covariate. Simulations demonstrate that our design identifies safe dose and schedule combinations as well as the traditional method that does not allow for intra-patient dose-schedule reassignments, but with a larger number of patients assigned to safe combinations. Supplementary materials for this article are available online.
Keywords: Bayesian statistics, Clinical trial, Dose-escalation study, Dynamic treatment regime, Non-mixture cure model
1. INTRODUCTION
Traditional Phase I trials assign a dose of a therapeutic agent to each subject and the subject receives that dose in a single administration. However, if the agent is safe at that dose, reason suggests that the patient should be given additional administrations of the agent at the same, or perhaps different, doses in hopes of maximizing any efficacy the agent may have with regard to treating or preventing disease.
Such was the motivation of the Phase I trial described by de Lima et al. (2010). Chemotherapy is often the first treatment given to patients with acute myelogenous leukemia (AML) or advanced myelodysplastic syndrome (MDS). If chemotherapy fails to force remission of a patient’s cancer, the next course of treatment is an allogeneic hematopoietic stem cell transplant (HSCT). Although short-term complete remission (CR) of cancer frequently occurs after HSCT, long-term cancer recurrence is still quite prevalent in HSCT recipients. Therefore, researchers hope to find interventions that can be given not only in proximity to HSCT, in order to promote a short-term CR, but also repeatedly after HSCT in order to maintain a CR for a longer period of time. One such intervention is azacitidine; however, the safety profile for multiple administrations of different doses of azacitidine in AML and MDS patients was unknown, thereby necessitating the design of the Phase I trial to address this question.
At the time that the azacitidine trial was being considered, there were no published designs for simultaneous dose- and schedule-finding in Phase I trials. Although Braun et al. (2005) proposed a design in which the time to toxicity was modeled using a triangular hazard model for each administration, their model assumed a single dose was under study. Liu and Braun (2009) later developed a more flexible model for the cumulative hazard of a dose-limiting toxicity (DLT) by introducing a non-mixture cure rate model and a smooth hazard function. However, their methods also assumed a single dose was being considered.
To meet the needs of the azacitadine trial, Braun et al. (2007) developed the first design for dose- and schedule-finding by generalizing the work of Braun et al. (2005) to incorporate different triangular hazard functions for each dose. However, as noted by Liu and Braun (2009), the method of Braun et al. (2007) can be inflexible mainly due to its computational difficulty, the finite support of the triangular hazard function and the difficulties with including patient-level or administration-level covariates.
The azacitidine Phase I trial was designed to identify which combination of three doses and four administration schedules was the maximum tolerated combination (MTC) of dose and schedule, defined as the combination estimated to have the probability of a DLT within 116 days of starting treatment closest to 0.30. In the design, each patient was adaptively assigned to whichever dose and schedule combination was believed to be the MTC, based upon the data collected on previously enrolled patients. One important characteristic of this trial was that once enrolled, a patient’s dose and/or schedule was to remain unchanged, except for reductions in dose and/or number of administrations due to complications unrelated to azacitidine such as infection. In the actual trial, three patients received reduction in their assigned dose, and about half of the patients had reductions to their planned number of administrations.
However, one could also envision patients who were assigned to combinations that during the trial are determined to have DLT rates well below that of the MTC. Patients assigned to such combinations who have not completed all their administrations might benefit from increases to the dose and/or number of administrations they receive. Such changes are not necessarily expected to increase correct identification of the MTC at the end of the study, but should increase the number of subjects during the trial who are assigned to combinations near the MTC. Although the model of Braun et al. (2007) could allow the possibility that the patient’s planned dose for each administration to be changed, the benefit of patient reassignments, as well as how and when appropriate reassignments of doses and/or schedules are determined, are areas that have not been studied.
These issues are the motivation of our current work. First, we generalize the methods of Liu and Braun (2009) to simultaneously optimize the dose and schedule assigned to each patient. Specifically, we extend their Bayesian non-mixture cure model by incorporating the per-administration dose as a covariate for modeling the cure fraction to allow for multiple dose levels. In addition, we derive a non-mixture cure rate model through a competing risks approach to accommodate multiple administrations one patient may receive. The second contribution of our work is to adaptively optimize the dose and schedule assignments both between patients and within patients. While new patients are given the most recent maximum-tolerated dose-schedule combination (MTC) estimate, our approach also re-evaluates the estimated DLT rate for the current assignment of each enrolled patient and automatically determines whether dose-schedule reassignment is needed. Patient accrual, data monitoring, and outcome-adaptive decision-making are done continuously throughout the trial under a Bayesian formulation. We describe the probability model and the dose-schedule-finding algorithm in Section 2, and we illustrate the proposed design in the context of a real trial and present a simulation study in Section 3. We conclude with a brief discussion in Section 4.
2. METHODS
2.1 Preliminary Notation
Typical dose-schedule finding trials aim to find the MTC within a J × K matrix consisting of J per-administration doses and K nested schedules. We denote the administration times for schedule k, k = 1, …, K, as s(k) = {s1, s2, …, sm(k)} such that s(1) ⊂ s(2) ⊂ ··· ⊂ s(K) and m(1) < m(2) < ··· < m(K), where m(k) is the number of administrations for schedule k. We focus on nested schedules because they have natural ordering and hence are of interest to the clinicians.
In our motivating example, there are J = 3 doses and K = 4 nested schedules. A course of administrations corresponds to daily administrations for the first 5 days followed by 24 days of rest, which we denotes as (5+, 24−). The first schedule is comprised of one single course, so the administration times s(1) = {0, 1, 2, 3, 4}. Schedule 2 consists of two courses with the additional course starting 28 days after the beginning of s(1), we have s(2) = {0, 1, 2, 3, 4, 28, 29, 30, 31, 32} = {s(1), s(1) + 28}, and so on. Ideally, we plan to give dose j = 1, 2, … J, at each administration in s(k), and we let dj denote the per-administration dose. The number of subjects enrolled by the end of the trial is N and each subject will be followed up to the maximum follow-up time ω = 116 days, which is determined by the clinical investigators and is a clinically meaningful duration of time that is sufficiently late enough to observe DLTs attributed to the longest schedule. A target DLT rate η = 0.30 is also elicited from clinicians and is defined as the targeted probability of cumulative toxicity by ω.
Note that dj and s(k) represent the combinations of doses and schedule that are possible assignments to each patient as they enter the study. In contrast, during a trial, the actual number of administrations and the dose at each administration for each patient may differ from each of those possible combinations. To make this concept distinct, we let mi denote the number of administrations patient i receives, si = {si,1, …, si,mi}, i = 1, …, N, denote the successive times at which patient i receives the agent and let di = {di,1, …, di,mi} where di,l ∈ {1, …, J} and l = 1, …, mi denote the per-administration doses for patient i at the administration times si.
2.2 Model for Time-to-DLT After a Single Administration
As noted by Liu and Braun (2009), a significant proportion of patients are “cured,” i.e. never experience DLTs after a single administration. Thus, they chose to model the time-to-DLT for a single administration using the non-mixture cure model proposed by Chen et al. (1999). Specifically, we take a standard cumulative distribution function F(ν|φ) with parameters φ, with a corresponding density function f(ν|φ), and scale F(ν|φ) by a parameter θ > 0 to create the respective survival and hazard functions S(ν|θ, φ) = exp[−θF(ν|φ)] and g(ν|φ, θ) = θf(ν|φ). We adopt S(ν| θ, φ) as the probability of no DLT by follow-up time ν after a single administration and interpret θ as a cure rate parameter because the cure fraction S(∞) = exp(−θ) is determined solely by θ. The Time-to-Event CRM (TITE-CRM) of Cheung and Chappell (2000) for traditional dose-finding can be viewed as a mixture cure model for the time-to-DLT, as outlined in Braun (2005). However, we have chosen to use a non-mixture cure rate model instead of a mixture cure model because the latter does not have a proportional hazards structure and is less feasible for Bayesian computations (Chen et al. 1999; Tsodikov et al. 2003).
However, the non-mixture cure model used by Liu and Braun (2009) must be extended to allow the cure fraction to vary by dose. To that end, we model the cure rate fraction for administration l of patient i as log(θi,l) = β0 +exp(β1)di,l, −∞ < β0, β1 < ∞, so that θi,l > 0. Note that we exponentiate β1 to ensure that the probability of DLT after a single administration increases with dose. As a result, the respective hazard and survival functions for a single administration l are g(νi,l|β, φ) = θi,lf (νi,l|φ) and S(νi,l|β, φ) = exp[−θi,lF (νi,l|φ)], in which β = (β0, β1). Thus, our proposed hazard is an increasing function of dose through the cure fraction, even though the parameters in f(·) do not involve dose. We feel that the log-linear model should be adequate in many settings for identifying the MTC since the sample size is usually small in Phase I trials and the overall model fit is not our primary interest (O’Quigley et al. 1990). However, if one were truly concerned about the log-linear assumption, one could always add more parameters in the model if needed. Although computationally challenging relative to the small sample size, one could propose several competing models and use Bayesian Model Averaging or select the best-fitting model at each interim analysis time as outlined by Raftery et al. (1997) and Yin and Yuan (2009).
With regard to f(·), we adopt the model of Liu and Braun (2009), a two-parameter Weibull density with φ = (α, γ). Such a choice has biologic appeal because the resulting hazard function increases with time to a certain time point and then attenuates afterward, as was suggested by clinical investigators in the azacitidine trial. Mathematically, we expect the mode of the hazard function to exist at exp(γ/α)(1 − 1/α)1/α, and we assume α > 1 so that the mode exists.
We did consider modeling φ as a function of dose, but did not because doing so would eliminate the proportional hazards structure of our model and there will be no guarantee that the hazard will increase with dose if φ is also a function of dose. Further support for our approach is given by Chen et al. (1999), who examined the standard cure model without proportional hazards and found both models (with or without proportional hazards) led to similar point and interval estimates. We also ran simulations (results not shown) with φ varying with dose and found that this added level of complexity to our model offered no benefit to identification of the MTC. The main reason for this result is Phase I trials seek to estimate well the DLT rate of the MTC and not necessarily the DLT rates for all dose-schedule combinations. Thus, overall model fit is not the primary interest and we prefer a parsimonious model with reasonable flexibility.
Thus the distribution of DLT times is controlled by the four parameters β0, β1, α, and γ, whose interpretations are as follows. If we denote pi,l as the DLT rate by the maximum follow-up time ω for a single administration l of patient i, then pi,l = 1 − S(ω|β, φ) = 1 − exp{−exp[β0 + exp(β1)di,l]F (ω|φ)}. Thus, with infinite follow-up, we have pi,l = 1 −exp{−exp[β0 + exp(β1)di,l]}, which is a complementary log-log model that could be used in the CRM with binary DLT outcomes. The intercept β0 quantifies the limiting probability of DLT for a single administration of a dose di,ℓ = 0, while β1 quantifies how the limiting probability varies with dose. The rate at which the limiting probability is reached for each dose is controlled by α and γ, in which α and γ determines the mode of the DLT times and increasing the value of γ quantifies later DLT times.
2.3 Model for Time-to-DLT After Multiple Administrations
We employ a competing risks cure rate model by treating yi,l, the time to the DLT after administration l of patient i, as a latent variable to incorporate the multiple administrations received by each patient. The patient time when patient i experiences a DLT is then defined as the random variable Yi = min {(s1 + yi,1), …, (smi + yi,mi)}. Therefore, under the assumption of independence of yi,1, …, yi,mi, the survival function for patient i at patient time t, is given by
| (1) |
and the density function is given by
| (2) |
where θi,l = exp[β0 + exp(β1)di,l] is the cure parameter and νi,l = t − si,l is the follow-up time for administration l of patient i. The hazard function is then given by , which indicates the cumulative effect of multiple administrations.
The assumption that the times-to-DLT after each administration, yi,1, …, yi,mi, are independent for the mi administrations of the same patient i might not hold, although the actual amount of correlation is not testable (Tsiatis 1975). A more general model could be based on an Archimedean copula-type model or a frailty model with a cure fraction (Hougaard 2000). For example, the above survival function could be generalized to
which is a Gumbel copula model with a correlation parameter ξ, in which ξ = 0 indicates independent DLT times. In this paper, we will assume independence for our model since it is simple and we feel that copula models could possibly impose strong and untestable assumptions on the correlation structure of DLT times.
Define the observed patient time Ti = min(Yi, Ui) and Ci = I(Yi ≤ Ui), where Ui denotes the censoring time and I(·) is the indicator function. Hence, we observe a DLT for patient i if Ci = 1. Since we perform interim analyses whenever a new patient in enrolled, by the time patient n+1 is enrolled, we denote the number of patients currently in the study as n and for each enrolled patient, we observe Ti, Ci, si and di, where si and di, as we defined previously, are the respective time and dose for each administration patient i have received, i = 1, …, n. Note Ui = min(Wi,n+1, ω), where Wi,n+1 the inter-patient time between patient i and n + 1. If n = N, the maximum number of patients for the study, then define Wi,n+1 as the time between patient i and the end of the study. It is reasonable to assume random censoring since Wi,n+1 is usually independent of the DLT time and ω is a fixed value. Based on the above information, Equations (1) and (2), the likelihood on the data
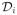 = (Ti = ti, Ci = ci,
si,
di) for patient i is given by
= (Ti = ti, Ci = ci,
si,
di) for patient i is given by
| (3) |
After determining the prior distribution p(β,
φ), then the posterior distribution of (β,
φ) based on
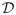 = {
= {
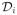 : i = 1, …, n} is
: i = 1, …, n} is
We can compute posterior quantities via adaptive Markov Chain Monte Carlo (MCMC) methods (Rosenthal 2007). Those posterior quantities will be used to identify the dose-schedule assignment for a new patient and a possibly new dose-schedule assignment for an existing patient as described in Section 2.5.
2.4 Establishing Prior Distributions
For the two parameters of the cure fraction, β, we assign independent Gaussian distributions with prior mean and prior variance (μ0,
) for β0 and (μ1,
) for β1. In order to determine values for the prior means μ0 and μ1, we ask the investigators to provide the “skeleton”
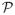 , which is a J × K matrix of a priori estimates of the DLT rates by ω for all dose-schedule combinations, in which element (j, k), denoted Pjk, corresponds to the combination of dose j and schedule k. We then fit the linear regression model log(−log[1 − Pjk]) = log(m(k)) + b0 + exp(b1)dj and use the ordinary least square estimates b̂0 and b̂1 as the respective values for μ0 and μ1.
, which is a J × K matrix of a priori estimates of the DLT rates by ω for all dose-schedule combinations, in which element (j, k), denoted Pjk, corresponds to the combination of dose j and schedule k. We then fit the linear regression model log(−log[1 − Pjk]) = log(m(k)) + b0 + exp(b1)dj and use the ordinary least square estimates b̂0 and b̂1 as the respective values for μ0 and μ1.
For the two parameters of the hazard, φ = (α, γ), we have chosen to make α fixed to maintain a parsimonious model and limit the number of parameters to estimate. In addition, preliminary simulations (results not shown) indicated that there was no meaningful change in operating characteristics when assigning a prior distribution to α. However, because the mode of the hazard for a single administration monotonically increases with γ, estimation of γ is important to the performance our algorithm. Therefore, we assign a Gaussian prior distribution for γ with mean μγ and variance . To determine values for α and μγ, we apply the method outlined in Liu and Braun (2009) for each dose and calculate the average. If the resulting value for α < 1, we set α = 1.01, so that the mode exists.
It is important to carefully calibrate the prior variances and as we can imagine that Phase I trials are usually sensitive to prior variances due to the small sample size. The prior variances should not be too small, otherwise the prior information dominates the trial. However, they cannot be too large either since we hope to incorporate the prior information for possibly more accurate estimation. We recommend calibrating the prior variances through simulations using a few different skeletons and prior variances. The prior variance that is the most insensitive to skeletons and leads to the best operating characteristics will be used for a real trial. We present an example of variance calibration related to the simulations of Section 3.
2.5 Algorithm for Adaptive Assignments for New Patients and Reassignments for Enrolled Patients
The algorithm for assigning a dose-schedule combination to a new patient is similar to that used in the CRM and many other Phase I designs. When a new patient enters the study, for every combination of a dose j and a schedule k, we compute p̂jk = 1 − ψ̂(ω|φ, β, s(k), dj), the posterior estimate of the DLT rate by the maximum follow-up time ω. In Phase I studies, ψ̂ is usually approximated by plugging in φ̂ and β̂, the respective posterior medians/means of φ and β. Given a desired DLT rate η, the dose-schedule combination that minimizes a distance measure d(p̂jk, η), which we denote (j*, k*) is assigned to the next patient, subject to one restriction. Both j* and k* cannot simultaneously be respectively more than one dose higher than ji−1, the dose assigned to the most recently enrolled patient, and ki−1, the schedule assigned to the most recently enrolled patient. Even though we use a “no-skipping” rule for dose-schedule escalation among successive patients, there is no such rule when it comes to de-escalation. We place no restriction on escalation of dose and schedule within a patient, which some may view as overly aggressive. However, in the simulation results presented in Section 3.2, we see no evidence of a higher than desired rate of DLTs. We also ran simulations in which the between-patient restriction on escalation to also applied within-patient (results not shown). We saw little change to the results presented in Table 4, except that patient assignments to acceptable combinations tended to lessen with the restriction than without it.
Table 4.
Simulation results for Design A (with reassignment) and B (without reassignment), prior standard deviation σ = 2 and Skeleton 2. For each design, there are four columns under “Selection” list the percentage of simulations in which the MTC was not identified, was identified at combinations with DLT rates below that desired, within that desired, and above that desired, respectively. Corresponding columns are listed under “Assignment” to describe the average percentage of patients assigned to each combination. DLT = mean proportion of patients who experienced DLT. The columns under “Reassignment” gives summary statistics on reassignment: Rp = average proportion of patients receiving at least one reassignment during the study, Rm (Rsd) = mean (standard deviation) of number of reassignments a patient received, R1 (Rn) = the average minimum (maximum) number of reassignments a patient received.
| Scen | Design | Selection
|
Assignment
|
DLT | Reassignment
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | L | In | H | L | In | H | Rp | Rm | Rsd | R1 | Rn | |||
| 1 | A | 0 | 5 | 95 | 0 | 10 | 90 | 0 | 27 | 38 | 0.9 | 1 | 0 | 4.1 |
| B | 0 | 4 | 96 | 0 | 12 | 88 | 0 | 27 | ||||||
| 2 | A | 0 | 13 | 83 | 3 | 19 | 63 | 18 | 31 | 56 | 1.2 | 1.3 | 0 | 5.2 |
| B | 0 | 12 | 86 | 3 | 29 | 52 | 18 | 31 | ||||||
| 3 | A | 1 | 14 | 71 | 14 | 22 | 53 | 24 | 32 | 53 | 1 | 1.2 | 0 | 4.7 |
| B | 0 | 25 | 62 | 13 | 29 | 48 | 23 | 33 | ||||||
| 4 | A | 0 | 27 | 53 | 20 | 19 | 58 | 23 | 30 | 68 | 1.6 | 1.5 | 0 | 5.8 |
| B | 0 | 32 | 48 | 20 | 33 | 29 | 38 | 31 | ||||||
| 5 | A | 2 | 2 | 78 | 17 | 7 | 62 | 29 | 35 | 43 | 0.7 | 0.9 | 0 | 3.8 |
| B | 2 | 2 | 81 | 16 | 5 | 63 | 31 | 36 | ||||||
| 6 | A | 1 | 18 | 56 | 25 | 18 | 52 | 29 | 34 | 44 | 0.7 | 0.9 | 0 | 3.7 |
| B | 1 | 12 | 64 | 23 | 21 | 44 | 35 | 34 | ||||||
| 7 | A | 11 | 0 | 69 | 20 | 0 | 58 | 33 | 36 | 20 | 0.3 | 0.6 | 0 | 2.5 |
| B | 9 | 0 | 66 | 24 | 0 | 54 | 39 | 37 | ||||||
| 8 | A | 0 | 12 | 56 | 32 | 14 | 58 | 28 | 32 | 73 | 1.7 | 1.5 | 0 | 5.9 |
| B | 0 | 15 | 58 | 27 | 25 | 36 | 38 | 32 | ||||||
| 9 | A | 6 | 18 | 49 | 28 | 18 | 38 | 40 | 34 | 25 | 0.4 | 0.7 | 0 | 2.7 |
| B | 3 | 14 | 54 | 29 | 17 | 38 | 44 | 36 | ||||||
| 10 | A | 0 | 25 | 53 | 22 | 16 | 53 | 31 | 30 | 62 | 1.5 | 1.5 | 0 | 5.6 |
| B | 0 | 26 | 53 | 21 | 30 | 26 | 44 | 30 | ||||||
| 11 | A | 0 | 10 | 79 | 11 | 15 | 64 | 22 | 31 | 67 | 1.6 | 1.5 | 0 | 5.7 |
| B | 0 | 12 | 76 | 13 | 21 | 48 | 31 | 31 | ||||||
| 12 | A | 2 | 5 | 75 | 18 | 9 | 59 | 30 | 35 | 37 | 0.6 | 0.9 | 0 | 3.5 |
| B | 2 | 4 | 74 | 20 | 9 | 53 | 36 | 36 | ||||||
| 13 | A | 0 | 14 | 67 | 19 | 15 | 63 | 22 | 33 | 56 | 1.1 | 1.2 | 0 | 4.8 |
| B | 0 | 13 | 69 | 17 | 24 | 52 | 24 | 33 | ||||||
| 14 | A | 3 | 8 | 61 | 28 | 12 | 57 | 28 | 35 | 32 | 0.5 | 0.8 | 0 | 3.2 |
| B | 3 | 7 | 58 | 32 | 13 | 51 | 35 | 36 | ||||||
| 15 | A | 0 | 17 | 74 | 8 | 16 | 64 | 20 | 30 | 64 | 1.5 | 1.5 | 0 | 5.7 |
| B | 0 | 26 | 65 | 9 | 26 | 44 | 30 | 30 | ||||||
| 16 | A | 89 | 0 | 0 | 11 | 0 | 1 | 37 | 21 | 5 | 0.1 | 0.3 | 0 | 1.4 |
| B | 87 | 0 | 0 | 13 | 0 | 0 | 40 | 22 | ||||||
We adopt the measure d(p̂jk, η) = |p̂jk − η|, although we could adopt a different metric in order to penalize selection of toxic regimens, like that proposed in the Escalation with Overdose Control (EWOC) design of Babb et al. (1998). EWOC selects the dose that minimizes the distance (p̂jk − η)(1 − δ)I(p̂jk > η) + (η − p̂jk)δI(p̂jk < η), and with δ < 0.5, will penalize the selection of toxic dose-schedule combinations more than our metric |p̂jk − η|. Furthermore, a stopping rule for excessive toxicity could be easily incorporated into our design. For example, in our simulations, we use a stopping rule stating that a trial is halted if at least three patients have been enrolled and p̂11 > η + 0.15, in which p̂11 is the DLT rate estimate for the lowest dose-schedule combination. A similar stopping rule when all DLT rates are too low could also be used.
We emphasize that reassignment of dose and/or schedule does not apply to patients who have experienced DLT, nor to those who finished their originally assigned treatment, nor those whose treatment was terminated early. For the remaining n* ≤ n patients who are still planning to receive additional administrations, we compute p̂ℓ = 1 − ψ̂(ω|φ, β, sℓ, dℓ), which is the estimated DLT rate of the administrations received so far by patient ℓ = 1, 2, … n*. We immediately terminate the treatment of any patient ℓ for whom p̂ℓ ≥ η + 0.1, as they have already received a combination that appears to be overly toxic and further treatment would be unethical. Once the treatment is terminated, no additional administrations will be given to the patient but this patient is still under follow-up until a DLT occurs or the maximum follow-up time ω is reached.
For each of the remaining patients for whom p̂ℓ < η + 0.1, we need to consider how many more administrations might be given and which dose would be given at each of those administrations. Specifically, if mℓ is the number of administrations received so far, we compute , for each schedule k, including the schedule to which the patient was originally assigned. Among all schedules with , let denote the remaining administration times for schedule k that could still be assigned to patient ℓ. We consider the combination of each with each dose j and let denote the remaining dose assignments, which is a vector of elements each with the value dj. We then compute , which is the probability of DLT by ω for patient ℓ for each of these possible reassignments appended to what he has already received. We will reassign patient ℓ according to whichever is closest to the targeted DLT rate, η. We emphasize again that one of the possible “reassignments” is simply the assignment currently belonging to patient ℓ.
To clarify our notation, we consider a hypothetical study of J = 3 doses and K = 5 schedules in which schedule k is comprised of k consecutive (5+, 24−) courses as described in Section 2.1. Imagine that a new patient is to be enrolled in the study and that we have an enrolled patient ℓ who was assigned to schedule 3, has not yet experienced a DLT, and has respective administration times and doses for each administration sℓ = {0, 1, 2, 3, 4, 28, 29, 30, 31, 32, 56, 57} and dℓ = {8, 8, 8, 8, 8, 16, 16, 16, 16, 16, 32, 32} mg/m2. As each schedule had a total of five planned administrations, we see that patient ℓ has completed two courses and has three administrations remaining in her third course. Assuming that the treatment received so far does not have an estimated DLT rate 10 points above the target, Table 1 delineates the nine possible remaining assignments that could now be given to patient ℓ. Whichever of these nine combinations, when appended to sℓ and dℓ, leads to an estimated DLT rate by ω closest to the target DLT rate is the reassignment given to patient ℓ.
Table 1.
Nine possible remaining dose and schedule assignments for a hypothetical patient who has not completed their originally assigned treatment and remains under observation without DLT. Vectors of remaining administration times are , and .
| Decision | Dose at Each Administration | Times of Administration | |
|---|---|---|---|
| No change | 32 |
|
|
| Change dose only | 8 |
|
|
| 16 |
|
||
| Change schedule only | 32 |
|
|
| 32 |
|
||
| Change dose & schedule | 8 |
|
|
| 8 |
|
||
| 16 |
|
||
| 16 |
|
This example emphasizes the fact that we attempt to keep the dose constant within a patient as much as possible, i.e. each administration for a patient will be at the same dose until a reassignment occurs. Thus, the hypothetical patient ℓ described above had already received two previous changes to her assignment, as her dose was increased from 8 mg/m2, then to 16 mg/m2, and then again to 32 mg/m2. Of course one could consider a setting in which the best treatment plan would be contrary to this, i.e. perhaps alternating back-and-forth between two doses. However, such a treatment plan, or one that considers any of the J doses at each administration period would be infeasible in practice and would likely lead to treatment errors if the treatment plans assigned to several patients were all different and impossible to remember.
Furthermore, we have chosen to only consider reassignments when a new patient is enrolled. This certainly is not the only benchmark at which we might consider reassigning patients. For example, we might instead (or also) re-evaluate the data collected so far each time a patient completes their follow-up, either by reaching ω without a DLT or experiencing a DLT sometime before ω. Or we could re-evaluate the data each time a patient completes a course, thereby allowing a course-by-course evaluation for every patient. And if we truly wanted to optimize the treatment of every patient in the study, it would seem most sensible to evaluate each patient after every single administration. However, most of these alternate approaches are unrealistic in practice as the frequency of the necessary computations would become administratively impossible. On the opposite end of the spectrum, we could administratively set times, i.e. every three months, when we might consider reassignments that have nothing to do with patient outcomes but makes the process of re-assignment known before the trial begins. However, we feel our approach of re-evaluating assignments when each new patient is enrolled is a good compromise between optimizing the treatment of each patient as much as possible and maintaining a feasible level of computation.
2.6 Conduct of the Trial
We plan on enrolling a maximum of N patients in the trial, and each patient will be followed for ω days after enrollment. The first patient is enrolled at study time t = 0 and is assigned to the shortest schedule (k = 1) with the lowest dose (j = 1). When patient i = 2, …, N is to be enrolled in the study at study time t, we perform the following steps:
Place each enrolled patient i′ = 1, 2, … i − 1 into one of two groups, either those without DLT or those with DLT;
-
For patients without DLT, record:
Ci′ = 0, indicating no DLT
Ti′ = min{Wi′,i, ω}, where Wi′,i is the inter-patient time between patient i′ and i;
-
For patients with DLT, record:
Ci′ = 1, indicating DLT
Ti′ = Yi′, the patient time when a DLT occurred;
For all enrolled patients, record si′, the vector of times of each administration received, and di′, the vector of doses given at each administration;
Use the information recorded from (2)-(4) above to compute the likelihood given in Equation (3). Specifically, patients without DLT will contribute an amount given in Equation (1) and patients with DLT will contribute an amount given in Equation (2);
Combine the likelihood with the prior distributions described in Section 2.4 to compute the posterior medians of φ and β;
Apply the methods described in Section 2.5 to determine whether to terminate the trial, and if not, determine for each patient whether to assign a new dose and/or schedule or terminate their treatment altogether;
Determine the dose and schedule assignment for patient i using the methods described in Section 2.5;
Once all N patients have been enrolled, use all accumulated data to compute final posterior estimates of the DLT rates of each dose and schedule combination and select the combination with estimated DLT rate closest to η as the optimal combinations
3. APPLICATION
3.1 Simulation Design
In the motivating azacitidine trial, there were J = 3 doses of interest: 8, 16 and 24 mg/m2, and K = 4 schedules with respective numbers of administrations m(1) = 5, m(2) = 10, m(3) = 15 and m(4) = 20, for a total of 12 combinations. A course consists of five daily consecutive administrations followed by 28 days of rest as described in the example in Section 2.1, and schedule k consists of k consecutive courses. Investigators would like to determine which of the 12 combinations has a DLT rate close to η = 0.30. The maximum follow-up time for each patient is ω = 116 days. We consider the dose-schedule combinations with DLT rates of η ± 0.10 to be acceptable choices of the MTC, since a small deviation from η is acceptable for the investigators (Braun et al. 2007). A maximum of N = 60 patients will be enrolled.
We considered two skeletons that we feel would reflect those most commonly used in practice. Skeleton 1 specifies the a priori MTC to exist at middle combinations whereas Skeleton 2 specifies the highest combinations as the a priori MTC; the actual values of the skeletons can be found in Table 2. For each skeleton, we used the methods described in Section 2.5 to calculate the prior means. For Skeleton 1, this leads to μ0 = −4.80, μ1 = −0.32, μγ = −0.818 and α = 1.73. The corresponding values for Skeleton 2 were μ0 = −5.50, μ1 = −0.43, μγ = −0.822 and α = 1.72. With either skeleton, the mode of the hazard function is around four days after administration. For both skeletons, we calibrated the prior variances of our model parameters through a process outlined in the Supplemental Materials.
Table 2.
The two skeletons used in the simulation study. The boldfaced values correspond to acceptable combinations.
| Skeleton | Dose(mg/m2) | Schedule
|
|||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 8 | 0.03 | 0.12 | 0.30 | 0.50 |
| 16 | 0.15 | 0.30 | 0.50 | 0.60 | |
| 24 | 0.30 | 0.50 | 0.60 | 0.75 | |
| 2 | 8 | 0.02 | 0.06 | 0.15 | 0.25 |
| 16 | 0.08 | 0.15 | 0.25 | 0.30 | |
| 24 | 0.15 | 0.25 | 0.30 | 0.38 | |
We examined our approach in 16 different scenarios that are summarized in Table 3. The true DLT rates of every combination of dose and schedule were not generated by the model used in our methods but were instead created using an approach outlined in the Supplementary Materials.
Table 3.
Summary of the 16 scenarios studied, including the actual DLT rates of each dose and schedule combination and three metrics that measure the difficulty of identifying an MTC. Boldfaced values indicate dose and schedule combinations with DLT rates within 10 points of the desired DLT rate η = 0.30.
| Method | Scenario | Dose(mg/m2) | Schedule
|
pd | Nc | MSE | SD | ξ | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||||||
| Independent | 1 | 8 | 0.05 | 0.10 | 0.14 | 0.18 | 0.010 | 3 | 0.03 | 0.08 | n/a |
| 16 | 0.06 | 0.12 | 0.18 | 0.23 | 0.013 | ||||||
| 32 | 0.09 | 0.17 | 0.24 | 0.30 | 0.018 | ||||||
| 2 | 8 | 0.05 | 0.10 | 0.14 | 0.18 | 0.010 | 3 | 0.32 | 0.23 | n/a | |
| 16 | 0.09 | 0.17 | 0.24 | 0.30 | 0.018 | ||||||
| 32 | 0.30 | 0.52 | 0.66 | 0.77 | 0.070 | ||||||
| 3 | 8 | 0.02 | 0.05 | 0.07 | 0.10 | 0.005 | 1 | 0.35 | 0.32 | n/a | |
| 16 | 0.18 | 0.32 | 0.44 | 0.54 | 0.038 | ||||||
| 32 | 0.47 | 0.72 | 0.85 | 0.92 | 0.120 | ||||||
| 4 | 8 | 0.03 | 0.07 | 0.10 | 0.13 | 0.007 | 1 | 0.42 | 0.15 | n/a | |
| 16 | 0.05 | 0.09 | 0.13 | 0.17 | .0095 | ||||||
| 32 | 0.17 | 0.31 | 0.42 | 0.52 | 0.036 | ||||||
| Gumbel | 5 | 8 | 0.18 | 0.31 | 0.41 | 0.50 | 0.048 | 4 | 0.06 | 0.16 | 0.88 |
| 16 | 0.22 | 0.36 | 0.48 | 0.57 | 0.058 | ||||||
| 32 | 0.29 | 0.47 | 0.59 | 0.69 | 0.080 | ||||||
| 6 | 8 | 0.13 | 0.18 | 0.23 | 0.27 | 0.050 | 3 | 0.30 | 0.20 | 0.60 | |
| 16 | 0.33 | 0.45 | 0.54 | 0.60 | 0.140 | ||||||
| 32 | 0.43 | 0.57 | 0.66 | 0.72 | 0.190 | ||||||
| 7 | 8 | 0.30 | 0.44 | 0.54 | 0.61 | 0.110 | 2 | 0.07 | 0.15 | 0.70 | |
| 16 | 0.35 | 0.50 | 0.60 | 0.68 | 0.130 | ||||||
| 32 | 0.46 | 0.63 | 0.73 | 0.80 | 0.180 | ||||||
| 8 | 8 | 0.02 | 0.06 | 0.11 | 0.17 | .0021 | 2 | 0.22 | 0.18 | 1.5 | |
| 16 | 0.07 | 0.17 | 0.30 | 0.42 | 0.006 | ||||||
| 32 | 0.11 | 0.27 | 0.44 | 0.59 | 0.010 | ||||||
| 9 | 8 | 0.17 | 0.28 | 0.36 | 0.43 | 0.049 | 2 | 0.29 | 0.25 | 0.81 | |
| 16 | 0.43 | 0.62 | 0.74 | 0.82 | 0.140 | ||||||
| 32 | 0.56 | 0.76 | 0.86 | 0.92 | 0.200 | ||||||
| 10 | 8 | 0.02 | 0.06 | 0.10 | 0.15 | .0018 | 1 | 0.29 | 0.12 | 1.5 | |
| 16 | 0.03 | 0.07 | 0.13 | 0.17 | .0023 | ||||||
| 32 | 0.07 | 0.17 | 0.30 | 0.42 | 0.006 | ||||||
| Frank | 11 | 8 | 0.05 | 0.09 | 0.13 | 0.17 | 0.010 | 3 | 0.03 | 0.14 | 1.5 |
| 16 | 0.09 | 0.17 | 0.24 | 0.30 | 0.020 | ||||||
| 32 | 0.19 | 0.32 | 0.42 | 0.50 | 0.043 | ||||||
| 12 | 8 | 0.19 | 0.32 | 0.43 | 0.51 | 0.044 | 3 | 0.08 | 0.16 | 1.5 | |
| 16 | 0.26 | 0.43 | 0.54 | 0.63 | 0.065 | ||||||
| 32 | 0.31 | 0.49 | 0.61 | 0.69 | 0.080 | ||||||
| 13 | 8 | 0.07 | 0.13 | 0.18 | 0.23 | .0146 | 3 | 0.13 | 0.21 | 1.5 | |
| 16 | 0.18 | 0.31 | 0.41 | 0.49 | 0.042 | ||||||
| 32 | 0.33 | 0.52 | 0.64 | 0.72 | 0.087 | ||||||
| 14 | 8 | 0.18 | 0.31 | 0.41 | 0.49 | 0.042 | 2 | 0.04 | 0.19 | 1.5 | |
| 16 | 0.29 | 0.47 | 0.59 | 0.67 | 0.075 | ||||||
| 32 | 0.42 | 0.62 | 0.74 | 0.82 | 0.120 | ||||||
| 15 | 8 | 0.03 | 0.06 | 0.08 | 0.11 | 0.006 | 2 | 0.31 | 0.13 | 1.5 | |
| 16 | 0.05 | 0.09 | 0.13 | 0.19 | 0.010 | ||||||
| 32 | 0.15 | 0.27 | 0.36 | 0.44 | 0.035 | ||||||
| 16 | 8 | 0.53 | 0.74 | 0.84 | 0.90 | 0.170 | 0 | 0.01 | 0.15 | 1.5 | |
| 16 | 0.53 | 0.75 | 0.85 | 0.91 | 0.175 | ||||||
| 32 | 0.55 | 0.75 | 0.86 | 0.91 | 0.178 | ||||||
Table 3 also contains three metrics that seek to measure how difficult finding the MTC might be in each scenario. The first value, Nc, is the number of combinations with DLT rates within 10 points of the target η, the second value, MSE, denotes the mean sum-of-squared-errors for the fit of the linear model log[− log(1 − pdj)] = β0 + exp(β1)dj, and the third value, SD, is the sample standard deviation of the 12 DLT rates. Thus, smaller values of Nc and SD would indicate greater difficulty of finding the MTC and larger values of MSE would indicate that the linearity assumed in our model may be suspect and lead to a poorer ability of correctly identifying an MTC.
We simulated patients to have exponentially distributed inter-arrival times with a mean of two weeks, and we divided all the follow-up times by 10 to achieve better numeric stability for our model. When a new patient is enrolled, an interim analysis is performed in which a single chain of 6, 000 samples, after a burn-in of 4, 000 samples, is drawn from the posterior distribution for each parameter. These posterior draws are then used to determine the dose and schedule assigned to the new patient as well as any dose and/or schedule reassignments for each currently enrolled patient still being followed. We then simulate for each a binary indicator of DLT using the method outlined in the Supplementary Materials depending upon the scenario examined. If a patient is simulated to have a DLT, the time of the DLT is drawn uniformly from the interval [4 + 24(k − 1), 4 + 24k] under their assigned schedule k, which also implies that all possible DLTs occur by ω = 116 days. We did perform simulations of our design using our assumed model to simulate DLTs and came to similar final conclusions, and we have omitted those results for brevity.
We compared the performance of our approach that allows for patient reassignment (Design A) with the traditional approach that does not allow for patient reassignment (Design B). We evaluated the performance of both approaches by comparing the correct selection frequency at the end of the study, the mean proportion of patients assigned to each dose-schedule combination and the mean proportion of patients who experienced DLTs. We performed 1, 000 simulations in each scenario; our computer code is available upon request.
3.2 Simulation Results
Table 4 contains a summary of the performance of Design A (with reassignment) and Design B (without reassignment) in the 16 scenarios described in Table 3. For each design, this summary is a series of eight columns. The first four columns describe the proportion of simulations in which the MTC selected at the end of the study was not found, had a DLT rate more than 10 points below the desired DLT rate η (column “L”), within 10 points of η (column “In”), or more than 10 points above η (column “H”). The next three columns have a similar interpretation related to the average percentage of dose-schedule assignments during the study. The eighth column, labeled “DLT” is the average of the proportion of observed DLTs among the 1,000 simulations.
Overall, we are able to identify acceptable dose-schedule combinations at the end of the study in a majority of simulations in the first 15 scenarios, whether or not reassignment is used, as well as terminate the study early in scenario 16. These results are not surprising, as the primary goal of reassignment is to optimize the assignments of patients enrolled in the study, rather than improve the final decision at the end of the study. Scenarios 4, 8, 9, and 10 have the lowest percentages of identifying the MTC at an acceptable combination, which is partially explained by the fact that these scenarios have only 1 or 2 acceptable combinations to choose from. These scenarios also have some of the largest values of MSE, indicating that the assumption of linearity in our model is suspect. Nonetheless, we emphasize that all 15 scenarios have DLT rates that come from models that are different from our assumed model, so that our approach works well even when the model is misspecified.
With regard to patient assignments during the study, we see that including reassignment leads to a higher proportion of patients assigned to acceptable combinations than without reassignment. For example, Design A assigned 58% of the patients to acceptable combinations in scenario 4, compared with only 29% for Design B, and the corresponding percentages in scenario 10 are 53% and 26%, respectively. Moreover, in all 15 scenarios, the average DLT rate when using reassignment is never more than the average observed DLT rate without reassignment and is always close to the desired DLT rate. Although Scenarios 7, 9 and 10 have 33%, 40% and 31% of patients, respectively, assigned to toxic combinations, most of the combinations in Scenarios 7 and 9 are overly toxic, and exposing a higher proportion of patients to toxic combinations in these scenarios seems unavoidable. Furthermore, in Scenario 10, all of the assignments to toxic combinations were to combinations with DLT rates in the range of 40% – 42%, and in Scenario 9, 25% of patients were assigned to combinations with DLT rates between 40% and 45%. We also conducted simulations using the EWOC distance measure described in Section 2.5, but due to space limitations, we omit these results. We found that using the EWOC distance measure led to treating fewer patients at overly toxic combinations in some scenarios, but this apparent increase in safety came with a reduced ability of finding the MTC at the end of the trial.
The final five columns of Table 4 contain a summary of the number of reassignments per patient that occurred in each of the 16 scenarios. Rates of reassignment above 0.60 were seen in scenarios 4, 8, 10, 11, and 15. Although the explanation for the high rate of reassignment is not immediately obvious, a partial explanation is that acceptable combinations in these scenarios appear with longer schedules of the highest dose, with even longer schedules then becoming overly toxic. In contrast, Scenario 1 has a much lower rate of reassignment because that scenario had no overly toxic combinations. We also see that less than two reassignments occurred per patient on average in all the scenarios and just under six reassignments was the maximum number of reassignments per patient on average in all scenarios.
We also examined the sensitivity of our design to the maximum sample size by repeating our simulations using sample sizes of 50 and 70, the results of which are summarized in Table 5. The results show that decreasing the sample size from 60 to 50 may result in a nontrivial loss is selecting correct combinations in Scenarios 4, 10 and 15. However, increasing the sample size from 60 to 70 only produces a minor increase in the selection of correct combinations. Therefore, we selected a maximum number of 60 patients for this study.
Table 5.
Simulation results for Design A with sample sizes of N = 50 and N = 70. For each design, columns “Selection” gives the percentage of identifying three categories of combinations as the MTC: unacceptable inefficacious combinations (“L”); acceptable combinations (“In”) and too toxic combinations (“H”). For each design, columns “Assignment” gives the mean proportion of patients assigned to the three categories, columns “DLT” give the mean proportion of patients who experienced DLTs.
| Scen | Design A with N = 50 | Design A with N = 70 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Selection
|
Assignment
|
Selection
|
Assignment
|
|||||||||||||
| None | L | In | H | L | In | H | DLT | None | L | In | H | L | In | H | DLT | |
| 1 | 0 | 6 | 94 | 0 | 11 | 89 | 0 | 27 | 0 | 5 | 95 | 0 | 9 | 91 | 0 | 27 |
| 2 | 0 | 17 | 79 | 4 | 21 | 58 | 21 | 31 | 0 | 11 | 86 | 2 | 17 | 66 | 17 | 31 |
| 3 | 0 | 16 | 66 | 17 | 24 | 49 | 26 | 33 | 0 | 12 | 73 | 15 | 20 | 56 | 23 | 32 |
| 4 | 0 | 32 | 45 | 24 | 20 | 54 | 26 | 30 | 0 | 25 | 57 | 18 | 18 | 61 | 21 | 30 |
| 5 | 2 | 3 | 78 | 18 | 8 | 58 | 32 | 35 | 1 | 2 | 82 | 15 | 7 | 66 | 26 | 34 |
| 6 | 1 | 19 | 55 | 25 | 18 | 50 | 31 | 35 | 1 | 12 | 64 | 22 | 16 | 55 | 27 | 34 |
| 7 | 9 | 0 | 66 | 25 | 0 | 55 | 38 | 37 | 9 | 0 | 73 | 18 | 0 | 61 | 32 | 35 |
| 8 | 0 | 16 | 55 | 30 | 16 | 54 | 30 | 33 | 0 | 12 | 57 | 31 | 14 | 61 | 25 | 32 |
| 9 | 4 | 17 | 48 | 31 | 20 | 34 | 43 | 36 | 3 | 16 | 53 | 28 | 19 | 39 | 40 | 35 |
| 10 | 0 | 28 | 50 | 22 | 18 | 48 | 34 | 30 | 0 | 26 | 54 | 20 | 17 | 54 | 29 | 30 |
| 11 | 0 | 14 | 74 | 12 | 16 | 60 | 24 | 31 | 0 | 10 | 80 | 11 | 15 | 65 | 20 | 31 |
| 12 | 3 | 5 | 68 | 25 | 10 | 53 | 35 | 36 | 2 | 4 | 78 | 17 | 9 | 62 | 28 | 35 |
| 13 | 1 | 15 | 64 | 20 | 15 | 59 | 25 | 33 | 0 | 13 | 70 | 16 | 14 | 66 | 20 | 32 |
| 14 | 3 | 9 | 54 | 34 | 12 | 54 | 31 | 36 | 1 | 7 | 61 | 31 | 11 | 61 | 26 | 35 |
| 15 | 0 | 22 | 68 | 10 | 18 | 58 | 23 | 30 | 0 | 18 | 75 | 7 | 15 | 66 | 18 | 30 |
| 16 | 83 | 0 | 0 | 17 | 0 | 1 | 42 | 24 | 89 | 0 | 0 | 11 | 0 | 1 | 34 | 19 |
Recall that we found that using a value of σ = 2 for the prior variances of the model parameters was insensitive to the skeleton used. To confirm this statement, we do not present the results when using Skeleton 1 in a tabular format like that of Table 4. Instead, Figure 1 contains a visual summary of the percentage of simulations in which the MTC was selected at an acceptable combination (left plot) and the percentage of patients assigned to acceptable combinations (right plot) in each of the 15 scenarios. As we found in Table 4, we are able to identify the MTC well whether or not reassignment is allowed, but that inclusion of reassignment greatly improves the treatment assignment of patients enrolled in the study.
Figure 1.
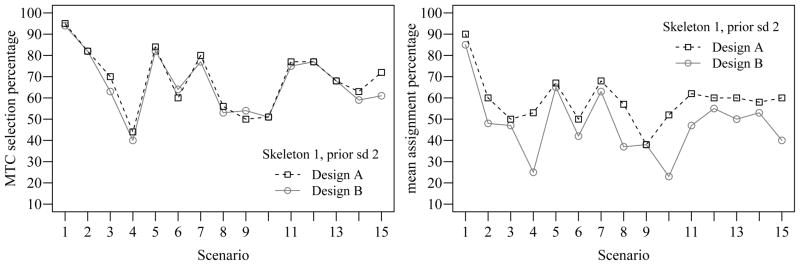
Comparison between Design A and B using Skeleton 1 and calibrated prior standard deviation 2.
4. DISCUSSION
In our methods, we reassigned the dose and/or schedule of each enrolled patient only when a new patient was enrolled in order to optimize the treatment of each patient but maintain a feasible level of computation. As a result, with an average arrival of a new patient every 14 days relative to a follow-up of 116 days in our simulations, we considered approximately no more than eight reassignments with each new enrollment. In a study with much faster accrual, there would be many more possible reassignments to consider at each new enrollment and many of the patients could have several reassignments occurring during their treatment. Investigators may feel that this level of possible reassignment impractical, requiring a different rule for determining when reassignment is possible. An interesting area of research is to compare our approach to other reassignment strategies to determine when fewer reassignments are allowed, yet do not lead to significantly worsened operating characteristics.
Although we restricted the estimate of the MTC at the end of the trial to only exist among dose-schedule regimens with dose constant within patient, our methods are flexible enough to regimens with dose variations within-patient that ultimately might provide a better MTC estimate since we are considering a richer set of candidate strategies. In addition, we could consider multiple MTC estimates each of which that are qualitatively different from each other. For example, we could consider two completing MTC estimates, one with a few administrations of a higher dose and another with many administrations of a lower dose. It is very possible that one schedule may be more effective or easier to administer and these facts are not yet part of our decision-making process. Certainly our methods can be generalized to incorporate more information and further the process of discovering new drugs and how to best administer them, and is an exciting avenue of research. Furthermore, our methods belong to the family of dynamic treatment regimes (Murphy 2003) and use of additional patient information, such as a key biomarker for response or risk factors for lack of response, might further the cause to “personalize” the dose and schedule assigned to each patient. However, the major limiting factor for all these extensions is the small sample size used in most early-phase clinical trials.
We introduce our design in the setting of dose-schedule finding studies, although our methods could be easily applied to other settings. If the schedule were fixed while the dose varied, our design would be similar to the TITE-CRM in which the weight function would be determined by the functional form of the hazard function of a single administration in our model. In Phase I/II studies, one can easily adapt our method to the work of Yuan and Yin (2009) to model late-onset toxicity/efficacy and introduce intra-patient dose changes. Similar modifications could be made to apply our approach to trials of combinations of two agents by specifying the hazard function of the toxicity or efficacy after a single administration to be a function of doses of both agents. However, the model that takes account of the joint distribution of toxicity and efficacy as a function of possibly multiple doses is not immediately obvious and should be carefully chosen. Lastly, in the motivating azacitidine trial, the highest dose and longest schedule was reached with no evidence of unacceptable toxicity and investigators decided to add more doses to the trial. The flexibility of our model would allow one to adaptively estimate the DLT rates of other doses and/or schedules to determine which, if any, might be added to the trial once it has begun.
Supplementary Material
Acknowledgments
The research is supported by National Institute of Health grant 5R01CA148713. The authors thank the editor, associate editor, and a referee for their constructive and helpful comments that substantially improved the manuscript.
Footnotes
Additional Results: The online supplemental file consists of three main parts. The first part introduces the models and algorithms we used for simulating true DLT rates. The second part describes the process of prior variance calibration. The third part displays an example to illustrate patient reassignments in our design.
Contributor Information
Jin Zhang, Email: zhjin@umich.edu.
Thomas M. Braun, Email: tombraun@umich.edu.
References
- Babb J, Rogatko A, Zacks S. Cancer phase I clinical trials: efficient dose escalation with overdose control. Statistics in Medicine. 1998;17:1103–1120. doi: 10.1002/(sici)1097-0258(19980530)17:10<1103::aid-sim793>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- Braun TM. Generalizing the TITE-CRM to Adapt for Early- and Late-Onset Toxicities. Statistics in Medicine. 2005;20:153–169. doi: 10.1002/sim.2337. [DOI] [PubMed] [Google Scholar]
- Braun TM, Thall PF, Nguyen H, de Lima M. Simultaneously Optimizing Dose and Schedule of a New Cytotoxic Agent. Clinical Trials. 2007;4:113–124. doi: 10.1177/1740774507076934. [DOI] [PubMed] [Google Scholar]
- Braun TM, Yuan Z, Thall PF. Determining a Maximum-Tolerated Schedule of a Cytotoxic Agent. Biometrics. 2005;61:335–343. doi: 10.1111/j.1541-0420.2005.00312.x. [DOI] [PubMed] [Google Scholar]
- Chen M, Ibrahim J, Sinha D. A New Bayesian Model for Survival Data with a Surviving Fraction. Journal of American Statistical Association. 1999;94:909–919. [Google Scholar]
- Cheung YK, Chappell R. Sequential Designs for Phase I Clinical Trials with Late-Onset Toxicity. Biometrics. 2000;56:1177–1182. doi: 10.1111/j.0006-341x.2000.01177.x. [DOI] [PubMed] [Google Scholar]
- de Lima M, Giralt S, Thall PF, Silva L, Jones RBKK, Braun TM, Nguyen HQ, Champlin R, Garcia-Manero G. Maintenance Therapy With Low-Dose Azacitidine After Allogeneic Hematopoietic Stem Cell Transplantation for Recurrent Acute Myelogenous Leukemia or Myelodysplastic Syndrome: A Dose and Schedule Finding Study. Cancer. 2010;116:5420–5431. doi: 10.1002/cncr.25500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hougaard P. Analysis of Multivariate Survival Data. New York: Springer; 2000. [Google Scholar]
- Liu C, Braun TM. Parametric Non-Mixture Cure Models for Schedule Finding of Therapeutic Agents. The Journal of the Royal Statistical Society, Series C (Applied Statistics) 2009;58:225–236. doi: 10.1111/j.1467-9876.2008.00660.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy SA. Optimal Dynamic Treatment Regimes. Journal of the Royal Statistical Society, Series B. 2003;65:331–336. [Google Scholar]
- O’Quigley J, Pepe M, Fisher L. Continual Reassessment Method: A Practical Design for Phase I Clinical Trials in Cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- Raftery AE, Madigan D, Hoeting JA. Bayesian Model Averaging for Linear Regression Models. Journal of the American Statistical Association. 1997;92:179–191. [Google Scholar]
- Rosenthal J. AMCMC: An R Interface for Adaptive MCMC. Computational Statistics and Data Analysis. 2007;51:5467–5470. [Google Scholar]
- Tsiatis A. A Nonidentiability Aspect of the Problem of Competing Risks. Proceedings of the National Academy of Sciences in USA. 1975;72:20–22. doi: 10.1073/pnas.72.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodikov A, Ibrahim J, Yakovlev A. Estimating Cure Rates from Survival Data: an Alternative to Two-component Mixture Models. Journal of American Statistical Association. 2003;98:1063–1078. doi: 10.1198/01622145030000001007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin G, Yuan Y. Bayesian Model Averaging Continual Reassessment Method in Phase I Clinical Trials. Journal of the American Statistical Association. 2009;104:954–972. [Google Scholar]
- Yuan Y, Yin G. Bayesian Dose Finding by Jointly Modelling Toxicity and Efficacy as Time-to-event Outcomes. The Journal of the Royal Statistical Society, Series C (Applied Statistics) 2009;58:719–736. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


