Abstract
Cryo-electron tomography allows the visualization of macromolecular complexes in their cellular environments in close-to-live conditions. The nominal resolution of subtomograms can be significantly increased when individual subtomograms of the same kind are aligned and averaged. A vital step for such a procedure are algorithms that speedup subtomogram alignment and improve accuracy for reference-free subtomogram classification, which will facilitate automation of tomography analysis and overall high throughput in the data processing. In this paper, we propose a fast rotational alignment method that uses the Fourier equivalent form of a popular constrained correlation measure that considers missing wedge corrections and density variances in the subtomograms. The fast rotational search is based on 3D volumetric matching, which significantly improves the rotational alignment accuracy in particular for highly distorted subtomograms with low SNR and tilt angle ranges in comparison to a fast rotational alignment based on matching of projected 2D spherical images. We further integrate our fast rotational alignment method in a reference free iterative subtomogram classification scheme, and propose a local feature enhancement strategy in the classification process. We can demonstrate that the automatic method can be used to successfully classify a large number of experimental subtomograms without the need of a reference structure.
Keywords: Cryo-electron tomography, subtomogram alignment and classification, fast rotational matching
1. Introduction
Cryo-electron tomography (cryoET) enables the visualization of a cell’s interior under close to live conditions (Beck et al., 2009; Nickell et al., 2006; Beck et al., 2011). The 3D tomogram is reconstructed from a set of two-dimensional micrographs, which are collected by tilting the sample around a single rotational axis. The reconstructed tomograms have typically resolutions that are sufficient to detect individual macromolecular complexes in their cellular context (Nicastro et al., 2006; Kühner et al., 2009; Medalia et al., 2002; Komeili et al., 2006). Once identified, subtomograms of the same complexes can then be aligned and averaged to achieve a higher nominal resolution and signal-to-noise ratio (SNR) of their 3D density maps (Frank, 2006).
Subtomogram alignment and subsequent classification is an integral part of this strategy. The alignment relies on the search for the best relative transformation of one subtomogram with respect to the second that maximizes the similarity measure between them. However, several factors make the alignment of subtomograms challenging. Tomograms contain relatively high noise levels (Frangakis and Förster, 2004) and are typically of low non-isotropic resolution (≥ 4 nanometers after averaging (Lucic et al., 2005; Förster et al., 2005; Briggs et al., 2009)). Moreover, tomograms are subject to distortions. One source of distortions is the variation of the Contrast Transfer Function (CTF) within and between individual micrographs used in the 3D density reconstruction (Förster et al., 2008). More critical are orientation specific distortions as a result of the so-called missing wedge effect, which is a consequence of the limited data collection due to the limited tilt ranges when collecting individual micrographs (with a maximal tilt range from −70 to +70 degrees). As a result, in Fourier space structure factors are missing in a characteristic wedge shaped region. This missing data leads to anisotropic resolution and different kinds of artifacts that depend on the structure of the object and its orientation with respect to the direction of the tilt-axis.
Several subtomogram alignment approaches take into account the missing wedge effects by using a constrained similarity measure (Förster et al., 2008; Bartesaghi et al., 2008; Amat et al., 2010; Volkmann, 2010). For instance, Förster et al. (2008) introduced a correlation metric that constrains the similarity measure only to the structure factors (i.e. Fourier coefficients) common to both pairs of subtomograms. Because sample thickness can be variable in a tomogram, this method also considers the local contrast difference in individual subtomograms by normalizing the similarity measure with respect to the mean and variance of the intensity distributions in both subtomograms (Förster et al., 2008).
In another method the influence of noise has been reduced in the alignment process by considering only a small percentage of high magnitude Fourier coefficients when computing the cross-correlation based similarity metric and therefore this method excludes those coefficients that are expected to be dominated by noise (Amat et al., 2010).
Most subtomogram alignment methods use an exhaustive scanning over all rotations of one subtomogram relative to the second to identify the orientation that maximizes the similarity metric (e.g. Förster et al., 2008; Amat et al., 2010; Volkmann, 2010). The scanning is performed at fixed angle intervals and at each sampled rotation a fast translational search is performed using the Fast Fourier Transform (FFT) (Frank, 2006). For highly accurate alignments, relatively small sampling intervals are needed, which significantly increases the cost of the rotational search. Exhaustive rotational scanning is computationally intensive, which limits its applicability when large data sets need to be aligned for subtomogram classification. This problem becomes even more relevant with increasing cryoET resolutions (Murata et al., 2010) and resulting larger subtomogram volumes. Therefore development of new algorithms that improve speed and accuracy of subtomogram alignment is a vital step in automation of tomography analysis and overall high throughput in data processing and reconstruction.
To enhance computational efficiency, Bartesaghi et al. (2008) use a fast rotational matching in which the best rotational transformation is computed rapidly using the convolution theorem within the Spherical Harmonics framework. Each subtomogram is transformed into a two-dimensional spherical image by integrating the magnitude of Fourier coefficients positioned along rays through the Fourier space origin. However, such a projection of the Fourier coefficient magnitudes onto the points of a unit sphere increases ambiguities in the alignment. Moreover, the applied alignment dissimilarity score is not normalized with respect to the mean and variance of two subtomograms, therefore does not consider the non-uniformness of the tomogram.
In this paper, we formulate a Fourier-space equivalent similarity measure for the normalized constrained correlation introduced by Förster et al. (2008) and combine it with a fast rotational alignment based on 3D volumetric rotational matching. We adapt a 3D volumetric rotational matching method that was previously used for fitting atomic structures into density maps (Kovacs and Wriggers, 2002; Garzon et al., 2007) and extend its applicability to subtomogram alignments by including missing wedge effects in the matching score. This method significantly increases the alignment speed in comparison to the standard exhaustive rotational scanning approach (Förster et al., 2008). It also significantly improves the alignment accuracy for subtomograms with low SNR and small tilt angle ranges in comparison to the fast rotational alignment approach based on the rotational matching of 2D spherical images (Bartesaghi et al., 2008). Moreover, using a Fourier equivalent score of the normalized constrained correlation corrects also for the non-evenness of contrast in tomograms.
As test case for our fast alignment method we perform reference-free subtomogram classifications. Reference-free classification is fundamental for providing an unbiased structural categorization of the macromolecular complexes in subtomograms because the initial classification is directly derived from the input data. Several types of reference-free subtomogram classification approaches exist, including methods based on maximum likelihood approaches (e.g. Scheres et al., 2009), methods using rotation invariant subtomogram features (Xu et al., 2009, 2011a), and finally methods that rely on iterative successive alignment and classification steps (i.e. the alignment-through-classification approach) (Bartesaghi et al., 2008; Winkler, 2007).
Our alignment method is sufficiently fast for carrying out all pair-wise alignments even for a relatively large number of subtomograms (e.g. a few thousands). Therefore we are able to embed the method into the alignment-through-classification framework, which is widely popular in 2D single particle averaging. Furthermore, we propose an additional generic and automatic local feature enhancement step to the framework. This step emphasizes the most discriminative local features between subtomograms, which improves the clustering performance. Moreover, we also integrate an automatic optimal cluster selection into the framework. We can demonstrate that the automated framework can successfully classify experimental subtomograms even for highly similar but distinct complexes.
2. Materials and methods
2.1. Fourier space equivalence of constrained correlation
Two subtomograms f and g are defined as two integrable functions . To calculate the similarity between two subtomograms, Förster et al. (2008) proposed a constrained correlation with missing wedge correction. It is based on a transform of the subtomograms that eliminates the Fourier coefficients in the missing wedge region. This goal is achieved by introducing a binary missing wedge mask function as . The missing wedge mask function defines valid and missing Fourier coefficients in Fourier space. For example, in single tilt electron tomography with tilt angle range ±θ, the missing wedge mask function can be defined as , where is the indicator function. Given , the real space subtomogram then excludes any coefficients located inside of any of the two missing wedge regions and is defined as
| (1) |
where ℜ denotes the real part of a complex function; ΛR is the rotation operator such that (ΛRe)(x) := e[R−1(x)] for any function is the Fourier transform operator; and ensures that only structure factors are considered that are defined in both subtomograms, therefore excluding any structure factors that are located in the missing wedge region of any of the two subtomograms. Correspondingly, the real space function of the second subtomogram is defined as
| (2) |
where τa is defined as the translational operator so that (τag)(x) := g(x − a) with a . Then the normalized constrained correlation value between two subtomograms f and g that also considers the missing-wedge corrections can be calculated as (Förster et al., 2008)
| (3) |
where μ is the mean operator that returns the mean value of a function h, and is defined as . is the size operator, and correspondingly returns the size of the subtomogram h (i.e. the total number of voxels in the subtomogram). Because this similarity measure is normalized by the mean and variance of intensity values of both subtomograms c considers the local contrast differences for individual regions in a tomogram.
To allow a fast rotational alignment of the local constrained similarity measure, we formulate an equivalent correlation measure directly in Fourier space. Given any two complex valued functions , according to the basic properties of the Fourier transform, we can formulate
| (4) |
where denotes the complex conjugate of q. Here the mean operator μ for complex Fourier space functions is defined in the same way as μ for real space functions. In addition,
| (5) |
Because , the Fourier transform of a mean subtracted function can always be obtained by changing to zero. Therefore, we assume and , correspondingly. When the Fourier transform is realized using FFT, and and have the same size (i.e. , the Fourier space form of c is calculated as
| (6) |
which is the real part of a complex valued function. According to the basic properties of the Fourier transform, we can reformulate c as
| (7) |
When using a binary mask , then . In summary, the general outcome of this section is the formulation of the constrained Fourier-space correlation measure c, which includes a missing-wedge correction and is normalized.
2.2. Fast rotational sampling by spherical harmonics convolution
Because we have formulated the constrained correlation measure in Fourier space it is possible to apply a fast rotational matching, which generates a small number of candidate rotational angles that are used for a subsequent fast translational alignment. Finding a good approximate translation-invariant rotational alignment is key in such a strategy. As mentioned in the last section, c is the real part of a complex valued function where the translation differences between subtomograms only lead to differences in the phase part of the complex valued function. Therefore, similar to an approach of (Bartesaghi et al., 2008), the fast rotational search can first be performed by removing phase information from c. Specifically, from Equation 7, a constrained local score can then be defined so that only magnitudes of the Fourier coefficients are included:
| (8) |
This score is then used in fast rotational matching.
In the previously published approach by Bartesaghi et al. (2008) fast rotational alignment is achieved by projecting all the Fourier coefficient magnitudes positioned along rays through the Fourier space origin onto the corresponding point on the unit sphere surface. Then 2D matching is applied on the corresponding two 2D spherical images (derived from the projected unit sphere surfaces). However, the compression of the Fourier coefficient magnitude values increases ambiguity in the alignment, which may cause problems in the alignment especially for subtomograms with high noise level (Amat et al., 2010).
Instead, here we apply a fast 3D volumetric rotational matching, previously used for efficient fitting of atomic structures into cryo-electron microscopy density maps (Kovacs and Wriggers, 2002) but adapt it here for subtomogram alignment by expanding it to include missing wedge corrections and density variances. It can be seen that Equation 8 can be formulated as being composed of three rotational correlation functions of the form , where p and q are component functions1. Specifically, we can represent c’ as
| (9) |
where , , , , , and .
When represented in spherical coordinates, the p and q components of these three functions cR can be approximated by a Spherical Harmonics (SH) expansion. Following (Garzon et al., 2007) the p and q components in Equation 9
where B is the bandwidth, and Clm(r) are the coefficients associated with the complex-valued spherical harmonic function Ylm(β, λ) with degree l and order m, where r, β and λ are the radial distance, co-latitude and longitude, respectively, which define the position in spherical coordinate. When a suitable parameterization of the three-dimensional rotational group is achieved, the rotation correlation function of all sampled rotations R can be represented as an inverse FFT of a 3D array of the of integrals as follows (Kovacs and Wriggers, 2002; Garzon et al., 2007):
| (10) |
where are real coefficients defining the elements of the Wigner small d-matrix evaluated at 90° (Biedenharn et al., 1981).
As a consequence of the above formulation the cross-correlation functions can be efficiently sampled by using FFT simultaneously over all sampled rotations (Kovacs and Wriggers, 2002). The sampling is given as twice the bandwidth used in the harmonic transformation of the maps. Therefore c’ can be efficiently computed over all sampled rotations R. The set of candidate rotations are then obtained by identifying the local maxima of c’ with respect to the rotational degrees of freedom. To obtain the optimal translation, a fast translational search is performed for each candidate rotation over the full correlation function c by using FFT. Finally, the best combination of rotation and translation is chosen.
2.3. Reference-free automatic classification and averaging of subtomograms with automatic local feature enhancement
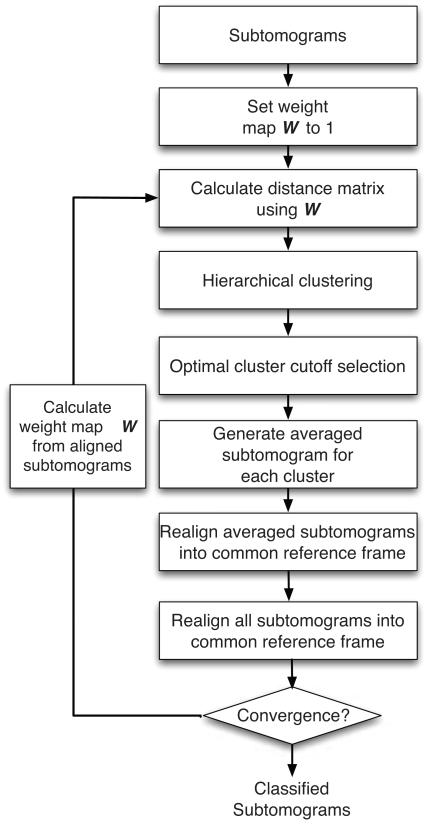
One of the main applications of fast subtomogram alignment is the classification of subtomograms into distinct complexes and the subsequent averaging of the classified subtomograms to determine a higher nominal resolution for the resulting density maps of macromolecular complexes (Bartesaghi et al., 2008; Förster et al., 2005). Before describing in detail the automatic reference-free subtomogram classification method (Figure 1), we first introduce an automatic local feature enhancement strategy, which will improve considerably the classification performance .
Figure 1.
Reference-free iterative subtomogram classification scheme with feature enhancement.
2.3.1. Automatic local feature enhancement strategy for subtomogram classification
Clustering of the aligned subtomograms is one of the main components in reference free classifications. However, clustering is challenging when the differences between the subtomograms are subtle, for instance when subtomograms contain variants of the same complex. Variants may only differ in a few regions of the subtomogram due to conformational differences and/or additional binding partners in one isoform. For example, subtomograms of GroEL and GroEL/ES (Förster et al., 2008) differ only slightly and at low SNR their subtomograms are difficult to differentiate. To classify complex isoforms it would be beneficial to define a distance measure that automatically focuses on those subtomogram regions that are most discriminative while at the same time are not background noise.
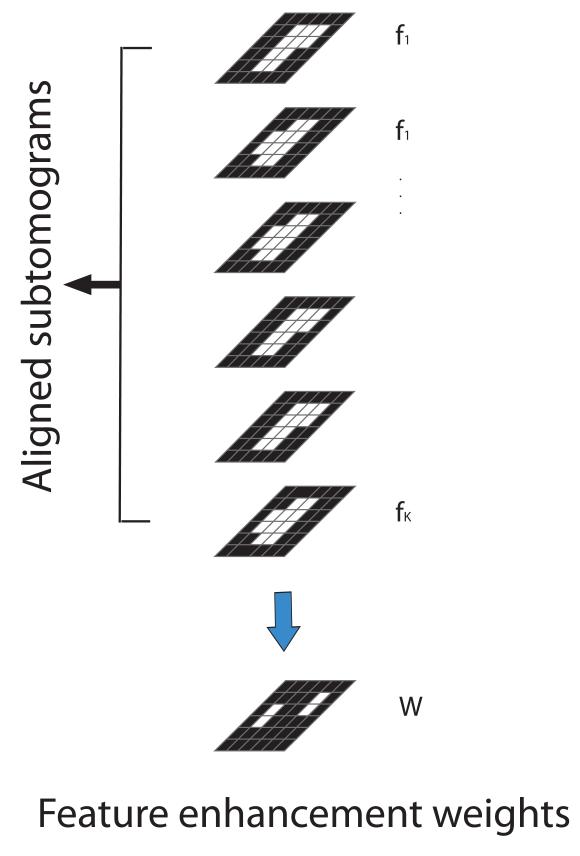
To achieve this goal we implement a local feature enhancement strategy by applying a real space weight mask to the constrained correlation measure (Figure 2). This weight mask reduces the influence of noise in empty regions and enhances the features that are most discriminative.
Figure 2.
Determining the feature enhancement map . Given a set of aligned subtomograms the feature enhancement for a given voxel is determined by a covariance measure of all voxel neighbors based on all aligned K subtomograms. The voxels are separated by the grid of gray lines.
For a given voxel x in an aligned subtomogram its weight is calculated as
| (11) |
where is the set of all neighbor voxels of x and COVxy is the covariance between voxel x and one of its neighbor voxels y. This covariance is defined as
| (12) |
where is the intensity value of voxel x in the kth subtomogram and is the mean intensity value of voxel x across all the K subtomograms . is defined accordingly. If the neighborhood region for voxel x is occupied predominantly by only one of the complex isoforms then voxels in this region tend to have high intensity values in all the subtomograms of this isoform, and low intensity values in all other subtomograms. Therefore, this region would have a large mean covariance value indicating that this neighborhood region can be effectively used to separate the subtomograms into distinct groups. Regions that are shared in all isoforms or regions that are highly variant in each subtomogram because they represent background noise have a low covariance value. This covariance measure therefore allows an effective way to enhance certain regions when calculating a distance measure based on the correlation between two maps. To incorporate the local feature enhancement, the constrained pairwise correlation measure between two subtomograms fj and fk can then be expressed as
| (13) |
with and , where τaj and ΛRj are translation and rotation of subtomogram j obtained at the iteration; (τak and ΛRk are defined accordingly).
2.3.2. Automatic iterative subtomogram classification and averaging with local feature enhancement
After having established the local feature enhancing map W we now describe the reference-free subtomogram classification. The classification process is performed in an iterative procedure containing 8 main steps (Figure 1):
Step 1
Calculation of a local feature enhancing map . The feature enhancing map is calculated from the aligned set of subtomograms in a cluster (Figure 2). However, at the initial step of the classification the subtomograms are not aligned and not clustered yet. In this case the elements of are set to 1. During each of the following iterations is recalculated from the aligned subtomograms.
Step 2
Calculation of a distance matrix using the feature enhancing map . To quantify the dissimilarity between two aligned subtomograms fj and fk we can calculate the Euclidean distance between the constrained transformation of fj and fk:
| (14) |
where and . Because of the subtomogram normalization, this constrained distance can be calculated from the constrained correlation:
| (15) |
To generate a distance matrix, all distances between all pairs of aligned subtomograms are calculated.
Step 3
Do hierarchical clustering. Based on the distance matrix in step 2, average linkage hierarchical clustering is applied (Johnson, 1967). Through hierarchical clustering a hierarchical tree is generated. In this tree, very similiar sub-tomograms are joined by short branches and increasingly different sub-tomograms by longer branches.
Step 4
Perform automatic cluster cutoff detection. In order to automatically determine the optimal set of clusters, we calculate the average Silhouette width for each clustering cutoff (Kaufman and Rousseeuw, 1990). The average Silhouette width is defined as follows. Assume that at a given clustering cutoff the input subtomograms are partitioned into k clusters S1, S2, …, Sk. Then the Silhouette width ωf of a single subtomogram f is defined as
| (16) |
where is the average dissimilarity between f and a subtomogram in a different cluster SJ that does not contain is the average dissimilarity between f and all subtomograms in the same cluster as f. The Silhouette width ranges between −1 and 1. The clustering cutoff is chosen that maximizes the average Silhouette width.
Step 5
Determine averaged tomogram for each cluster. After clustering, an averaged subtomogram template is generated by averaging all the aligned subtomograms in the same cluster.
Step 6
Alignment of averaged templates. In this step, all averaged cluster templates that are similar to each other are aligned to a common reference frame. First, all the templates are pairwise aligned using our fast alignment method and clustered using the constrained correlation defined in Equation 6 as similarity measure. Hierarchical clustering is combined with maximal average Silhouette to detect the optimal cutoff that result in a optimal set of template clusters. Then within each template cluster, all the averaged templates are aligned to the averaged template from the largest subtomogram cluster.
Step 7
Alignment of all subtomograms against the averaged subtomograms of each cluster. Every subtomogram is re-aligned to each of the averaged cluster templates and only the alignment with the best similarity score is then further considered. In this step it is possible that subtomograms are re-classified to different clusters.
Step 8
Testing for convergence. The convergence of the classification process is terminated when the maximum average Silhouette width calculated from the clustering reaches a plateau with increasing number iterations. If convergence is not reached the process is iteratively repeated starting with step 1.
2.4. Generating simulated cryo-electron tomograms
For a reliable assessment of the method, subtomograms must be generated by simulating the actual tomographic image reconstruction process, allowing the inclusion of noise, tomographic distortions due to missing wedge, and electron optical factors such as Contrast Transfer Function (CTF) and Modulation Transfer Function (MTF). We follow a previously applied methodology for simulating the tomographic image formation mechanism as realistically as possible (Beck et al., 2009; Förster et al., 2008; Nickell et al., 2005; Xu et al., 2011a). The electron optical density of a macromolecule is proportional to its electrostatic potential and the density map can be calculated from the atomic structure by applying a low pass filter at a given resolution. Here, density maps are generated at 4 nm resolution using the PDB2VOL program of the Situs 2.0 package (Wriggers et al., 1999) with voxel length of 1 nm. These initial density maps are then used as samples for simulating electron micrograph images at different tilt angles. In cryoET the sample is tilted in small increments around a single-axis. At each tilt angle a simulated micrograph is generated from the sample. As a result our data contains a wedge-shaped region in Fourier space for which no structure factors have been measured (i.e., the missing wedge effect), similar to experimental measurements. The missing wedge effect leads to distortions of the density maps. These distortions depend on the structure of the object and its orientation with respect to the direction of the tilt-axis. To generate realistic micrographs, noise is added to the images according to a given SNR level, defined as the ratio between the variances of the signal and noise (Förster et al., 2008). Moreover, the CTF and MTF describe distortions from interactions between electrons and the specimen and distortions due to the image detector (Frank, 2006; Nickell et al., 2005). Therefore, the resulting image is convoluted with a CTF, which describes the imaging in the transmission electron microscope in a linear approximation. Any negative contrast values beyond the first zero of the CTF are eliminated. We also consider the MTF of a typical detector used in tomography, and convolute the density map with the corresponding MTF. Typical acquisition parameters that were also used during actual experimental measurements (Beck et al., 2009) were used: voxel grid length = 1 nm, the spherical aberration = 2 × 10−3m, the defocus value = −4 × 10−6m, the voltage = 200kV, the MTF corresponded to a realistic electron detector (McMullan et al., 2009), defined as sinc(πω/2) where ω is the fraction of the Nyquist frequency. Finally, we use a backprojection algorithm (Nickell et al., 2005) to generate a tomogram from the individual 2D micrographs that were generated at the various tilt angles (Beck et al., 2009; Xu et al., 2011a). To test the influence of increasing noise, we add different amount of noise to the images, so that the SNRs range between 0.1 and 0.001, respectively (Figure 3).
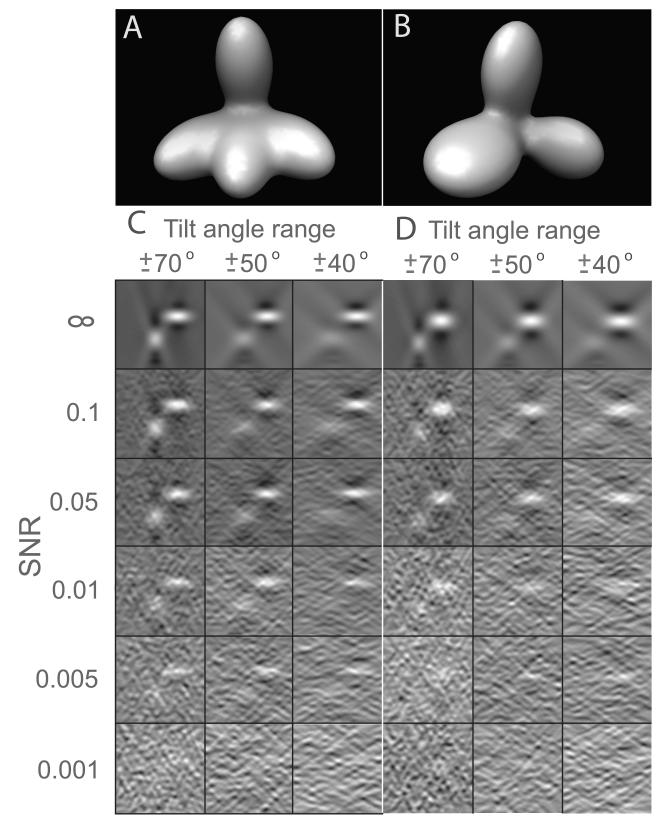
Figure 3.
Tomograms of phantom models simulated at various signal-to-noise ratios (SNR) and tilt angles ranges. Tomograms are of size 643 voxels. (A) Isosurface of model 1 consisting of four Gaussian functions of the same shape. The principal axis of three Gaussian functions are in the same plane, while the principal axis of the fourth Gaussian function is positioned orthogonal to the first three Gaussian functions. (B) Isosurface of model 2 consisting of three Gaussian functions with different intensity distributions. (C) Slices taken along direction through the tomograms at different levels of noise and tilt angle ranges. The Isosurface is plotted using the Chimera software (Pettersen et al., 2004).
2.4.1. Benchmark set
The classification is tested on simulated tomograms of two phantom models (Figure 3) and four different protein complexes taken from the Protein Data Bank (PDB) (Berman et al., 2000), as well as experimentally determined subtomograms (see text for details). For each simulated tomogram complexes were randomly oriented and placed and tomograms simulated at 6 different SNRs (0.001 0.005, 0.01, 0.05, 0.1, ∞) and variable tilt angle ranges (Figure 3 and Table 1).
Table 1.
Median rotational alignment error ΔE of all 100 pairwise alignments for phantom models 1 and 2. ΔE is defined as the difference between the rotational matrix determined by the fast rotational matching and the ground truth: ΔE = ∥Rdif − I∥. The maximum value of ΔE is 8. Grey fields are considered failed alignments, white fields are considered correct alignments.
| Model 1 | ||||||
|---|---|---|---|---|---|---|
|
|
∞ | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| ±90 | 0.00323 | 0.00382 | 0.00384 | 0.00558 | 0.0185 | 7.12 |
| ±80 | 0.00329 | 0.00309 | 0.00292 | 0.00739 | 0.0176 | 7.04 |
| ±70 | 0.00275 | 0.00329 | 0.00332 | 0.0116 | 0.0579 | 6.64 |
| ±60 | 0.00347 | 0.00339 | 0.0043 | 0.0104 | 6.54 | 6.82 |
| ±50 | 0.00388 | 0.00407 | 0.00555 | 7.26 | 6.93 | 6.26 |
| ±40 | 0.00648 | 0.0152 | 6.49 | 6.1 | 6.68 | 6.55 |
| Model 2 | ||||||
|---|---|---|---|---|---|---|
|
|
∞ | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| ±90 | 0.00353 | 0.00381 | 0.00384 | 0.0145 | 0.0397 | 6.65 |
| ±80 | 0.00386 | 0.00351 | 0.0047 | 0.0144 | 0.106 | 6.87 |
| ±70 | 0.0042 | 0.00361 | 0.00635 | 0.0115 | 5.03 | 6.79 |
| ±60 | 0.00437 | 0.0044 | 0.005 | 5.23 | 6.45 | 6.63 |
| ±50 | 0.00623 | 0.00721 | 5.38 | 7.38 | 6.58 | 6.15 |
| ±40 | 0.0077 | 4.79 | 6.42 | 6.31 | 5.92 | 6.4 |
2.5. Analyzing the computational efficiency
We test the computational efficiency by measuring the time for aligning 100 pairs of subtomograms of model 1 (Figure 3) using a computer with 2.67 GHz speed. Our fast alignment consists of two steps: 1) The rotational alignment step, which depends on the volume of the subtomogram and the angle sample interval; 2) the translational alignment and evaluation step of a candidate, which depends on the volume of the subtomogram. The average computation time is calculated from 100 repeated rotational alignments. Also, we measured the average time for evaluating each candidate translational alignment. The fast rotational alignments in Section 3.1 result in less than 100 candidate rotations per alignment. An upper bound for the total alignment time is therefore estimated by trotation+100×tcandidate, where trotation is the average time spent for the rotational alignment and tcandidate is the average time spent for translational alignment of a given candidate rotation. For comparison we also measure the total computational time used for the exhaustive rotational scanning by determining the the average time spent evaluating the constrained correlation score in (Förster et al., 2008), multiplied by the number of iterations required for the exhaustive search (Table 3). For comparison, both methods where implemented in MATLAB.
Table 3.
Estimated computational time in seconds, for our fast alignment method and the alignment using standard exhaustive rotational scanning (in parentheses), for different subtomogram volumes (in voxel number) and rotational angle intervals (RAI, in degrees).
|
|
163 | 323 | 643 |
|---|---|---|---|
| 10° | 13.0 (3:73 × 102) | 26.5 (1:96 × 103) | 94.9 (1:49 × 104) |
| 5° | 15.6 (3:04 × 103) | 32.1 (1:64 × 104) | 108 (1:21 × 105) |
| 2.5° | 39.2 (2:39 × 104) | 61.5 (1:30 × 105) | 153 (9:67 × 105) |
2.6. Software
For proof of principle the fast alignment method is implemented in MATLAB. For fast calculation of rotational correlation functions we use the DOTM library (Simons, 2001) to compute the Spherical Harmonics expansion and calculation of the Wigner d-matrix. A standalone program is in preparation and to be released upon completion.
3. Results
Our subtomogram alignment and reference-free classification approach is tested on realistically simulated cryo-electron tomograms of phantom models, structures of protein complexes, and cryo-electron subtomograms of purified complexes or complexes extracted from whole-cell tomograms.
3.1. Assessment of the alignment accuracy using phantom models
First, we assess the alignment accuracy on two asymmetric phantom models (Figure 3). For each of the two phantom models 100 pairs of subtomograms are generated where the phantom models are randomly oriented and placed and the subtomograms simulated for a variety of different SNR levels and tilt angle ranges (Figure 3). Then each pair of subtomograms is aligned and the determined relative rotations and translations compared with the ground truth, which is the rotational matrix that is used to generate the subtomogram orientation. To quantify the rotational alignment accuracy we calculate the difference between the rotational matrix of the optimal alignment and the ground truth. The difference between both matrices ΔE is measured as , where Ralign is the rotation matrix determined by the fast rotational alignment and Rtrue is the ground truth (i.e. the rotation matrix used to generate the subtomogram orientation); ∥ · ∥F denotes the Frobenius norm. The absolute error ΔE can range from 0 to a maximal value of 8 indicating that the object is placed in the opposite direction from the ground truth. Any ΔE value larger than 0.1 depicts a false alignment.
Our analysis shows that the accuracy of our fast rotational search method is very robust even at relatively high noise level and missing wedge distortions (Table 1). At SNR of 0.01 the fast rotational alignment is able to identify the correct alignment at tilt angle ranges that are typical used in tomographic experiments. Even at an SNR level of 0.005 our method can still accurately detect the optimal rotation. Only at extremely low SNR levels of 0.001 the method fails.
Next, we compare our fast rotational alignment based on 3D volumetric matching with the fast rotational search based on projected 2D spherical images published previously (Bartesaghi et al., 2008). To compare the two methods we calculate the ratios between the rotational error ΔE for both methods (Table 2). We observe that the 3D volumetric matching performs significantly better at lower SNR and smaller tilt angle ranges (Table 2). For instance, at SNR levels of 0.01 2D spherical image matching is unable to determine the correct alignment, while 3D volumetric matching is able to produce correct alignments at even lower SNR levels of 0.005. 3D volumetric matching therefore significantly extends the applicability for fast rotational matching to subtomograms with lower SNR (Table 2).
Table 2.
Ratio of the rotational alignment errors for a fast rotational alignment using 3D volumetric matching as described in this paper, and a fast rotational matching based on the alignment of 2D spherical images (see text for details) (Bartesaghi et al., 2008). Grey areas indicate subtomogram conditions where both methods fail to provide the correct alignment. Yellow areas indicate subtomogram conditions where 3D volumetric matching is able to provide a correct alignment while the 2D matching strategy fails.
| Model 1 | ||||||
|---|---|---|---|---|---|---|
|
|
∞ | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| ±90 | 1.02 | 1.06 | 1.12 | 2.51 | 202 | 0.959 |
| ±80 | 0.942 | 1.17 | 1.3 | 536 | 370 | 0.907 |
| ±70 | 0.97 | 1.07 | 1.09 | 573 | 119 | 0.996 |
| ±60 | 1.01 | 1.25 | 1.15 | 653 | 0.998 | 0.847 |
| ±50 | 1.04 | 0.974 | 1.3 | 0.907 | 0.875 | 0.971 |
| ±40 | 0.799 | 429 | 0.923 | 1.08 | 0.956 | 0.99 |
| Model 2 | ||||||
|---|---|---|---|---|---|---|
|
|
∞ | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| ±90 | 0.886 | 1.11 | 1.7 | 154 | 150 | 0.985 |
| ±80 | 1.04 | 1.54 | 1.93 | 405 | 63.9 | 0.985 |
| ±70 | 1.11 | 1.39 | 1.16 | 629 | 1.37 | 1.03 |
| ±60 | 0.721 | 1.31 | 1.69 | 1.38 | 0.993 | 1 |
| ±50 | 0.73 | 0.838 | 1.05 | 0.877 | 0.972 | 0.991 |
| ±40 | 0.848 | 1.39 | 0.97 | 1.03 | 1.02 | 0.943 |
3.2. Analysing the computational efficiency
Next, we compare the computational cost between the fast rotational matching and the exhaustive rotational scanning (Förster et al., 2008). For comparison we have implemented both methods in MATLAB and performed subtomogram alignments on model 1 (Section 2.5).
The exhaustive rotational scanning consists of a nested iteration over all sampled rotational angles. At each step the constrained correlation (Förster et al., 2008) is calculated. Its computation consists of several computational intensive operations, such as the FFT, element wise array products, and 3D summations, as well as 3D rotation, which are all efficiently implemented by the MATLAB system. Therefore we can expect that the efficiency of our rotational scanning implementation is similar in scope to the optimal implementations of the method in other programming language platforms.
Although the current implementation of our fast alignment method is not fully optimized for computational efficiency, we can already demonstrate that our fast rotational matching drastically decreases the computational time in comparison to the exhaustive rotational scanning (Table 3). In addition the method is also more scalable with increasing subtomogram size and decreasing angle sampling intervals. For example, with a subtomogram size of 643 voxels our method is on average ≈ 6000 times faster, with the correct alignment found at 153 seconds using a MATLAB implementation. By contrast, the standard exhaustive rotational scanning with an angle interval of 2.5° takes more than 10 days to find the correct alignment in a MATLAB implementation. Even with relatively small subtomogram volumes (i.e., 163 voxels) and a large rotational angle interval of 10 degrees, the standard exhaustive scanning approach still takes on average 373 seconds, while the fast rotational matching only takes 13 seconds.
3.3. Reference free alignment and classification of subtomograms
We now test our method for the reference free alignment and classification of subtomograms. The fast rotational matching allows very efficient alignments and therefore the comparison of a large number of subtomograms. We test our approach first on simulated subtomograms based on real protein complex structures extracted from the Protein Data Bank (PDB) (Berman et al., 2000). Then we test our method on experimental subtomograms, namely tomograms of purified GroEL and GroEL/ES complexes and finally experimental subtomograms extracted from whole-cell tomography.
3.3.1. Reference free classification of subtomograms simulated from protein complex structures
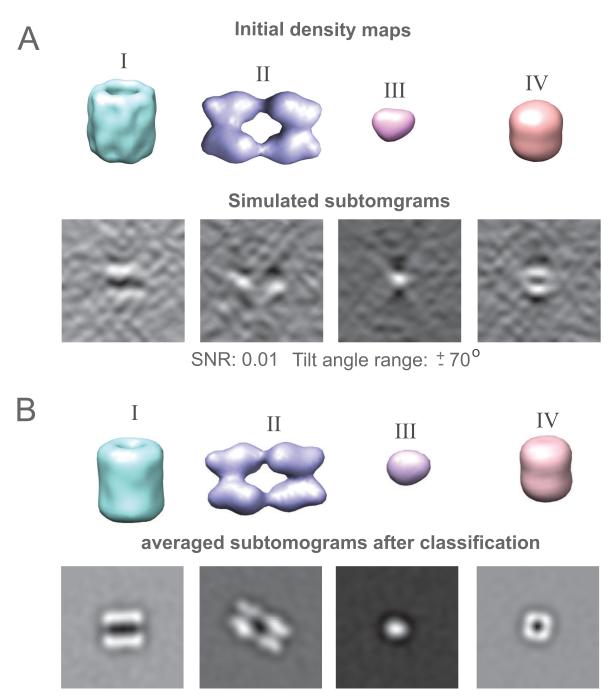
Structures of four protein complexes are obtained from the PDB: GroEL (PDBID: 1KP8), Carbamoyl phosphate synthase (PDBID: 1BXR), octameric enolase (PDBID: 1W6T), and ClpP (PDBID: 1YG6) (Figure 4A). For each of the four complexes 100 randomly oriented and placed subtomograms are generated at a SNR of 0.01 and a tilt angle range ±60° (Figure 4A) (Section 2.4).
Figure 4.
Reference-free subtomogram classification for simulated subtomograms from 4 different protein complexes. (A) Density map of selected protein complexes (I: GroEL (PDBID: 1KP8), II: Carboamoyl phosphate synthase (PDBID: 1BXR), III: octameric enolase (PDBID: 1W6T), IV: ClpP (PDBID: 1YG6 )) and a slice of a simulated subtomogram generated for SNR 0.01 and a tilt angle range ±60. The slice is taken along the y direction. (B) Density maps of complexes generated by averaging all the classified and aligned subtomograms in each class. Also shown is though the averaged tomograms .
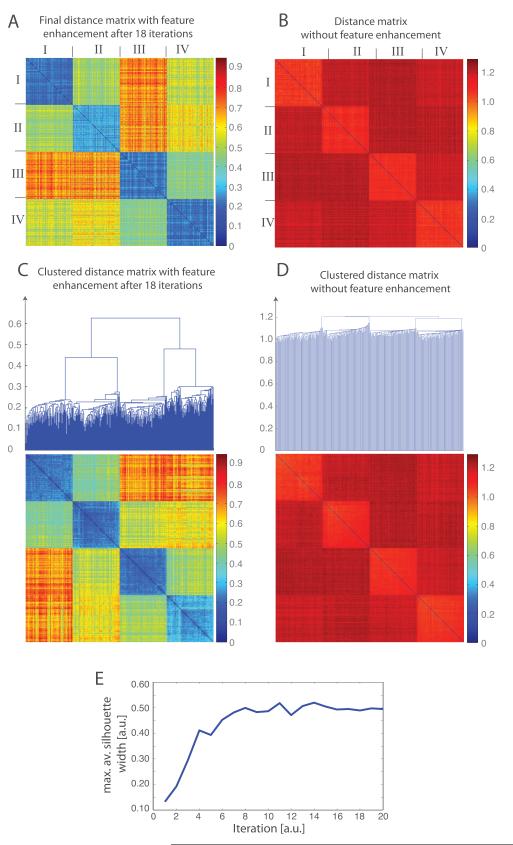
The reference free automatic classification procedure (Section 2.3.2) converges after 18 iterations and a clear classification into 4 different groups is evident (Figure 5 ACE). Notably, the final distance matrix calculated with feature enhancement is able to clearly differentiate the 4 classes of subtomograms (Figure 5C) with 100% classification accuracy. Distances between subtomograms of the same complex are very small, while distances between different complexes are relatively large (Figure 5B). Averaging all aligned subtomograms in each class reproduces well the initial density maps of the complexes (Figure 4B).
Figure 5.
Reference-free subtomogram classification for the simulated subtomograms of 4 different protein complexes as shown in Figure 4. (A) Distance matrix after 18 iterations of reference-free subtomogram classification with the feature enhancement weight . The order of subtomograms is according to the ground truth. The distance matrix is calculated using the feature enhancement weight. (B) Distance matrix calculated without feature enhancement weight after all subtomograms are aligned to their respective template density map. The order of subtomograms is according to the ground truth. (C) Clustered distance matrix after 18 iterations of the reference-free classification process using the feature-enhancement weight . Four different clusters can be clearly differentiated. (D) Clustering of the distance matrix from C. (E) Convergence of the classification process. The maximal average Silhouette width is calculated from the resulting subtomogram clusters at each iteration of the classification process. The convergence is reached when the maximal average Silhouette width reaches a plateau with increasing iterations.
In contrast, without feature enhancement the distinction between the groups of complexes is more challenging (Figure 5BD). When subtomograms are aligned to their templates without feature enhancement the resulting distances are relatively large, and therefore the variance of distances between subtomograms of different complexes is relatively small (Figure 5BD). Clustering into distinct complex groups is more challenging (Figure 5D). Therefore, the feature enhancement is clearly of great benefit for subtomogram classification.
3.3.2. Reference free alignment and classification of subtomograms of purified complexes
We now further test our reference free classification method on a set of experimental tomograms, namely tomograms of purified GroEL and GroEL/GroES complexes previously published in (Förster et al., 2008). The dataset consists of two sets of subtomograms. 214 subtomograms obtained from 13 cryo-electron tomograms of purified GroEL complexes, and 572 subtomograms obtained from 11 cryo-electron tomograms containing GroEL/GroES complexes. The differences between the subtomograms of the two different complexes are subtle and the classification and averaging is challenging.
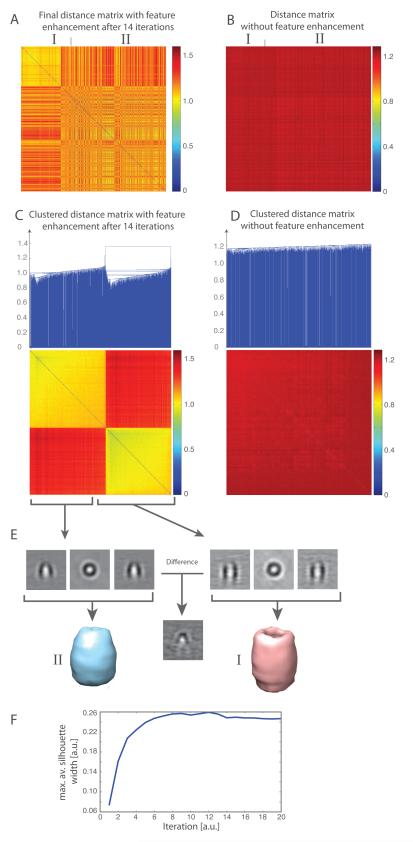
After about 14 iterations and automatic cluster cutoff detection, the iterative classification procedure (Section 2.3) can separate the subtomograms into two distinct clusters corresponding to the two classes of complexes (Figure 6ACF) with a classification accuracy of 68.2%. Note that the classification and averaging of this data might not only be affected by the subtleness of differences between the two types of complexes but also the impurity in the data (Scheres et al., 2009). The subtomogram averages obtained from each of the two clusters show the distinct features of the GroEL and GroEL/ES complexes (Figure 6E). Differences between the two complexes are clearly visible. When using a distance measure without feature enhancement it is not possible to dissect the two sets of subtomograms into two classes by hierarchical clustering (Figure 6BD), in agreement with a previous study (Förster et al., 2008).
Figure 6.
Reference-free classification of 786 experimental subtomograms, containing GroEL and GroEL/ES complexes. (A) Distance matrix after 14 iterations of reference-free subtomogram classification with the feature enhancement weight . The order of subtomograms is based on the tomogram type. The distance matrix is calculated using the feature enhancement weight. (B) Distance matrix calculated without feature enhancement weight after all subtomograms are aligned to a reference subtomogram. The order of subtomograms is identical to those in panel A. (C) Clustered distance matrix after 14 iterations of the reference-free classification process. Two different clusters are clearly detected by the automatic cutoff detection. (D) Clustering of distance matrix as shown in panel B. The clustering into the two subgroups fails without feature enhancement and reference-free classification. (E) Averaged subtomograms after iterative classification and alignment. (Upper panel) slices through the averaged subtomograms and (lower panel) isosurface of the averaged subtomograms of each cluster. Clearly shown are the distinct features for the GroEL complex (left panel) and the GroEL/ES complex (right panel). A slice through the difference map of both subtomograms shows the distinct differences in both complexes. (F) Convergence of the classification process. The maximal average Silhouette width is calculated from the resulting subtomogram clusters at each iteration of the classification process. The convergence is reached when the maximal average Silhouette width reaches a plateau with increasing iterations.
3.4. Reference free alignment and classification of subtomograms extracted from whole cell tomogram
Finally, we test our method on subtomograms extracted from a whole cell tomogram of Leptospira interrogans in undisturbed conditions (Beck et al., 2009). The classifications of subtomograms from whole-cell studies is significantly more challenging because the heterogeneity of complexes is expected to be much higher when subtomograms are extracted from crowded whole cell tomograms and because the SNR levels and resolution of these subtomograms is typically much lower in comparison to the tomograms of purified complexes. Beck et al., 2009 have identified several types of complexes in the tomogram using template matching (Best et al., 2007). The templates were generated by simulating subtomograms of structures from the PDB (Berman et al., 2000) and convoluted with CTF and MTF. As a test case, we selected the two complexes with the highest cellular abundance in the whole cell tomogram (i.e., the ribosome and ATP synthase, with more than 200 instances for each complex in the tomogram). To ensure high confidence for our data set, we only identified the 100 best scoring template matches for each of the two complexes. For each of these matches we extracted a subtomogram of size 323 voxels that was large enough to contain an instance of the complex.
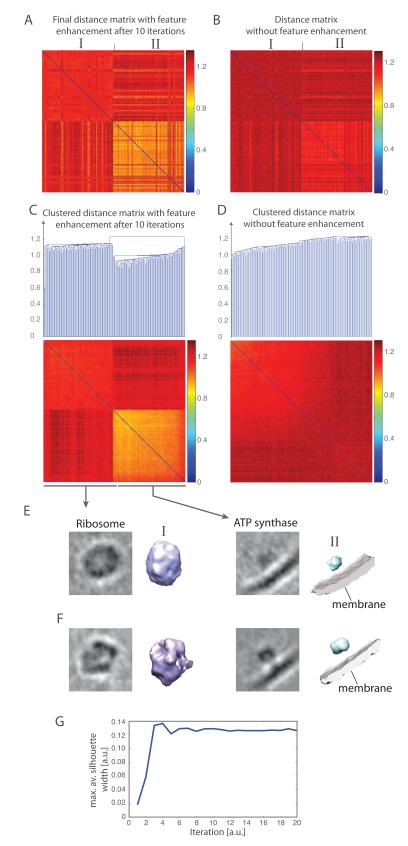
The reference-free classification with feature enhancement combined with automatic cluster cutoff determination is able to detect correctly the two classes of subtomograms (Figure 7AC) with a classification accuracy of 99% when the subtomograms from template matching are taken as ground truth. The classification converges after around 9 iterations (Figure 7G). In contrast, the distance matrix for the same subtomograms calculated without feature enhancement is unable to discriminate between the two classes, even if all the subtomograms are first aligned to a corresponding reference subtomogram (Figure 7BD). Clustering of this distance matrix does not allow the distinction between the two complex classes (Figure 7D).
Figure 7.
Reference-free classification of 200 experimental subtomograms, extracted from a whole cell cryo-electron tomogram of L. interrogans (Beck et al., 2009). (A) Distance matrix after 10 iterations of reference-free subtomogram classification with the feature enhancement weight . The order of subtomograms is based on the result of template matching. The distance matrix is calculated using the feature enhancement weight. (B) Distance matrix calculated without feature enhancement weight after all subtomograms are aligned to the corresponding subtomograms with the highest matching score in template matching (Best et al., 2007). The order of subtomograms is identical to those in panel A. (C) Clustered distance matrix after 10 iterations of the reference-free classification process. Two different clusters are detected by the automatic cutoff detection, differentiating the ATP synthase complexes from the ribosome complexes. (D) Clustering of distance matrix as shown in panel B. The clustering into the two subgroups fails without feature enhancement and reference-free classification. (E) Averaged subtomograms after iterative classification. Shown are slices through the averaged subtomograms and the isosurface of the averaged subtomograms of each cluster. (F) Averaged subtomograms when all the subtomograms in each determined cluster are aligned to the respective ground truth template. Shown are slices through the averaged subtomograms and the isosurace of the averaged subtomograms. (G) Convergence of the classification process. The maximal average Silhouette width is calculated from the resulting subtomogram clusters at each iteration of the classification process. The convergence is reached when the maximal average Silhouette width reaches a plateau with increasing iterations.
4. Conclusion
Fast and accurate subtomogram alignments are key for reference-free subtomogram classification and averaging. However, most of existing alignment methods rely on exhaustive rotational scanning of one subtomogram with respect to the other. However, the computational cost of such rotational scanning is often the limiting factor in reference-free subtomogram classifications in particular with the increasing number, and size of subtomograms and alignment precision.
In this paper, we propose a fast rotational alignment method based on the Fourier equivalent form of a popular constrained correlation measure. The constrained correlation takes into account mean and variance of subtomograms, therefore corrects for the non-evenness of tomograms due to the imaging process. The fast rotational search is based on 3D volumetric matching. We demonstrate that the use of 3D volumetric matching improves significantly the alignment accuracy, in particular for highly distorted subtomograms with low SNR and tilt angle ranges, compared to the matching based on projected 2D spherical images (Bartesaghi et al., 2008). To further increase alignment accuracy, the alignment can be refined using gradient guided methods (Bartesaghi et al., 2008; Xu et al., 2011b).
We apply a reference-free iterative classification framework with our fast alignment method, and propose a local feature enhancement strategy. We can demonstrate that the method can be used to successfully classify subtomograms extracted from tomograms of purified protein complexes and whole cell tomograms.
For proof of principles we have used the popular hierarchical clustering approach. However, in future the clustering step can be improved using a wide range of other clustering methods, especially those specifically designed for subtomogram clustering (e.g. Yu and Frangakis, 2011).
5. Acknowledgements
The authors would like to thank Dr. Friedrich Förster for providing the GroEL and GroEL/ES subtomograms for classification. This work is supported by the Human Frontier Science Program grant RGY0079/2009-C to F.A., Alfred P. Sloan Research foundation grant to F.A.; NIH grants 1R01GM096089 and 2U54RR022220 to F.A.. F.A. is a Pew Scholar in Biomedical Sciences, supported by the Pew Charitable Trusts.
Footnotes
When q is a real valued function, the complex conjugate .
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amat F, Comolli L, Moussavi F, Smit J, Downing K, et al. Subtomogram alignment by adaptive Fourier coefficient thresholding. Journal of structural biology. 2010 doi: 10.1016/j.jsb.2010.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartesaghi A, Sprechmann P, Liu J, Randall G, Sapiro G, et al. Classification and 3D averaging with missing wedge correction in biological electron tomography. Journal of structural biology. 2008;162(3):436–450. doi: 10.1016/j.jsb.2008.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck M, Malmström J, Lange V, Schmidt A, Deutsch E, et al. Visual proteomics of the human pathogen Leptospira interrogans. Nature methods. 2009;6(11):817–823. doi: 10.1038/nmeth.1390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck M, Topf M, Frazier Z, Tjong H, Xu M, Zhang S, et al. Exploring the Spatial and Temporal Organization of a Cell’s Proteome. Journal of Structural Biology. 2011;173(3):483–496. doi: 10.1016/j.jsb.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H, Westbrook J, Feng Z, Gilliland G, Bhat T, et al. The protein data bank. Nucleic acids research. 2000;28(1):235. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best C, Nickell S, Baumeister W. Localization of protein complexes by pattern recognition. Methods in cell biology. 2007;79:615–638. doi: 10.1016/S0091-679X(06)79025-2. [DOI] [PubMed] [Google Scholar]
- Biedenharn L, Louck J, Carruthers P. Angular momentum in quantum physics: theory and application. Addison-Wesley; Reading, MA: 1981. [Google Scholar]
- Briggs J, Riches J, Glass B, Bartonova V, Zanetti G, Kräusslich H. Structure and assembly of immature hiv. Proceedings of the National Academy of Sciences. 2009;106(27):11090–11095. doi: 10.1073/pnas.0903535106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Förster F, Medalia O, Zauberman N, Baumeister W, Fass D. Retrovirus envelope protein complex structure in situ studied by cryo-electron tomography. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(13):4729. doi: 10.1073/pnas.0409178102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Förster F, Pruggnaller S, Seybert A, Frangakis A. Classification of cryo-electron sub-tomograms using constrained correlation. Journal of structural biology. 2008;161(3):276–286. doi: 10.1016/j.jsb.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Frangakis A, Förster F. Computational exploration of structural information from cryo-electron tomograms. Current opinion in structural biology. 2004;14(3):325–331. doi: 10.1016/j.sbi.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Frank J. Three-dimensional electron microscopy of macromolecular assemblies: visualization of biological molecules in their native state. Oxford University Press; USA: 2006. [Google Scholar]
- Garzon J, Kovacs J, Abagyan R, Chacon P. ADP EM: fast exhaustive multi-resolution docking for high-throughput coverage. Bioinformatics. 2007;23(4):427. doi: 10.1093/bioinformatics/btl625. [DOI] [PubMed] [Google Scholar]
- Johnson S. Hierarchical clustering schemes. Psychometrika. 1967;32(3):241–254. doi: 10.1007/BF02289588. [DOI] [PubMed] [Google Scholar]
- Kaufman L, Rousseeuw P. Finding groups in data: an introduction to cluster analysis. Vol. 39. Wiley Online Library; 1990. [Google Scholar]
- Komeili A, Li Z, Newman D, Jensen G. Magnetosomes are cell membrane invaginations organized by the actin-like protein mamk. Science. 2006;311(5758):242. doi: 10.1126/science.1123231. [DOI] [PubMed] [Google Scholar]
- Kovacs J, Wriggers W. Fast rotational matching. Acta Crystallographica Section D: Biological Crystallography. 2002;58(8):1282–1286. doi: 10.1107/s0907444902009794. [DOI] [PubMed] [Google Scholar]
- Kühner S, Van Noort V, Betts M, Leo-Macias A, Batisse C, Rode M, Yamada T, Maier T, Bader S, Beltran-Alvarez P, et al. Proteome organization in a genome-reduced bacterium. Science. 2009;326(5957):1235. doi: 10.1126/science.1176343. [DOI] [PubMed] [Google Scholar]
- Lucic V, Förster F, Baumeister W. Structural studies by electron tomography: from cells to molecules. Annu. Rev. Biochem. 2005;74:833–865. doi: 10.1146/annurev.biochem.73.011303.074112. [DOI] [PubMed] [Google Scholar]
- McMullan G, Chen S, Henderson R, Faruqi A. Detective quantum efficiency of electron area detectors in electron microscopy. Ultramicroscopy. 2009;109(9):1126–1143. doi: 10.1016/j.ultramic.2009.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medalia O, Weber I, Frangakis A, Nicastro D, Gerisch G, et al. Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science. 2002;298(5596):1209. doi: 10.1126/science.1076184. [DOI] [PubMed] [Google Scholar]
- Murata K, Liu X, Danev R, Jakana J, Schmid M, et al. Zernike Phase Contrast Cryo-Electron Microscopy and Tomography for Structure Determination at Nanometer and Subnanometer Resolutions. Structure. 2010;18(8):903–912. doi: 10.1016/j.str.2010.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicastro D, Schwartz C, Pierson J, Gaudette R, Porter M, et al. The molecular architecture of axonemes revealed by cryoelectron tomography. Science. 2006;313(5789):944. doi: 10.1126/science.1128618. [DOI] [PubMed] [Google Scholar]
- Nickell S, Förster F, Linaroudis A, Net W, Beck F, et al. TOM software toolbox: acquisition and analysis for electron tomography. Journal of Structural Biology. 2005;149(3):227–234. doi: 10.1016/j.jsb.2004.10.006. [DOI] [PubMed] [Google Scholar]
- Nickell S, Kofler C, Leis A, Baumeister W. A visual approach to proteomics. Nature reviews Molecular cell biology. 2006;7(3):225–230. doi: 10.1038/nrm1861. [DOI] [PubMed] [Google Scholar]
- Pettersen E, Goddard T, Huang C, Couch G, Greenblatt D, et al. UCSF Chimeraa visualization system for exploratory research and analysis. Journal of computational chemistry. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Scheres S, Melero R, Valle M, Carazo J. Averaging of electron subtomograms and random conical tilt reconstructions through likelihood optimization. Structure. 2009;17(12):1563–1572. doi: 10.1016/j.str.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons F. Dotm library. 2001 Http://geoweb.princeton.edu/people/simons/software.html.
- Volkmann N. Methods for Segmentation and Interpretation of Electron Tomographic Reconstructions. Methods in Enzymology. 2010:31–46. doi: 10.1016/S0076-6879(10)83002-2. [DOI] [PubMed] [Google Scholar]
- Winkler H. 3d reconstruction and processing of volumetric data in cryo-electron tomography. Journal of structural biology. 2007;157(1):126–137. doi: 10.1016/j.jsb.2006.07.014. [DOI] [PubMed] [Google Scholar]
- Wriggers W, Milligan R, McCammon J. Situs: A Package for Docking Crystal Structures into Low-Resolution Maps from Electron Microscopy. Journal of Structural Biology. 1999;125(2-3):185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- Xu M, Beck M, Alber F. Template-free detection of macromolecular complexes in cryo electron tomograms. Bioinformatics. 2011a;27(13):i69. doi: 10.1093/bioinformatics/btr207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu M, Zhang S, Alber F. 3d rotation invariant features for the characterization of molecular density maps. 2009 IEEE International Conference on Bioinformatics and Biomedicine; IEEE; 2009. pp. 74–78. [Google Scholar]
- Xu M, Zhang S, Alber F. Gradient-based high precision alignment of cryo-electron subtomograms. 2011 IEEE International Conference on Systems Biology; IEEE; 2011b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z, Frangakis A. Classification of Electron Sub-Tomograms with Neural Networks and its Application to Template-Matching. Journal of structural biology. 2011 doi: 10.1016/j.jsb.2011.02.009. [DOI] [PubMed] [Google Scholar]