A signal detection analysis of gist-based discrimination of genetic breast cancer risk

Abstract

Pervasive biases in probability judgment render the probability scale a poor response mode for assessing risk judgments. By applying fuzzy trace theory, we used ordinal gist categories as a response mode, coupled with a signal detection model to assess risk judgments. The signal detection model is an extension of the familiar model used in binary choice paradigms. It provides three measures of discriminability—low versus medium risk, medium versus high risk, and low versus high risk—and two measures of response bias. We used the model to assess the effectiveness of BRCA Gist, an intelligent tutoring system designed to improve women’s judgments and understanding of genetic risk for breast cancer. Participants were randomly assigned to the BRCA Gist intelligent tutoring system, the National Cancer Institute (NCI) Web pages, or a control group, and then they rated cases that had been developed using the Pedigree Assessment Tool and also vetted by medical experts. BRCA Gist participants demonstrated increased discriminability for all three risk categories, relative to the control group; the NCI group showed increased discriminability for two of the three levels. This result suggests that BRCA Gist best improved discriminability among genetic risk categories, and both BRCA Gist and the NCI website improved participants’ ability to discriminate, rather than simply shifting their decision criterion. A spreadsheet that fits the model and compares parameters across the conditions can be downloaded from the Behavior Research Methods website and used in any research involving categorical responses.

The ability to accurately judge risk is an important cognitive ability with far-reaching implications for one’s well-being. One important example involves the decision to undergo genetic testing for breast cancer. Numerous costs are associated with genetic testing, including, but not limited to, the cost of the test itself, the potential for genetic discrimination by employers and insurers, possible conflicts among family members, and increased anxiety (e.g., Brewer, Richman, DeFrank, Reyna, & Carey, 2012). Given these stakes, it is necessary to accurately judge risk in order to properly weigh potential costs against potential benefits.

Probability theory serves as the normative model of risk judgment, in which judgments vary on a continuum ranging from 0 (impossible) to 1 (certain). The axioms of probability theory ensure that risk judgments are coherent (internally consistent), whereas careful measurement and sound methodology can provide reasonable calibration (external validity) (Reyna & Adam, 2003). Although there are clear benefits of using probability as a normative model, pervasive judgment biases suggest that probability theory is a poor descriptive model of judgment and may be of limited use as a prescriptive model. Some examples of judgment biases include the conjunction fallacy (Wolfe & Reyna, 2010), base-rate neglect (Barbey & Sloman, 2007; Reyna & Brainerd, 2008), and the lack of semantic coherence in conditional probability judgments (Fisher &Wolfe, 2011;Wolfe, Fisher, & Reyna, 2012). These problems are further exacerbated by poor numeracy, defined as the ability to reason with basic quantitative concepts (Reyna, Nelson, Han, & Dieckmann, 2009).

For the reasons cited above, the probability scale is a poor response mode for assessing subjective risk judgment (see also Haase, Renkewitz, & Betsch, 2013). As a prescriptive alternative, we propose a gist-based response mode consisting of the ordinal categories low, medium, and high. The use of ordinal gist categories is theoretically grounded in fuzzy trace theory (FTT; Reyna, 2008), but it may be compatible with other theoretical orientations and has clinical applications. In the remainder of this article, we briefly describe FTT as it applies to risk judgment, the development of materials defined by externally validated risk categories, and an arguably underutilized signal detection model that can be applied to more than two response categories. We end with a discussion of the approach within the larger domain of risk judgment and a discussion of the assumptions of the model.

Fuzzy trace theory

FTT is a theory of memory that has implications for risk judgment (Reyna, 2008). According to FTT, memory is multifaceted, with multiple representations ranging from verbatim to gist. In FTT, the terms “verbatim” and “gist” retain much of their colloquial meaning. Verbatim refers to exact, surface-level details of risk, whereas gist refers to its qualitative meaning, including one’s affective response. One tenet of FTT is that people prefer to reason with the most gist-like representation that is applicable to a given situation. In terms of risk judgment, a mental representation consisting of an exact numerical probability would be located at the verbatim end of a continuum, whereas risk present/absent would be located at the gist end of the continuum. FTT suggests that the ordinal gist categories “low,” “medium,” and “high” reflect a level of resolution frequently used by laypeople when assessing levels of risk (Reyna, 2012).

Signal detection theory

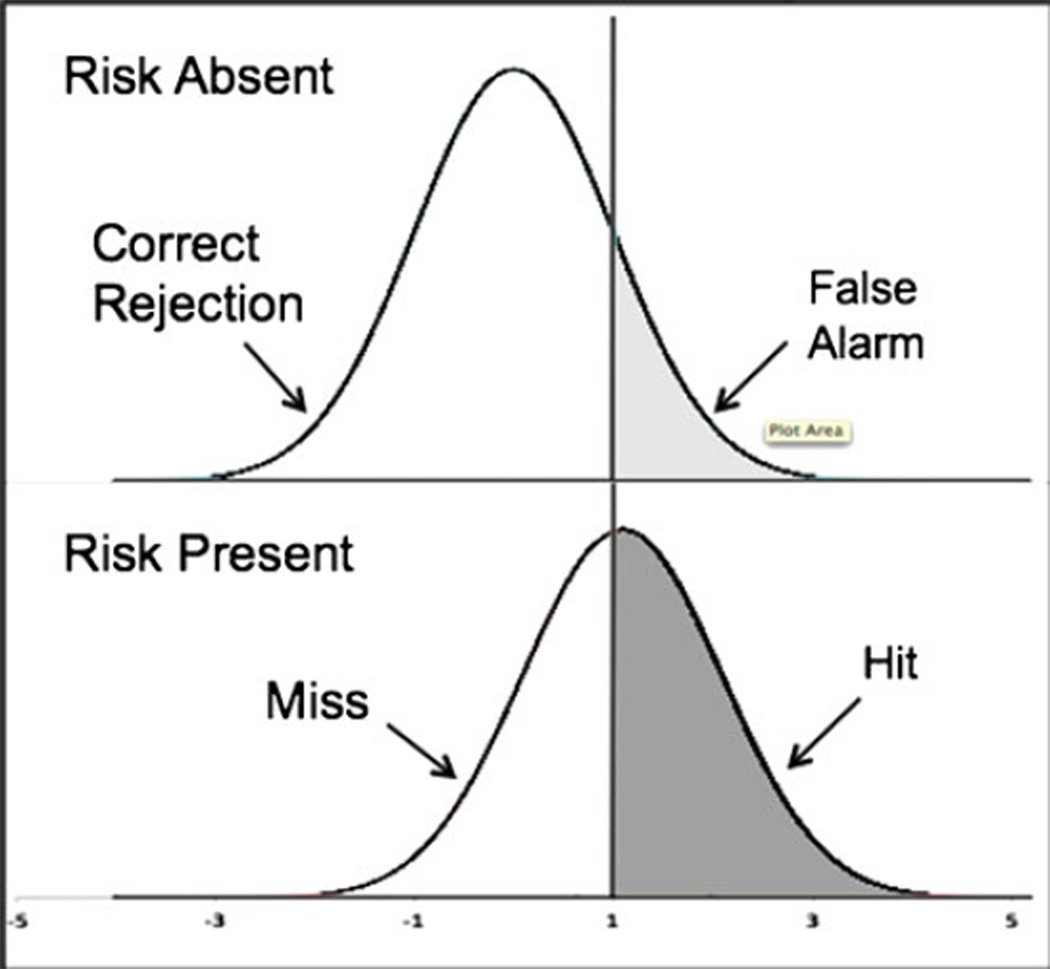
Signal detection theory (SDT) is a formal framework for assessing performance in discrimination and categorization, which has been successfully applied in psychophysics and memory research (Wickens, 2002). According to SDT, a quantity such as subjective risk can be represented as an underlying continuum upon which a response criterion is set to define response categories. The process is error-prone and can accordingly be represented as overlapping distributions, as is shown in Fig. 1. The benefit of using SDT is that it can disentangle two important aspects of judgment: discriminability and the judgment criterion. Discriminability, as measured by d′, refers to the ability to differentiate risk categories. The parameter d′ is defined as the standardized difference between the distributions and conceptually represents the degree of overlap between the distributions. A d′ value can be compared with chance performance and perfect performance as benchmarks to aid in interpretation. At one extreme, d′ equals 0 when performance is at chance levels. At the other extreme, d′ approaches infinity as performance increases.

Fig.1.

Depiction of signal detection with two responses

Criterion refers to the threshold that separates one response category from another. In Fig. 1, the black vertical line represents the criterion. It is often measured with respect to the intersection of the distributions, which indicates equal weighting of two possible errors: misses (e.g., failing to detect the presence of risk) and false alarms (e.g., incorrectly stating the presence of risk when it is absent). This is known as response bias, denoted c′. Values of d′ and c′ are estimated in the model through the unique combination of hit rates (correctly identifying the presence of risk) and false alarm rates.

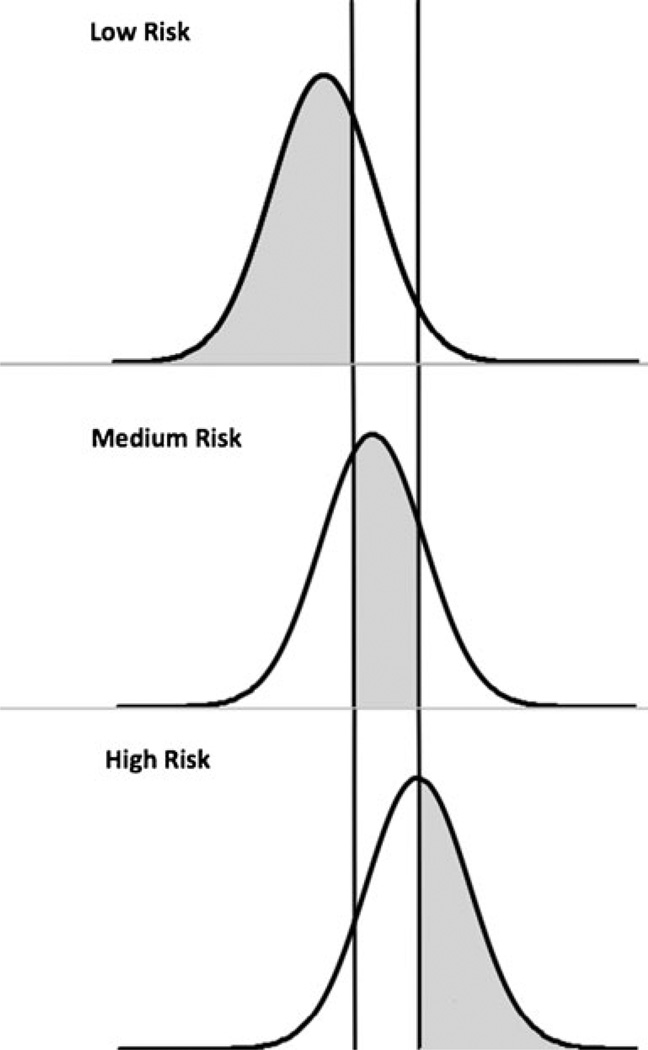
Figure 1 is an example of the two most common SDT paradigms: the yes–no experiment and two-alternative forced choice. The common feature between these paradigms is the use of binary responses. These paradigms can be generalized to a k-alternative identification paradigm with k(k−1)/2 measures of discriminability and k−1 measures of response bias (Wickens, 2002 p.124). In the present article, we describe a three-alternative identification model. As is shown in Fig. 2, the three distributions correspond to the ordinal gist categories of low, medium, and high risk. As we previously noted, FTT suggests that people represent risk at the resolution of three ordinal gist categories. The model contains three parameters for discriminability, one for each of the three pairwise comparisons between distributions. These are d′_lm, d′_lh, and d′_mh, where l, m, and h denote “low,” “medium,” and “high,” respectively; d′_lm measures discriminability between the low- and medium-risk categories, d′_lh measures discriminability between the low- and high-risk categories, and d′_mh measures discriminability between the medium- and high-risk categories. In addition, the model has two parameters for response bias, one that separates low from medium judgments, and a second that separates medium from high judgments, denoted c′_lm, and c′_mh, respectively. For simplicity, the model assumes equal variances.

Fig.2.

Depiction of the three-alternative identification model. Gray areas represent a hit for each of the risk categories. The left vertical black line is the criterion separating low- from medium-risk responses, and the right vertical line is the criterion separating medium- from high-risk responses

Simple binary SDT models, such as yes–no and two-alternative forced choice, have been used extensively in the literature. Tutorials (Stanislaw & Todorov, 1999) and spreadsheets (Sorkin, 1999) have been devoted to their use. By contrast, the k-alternative identification model has received considerably less attention in the literature. In this article, we build upon previous work by describing the computational details and implementation of the theoretically motivated three-alternative identification model, which can easily be extended to accommodate an arbitrary number of categories. The model can easily be implemented in standard programs such as Microsoft Excel, MATLAB, and R, using cumulative normal distribution functions and an optimization algorithm. We provide a ready-to-use spreadsheet for the three-alternative identification model that can be found in the supplementary materials available on the Behavior Research Methods website. Unlike previous efforts, our spreadsheet also includes several useful features, such as the standard errors of the parameter estimates, hierarchical model comparisons for testing differences in the parameters, and posterior probability approximations using the Bayesian information criterion (see Appendix A for computational details).

Research materials

An important prerequisite for using SDT is the development of stimuli that fall into objectively defined categories, a difficult but not impossible task that lies outside of psychophysics. Genetic risk level in this study was validated with the Pedigree Assessment Tool (PAT; Hoskins, Zwaagstra, & Ranz, 2006). The PAT estimates genetic risk on the basis of empirically verified risk factors, including family history of breast cancer and ethnicity. Ordinal gist categories were defined using cutoff values for the PAT (see Appendix B). Importantly, the cutoff values were also vetted by a nationally recognized medical expert in women’s health and clinical decision-making, as defining low-, medium-, and high-risk categories.

On the basis of these defined categories, we developed 12 cases of hypothetical women who varied in genetic risk for breast cancer. These included four low-, medium-, and high-risk cases. A complete listing of the 12 cases can be found in Appendix B. Careful attention was given to the development of tightly controlled and standardized cases. Each case included the following information: name, age, ethnicity, hometown, and family and personal health history. Given that age is a strong, nongenetic predictor of breast cancer, age was equated across the risk categories. The 12 cases were also equated in terms of word length and linguistic complexity, as measured by the Flesch–Kincaid Grade Level score and the Flesch Reading Ease score. This precluded the possibility that higher risk judgments would superficially be given to scenarios that contained more words, were more difficult to read, or were more jargon-laden.

An empirical study

We used the SDT model with these 12 breast cancer risk cases to test the efficacy of the Breast Cancer Genetics Intelligent Semantic Tutor (BRCA Gist). BRCA Gist is an intelligent tutoring system created using AutoTutor Lite (Hu et al., 2009) to teach women about genetic breast cancer risk (see also Graesser et al., 2004). AutoTutor Lite is a Web-based instantiation of AutoTutor, which has been implemented successfully in knowledge domains as diverse as physics (Jackson, Ventura, Chewle, Graesser, & the Tutoring Research Group, 2004), computer science (Craig, Sullins, Witherspoon, & Gholson, 2006), and behavioral research methods (Arnott, Hastings, & Allbritton, 2008). AutoTutor Lite has shown some successes in improving coherence in probability judgments (Wolfe, Fisher, Reyna, & Hu, 2012). BRCA Gist consists of a human-like avatar that communicates to the user verbally and can provide information by means of a variety of multimedia channels, including spoken and written text, video, and graphics. During tutorial interactions, BRCA Gist poses questions, and the user responds by typing into a dialog box. Throughout the tutorial interaction, BRCA Gist provides feedback and encouragement, prompting the user to elaborate on her answers. In combination with content that focuses on bottom-line gist, this process of tutorial interaction is used to increase learning.

In this experiment, 200 women were randomly assigned to either BRCA Gist (N= 68) or one of two comparison conditions: the National Cancer Institute (NCI; N= 65) website, or an irrelevant nutrition control group (N= 67). To control for time on task, the control and NCI conditions had a completion time of 60 min, which is comparable to the length of the BRCA Gist tutorial. The nutrition control group received irrelevant nutrition information, and thus served as a point of reference to assess learning gains. The NCI group read information related to genetic risk of breast cancer from the NCI website. We made PDFs of 26 NCI web pages and hosted them on the experimenter’s server. Thus, participants read and saw all of the relevant content and navigated among pages with the aid of a navigation bar, but they could not follow any hyperlinks. This also prevented potential changes in content during the experiment. The NCI group allowed us to compare the efficacy of BRCA Gist to that of the NCI website, an information source developed by experts on genetic risk of beast cancer that was the major source used in the development of BRCA Gist.

BRCA Gist covered many of the same topics covered in the NCI group, but it also included graphics and videos designed to help participants develop the appropriate gist representation of key concepts such as the relationship between BRCA mutations and breast cancer in the population of American women. The BRCA Gist materials were vetted by a medical expert. An animated avatar presented information verbally, with key concepts being presented concurrently in text. Women engaged in five tutorial interactions throughout the experiment. During the interactions, BRCA Gist posed a question such as “What should someone do if she receives a positive result for genetic risk of breast cancer?” and women typed responses into a dialog box. BRCA Gist provided feedback and encouraged elaboration on the basis of the relevance and thoroughness of the answers. See Wolfe et al. (2013) for a more thorough discussion of these tutorial dialogues.

After completing the learning phase, participants judged the genetic breast cancer risk for each of 12 randomly ordered cases as a measure of distant transfer—that is, their ability to apply what they have learned to hypothetical cases. On each trial, participants read one randomly selected case and categorized it as low, medium, or high risk. Other measures were collected, such as a declarative knowledge assessment, the State–Trait Anxiety Inventory (Spielberger, Gorsuch & Lushene, 1970), and the PAT. However, a detailed discussion of these measures is beyond the scope of this article.

Results

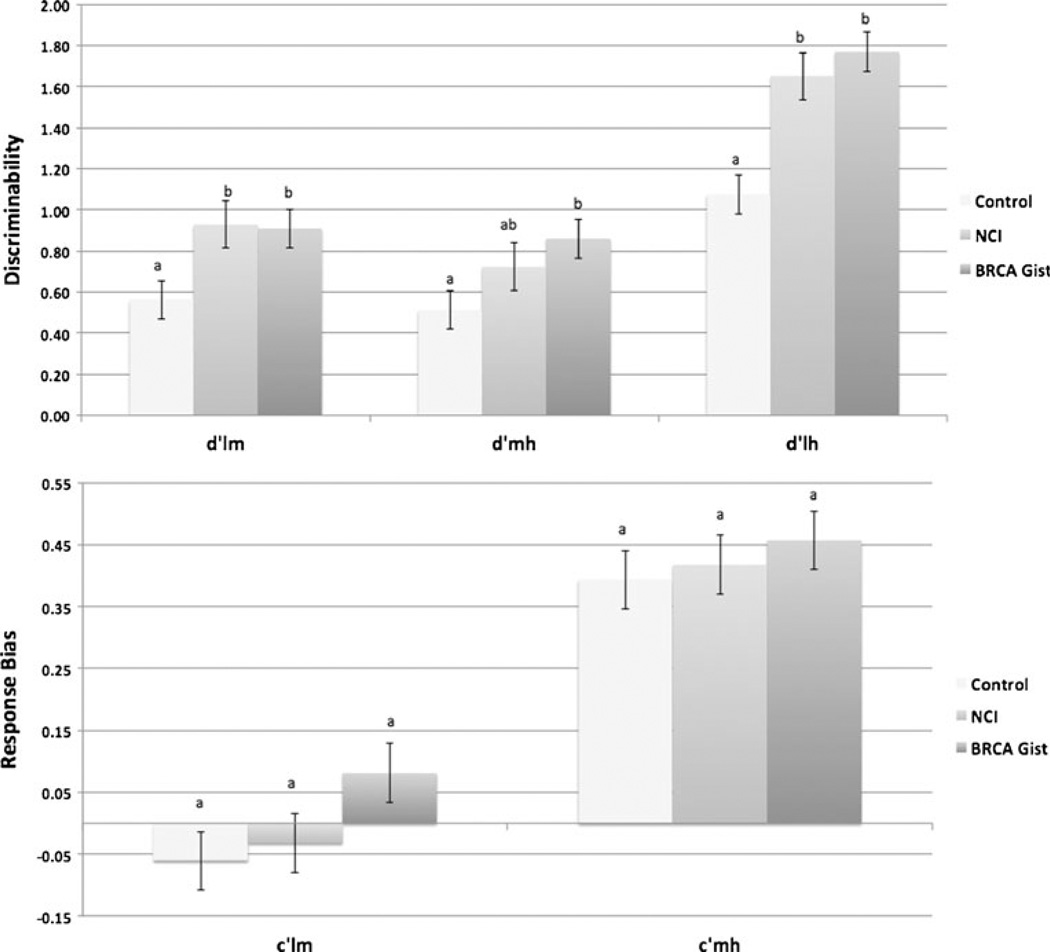
Responses were organized into the nine response categories formed by a 3× 3 confusion matrix (see Appendix A) and aggregated for each group (see Table 1). Model fitting and model comparison were performed using the spreadsheet developed by the authors, which can be downloaded from the Behavior Research Methods website. The spreadsheet includes the data from the present study and a worked example. The model fits for the nutrition control, G²(df= 2)= .71, p= .70, and NCI, G²(df= 2)= .79, p= .67, conditions were good. The model departed from the data in the BRCA Gist condition, G²(df= 2)= 16.86, p< .001. However, the magnitude of departure was very small, w= .14. On this basis, the model is arguably a satisfactory fit. Figure 3 shows the best-fitting parameter estimates of d′ and c′ for each condition.

Table 1.

Observed and expected response probabilities by condition

	Control			BRCA Gist			NCI
Response	Low	Medium	High	Low	Medium	High	Low	Medium	High
Low	.59 (.59)	.37 (.37)	.19 (.20)	.72 (.70)	.31 (.35)	.13 (.11)	.67 (.67)	.30 (.31)	.12 (.11)
Medium	.29 (.30)	.36 (.38)	.38 (.36)	.21 (.26)	.54 (.46)	.37 (.40)	.28 (.29)	.49 (.47)	.40 (.41)
High	.12 (.11)	.26 (.26)	.44 (.45)	.06 (.04)	.14 (.19)	.50 (.49)	.05 (.04)	.21 (.22)	.48 (.48)

Expected response probabilities are in parentheses

Fig.3.

Group comparisons of d′ (top panel) and c′ (bottom panel). Error bars represent standard errors. Groups marked by different letters are statistically different at p< .05

A hierarchical model comparison was used to test the pairwise differences in parameters for the BRCA Gist, NCI, and the control conditions (see Appendix A for computational details). BRCA Gist showed increased discriminability for all risk categories, relative to the nutrition control. As compared with the nutrition control, NCI showed increased discriminability only for d′_lm and d′_lh. However, BRCA Gist was not statistically different from NCI (see Table 2). These results suggest that both BRCA Gist and NCI generally improved women’s ability to discriminate among levels of genetic breast cancer risk, but that differences were slightly more robust for BRCA Gist (but not statistically better than reading the NCI website). In addition, we found no differences in response bias between the groups for either measure. Taken together, these results suggest that the increases in performance for both BRCA Gist and the NCI website were due to improved risk discrimination, rather than a simple shifting of response criteria.

Table 2.

Pairwise comparisons for each d′ and c′ parameter

Parameter	Control vs. BRCA Gist	NCI vs. BRCA Gist	Control vs. NCI
d′lm	5.82*	0.02	6.42**
d′mh	6.27**	0.95	2.26
d′lh	21.75**	0.57	14.92**
c′lm	3.47	2.12	0.14
c′mh	0.66	0.24	0.10

Inferential statistics are ΔG² values, with Δdf=1 for all comparisons.

^*p≤ .05.

^**p≤ .01

Discussion

SDT is a useful formal framework for assessing performance in discrimination and categorization tasks for which objective categories can be defined. We demonstrated that it is possible to apply SDT to perceptions of risk. With the aid of the PAT and expert medical judgment, we were able to estimate the risk of individuals (presented as case-based scenarios) with reasonable accuracy. Moreover, the case materials in Appendix B were standardized in terms of several dimensions, including word length, linguistic complexity, and nongenetic risk factors for breast cancer, such as age.

One major advantage of using SDT, as opposed to simple percentages correct, is that it can disentangle risk discriminability from the response bias (i.e., decision threshold) on which judgments of risk are based. In this experiment, BRCA Gist, an intelligent tutoring system, and the NCI website both increased women’s ability to discriminate genetic risk for breast cancer, although BRCA Gist supported differentiating low, medium, and high risk. However, no differences in response bias emerged among any of the groups, suggesting that BRCA Gist and NCI do not appreciably alter how women weight errors (misses vs. false alarms). Thus, participants did not improve accuracy by simply having a more strict or lenient decision criterion. The lack of a change in response bias is a desirable outcome, considering that it is a subjective component of risk judgment. Without a mathematical model, such as SDT, it would have been impossible to isolate these components of risk judgment.

To illustrate the utility of the SDT model, it has informed our ongoing efforts to develop and improve the BRCA Gist tutorial. For example, BRCA Gist improved declarative knowledge of genetic breast cancer risk relative to the NCI website (results not reported here). A model-based analysis indicated that this gain in knowledge did not necessarily transfer to the more distal task of risk judgment. Bearing these results in mind, we are modifying BRCA Gist to place greater emphasis on conveying the gist of risk. Alternatively, BRCA Gist could provide training in risk judgment with explicit feedback.

Another advantage of SDT is its flexibility. By far the most common paradigms are the yes–no and two-alternative forced choice paradigms, each involving simple binary choice. However, SDT can be generalized to a larger number of categories. As a result of this flexibility, we were able to model risk judgment using three ordinal gist categories—low, medium, and high—that were theoretically grounded in FTT.

One potential issue is that the assumptions of the model may not hold perfectly, a common problem in mathematical modeling. In particular, the model assumes normality, equal variances, and the unidimensionality of risk. We have several grounds for believing that these assumptions are reasonable, even if not fully satisfied. First, the model provided a good fit to the data in the nutrition control and NCI groups. Adding more parameters would have diminishing returns, and would likely decrease the generalizability of the model to replications of the same experiment (Pitt & Myung, 2002). Although the model did not fit the BRCA Gist group as well, the magnitude of the discrepancy was small. However, given the relatively high value of G², the finding that the BRCA Gist tutorial increased sensitivity without affecting response bias—that is, the independence of d′ and c′—must be interpreted with caution. Ultimately, further investigation will be needed to refine the model and evaluate the tenability of its assumptions. What we have provided here is the initial computational and methodological groundwork for extending SDT into the domain of risk judgment.

Our theoretical rationale for using three ordinal gist-based risk categories is motivated by FTT and by research supporting the psychological reality of ordinal categories. However, the approach that we have outlined is compatible with other theoretical frameworks. Moreover, FTT does not limit its potential clinical application; on the contrary, FTT has been tested empirically in other domains of health and medical decision making (e.g., Reyna & Lloyd, 2006). Although the present study involved genetic risk of breast cancer, our approach is broadly applicable to other risk domains and can provide insight into peoples’ ability to understand and judge risk. Risk communication, especially communicating meaningful gist, is particularly important in light of the shift toward patient-centered care, in which patients assume more involvement in the decision-making process (Elwyn et al., 2012; Reyna et al., 2009).

Appendix A: Computational details

Responses can be organized in a 3×3 confusion matrix, as shown below. The diagonals represent correct responses, whereas the off-diagonals represent incorrect responses

		Stimulus
		Low	Medium	High
Response	Low	Correct	Incorrect	Incorrect
	Medium	Incorrect	Correct	Incorrect
	High	Incorrect	Incorrect	Correct

Model formulae

Let r index the response and s the stimulus. l, m, and h denote low, medium, and high risk, respectively.

$$r=[l,m,h]s=[l,m,h]$$

O_rs denotes the observed frequency of response r for stimulus s. θ is a vector of parameters in which C_s is the criterion, M_s is the mean, and σ_s is the standard deviation.

$$\theta =[C_s,M_s,{\sigma }_s]$$

ρ̂_rs denotes the estimated probability of responding r on stimulus s, and Φ is a normal cumulative distribution function.

The predicted probabilities for each response and stimulus combination are displayed below. As a point of reference, M_l = 0 and all σ_s=1, according to our assumption of equal variances.

$${\mathrm{\rho ̂}}_{11}=\mathrm{\Phi }\left(\frac{C_1-M_1}{{\sigma }_1}\right),{\mathrm{\rho ̂}}_{ml}=\mathrm{\Phi }\left(\frac{C_m-M_l}{{\sigma }_l}\right)-\mathrm{\Phi }\left(\frac{C_l-M_l}{{\sigma }_l}\right){\mathrm{\rho ̂}}_{hl}=1-\mathrm{\Phi }\left(\frac{C_m-M_l}{{\sigma }_l}\right){\mathrm{\rho ̂}}_{lm}=\mathrm{\Phi }\left(\frac{C_l-M_m}{{\sigma }_m}\right){\mathrm{\rho ̂}}_{mm}=\mathrm{\Phi }\left(\frac{C_m-M_m}{{\sigma }_m}\right)-\mathrm{\Phi }\left(\frac{C_l-M_m}{{\sigma }_m}\right){\mathrm{\rho ̂}}_{hm}=1-\mathrm{\Phi }\left(\frac{C_m-M_m}{{\sigma }_m}\right){\mathrm{\rho ̂}}_{lh}=\mathrm{\Phi }\left(\frac{C_l-M_h}{{\sigma }_h}\right){\mathrm{\rho ̂}}_{mh}=\mathrm{\Phi }\left(\frac{C_m-M_h}{{\sigma }_h}\right)-\mathrm{\Phi }\left(\frac{C_l-M_h}{{\sigma }_h}\right){\mathrm{\rho ̂}}_{hh}=1-\mathrm{\Phi }\left(\frac{C_m-M_h}{{\sigma }_h}\right)$$

Model parameters are estimated by maximizing the log multinomial likelihood function, which is displayed below.

$$P(O|\theta )=\sum _r^R\sum _s^S\text{ln}({\mathrm{\rho ̂}}_{rs}^{\mathrm{o}rs}),$$

where O_rs is the observed frequency of responding r to stimulus s.

The fit of the model can be evaluated with the likelihood ratio statistic shown below:

$$G^2=2\sum _r^R\sum _s^S{O}_{rs}\text{ln}\left(\frac{O_{rs}}{E_{rs}}\right),$$

where E_rs is the expected frequency of responding r to stimulus s. The model is evaluated at two degrees of freedom. The degrees of freedom are computed from the following formula (Wickens, 2002, p.247): df= categories− constraints− free parameters= 9− 3− 4= 2. There are three constraints because the columns in the confusion matrix must sum to the number of stimulus trials. The free parameters are M_m, M_h, C_m, and C_h.

Parameters

The d′ and c′ parameters are computed from the four free parameters M_m, M_h, C_m, and C_h:

$${d\prime }_{\mathrm{l}\mathrm{m}}=M_{\mathrm{m}},{d\prime }_{\mathrm{l}\mathrm{h}}=M_{\mathrm{h}},{d\prime }_{\mathrm{m}\mathrm{h}}={d\prime }_{\mathrm{l}\mathrm{h}}-{d\prime }_{\mathrm{l}\mathrm{m}},{c\prime }_{\mathrm{l}\mathrm{m}}=C_1-.5{d\prime }_{\mathrm{l}\mathrm{m}},\text{and}{c\prime }_{\mathrm{m}\mathrm{h}}=(C_{\mathrm{m}}-M_{\mathrm{m}})-.5(M_{\mathrm{h}}-M_{\mathrm{m}}).$$

Standard errors

The standard errors were adapted from Macmillan and Creelman (2005, p.325). π_rs denotes the observed proportion of responses associated with stimulus s and response r; N_s denotes the number of responses on stimulus trials s; and ϕ denotes the ordinate of the normal distribution.

$${\mathrm{\sigma }}_{{\mathrm{d}\prime }_{\mathrm{l}\mathrm{m}}}=\sqrt{\frac{{\mathrm{\pi }}_{\mathrm{m}\mathrm{m}}(1-{\mathrm{\pi }}_{\mathrm{m}\mathrm{m}})}{{\mathrm{N}}_{\mathrm{m}}{[\varphi ({\mathrm{\pi }}_{\mathrm{m}\mathrm{m}})]}^2}+\frac{{\mathrm{\pi }}_{\mathrm{m}\mathrm{l}}(1-{\mathrm{\pi }}_{\mathrm{m}\mathrm{l}})}{{\mathrm{N}}_1{[\varphi ({\mathrm{\pi }}_{\mathrm{m}\mathrm{l}})]}^2}}{\mathrm{\sigma }}_{{\mathrm{d}\prime }_{\mathrm{m}\mathrm{h}}}=\sqrt{\frac{{\mathrm{\pi }}_{\mathrm{h}\mathrm{h}}(1-{\mathrm{\pi }}_{\mathrm{h}\mathrm{h}})}{{\mathrm{N}}_{\mathrm{h}}{[\varphi ({\mathrm{\pi }}_{\mathrm{h}\mathrm{h}})]}^2}+\frac{{\mathrm{\pi }}_{\mathrm{m}\mathrm{h}}(1-{\mathrm{\pi }}_{\mathrm{h}\mathrm{m}})}{{\mathrm{N}}_{\mathrm{m}}{[\varphi ({\mathrm{\pi }}_{\mathrm{h}\mathrm{m}})]}^2}}{\mathrm{\sigma }}_{{\mathrm{d}\prime }_{\mathrm{l}\mathrm{h}}}=\sqrt{\frac{{\mathrm{\pi }}_{\mathrm{h}\mathrm{h}}(1-{\mathrm{\pi }}_{\mathrm{h}\mathrm{h}})}{{\mathrm{N}}_{\mathrm{h}}{[\varphi ({\mathrm{\pi }}_{\mathrm{h}\mathrm{h}})]}^2}+\frac{{\mathrm{\pi }}_{\mathrm{l}\mathrm{h}}(1-{\mathrm{\pi }}_{\mathrm{h}\mathrm{l}})}{{\mathrm{N}}_1{[\varphi ({\mathrm{\pi }}_{\mathrm{h}\mathrm{l}})]}^2}}{\mathrm{\sigma }}_{{\mathrm{c}}_{\mathrm{l}\mathrm{m}}^{\prime }}=\sqrt{.25{\mathrm{\sigma }}_{{\mathrm{d}\prime }_{\mathrm{l}\mathrm{m}}}^2}{\sigma }_{{\mathrm{c}}_{\mathrm{m}\mathrm{h}}^{\prime }}=\sqrt{.25{\mathrm{\sigma }}_{{d\prime }_{\mathrm{m}\mathrm{h}}}^2}$$

Hierarchical model comparison

Hierarchical model comparison can be used to test the null hypothesis that two parameters are equal. Instructions for this procedure can be found in the supplementary spreadsheet. A full model and a nested model are compared in terms of their abilities to fit the data. In the full model, all of the parameters are free to vary. However, in the nested model, the parameters of interest (e.g., the d′s for two different groups) are constrained to be equal, whereas the remaining parameters are free to vary. According to the logic of hierarchical model comparison, a statistically significant reduction in fit between the nested model and the full model would indicate that different parameter values are necessary to explain the data. In this case, one could infer that the parameter values are different. This would be evaluated statistically as follows:

$$\Delta G^2={G^2}_{\text{nested}}-{G^2}_{\text{full}},$$

with

$$\Delta df=d{f}_{\text{nested}}-d{f}_{\text{full}}.$$

The spreadsheet includes two supplementary indices to assess the difference between the full and nested models. w is a measure of effect size that is used for goodness of fit and is a member of the r family of effect sizes:

$$w=\sqrt{\frac{G^2}{N}},$$

where N is the total number of observations (Cohen, 1988, p.216). The spreadsheet also includes the posterior probability of the nested model, assuming that both models are weighted equally a priori. Bayesian methods have been proposed as an alternative to p values (Wagenmakers, 2007). One advantage is that, unlike the p value, the posterior probability also quantifies support for the null hypothesis (nested model, in this case). The posterior probability of the nested model is defined as in Lewandowsky and Farrell (2010):

$$P(M_{\text{nested}}/\text{Data})=\frac{1}{1+e^{2({\text{BIC}}_{\text{nested}}-{\text{BIC}}_{\text{full}})}},$$

where the Bayesian information criterion for the mth model is

$${\text{BIC}}_m=-2\text{ln}[P(O|\theta )]+p_m\text{ln}(N),$$

and p_m is the number of parameters in the mth model. A tutorial on Bayesian methods can be found in Fisher and Wolfe (2012).

Appendix B: Scenarios for genetic risk of breast cancer

Each description has the following information: name, age, ethnicity, hometown, family health facts, and personal health facts. Conditions are equated for age. The range of words is 56– 60, the range of Flesch Reading Ease scores is 56.9–62.9, and the range of Flesch–Kincaid Grade Level scores is 7.3–7.9.

Highest risk: PAT score of 8–10

Rachel, PAT Score 10; Words: 56; Flesch Reading Ease Score: 62.5; Flesch–Kincaid Grade Level Score: 7.3.

Rachel is a 47-year-old Chicago woman. Her parents came to this country from Eastern Europe and her family background is Ashkenazi Jewish. She has two cousins on her mother’s side who have breast cancer. Her cousin Joanne was diagnosed with breast cancer at age 56, and Elaine at age 61. Rachel has generally been healthy.

Anabelle, PAT Score 10;Words: 57; Flesch Reading Ease Score: 57.6; Flesch–Kincaid Grade Level Score: 7.5.

Anabelle is a healthy 55-year-old Italian-American. She lives in Providence, Rhode Island. Anabelle comes from a family of nine children. Two of her sisters are breast cancer survivors. Her sister Grace was diagnosed with breast cancer at the age of 49, and Faith when she was 53. Her 66-year-old cousin Maria also had breast cancer.

Sarah, PAT Score 9; Words: 58; Flesch Reading Ease Score: 62.3; Flesch–Kincaid Grade Level Score: 7.4.

Sarah is 66 years old and lives in Boca Raton, Florida. She lives with her husband and pet dogs Baby and Dolly. She is of Ashkenazi Jewish descent, but she and her husband are not very religious. Sarah likes playing golf, and she has always been healthy and active. Recently her younger sister was diagnosed with ovarian cancer.

Claire, PAT Score 8; Words: 59; Flesch Reading Ease Score: 62.9; Flesch–Kincaid Grade Level Score: 7.4.

Claire is an unattached 35-year-old New Yorker. She has a vegan diet, and is an avid jogger. Her family is of Scottish-Irish heritage. Recently, her 51-year-old uncle Sean was diagnosed with cancer of the breast. Claire has several siblings and, to the best of her knowledge, her uncle Sean is the only family member with breast cancer.

Medium risk: PAT score of 3–5

Kim, PAT Score 5; Words: 56; Flesch Reading Ease Score: 57.9; Flesch–Kincaid Grade Level Score: 7.9.

Kim is a 66-year-old Korean American mother who lives in San Jose, California, with her family. Kim suffers from migraine headaches. Her 59-year-old sister Sun is a 5-year ovarian cancer survivor. That is the only cancer in her family that she knows about. Kim eats healthy foods, but does not get enough exercise.

Hanna, PAT Score 4; Words: 59; Flesch Reading Ease Score: 59.1; Flesch–Kincaid Grade Level Score: 7.4.

Hanna is a 55-year-old mother of Ashkenazi Jewish descent. Her ancestors are from Eastern Europe. She lives in Cleveland Heights, Ohio, with her husband and youngest daughter. No one in her extended family has ever had cancer. She likes to walk to work for exercise when the weather is good. However, she suffers from asthma and seasonal allergies.

Olive, PAT Score 4; Words: 60; Flesch Reading Ease Score: 62.1; Flesch–Kincaid Grade Level Score: 7.5.

Olive is 47 years old, the exact same age that her mother was when she died of breast cancer complications. She also lost an uncle to lung cancer. No one else in her French-Canadian family has had breast or ovarian cancer. Olive is considered medically obese, and her weight frequently fluctuates. She lives in Los Angeles with her roommate.

Janet, PAT Score 3; Words: 57; Flesch Reading Ease Score: 60.2; Flesch–Kincaid Grade Level Score: 7.6.

Janet is a 35-year-old Denver woman of English and Scottish ancestry. Janet is prone to kidney stones, and her urologist has her on a diet low in red meat. Her 61-year-old cousin was recently diagnosed with breast cancer. No one else in the family has had cancer, but her mother has diabetes. Janet herself battles obesity.

Low risk: PAT score of 0

Alegria, PAT Score 0; Words: 60; Flesch Reading Ease Score: 62.1; Flesch–Kincaid Grade Level Score: 7.5.

Alegria is a 47-year-old Mexican American. She lives in Phoenix, Arizona, with her husband. Alegria is a heavy cigarette smoker. Her best friend is a 10-year breast cancer survivor, but this has not been enough to get her to give up her two-pack-a-day cigarette habit. No one in her family has ever had breast cancer.

Natalie, PAT Score 0; Words: 60; Flesch Reading Ease Score: 59.2; Flesch–Kincaid Grade Level Score: 7.9.

Natalie is a 66-year-old woman who lives with her husband Charlie in Cincinnati. She does not have any children. Her ancestors were German Lutherans, but her husband is of Ashkenazi Jewish descent. Although they have both been healthy, recently her husband Charlie was diagnosed with cancer of the breast. No one else in her family has ever had cancer.

Kate, PAT Score 0; Words: 57; Flesch Reading Ease Score: 61.1; Flesch–Kincaid Grade Level Score: 7.4.

Kate is 55-years old, divorced, and lives by herself in a townhouse in Atlanta. Kate frequently feels exhausted even when she has not physically exerted herself. Her family can trace many of their ancestors back to England. Five years ago, Kate had basal cell carcinoma removed from her scalp. Her father also had skin cancer removed.

Rheana, PAT Score 0; Words: 60; Flesch Reading Ease Score: 60.4; Flesch–Kincaid Grade Level Score: 7.3.

Rheana is a 35-year-old African American woman from Columbus. Her family has a history of diabetes and hypertension. For this reason, she goes out of her way to cook healthy meals for her family. Her brother was recently diagnosed with prostate cancer. No one else in the family has ever had cancer. Rheana considers herself blessed with good health.