Respiration and heart rate complexity: Effects of age and gender assessed by band-limited transfer entropy

Abstract

Aging and disease are accompanied with a reduction of complex variability in the temporal patterns of heart rate. This reduction has been attributed to a break down of the underlying regulatory feedback mechanisms that maintain a homeodynamic state. Previous work has established the utility of entropy as an index of disorder, for quantification of changes in heart rate complexity. However, questions remain regarding the origin of heart rate complexity and the mechanisms involved in its reduction with aging and disease. In this work we use a newly developed technique based on the concept of band-limited transfer entropy to assess the aging-related changes in contribution of respiration and blood pressure to entropy of heart rate at different frequency bands. Noninvasive measurements of heart beat interval, respiration, and systolic blood pressure were recorded from 20 young (21–34 years) and 20 older (68–85 years) healthy adults. Band-limited transfer entropy analysis revealed a reduction in high-frequency contribution of respiration to heart rate complexity (p < 0.001) with normal aging, particularly in men. These results have the potential for dissecting the relative contributions of respiration and blood pressure-related reflexes to heart rate complexity and their degeneration with normal aging.

1. Introduction

Although it is known that aging is associated with increased cardiovascular risk (Lakatta et al., 2009; Najjar et al., 2005; Ryan et al., 1994; Shiogai et al., 2010), the underlying mechanisms are poorly understood. Furthermore, diseases such as obstructive sleep apnea, which are independent risk factors for cardiovascular disease, increase in prevalence with age (Ancoli-Israel et al., 1996; Wellman et al., 2007; Young et al., 2002), and may contribute to overall cardiovascular risk. In order to assess the relationships between age and cardiovascular control, investigators have used indices of heart rate (HR) variability (based on the variance of HR time series) and complexity (based on predictability and nonlinear relationships in HR time series), with most studies demonstrating a reduction in HR variability and complexity with age (Goldberger et al., 2002; Nolan et al., 1998; Ponikowski et al., 1997; Tsuji et al., 1996). However, the specific mechanisms for this reduction are not known.

There are a number of mechanisms that contribute to variability in HR; among them are those linked to variability in blood pressure and respiration (including periodic and aperiodic oscillations). They may emerge as a result of various delayed feedback and feedforward pathways between the system variables (Bruce, 1996; deBoer et al., 1987; Nemati et al., 2011), as well as the influence of signals from the afferent and efferent nerves influencing vagal-cardiac motoneuron and pacemaker cells involved in generation of heart beat and respiration (Del Negro and Hayes, 2008; Eckberg, 2009). Quantification of the coupling between HR and factors such as blood pressure and respiration is therefore necessary to probe the origin of the reduction in HR variability and complexity with age. Using spectral analysis of HR and respiration, several authors have shown a significant reduction with age in HR variability in the frequency ranges associated with breathing (Pinna et al., 2006; Singh et al., 2006). However, techniques using spectral analysis make major assumptions about the underlying system dynamics including linearity and stationarity. Such limitations are important given that previous research has suggested that the coupling between respiration and cardiovascular system is strongly nonlinear (Novak et al., 1993; Wessel et al., 2009), and in this case, spectral analysis is not appropriate.

Given these limitations, Goldberger et al. have successfully used techniques from nonlinear dynamics, such as fractal scaling and entropy, to characterize subjects according to the nonlinear complexity of their HR (Goldberger et al., 2002; Iyengar et al., 1996; Lipsitz and Goldberger, 1992; Ryan et al., 1994). The concept of entropy for assessing higher order temporal structures in the time series has been emphasized (Ryan et al., 1994; Takahashi et al., 2012), since it does not make any assumptions about the linearity of the system. Notably, a conditional variant of entropy known as sample entropy has been widely used to assess the complexity of HR (Humeau et al., 2008; Lake et al., 2002; Moorman et al., 2011; Vaillancourt et al., 2004). By extension, multiscale entropy, which examines the entropy at different time-scales, has been suggested as an effective tool to assess physiological systems (Costa et al., 2002). However, a limitation of all these techniques (including spectral methods when applicable) is that they do not assess directional relationships (e.g., the nonlinear influences of respiration and blood pressure on HR), and therefore, without substantial prior physiological knowledge, have limited power to reveal the underlying mechanisms responsible for the changes in complexity.

As such the major aim of the current work is to develop a technique based on the concept of band-limited transfer entropy to quantify the contribution of both respiration and blood pressure to HR complexity over multiple frequency bands. The proposed technique aims to track the directional coupling between both respiration and blood pressure with HR over low and high frequency bands, which are influenced by the sympathetic and parasympathetic regulatory reflexes (Robinson et al., 1966; Shannon et al., 1987). Previously, Iyengar et al. (1996) demonstrated a reduction in complex variability of HR (based on the concept of fractal scaling) with aging in a subset of subjects from the Physionet Fantasia database. Here we confirm the findings of that study within the entire Fantasia dataset (Goldberger et al., 2000) using a conditional entropy analysis, and then assess the aging-related changes in contribution of respiration and blood pressure to HR complexity within the male and female populations using the technique of band-limited transfer entropy.

2. Methods

2.1. Dataset

Our cohort consisted of a group of healthy subjects from the Physionet Fantasia database (Goldberger et al., 2000; Iyengar et al., 1996), which consisted of 20 young subjects (21–34 years) and 20 older adults (68–85 years). Each group was made up of equal numbers of males (n = 10) and females (n = 10). The subjects underwent two hours of continuous monitoring in supine resting position while watching the Disney movie ‘Fantasia’. Continuous time-synchronized measurements of electrocardiogram (ECG) and respiration (impedance plethysmography) were collected in all subjects. Additionally, non-invasive measurements of blood pressure (tonometric pressure, Colin Electronics) were recorded in a subset of 10 young and 10 older adults. All waveforms were recorded at 250 Hz sampling frequency. All of our analyses are limited to artifact-free segments of the data, determined according to the signal quality assessment procedure described below.

2.2. Preprocessing and extraction of beat-by-beat time series

An example of the processed waveforms and time series is shown in Fig. 1. We used the automatically detected, visually verified and corrected ECG R-peak annotations available on the Fantasia website (Goldberger et al., 2000) to derive time series of peak-to-peak (RR) intervals. Within each RR interval, a search was performed to find the location of peaks of the blood pressure; these constituted our systolic blood pressure (SBP) time series. The onset of each breath was detected as follows (Nemati et al., 2011). We first removed the baseline drift (often seen in impedance plethysmography-based measurement of respiratory volume) by fitting a cubic spline function through all the breath onsets, and subtracting the resulting “baseline” curve from the respiratory waveform; the resulting volume waveform started at zero upon the onset of each breath. Next, we constructed a respiratory volume time series for each RR interval from the volume difference at the times of the R wave peaks (see Fig. 2, panels A, C, and E).

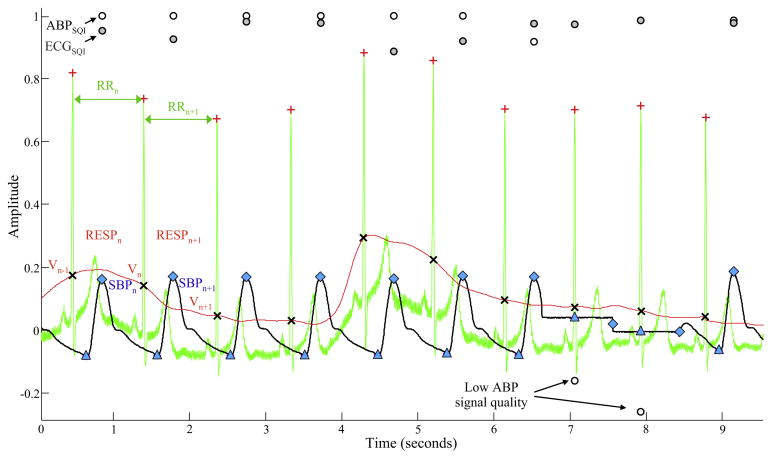
Fig. 1.

Example of raw waveforms and signal quality indices from a 10 s recording of ECG (green trace), blood pressure (black trace), and impedance plethysmography-based respiratory volume waveforms (red trace). All waveforms were scaled to fit on the same graph. The location of each ECG R-peak is marked by the plus symbol (+), and two consecutive RR intervals are denoted as RR_n and RR_n+1. Moreover, the systolic and diastolic blood pressure values are marked by diamond (◆) and triangle (△) symbol on the blood pressure waveform, and two consecutive systolic blood pressure values (corresponding to the two RR intervals) are denoted as SBP_n and SBP_n+1. The respiratory volume time series sample for the RR_n interval (denoted by RESP_n) was calculated as the difference between the values of the respiratory volume waveform at the boundaries of the RR_n denoted by cross symbol (×) (that is RESP_n = V_n−V_n−₁). At approximately 7 s the blood pressure signal is lost for two heart beats due to an automated calibration procedure, which results in the signal quality index of blood pressure (ABP_SQI; open circles) to drop below zero. Note that, the ECG signal quality index (ECG_SQI; closed circles) remains unchanged.

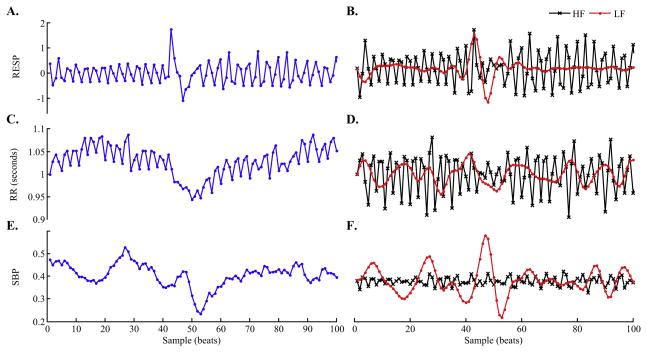
Fig. 2.

Example of extracted time series. Panels A, C, and E show 100 samples of time series of respiration, RR intervals and systolic blood pressure, respectively. The corresponding low-passed (LF) and high-passed (HF) time series, respectively, are shown in panels B, D, and F. Note that both the respiration and blood pressure measurements were uncalibrated.

Due to the presence of artifacts in ECG and blood pressure waveforms, we also calculated indices of waveform signal quality via constructing template (or average) beats and assigning a signal quality index (SQI) to every ECG and blood pressure beat according to their correlation coefficient with their corresponding templates; where a correlation coefficient near unity represents a high quality signal. For each subject, a separate template beat for ECG and blood pressure was constructed by placing a temporal window of size equal to median RR interval (symmetric around the waveform peaks) on each beat and averaging the windows over all the beats. Next, each record was segmented into continuous artifact-free blocks of ECG (and when available blood pressure) with SQIs of larger than 0.7. Finally, all samples within each time series were replaced with their ranks (similar to nonparametric statistical tests) (Lee et al., 2012) in order to eliminate the problem of data outliers while still preserving all the joint information among time series (Darbellay and Vajda, 1999; Hudson, 2006b). We used the resulting time series within all the artifact-free data blocks for the estimation of transfer entropy.

2.3. Transfer entropy

Recent techniques for studying nonlinear directional relationships among discretized physiological variables have been based on utilizing the concept of transfer entropy (Lee et al., 2012; Porta et al., 2011). Briefly, given two time series X = {x₁, x₂,…, x_N} and Y = {y₁, y₂, …, y_N}, the transfer entropy from X to Y, denoted T_X→Y (Lee et al., 2012) is defined by:

$$T_{X\to Y}=H(y_i\mid y_{i-1})-H(y_i\mid y_{i-1},x_{i-\tau }),$$ (1)

where for an arbitrary time series Z with probability density P(z_i), its entropy H(Z) = −Σ_zi P(z_i) log P(z_i) is related to the amount of information needed to predict the future values of the time series. Thus, a time series with a high level of entropy tends to be more random and have greater complexity. Furthermore, the conditional entropy term H(z_i|z_{i− τ}) = Σ z_i, z_i−1 P(z_i, z_{i− τ}) log(P(z_{i− τ})/P(z_i, z_{i− τ})), where P(z_i, z_{i− τ}) is the joint probability density, is the amount of information needed to predict the future values of Z if we know its past value at some lag τ. For example, the conditional entropy of RR intervals, denoted as H(RR_i|RR_i−1), is the amount of information needed to predict the future value of RR given that we know its current value at time i. Thus in Eq. (1), the transfer entropy from X to Y, T_X→Y, quantifies the amount the history of X at lag τ (i.e., x_i−τ) predicts the current value of Y (i.e., y_i) beyond the amount it is already predicted by its own immediate history (i.e., y_i−1). When considering the transfer entropy from both SBP and RESP to RR intervals, we varied the lag parameter τ from 1 to 6, and we report the lag with the maximal transfer entropy. The fast parasympathetic (or vagal) responses allow the SBP and RESP to affect RR interval within one beat, while the slower sympathetic response may take two or three beats to attain its maximal effect (deBoer et al., 1987; Eckberg, 2009).

Calculation of the conditional entropy quantities in Eq. (1) requires estimation of joint probability distributions among the variables of interest. Typically this procedure is done by binning the data in a manner similar to constructing histograms, which requires an often arbitrary decision regarding the number and size of bins. In this work, we adopted the technique described in Hudson (2006a) which uses the Darbellay–Vajda (DV) partitioning algorithm to adaptively assign bins of varying sizes to different regions within the variable space, thus obviating the need for arbitrary choices of bin sizes or other parameter settings that are often needed with other continuous variable density estimation techniques, such as selecting a bandwidth in kernel density estimation (Scott and Sain, 2005). Moreover, the DV partitioning technique has advantage of being able to perform well given small number (i.e., a few hundred) of time series samples (Lee et al., 2012). Intuitively, the technique adaptively assigns larger size bins to regions where there is low concentration of data points and vice versa. A larger bin size results includes more samples for estimating the probability of an event, at the cost of having less certainty regarding the exact values defining that event. In this work we extended the two-dimensional DV partitioning (Hudson, 2006a) to include a third variable (lagged HR). Note that Hudson’s formula (Hudson, 2006a) for Pearson’s χ² test of uniformity used in adaptive partitioning neglects normalization of the squared residuals by the expected probabilities; this was corrected in the current work. Additionally, assuming stationarity across multiple blocks of data from the same record, we combined the time series across all the artifact-free blocks to estimate the joint probability distributions. Therefore, our technique uses all the available data to produce a single index of entropy (either conditional or transfer) for the entire record.

2.4. Band-limited transfer entropy

Physiological regulatory mechanisms often operate across multiple time scales. For instance, the sympathetic autonomic control is known to be slow acting, while the parasympathetic system has a faster response (Robinson et al., 1966). Therefore, we extended our transfer entropy estimation framework (Lee et al., 2012) to study entropy transfer at two different frequency-bands; a high frequency (HF) band (corresponding to periods of 2–5 beats; reflecting fast changes over short time-scales) and a low frequency (LF) band (corresponding to periods of 6–20 beats; reflecting slow changes). The time series of RESP, RR, and SBP were band-pass filtered (using a 7th order Butterworth digital filter) using zero-phase filtering¹ (thus avoiding possible phase distortions) to generate the HF and LF band-limited signals for each time series (Fig. 2, panels B, D, and F). Finally, our transfer entropy estimation technique was applied to the associated band-limited time series separately within the LF and HF bands.

2.4.1. Surrogate test of significance

In a similar fashion to analyses using correlation, random coincidences may result in spurious measurements of transfer entropy, requiring care in establishing the statistical significance of the transfer entropy results. In the current work, significance of the entropy transfer from time series X to Y was determined by Monte Carlo surrogates, through temporally shuffled time series (Lee et al., 2012). The idea is that any significant transfer entropy ought to be due solely to the specific temporal relationships between X and Y time series. Shuffling destroys these relations and therefore any remaining entropy transfer is taken as random coincidences. In our work, the source time series was shuffled 100 times and T_X→Y was calculated for each case. The transfer entropy from the original source time series was assessed significant if it was greater than the 95th percentile of the surrogate results.

The Matlab script used for generating time series and SQIs from the waveforms, as well as our Matlab implementation of multiblock band-limited transfer entropy with adaptive partitioning is available on the Physionet (Goldberger et al., 2000) website.

2.5. Statistical analysis

Kruskal–Wallis nonparametric ANOVA test (with Tukey’s significant difference criterion) (Hochberg and Benjamini, 1990) was used for comparing groups across four categories of young females (FY), young males (MY), older females (FO), and older males (MO). When comparing the combined group of men and women for young versus older subjects we used the unpaired t-test. For all tests, p < 0.05 was considered statistically significant.

3. Results

Time series of RR intervals, SBP, and RESP were constructed from the corresponding waveforms as described in Section 2.2. Approximately 88 ± 13% of the time series from the combined young group were assessed as high quality (amounting to ~6500 ± 1400 samples) compared with 84 ± 15% of data from the combined older group (amounting to ~5700 ± 1450 samples). To ensure our analysis was not influenced by varying sample sizes we used the first 2500 samples for the entropy analyses that follows.

3.1. Conditional entropy analysis

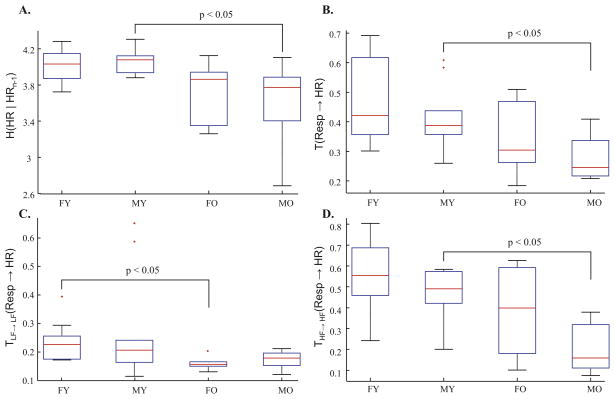
The results of the RR interval conditional entropy analysis are summarized in Table 1 (first row). Conditional entropy was significantly lower in the old group compared with the younger group. The multiple comparisons test shown in Fig. 3 (panel A) demonstrated that the significant reduction in conditional entropy with aging was driven by the reduction in males.

Table 1.

Effects of respiration and blood pressure on various entropy measures, pooled over sex.

	Young	Old
H (HR|HRn−1)	4.08 [3.89 4.13]	3.84 [3.39 3.94]*
T (Resp → HR)	0.41 [0.36 0.52]	0.27 [0.22 0.38]†
THF→HF (Resp → HR)	0.49 [0.44 0.60]	0.27 [0.15 0.41]†
TLF→LF (Resp → HR)	0.22 [0.18 0.24]	0.17 [0.15 0.19]†
T (SBP → HR)	0.18 [0.16 0.19]	0.19 [0.18 0.21]
THF→HF (SBP → HR)	0.23 [0.15 0.31]	0.17 [0.11 0.28]
TLF→LF (SBP → HR)	0.25 [0.21 0.29]	0.20 [0.17 0.23]

Median, first and third quartiles (inside the brackets) of conditional entropy (H), transfer entropy (T), and band-limited transfer entropy; within the low frequency (T_LF→LF) and high frequency (T_HF→HF) bands. The symbols * and ^† indicates a statistically significant change in the median values between the young and the older populations (p < 0.05 and p < 0.01, respectively).

Fig. 3.

Summary of entropy analysis results, broken down with respect to age (Y: young versus O: old) and gender (M: male versus F: female). Conditional entropy of RR intervals (panel A) shows a significant reduction in older men, which is associated with a reduction in transfer entropy from respiration to RR intervals (panel B). The transfer entropy reduction was significant in both the LF band (panel C) and HF band (panel D).

3.2. Transfer entropy from RESP to RR intervals

All subjects passed the surrogate test of significance for at least one lag. The results presented in Table 1 (second row) are based on the maximal significant lag, which was defined as the significant lag (according to the surrogate test) for which transfer entropy was largest in magnitude. The median value of the maximal significant lag for transfer entropy in the young group was 1 [1, 2] (median [interquartile-range]), versus in the older group it was 2 [2, 2.5] (p < 0.05; Wilcoxon rank-sum test). We observed a significant reduction in transfer entropy with aging. Fig. 3 (panel B) demonstrates that the older subjects exhibit significantly lower transfer entropy when compared to the younger group, a reduction driven by the male subjects.

3.3. Band-limited transfer entropy from RESP to RR intervals

All subjects passed the surrogate test of significance for at least one lag. Table 1 (row three and four) shows that there was a significant reduction in transfer entropy in both the LF and HF bands with aging. Furthermore, Fig. 3 (panels C) demonstrates that the LF band transfer entropy was significantly lower in the older females compared to the younger females. Within the HF band, there was a significant reduction in transfer entropy within males. Within the LF band, 10% of the subjects did not pass the surrogate test of significance. The median maximal significant lag for transfer entropy in the young group was 1 [1, 4] versus in the older group it was 2 [1, 4]. Moreover, within the HF band, all subjects passed the surrogate test of significance for at least one lag. The median maximal significant lag in the young group was 1 [1, 1] versus in the older group it was 1 [1, 2].

3.4. Transfer entropy from blood pressure to RR intervals

Both the transfer entropy and the HF band transfer entropy from blood pressure to HR were approximately half of the corresponding values for respiration, while in the LF band the values were comparable (see Table 1 rows 5–7). We did not observe any significant change in entropy transfer from SBP to RR with aging, using either transfer entropy or the band-limited transfer entropy.

4. Discussion

The current study goes beyond a descriptive index of RR interval complexity at a single time-scale, by quantifying the influence of lagged values of RESP and SBP on RR interval entropy within two different time-scales corresponding to the LF and HF bands. Our results suggest that there is a significant reduction in RESP to RR transfer entropy with age, which is particularly apparent in men. The reduction in transfer entropy within the male population was driven by the pronounced reduction in the HF band. This observation leads us to hypothesize that in men the reduction in heart rate complexity with age, known to be linked to increased adverse prognosis, may partially be explained by a reduction in the influence of respiration within the HF bands on RR intervals.

The transfer entropy technique has gained popularity over the past decade in the study of directional relationships among variables from both linear and nonlinear systems due to its many strengths over existing techniques (Hlavackova-Schindler et al., 2007; Porta et al., 2011). Our implementation of the transfer entropy technique has the additional advantage of not requiring any user specified parameters for estimating the joint probability distributions needed for evaluating Eq. (1), which mitigates the problems associated with subjective settings of parameters, particularly those of binning. Furthermore, we adopted a data segmentation scheme based on the signal quality indices that mitigates the problem of recording artifacts. Importantly, the band-limited transfer entropy technique used in the present study allows directional relationships to be analyzed at multiple time-scales corresponding to different physiological control mechanisms. Band-limited analysis, via band-pass filtering in order to remove low frequency trends as well as high frequency noise, improves time series stationarity and robustness of the transfer entropy estimation technique to noise. Finally, the ranking step used in calculation of joint-probability distributions, while preserving non-linear relationships (Darbellay and Vajda, 1999; Hudson, 2006b), makes the technique robust to outliers such as a spontaneous sigh during regular breathing or an ectopic heart beat.

4.1. Comparison with other approaches

Our results confirm and extend previous findings (Shiogai et al., 2010), demonstrating a reduction in the influence of the phase of respiration on the phase of RR interval with aging, by additionally examining influence of respiratory amplitude on RR complexity. Inclusion of amplitude of respiration (in addition to phase) is physiologically important, since a large increase in tidal volume will have a larger influence on intrathoracic pressure, the cardiac output, and ultimately the baroreflex control of HR.

A number of studies have employed variations of transfer entropy, such as time-delayed mutual information (Pompe et al., 1998) and conditional mutual information (Porta et al., 2011), to investigate relationships between cardiovascular variables. Time-delayed mutual information does not take into account possible temporal dependencies within a given time series (i.e., does not condition on the history of the time series itself) when assessing information flow from another time series at different time lags. Therefore, the standard time delayed mutual information cannot distinguish between information that is due to common history and inputs and the information that is exchanged (Schreiber, 2000). Conditional mutual information, when histories of both time-series are taken into account, has been shown to be equivalent to transfer entropy (Paluš and Vejmelka, 2007).

An important strength of our technique is that it assesses the influence of respiration on RR intervals at different lags. Notably, within the younger subjects the previous value of respiration yielded the greatest amount of information about the current value of RR interval (i.e., the largest reduction in uncertainty) whereas in older adults it was the values of respiration at two lags back that was most significant. The influences of change in pleural pressure associated with respiration on the observed changes in RR intervals are complex and may involve time delays. In particular, mechanical heart/lung interactions include ventricular interdependence, changes in preload/afterload, volume status, and cardiac function. Our findings therefore suggest that the net effect of these interactions may become progressively slower with aging.

4.2. Methodological considerations

The simplified transfer entropy definition used in this work has limitations that must be considered. First, only the immediate history of RR time series was considered when estimating the transfer entropy quantities. The main reason for this choice was methodological simplicity and our prior experience with the technique (Lee et al., 2012). Nevertheless, it is conceivable that the current value of RR is influenced by the intrinsic “memory” within the sinoatrial node (or the brain-stem neurons projecting thereto) and this memory in principle can go back several heartbeats. Moreover, this intrinsic memory property could change with aging. However, this would not be expected to significantly affect our transfer entropy estimates, since the influence of the immediate past history is included in the two conditional entropy terms that constitute Eq. (1).

Filtering a signal can distort the phase relationships of the various frequency components of a signal and therefore may complicate interpretation of band-limited transfer entropy quantities; especially since nonlinear systems can exhibit cross-frequency interactions. To avoid this problem, we utilized zero-phase filtering which preserves the original phase relationships. However, filtering also involves weighted averaging which introduces spurious correlations among the consecutive values of a time series. This bias may contribute to the change in maximal lag time between transfer entropy and HF band transfer entropy seen in older subjects, in addition to the lower magnitude of transfer entropy in these subjects.

4.3. Utility of our analytic approach

In our previous work, we showed that the transfer entropy technique can be used to characterize the changes in influences of blood gases on respiration after administration of the dopamine antagonist domperidone (Lee et al., 2012) which acts to enhance chemosensitivity (Edwards et al., 2008). Similarly, when dealing with interventions that alter HR complexity, the current technique can quantify and track the therapeutic outcomes aimed at improving and enhancing healthy HR complexity. More generally, our technique allows us to go beyond descriptive indices of complex variability in physiological signals and probe specific sources of variability, constituting a systems view of variability. Such knowledge is important in disease diagnosis and treatment (Buchman, 2004) through interventions aimed at reducing pathological oscillations (e.g., Cheyne–Stokes respiration) or enhancing favorable oscillations (e.g., healthy variability in HR dynamics (Costa et al., 2002; Ivanov et al., 1999)).

It is important to note that the Fantasia cohort consisted of entirely healthy subjects, and therefore the reduction in transfer entropies reported in the current work should be attributed to healthy aging. An intriguing question is how and the extent to which the compounding effects of cardiovascular risk factors, such as obstructive sleep apnea (Ancoli-Israel et al., 1996; Wellman et al., 2007; Young et al., 2002), contribute to the reduction in heart rate complexity and transfer entropies in a longitudinal study.

5. Conclusion

We showed that the known age-related reduction in complexity (as measured by entropy) of heart rate is associated with (1) a significant reduction in transfer entropy from respiration to heart rate, and (2) an increase in the lag where respiration has its maximal influence on heart rate. Moreover, the reduction in entropy was larger in the high frequency band, which was particularly pronounced within the male population. Surprisingly, the transfer of entropy from blood pressure to heart rate was both modest and did not change significantly with normal aging, suggesting the possible involvement of non-baroreflex mechanisms responsible for the reduced influence of respiration on heart rate complexity. Application of this technique may shed light on the origin of pathological alterations in HR complexity in different disease populations (Goldberger et al., 2002), thus allowing therapies to be directed at the specific underlying mechanisms responsible for deterioration of healthy HR complexity.