Microscopic insights into the NMR relaxation based protein conformational entropy meter

Abstract

Conformational entropy is a potentially important thermodynamic parameter contributing to protein function. Quantitative measures of conformational entropy are necessary for an understanding of its role but have been difficult to obtain. An empirical method that utilizes changes in conformational dynamics as a proxy for changes in conformational entropy has recently been introduced. Here we probe the microscopic origins of the link between conformational dynamics and conformational entropy using molecular dynamics simulations. Simulation of seven pro! teins gave an excellent correlation with measures of side-chain motion derived from NMR relaxation. The simulations show that the motion of methyl-bearing side-chains are sufficiently coupled to that of other side chains to serve as excellent reporters of the overall side-chain conformational entropy. These results tend to validate the use of experimentally accessible measures of methyl motion - the NMR-derived generalized order parameters - as a proxy from which to derive changes in protein conformational entropy.

Introduction

The thermodynamic nature of the folded state of proteins governs their biological function in innumerable ways. Indeed, the many forces that govern the stability of the native state are complex and continue to be difficult to unravel and dissect through experiment, simulation or theory.^1,2 This is particularly true for the residual conformational entropy of proteins, which is potentially a central component of the thermodynamics governing protein function.^3-5 Historically, it has been impossible to experimentally determine the contribution of residual protein entropy to fundamental protein activities such as the binding of ligands, vital for protein function. Recent progress has illuminated the possibility of employing NMR relaxation methods to quantitatively determine the role of changes in conformational entropy in molecular recognition by proteins.⁶ The approach rests on using fast internal protein dynamics as a proxy for conformational entropy.⁷ The initial approach was to effectively take an inventory of the change in motion at a limited number of sites and interpret this within the context of a simple physical model such as the harmonic oscillator⁸ or diffusion within an infinite square well.⁹ This raises several obvious issues such as the effects of correlated motion, the operation of a more complex potential energy function, the completeness of the oscillator count, and so on.⁷ More recently this issue was sidestepped by using an empirical calibration of the dynamical proxy for conformational entropy. Rather than attempt a model-dependent interpretation of an inventory of changes in local dynamics, an empirical scaling between the experimental measures of local dynamics and local disorder (entropy) was attempted.¹⁰ The idea rests on the assumption that the experimentally accessible methyl-bearing side chains are numerous enough to provide good coverage of internal motion and are sufficiently coupled to neighboring side chains to report on the entropy.⁶ With an appropriate experimental system, this leads to a rather simple relationship between what can be measured (protein motion and total binding entropy) or confidently calculated (solvent entropy) and what is desired (conformational entropy).¹⁰ Thus by comprehensively measuring the change in motion of methyl-bearing side chains on the nanosecond time scale using classical NMR relaxation methods^11-15 one could obtain a quantitative measure of the underlying change in conformational dynamics.¹⁰ This approach was first introduced using the binding of calcium-saturated calmodulin to a series of calmodulin-binding domains.¹⁰ The results demonstrated that changes in conformational entropy were important to ligand binding and also confirmed an earlier suggestion¹⁶ that conformational entropy contributes to the tuning of the free energy of binding in this system.¹⁰ Recently, a second example has appeared where Tzeng & Kalodimos used an impressive collection of mutants of the catabolite activator protein (CAP) to undertake a similar analysis of the thermodynamic origins of high affinity binding of DNA to the cAMP-activated protein.¹⁷ The advantage of the CAP system is that the same binding ligand (DNA) was used, the structure does not change appreciably upon binding the DNA and an array of structurally benign mutations remote from the binding interface were available. This eliminated most of the uncertainties that may have hampered the analysis of the calmodulin complexes described above. The resulting empirical calibration for CAP was most impressive and led to a convincing analysis of the role of conformational entropy in the binding of ligands to the CAP protein and its potential role in its allosteric regulation.¹⁷

Here we attempt to understand the microscopic origins of the apparent success of the empirical “entropy meter” based on a dynamical proxy measured through NMR relaxation methods. We employ extensive molecular dynamics simulations in explicit water to examine the ability of measures of fast motion of methyl groups in proteins to adequately represent the conformational entropy of the protein. In addition, we explore several issues as such as the degree to which correlated or conditional motion affects the analysis. In order to rely on such an analysis, it is required that the molecular dynamics simulations faithfully represent those motions contributing to experimentally observables such as NMR relaxation. Although there have recently been significant advances in computational approaches, particularly with respect to long-time scale dynamics,^18,19 there has been very little bench marking of molecular dynamics simulations with experimental measures of methyl-bearing side chain motion derived from NMR relaxation.²⁰ With one exception,²¹ the correspondence between Lipari-Szabo (L-S) methyl group squared generalized order parameters derived from molecular dynamics and experiment in the few cases examined has been mixed and insufficient to promote detailed analysis in this context. In a preamble to the main thrust of this paper, we compare L-S squared generalized order parameters of methyl group symmetry axes derived from deuterium or carbon relaxation methods. Using NAMD^22,23 simulations of seven proteins with the CHARMM27 force field,^24,25 we find excellent agreement with experiment, which provides a solid foundation for addressing the microscopic origins of the “entropy meter” established using NMR relaxation methods. Analysis of the simulations then reveals that the experimentally accessible motions of methyl-bearing side chains are sufficiently coupled to the motion of other side chains to serve as excellent reporters of the protein conformational entropy: The total side chain conformational entropy can be accurately recapitulated using only measures of side-chain methyl motions. The conformational entropy varies mostly through changes in populations of rotameric states rather than by variation in the effective potential defining each rotameric well, although some well narrowing is seen at very rigid sites. Importantly, a statistical analysis reveals that correlated motion is sufficiently limited to have little impact on the relationship between the NMR measure of methyl dynamics and the derived entropy. These results validate the use of conformational dynamics derived experimentally from NMR relaxation as a proxy from which to obtain quantitative estimates of changes in protein conformational entropy.

Methods

Molecular dynamics simulations

Molecular dynamics simulations of the seven proteins listed in Table 1 were carried out with NAMD2²³, using the CHARMM27²⁴ all-atom parameter set and the TIP3P²⁶ water potential. Hydrogen atoms were added to the PDB structures with VMD.²⁷ Using VMD²⁷ individual proteins were centered in a TIP3P water box such that protein atoms were at least 8 Å from the boundary except in the case of the two small proteins, ubiquitin and α₃D, where the solvent layer was at least 5 Å and 6 Å, respectively.

Table 1.

Characteristics of the protein set used for molecular dynamics simulations

Proteinsa	Residues	PDBb	T (°C)c	Watersd	Lengthe (ns)
ALBP	131	1LIB	20	4008	112
a3D	73	2A3D	30	2532	160
Cyt c2	116	1C2R	30	5116	120
CaM-smMLCKp	167	1CDL	35	5228	1280f
CaM-nNOSp	168	2O60	35	4957	1120f
HEWL	129	1LZA	35	4133	240
Ubiquitin	76	1UBQ	25	2238	260f

^aAbbreviations: ALBP, adipocyte lipid binding protein; Cyt c2, cytochrome c2; CaM-smMLCKp, calcium-saturated calmodulin (CaM) in complex with a peptide corresponding to the smooth muscle myosin light chain kinase calmodulin-binding domain (smMLCKp); CaM-nNOSp, calcium-saturated calmodulin in complex with a peptide corresponding to the neuronal nitric oxide synthase calmodulin-binding domain (nNOSp); HEWL, hen egg white lysozyme

^bPDB code of starting structure

^cTemperature of simulation and NMR experiments

^dNumber of waters in the simulation

^eLength of the simulation

^fUtilized Anton (see Methods)

Simulations were performed using a time step of 2 fs. Bonds to hydrogen atoms were constrained using the SHAKE algorithm.²⁸ A switching distance of 10 Å and cut-off of 12 Å were used for the non-bonded interaction interactions, combined with a Particle Mesh Ewald summation with 1 Å grid spacing for long-range electrostatics. Simulations were run at constant temperature and pressure of 1 Atm, controlled using the extended Langevin method. Simulation temperatures corresponded to those at which the NMR relaxation experiments were performed (Table 1). Following equilibration runs of at least 1 ns, several 60 ns data production runs were performed with every subsequent 60 ns simulation starting from the final coordinates of the earlier run but with different initial velocities. For three protein systems, ubiquitin, calmodulin-smMLCKp complex and calmodulin-nNOSp complex, longer simulations were also run on the Anton supercomputer at the Pittsburgh Supercomputer Center run using the same force field and simulation conditions except for a non-bond cutoff of 14 Å.

Analysis of internal motion

The Lipari-Szabo²⁹ squared generalized order parameters (O²) were calculated from MD simulations by overlaying snapshots of the protein from the trajectories using a standard rigid-body alignment (Cα) procedure. For each snapshot, the unit vector along the methyl symmetry axis was obtained in terms of its vector components in Cartesian axes, x, y, and z. The O² parameter for a given methyl is then calculated using:³⁰

$$O^2=\frac{3}{2}\left[{\langle x^2\rangle }^2+{\langle y^2\rangle }^2+{\langle z^2\rangle }^2+2{\langle xy\rangle }^2+2{\langle yz\rangle }^2+2{\langle xz\rangle }^2\right]-\frac{1}{2}$$ (1)

where <> indicates the average over the trajectory. For comparison with experiment, the order parameter was derived from the measured order parameter for the methyl C-H bond by assuming free rotation around the symmetry axis and ideal tetrahedral geometry (θ = 109.5°) by: ³¹

$$O_{obs}^2=O_{rot}^2\times O_{axis}^2=\frac{{(3{\cos }^2\theta -1)}^2}{4}{O}_{axis}^2=0.1108\times O_{axis}^2$$ (2)

Order parameters from independent simulations on the same protein were first computed using equation (6), averaged and then compared to those obtained experimentally using NMR relaxation through equation (7).

Calculation of rotameric entropy

Side chain χ angles for each amino acid were calculated from the MD trajectories and binned into one of three conformational states based on the dihedral angle: gauche₊ - [0°, 120°], trans - [120°, 240°]; and gauche_- - [240°, 360°]. The rotamer probability distribution function (pdf) of all 3^Nχ rotamers of each side chain was constructed from the χ angle histograms, where Nχ is the number of side chain χ angles. Only unique side chain torsion angles were considered (e.g. the isopropyl group contributes to one giving Leu 2 and Val 1 side chain torsion angles). The side chain rotamer entropy is:

$$S∕k_b=-\sum _i{p}_i\ln p_i$$ (3)

where k_B is the Boltzmann constant, p_i is the probability of the i^th rotamer. S_b=S/k_b is the entropy given in dimensionless units, and the normalized entropy is then defined as S_b/Nχ,.

Calculation of the influence of correlated motions on side-chain entropy

To quantify the effect of correlated motions of side-chains on their entropy, one-dimensional, two-dimensional and three-dimensional pdfs for every side-chain torsion angle, doublet or triplet combination, respectively, were constructed from the trajectories. The torsion angles were again binned into gauche+, gauche- and trans conformations. The one-dimensional (i.e. uncorrelated) entropy, S_1D was obtained by summing –P(χ)ln P(χ) over each one-dimensional pdf, P(χ), and then summing over all residues in the protein. The total side-chain entropy, including the effect of correlated motions of side-chains was then estimated using the maximum information spanning tree (MIST) method.³² A second order MIST approximation was obtained by computing pair-wise second order mutual information terms (I₂) from the one-dimensional and two-dimensional pdfs as:

$$I_2(j,k)=\sum _{l=1}^3\sum _{m=1}^{3}P({\chi }_l^j,{\chi }_m^k)\ln \left(\frac{P({\chi }_l^j,{\chi }_m^k)}{P\left({\chi }_l^j\right)P\left({\chi }_m^k\right)}\right)$$ (4)

where the two-dimensional pdf $P({\chi }_l^j,{\chi }_m^k)$ expresses the joint probability that side-chain torsion angles j, k are in the I’th and m’th conformations respectively. $P\left({\chi }_l^j\right)$ and $P\left({\chi }_m^k\right)$ are the corresponding one-dimensional pdfs. Given all the I₂'s, the second order MIST expansion is then obtained by selecting a spanning set of I₂'s to maximize:

$$I_2^{MIST}=\sum _{i=2}^n{I}_2(j,i)$$ (5)

where n is the total number of side-chain torsion angles in the protein. To construct this spanning set, for each i, the index j is chosen from the set {1,2..,i-1} which gives the largest I₂(i,j). Similarly, a third order mutual information term (I₃):

$$I_2(i,j,k)=\sum _{o=1}^3\sum _{l=1}^3\sum _{m=1}^{3}P({\chi }_o^i,{\chi }_l^i,{\chi }_m^k)\ln \left(\frac{P({\chi }_o^i,{\chi }_l^j,{\chi }_m^k)}{P({\chi }_o^i,{\chi }_l^j)P\left({\chi }_m^k\right)}\right)$$ (6)

expresses the change in mutual information between i and j by including the k’th torsion angle. A third order MIST approximation is built up analogously by choosing a spanning set of I₃'s to maximize:

$$I_3^{MIST}=I_2(1,2)+\sum _{k=3}^n{I}_3(i,j,k)$$ (7)

where for each k, the indices i and j are chosen from the set {1,2..,k-1} which gives the largest I₃(i,j,k). Then an upper bound estimate for the total entropy including correlations at order O is: ³²

$$S_{MIST-O}^{total}=S_{1D}-I_O^{MIST}(O=2,3)$$ (8)

Results

Seven proteins ranging in size from 73 to 168 residues were selected for study (Table 1). Some have bound metals (calmodulin) or prosthetic group (cytochrome c2). Two are high-affinity complexes of small peptides with calmodulin. All have an extensive experimental reference sets for dynamics derived from site-resolved solution NMR relaxation studies. The methyl group Lipari-Szabo squared generalized order parameters (O²_axis) were taken from published deuterium methyl relaxation studies: α₃D,³³ adipocyte lipid binding protein,³⁴ cytochrome c₂,³⁵ calcium-saturated calmodulin (CaM) complexes with peptides corresponding to the calmodulin-binding domain of the smooth muscle myosin light chain kinase (smMLCKp) and the neuronal nitric oxide synthase (nNOSp),¹⁶ hen egg white lysozyme³⁶ and ubiquitin.³⁷ The average dynamical properties of the proteins range from quite rigid (e.g. cytochrome c₂ and lysozyme) to quite internally dynamic (e.g. α₃D). The molecular coordinates for the proteins used in the simulations were derived from structures deposited in the Protein Data Bank: ubiquitin,³⁸ α₃D,³⁹ (Ca²⁺)₄-calmodulin-smMLCK,⁴⁰ (Ca²⁺)₄-calmodulin-nNOS (unpublished), hen egg white lysozyme,⁴¹ adipocyte lipid binding protein,⁴² and cytochrome c₂⁴³ (Table 1).

Comparison of simulation and experimental methyl side-chain dynamics

The primary goal of this work is to discover the microscopic origins of the apparent success in using a dynamical proxy employing motion of methyl-bearing side chains for the determination of conformational entropy of proteins. As a first step towards this goal, it is important to determine the reliability and accuracy of molecular dynamics simulations in capturing the experimentally determined side chain motion. Here we employ the CHARMM27 potential²⁴ in implemented in the context of the NAMD molecular dynamics environment.²³ Trajectories were carried out in explicit water at the temperature at which the experimental measurements were made (Table 1). Methyl group symmetry axis L-S squared generalized order parameters (O²_axis) were calculated from the trajectories using Eq. 6. Convergence of the simulations with regard to O²_axis values was confirmed by examination of the full time correlation function C(t)=P₂(<μ(t+T)·μ(t)>) for selected methyl groups spanning the range of observed O² values, and by the variation in O²_axis calculated from different batches of individual trajectories (Supplementary Figure S1)

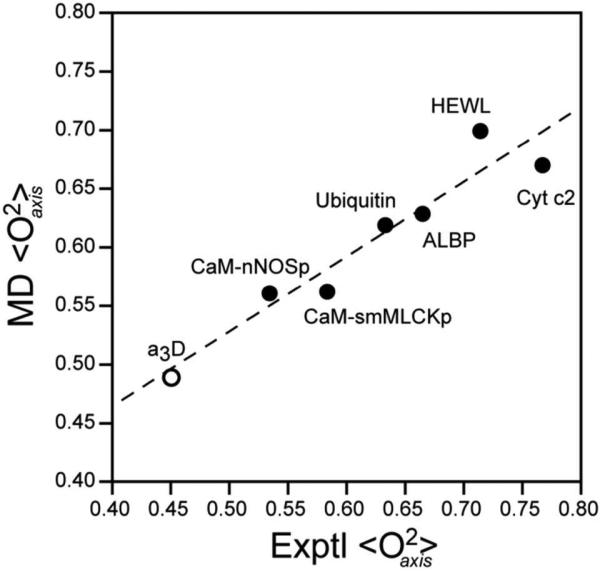
In detail, a methyl-by-methyl comparison reveals considerable variation between the calculated and simulated L-S O²_axis parameters with both over- and underestimation being evident (Table 2 and Supplementary Figure S2). Table 2 summarizes the statistical comparison of O²_axis parameters obtained from simulation and by experiment. With the exception of cytochrome c₂, the correlation coefficients (R²) are all above 0.5, with the highest value of 0.85 being achieved for ubiquitin. Importantly, there is a good correlation between the calculated and observed average order parameters for each protein (Figure 1). This provides a solid foundation for exploring the microscopic basis for fast methyl-bearing side motion as a proxy for conformational entropy.

Table 2.

Correspondence between simulated and observed motion of methyl-bearing amino acid side chains

Proteins	Expt'l <O2axis>	Mol. Dyn. <O2axis>	R2	Slope
ALBP	0.633	0.619	0.75	0.88
a3D	0.451	0.571	0.76	1.25
Cyt c2	0.767	0.670	0.47	0.68
CaM-smMLCKp	0.583	0.562	0.62	0.83
CaM-nNOSp	0.534	0.560	0.50	0.77
HEWL	0.713	0.699	0.64	0.67
Ubiquitin	0.664	0.629	0.85	0.86
Average	0.620 ± 0.11	0.616 ± 0.05	0.65 ± 0.14	0.85 ± 0.13

Figure 1.

Comparison of the average experimentally determined L-S squared generalized order parameters of the methyl group symmetry axis (<O²_axis>) with that calculated from the molecular dynamics (MD) simulations. The experimental average includes all available data. With the exception of α₃D, the molecular dynamics average includes all methyl groups. In the case of α₃D, the experimentally accessible sites are compared directly with the MD average of those sites to avoid an apparent an artifact of limited experimental sampling. Linear regression yields an excellent correlation (R² = 0.92) with slope 0.64 ± 0.09 and intercept 0.21 ± 0.05. Forcing the fitted line through an intercept of zero yields a slope 0.92 with a slightly lower R². Individual site-to-site correlation plots for each protein are provided in the Supplementary Figure S2. The correlation coefficients and the slope values for each protein are summarized in Table 2.

The correlation of methyl-bearing side chain motion and rotamer entropy

A fundamental aspect of the empirical “entropy meter” approach outlined by Marlow and coworkers is the need for a quantitative linkage between the motional averaging of the methyl group symmetry axis and the underlying conformational entropy.¹⁰

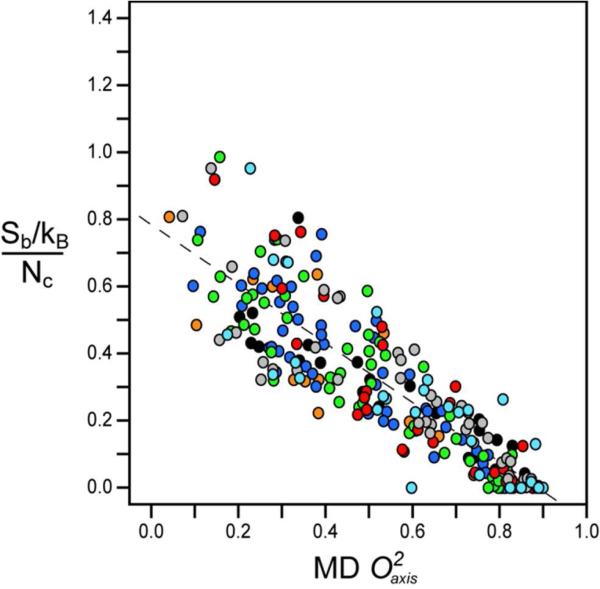
To examine this question, the rotamer population distributions of all the methyl containing amino acids were calculated for each of the protein simulations. The corresponding side chain rotamer entropies were calculated as described by Equation 3. The resulting entropies are plotted against the corresponding calculated methyl order parameters in Figure 2. There is an excellent linear correlation between the rotamer entropy (S_b) of each methyl containing amino acid when normalized by the number of side-chain torsion angles (N_χ) in that residue and the respective methyl side chain order parameters calculated from the MD simulations. Moreover, the distributions from the different proteins overlay each other, strongly suggesting that the empirical scaling of motion to the corresponding entropy should be universal. Correlations of rotamer entropy and O²_axis parameters for the individual proteins are provided in the Supplementary Figure S3 and summarized in Supplementary Table S1.

Figure 2.

Correlation of the methyl rotamer entropy versus O²_axis from MD simulations. Normalized entropy S_b/Nχ given for every side chain methyl probe. The correlation was highly linear (R² of 0.77) with a slope of −0.88 ± 0.03 and an intercept of 0.78 ± 0.02. The different proteins are represented as follows: () Ubiquitin, () α₃D, () Calmodulin-smMLCkp, () Calmodulin-nNOSp, () Hen Egg White Lysozyme, () Adipocyte lipid binding protein, () Cytochrome c₂.

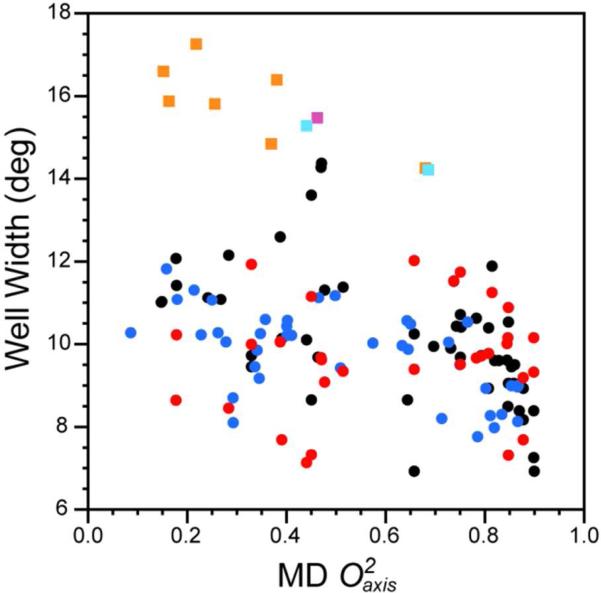
In principle, the entropic content represented by the O²_axis parameter could arise not only from the distribution between rotamer wells but also from the distribution within each rotamer well and the associated vibrational entropy.^5,44,45 With this in mind, for each methyl group we examined the fine distribution of torsion angles using a resolution of 3°. The width of a rotameric well is characterized by the root mean square deviation (rmsd) of its χ-angles. Weighting the width of each well of a given torsion by its overall occupancy gives the mean width. This width is shown as a function of the calculated O²_axis parameter for the corresponding residue in Figure 3. The within-well distributions of non-Methionine rotamer angles is largely insensitive to values of O²_axis below ~0.8. At higher O²_axis values some narrowing of the within-well distribution is indicated. Met methyl groups behave somewhat differently: Within-well widths are modestly correlated with O²_axis (R²=0.30), suggesting that the energy well governing the directly connected torsion angle of the Met methyl group is somewhat plastic.

Figure 3.

Correlation of the within-well width distribution of side-chain torsion angles with the directly connected methyl group symmetry axis L-S squared order parameters calculated from MD simulations. The width of the distribution is given by the r.m.s.d. Protein and residue types indicated by () Ubiquitin – (LEU, ILE, VAL, THR), () Calmodulin-smMLCKp – (LEU, ILE, VAL, THR), () Hen Egg White Lysozyme – (ILE, LEU, VAL, THR). Methionines are indicated by square symbols with () from the CaM complexes, () from ubiquitin and () from HEWL.

Given the rarity of Met residues the generality and origin of this remains to be established. Overall, the high correlation between the normalized rotameric entropy of methyl containing amino acids and the O²_axis parameters of the attached methyl groups indicates that methyl probes serve as excellent reporters of the conformational entropy of methyl containing amino acids in proteins. Two conclusions can be drawn. First, since the residues of seven quite different proteins have indistinguishable correlations between rotamer entropy S_b and the O²_axis parameter, there appears to be a universal relationship between these two quantities. Second, the O²_axis parameter appears to be determined primarily by between-well rotamer transitions.

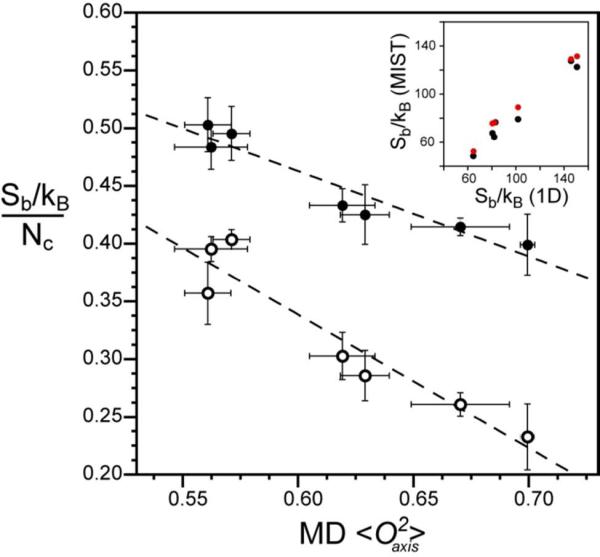
Though there is significant variation in the normalized rotamer entropy associated with a specific value of O²_axis on a per-residue basis, particularly at lower order parameters (Figure 2 and Supplementary Figure S3), this variation is much smaller when considering the average behavior over the entire protein. The average normalized rotamer entropy shows an excellent correlation (R² = 0.91) with the average O²_axis parameter (Figure 4). This suggests that the NMR O²_axis parameter and the normalized rotamer entropy are effectively transforms of each other and follow a simple protein-independent linear relationship. Thus, though our current ability to accurately simulate individual experimental order parameters is limited (Table 2 and Supplementary Figure S2), the accuracy of the corresponding derived entropy greatly improves when one uses averages over the entire molecule (Figure 4 and Supplementary Figure S4) and one is not trying to simulate order parameters but has known values from NMR.

Figure 4.

The dynamic proxy of methyl groups is an excellent reporter of both methyl and total side-chain rotameric entropy. (o) The normalized methyl rotameric entropy for each protein is calculated as the summation of S_b for individual methyl-bearing amino acids divided by the number of associated rotamer angles (Nχ). () The total rotameric entropy for each protein is calculated as the summation of S_b for all residues and is normalized by the respective total number of rotamer angles (Nχ). The average methyl O²_axis parameter for all methyl-bearing residues including Ala is that obtained from MD simulations. A very high linear correlation is observed for both methyl-side chain rotamer entropy [slope = −1.16 ± 0.17, R² = 0.90] and total rotamer entropy [slope = −0.74 ± 0.10, R² = 0.91 ]. The inset shows the correlation of the uncorrected entropy with the entropy corrected for correlated motions using () second–order and () third-order MIST estimates of inter-residue correlations. Both correlations are highly linear with a slope of −0.89 (R² = 0.99) and slope = −0.83 (R² = 0.96) for second-order and third-order MIST calculations, respectively.

The essence of the “entropy meter”

A critical assumption in the use of the dynamical proxy of methyl group motion for conformational entropy of the entire protein is that the motion of the methyl group is sufficiently coupled to its surroundings to faithfully report on local disorder.¹⁰ To examine this central issue, we calculated the total side chain rotamer entropy from the probability distributions for all side-chain torsion angles. The linear correlation between the dynamical proxy (methyl group dynamics) and total conformational entropy is excellent (Figure 4). Thus averaged over a protein, the methyl order parameters report well on the total side chain entropy. This can be expressed using the remarkably simple equation:

$$\frac{\sum S_b}{\sum N_{\chi }}=0.91-0.74\langle O_{axis}^2\rangle \text{MD}-\text{uncompensated}$$ (9)

which, as noted, is uncompensated for correlated states. Thus far the rotamer entropy has been calculated from entirely intra-side chain rotamer pdfs. Correlations between χ angles within each residue are accounted for by the exhaustive enumeration of individual side chain torsion angle combinations (see Methods). However, the effect of inter-residue correlations between torsional motions is absent. Such correlations will result in lowering of the derived protein conformational entropy. In order to quantify the effect of such correlations, doublet and triplet torsion angle distributions of side-chains in all the proteins were accumulated and analyzed. The contributions of inter-residue correlations to the total entropy were calculated using the MIST formulation of Tidor and coworkers.^32,46 The proportional degree of reduction in total conformational entropy is very similar across the set of proteins studied. Both second and third order corrections for inter-residue correlated motion gave resulting entropies that showed excellent linear correlations with the uncorrected entropy (Inset, Figure 4). Moreover, the correction from third-order (17%) is not much higher than for second order (11%) indicating that the bulk of the correction due to all orders of correlation is captured by these lower order, calculable effects. This leads to a simple correction to Equation 1 so that one can obtain an estimate of the total side chain entropy of a protein, including both methyl and non-methyl containing residues, intra- and inter residue correlation effects from the following equation

$$S_{sc}^{tot}=0.83\sum N_{\chi }\left(0.91-0.74\langle O_{axis}^2\rangle \right)\mathrm{MD}$$ (10)

which is corrected for inter-residue correlations.

In summary, the side-chain rotamer entropy and methyl order parameters are closely related measures of the dynamics of methyl bearing side chains. In addition, the major determinants of side chain entropy changes are shifts in rotamer populations, which are visible to NMR. Moreover, when averaged over the whole protein, methyl order parameters report with identical fidelity on all side-chain motions. Thus NMR measurements of average methyl order parameter values can be leveraged into estimates of total side-chain entropy.

Reformulation of the “entropy meter”

The original construction of the conformational “entropy meter” based on the dynamical proxy of fast methyl group motion was admittedly crude.^6,10 This was especially true on how to project the measured motion of methyl groups across the protein. A simple residue-weighting scheme was used. Briefly, the approach rested on relating what could be easily measured (total binding entropy via isothermal titration calorimetry) or calculated (solvent entropy via changes in accessible surface area) to the dynamical proxy. The approach assumed that additional sources of entropy, such as rotational-translational entropy or undocumented entropy were constant across a family of protein-ligand interactions. It was further assumed that measured changes in methyl-group motion were linearly related to changes in changes in local motion (disorder) that not only reflected the methyl-bearing side chain but also that of the surrounding side-chains. Linear correlation between side-chain motion and entropy was suggested by simple models,^8,9,47 and by the molecular dynamics simulations presented here. These considerations led to the following formulation of the “entropy meter:”¹⁰

$$(\Delta S_{tot}-\Delta S_{solv})=m\left[\left(n_{res}^{prot}\right){\langle \Delta O_{axis}^2\rangle }^{prot}+\left(n_{res}^{lig}\right){\langle \Delta O_{axos}^2\rangle }^{lig}\right]+(\Delta S_{RT}+\Delta S_{other})$$ (11)

where ΔS_tot, ΔS_solv, ΔS_conf, ΔS_RT and ΔS_other are the changes in total system entropy, solvent entropy, conformational entropy, rotational-translational entropy and otherwise undocumented entropy, respectively. As noted in detail elsewhere,⁶ the two protein systems where this approach was taken give decidedly different conversion constants (m). Though it may indeed be possible that different proteins have qualitatively different dynamics it does seem puzzling.⁶ We resolve this below.

The ability to recapitulate semi-quantitatively experimentally derived order parameters via molecular dynamics trajectories allows for the rapid exploration of the generality of slight reformulations of the experimental “entropy meter.” The computational results described here suggest a modest refinement. Due to the excellent correlation between measures of angular disorder (O²_axis) and the conformational entropy normalized by the number of involved torsion angles (Figure 4), we reanalyzed the empirical calibration of conformational entropy from the study on calmodulin and its binding partners¹⁰ and cAMP activated CAP and its mutants binding to DNA¹⁷. Now the NMR order parameter derived proxy is given by:

$$N_x^{prot}\left[{\langle O_{axis}^2\rangle }_{complex}^{prot}-{\langle O_{axis}^2\rangle }_{free}^{prot}\right]+N_x^{lig}\left[{\langle O_{axis}^2\rangle }_{complex}^{lig}-{\langle O_{axis}^2\rangle }_{free}^{lig}\right]\text{Experiment}$$ (12)

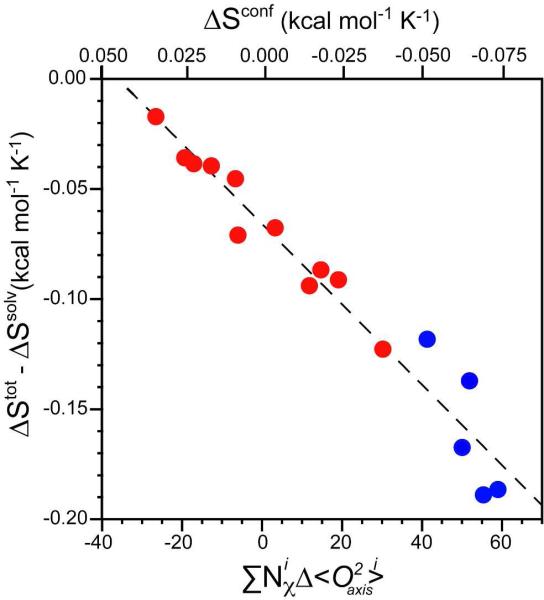
where Nχ^prot and Nχ^lig are the total number of side-chain torsion angles in the protein and ligand, respectively. Using this formulation of the dynamical proxy, a single linear calibration line applies to both the CaM and CAP protein complexes (Figure 5).

Figure 5.

Calibration of the experimental dynamic proxy for protein conformational entropy. The points corresponding to both wild-type and mutants of CAP binding to DNA (red)¹⁷ and CaM binding to its partners (blue)¹⁰ follow the same empirical relationship when correlated using the average change in methyl order parameter weighted by the total number of torsion angles. An excellent linear correlation is seen (R² = 0.95) suggesting a common relationship between the conformational entropy of proteins and their respective change in dynamics as represented by the methyl groups. A slope of −0.0018 ± 0.0001 kcal mol⁻¹ K⁻¹ ∑Nχ⁻¹ provides a conversion between the dynamical proxy and conformational entropy, as illustrated by the top abscissa axis.

Discussion

Here we have employed molecular dynamics simulations to investigate the validity of several assumptions that are fundamental to the idea of using dynamical information gathered from NMR relaxation in methyl groups of amino acid side chains as a quantitative proxy for conformational entropy. Since the pioneering introduction of molecular dynamics simulations for comprehensive studies of internal protein motion several decades ago,⁴⁸ the capabilities and accuracy of such simulations have expanded greatly with increases in computational power and significant improvements in various aspects of the force fields employed.¹⁹ Perhaps surprisingly, the accuracy of molecular dynamics simulations have not been extensively tested in the ps-ns time regime against the sizable database of side chain order parameters obtained by solution NMR relaxation methods.^18-20 Using the NAMD implementation of the CHARMM27 potential in a largely “out of the box” fashion, reasonable “site-to-site” agreement with experiment. These results compare favorably with evaluations of various AMBER potentials employing calbindin and ubiquitin as test proteins.^49,50 More importantly, we find excellent on average agreement between experimental Lipari-Szabo squared generalized order parameters and those extracted from molecular dynamics trajectories. There exists a large site-to-site variance between experiment and simulation that remains to be explained and corrected. However, the overall agreement with experiment is sufficiently good to promote use of simulations to illuminate critical aspects of the use of the dynamical proxy as a means to quantify conformational entropy.

A central feature of the dynamical proxy to act as a measure of the distribution of states is the notion that motion between states can be linearly related to the underlying conformational entropy.⁷ This was initially promoted by examination of a number of simple motional models.^8,9,47 The molecular dynamics studies of the seven protein systems described here fully reinforce this expectation. There is a robust linear relationship observed between the calculated rotamer entropy of each methyl bearing side chain - normalized by the number of associated χ torsion angles - and its respective methyl order parameter for each protein. This is perhaps not unexpected given that the motion of terminal methyl groups arises from motion about all torsions connecting it to the backbone. Indeed, this type of motion is mirrored in the product of the corresponding generalized order parameters.^29,51 This indicates that methyl groups are excellent reporters of their own side-chain conformational entropy. Importantly, this relationship is uniform across all the proteins studied here suggesting that it is general (Figure 2). Further evidence for this generality comes from a recent and parallel analysis of apo HIV protease simulations.⁵² Glass et al⁵² also find a linear dependence of methyl group entropy on O² over the range 0.1-0.8, with a slope, when expressed in dimensionless units, very similar to that of Figure 2. It is important to note in this regard that the motions detected by the NMR relaxation discussed here are restricted to timescales faster than overall tumbling of the macromolecule,²⁹ which is on the order of ten nanoseconds or less for the proteins examined in this study. Interestingly, the molecular dynamics simulations exceed this by an order of magnitude. Thus, the high correlation suggests that the ensemble of states that is experimentally accessible accurately reflects that sampled on longer timescales. It is important to note that all methy-bearing side chains, except for Thr, show extensive rotamer interconversion during the trajectories. In principle, it is possible that longer time scale motion may interconvert states that are not similarly sampled in the time regime relevant to the generalized order parameter obtained by classical NMR relaxation.⁵³ Fortunately, the high empirical correlation found (Fig. 5) suggests that the possible distortion of the relationship between local entropy and the generalized order parameter due to slow rotamer interconversion is small.

In the “entropy meter” treatment of Marlow and coworkers¹⁰ it is assumed that the motion of the experimentally accessible methyl group not only reflects the motional disorder of the entire methyl-bearing side chain but that it also linearly reflects motion (disorder) of the surrounding non-methyl bearing side chains. This coupling of motion is clearly evident in the molecular dynamics simulations where a remarkably robust linear relationship exists between the total normalized rotamer entropy of a protein and the appropriately weighted change in effective amplitude (i.e. the angular disorder represented by the L-S O²_axis parameter) of fast methyl group motion. The normalization by Nχ provides an unbiased view of the relationship between rotamer entropy, expressed now as an intensive quantity, and methyl dynamics for different length side-chains e.g. methionine versus valine etc. Furthermore, this linear relationship is valid for the entire range of order parameter i.e. from 0 to 1 irrespective of the type of methyl side-chain, i.e. the relative contribution to entropy from a residue with a given order parameter depends only on <O²_axis> and Nχ not the type of side chain.

The microscopic origins of this rotamer entropy and its subsequent linear relationship to methyl side-chain order parameters are intrinsically related to the population distribution between the different energy states of the side-chain i.e. different rotamer wells. The relationship is largely insensitive to the distributions within a rotamer well except for perhaps methionine (Figure 3). In principle, the total side-chain conformational entropy arises from the combined effect of both transitions between rotamer wells (‘conformational entropy’) and distributions within a rotamer well (‘vibrational entropy’).⁵ However, differences in entropy that distinguish more dynamic or less dynamic residues, or that distinguish more dynamic proteins such as α₃D from less dynamic ones such as HEWL arise almost entirely from the conformational component. This insensitivity of the torsional distributions within rotamer wells is attributable to the fact that the energies involved in stabilization of protein structure and in binding ligands are rather modest. They are apparently sufficient to modulate softer modes of motion such as transitions between rotamers, but not enough to greatly affect vibrational contributions such as motion within torsion wells nor indeed the much stiffer vibrational contributions from bond angle and bond stretch motions.

A logical consequence of the coupling of motion is the need to consider how correlation might affect the quantification of conformational entropy via a dynamical proxy. Although exhaustive enumeration of rotamers within a side chain is computational feasible and was carried out explicitly, complete inter-residue correlations are not computationally tractable but were estimated here using the MIST algorithm.³² These calculations indicate that only a small linear scaling of the uncorrected entropy is required. This picture of rather restricted, local effects of correlation is consistent with other recent studies of conformational entropy in proteins.^54-56 Given the generally linear relationship revealed by simulations, the experimental “entropy meter” should represent the true conformational entropy change as the effects of correlated motion are encapsulated within the empirical calibration, assuming the absence of significant solvent-protein coupling (see equation 3). As emphasized above, the conformational entropy calculated from molecular dynamics derived <O²> values alone would be insufficiently accurate. In contrast, the empirical entropy meter based on the measured methyl-group dynamical proxy would more accurately relate side chain motion to the underlying conformational entropy, and does so through a remarkably simple relationship:

$$\Delta S_{sc}^{tot}∕k_B=0.92\sum N_{\chi }\Delta \langle O_{axis}^2\rangle \text{Experiment}$$ (13)

Conclusions

Using molecular dynamics simulations as a guide, we have resolved the apparent discrepancy between the applications of a dynamical proxy for conformational entropy to the binding of ligands by calmodulin and the catabolite activation protein. A simple normalization based on the number of degrees of freedom (torsion angles) is sufficient. The molecular dynamics simulations also suggest that the “entropy meter” derived from this approach may be generally applicable. Further experiments are required to confirm this. Nevertheless, the apparent robustness of the dynamical proxy for conformational entropy from the perspective of both simulation and experiment reinforces the conclusion that conformational entropy can indeed play a significant and potentially determining role in associations involving proteins.⁶ Looking forward, these results promote a more exhaustive examination of the quantitative role of conformational entropy in the free energy governing protein-ligand associations. This may be particularly important in the context the interaction of proteins with unnatural man-made pharmaceuticals where the influence of conformational entropy remains largely unknown.⁵⁷