Abstract
Cardiovascular variables such as heart rate (HR) and blood pressure (BP) are robustly regulated by an underlying control system. Time series of HR and BP exhibit distinct dynamical patterns of interaction in response to perturbations (e.g., drugs or exercise) as well as in pathological states (e.g., excessive sympathetic activation). A question of interest is whether “similar” dynamical patterns can be identified across a heterogeneous patient cohort. In this work, we present a technique based on switching linear dynamical systems for identification of shared dynamical patterns in the time series of HR and BP recorded from a patient cohort. The technique uses a mixture of linear dynamical systems, the components of which are shared across all patients, to capture both nonlinear dynamics and non-Gaussian perturbations. We present exploratory results based on a simulation study of the cardiovascular system, and real recordings from 10 healthy subjects undergoing a tilt-table test. These results demonstrate the ability of the proposed technique to identify similar dynamical patterns present across multiple time series.
Index Terms: Cardiovascular control, switching linear dynamical systems, baroreflex
I. INTRODUCTION
Physiological systems often involve many variables which are both subject to noise and interaction via feedback. The resulting multivariate time series of such physiological variables exhibit rich dynamical patterns, which are altered under pathological conditions [1]. A long-term objective of physiological data analysis is to automatically discover these pathology-driven alterations and use them to inform clinical decisions. This paper examines the problem of segmenting physiological time series into stereotypical dynamics across a cohort of patients, with the objective of extracting features that will be useful for predicting physiological properties that cannot be directly observed.
Models of these physiological time series have been used by several authors to infer the properties (e.g., transfer functions, phase relationships, etc) of the underlying dynamical systems [2–5]. For instance, several authors have used the time series of heart rate (HR) and blood pressure (BP) to obtain estimates of baroreflex gain [6–8], or more generally to characterize the feedback control system regulating the cardiovascular variables [9]. The linear techniques commonly used (often based on variants of autoregressive modeling) have the advantage of revealing the individual relationships among the observed variables (e.g., the baroreflex gain describes the relationship between HR and BP, excluding the possible influence of respiration). On the other hand, nonlinear indices of complexity are capable of capturing a richer set of dynamical behavior [10, 11], but often lack physiological interpretability in terms of specific underlying mechanisms.
In this work, we assume that, although the underlying dynamical system may be nonlinear and the stochastic noise components can be non-Gaussian, the dynamics can be well approximated by a mixture of linear dynamical systems. We will refer to the components of such a mixture as modes. Specifically, we present a technique based on a switching linear dynamical system [12], that is: (i) sufficiently simple to allow for a physiologically-interpretable model for the interaction between HR and BP, (ii) sufficiently complex to provide a realistic representation of the underlying physiology, and (iii) provides a framework for defining a measure of similarity among multivariate physiological time series based on their underlying shared dynamics.
The mixture modeling approach provides a framework for automatic segmentation of time series into regions with similar dynamics (i.e., time-dependent rules describing how the future state of the system evolves from the current state). Furthermore, we assume that “similar subjects” respond similarly to perturbations (such as tilting), and therefore they share dynamical modes. The latter assumption allows us to define a notion of similarity across segments from multiple time series. This approach provides a potential improvement over time series similarity measures which are based on symbolic representations [13] or simple trend-detection [14]. These measures often ignore the joint temporal information that is embedded in the dynamics of interaction among physiological variables.
I. METHODS
A. Cardiovascular Simulation
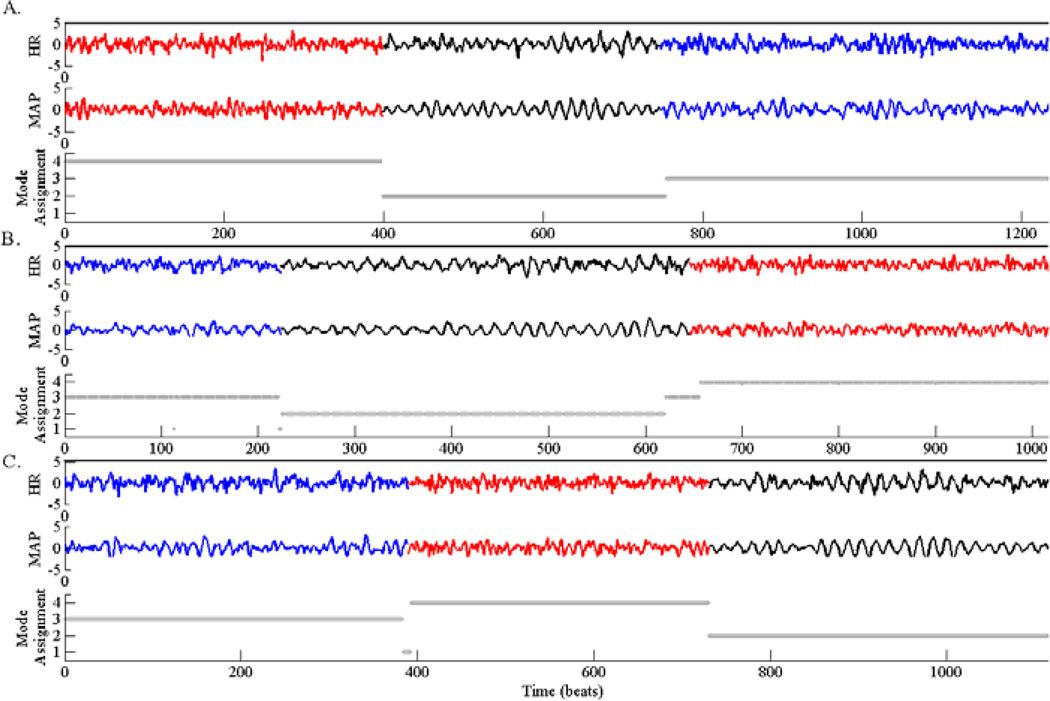
We simulated time series of cardiovascular control system variables based on a delay recruitment model of the cardiovascular control system, as described in Fowler & McGuinness [15] and McSharry et al. [16]. The model included a coupled system of nonlinear delayed differential equations, controlling HR and BP, with respiration as an exogenous input. We simulated 10 different multivariate time series of HR and mean arterial BP (MAP), each including three different dynamics that become dominant in a random order and last for a variable length of time. The three dynamics (color-coded as red, blue, and black, respectively, in Fig. 1) approximate aging-related autonomic changes; a progressive reduction in parasympathetic gain (from 0.40 to 0.13 to 0.07 in normalized units; see [15]) and an increase in sympathetic delay (from 3 to 5 seconds).
Figure 1.
Simulation study of the cardiovascular system. Three examples (out of the 10 simulated time series) of HR and MAP (after filtering) are shown in panels A, B and C. In each case, the actual dynamics are color coded. The horizontal gray lines show the inferred segmentations based on the switching Kalman filter (SKF). Note that, the SKF consistently assigned modes 2, 3 and 4 to the dynamics color-coded as black, blue and red, across all the simulated time series
B. Tilt-Table Experiment
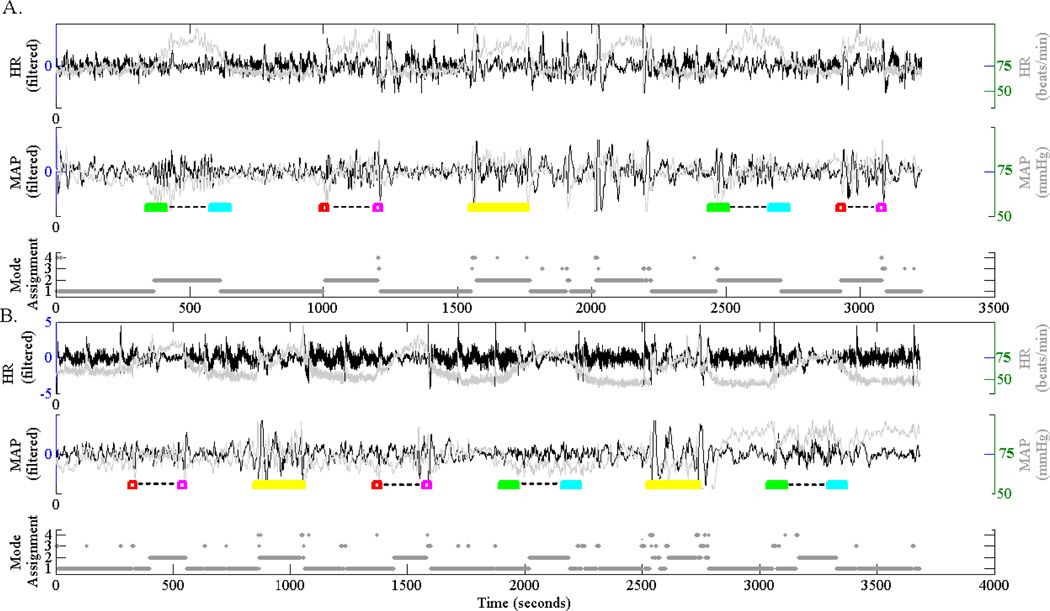
Time series of HR and MAP were acquired from 10 healthy subjects undergoing a tilt-table experiment. The details of the protocol is described in Heldt et al. [17]. Briefly, subjects were placed in supine position and secured to the table with straps. Tilting was performed from horizontal position to vertical position and back to supine. Examples of the resulting time series are shown in Fig. 2.
Figure 2.
Tilt-table study. Two examples out of the 10 recording of HR and MAP from the tilt-table experiment are shown in panels A, B. Within each panel, from top to bottom, HR and MAP (actual values in gray and filtered values in black), and SKF-based segmentation are shown. In each case, the actual true dynamics are color coded (green to cyan: slow tilt up and down to supine; red to pink: rapid tilt up and down to supine; yellow: stand up and back to supine). Note that the SKF consistently assigns the modes one and two to the supine and non-supine states, respectively. The other two modes seem to capture the high-frequency noise components of the time series.
C. Data Pre-processing
Since we are interested in the dynamics of interaction between HR and MAP in the frequency range pertinent to sympathetic and parasympathetic regulation [18], time series of HR and MAP were high-pass filtered to remove the steady-state baseline and any oscillation in the time series slower than 100 beats/cycle. This filtering was done using a 7th order Butterworth digital filter with cutoff frequency of 0.01 cycles/beat. All time-series were further normalized to have a standard deviation of one.
D. Switching Kalman Filter with Dynamic Sharing
Our starting point for the modeling of physiological time series is the multivariate autoregressive (AR) model. Let yt be a K-dimensional vector of physiological variables at time t. An AR model captures their discrete-time dynamics via:
| (1) |
where p is the time lag, up to the model order P (P=3 in the present study). The Hp are K×K matrices of linear dynamics relating yt-p to yt; wt captures variations in yt that are not explained by the linear dynamics of the physiological variables, and are therefore considered to be noise. Models of the type described by Eq. (1) have been successfully used by researchers to model the cardiovascular [6, 7] and respiratory [5] control systems, with appropriate physiological constraints imposed on the model coefficients. Note that, Eq. (1) does not explicitly model measurement-related noise. Moreover, it assumes a static linear model with stationary Gaussian noise. Unfortunately, recordings of physiological variables are often corrupted by measurement-related artifacts and noise due to, e.g., muscle artifacts, electrode movement, etc. A solution to this problem is provided by the switching Kalman filter (SKF) framework [12], where a bank of M different linear models, along with transition dynamics between them is used to explain the observed data. Under this setup, nonlinear dynamics can be approximated in terms of switches between linear models, and non-Gaussian noise can be approximated using a mixture of Gaussians.
To facilitate this approach, we cast the model of Eq. (1) into a state-space framework and use machine learning tools to identify the model parameters. Vector AR models can be described in a state-space form [19]:
| (2) |
| (3) |
where A are the AR coefficients (perhaps with application-dependent physiological constraints), C relates the latent state of the system, xt, to the observations yt, qt is the AR noise, and νt is measurement noise.
Let us define a mode (or dynamic) as a set of model parameters Θ={A, C, Q, R}. We further assume a set of indicator (switching) variables st that specify which of the M modes is active at time t. We take M=4 in both studies. The SKF algorithm [12] assumes st follows a Markov chain with transition matrix Z (M×M) and initial distribution vector π (1×M).
In practice, we neither know the set of switching variables (i.e., segmentation of the time series) nor the modes. In this work, we performed expectation-maximization (EM) [12] to find the maximum-likelihood set of model parameters. EM also provides us with a factored estimate of the posterior distribution over the latent switching variables. Here we skip the details of EM algorithm, but highlight the main intuition behind EM, as well as our modification to impose physiological constraints on the dynamics for each mode and learn sharing of the modes across all the patients.
Consider a set of N patients with time series y(n) of length Tn. EM is an iterative procedure for finding a maximum likelihood estimate. We choose a random initialization of Θ(m), Z, and π. The E-step involves constructing an approximating distribution over the hidden states xt(n) and the corresponding switching variables st(n), using a modified Kalman smoother [12]. We run the E-step separately on each of the N time series.
Next, given the observations yt(n), and the approximate distributions over xt(n) and st(n), the M-step maximizes the expected complete data log likelihood by adjusting the model parameters across all the modes (via constrained least squares optimization to maintain the structure of the A matrices), as well as the Markov chain parameters Z and π. Therefore, learning of the model parameters is done by pooling together all the observed and inferred hidden variables across all the subjects. Iteration through several steps of the EM algorithm will result in learning a set of M shared modes and a global transition matrix Z for all the patients. In addition, to minimize the influence of initialization on the final learned parameters and to reduce the chance of trapping in local minima, we implemented a deterministic annealing step within the EM algorithm [12].
II. RESULTS
A. Simulation study
Fig. 1 A–C shows three examples of simulated time series with the inferred SKF-based segmentations. In all 10 simulated cases the SKF algorithm was able to find the correct segmentation of each time series, as well as the sharing of the dynamics across multiple time series.
B. Tilt-table experiment
We constructed a binary classification problem of determining supine versus non-supine segments (see Fig. 2). There were a total of seven supine positions and six non-supine positions per subject (total of 13×10=130 binary outcomes). We used the average probability of belonging to each of the four SKF states (M=4) as our feature vector (i.e., average value of P(st) within each position), resulting in a 130×4 input matrix. Application of logistic regression with 10-fold cross-validation yielded an AUC of 0.97±0.01, indicating an excellent discriminatory power.
III. Discussion and Future direction
We presented a technique for extracting shared physiological dynamics within a cohort. It was shown that quantum changes in the dynamics of HR and BP, either as a result of an altered underlying control system (decreased sympathetic regulation) or due to external perturbations (tilting), can be captured in an automated fashion.
Since an AR model of HR and BP regulation was used, the proposed framework allows us to extract useful indices of baroreflex activity from the learned AR coefficients [5, 9]. Therefore, the discovered dynamical patterns are physiologically interpretable.
Future work involves exploring the full potential of the SKF framework to model nonlinear dynamics and non-Gaussian physiological and measurement-related noise. The technique is most useful in modeling systems with rapid transition among physiological states (e.g., study of changes in autonomic regulation with sleep stages).
Other possible applications include monitoring of patients’ “state” in a hospital setting, where transition to certain “high risk” dynamical modes could be used to sound alarms. Such modes can be learned from a database of patients were outcome measures are available. Therefore, real-time monitoring can be achieved by only doing a forward E-step to infer the most probable patient state, given a dictionary of dynamics previously learned.
Acknowledgment
We are grateful to Thomas Heldt (Harvard-MIT Division of Health Sciences and Technology) for kindly providing the tilt-table data analyzed in this study.
This work was supported in part by the National Institutes of Health (NIH) training grant T32-HL07901, the National Institute of Biomedical Imaging and Bio-engineering and by the National Institute of General Medical Sciences, under NIH cooperative agreement U01-EB-008577 and NIH grant R01-EB001659. The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the NIBIB or the NIH.
Contributor Information
Shamim Nemati, Massachusetts Institute of Technology, 45 Carleton Street, Cambridge, MA 02142, USA..
Li-wei H. Lehman, Massachusetts Institute of Technology, 45 Carleton Street, Cambridge, MA 02142, USA.
Ryan P. Adams, Harvard School of Engineering and Applied Sciences, 33 Oxford Street, Cambridge, MA 02139, USA.
Atul Malhotra, Division of Sleep Medicine, Brigham and Women’s Hospital and Harvard Medical School, 221 Longwood Avenue, Suite 438, Boston, MA 02115, USA..
References
- 1.Goldberger AL, Amaral LA, Hausdorff JM, Ivanov P, Peng CK, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci U S A. 2002 Feb 19;vol. 99(Suppl 1):2466–2472. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kalli S, Gronlund J, Ihalainen H, Siimes A, Valimaki I, Antila K. Multivariate autoregressive modeling of autonomic cardiovascular control in neonatal lamb. Comput Biomed Res. 1988 Dec;vol. 21:512–530. doi: 10.1016/0010-4809(88)90009-2. [DOI] [PubMed] [Google Scholar]
- 3.Korhonen I. Multivariate closed-loop model for analysis of cardiovascular dynamics. Methods Inf Med. 1997 Dec;vol. 36:264–267. [PubMed] [Google Scholar]
- 4.Khoo MC, Yang F, Shin JJ, Westbrook PR. Estimation of dynamic chemoresponsiveness in wakefulness and non-rapid-eye-movement sleep. J Appl Physiol. 1995 Mar;vol. 78:1052–1064. doi: 10.1152/jappl.1995.78.3.1052. [DOI] [PubMed] [Google Scholar]
- 5.Nemati S, Edwards BA, Sands SA, Berger PJ, Wellman A, Verghese GC, Malhotra A, Butler JP. Model-based characterization of ventilatory stability using spontaneous breathing. J Appl Physiol. Jul;vol. 111:55–67. doi: 10.1152/japplphysiol.01358.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Parati G, Saul JP, Di Rienzo M, Mancia G. Spectral analysis of blood pressure and heart rate variability in evaluating cardiovascular regulation. A critical appraisal. Hypertension. 1995 Jun;vol. 25:1276–1286. doi: 10.1161/01.hyp.25.6.1276. [DOI] [PubMed] [Google Scholar]
- 7.Di Rienzo M, Parati G, Mancia G, Pedotti A, Castiglioni P. Investigating baroreflex control of circulation using signal processing techniques. Engineering in Medicine and Biology Magazine, IEEE. 1997;vol. 16:86–95. doi: 10.1109/51.620499. [DOI] [PubMed] [Google Scholar]
- 8.Porta A, Bassani T, Bari V, Tobaldini E, Takahashi AC, Catai AM, Montano N. Model-based assessment of baroreflex and cardiopulmonary couplings during graded head-up tilt. Comput Biol Med. Mar;vol. 42:298–305. doi: 10.1016/j.compbiomed.2011.04.019. [DOI] [PubMed] [Google Scholar]
- 9.Mukkamala R, Mathias JM, Mullen TJ, Cohen RJ, Freeman R. System identification of closed-loop cardiovascular control mechanisms: diabetic autonomic neuropathy. Am J Physiol. 1999 Mar;vol. 276:R905–R912. doi: 10.1152/ajpregu.1999.276.3.r905. [DOI] [PubMed] [Google Scholar]
- 10.Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of complex physiologic time series. Phys Rev Lett. 2002 Aug 5;vol. 89:068102. doi: 10.1103/PhysRevLett.89.068102. [DOI] [PubMed] [Google Scholar]
- 11.Ivanov PC, Amaral LA, Goldberger AL, Havlin S, Rosenblum MG, Struzik ZR, Stanley HE. Multifractality in human heartbeat dynamics. Nature. 1999 Jun 3;vol. 399:461–465. doi: 10.1038/20924. [DOI] [PubMed] [Google Scholar]
- 12.Murphy KP. Switching Kalman filter. Compaq Cambridge Research Laboratory, Tech. Rep. 98-10. 1998 [Google Scholar]
- 13.Saeed M, Mark R. A novel method for the efficient retrieval of similar multiparameter physiologic time series using wavelet-based symbolic representations. AMIA Annu Symp Proc. 2006:679–683. [PMC free article] [PubMed] [Google Scholar]
- 14.Avent RK, Charlton JD. A critical review of trend-detection methodologies for biomedical monitoring systems. Crit Rev Biomed Eng. 1990;vol. 17:621–659. [PubMed] [Google Scholar]
- 15.Fowler AC, McGuinness MJ. A delay recruitment model of the cardiovascular control system. J Math Biol. 2005 Nov;vol. 51:508–526. doi: 10.1007/s00285-005-0339-1. [DOI] [PubMed] [Google Scholar]
- 16.McSharry PE, McGuinness MJ, Fowler AC. Confronting a cardiovascular system model with heart rate and blood pressure data. Computers in Cardio. 2005:587–590. [Google Scholar]
- 17.Heldt T, Oefinger MB, Hoshiyama M, Mark RG. Circulatory response to passive and active changes in posture. Computers in Cardiology. 2003;vol. 30:263–266. [Google Scholar]
- 18.Heart rate variability: standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysio. Circulation. 1996 Mar 1;vol. 93:1043–1065. [PubMed] [Google Scholar]
- 19.Lardiès J. Relationship between state-space and ARMAV approaches to modal parameter identification. Mechanical Systems and Signal Processing. 2008;vol. 22:611–616. [Google Scholar]