Predictive coding and pitch processing in the auditory cortex

Abstract

In this work, we show that electrophysiological responses during pitch perception are best explained by distributed activity in a hierarchy of cortical sources and, crucially, that the effective connectivity between these sources is modulated with pitch-strength. Local field potentials were recorded in two subjects from primary auditory cortex and adjacent auditory cortical areas along the axis of Heschl's gyrus (HG) while they listened to stimuli of varying pitch strength. Dynamic Causal Modelling was used to compare system architectures that might explain the recorded activity. The data show that representation of pitch requires an interaction between non-primary and primary auditory cortex along HG that is consistent with the principle of predictive coding.

Introduction

Mechanisms for pitch perception are a subject of controversy with some studies suggesting the existence of single areas (Bendor & Wang, 2005; Krumbholz, Patterson, Seither-Preisler, Lammertmann, Lutkenhoner, 2003; Penagos, Melcher, Oxenham, 2005) and others suggesting distributed processing over areas (Griffiths et al 2010; Bizley, Walker, Silverman, King, Schnupp, 2009). We consider here the idea that pitch perception requires a functional system comprising several areas with specific patterns of effective connectivity between them. We test this idea by comparing different dynamic causal models of electrical activity recorded directly from human auditory cortex using depth electrodes: we were particularly interested in testing biophysical models with a hierarchical connectivity, based on a predictive coding account of pitch perception.

From a psychophysical perspective, pitch is a fundamental auditory percept with a complex relationship to the structure of the sound in frequency and time (see de Cheveigne, 2005 for review). From a biological perspective, this suggests that the representation of pitch by the brain will not rest on a simple mapping of stimulus properties such as frequency. The auditory cortex of mammals contains multiple areas, each containing systematic frequency mappings, with mirror reversal of frequency gradients between areas (Kaas & Hackett, 2000). Recordings from single neurons have looked at whether some of these areas might be specialised for the representation of pitch. In the marmoset, neurons that show a form of ‘pitch tuning’ have been demonstrated in a low-frequency area abutting primary cortex in A1 (Bendor & Wang, 2005), while in the ferret, selective responses to pitch (based on a less strict criterion for pitch responsiveness) have been demonstrated in multiple areas (Bizley, Walker, Silverman, King, Schnupp, 2009).

In humans, direct recordings of local field potentials (LFPs) show responses to temporally regular sounds when these have rates associated with pitch (Griffiths et al, 2010). The responses are found in human primary cortex in medial Heschl's Gyrus (HG) and adjacent non-primary areas in HG. Functional magnetic resonance imaging (fMRI) studies (Patterson, Uppenkamp, Johnsrude, Griffiths, 2002; Penagos, Melcher, Oxenham, 2005; Puschmann, Uppenkamp, Kollmeier, Thiel, 2010) demonstrate maximal activity in lateral HG activity during pitch perception, although activity does occur in more medial areas too; see Griffiths et al (2010) for discussion. Megnetoencephalography (MEG) studies (Krumbholz, Patterson, Seither-Preisler, Lammertmann, Lutkenhoner, 2003; Gutschalk, Patterson, Rupp, Uppenkamp, Scherg, 2002; Gutschalk, Patterson, Scherg, Uppenkamp, Rupp, 2004) have also demonstrated activity that is lateral to primary auditory cortex. These studies beg the question as to how activity in the primary auditory cortex in medial HG and non-primary auditory cortex in more lateral parts of HG is related.

Predictive coding (Mumford, 1992; Rao & Ballard, 1999; Friston, 2002, 2005, Friston & Kiebel, 2009) as a model for perception posits that the brain uses a hierarchical generative model to predict and explain sensations. Representations of the causes of sensory input (e.g. temporal regularity for pitch perception) are optimised by minimising prediction error: predictions are passed to lower levels of a cortical sensory hierarchy by backward connections where they are compared with low-order representations (or sensory input at the lowest level) to produce a prediction error. The prediction error is then sent back to the level above via forward connections, to improve the predictions and hence reduce prediction error. This iterative process continues until the prediction error is minimized and an optimal hierarchical representation is formed. This model forms a theoretical basis for both visual (Kersten, Mamassian, Yuille, 2004; Rao & Ballard, 1999) and auditory (Vuust, Ostergaard, Pallesen, Bailey, Roepstorff, 2009) perception. We hoped to find evidence for this hierarchical message-passing by comparing different (hierarchical and non-hierarchical) connectivity models of observed electrophysiological responses.

In the present study, local field potentials (LFPs) were recorded from primary auditory cortex and adjacent auditory cortical areas along the axis of HG, while subjects listened to stimuli with varying pitch strength. We examined effective connectivity using dynamic causal modelling (DCM) (David et al, 2006) and Bayesian model selection (Stephan, Penny, Daunizeau, Moran, Friston, 2009; Penny et al, 2010) to determine (i) the effective connectivity between medial, middle and lateral HG and (ii) how these connections are modulated with varying pitch strength.

In addition to quantifying effective connectivity between areas, DCM allows the comparison of hierarchical architectures within the auditory system by defining forward connections (from lower to higher areas), parallel connections (between areas at the same level in the hierarchy) and backward connections (from higher to lower areas). In our DCM, forward connections are modelled as originating in pyramidal cells and targeting granular layers, whereas backward connections target supra-granular and infra-granular layers (cf. Felleman and Van Essen 1991). We hypothesised (i) that lateral HG is at a higher level in the auditory hierarchy than medial HG, and (ii) that the top-down influence of higher areas (lateral HG) would increase with the predictability (strength) of pitch, in accord with the predictive coding model; i.e., backward connections would predominate over forward connections. Our results demonstrate prominent effective connectivity between the three areas consistent with a hierarchical architecture and pitch-strength dependent changes in effective connectivity between lateral HG and lower areas that are consistent with predictive coding.

Materials and Methods

Dynamic Causal Modelling: Theory

In conventional non-invasive studies of brain function, brain responses using electroencephalography (EEG) and MEG or fMRI are routinely measured in response to a stimulus or when a cognitive/motor task is performed. However, most of the interesting things that happen when the brain is activated are hidden (that is, not directly measurable). For example, activity measured at one site of the brain may not be the sole result of processing at that site but it may also reflect neuronal interactions between areas. The goal of DCM is to make inferences about the hidden parameters and variables using measured variables. Specifically, DCM tries to explain the observed brain responses in terms of underlying causal interactions between different areas at the neuronal level. The technique was first used to infer the neuronal interactions from the measured BOLD signals from fMRI (Friston, Harrison, Penny, 2003). Subsequently, it has been extended to EEG/MEG (David et al, 2006) and local field potentials (Moran et al, 2009). Here we apply DCM to LFPs recorded directly from human auditory cortex. DCM has four components: (i) specification of a biologically realistic neuronal model for each area (ii) specification of models of causal interactions or extrinsic coupling among different areas, (iii) selection of the best model or architecture based on the evidence in the data, and (iv) inference of the parameters of the best model, given those data.

A single source in DCM is modelled by ‘a neural mass model’. The idea behind the neural mass model is that the state of an ensemble of neurons at a given time can be characterized by the mean activity of the ensemble. The dynamics of an ensemble over time can therefore be characterized by how this mean activity evolves over time and can be specified formally with biologically constrained differential equations (see Deco, Jirsa, Robinson, Breakspear, Friston, 2008 for a review of neural mass models). The neural mass model used in DCM was first described by Jansen & Rit (1995) and comprises three populations of neurons: a population of (excitatory) pyramidal cells receive inputs from excitatory and inhibitory interneurons (Supplementary Figure S1 (A)). In DCM each source is modelled with a three-population Jansen and Rit model, where the subpopulations are assigned to three layers: supragranular, granular and infragranular layers. Supragranular and infragranular layers comprise the superficial and deep pyramidal cells respectively along with a population of inhibitory interneurons. The ganular layer consists of excitatory interneurons (c.f. spiny stellate cells) only (Supplementary Figure S2(A)). Synaptic dynamics are modelled as a linear system, which is characterized by a (post synaptic response) kernel with two parameters for each subpopulation: a time constant and a maximum amplitude. Pre-synaptic activity is convolved with the kernel to produce postsynaptic activity. This is transformed by a nonlinear sigmoid function to firing rate (see Jansen & Rit (1995) and David et al (2006) for details). The output measured at a given area is modelled as a mixture of depolarization of each of the three populations (that is dominated by contributions from the pyramidal cells).

Cortico-cortical connections between different areas are arranged hierarchically. This hierarchy is reflected in the laminar pattern of origin and termination of connections between the two areas (Felleman & Van Essen, 1991). Specifically, forward connections originate in the supragranular layers and terminate in the granular layer, while backward connections originate in the infragranular layers and terminate in agranular layers and lateral connections connect agranular layers (Supplementary Figure S2(B)). This means that different areas can be connected by extrinsic connections that follow these anatomical rules. Each pattern of connections represents a different hypothesis about the functional architecture and corresponds to a competing model or DCM. Implementation of these connections using the Jansen and Rit (1995) model is shown in Supplementary Figure S1(B).

The final stage of DCM is the selection and optimisation of their parameters using measured brain responses. Mathematically, any DCM can be described by two equations:

$$\begin{array}{c}\frac{dx}{dt}=f(x,u,\theta )\\ y=g(x,\theta )\end{array}$$ (1)

The first (state) equation specifies how the experimental input u(t) influences the dynamics of hidden states x(t) and the second (observer) equation links the hidden states x(t) to measured brain responses y(t). θ represents the unknown parameters of model like connection strengths and synaptic parameters, which are to be estimated. The parameters are estimated using Bayesian statistics, which specify the posterior density of parameters θ, given the data:

$$p(\theta |y,m)=\frac{p(y|\theta ,m)p(\theta |m)}{p(y|m)}$$ (2)

Where p(y | θ, m) and p(θ | m) are the likelihood and prior density of parameters θ respectively of a given model m. The denominator p(y | m) is called the model evidence and is calculated as:

$$p(y|m)=\int p(y|\theta ,m)p(\theta |m)d\theta$$ (3)

An iterative method called variational Bayes (Friston, 2002) is used to estimate the posterior density p(θ | y, m) and the model evidence p(y | m). In this method, posterior density is approximated by density q(θ) that is assumed to be Gaussian. The idea behind variational Bayes is that the model evidence can be expressed as:

$$lnp(y|m)=F(q,\theta ,m)+D(q\Vert p(\theta |y,m)$$ (4)

or

$$F(q,\theta ,m)=lnp(y|m)-D(q–p(\theta |y,m)$$ (5)

where F is the free energy and D(q ║ p(θ | y, m). is Kullback-Leibler distance between density q and posterior density p(θ | y, m). Since Kullback-Leibler distance is non-negative, maximization of free energy minimizes the distance between q and posterior density. That is, q approximates the posterior density: q → p(θ | y, m). Furthermore, the maximum value of free energy approximates model log-evidence, that is:

$$lnp(y|m)\approx F(q,\theta ,m)$$ (6)

The log-evidence for different models can be used to determine the best model, given some data. DCM is usually used as a hypothesis-driven technique, where a number of models or hypotheses are specified in advance and the log-evidence for each model is calculated using the free energy approximation above. A complete list of parameters θ that are optimized is given in David et al (2006).

Subjects, surgery and recording

Local field potentials (LFPs) were recorded from two adult subjects, R154 and L156, undergoing intracranial electrophysiological recording to localise epileptic foci. Both subjects had normal hearing as confirmed by audiometric testing prior to implantation of electrodes. Hybrid depth electrodes (Howard et al, 1996; Reddy et al., 2010) with 14 high impedance contacts (70 - 300 kΩ) were implanted along the long axis of HG in one hemisphere. The electrode contact positions were determined by co-registering electrode locations identified on postoperative MRI scans with the subject's pre-operative 3-dimensional brain MRI. The localisation procedure demonstrated that all experimental high impedance electrode contacts in subject R154 and all but contacts 13 and 14 in subject L156 were in gray matter, along the axis of HG. The research protocols were approved by the University of Iowa Human Subjects Review Board. Prior informed consent was obtained from each subject before the study. Figure 1 shows the electrode locations in the two subjects.

Figure 1.

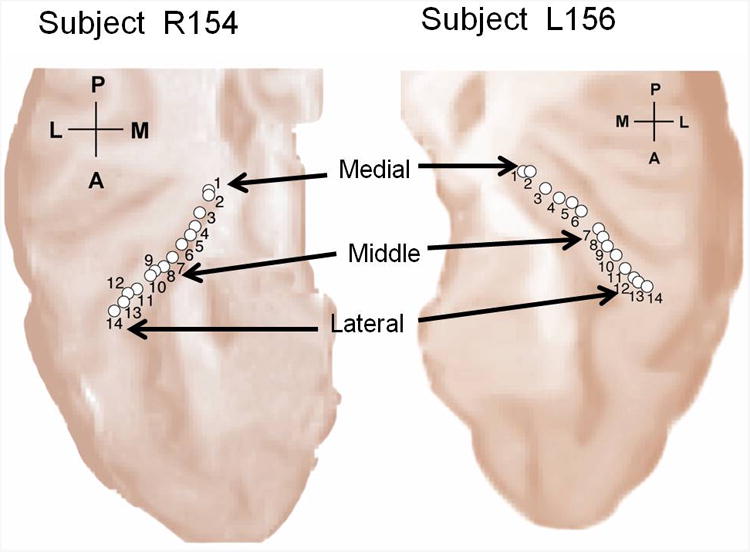
Electrode locations for the two subjects (subject R154 and L156) along the axis of HG overlaid on the MRI of the superior temporal plane. Three contacts, one each in the medial, middle and lateral part of HG were considered in the effective connectivity analyses. For subject R154, the chosen contacts were 1, 8 and 14 and for the subject L156 the contacts were 1, 7 and 12.

Electrical activity and effective connectivity were examined for three contacts in the medial, middle and lateral part of HG in each subject. For subject R154, the selected representative contacts were 1, 8 and 14; for subject L156, the contacts were 1, 7 and 12. The corresponding Talairach coordinates for these electrodes (Supplementary Information, Tables T1 and T2) show that they are located at three sites of maximal activity for sound minus silence contrasts in fMRI (Patterson et al, 2002), where the medial site corresponds to primary auditory cortex (human homologue of A1). The lateral maxima may correspond to homologues of non-primary areas in macaque (Brugge et al, 2009, Hackett, 2007).

Stimuli

The stimuli consisted of a 1-s burst of broadband noise followed by 1.5 s of regular interval noise (RIN). The RIN was created using a delay-and-add algorithm (Yost, 1996). RIN is also known as “iterated rippled noise” because of the ripples that the delay-and-add process induces in the frequency magnitude spectrum of the stimulus. We use the term RIN here to emphasise the temporal cue observed in the pattern of neural firing in the auditory nerve, and the temporal cue used in models of RIN perception (Yost, Patterson, Sheft, 1996; Patterson, Handel, Yost, Datta, 1996). The delay in the delay-and-add cycle determines the pitch value that the listener hears, and the number of cycles, or iterations, determines the pitch strength or salience (Yost et al. 1996; Patterson et al., 1996). The stimuli were normalised to a common power spectral density, high-pass filtered using a cut-off frequency of 800 Hz (to remove spectral ripples that might be resolved by the cochlea) and masked with broadband noise below the cut-off frequency (Griffiths et al., 2010).

Paradigm

Recordings were made in a dedicated recording facility in a shielded room. The experiments employed a passive listening paradigm. Subjects were awake with eyes open and relaxed during the recording sessions. The stimuli were delivered diotically via Etymotic ER4B earphones in custom earmolds at a comfortable sensation level of 45-55 dB. The DCM analysis was based on data acquired with RIN constructed with 8, 16, and 32 iterations and a fixed pitch value of 128 Hz. There was also a baseline condition with 0 iterations, that is, a spectrally-matched noise with no pitch. Time series were recorded from each electrode and averaged over 50 repetitions for each stimulus condition.

Data Preparation

LFPs were down sampled to 250 Hz, band-pass filtered between 4 and 16 Hz and averaged across trials. This narrow range of frequency band was chosen to analyze only the evoked responses time locked to stimulus onset. Evoked responses during the first 300 ms after RIN onset were analyzed.

DCM Specification

The principle objective of the present analysis was to ask: 1) what types of connections (forward, backward or lateral) couple the medial, middle and lateral areas of HG; 2) how are these connections modulated during the processing of stimuli with increasing pitch strength? To address the first question, a model space (set of models) was constructed based on the following biologically informed criteria:

• If an area A sends forward connections to area B then B sends backward connections to area A.

• If an area A sends lateral connections to area B then B sends lateral connections to area A.

Since there are 6 connections among the three areas and three are fixed by the above constraints (for example, if the connection between regions A and B is specified as forward then it follows that connection from B to A is backward), there are three unspecified connections, each of which could be forward, backward or lateral). This gives 3³ = 27 possible models.

To address the second question, a model space was constructed in which every connection in the model is either modulated or not modulated by temporal regularity. Since there are 6 connections there are 2⁶ = 64 models for each combination of connection types.

To finesse an exhaustive search over (27 × 64) models with different connections and modulations, we used a heuristic search strategy in which we first optimized the connection types (over subjects and pitch strength) and then optimized modulation-type models with the ensuing connection-types.

The DCMs exogenous inputs (u(t) in equation 1 above) comprise input relayed by sub-cortical structures and were modelled by gamma functions (David et al, 2006). In the present study, we used four gamma functions (Supplementary Figure S3). A gamma function models the event-related input that is delayed with respect to stimulus onset (this parameterisation of the inputs was optimised using Bayesian model comparison, with one to six gamma functions). This exogenous input entered all three regions of HG. We used multiple input components (gamma functions) to model the unknown convolutions of sensory discharges by earlier (subcortical) systems.

Family-wise model comparison

Since the connections types among medial, middle and lateral regions are not constrained by the nature of the exogenous input, all 27 connection-type models were inverted for different levels of temporal regularity (8, 16 and 32 iterations) and both subjects. To determine the type of a given connection (e.g. between medial and middle regions), all the models (across all regularity and subjects) were divided into three families: Family F1, in which the connection was forward, family F2 in which the connection was backward and family F3, in which the connection was lateral. The posterior probability that each connection was forward, backward or lateral was computed by summing the posterior probabilities of all (9) models in each family. The posterior probability of each model was evaluated by summing the log-evidence for each of the (27) models over subjects and regularity (under the assumption of independent data from each observation). The exponential of these pooled log-evidences was normalised so that their sum was unity. This gives the posterior model probability, under prior assumptions that each model was equally probable. Having established the optimum connection-types, we then inverted all 64 modulation-type models and examined the best models to see how temporal regularity (pitch strength) modulated those connections.

Results

Type of connections between medial, middle and lateral regions of HG

We constructed a model space consisting of 27 models that spanned all possible hypotheses about the types of connections between medial, middle and lateral regions of HG). The family-wise posterior probabilities for each connection being forward, backward or lateral are shown in Figure 2. This figure shows that medial and middle regions are connected to each other by lateral connections, whereas the lateral part of HG receives forward connections from, and sends backward connections to, both the medial and middle part of HG. A schematic representation of this architecture is shown in Figure 3. Based upon the hierarchal specificity of laminar projections (Felleman & van Essen, 1991, Maunsell & van Essen, 1983), these results suggest that:

• The medial and middle part of HG are reciprocally connected by lateral connections and are at a similar level of hierarchy.

• The lateral part of HG is at a higher level of the auditory hierarchy than medial and middle parts.

Figure 2.

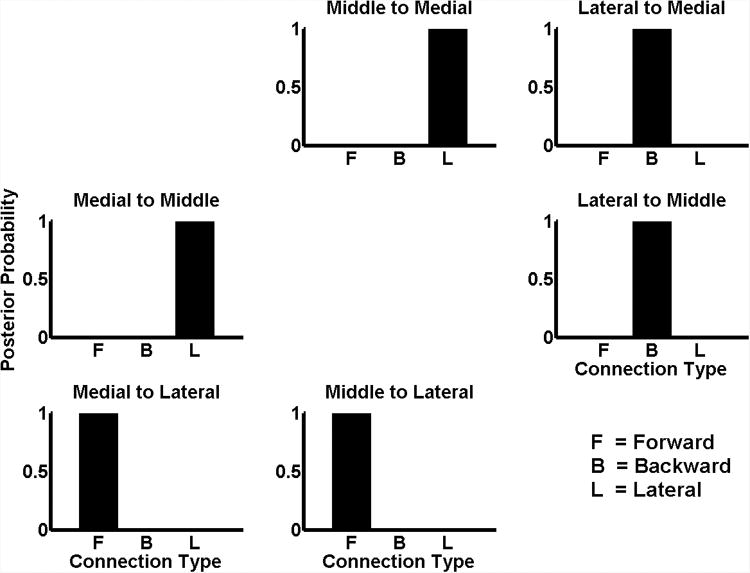
Posterior probability of model families, where each family (or partition of model space) was defined in terms of the connection type for each connection. The posterior probability was computed using fixed effect analysis over three conditions (8, 16 and 32 iterations) and two subjects.

Figure 3.

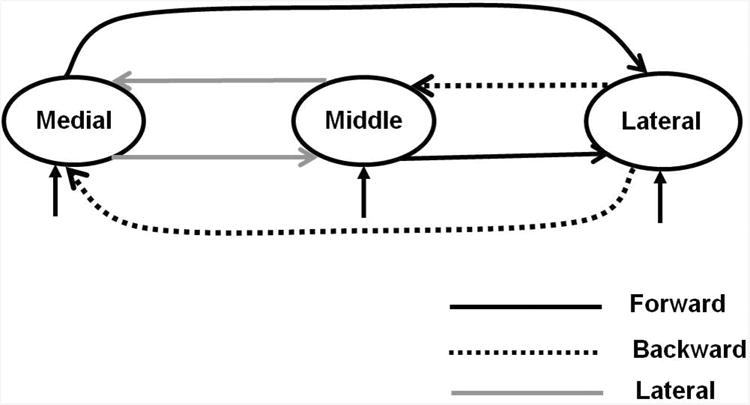
Most probable connection types between medial, middle and lateral parts of HG

Modulation of connectivity by temporal regularity

Having established the types of connection, we next investigated how these connections were modulated by the temporal regularity of the RIN. Event-related responses to RIN with 0, 8, 16 and 32 iterations from the medial, middle and lateral HG were analysed together in a single DCM. This involved optimising additional parameters that controlled how pitch strength (number of RIN iterations) modulated the strength of connections monotonically, over the four ERPs (as in Garrido et al 2008). We constructed 64 variants of the model shown in Figure 3. These models were based on all possible combinations of how pitch strength could modulate extrinsic connections among the three areas. Posterior probabilities for each of these 64 models for the two subjects R154 and L156 are shown in Figure 4(a) and 4(b) respectively. For subject R154, there are two comparably plausible models (64 and 48) that have posterior probabilities of 0.52 and 0.37 respectively. For subject L156, the best model (model 60) has a posterior probability of 0.78 and the second best model (model 44) has a posterior probability of 0.20. The best models (64 and 48 for subject R154 and 60 and 44 for subject L156) for the two subjects are shown in Figure 5. Red and green triangles denote those connections that are modulated by pitch strength. These results show that in subject R154 (Figure 5(A)), the two winning models have a very similar structure: in model 64 (posterior probability 0.52) all the connections are modulated, whereas in model 48 (posterior probability 0.37), all but the middle to medial connection are modulated by temporal regularity. In subject L156 (Figure 5(B)), the best model (model 60 posterior probability 0.78) requires modulation of all connections with the exception of lateral to middle whereas in the second best model (model 44, posterior probability 0.2), in addition to the connection in the best model, connection from middle to medial is also not modulated.

Figure 4.

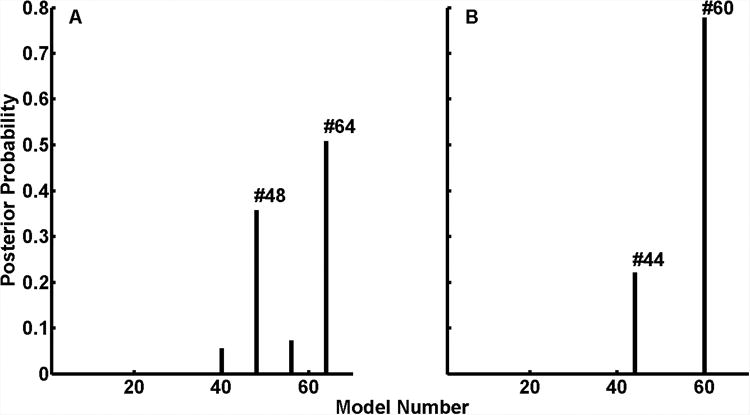
Posterior probabilities of 64 modulation-type models; (a) for subject R154 and (b) for subject L156

Figure 5.

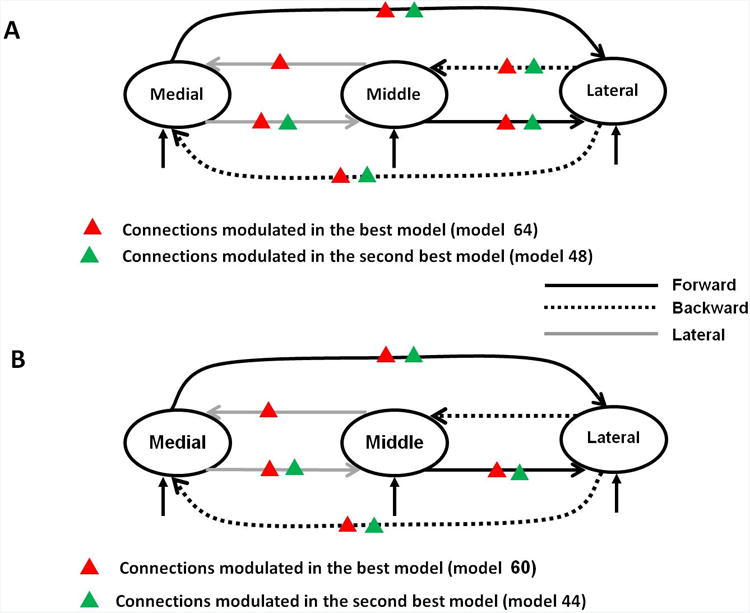
Structure of the best models; (a) for subject R154 and (b) for subject L156.

Figure 6 plots the change in connection strength with temporal regularity for both subjects. Modulation of connectivity for the best model (model 64 in subject R154, Figure 6(a) and model 60 in subject L156, Figure 6(b)) is shown in black. Modulation for the second best model (model 48 in subject R154 and model 44 in L156) is shown in grey. The profile of modulation is remarkably consistent between the two subjects and shows distinct effects of pitch strength on different connections within the system. The following generalisations can be drawn from these results:

• For subject R154, all connections show very similar patterns of pitch-strength modulation, except the connection from middle to medial region, which is modulated in one model (model 64) but not the other (model 48)

• For subject L156, the pattern of connectivity is again very similar except in the middle to medial region which is modulated in the best model (model 60) but not in the second best model (model 44)

• Backward connections from lateral HG (to both medial and middle HG in subject R154 and to only medial HG in subject L156) increase with temporal regularity. In both subjects, there is almost a doubling of connection strength with increasing temporal regularity.

• Forward connections from both the medial and middle HG decrease with temporal regularity.

• Lateral connection strengths (from medial to middle and middle to medial) increase with temporal regularity. However, the medial to middle connection changes much more than the reciprocal connection.

Figure 6.

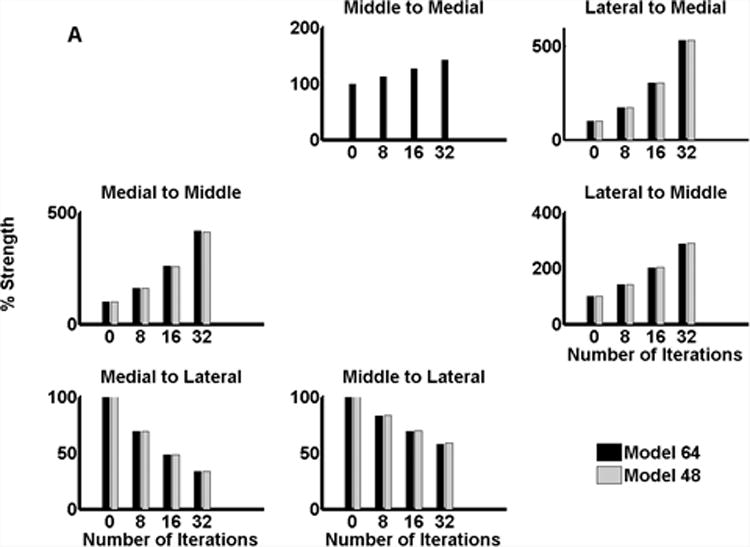
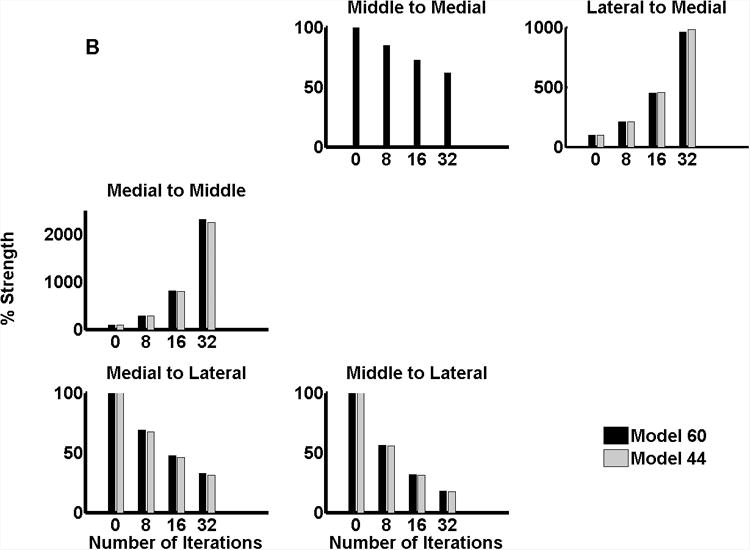
Modulation of connectivity with temporal regularity; (a) subject R154 (b) subject L156.

Discussion

Connection types in HG

Based on cytoarchitectonics, Brodmann (1909) localized primary auditory cortex to HG. However, further studies have shown that HG is not a single homogeneous area but consists of at least two areas (von Economo and Koskinas' (1925) areas TC and TD; and Galaburda and Sanides' (1980) KAm and kAlt) or three areas (Morosan et al (2001), Te 1.0, Te 1.1 and Te 1.2). To the best of our knowledge, however there is no literature on the types of connections that exist between these distinct regions in humans. We applied dynamic causal modelling to depth electrode data recorded from the medial, middle and lateral regions of HG to infer the types of (effective) connections between them. Our results suggest that medial and middle regions are connected by lateral connections, whereas the lateral region receives forward projections from, and sends backward connections to the other two regions of HG. This implies that lateral HG is at a higher level of the auditory hierarchy than the medial and middle regions (Felleman & von Essen (1991) and medial and middle regions of HG occupy similar levels.

The notion that lateral HG is at a higher level of hierarchy than medial HG agrees with a number of previous studies. Cytoarchitectonic studies in humans (Galaburda & Sanides, 1980; Morosan et al, 2001) have shown that lateral HG is less ‘primary-like’ than medial and middle HG. Von Economo and Koskinas (1925) described this area as a ‘transition zone between primary and non primary areas’ (Morosan et al, 2001). Although the homology between the auditory areas of macaque and human is not well established, functional studies using same stimuli in both humans and macaque have suggested that lateral HG may correspond to area R/RT (Baumann et al, unpublished observations) or may correspond to a belt area (Brugge et al, 2009) in macaques. Moreover, the possibility that medial and middle regions of HG are at a similar hierarchical level is consistent with functional studies which shows that medial and middle HG have similar responses and may both lie in the core area (Brugge et al, 2009).

Modulation of connectivity strength with increasing temporal regularity

We have shown that backward connections from lateral HG (to medial and middle HG) increase with temporal regularity and forward connections (from medial and middle HG) decrease with temporal regularity. These results can be explained by predictive coding (Mumford, 1992; Barlow, 1994; Friston, 2002; 2005, Friston & Kiebel, 2009; Rao & Ballard, 1999). The idea behind predictive coding is that, in a hierarchically organized brain, areas higher in the hierarchy (here lateral HG) use a generative model of the world to make predictions of representations at lower levels. These predictions are passed to lower areas by means of backward connections (here medial and middle HG). The difference between the actual representation at the lower area and the prediction is the prediction error. This is passed back to the higher area by means of forward connections to adjust the higher level representation: if the error is large then the model of the world ‘stored’ in higher order area is not correct and needs updating. This recursive message passing entails an iterative process, which aims at minimizing prediction error at all levels in the hierarchy, to describe the causes of sensory input at multiple levels. Clearly, our use of RIN speaks directly to the predictability of stimuli and the perceptual inferences about pitch. Our hypothesis assumed that as the predictability of stimuli increased the top down influences mediating predictions would become stronger relative to bottom up passing of prediction errors. The theoretical mechanism behind this effect is quite simple: in computational models of predictive coding the precision (inverse variance) of prediction error is encoded by the post synaptic sensitivity of prediction error units, generally thought to be superficial pyramidal cells. This means that when stimuli are predictable (and prediction errors are low) the responsiveness of pyramidal cells to top-down predictions increases (because precision is high). This is what we observed empirically in the DCM. Similar results have also been found in studies of perceptual discrimination using endogenous fluctuations in activity or sensitivity (e.g., Hesselmann et al., 2010). This finding is also consistent with the relative decrease in the strength of forward connections for standard stimuli relative to unpredicted oddball stimuli using DCM and the mismatch negativity paradigm (e.g., Garrido et al., 2009).

The lateral connections between medial and middle HG are also modulated by temporal regularity. The medial to middle connection increased in both subjects and middle to medial connection increased for one subject and decreased for the other. One possible functional role of lateral connections is to decorrelate regions of the network which respond to the same feature of the stimulus (Foldiak, 1990; Sirosh and Mikkulainen, 1996). For example, if two regions respond to the same stimulus feature, then responses of these two regions will be correlated. Lateral connections using mutual inhibition reduce this redundancy and make the representations more efficient (a sparse representation). This can be shown formally to be an emergent property of predictive coding (Friston, 2008).

There is a close relationship between the number of iterations used to generate a RIN and the strength of the pitch that listeners hear, and so the model of regularity processing has direct implications for models involving perceptual inferences about pitch and pitch strength. A number of previous fMRI studies (Patterson et al, 2002; Penagos et al, 2005) have emphasized a role for lateral HG in the processing of temporal regularity and the perception of pitch. Our results suggest a specific role for lateral HG in pitch prediction as part of a constructive (predictive) hierarchical model, distributed within an auditory pitch system.

A number of computational models for pitch perception have been proposed in the literature (de Cheveigne, 2005). Most of these models lack biological realism because (i) they are driven bottom-up: these models compute some feature (e.g. spectrum or autocorrelation of the stimulus without using any top-down information (ii) they are non-hierarchical: they extract the percept only at one scale. The current theories of brain function suggest that the percept is computed hierarchically at different time scales and is driven both by bottom-up and top down flow of information (Friston, 2008). One such model (Balaguer-Ballester, Clark, Coath, Krumbholz, Denham, 2009), emphasizing the role of hierarchies and top-down effects in computing pitch, was proposed recently. In this model, higher areas optimise the temporal scale over which information is integrated in lower areas. Thus, different temporal scales are invoked, depending on the (slow or fast) dynamics of the stimulus. We suggest that lateral HG may play a similar role and adapts the time scale of integration in lower areas (primary auditory cortex and sub-cortical areas) in a context-sensitive manner. This might be achieved using the prediction signal from the lateral HG or the local prediction error signal (for example in the primary auditory cortex) to adapt processing in the primary auditory cortex. Please see (Kiebel, Kriegstein, Daunizeau, Friston, 2009) for a discussion of related mechanisms in tracking auditory sequences under the predictive coding framework.

The predictive coding hypothesis has a number of consequences, some of which we have exploited when comparing different explanations (DCMs) for our data: These include (i) a hierarchy of cortical levels; (ii) forward and backward message-passing that entails reciprocal and directed connectivity; (iii) Functional asymmetries in forward and backward connections (modelled here in terms of the subpopulations targeted); (iv) Top-down influences can only be expressed when predictions can be formed, suggesting a predictability-dependent (pitch salience-dependent) expression of backward effective connectivity.

Although not explicitly tested here, predictive coding also suggests: (i) Areas higher in the hierarchy (lateral HG in the present study) will have a longer temporal window of integration. This is because higher areas (which predict activity in lower areas) receive inputs (prediction errors) from a number of areas below, each of which integrates input using a smaller temporal window (ii) the dynamics of areas higher in the hierarchy will unfold more slowly than areas lower in the hierarchy (iii) Responses (context-sensitive predictions) to a given event depend on the context surrounding the event. For example, an MEG study (Chait, Poeppel, Simon, 2007) showed that responses to transitions from an ordered train of tone pips to a disordered train is different when the transition is made in the reverse direction (that is, from ordered tone pips to disordered tone pips). See Friston (2008) for a fuller discussion of these issues.

One possible criticism of our study could be that we have used only one type of stimulus (RIN) and the analysis is restricted to areas lying along the HG. A recent fMRI study (Hall & Plack, 2009) using a broader range of pitch producing stimuli has shown that pitch related activity may extend to areas beyond HG. However, the role of lateral HG in pitch perception is not restricted to RIN stimulus only. Studies from several groups using stimuli other than RIN have shown role of lateral HG in pitch perception. These stimuli include, harmonic complexes (Penagos et al, 2005; Warren, Uppenkamp, Patterson, Griffiths, 2003), Huggins pitch (Puschmann et al, 2010) and click trains (Gutscahalk et al, 2002; Gutscahalk et al, 2004). It will be interesting to see how specific the system we have identified is to the type of pitch used.

In our previous study (Griffiths et al, 2010), we observed both evoked and induced high frequency gamma (80-120 Hz) in response to RIN all along the HG. The latter particularly occurring when the RIN frequency was above the lower limit of frequency that is perceived as pitch. In the current study, we have only focussed on how to explain the evoked responses in terms of interactions between the medial, mid and lateral part of HG. Interactions between these regions in the gamma range will be addressed in future studies using DCM for induced responses (Chen, Kiebel, Friston, 2008)

Supplementary Material

Supplementary Figure 1

Figure S1: (A) Schematic representation of the Jansen and Rit model for a single source (B) Hierarchical connections between Jansen and Rit units based on Felleman and Van Essen (1991) rules.

Figure S2: (A) Schematic representation of the laminar structure of the cortex modelled in DCM. (B) Hierarchical connections between different regions of the cortex based on Felleman and Van Essen (1991) rules.

Figure S3: Input used in the DCM models. It models input relayed by sub-cortical structures and consists of four gamma functions. The choice of four gamma functions was determined using Bayesian model comparison.

Table T1: Talairach coordinates of high impedance contacts in right auditory cortex for subject 154

Table T2: Talairach coordinates of high impedance contacts in left auditory cortex for subject 156