Single-Molecule Analysis of the Rotation of F₁-ATPase under High Hydrostatic Pressure

Abstract

F₁-ATPase is the water-soluble part of ATP synthase and is an ATP-driven rotary molecular motor that rotates the rotary shaft against the surrounding stator ring, hydrolyzing ATP. Although the mechanochemical coupling mechanism of F₁-ATPase has been well studied, the molecular details of individual reaction steps remain unclear. In this study, we conducted a single-molecule rotation assay of F₁ from thermophilic bacteria under various pressures from 0.1 to 140 MPa. Even at 140 MPa, F₁ actively rotated with regular 120° steps in a counterclockwise direction, showing high conformational stability and retention of native properties. Rotational torque was also not affected. However, high hydrostatic pressure induced a distinct intervening pause at the ATP-binding angles during continuous rotation. The pause was observed under both ATP-limiting and ATP-saturating conditions, suggesting that F₁ has two pressure-sensitive reactions, one of which is evidently ATP binding. The rotation assay using a mutant F₁(βE190D) suggested that the other pressure-sensitive reaction occurs at the same angle at which ATP binding occurs. The activation volumes were determined from the pressure dependence of the rate constants to be +100 Å³ and +88 Å³ for ATP binding and the other pressure-sensitive reaction, respectively. These results are discussed in relation to recent single-molecule studies of F₁ and pressure-induced protein unfolding.

Introduction

Pressure is one of the most fundamental thermodynamic parameters and it modulates chemical equilibrium of conformational stability as well as the catalytic power of proteins. Although pressure is not generally an option for physical perturbation of chemical reactions due to the technical complexity involved, experiments under high hydrostatic pressure offer unique opportunities to elucidate the molecular mechanism. Equilibrium shift of chemical reactions under high pressure obeys Le Chatelier’s principle; when the reaction product has a smaller partial molar volume than the reactant, the reaction is promoted by pressure. A prominent and well-studied effect of hydrostatic pressure on proteins is pressure-induced unfolding (1); when hydrostatic pressure is applied at more than several hundred MPa, some proteins unfold by swelling with water molecules. From a thermodynamic point of view, this means that the water-swollen state has a smaller partial molar volume.

Hydrostatic pressure also affects the catalytic reaction rate of proteins. The activation volume, ΔV^‡, which is the partial molar volume change upon transition-state formation, characterizes modulation of catalytic power by pressure; when ΔV^‡ is positive, the reaction is decelerated by pressure, and vice versa. For instance, the activities of dihydrofolate reductase, tryptophan permease, and kinesin were suppressed by high pressure (2–4). In contrast, thermolysin, α-chymotrypsin, and α-cyclodextrin are activated by pressure (5–7). In the former cases, ΔV^‡ is considered to be positive, whereas in the latter cases it would be negative. Thus, pressure sensitivity gives insights about the conformational state of enzymes at the transition state.

The structural details and kinetic features of pressure-induced protein unfolding have been well studied in NMR (1,8,9) and other spectroscopic measurements (10–15). However, the dynamical features of proteins during catalytic turnover under high pressure have not been well understood. To investigate the effects of pressure on the morphology of the cellular cytoskeleton network, several research groups developed a high-pressure chamber system for microscopic imaging (16,17). Salmon observed depolymerization of the spindle microtubule in cells when pressure of several dozens of MPa was applied (18). Recently, we developed a high-pressure chamber that allows us to monitor the real-time dynamics of protein molecules under pressure of up to 200 MPa (4). It was revealed by in vitro motility assay that hydrostatic pressure suppresses the gliding velocity of microtubule filaments moved by kinesin motors. Our results showed that the pressure mainly affects the stepping motion, but not the ATP binding reaction. These activation volumes were 88 and 15 Å³, respectively. The high-pressure microscopy system has also been used to study how pressure affects the bacterial flagella motor (19–21). In this study, we used a high-pressure microscope to conduct a single-molecule rotation assay of F₁-ATPase to elucidate the effects of pressure on the catalysis of F₁ resolving into individual reaction steps.

F₁-ATPase is the water-soluble part of F₀F₁-ATP synthase and is an ATP-driven rotary molecular motor (22). The bacterial F₁-ATPase is composed of α₃β₃γδε subunits. The minimum complex as a motor is the α₃β₃γ subcomplex, hereafter referred to for simplicity as F₁. The α₃β₃ forms the stator ring and the γ subunit is the rotary shaft. The reaction centers reside at three α-β interfaces, mainly on β subunits (23). Catalysis on the β subunits is highly cooperative (24); each β sequentially hydrolyzes ATP, changing the conformational state in a unique order to induce the unidirectional rotation of the γ subunit (25,26). An elementary step of the mechanochemical reaction of F₁ is 120° rotation that is coupled with a single turnover of ATP hydrolysis (27). The 120° step rotation can be resolved into the 80° and 40° substeps, each triggered after ATP binding or ATP hydrolysis, respectively (28,29). Therefore, the angular positions before the 80° and 40° substeps are termed the binding angle and the catalytic angle, respectively. Further analysis revealed that ADP release and a highly temperature-sensitive (TS) reaction occur at the binding angle (30,31). The TS reaction is considered a conformational rearrangement reaction of β before or after ATP binding (32). It has been suggested that release of inorganic phosphate (P_i) takes place at the catalytic angle (30,33). In addition, the rotation mechanism has been studied by various theoretical methods, such as mathematical modeling (34), quantum chemical calculations (35–37), normal-mode analysis (38), water-entropy effect (39,40), and molecular dynamics simulations (41–45). Thus, the mechanochemical coupling reaction scheme of F₁ has been well studied. However, the molecular basis of the individual catalytic reaction steps is not understood.

The effect of hydrostatic pressure on the catalytic activity of F₁ and F₀F₁-ATP synthase was studied in biochemical assays, which, however, focused on the pressure-induced unfolding and/or dissociation of constituent subunits of F₁ and F₀F₁ complex (46–50). In this study, we used the F₁-ATPase from thermophilic Bacillus PS3, which is not only tolerant of heat treatment but also stable against denaturing conditions and reagents. The thermostable F₁ retained the active complex even at 140 MPa and showed the unidirectional rotation, allowing us to investigate the effect of hydrostatic pressure on catalysis at the single-molecule level. This work clearly showed that F₁ has at least two pressure-sensitive reactions, one of which is the ATP-binding process. Another pressure-sensitive reaction was also found. This reaction is a post-ATP-binding reaction but occurs at the ATP-binding angle. The result is discussed with regard to the torque-generation mechanism of F₁ and recent studies on pressure-induced protein unfolding.

Materials and Methods

Preparation of F₁

The α₃β₃γ subcomplex from thermophilic Bacillus PS3 that was genetically modified for single-molecule rotation assay and the α(His₆ at N-terminus/C193S)₃β(His₁₀ at N-terminus)₃γ(S108C/I211C) were expressed in Escherichia coli, purified, and biotinylated as in a previous work (51). The mutant F₁ retained the genuine catalytic activity at ambient pressure and temperature conditions and was used as the wild-type F₁-ATPase in this study. Another mutant F₁, F₁(βE190D) in which βE190D mutation (29) was introduced in addition to the above mutations, was prepared in the same way as the wild-type.

High-pressure microscope

Fig. 1 A shows a schematic illustration of the high-pressure microscope (19). The pressure apparatus consisted of a high-pressure chamber, separator (4), pressure gauge (PG-2TH, Kyowa, Kyoto, Japan), and hand pump (HP-150, Syn, Kyoto, Japan). Hydrostatic pressure was applied using the hand pump, and then the water pressure was properly transduced to the assay buffer in the separator, as described previously.

Figure 1.

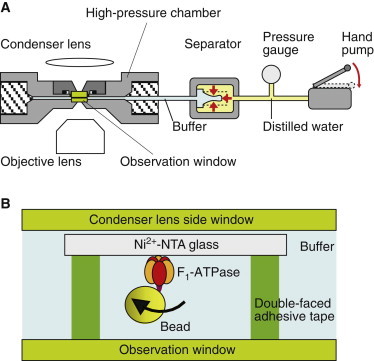
Direct observation of rotation of single F₁-ATPase molecules at high pressure (not to scale). (A) Schematic diagram of the high-pressure microscope (19). (B) Experimental system. F₁-ATPase molecules were fixed on the surface of Ni²⁺-NTA glass set on the observation window with double-faced adhesive tape. The bead for visualization was attached onto the γ-subunit of F₁-ATPase. The rotational direction was clockwise from the view of bottom side. To see this figure in color, go online.

The chamber was equipped with two optical windows that allowed us to acquire microscopic images. Due to the thickness of the glass and physical hindrance at an opening of the chamber with the objective lens, the image was obtained with a long-working-distance objective (LUCPlanFLN ×40/NA 0.6, Olympus, Tokyo, Japan). The chamber was mounted on the stage of an inverted microscope (IX-71, Olympus). The bright-field images were recorded at 30–100 frames s⁻¹ with a high-speed camera (LRH20000B, digimo, Tokyo, Japan) (19). The recorded images were analyzed with tracking analysis software (G-track, G-Angstrom, Sendai, Japan) or a custom-made program (K. Adachi, Waseda University, Tokyo, Japan).

Rotation assay

A flow cell for the rotation assay was constructed on the observation window of the high-pressure chamber with a small piece of a nickel-nitrilotriacetic acid (Ni²⁺-NTA) glass and two strips of double-faced adhesive tape (Fig. 1 B). Solution of F₁ molecules in the basal buffer (50 mM MOPS-KOH, pH 7.0, and 50 mM KCl) was introduced into the flow cell to immobilize F₁ molecules on the Ni²⁺-NTA glass surface. After 10 min incubation, unbound F₁ molecules were washed out with bovine serum albumin (BSA) mixture (5 mg ml⁻¹ BSA in basal buffer). Streptavidin-coated magnetic beads (≥0.2 μm, Seradayn, Thermo Scientific, Waltham, MA) were introduced for attaching to the biotinylated γ-subunit of F₁. After 20 min incubation, unbound beads were washed out with the BSA mixture, and then the ATP mixture (2 mM MgCl₂ and the indicated amount of ATP) was injected into the flow cell. The ATP regenerating system (1 mM phospho(enol)pyruvate and 0.1 mg/mL pyruvate kinase) was also included in the ATP mixture under conditions of <2 mM ATP concentration. Then, ATP mixture was poured into the remaining space of the chamber and separator to fill up. The chamber was set on the microscope stage, connected with the separator, and then the hatch was closed. The rotation assays were performed at room temperature (23–26°C).

Analysis

Because the Ni²⁺-NTA glass was set to cover the observation window, F₁ showed the rotation with the protruding part facing downward (Fig. 1 B). Therefore, the rotary direction of the recorded rotations was clockwise. The data were analyzed after correcting the rotary direction. We analyzed only F₁ molecules that showed continuous rotation at any condition, meaning that data derived from the inactive form of F₁ were excluded from the analysis. The rotational rate of F₁ was measured from the slope of the time course of rotations. The rotary fluctuation during pause was determined from the standard deviation of the Gaussian curve for fitting the pauses recorded at 100 frames s⁻¹. The concentration of ATP was corrected from the density of distilled water at each pressure (52).

Results

Effect of pressure on the rotational rate of wild-type F₁

Fig. 2, A and B, displays the time courses and xy plots of rotation of single F₁ molecules under ATP-saturating (2 mM) and ATP-limiting concentrations (200 nM), respectively. At 0.1 MPa and 2 mM ATP, F₁ showed smooth rotation without evident pauses, as previously reported (Fig. 2 A, blue line and trajectory) (25,27). When 140 MPa pressure was applied to the system under ATP-saturating condition (2 mM), the rotary motion drastically changed (Fig. 2 A, red line and trajectory); F₁ showed discrete 120° steps, showing that applied pressure did not change the step size and directionality of the rotation. To investigate the reversibility of the pressure-induced change, the pressure was changed from 0.1 MPa to 140 MPa, and then returned to 0.1 MPa during the observation of particular rotating molecules (Fig. 2 C). The mean rotational rate at 0.1 MPa was 9.5 ± 3.5 rps (mean ± SD). At 140 MPa, the rotational rate decreased to 3.0 ± 1.1 rps, and then recovered to the initial rate, 9.3 ± 4.3 rps, when pressure was returned to 0.1 MPa.

Figure 2.

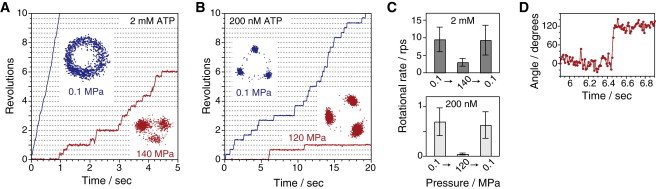
Rotation of wild-type F₁-ATPase. (A and B) Time courses and their centroid traces of the rotation of F₁-ATPase at two concentrations, [ATP] = 2 mM (A) and [ATP] = 200 nM (B). Data were obtained from different molecules at each condition. (C) Reversible inhibition of rotation of F₁-ATPase at 2 mM (upper; n = 18–43, total = 87) and 200 nM ATP (lower; n = 38–56, total = 148) (mean ± SD). (D) Rising phase of single 120° step at 120 MPa and 200 nM ATP. Data were recorded at 100 frames s⁻¹. To see this figure in color, go online.

Similar pressure effects were also observed under ATP-limiting conditions (200 nM). At 0.1 MPa, F₁ showed the clear 120° steps pausing at three ATP-binding angles (Fig. 2 B, blue line and trajectory). At 120 MPa, the dwell time was evidently lengthened (Fig. 2 B, red line and trajectory). The rotational rate decreased from 0.69 ± 0.28 rps at 0.1 MPa to 0.045 ± 0.019 rps at 120 MPa (Fig. 2 C). The pressure effect under the ATP-limiting condition was also reversible; after the pressure was released, rotation of F₁ recovered to the initial rate, 0.63 ± 0.27 rps. Thus, under high pressure, F₁ showed distinctive pauses at three positions in both ATP-saturating and ATP-limiting conditions.

Next, we examined whether F₁ retains a stable conformation even under high pressure. The rotary fluctuations during the ATP waiting pause were measured under 0.1 and 120 MPa. The standard deviations during the pauses were determined from Gaussian fitting of the angle distribution. The mean ± SD was 12 ± 2° (n = 21 angles from seven molecules) and 12 ± 4° (n = 15 angles from five molecules) for 0.1 and 120 MPa, respectively. This suggests that high pressure does not greatly affect the conformational stability of F₁ motors.

Finally, we checked whether high hydrostatic pressure affects the driving torque for a 120° step. In the rotation assay, the torque is balanced with the hydrodynamic friction on the rotating probe, and the value is proportional to the angle velocity and drag coefficient. Fig. 2 D displays the typical time course of a 120° step at 120 MPa and 200 nM ATP on an expanded timescale. Most steps took place rapidly, independent of pressure. This means that the application of pressure did not seriously affect the angle velocity at the rising phase of the 120° step. In addition, note that although water viscosity increases under high pressure, the increment of the viscosity at 150 MPa is only +9% (4), and thus is negligible in this study. These results thus indicate that hydrostatic pressure does not significantly affect the torque of F₁.

Michaelis-Menten kinetic analysis of rotation of wild-type F₁-ATPase

Rotation assays were performed at various ATP concentrations. Fig. 3 A shows the typical time courses of the rotation at 120 MPa. The mean rotational rate decreased from 4.1 ± 1.5 to 0.045 ± 0.019 rps when [ATP] was decreased from 2 mM to 200 nM. The rotation time courses show clear 120° stepping rotation at all [ATP]s. Histograms of the angular position of rotation (Fig. 3 B) also show 120° stepping rotation. The following analysis showed that the Michaelis-Menten constant, K_m, is 18 μM at 120 MPa. Even at 20 μM ATP, close to the K_m at which the time constants of ATP binding and the subsequent reactions are comparable, F₁ still showed only 120° stepping rotation (Fig. 3 B). This is in contrast to the rotation under ambient pressure; F₁ shows 80° and 40° substeps, pausing at six positions, three binding angles, and three catalytic angles at [ATP] around K_m (28). An attempt was made to find the rotation with 80° and 40° substeps under different pressures. However, the time courses and histograms for angular position showed no evidence of substeps. These observations strongly suggest that one or a few pressure-sensitive reactions occurred at the angular positions for ATP-binding. This point was verified by the rotation assay using a mutant F₁, F₁(βE190D) (see below).

Figure 3.

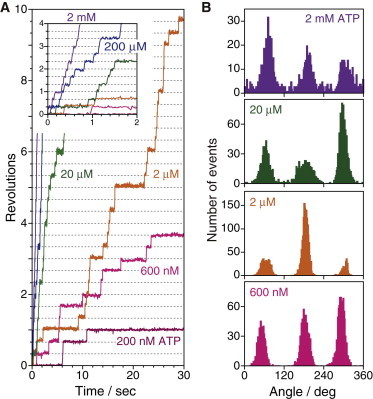
Stepping rotation of wild-type F₁-ATPase (A) Time courses of rotation of F₁-ATPase at 120 MPa, at various ATP concentrations. (B) Histograms of the angle from the traces in A. To see this figure in color, go online.

We performed systematic analysis of the rotational rate of single F₁ motors under various concentrations of ATP (from 200 nM to 2 mM) and hydrostatic pressures (from 0.1 to 120 and 140 MPa at 200 nM and 2 mM ATP, respectively). The rotational rate gradually decreased with increased pressure at each concentration of ATP (Fig. 4 A). The pressure and rotational rate curve was similar to a linear relation at limiting [ATP] (200 nM). On the other hand, at saturating [ATP] (2 mM), the pressure dependence of the rotational rate was relatively weak, indicating that the rate-limiting process at ambient condition was not highly sensitive to applied pressures.

Figure 4.

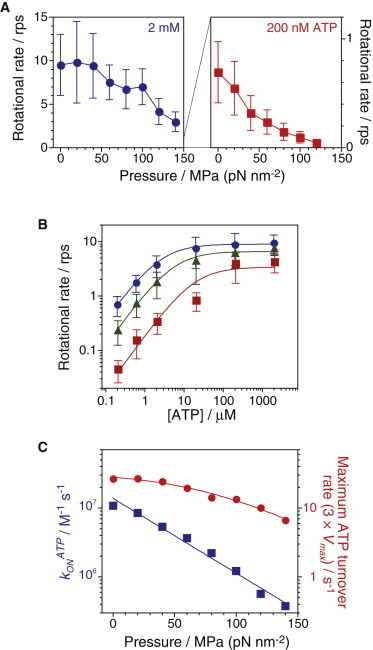
Rotational rate of wild-type F₁-ATPase. (A) Pressure dependence of rotational rates under saturating (2 mM, n = 12–43, total = 173) and limiting ATP concentrations (200 nM, n = 38–75, total = 406) (mean ± SD). (B) Rotational rates (mean ± SD) as a function of ATP concentration at 0.1 (circles, n = 22–81, total = 314), 60 (triangles, n = 12–102, total = 294), and 120 MPa (squares, n = 25–79, total = 283). Curves show the fitting line with the Michaelis-Menten equation, V = V_max × [ATP]/(K_m + [ATP]); V_max = 8.9 ± 0.3, 6.5 ± 0.5, and 3.4 ±1.1 s⁻¹; K_m = 2.4 ± 0.1, 5.3 ± 0.6, and 18 ± 8 μM at 0.1, 60, and 120 MPa, respectively. (C) Pressure dependence of the apparent ATP binding rate, k_on^ATP (squares) and maximum ATP turnover rate, 3 × V_max (circles). The plots of k_on^ATP were fitted by Eq. 1 with k_on^ATP(0.1) = 14 ± 2 ×10⁶ M⁻¹ s⁻¹ and ΔV^‡ = +100 ± 10 Å³. The plots of 3 × V_max were fitted by Eq. 2 with k_p-ind = 33 ± 5 s⁻¹, k₀ = 180 ± 90 s⁻¹ and ΔV^‡ = +88 ± 15 Å³. To see this figure in color, go online.

Fig. 4 B summarizes the ATP concentration dependence of the rotational rate at 0.1, 60, and 120 MPa. Each data set was fitted with a simple Michaelis-Menten equation to determine the maximum rate, V_max, and the Michaelis constant, K_m (28,53). When the pressure was increased from 0.1 to 120 MPa, V_max decreased from 8.5 to 3.4 s⁻¹, whereas the K_m increased from 2.4 to 18 μM. These parameters at 120 MPa were similar to those at 0.1 MPa and 4°C (V_max = 2.0 s⁻¹ and K_m = 12 μM) (31), showing that increased pressure and low temperature apparently caused similar effects on the rotation of F₁.

Fig. 4 C shows the pressure dependence of the apparent ATP binding rate, k_on^ATP (3 × V_max/K_m), and the maximum ATP turnover rate, 3 × V_max. It clearly shows that ATP-binding and post-ATP-binding steps are pressure-sensitive reactions. The value of k_on^ATP decreased from 11 × 10⁶ M⁻¹ s⁻¹ at 0.1 MPa to 0.57 × 10⁶ M⁻¹ s⁻¹ at 120 MPa. The relationship between pressure and k_on^ATP was linear on a log scale. It can be characterized by

$$k_{\text{on}}^{\text{ATP}}\left(P\right)\mathrm{=}{k}_{\text{on}}^{\text{ATP}}\left(0.1\right)\times \exp \left(\frac{\mathrm{-}\left(P\mathrm{-}0.1\right)\mathrm{\times }\Delta V^{\mathrm{‡}}}{k_{\text{B}}T}\right),$$ (1)

where k_on^ATP(0.1) is the basal rate at 0.1 MPa, P is the pressure, ΔV^‡ is the activation volume, k_B is the Boltzmann constant, and T is the absolute temperature (4). The plots were fitted by Eq. 1 with k_on^ATP(0.1) = 14 × 10⁶ M⁻¹ s⁻¹ and ΔV^‡ = +100 Å³. On the other hand, the relationship between pressure and 3 × V_max deviated from a straight line. It can be described by

$$k\left(P\right)\mathrm{=}\frac{1}{1/k_{p\text{-}\text{ind}}\mathrm{+}1/\left(k_0\times \exp \left(\mathrm{-}\left(P\mathrm{-}0.1\right)\mathrm{\times }\Delta V^{\mathrm{‡}}/k_{\text{B}}T\right)\right)},$$ (2)

where k_p-ind is the rate constant of the pressure-independent step for 120° step rotation and k₀ is the basal rate of the pressure-dependent step at 0.1 MPa. The plots were fitted by Eq. 2 with k_p-ind = 33 s⁻¹, k₀ = 180 s⁻¹, and ΔV^‡ = +88 Å³. The activation volume for the other pressure-sensitive reaction was similar to that of the ATP-binding reaction.

Rotation assay of mutant F₁(βE190D) upon applying pressure

Our results suggest that the pressure-sensitive reaction after the ATP-binding step occurs at the ATP-binding angle. This point was further verified using the mutant F₁(βE190D). It is known that the βE190D mutation significantly retards the hydrolysis step, causing an evident pause at the catalytic angle (29). This mutation also causes pause at the ATP-binding angle due to the lengthened TS reaction (32). Although the TS pause is relatively shorter than the catalytic pause, F₁(βE190D) clearly shows six pauses/turn. The angular positions before +40° and +80° substeps correspond to the catalytic angle and the binding angle, respectively. To study the angular position of the pressure-sensitive reaction, we performed a rotation assay of the mutant F₁(βE190D) at a saturating [ATP], 2 mM, under various pressures.

We tracked the rotation of F₁(βE190D) molecules under saturating (2 mM) ATP concentrations and various pressure conditions (Fig. 5 A). This allowed us to construct angular histograms of the rotation of each F₁(βE190D) molecule at different pressures (Fig. 5 B). At 0.1 MPa, the histogram displayed three pairs of peaks. The left and right peaks in a pair correspond to catalytic and binding angles due to the slow-hydrolysis and TS reactions, respectively (Fig. 5 B, upper). When the pressure was changed to 40 MPa, F₁(βE190D) slowed the rotation (Fig. 5 A) with an accompanying pressure-induced pause, distinct from the catalytic angles (Fig. 5 B, lower). The angular distribution of the peaks was fitted by the sum of a pair of Gaussian curves. Fig. 5 C shows a histogram of angle distance of the pressure-induced pause (θ₂ at 40–60 MPa in Fig. 5 B) from the catalytic pause (θ₁ at 0.1 MPa in Fig. 5 B), Δθ. The mean angular shift upon application of pressure was +45 ± 9°, from the catalytic angle to the binding angle, suggesting that the pressure-sensitive reaction after ATP binding occurs at the binding angle.

Figure 5.

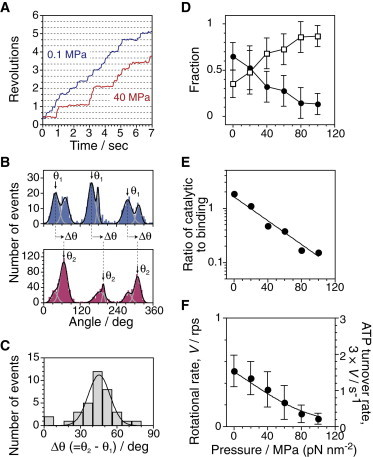
Rotation of a mutant F₁(βE190D). [ATP] = 2 mM. (A) Time courses of rotation at 0.1 and 40 MPa, respectively. (B) Histograms of the angle from traces in A at 0.1 (upper) and 40 MPa (lower). Each pair of two peaks was fitted by a sum of two Gaussian curves to determine the peak positions and area intensities. Arrows indicate major peaks at every pair. (C) Histogram of the angular distance, Δθ, between the emerging angle position at 40–60 MPa (θ₂) and the nearest catalytic angle position on the minus direction side at 0.1 MPa (θ₁). The peak angle was 45 ± 9° (mean ± SD, n = 36). (D) Fraction of area intensity of left (circles) and right peaks (squares) (mean ± SD). Each peak intensity was obtained from the angular histograms as shown in C. (E) Ratio of catalytic angle position to binding angle position. (F) Rotational rate as a function of pressure (mean ± SD, n = 25–47, total = 217). The plots in E and F were fitted by k_p-dep/k_p-ind and Eq. 2, respectively, with k_p-ind = 2.5 ± 0.7 s⁻¹, k₀ = 4.0 ± 1.9 s⁻¹, and ΔV^‡ = +100 ± 30 Å³. To see this figure in color, go online.

Fig. 5 D displays the fractions of pause time at the catalytic (circles) and binding angles (squares). Each value was calculated from the area intensity in paired peaks. As the pressure increased, the fraction of the pause time at binding angles gradually increased with pressure. The ratio of the catalytic to the binding angles decreased linearly at log scale (Fig. 5 E). Finally, we checked the pressure dependence of the rotational rate of F₁(βE190D) at 2 mM ATP. The rotational rate gradually decreased with increased pressure (Fig. 5 F). The ATP turnover rate was calculated from the rotational rate multiplied by 3, as indicated on the right axis. A global-fit analysis was performed for characterizing the pressure-sensitive process. We assumed that a pressure-sensitive reaction exists in the binding pause, but not the catalytic one. The reaction rates can be described as k_p-dep and k_p-ind, respectively. The plots in Fig. 5, E and F, were fitted by k_p-dep/k_p-ind and Eq. 2, respectively, with k_p-ind = 2.5 s⁻¹, k₀ = 4.0 s⁻¹ and ΔV^‡ = +100 Å³. The value of ΔV^‡ is close to ΔV^‡ of the pressure-sensitive reaction for the wild-type F₁, +88 Å³.

Discussion

It is reported that protein complexes are unstable when subjected to ∼100 MPa pressure and may dissociate into individual monomer subunits (54). However, this is evidently not the case for the thermophilic F₁ used in this study, because F₁ actively continued rotation at high pressure, pausing at three positions equivalently. Partial denaturation or unfolding is also highly unlikely, taking into account that most steps took place rapidly in the hydrolyzing direction, even under pressure (Fig. 2 D). Torque was not affected. This implies that the rotary potential between the α₃β₃ stator ring and the rotary shaft, γ, was not impaired. The rotary fluctuation during the pauses at the ATP-binding angle was also analyzed to examine the effect of high pressure on the conformational stability from the rotary potential of F₁ in pausing states. These observations also support the above contention. Thus, these results mean that pressure did not change the rotary potential shape.

On the other hand, the kinetics of F₁ was significantly changed upon pressure; the rotational rate was remarkably slowed down under high-pressure conditions due to the lengthened intervening pauses. In previous studies, it was reported that F₁ showed 80° and 40° substeps, pausing at six positions, three binding angles, and three catalytic angles at [ATP] around the K_m (28). It was expected that F₁ would rotate with 80° and 40° substeps at certain pressure and [ATP] conditions, but our results showed that wild-type F₁ rotated with only 120° steps. This means that pressure-sensitive reactions occurred at ATP-binding angles, but not catalytic ones. This point was further verified by rotation assays of F₁(βE190D) at 2 mM ATP. Application of pressure lengthened the pause time at ATP-binding angles, but not at catalytic angles.

Kinetic analysis revealed that F₁ has two pressure-sensitive reactions at ATP binding angles; one is the ATP-binding step, and the other is a post-ATP-binding step. The values of ΔV^‡ were similar in both reactions (∼100 Å³). How is the ATP-binding step changed by applied pressure? Here, we consider ATP binding, resolving into two steps: the first docking of ATP from medium and the subsequent conformational rearrangement of the β-subunit triggered by ATP docking (induced fit). Our previous study revealed that the ATP docking process determines the apparent rate constant of ATP binding, whereas the subsequently induced conformational rearrangement of β is responsible for torque generation (55). The results presented here show that hydrostatic pressure does not affect the angle velocity for the torque generation step (Fig. 2 D). Therefore, the pressure sensitivity is attributed to the docking process of ATP from medium.

Recent experiments on pressure-induced unfolding of proteins suggest that the critical determinant driving the unfolding is void volumes (cavities) inside the folded structure; at high pressure, water molecules penetrate into the cavities, reducing the partial molar volume (56,57). Theoretical studies with molecular liquid theory or molecular dynamics simulation also support this view (58,59). These findings evoke a simple explanation for the pressure sensitivity of ATP binding, which is that the transition state of the ATP docking process accompanies void-volume formation; before ATP can bind, dehydration of ATP and the binding residues of F₁ have to occur. A recent nonbiased molecular simulation suggests that dehydration is the kinetic bottleneck of the ligand docking process of G-protein-coupled receptors (60). The transiently formed intermolecular void space between ATP and binding residues of F₁ may confer the observed pressure sensitivity. The activation volume of ATP binding, +100 Å³, which corresponds to the volume of three water molecules, seems feasible in this context. However, we should note that there are other determinants of the apparent activation volume, such as the water-accessible surface, thermal volume, and interaction volume (58,61).

A more general explanation for the pressure sensitivity of the intermolecular association process has also been proposed on the basis of the translational entropy of water (61–63). This theory predicted well that the kinetic free-energy barrier for molecular association in general increases with pressure (T. Yoshidome and M. Ikeguchi, Yokohama City University, Yokahama, Japan, personal communication, 2013). More elaborate experimental and theoretical studies are required to elucidate the molecular mechanism of the pressure sensitivity of ATP docking.

Another question is what the other pressure-sensitive reaction is. Considering that this reaction occurs at the binding angle, there are at least two possibilities: ADP release or TS reaction, both of which occur at the binding angle (32). The rotation assay of F₁(βE190D) showed that the dwell time of the TS reaction was apparently lengthened under high pressure. However, this observation does not exclude the possibility that an ADP-release step dominates the pausing time under high-pressure conditions. A rotation assay at low temperature and under high pressure would address this issue.