Reinforcement Mechanisms in Putamen during High Frequency STN DBS: A Point Process Study

Abstract

Despite a pivotal role in the motor loop, dorsolateral striatum (putamen) has been poorly studied thus far under Parkinsonian conditions and Deep Brain Stimulation (DBS). We analyze the activity of the putamen in a monkey by combining single unit recordings and point process models. The animal received DBS (30–130Hz) in the subthalamic nucleus (STN) while at rest and recordings were acquired both before and after treatment with 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP), which induced Parkinsonian-like motor disorders. 141 neurons were collected and, for each neuron, a point process model captured DBS-evoked discharge patterns. In the normal animal, spike trains at rest had Poisson like distribution with non-stationary recurrent patterns (RPs) of period 3–7ms and were mildly changed by low frequency (LF, i.e., <100Hz) DBS (i.e., <20% of neurons affected). With high frequency (HF, i.e., 100–130Hz) DBS, instead, up to 59% of neurons were affected, the DBS history significantly impacted the neuronal spiking propensity, and the RPs and the post-stimulus activation latency decreased. MPTP evoked inter-neuronal dependencies (INDs) at rest and, compared to normal, LF DBS of the MPTP animal increased RPs and INDs, while HF DBS elicited a faster and wider post-stimulus activation. Overall, HF DBS reduced ongoing non-stationary dynamics by regularizing the discharge patterns both in MPTP and normal putamen, while the combination of MPTP and LF DBS enhanced such dynamics.

I. Introduction

High frequency (HF) Deep Brain Stimulation (DBS) of the basal ganglia (BG) and thalamus is clinically recognized to treat movement disorders in Parkinson’s disease (PD) and several other neurological disorders but its therapeutic mechanisms still require investigation [1]–[5]. Most of the studies conducted thus far on single unit recordings, both from humans and animals, have been focused on the effects of DBS on the stimulation target and structures downstream (i.e., subthalamic nucleus [STN], globus pallidus [GPi, GPe], thalamus, or cortex) [6]–[11]. Very little attention has been paid to the structures upstream (e.g., striatum), even though changes in these structures are presumably important [12].

Studies in monkeys at rest reported abnormal modulation of the neuronal spiking activity in the dorso-lateral striatum (putamen) after treatment with 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP) and an increased probability of spiking 4–6ms after each DBS pulse during 50, 100, and 130Hz STN DBS [5][13]. Studies in 6-hydroxydopamine-lesioned rats performing a motor task, instead, reported that STN DBS evokes rebound excitatory responses but no significant variation of the mean discharge rate in the dorsal striatum [14].

It is still debated, however, (i) how STN DBS affects the discharge patterns and pair-wise relationships between neurons (inter-neuronal dependencies) in the putamen, (ii) if the effects of DBS vary with the stimulation frequency, and (iii) how PD impacts the response to DBS in the putamen.

We addressed these questions by analyzing 141 neurons collected in the putamen of a monkey that quietly sat in a loosely restraining chair while regular STN DBS was applied. The animal was not involved in any motor task to avoid movement-related changes in putamen activity [15]. Multiple DBS frequencies were tested for each neuron (30 to 130Hz) and the recordings were performed before and after treatment with MPTP. For each neuron, disease condition, and stimulation setting, a point process model (PPM) [16] was computed to capture recurrent non-stationary patterns and inter-neuronal dependencies before and during DBS.

Point process models have been applied to a wide range of neural systems [17]–[20] and describe the spiking propensity of a neuron as a function of multiple factors (e.g., DBS, ensemble neurons’ spiking history, etc.). PPMs were recently used to analyze the discharge pattern of neurons in STN, GPi and motor cortex in PD patients and MPTP-treated monkeys [21]–[23]. In [24] we used PPMs and a preliminary dataset of multi-site single unit recordings from a resting monkey to study the ongoing relationships between putamen, somatosensory cortex, and GPe both before and after treatment with MPTP. We found positive correlation between neurons in putamen and cortex with delays ranging from 3 to 10ms after MPTP treatment, which suggests cortico-striatal synchronization, and mild negative correlation between neurons in putamen and GPe (lag ranging from 1 to 5ms), which would be consistent with pallido-striatal inhibition.

II. Methods

A. Experimental Setup

A male macaca mulatta was trained to sit quietly in a loosely restraining chair designed to allow passive movements of the upper and lower limbs while preventing the animal from disturbing the recording instruments. The research protocol was in compliance with “The National Institutes of Health Guide for Care and Use of Laboratory Animals” and approved by the Institutional Animal Care and Use Committee. Details are in [13][24][25].

Briefly, the animal was implanted with a recording chamber and received STN DBS via a reduced scale model of the human DBS lead (four contacts lead, each contact being 0.525mm in diameter, 0.5mm long, 0.5mm between contacts, area 0.82mm²). The electrical stimulation consisted of constant-current symmetric biphasic square-wave pulses, which were delivered between the most distal and the most proximal contact. For each pulse the cathodic phase preceded the anodic phase at the most distal contact (reverse for the most proximal one). Pulse width was 90μs/phase and amplitude was 80% of the current inducing tonic contraction during 130Hz DBS (0.55mA). DBS frequencies included in this study are: 30, 50, 80, 100, and 130Hz.

Microelectrode recordings were collected from separate sites of the putamen on a semi-daily basis. For each recording site, multiple sessions of STN stimulation were made at the frequencies described above and, for each session, recordings were collected continuously 30s before and 30 to 42s during DBS. Extracellular action potentials were acquired through platinum-iridium microelectrodes (tip exposure: 10 to 20μm; impedance: 0.4 to 0.6MΩ; FHC, Inc., Bowdoinham, ME). Electrophysiological signals were band pass-filtered and digitally converted (sampling rate: 25 kHz) for off-line analyses. Action potentials were isolated from background noise and clusterized by using validated off-line software [25]. Four months after the beginning of the study, the animal received an initial infusion of MPTP via the right intracarotid artery (0.04mg/kg) and, then, three systemic doses of 0.2mg/kg, administered intravenously over several weeks, until the animal demonstrated a consistent motor impairment.

B. Point Process Modeling

A neural spike train is treated as a series of random binary events (0s and 1s) that occur continuously in time (point process), where the 1s are spike times and the 0s the times at which no spikes occur [16]–[18]. A PPM of a neural spike train is completely characterized on any interval (0, T] by defining the conditional intensity function (CIF)

$$\lambda (t\mid H_t)=\underset{\mathrm{\Delta }\to 0}{lim}Pr(N(t+\mathrm{\Delta })-N(t)=1\mid H_t)/\mathrm{\Delta }$$ (1)

where N(t) is the number of spikes counted in interval (0, t] for t in (0, T], H_t is the history of spikes up to time t and Pr (·) is the probability [16]. λ(t|H_t) is a generalized history-dependent rate function and λ(t|H_t)Δ approximately gives the spiking propensity at time t if Δ is small. Because the CIF completely characterizes a spike train, defining a model for the CIF defines a model for the spike train [18]. For each neuron, we defined the following model structure:

$$\lambda (t\mid H_t,\mathrm{\Theta })=e^{\sigma }{\lambda }_O(t\mid H_t^O,\mathrm{\Theta })·{\lambda }_E(t\mid H_t^E,\mathrm{\Theta })·{\lambda }_S(t\mid H_t^S,\mathrm{\Theta })$$ (2)

where e^σ (in spikes/s) accounts for the average history-independent (i.e., Poisson-like) activity, and λ_O, λ_E, and λ_S are dimensionless functions of the neuron’s own spiking activity $H_t^O$, the spiking activity $H_t^E$ of any other neuron in the same ensemble, and the DBS stimulus sequence $H_t^S$ (if applied), respectively. Θ is a parameter vector to be estimated from data. We set Δ = 1ms and assumed that λ_O, λ_E, and λ_S belong to the class of generalized linear models [26]:

$$log({\lambda }_O)={\sum }_{r=1}^{10}{\beta }_{r}dN(t-r\mathrm{\Delta },t-(r+1)\mathrm{\Delta })+{\sum }_{r=11}^{18}{\beta }_{r}dN(t-5(r-8)\mathrm{\Delta },t-5(r-9)\mathrm{\Delta })$$ (3)

$$log({\lambda }_E)={\sum }_{q=1}^Q\{{\sum }_{h=1}^{10}{\delta }_{h,q}{dN}_q(t-h\mathrm{\Delta },t-(h-1)\mathrm{\Delta })+{\sum }_{r=11}^{18}{\delta }_{h,q}{dN}_q(t-5(h-8)\mathrm{\Delta },t-5(h-9)\mathrm{\Delta })\}$$ (4)

$$log({\lambda }_S)={\sum }_{v=1}^8{\gamma }_v{dN}_S(t-v\mathrm{\Delta },t-(v-1)\mathrm{\Delta })$$ (5)

where dN(a, b) and dN_q(a, b) are the number of spikes fired by the given neuron or the q-th neuron in the ensemble in the interval (a, b) (in ms), dN_s(a, b) is the number of DBS pulses, and $\mathrm{\Theta }=\left[\sigma ,{\beta }_1,\dots ,{\beta }_{18},{\gamma }_1,\dots ,{\gamma }_8,{\{{\delta }_{1,q},\dots ,{\delta }_{18,q}\}}_{q=1}^Q\right]$.

For each neuron, both with and without DBS, an estimation of Θ and the 95% lower confidence bounds was provided by maximizing the likelihood of observing the recorded spike trains [18][20]–[24]. For each neuron, 80% of spike trains were for parameter estimation and the last 20% for validation. The set of history bins (a and b in dN(a, b)) in (2–5) was chosen by minimizing the Akaike’s information criterion [27]. The goodness-of-fit of each PPM was assessed on the validation data set with the KS plot after time rescaling of the spike trains [18]. Only neurons whose PPM passed this test (p < 0.05) were included in this study (Table I).

TABLE I.

Experimental Dataset

	DBS Frequency (Hz)	Normal	MPTP
# of Neurons	0 (no DBS)	95	46
	30	35	-
	50	71	15
	80	36	8
	100	71	-
	130	48	30
# of Neuron Pairs	0 (no DBS)	334	237
	30	187	-
	50	258	44
	80	167	23
	100	268	-
	130	162	97

C. Statistical Inferences from Point Process Models

A neuron shows a recurrent pattern (RP) with period Δ_p if, at any time t, the probability that it spikes is higher than the probability for e^σ, provided that the neuron spiked Δ_p ms earlier. An RP with period in (a, b) was inferred if the lower 95% confidence bound of e^β_r in λ_O was > 1.05, where β_r multiplies the number of spikes dN(a, b) in (3), i.e., an RP was inferred if the probability of spiking at t increased by >5% over e^σ, given that a spike occurred (a,b) ms before t.

Given a pair of neurons (n₁,n₂) in the same ensemble (i.e., simultaneously recorded), n₁ has inter-neuronal dependency (IND) with lag L_p on n₂ if, at any time t, the probability that n₁ spikes is higher than the probability for e^σ, provided that n₂ spiked L_p ms earlier. An IND between the modeled neuron and any other neuron q in the same ensemble with lag in (a, b) was inferred if the lower 95% confidence bound of e^δ_h,q in λ_E was > 1.05, where δ_h,q multiplies dN_q(a, b) in (4).

III. Results

A. Poisson Factor in Normal Conditions

For each neuron, we tested whether the discharge rate changed significantly (either increased or decreased) during DBS vs. rest conditions. We found that the percentage of neurons with significant change was small under low frequency (LF, i.e., <100Hz) DBS (11.5±8.5%, mean±std. dev.) and no trend was noticeable as the frequency increased. 130Hz DBS, instead, affected a higher percentage of neurons (59.3%), with a significant increment over the percentage of responsive cells measured under LF DBS (t-test, p<0.001). The population-mean discharge rate, instead, was lower during 130Hz DBS than at rest (Fig. 1a), thus indicating a decreased discharge activity.

Fig. 1.

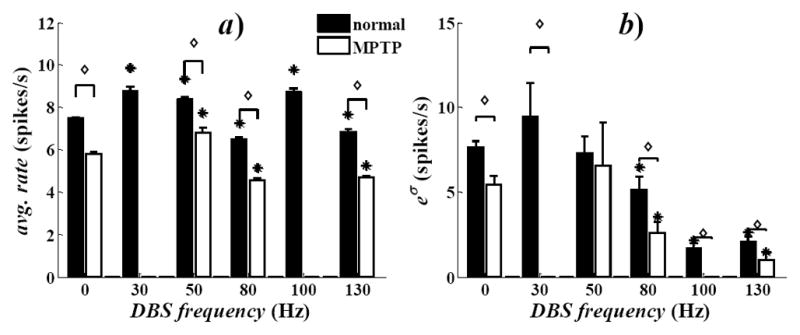
a) Population-mean average discharge rate at rest (0Hz) and during STN DBS. b) Population-mean value of the Poisson factor e^σ in (2). Values are mean±s.e.m. Asterisks denote significant differences during DBS vs. rest. For each DBS setting, diamonds denote significant differences in MPTP vs. normal conditions. Significance: t-test, p<0.001.

The reduction of the population-mean rate was associated with a reduction of the Poisson factor e^σ in (2) (Fig. 1b). The Poisson factor accounts for the incidence of covariates and the variability of the discharge patterns across the population. High values of e^σ, indeed, correspond to high variability and low impact of the spiking histories. Also, e^σ measures the similarity between the neuron’s own discharge pattern and a Poisson process. Overall, we found that e^σ decreased when DBS frequencies ≥50Hz were used but the reduction was significant (p<0.001) only under high frequency (HF, i.e., 100–130Hz) DBS (Fig. 1b), which suggests a reduced variability during HF DBS. Also, e^σ was close to the average discharge rate during 30, 50, and 80Hz DBS, while it was significantly lower than the correspondent rate during HF DBS, which indicates that HF DBS disrupted pre-existent Poisson-like patterns and increased the impact of the spiking and DBS histories on the neuronal propensity to spike.

B. Effects of DBS on Discharge Patterns in Normal Conditions

The influence of the DBS history was quantified by using the point process model parameters γ_ν ν = 1,…,8 in (5). Fig. 2 reports the population-mean value of e^γ_ν both for LF and HF DBS in normal conditions. Values e^γ_ν ≫ 1 for any neuron n* indicate that the probability of spiking of n* at a given time t increases over a baseline Poisson process of similar rate, provided that a DBS pulse was timely delivered in the past 8ms before t. Fig. 2 shows that, while the impact of LF DBS on the spiking propensity was low and vanishing toward the end of the inter-pulse period (i.e., e^γ_ν ≅ for all ν), HF DBS strongly increased the spiking likelihood and such contribution was significantly larger during 130 vs. 100Hz DBS. Also, during 130Hz DBS, a peak of contribution was noted between 3 and 5ms (4 ≤ ν ≤ 6) and, both with 100 and 130Hz DBS, the average value of e^γ_ν was significantly larger than the value of parameters e^β_r and e^δ_h,q in (3)–(4) (data not shown), which means that HF DBS likely elicited a strong phase-locked response in the neurons that presumably overrode the dependency from the previous spiking history. DBS also evoked a transient post-stimulus modulation of the discharge patterns during the inter-pulse interval, as indicated by the post-stimulus time histogram (PSTH). The PSTH consists of counts of neuronal discharges in 0.08ms-long consecutive time bins within the inter-stimulus interval following each DBS pulse, normalized to the pre-stimulation baseline activity (z-score) [10]. A z-score >1.96 (<−1.96) indicates significant (p<0.05) neuronal activation (inhibition) within the inter-pulse interval and can be used to determine the most likely latency between DBS pulses and neuronal spikes [10]. We found that the percentage of neurons with significant activation within an inter-pulse interval increased with the DBS frequency. In particular, the number of neurons with a significant response in three consecutive windows after the DBS pulse (1.2–2.2, 2.3–4.2, 4.5–6.0ms) was significantly higher with HF DBS than LF DBS. Also, the latency between the DBS pulse and the first bin with z-score >1.96 was significantly lower during 130Hz DBS than other settings, while the correspondent value of the z-score was significantly higher (Fig. 3a,b). This suggests that, under HF DBS, distinct neurons were likely to respond similarly right after a DBS pulse, with no regards to the pre-DBS pattern.

Fig. 2.

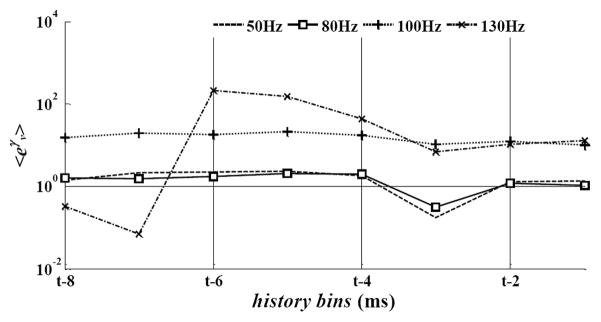
Population-mean value of the model parameters e^γ_>ν, ν =1,…,8 in (5) for several DBS frequencies in normal conditions. Parameters were depicted vs. the history bins for a generic time t.

Fig. 3.

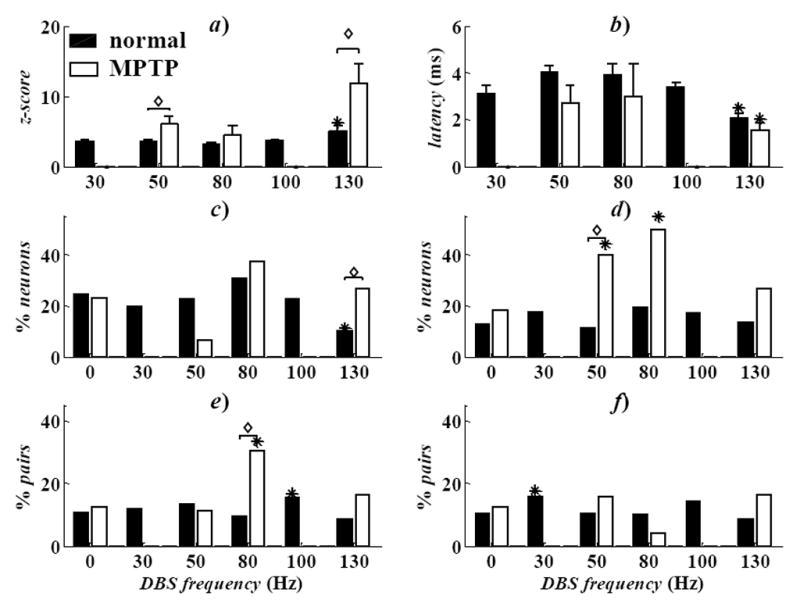
a, b) Population-mean z-score (a) and correspondent mean latency (b) in activated (z-score>1.96) neurons. Values are mean±s.e.m. Asterisks denote significant difference at 130Hz DBS vs. the remaining conditions (one-way ANOVA, Tukey’s post-hoc test, p<0.05). For each DBS setting, diamonds indicate differences MPTP vs. normal conditions (t-test, p<0.05). c–f) Percentage of neurons with RPs of period 3–7ms (c) and 30–50ms (d), and with INDs of period 10–30ms (e) and 30–50ms (f). In c–f): asterisks denote differences with DBS vs. rest. For each DBS setting, diamonds indicate differences MPTP vs. normal conditions (χ²-test, p<0.05).

Finally, PPM parameters in (3)–(4) were used to infer RPs and INDs. We found that RPs and INDs with periods ranging from 3 to 50ms occurred in ~20% of neurons at rest (Fig. 3c–f). LF DBS did not significantly vary the occurrence of RPs and INDs, while 130Hz DBS mainly reduced the RPs with period of 3 to 7ms. INDs, instead, were less frequent than RPs and less sensitive to the DBS treatment under normal condition.

C. Effects of DBS in MPTP vs. Normal Conditions

At rest, MPTP decreased the population-mean discharge rate and the Poisson factor (Fig. 1), and increased the fraction of neurons with RPs and INDs of period 30–50ms (Fig. 3d,f), which is consistent with emerging (non-stationary) oscillatory patterns in the beta frequency band (13–30Hz).

DBS determined two major differences between normal and MPTP condition. First, 130Hz DBS significantly reduced the latency between the DBS pulse and first post-stimulus response and increased the correspondent value of the z-score (Fig. 3a,b), which means that the neurons were more likely to spike after the DBS pulses and with shorter latency. Secondly while 130Hz DBS had similar effects on RPs and INDs both in the normal and MPTP animal, LF DBS had stronger effects after the MPTP treatment and significantly increased the incidence of RPs (main period: 30–50ms, Fig. 3d) and INDs (10–30ms, Fig. 3e) over the baseline values at rest.

Overall, these results suggest that non-stationary RPs and INDs increased under dopamine depletion and were further facilitated by LF DBS. This is consistent with the fact that LF DBS in PD subjects usually worsens the movement disorders [4][5] and suggests that RPs and INDs might be pathological features associated with the emerging of movement disorders. 130Hz DBS, instead, reduced such features by increasing the probability of short-latency post-stimulus responses and decreasing any late post-stimulus modulation, which would indicate a regularization of the discharge patterns.