Retrospective Analysis of Midsummer Hypoxic Area and Volume in the Northern Gulf of Mexico, 1985–2011

Abstract

Robust estimates of hypoxic extent (both area and volume) are important for assessing the impacts of low dissolved oxygen on aquatic ecosystems at large spatial scales. Such estimates are also important for calibrating models linking hypoxia to causal factors, such as nutrient loading and stratification, and for informing management decisions. In this study, we develop a rigorous geostatistical modeling framework to estimate the hypoxic extent in the northern Gulf of Mexico from data collected during midsummer, quasi-synoptic monitoring cruises (1985–2011). Instead of a traditional interpolation-based approach, we use a simulation-based approach that yields more robust extent estimates and quantified uncertainty. The modeling framework also makes use of covariate information (i.e., trend variables such as depth and spatial position), to reduce estimation uncertainty. Furthermore, adjustments are made to account for observational bias resulting from the use of different sampling instruments in different years. Our results suggest an increasing trend in hypoxic layer thickness (p = 0.05) from 1985 to 2011, but less than significant increases in volume (p = 0.12) and area (p = 0.42). The uncertainties in the extent estimates vary with sampling network coverage and instrument type, and generally decrease over the study period.

1. Introduction

A large hypoxic zone has formed nearly every year in the northern Gulf of Mexico over at least the last few decades.¹⁻³ It is the largest human-caused coastal hypoxic zone in the western hemisphere and one of the largest worldwide.^1,4 Because of its negative ecological impacts and potential fisheries impacts,⁵ the hypoxic zone has received attention from various stakeholders and policy makers who have developed plans to reduce its average size.^6,7

The hypoxic zone is generally largest in summer due to the seasonal cycles of phytoplankton production and water column stratification, which are the two primary factors leading to dissolved oxygen (DO) depletion.⁸⁻¹⁰ Both factors are related to the outflow from the Mississippi River Basin, which typically peaks in March–May. Nutrient loads from the Basin stimulate phytoplankton production in offshore waters, and much of the resulting organic matter eventually settles along the Louisiana–Texas shelf. Aerobic bacteria decompose the organic matter, consuming large quantities of DO. At the same time, freshwater outflows from the Basin promote stratification through a fresher surface layer, which warms in spring and summer, and overlays a colder, saltier water layer, inhibiting reoxygenation of bottom waters.¹

The hypoxic extent, operationally defined as the region (area or volume) where DO concentrations are below 2 mg L^–1, is often assessed using data from “shelfwide” sampling cruises. The cruises are considered “quasi-synoptic” because changes in weather conditions (e.g., tropical storms) preceding or during the cruises can disrupt typical seasonal patterns in hypoxia. Cruises to document the occurrence of hypoxia, as well as related physical and biological parameters, have been performed by the Louisiana Universities Marine Consortium (LUMCON) beginning in 1985.^1,2 The estimated bottom-water hypoxic area² has been determined by interpolating between sampling locations and hand-contouring parallel to isobaths over a calibrated (planimeter) grid. These estimates have been used in multiple modeling studies linking hypoxia to nutrient loads from the Mississippi River basin and other environmental factors¹¹⁻¹⁴ and for setting policy goals to reduce the severity of hypoxia.^6,7 However, these estimates are generally conservative in that the most inshore, most offshore, and most western extents of hypoxia are not always captured because of logistical constraints.^15,16 Also, these estimates do not quantify the uncertainty inherent in making estimates from limited observations.^17,18 Quantified uncertainties are useful for assessing the adequacy of existing sampling programs and for improving models that link hypoxic extent to environmental causes and effects.

Hypoxic area estimates only partially characterize the hypoxic extent. The thickness and volume of hypoxia are also important, as they relate to how hypoxia affects pelagic organisms.^19,20 In addition, hypoxic volume, rather than area, should be more closely related to the total oxygen deficit of the system, potentially making it a more useful metric for biogeochemical modeling studies.⁴ While hypoxic volume measurements are available for other systems, such as Chesapeake Bay,^21,22 estimates for the Gulf have only been available for a subset of years, using an unpublished methodology.⁴

The primary goal of this study is to improve our knowledge of the Gulf’s hypoxic extent over the 27-year study period (1985–2011) by systematically estimating midsummer hypoxic area and volume. These are the first Gulf hypoxic extent estimates to include “instrument bias adjustments” that account for the use of different sampling instruments, capable of being lowered to within different proximities of the sea floor, in different years.²³ Our approach also uses trends between DO, hypoxic fraction, depth, and spatial position to account for consistent, large-scale spatial patterns in DO, thereby improving the explanatory power of the model.¹⁸ Our extent estimates are developed using a Monte Carlo-type simulation approach, rather than traditional interpolation, allowing for uncertainty quantification (i.e., confidence intervals).^17,18 These confidence intervals reflect the spatial stochasticity of the system, uncertainties in trends among variables, and uncertainties in instrument bias adjustments. Hypoxic volume is estimated using a novel two-step approach where DO is simulated first, and hypoxic fraction (i.e., the fraction of the water column that is hypoxic) is simulated second using DO as a trend variable.

2. Methods

2.1. Data and Study Boundaries

We use DO data from LUMCON midsummer sampling cruises conducted between 1985 and 2011. Data for 1998–2008 are retrieved from the National Ocean Data Center, while data for other years are obtained directly from LUMCON.²⁴ Sampling locations are geo-referenced using the Universal Transverse Mercator (UTM) Zone 15 projection, and bathymetry is determined from a 3-arc-second digital elevation model obtained from the National Oceanic and Atmospheric Administration (NOAA).²⁵

During cruises, DO is sampled using one or two types of instruments (Figure 1): a rosette-mounted DO probe and a hand-held DO probe, with the latter capable of being lowered closer to the sea floor.^9,23 (Hereafter, we refer to these instruments as the “rosette sampler” and “handheld sampler”.) While instrument technology has changed over time, all instruments were calibrated against Winkler titrations, and postcruise corrections were made as necessary. For sampling events where both instruments were used, data are combined into synthesized profiles.⁹ (Here, a “sampling event” refers to the depth profile of data collected at a specific latitude/longitude and time.)

Figure 1.

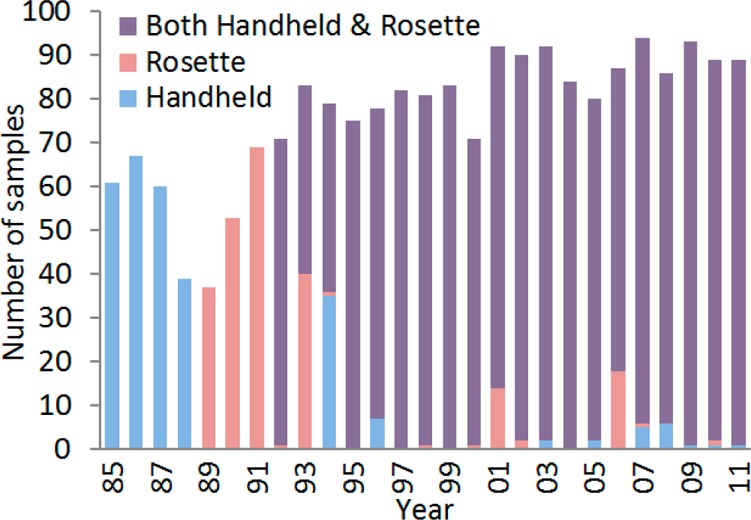
Number of locations sampled during the annual midsummer shelfwide cruises using hand-held and rosette instruments.

We extract bottom water dissolved oxygen (BWDO) and minimum dissolved oxygen (MinDO) concentrations from the DO profiles. BWDO and MinDO concentrations greater than 7 mg L^–1 (less than 1% of total samples), are treated as 7 mg L^–1, because higher concentrations are outliers representing supersaturation conditions that are not of interest in this study. For sampling events where hypoxia was present, we also extract the fraction of the water column that is within the hypoxic bottom layer (hereafter, bottom water hypoxic fraction, or BWHF) and, where other hypoxic layers are present, the total hypoxic fraction (THF) of all hypoxic layers. Bottom and upper layers of hypoxia are observed at 49% and 12% of sampling events, respectively. Here, we focus on the models for BWDO and BWHF because bottom layer results are most comparable to previous studies.^2,16 The models for MinDO and THF are formulated in the same way and yield comparable results, but for brevity are discussed only in Supporting Information (SI) Section S7.

In this study, adjustments are made to address biases that arise from the use of different sampling instruments. For cruises when only the rosette sampler was used (Figure 1), one would expect the hypoxic extent to be underestimated because the rosette sampler does not reach as close to the sea floor as the hand-held sampler. We quantify this bias using data from sampling events where both instruments were used together. For these cases, observed BWDO and BWHF are calculated for both the synthesized profile and rosette-only profile. Probabilistic relationships are then developed between the synthesized results and the rosette-only results (Section S1 of the SI). When performing simulations (described below), we adjust the rosette-only observations by sampling from these relationships. A larger bias adjustment is required for the first 38 sampling events in 1991 because the ship’s fathometer was not properly calibrated, causing the rosette sampler to be lowered 1.5 m less than it would have been otherwise (N.N. Rabalais, cruise records). For these observations, the probabilistic relationships between synthesized and rosette-only results are again determined based on sampling events where both instruments were functioning properly (as described above) but with the bottom 1.5 m of the rosette-only profiles removed.

Geostatistical modeling is performed on a 5 × 5 km² grid of estimation points (Figure 2), covering 342.5–837.5 km UTM easting and 3122.5–3292.5 km UTM northing, reflecting the general extent of sampling. The estimation grid is limited to depths between 3 and 80 m, which are typical of the Louisiana–Texas shelf region where hypoxia occurs.

Figure 2.

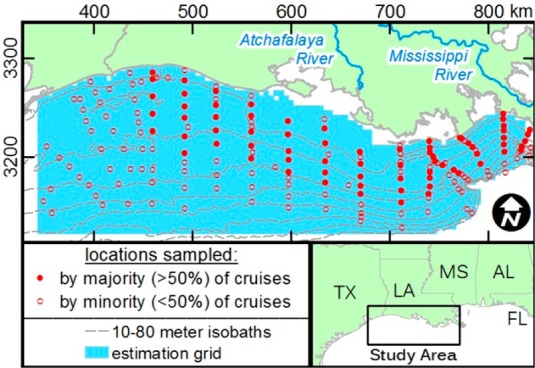
Study area bathymetry, sampling, and estimation locations.

2.2. Model Formulation

Geostatistical methods provide an effective means to model data that exhibit spatial correlation.^17,26 The efficacy of these methods has been demonstrated in previous environmental analyses of rainfall, snow depth, soil phosphorus, and water quality indicators.^{18,21,27−29} Many of these studies have focused on mapping through spatial interpolation, and comparison studies have demonstrated that geostatistical interpolation outperforms simpler interpolation methods, such as inverse distance weighting.^21,28

In a geostatistical model, the response variable, z, is represented as a combination of deterministic and stochastic components:²⁶

1

This formulation is similar to linear regression, but includes an additional term, η, representing spatially correlated stochasticity, in addition to the more commonly modeled uncorrelated stochasticity, ε. As in linear regression, Xβ is the portion of z that can be expressed as a deterministic function of categorical and/or trend variables (X) and their corresponding regression coefficients (β). If the X term includes only cruise-specific categorical variables (vectors of zeros and ones that bin the data by cruise), then the model can essentially be used to perform ordinary kriging (OK). If X also includes trend variables, then it can be used to perform universal kriging (UK).¹⁷

In this study, the stochastic components (η and ε) are found to be well represented by the commonly used exponential covariance function with a nugget effect,²⁶ defined as follows:

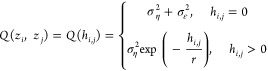2

where Q is the covariance between two observations (z_i and z_j) separated by distance (h_i,j); σ_ε² and σ_η² are parameters representing the variances of the stochasticity that is spatially correlated and is not spatially correlated, respectively; and r is a range parameter (3r is approximately the distance at which observations are no longer spatially correlated). We allow for anisotropy in the covariance model by scaling h_i,j using parameter α, which represents the ratio of east–west to north–south correlation ranges. Covariance function parameters are estimated using restricted maximum likelihood^30,31 and deterministic component parameters (β) are estimated using generalized least-squares, as outlined in a previous study by Obenour et al.⁹ that used geostatistical methods to explore biophysical drivers of DO depletion.

Geostatistical models are developed for both BWDO and BWHF to determine bottom layer hypoxic area and volume, respectively. The model for BWDO uses all observations, while the model for BWHF uses only observations from locations where BWDO is below the hypoxic threshold. Both models use the UK formulation to take advantage of potential relationships between the response variables and available trend variables.¹⁸

The deterministic components of the models include two types of trends. First, “constant trends” represent relationships between response and trend variables using regression coefficients that are the same for all cruises. For the BWDO model, potential constant trends include linear and quadratic trends with depth (Depth and Depth²), easting (Easting and Easting²), and northing (Northing and Northing²). On the basis of an examination of model residuals, it was noted that the overall trend between depth and BWDO does not continue for depths greater than 40 m, and so depths of greater than 40 m are treated as 40 m in the final BWDO model development. This approach is justified because model residuals are evenly distributed across all depths when depths greater than 40 m are modified as described here (see Figure S3 of the SI). For BWHF, potential constant trends include linear and quadratic trends with easting, northing, and BWDO.

Second, “cruise-specific trends” (with cruise-specific regression coefficients for Easting) represent relationships that are specific to individual cruises. Allowing these trends was motivated by previous studies^16,23 that indicate the east–west distribution of hypoxia is influenced by alongshore current velocity, which can vary interannually in response to prevailing winds. When selected, these cruise-specific trends modify the constant trend.

To prevent overparameterization of the model, we use only trend variables selected through a geostatistical adaptation of the Bayesian information criterion (BIC),^9,32,33 wherein models with different subsets of trend variables are compared based on their BIC score, and the model with the lowest BIC score is optimal in terms of its explanatory power relative to its complexity. Because of the large number of variables considered in this study, an initial optimal model is first selected among those formed from constant trend variables only. Cruise-specific trend variables are then individually tested relative to that model, and only cruise-specific trends that improve the BIC score are included in the final model.

The deterministic portion of the model also includes categorical variables that bin data by cruise, reflecting the fact that the mean BWDO varies from cruise to cruise. In UK, the categorical variables essentially allow for different “intercepts” (as in linear regression), that shift the trend up or down to best fit the observations from each cruise. In OK, these categorical variables simply allow for a different mean for each cruise.

The covariance model, selected deterministic variables, and categorical variables are used to determine a set of geostatistical weights, Λ, that are applied to observations when performing geostatistical interpolation and simulation. For each cruise, y, a unique set of weights, Λ_y, are determined by solving a system of linear equations:

3

where Q_oo is an n × n covariance matrix for the n observation locations (all cruises), with elements determined from eq 2. Because we did not assume correlation among stochasticity from different cruises, intercruise covariances are assigned a value of zero. Similarly, Q_oe,y is an n × m covariance matrix of n observation locations and m estimation locations, and the rows of Q_oe,y that correspond to observations from cruises other than cruise y are assigned a value of zero. The matrix X_o is n × p and includes the p deterministic variables (trend and categorical) for the observation locations, and the matrix X_e (m × p) includes the same variables for the estimation locations. The trend variables are normalized to a mean of zero and variance of one. Note that terms with a “y” subscript are cruise-specific.

In eq 3, Λ_y is an n × m matrix of cruise-specific weights that reflect both the spatial correlation structure and the deterministic trends. Also, G_y is a p × m matrix of Lagrange multipliers that can be used with Λ_y to determine location-specific estimation uncertainties. Using the weights, along with the observations z_o (an n × 1 vector), one can develop estimates of the response variable across the estimation grid:

4

where z_e,y⁰ is an m × 1 vector of interpolated BWDO or BWHF values for cruise y.

Although we use a UK model formulation, hypoxic area and volume are not determined by kriging (i.e., spatial interpolation), but instead by developing “spatially consistent Monte Carlo simulations”¹⁷ which are often referred to as conditional realizations (CRs). While both kriging and CRs provide equivalent information for individual estimation locations, CRs are necessary to estimate spatially aggregated quantities (e.g., area and volume) probabilistically. A CR is performed by first creating an “unconditional realization” and then “conditioning” it to the observed data and deterministic trend.¹⁷ Unconditional realizations (eq 5) include simulated values at the estimation locations (z_e,y^u) as well as at the observation locations (z_o,y):

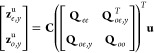5

Note that the vector z_o,y^u includes simulated values corresponding to the observations from all cruises, but only observations from cruise y have their stochasticity correlated with that of the estimation locations. Here, Q_ee is the m × m covariance matrix between estimation locations, and u is an (m + n) × 1 vector of random independent samples from the standard normal distribution. The operator C( ) returns the triangular matrix resulting from Cholesky decomposition of the subject matrix.

The unconditional realizations are then conditioned to the observed data and deterministic trends through:

6

Here, z_o is the n × 1 vector of the observed values, and z_e,y^c is the resulting cruise-specific CR, an m × 1 vector of values corresponding to the estimation locations.

The CRs are performed in two steps. First, BWDO concentration is simulated across the entire estimation grid. Then, BWHF is simulated over those locations where the simulated BWDO is below the hypoxic threshold. At hypoxic estimation locations, the simulated BWDO values are used as a trend variable in the BWHF model. Simulated values are limited to within realistic ranges (determined to be 0–7 mg L^–1 for BWDO and 0.001–0.8 for BWHF, based on a review of the observed data). Without these constraints, the estimated hypoxic volume would be 6% smaller, on average, as a result of (unrealistic) negative hypoxic thicknesses.

The two-step CR process is repeated 1000 times for each cruise, resulting in 1000 realizations of both BWDO and BWHF. For each realization of BWDO, the hypoxic area is calculated as the number of estimation locations simulated to be hypoxic multiplied by the grid cell area (25 km²); and for each realization of BWHF, the hypoxic volume is calculated as the vector of simulated BWHF values multiplied by the corresponding vector of water column depths, all multiplied by the grid cell area. From this ensemble of results, we determine the mean and 95% confidence intervals for the hypoxic area and volume for each cruise.

3. Results

The BWDO and BWHF models include several parameters that characterize the deterministic and stochastic model components (eq 1). Regression coefficients for the BIC-selected trend variables, explaining a portion of the spatial variability in observed BWDO and BWHF, are provided in Table 1. The standard errors of these coefficients are low (i.e., p < 0.05), suggesting these trends are statistically significant. The coefficients for the cruise-specific categorical variables, accounting for year-to-year variability in the responses, are included in Section S3 of the SI. Overall, the deterministic model components explain 28% and 32% of the total (spatial plus interannual) variability in BWDO and BWHF, respectively, while the stochastic components of the models explain the remainder of the spatial variability. If trend variables are omitted (i.e., the OK formulation), then the deterministic components only account for interannual variability, and only 12% and 11% of the total variability in BWDO and BWHF is explained, respectively. A check of the linearity assumption implicit in these deterministic relationships is included in Section S2 of the SI.

Table 1. Regression Coefficients (β̂) with Standard Errors (σ_β̂) for Normalized, BIC-Selected Trend Variables in BWDO and BWHF Models^a,

^b

variable	BWDO (mg L–1)		BWHF
	β̂	σβ̂	β̂	σβ̂
Easting	–0.62	0.09	0.018	0.007
Easting2	0.25	0.07	–0.020	0.006
Northing	–0.36	0.09	n.s.
Depth	–2.31	0.18	n.a.
Depth2	2.45	0.17	n.a.
BWDO	n.a.		–0.065	0.005
c.s.E 1998	–1.35	0.45	n.s.

^aParameters optimized by generalized least squares.

^bc.s.E = cruise specific trend for Easting, n.s.=not selected, n.a.=not available.

The BWDO model includes trends with easting, northing, and depth. The trend between BWDO and easting is quadratic with a minimum at 794 km easting (UTM coordinate, Figure 2), between the Mississippi and Atchafalaya river outfalls, which is reasonable given that these rivers provide the freshwater flows and nutrients that are important for hypoxia formation. In 1998, the only year for which a cruise-specific east–west trend with BWDO is selected, the minimum is shifted to 1111 km easting, outside of the study area, indicating that BWDO concentrations decrease monotonically with easting within the study area. The unique spatial distribution in 1998 has been noted previously, and is generally attributed to unusually persistent eastward currents.¹⁶ A similar BWDO pattern has been noted for 2009,²³ but it was not sufficiently strong to result in a cruise-specific trend in this analysis. The trend between BWDO and northing is linear, and suggests that BWDO concentrations are higher to the south. The trend between BWDO and bathymetry (depth) is quadratic with a minimum at 22 m. The overall deterministic trends in BWDO (Figure S7 of the SI) compare well with spatial patterns in hypoxic frequency, as mapped by Walker and Rabalais.³⁴

Because BWHF is modeled as a function of BWDO, it effectively inherits the trends from the BWDO model. The trend with BWDO is linear and suggests that BWHF is larger where BWDO concentrations are lower. The model for BWHF also includes a quadratic trend with easting, suggesting a maximum at 701 km, about 30 km east of the Atchafalaya outfall location (although the overall trend in BWHF is also affected by the trends in BWDO). No cruise-specific east–west trends were selected for the BWHF model.

The models also include covariance parameters that characterize their stochastic components. For BWDO, σ_ε² and σ_η², commonly referred to as the nugget and partial sill, were 0.39 and 2.33 (mg² L^–2), respectively. Since σ_ε² is smaller than σ_η², the majority of the stochasticity in the model is spatially correlated. The approximate range of spatial correlation (3r, per eq 2) is 94 km in the east–west direction and 53 km in the north–south direction. The greater correlation distance in the east–west direction was expected due to the dominant east–west current pattern.^35,36 For BWHF, the spatial correlation of the stochasticity is somewhat weaker with σ_ε² and σ_η² similar in magnitude, having values of 0.009 and 0.011 (unit-less), respectively. Also, the correlation range was 63 km in all directions (anisotropy was negligible). Overall, spatially correlated stochasticity accounts for the greatest portion of the variability in both BWDO and BWHF. As discussed in Obenour et al.,⁹ the spatial correlation of the stochasticity is consistent with the effects of varying coastal current patterns, influencing the distribution of hypoxia over the spatial scales described above. In general, the correlation ranges are considerably longer than the typical distances between sampling locations (Figure 2), especially on the eastern shelf, suggesting that the sampling network is adequate for resolving the spatially correlated stochasticity of the system.

Using CR, we determined the mean and 95% confidence intervals for hypoxic area and volume of each cruise (Figure 3). The largest estimated hypoxic area was for 1996, but it was not significantly different from 1991, 1993, 1995, 1997, 1999, 2001, 2002, 2007, or 2008 (p > 0.05), given the uncertainty in the area estimates. The largest hypoxic volume estimate was for 2008, but it was not significantly different from 1993, 1996, 1999, 2004, or 2007 (p > 0.05). Both hypoxic area and volume were lowest in 1988, a drought year.¹⁶

Figure 3.

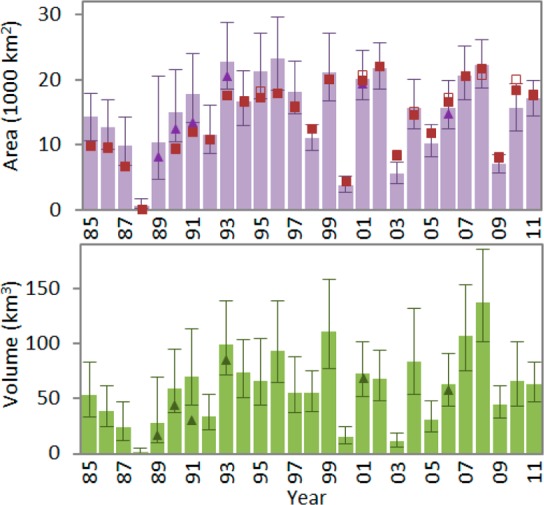
Bottom layer hypoxic extent estimates with 95% confidence intervals by year; estimates prior to making adjustments for instrument bias as triangles; previous LUMCON area estimates as open squares; revised LUMCON area estimates as solid squares.

Two sets of hypoxic area estimates, determined by LUMCON, are also included in Figure 3 for comparison. The first set are the original LUMCON estimates, determined by hand contouring, as described above.^2,19 The second set are revised estimates developed as part of this study; also by hand contouring, but using the updated BWDO values for this study (which are superior because they reflect postcruise DO calibrations). In most cases, the original LUMCON estimates (Figure 3, open squares) overlap the revised estimates (solid squares), and the majority of the LUMCON estimates fall within the 95% confidence intervals determined by this study. However, for the first third of the study period (1985–1993), the new estimates are consistently higher than the LUMCON estimates.

LUMCON did not make an estimate for 1989, because only a portion of the shelf was sampled that year. Our method does allow for extent estimates for 1989, and the wide confidence intervals (Figure 3) reflect the relatively large uncertainties. Even though data for 1989 were limited, the overall spatial trends (based on the data from all years) help to constrain the variability in the CRs to within realistic ranges, across the study area. We note that the 1989 estimate presented here is consistent with previous estimates developed from nutrient loading models.^37,38

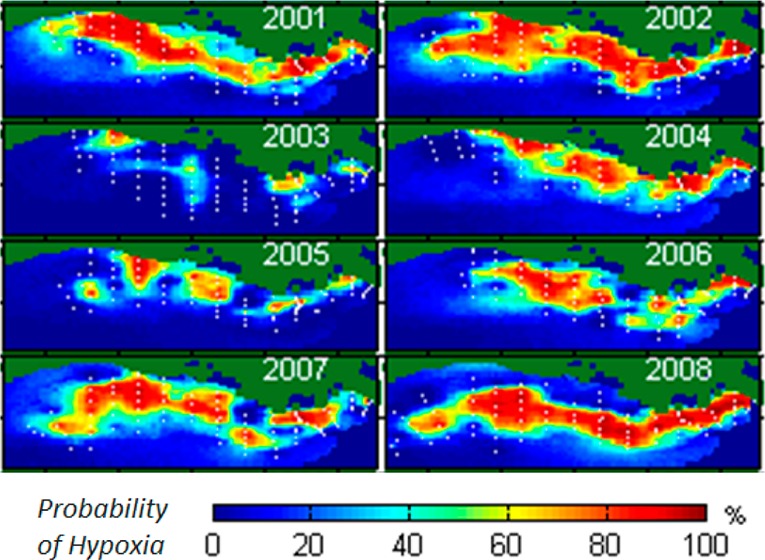
There was considerable interannual variability in the spatial distribution of hypoxia and in the thickness of the hypoxic bottom layer (Figure 4). Years with similar hypoxic areas may have very different average hypoxic thicknesses and thus volumes. For example, 2002 and 2008 have similar hypoxic areas, but they are very different in terms of hypoxic thickness, such that 2008 has approximately twice the hypoxic volume of 2002. The results indicate that the average bottom layer hypoxic thickness for the 27-year study period was 3.9 m, with the thickest average layers of approximately 6.2 and 6.3 m occurring in 2008 and 2009, respectively. Over the 27-year study period, hypoxic volume is correlated with area (r² = 0.77). Interestingly, hypoxic area and thickness are also somewhat positively correlated over most years (r² = 0.37, not including 1998 and 2009, which were subject to unusually strong eastward currents^16,23), such that volume increases exponentially relative to area. Tabulated results and additional maps showing estimated BWDO, estimated hypoxic thickness, probability of hypoxia, and example CRs for the entire study period are included in Sections S4 and S5 of the SI.

Figure 4.

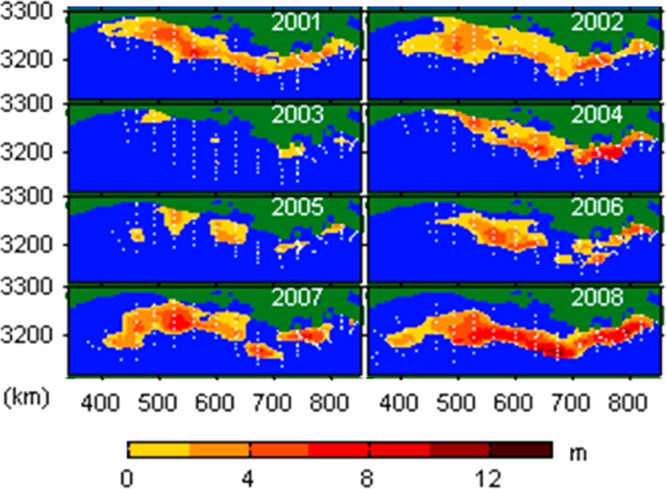
Example maps of estimated bottom layer hypoxic thickness (median values from CRs), 2001–2008; observation locations shown as white dots.

4. Discussion

The geostatistical modeling results can be used to assess temporal trends in hypoxic zone size for the 27-year study period. Hypoxic volume increased by an average of 2.3% per year as a linear trend with time (1.4 km³ yr^–1, percent increase determined by dividing by the 27-year mean hypoxic extent), but this trend was not significant (p = 0.12). Hypoxic area increased at a lesser rate of 0.9% per year (140 km² yr^–1) and was also not significant (p = 0.42). However, the relatively large increase in volume relative to area reflects a significant increasing trend in hypoxic layer thickness (1.8% per year, 0.069 m yr^–1, p = 0.05). Note that trend significance is affected by the uncertainty in the geostatistical estimates; trend significance is determined using a Monte Carlo approach where temporal trend coefficients are developed for each of the 1000 sets of CRs, and an overall probability distribution is developed by sampling from the uncertainty in these trend coefficients (note p-values are based on a two-sided test). Without accounting for uncertainty, the volume, area, and thickness trends would have p-values of 0.09, 0.38, and 0.01, respectively.

The new hypoxic area estimates can be compared to the previous hypoxic area estimates developed by LUMCON.^2,16 For the 27-year study period, the previous area estimates increased at a highly significant rate of 2.6% per year (360 km² yr^–1, p = 0.01), substantially greater than the 0.9% rate for the new estimates. This dissimilarity is due primarily to differences in estimates for the earlier years of the study period (Figure 3). For 1985–1987, the new estimates are consistently higher than the previous estimates primarily because the geostatistical methodology accounts for the possibility of hypoxia occurring outside the envelopes of the cruises, which were relatively small in these years. For 1990, 1991, and 1993, the new estimates are also higher because of the instrument bias adjustments developed in this study. For 1985–1993 (except 1989, for which there is no previous estimate), the mean geostatistically determined hypoxic area is 39% (3650 km²) greater than that of the previous estimates.

For 1994–2011, the new area estimates are in general agreement with the previous area estimates. Over this time period, the two sets of estimates are highly correlated (r² = 0.88), the means of the two data sets are of negligible difference, and only three of the previous estimates (1996, 2003, and 2010) fall outside the 95% confidence intervals of the new estimates (Figure 3). This suggests that when the biasing issues noted above are avoided, there is approximate agreement between the geostatistical and hand-contouring estimates.

The new extent estimates have implications for our understanding of how hypoxia is changing over long temporal scales. Multiple studies using nutrient loads to predict the previous hypoxic area estimates have suggested the Gulf is becoming increasingly susceptible to hypoxia, based on increasing hypoxic area relative to nutrient loading.^11,12,39,40 (Nutrient loading increased greatly in the 1970s but remained relatively stable throughout the study period.)^37,41 Increases in hypoxic susceptibility have also been suggested in other studies of the Gulf and other coastal systems.⁴²⁻⁴⁴ The new hypoxic area estimates, however, exhibit relatively little increase over time, especially when compared to the previous estimates, potentially suggesting less system change during the study period than previously thought. But, the new hypoxic thickness and volume estimates do increase to a greater degree, potentially suggesting a more vertically oriented increase in hypoxic extent. Future studies could focus on recalibrating existing nutrient-loading models to these new hypoxic extent estimates to develop a refined understanding of how Gulf hypoxia may be changing over time.

Uncertainties in the new hypoxic extent estimates, represented by the 95% confidence intervals (Figure 3), reflect the limited spatial scope and resolution of shelfwide cruise sampling. Uncertainties are generally greatest in the earlier years when cruises were smaller and did not always use instruments that reached the sea floor. From 1985 to 1993, the mean relative standard error for hypoxic area was 23%, but it decreased to 11% for 1994–2011. Uncertainties also appear to be larger in years with relatively severe hypoxia (i.e., lower average BWDO and larger hypoxic area), likely because more of the estimation grid is subject to the possibility of hypoxia (in years with higher average BWDO, most of the estimation grid is determined to be well above the hypoxic threshold, such that simulated values rarely fall below the hypoxic threshold). In the future, the modeling framework presented here could be used to evaluate different sampling designs based on how well they constrain estimate uncertainty. The modeling approach could also be used to compare hypoxic extent results and associated uncertainties using hypoxic threshold choices other than 2 mg L^–1.

Regardless of the precision of the estimates, it is important to remember that they represent conditions at only certain points in time (i.e., during the shelfwide cruises), and that hypoxic extent can vary substantially throughout the summer due to changes in organic matter production, wind-driven mixing events, and fluctuating current patterns.^10,45,46 As a result, these estimates do not necessarily reflect hypoxic conditions over the entire summer (although back-to-back cruises have demonstrated fairly consistent hypoxic areas under stable weather conditions).¹⁵ More detailed monitoring and biophysical modeling are needed to better understand the short- and long-term dynamics of hypoxia formation, and to mechanistically interpret the temporal variability in the extent estimates presented here.

The primary feature of the geostatistical approach, when compared to more traditional, interpolation-based approaches, is the use of simulations (i.e., CRs).¹⁸ The most obvious benefit is the ability to quantify the uncertainty in extent estimates. A second benefit is that CRs provide more realistic extent estimates than can be derived from kriging (or largely equivalent methods such as Gauss-Markov smoothing⁴⁷) alone. In this study, hypoxic area estimates derived from kriged maps (UK interpolation, Figure S14 of the SI) were substantially lower than both our CR estimates and the LUMCON estimates. This is because the kriged maps (Figure S9 of the SI) tend to characterize large portions of the estimation grid as slightly above the hypoxic threshold. However, due to the stochasticity of the system, these locations still have some probability of being hypoxic. The CR approach, which samples from the uncertainty in the system, accounts for this possibility, and thus results in larger hypoxic area estimates. This is consistent with Chiles and Delfiner,¹⁷ who argue that CR, rather than kriging, is the more appropriate approach for determining spatially aggregated quantities. A third advantage of the CR approach is that it provides a framework for performing instrument bias adjustments probabilistically, such that adjustment uncertainty is propagated to the hypoxic extent estimates. Finally, CR was fundamental to probabilistically determining hypoxic volume (in addition to area). The two-step CR approach, developed here, can be compared to other volume estimation methods, such as multilayer kriging²¹ and three-dimensional CR,²² which have been applied in Chesapeake Bay. A benefit of our approach is that it allows uncertainty quantification of hypoxic volume within a relatively simple (two-dimensional) geostatistical framework.

This study also demonstrates the benefits of including trend variables within the geostatistical model (i.e., the UK formulation) because the deterministic trends help reduce model uncertainty and result in more realistic extent estimates (Section S6 of the SI). The advantages of UK have been demonstrated previously for Lake Erie and Chesapeake Bay hypoxia,^18,21 but are perhaps even more salient for an open system such as the Gulf shelf. When trends in DO are not modeled, it has been necessary to limit the estimation grid around the bounds of the sampling cruise,^15,48 such that the size of the cruise can potentially bias the inferred hypoxic area. By including trend variables that explain the large-scale spatial patterns in BWDO and BWHF, it is possible to develop realistic CRs of DO across the entire study area, so the same estimation grid can be used for all cruises.

Finally, the results confirm that the hypoxic area on the Louisiana-Texas shelf greatly exceeds the Hypoxia Task Force goal of 5000 km² as a five-year running average.^6,7 The most recent five-year period from our study, 2007–2011, has a mean hypoxic area of 16 600 km² with a 95% confidence range of 15 100–18 000 km². Clearly, additional management measures are required if the hypoxic extent is to be reduced to comply with the Task Force goal.

Supporting Information Available

A description of the instrument bias adjustments, a graphical test of linearity for the deterministic components of the models, the intercept parameters for the categorical variables, a set of results maps, tabulated bottom layer hypoxic extent results, and a summary of the models for MinDO and THF. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.