Abstract
Purpose
Gradient nonlinearity of MRI systems leads to spatially-dependent b-values and consequently high non-uniformity errors (10–20%) in ADC measurements over clinically relevant field-of-views. This work seeks practical correction procedure that effectively reduces observed ADC bias for media of arbitrary anisotropy in the fewest measurements.
Methods
All-inclusive bias analysis considers spatial and time-domain cross-terms for diffusion and imaging gradients. The proposed correction is based on rotation of the gradient nonlinearity tensor into the diffusion gradient frame where spatial bias of b-matrix can be approximated by its Euclidean norm. Correction efficiency of the proposed procedure is numerically evaluated for a range of model diffusion tensor anisotropies and orientations.
Results
Spatial dependence of nonlinearity correction terms accounts for the bulk (75–95%) of ADC bias for FA = 0.3–0.9. Residual ADC non-uniformity errors are amplified for anisotropic diffusion. This approximation obviates need for full diffusion tensor measurement and diagonalization to derive a corrected ADC. Practical scenarios are outlined for implementation of the correction on clinical MRI systems.
Conclusions
The proposed simplified correction algorithm appears sufficient to control ADC non-uniformity errors in clinical studies using three orthogonal diffusion measurements. The most efficient reduction of ADC bias for anisotropic medium is achieved with non-lab-based diffusion gradients.
Keywords: diffusion MRI, gradient nonlinearity, ADC systematic bias
Introduction
Diffusion weighted imaging (DWI) is a widely used magnetic resonance (MR) modality for noninvasive diagnostics (1–3). The most common diffusion quantity of interest in clinical oncology applications, such as therapeutic response assessment, is mean diffusivity (4–7). This quantity indirectly reflects tissue cellularity via water mobility and has the desirable property of being independent of the relative orientation between the applied diffusion gradient directions and directional tissue cytoarchitecture (8,9). Mean diffusivity, commonly referred to as “apparent diffusion coefficient” (ADC), may be determined from a variety of tissue/media-based models of how DWI signal changes with applied diffusion gradient strength (10–12). ADC has been suggested as a potential biomarker for cancer diagnosis and treatment monitoring (4–7). To detect clinically significant changes in diffusion measurements, the sources of technical variability and bias have to be well-characterized separately from biologic and therapy-induced changes (13–15). Ultimately, for diffusion to be used as a quantitative biomarker in clinical studies, measurement methodology must be standardized across multiple MRI platforms (7,15–17).
Recently, a significant platform-dependent variation has been identified as a source of spatial-dependent error in ADC measurement (18,19). Such errors have been demonstrated on commercial MRI equipment (19) by using a temperature-controlled (ice water) phantom for a precisely known diffusion fluid (18). Testing showed that gradient nonlinearity was the primary source of the error leading to a spatially-dependent b-value and subsequent ADC bias that can exceed 10–20% over a clinically relevant field-of-view (FOV) on some systems (19,20). This platform-dependent bias results in spatial non-uniformity errors that substantially deteriorate quantitative DWI measurements. The early accounts of DWI errors related to gradient nonlinearity are now a decade old (21,22), but the systematic bias problem has clearly persisted for contemporary clinical systems. This is presumable due to lack of practical correction procedures for vendor implementation. Gradient nonlinearity is a static characteristic of the gradient coil system (23) known to system engineers and universally utilized for correction of geometric distortions (24,25) for routine MRI scans.
Previous research on nonlinearity correction for diffusion gradients (26) described an approach for correction of diffusion tensor imaging (DTI) that required full spatial-mapping of the gradient coil fields (24) as well as collection of at least 6 DWI gradient directions in each experiment. This comprehensive approach accounted for both direction and magnitude errors in diffusion tensor due to gradient nonlinearity, although the underlying tensor diagonalization algorithm can be susceptible to measurement noise (27) and fitting errors (28). Optimized sampling of many directions, as required for DTI (29), prolongs image acquisition beyond the desired scan time in many clinical applications, when only a measure of mean diffusivity is sought (5,6). Full DTI determination becomes more impractical for multi-b-value studies (12,30). To streamline correction for background and imaging gradient errors in DTI, a simplified empiric calibration algorithm was introduced (31) based on a regression model, without reference to the system’s hardware characteristics. Such approach is dependent upon specific gradient hardware and waveforms, and may require recalibration and error analysis for each clinical scan. Other methods have incorporated the interaction of imaging gradients with diffusion gradients in the model (32), but did not account for gradient nonlinearity and spatial cross-terms (26). In short, the corrective techniques suggested thus far have not been successful in practical implementation of simultaneous corrections for spatial gradient nonlinearity and time-domain cross-terms that corrupt ADC measurement for conventional (three-direction) DWI scanning.
For clinical studies focused on mean diffusivity and not anisotropy, such as usually is the case for body oncology applications (5,6), there is a desire to perform imaging using the fewest number of directional DWIs. This is particularly, true when multiple b-values are acquired to separate ADC components (12,30). In the absence of gradient nonlinearity, three orthogonal gradient directions are adequate (3,5,33). However, as surmised in Ref.(26), due to spatial cross-terms with tissue diffusion tensor, gradient nonlinearity required solution via acquisition of at least six directions to derive three eigenvalues of the diffusion tensor from which a corrected mean diffusivity was calculated. Our work seeks a practical procedure that both builds on comprehensive physical system characteristics (10,23,24,26,32,34) and minimizes acquisition and analysis time to achieve quantitative control of spatial bias error.
This work describes the simplified procedure that corrects ADC non-uniformity for conventional (three orthogonal direction) DWI acquisition (3,33) by concentrating energy of the b-matrix in to a single map (per DW direction) that approximates the spatial nonlinearity bias. In this form, the correction scales with effective b-value at isocenter and can be applied for an arbitrary diffusion gradient waveform from an orthogonal set, independent of other experimental settings. By design, the DWI waveforms include time-compact imaging gradients that minimize imaging cross-terms (35). Correction efficiency of the suggested procedure as well as residual spatial bias in ADC due to nonlinearity cross-terms are evaluated for a range of tissue-like diffusion tensor anisotropies and orientations. Despite tissue anisotropy, spatial gradient nonlinearity and imaging gradient cross-terms, the proposed correction procedure allows sufficient reduction of ADC bias with only three-orthogonal gradient measurements as is preferred in clinical oncology practice (5–7). The theoretical model and simulation of bias error is verified with actual phantom data for isotropic medium. Both correction and residual bias analysis are performed numerically excluding random measurement errors. Theoretical formalism is presented to summarize the workflow and correction algorithm for implementation by clinical MRI vendors.
Theory
The trace of diffusion tensor, D, is invariant to rotation of coordinate system and is known as the mean diffusivity or apparent diffusion coefficient, ADC. Therefore, this property can be measured for any three orthogonal DWI directions independent of both overall diffusion tensor orientation (8–10) and selected DW-frame ((3,33), see Appendix, Eq.[A7]):
| [1] |
Here, is measured signal intensity ratios for any image pixel of zero to non-zero diffusion gradient conditions for each of three kth orthogonal measurements, and is an effective spatially independent b-value given by the Frobenius norm of b0-matrix (at isocenter), which generally includes incremental b-components due to time-domain cross-terms between diffusion and imaging gradients: (Eqs.[A2–A3], (32,34)).
Spatial nonlinearity of the gradient coils (23,24), characteristic of wide-bore clinical magnets (25), can be described by static dimensionless nonlinearity tensor L(r) (23,26) independent of desired gradient strength at isocenter. For linear systems, L = I, for any image voxel r = (x, y, z)T. In presence of spatial gradient nonlinearity (23–26), spurious gradients are produced that significantly alter both direction and norm of effective DWI waveform, Eq.[A9]. These result in a b′-matrix (26), Eq.[A10], with spatially dependent norm ‖b′‖(r) ≠ ‖b0‖. The “true” (unbiased) apparent diffusion coefficient, as follows from Eq.[A1],
| [2] |
now includes contribution from spatial and imaging cross-terms with the diffusion tensor. For any three orthogonal diffusion gradient directions, each kth b′-matrix in Eq.[2] can be transformed to DW-frame by rotation UUT = I3 ≡ I:
| [3] |
where , U = (u1, u2, u3), and unit vector uk = (uxk, uyk, uzk)T defines the kth DW direction in the gradient coil coordinates. This single transformation simultaneously preserves the bulk of the norm (power) for each of the three bk-matrices in the leading term along the corresponding DW direction (Eqs.[A3, A11]): , and effectively reduces all cross-terms in Eq.[2]: .
As shown in Appendix, Eqs.[A11]–[A13], to reduce Eq.[2] to its simplified analogue of Eq.[1] in presence of nonlinearity, spatial bias map for each applied DW gradient can be approximated by:
| [4] |
and corresponding “corrected” b-value map is then obtained from:
| [5] |
Note that for DW-gradient directions along the LAB axes, U=I, Eqs.[4,5] can be further simplified to produce: . Residual error of the leading b-correction term, Eqs.[A3, A14], is negligible and depends on selected DW direction and relative strength of cross-terms with imaging gradients at isocenter.
Finally, the unbiased ADC value can be approximated using Eq.[1] and replacing “assumed” b-value with “corrected” map, Eq.[5]. When the DWI sequence is designed so that effective b-value is independent of direction, , it can be factored out from expression for corrected ADCc:
| [6] |
Residual error of ADC-correction, will be defined by contribution of spatially-dependent cross-terms of Eq.[3] in Eq.[2] with diffusion tensor components in DW-frame, . This error will depend on mutual orientation of selected DW directions and principal axis system of diffusion tensor, as well as its anisotropy and relative strength of cross-terms with imaging gradients.
In practice, it may be more desirable to directly correct either b-values, Eq.[5], or actual DWI pixel intensity as a function of space before ADC calculations (e.g., for multi-exponential model fit (12,30)). Intensity correction for each orthogonal DWI direction can be achieved by:
| [7] |
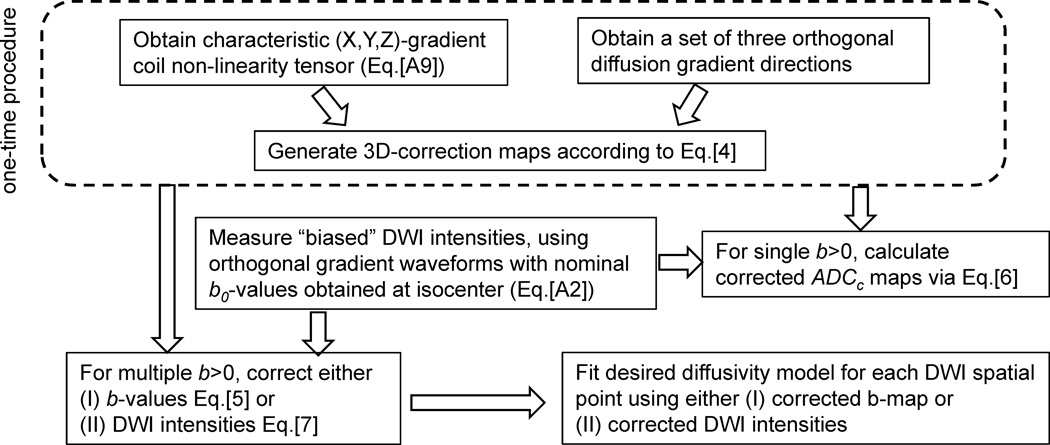
The proposed correction workflow is summarized in Figure 1. Note that described ADC bias correction procedure uses only three orthogonal measurements for a given b-value and avoids matrix inversion, fitting approximation (28) or direct solution of DTI eigenvalue problem for Eq.[2] (26), which are more sensitive to the measurement noise (27).
Figure 1.
Schematic of proposed ADC correction workflow. Dashed outline marks one-time procedure to obtain corrector maps for a specific MRI scanner. This is followed by description of allowed correction routes for a DWI scan to remove ADC bias.
Methods
(1) Hardware model parameters
Gradient waveforms and corresponding b-matrices, Eq.[A2], (32,34) were modeled numerically (Matlab 7, MathWorks Inc.) for a time-compact pulse sequence (35) using two scenarios for three orthogonal diffusion gradients: (1) “LAB” -- DW gradients applied independently along X, Y, Z directions (‖b0‖ = 1010, U = I = [(1, 0,0)T, (0, 1,0)T, (0, 0,1)T]), and “OVP” -- DW gradients combined along X+Y+Z axes (‖b0‖ = 1510, . Low nominal b-value of ‖b0‖ = 101 was also modeled to estimate relative contribution of imaging cross-terms. Square waveforms were used as diffusion pulse models. The duration of the DW pulses was 30ms, 4ms slice select and SE pulse, TE = 100ms, with 3.2ms read-out. For time-compactness (35), read-out pre-phase pulse immediately preceded the read-out gradient at TE. Imaging gradient contribution to time-domain cross-terms was included through numerical time-integration of gradient waveforms Eq.[A2] (32,34). Following Janke, et al, (24) spatial dependence of gradient coil fields was described via spherical harmonic expansion to the 7th order skipping all even terms (using characteristic magnet bore diameter rc = 400 mm). Magnetic field for the Y-coil was obtained by 90° rotation of the X-gradient field. Nine 3D-elements of gradient nonlinearity tensor were obtained by numeric differentiation of the gradient coil fields along three Cartesian axes and subsequent normalization by the effective gradient strength at isocenter, Eq. [A9]. The spatial dependence of bij (r)-terms was then modeled numerically, Eq.[A10], using nonlinearity tensor according to the formalism introduced in Ref.(22), within a 300×300×300 mm3 volume sampled every 5 mm. The spatial dependence of residual cross-terms after correction was obtained via Eq.[3].
(2) Tissue diffusion model
Diffusion properties of the media were modeled numerically using diffusion tensor (8,10) with tissue-like characteristics: ADC =1.0×10−3 mm2/s and fractional anisotropy FA = 0.0, 0.3, 0.5, 0.7 and 0.9. Model ADC was uniform across FOV. Diffusion tensor orientation was varied uniformly in respect to the lab (gradient) system by consecutive rotations around X−Y−X axes (0..π/2, 0..π/2, 0..2π) with a constant step of 9° for the first rotation around X and around Y, and scaled by sin(αY) (to achieve constant solid angle arc length) for the second rotation around X, resulting in 2510 uniform D-tensor orientations. This sampling rate was empirically determined to provide adequate orientation density coverage for the error histogram shape and width analysis downstream. The uniformity of sampling ensured absence of orientation clustering and under-binning of the error histograms. The uniformity was checked by visualization of D-ellipsoid rotation for 100–300 orientations. “True” (uniform) ADC was obtained according to Eq.[2] including full gradient nonlinearity, imaging cross-terms and tissue model description, Eqs.[A1,A2,A9,A10]. The “assumed ADC”, ADCa, was obtained according to Eq.[1], using effective b-values at isocenter (ignoring spatial dependence). The “corrected ADC”, ADCc, (Eq.[6]) was calculated using spatially dependent “corrected” -terms, Eq.[5], substituted into Eq.[1]. The corresponding corrector maps, Eq.[4], were obtained assuming only knowledge of hardware parameters (DWI gradient waveform and nonlinearity tensor, Figure 1).
(3) ADC error analysis
ADC errors were calculated as deviation from true (uniform model) value for each pixel in 3D-volume within 300 mm FOV. Error statistics histograms were compared for ADC with, Eq.[6], and without, Eq.[1], bias correction. Fixed binning step (0.005) and range (−0.2 to 0.35) was used for all fractional error histograms independent of model FA and DWI gradient orientation to provide uniform statistics independent of sampling. The appropriate range and binning step were determined from the model with FA = 0.9 corresponding to the widest error range. The histograms were characterized by mean, median, 95-percentile, range and root-mean-square-error (RMSE) measured over the full image volume. To characterize orientation dependence of the error, whole-volume RMSE histograms were explored. The figure of merit for the correction procedure was defined as orientation-mean of the whole-volume RMSE. The total efficiency of the correction was measured as percent corrected mean RMSE. To confirm that error statistics are independent of model parameters, in addition to the model parameters listed above, b-value of 1000 and ADC = 2×10−3 mm2/s were also tested with OVP for extreme anisotropy values of FA=0 and FA=0.9. Lastly, the simulated one-dimensional ADC = 1.1×10−3 mm2/s dependence along Z and X were compared to experimental phantom results with superior-inferior (SI) and right-left (RL) offset, respectively.
(4) Phantom
An ice-water based isotropic DWI phantom was devised with known diffusion coefficient of 1.1×10−3 mm2/s (36) (denoted as “ADC” for consistency). One long 30mm diameter tube filled with distilled water at thermal equilibrium with an ice-water envelop provided the universal ADC standard (18). The phantom was constructed similar to Ref.(18) from a single tube (29×260 mm) and 3000-mL polypropylene wide-mouth jar. The 172-mL tube was filled with distilled water, capped with insulation and cemented to the underside of the 3785 mL jar top. Prior to diffusion measurements, cubed or crushed ice and water were added such that ice filled the full extent of the jar. By screwing on the jar top, the 172-mL tube of water was held in the center ice-water mixture. The phantom was wrapped in a foam insulation and zip-lock plastic bag to keep surface condensate off MR components. Following preparation of the phantom, 60 minutes was allowed to reach thermal equilibrium. The ice-water mixture provided temperature control to 0°C for several hours and allowed ADC measurement accuracy within 2% (18,19).
(5) MRI data acquisition protocol
A 3T clinical MR system (Philips Ingenia) was used. Acquisition conditions: TR = 8000ms; TE = 98 ms; acquisition matrix = 128×128; FOV = 240×240mm; 25 slices, 6mm thick, 4mm gap; bandwidth = 2.65kHz/pixel; NEX = 1; no parallel imaging. Two DWI pulse sequences were considered with gradient waveforms applied on three orthogonal axes. The first sequence, denoted “LAB”, had nominal b-value = 1000s/mm2and only one DWI gradient channel was active at a time (DW axes = X, Y, Z); whereas for the second sequence, denoted overplus (OVP), applied multiple gradient channels simultaneously for nominal b-value = 1000s/mm2. For the LAB sequence, ADC measurements on the isotropic ice-water phantom were performed both for three separate direction measurements and the resultant trace DWI defined as the geometric mean of individual axis DWx,y,z. Off-center measurements were performed using torso coil and repositioning the phantom with 50 mm overlap in superior/inferior (SI) and right/left (RL) directions. Axial and sagittal slices were acquired for SI and RL offset directions, respectively. The axis of the 172mm tube was oriented perpendicular to the slices. Measurements along the tube axis provided a spatial extent of approximately +/−150 mm in the SI and RL directions.
Results
Nonlinearity bias error was analyzed numerically using hardware and tissue model parameters described above. The base-level error due to time-domain cross-terms with imaging gradients was provided by numerical integration of gradient waveforms including imaging gradients or excluding them according to Eq.[A2–A3] (32). For the LAB and OVP gradient waveforms used in this work (see Methods), the effect of cross-terms with imaging gradients on bij-elements in the absence of spatial bias was numerically estimated to be less than 1.3% for low b-value of 100 and less than 0.4% for b-values above 1000. DWI-orientation error term induced by imaging gradients (~1.5%) was found to be approximately 3-times higher than the b-magnitude error (<0.5%, Eq.A3). Overall, small contribution of both magnitude and direction error due to imaging cross-terms was included into general ADC correction formalism as an error term matrix ε, Eq.[A3], with the elements max(|εij|) ≤ ‖ε‖~o(0.03 · ‖b‖D), where bD is obtained for the DW gradient waveform in the absence of the imaging gradients.
Further numerical simulations ascertained that time-integral and spatial bias terms still commute when gradient waveforms include imaging gradients, Eq.[A2], thus allowing independent calculation of b0-matrix at isocenter once and propagating the spatial bias through Eq.[A10] (26). Introduction of spatial bias and spatial gradient cross-terms, Eq.[A9], (26) lead to relative enhancement of the cross-terms with imaging gradients. However, spatial bias due to cross-terms with imaging gradients alone accounted for < 0.5% of total spatial bias for each voxel. The bulk of nonlinearity bias (>99.5%) was due to spatial cross-terms between diffusion gradients. Total bias including diffusion and imaging gradients was numerically evaluated and visualized through spatial dependence of diagonal and off-diagonal terms of biased b’-matrix.
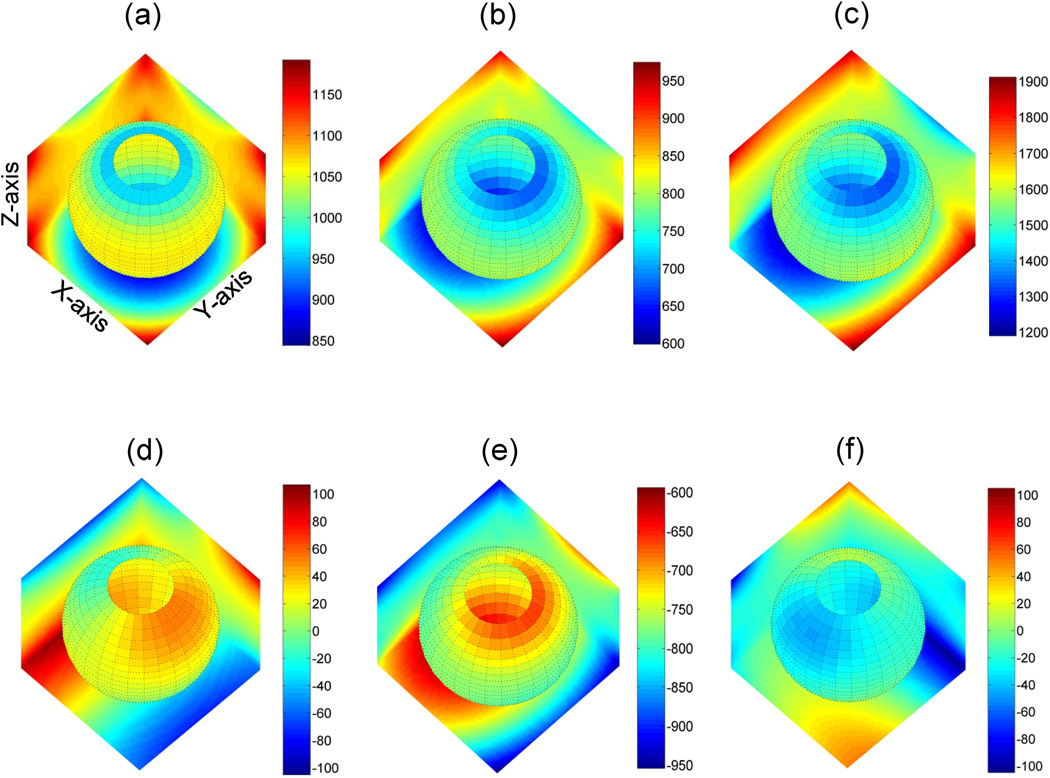
The effect of nonlinearity on spatial bias of b’-matrix including imaging gradients, Eqs.[A2,A9], (26) is illustrated in Figure 2 for a single representative DWI direction for LAB (u3 = (0, 0,1)T: Fig.2a,d), OVP : Fig.2b,e) and corrected OVP (Fig.2c,f; Eqs.[3–4]) scenarios. Spatial dependence is depicted as 3D color-map for one diagonal (bzz, Fig.2a–c) and one off-diagonal (bzx, Fig2.d–f) element of 3×3 b-matrix. Spatial non-uniformity of b-value is reflected in color gradient of the planes and spherical surfaces within the volume. The relative power of diffusion weighting across 3D map is represented by color-bar scale.
Figure 2.
Effect of gradient nonlinearity on spatial non-uniformity of diagonal (a–c) versus off-diagonal (d–f) elements of b-matrix over FOV = 300×300×300mm is illustrated for DWI gradients along “Z”-LAB (a,d), “Z”-OVP (b,e), and corrected “Z”-OVP (c,f). Spatial dependence is represented by color gradient at boundary planes (X=150mm, Y=150mm, Z=−150mm) and spherical slice through the FOV. Color-bars to the right of each 3D-map provide the scale for depicted b-values (s/mm2). The unbiased (uniform) b-value corresponds to 1010 (a), 755 (b) and 1510s/mm2 (c) at isocenter. The deviation from uniformity is visually estimated by the color gradient scale away from isocenter. The color gradient of the corrected map (c) preserves all spatial non-uniformity information of (b) to remove nonlinearity bias via Eqs.[4,5]. The residual non-uniformity error, Eq.[2], of b-matrix is represented by the spatial bias and relative scale of the off-diagonal b-elements (d–f).
In the absence of nonlinearity, the 3D map would be colored uniformly according to the nominal b-value at the isocenter (bLAB=1010, bOVP = 1510; see Methods). As evident from the color gradient, due to nonlinearity, spatial deviation from nominal value increases towards the FOV boundaries both for LAB (850–1200 scale, Fig.2a) and OVP (600–950 scale, Fig.2b) gradients. For LAB-DW scenario (Fig.2a), spatial bias introduced by nonlinearity along Z-direction, retains characteristic cylindrical symmetry of Z-coil gradient field, as prescribed by lzz (consistent with Theory, and Ref.22). Similar observations were made for the LAB-X and LAB-Y DW-directions (bxx and byy not shown). For the described correction procedure, Eq.[3,4], spatial bias of the leading b-element for LAB gradients provides the corrector map, Eq.[4], for the corresponding direction (i.e. corrected bzz has the same appearance as bzz nonlinearity map in Fig.2a).
As is evident from boundary plane projections for OVP scenario (Fig.2b), spatial symmetry of the diagonal bzz-term no longer directly reflects individual gradient coil field (unlike LAB(20)), but represents a mixed effect of nonlinearity from gradient coils simultaneously active for this OVP direction (Methods). Unlike LAB, for OVP corrected bzz non-uniformity scale (1200–1900; Fig.2c) is different from the one before correction (600–950; Fig.2b), indicating that OVP corrector map includes nonlinearity contribution from all active gradient coils (Eq.[4]). The color gradient of the corrected map (Fig.2c, Eq.[4]) preserves all spatial non-uniformity information and thus substantially removes nonlinearity bias error in ADC by Eq.[6]. Spatial dependence and scale for off-diagonal b-elements (Fig.2d–f) reports on the nonlinearity bias that propagates into ADC errors in Eqs.[2,3]. At each point in space, the contribution of off-diagonal element, byz, is below 10% of the diagonal values, bzz, both for LAB and corrected OVP scenario, but is much higher (up to 95%) for OVP before correction (see corresponding numerical color-bar scales).
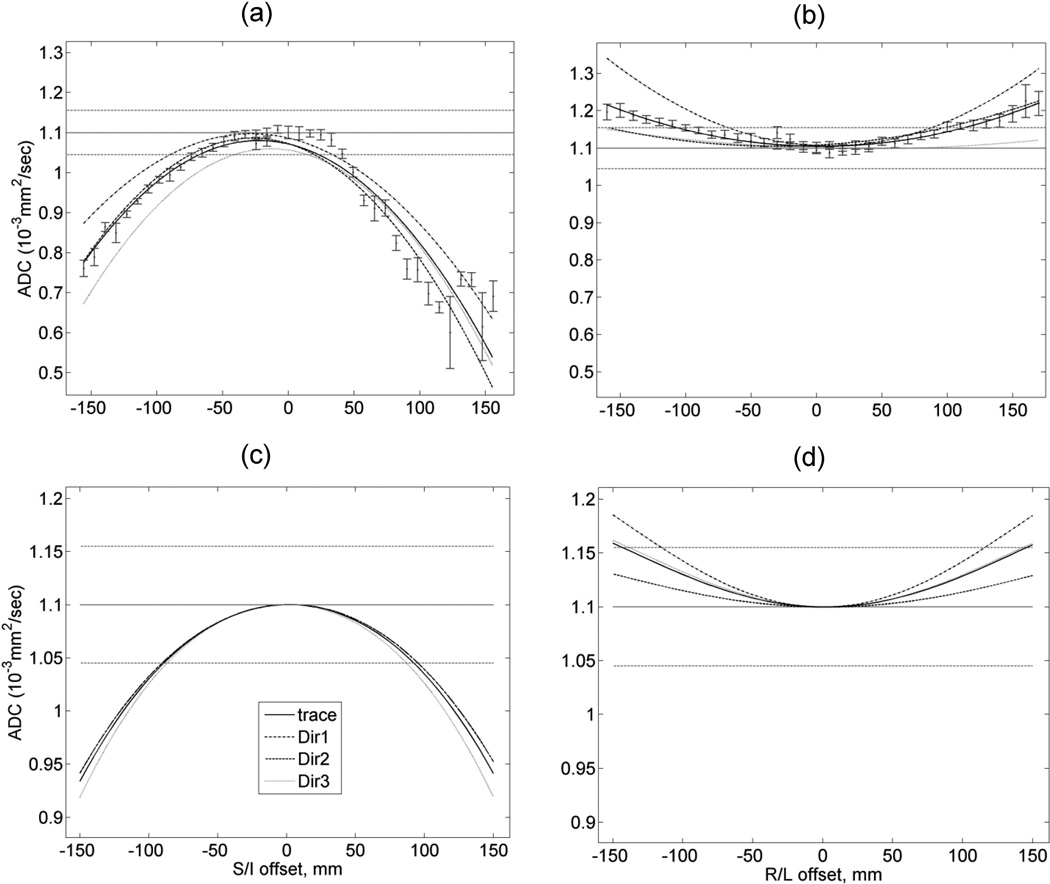
Figure 3 illustrates qualitative agreement between calculated 1D-spatial dependence of ADC and our experimental observations for an isotropic ice-water phantom run on a clinical scanner with the LAB DWI-gradients. For all three separate gradient directions and the trace, both observed (Fig.3a,b) and calculated (Fig.3c,d) ADC are quadratically underestimated along SI, while overestimated along RL compared to true values (solid horizontal line). The absolute bias along SI is more than two times higher than that along RL (Fig.3a,c versus Fig.3b,d). The model correctly reflects differences in spatial bias for individual DW gradient directions (e.g., direction 1 versus 2 in Fig.3b,d).The trace ADC bias error for OVP gradients (not shown) was 12 the same as for LAB. For FOV > 50 mm, the observed non-uniformity bias is significantly higher (> 10%) than either standard deviation of the measurement within ROI (< 2%, error bars) or error terms due to imaging gradients (< 2%, vertical shift near zero-offset).
Figure 3.
Comparison of measured spatial bias for ADC (a,b) for isotropic ice-water phantom) to the model (c,d) in case of LAB-DWI gradients plotted for three separate directions (dashed, dotted curves) and the trace (solid curve): (a,c) SI offset; (b,d) LR offset. Dotted horizontal lines mark 5% deviations from reported ADC ≡ 1.1×10−3mm2/s value of water (36) at 0 °C (solid line). Error bars for the measured trace ADC correspond to a standard deviation over 10 mm diameter circular ROI (approx. 90 pixels). Spatial non-uniformity bias away from isocenter exceeded experimental measurement errors.
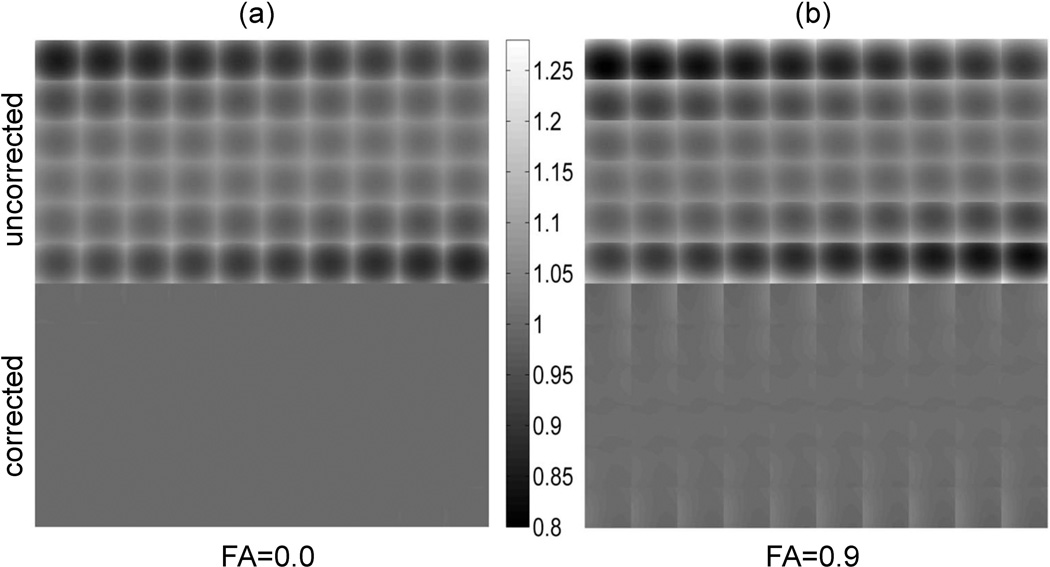
Figure 4 compares tiled 2D ADC Z-slice images obtained with the complete nonlinearity model, Eq.[2], for three orthogonal OVP DWI-gradients (top row) to those after correction (below) according to Eq.[6] in case of isotropic (FA=0, Fig.4a) and highly anisotropic (FA=0.9, Fig.4b) diffusion media. The orientation of diffusion tensor in respect to magnet axis happened to be (π/10, π/3, 0) which was representative of the typical bias error. Non-uniformity of uncorrected ADC, as indicated by gray-scale gradient, is higher for anisotropic medium (Fig.4b), while correction efficiency (uniformity of corrected ADC gray-scale-maps) is lower, especially toward the FOV edges of each slice-tile, indicating higher residual bias errors. True (model) ADC is uniform across FOV (Methods). For the isotropic case, ADC non-uniformity is effectively removed by correction producing uniform gray-scale-map in Fig.4a.
Figure 4.
Corrected versus uncorrected ADC gray-scale maps for 60 image slices (6×10 tiles) through FOV = 300×300×300 mm3 for (a) isotropic media FA=0 and (b) an arbitrary diffusion-tensor orientation with FA=0.9. Gray color-bar scale is 10−3 mm2/s. ADC non-uniformity bias is depicted by deviation from true (uniform model) ADC ≡ 1×10−3mm2/s across FOV.
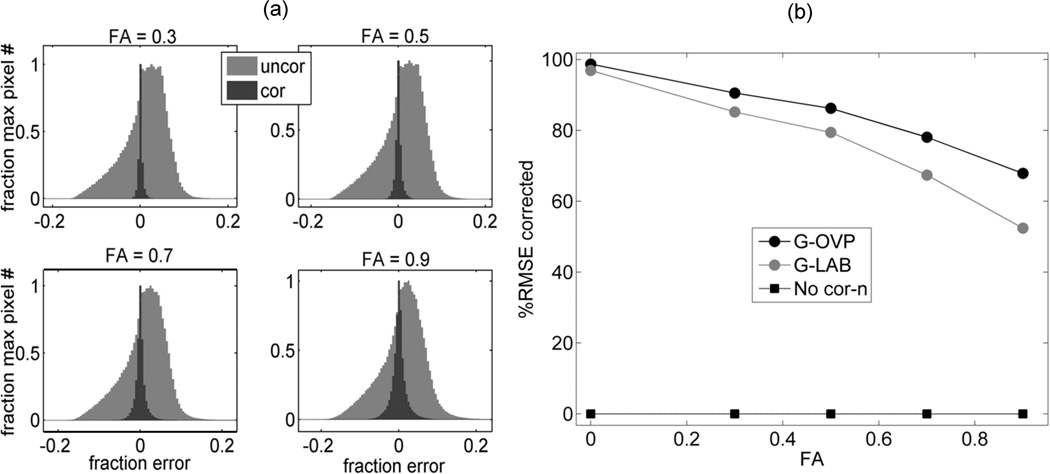
The absolute ADC non-uniformity error within FOV is summarized for several anisotropy values in histograms of Figure 5a. Figure 5b shows the average correction efficiency for two DWI gradient direction scenarios. Both uncorrected (light) and residual (dark) error histograms become broader with increasing FA of the medium (Fig. 5a). The number of voxels with high nonlinearity bias decreases as absolute bias value increases. The relative width of the histograms described by the ratio of their corresponding mean RMSE (averaged over 2510 uniform diffusion tensor orientations) is shown in Figure 5b. This ratio reflects efficiency of the correction procedure, which decreases with increasing FA. Higher overall efficiency is achievable for OVP gradients that include off-diagonal nonlinearity terms in corrector, Eq.[4]. The absolute error reduction for ADC non-uniformity achieved through leading-term correction procedure, Eqs.[4,6], was from 90 to 70% for FA from 0.3 to 0.9 respectively; and better than 97% for FA=0. More than 90% error is corrected for OVP and 80% for LAB scenario for FA<0.5. The histogram statistics did not change when using model ADC = 2×10−3mm2/s versus 1×10−3mm2/s or b-value of 1510s/mm2 versus 1010s/mm2 for FA=0 and 0.9.
Figure 5.
(a) corrected (dark) versus uncorrected (light grey) error histograms (scaled to maximum pixel number) for four FAs and 2510 uniform diffusion-tensor orientations within FOV = 300×300×300mm; (b) total correction efficiency (%RMSE) as a function of FA for all pixels within FOV averaged over 2510 diffusion tensor orientations for LAB (gray circles) versus OVP (black circles) DWI. Squares illustrate baseline efficiency without bias correction.
Discussion
The objective of this work was to find a viable correction procedure for the observed spatial non-uniformity bias of ADC for media of arbitrary anisotropy in the fewest number of measurements. Such procedure (Fig.1) was devised for any three orthogonal DWI-measurements based on fundamental property of ADC invariance under rotation and intrinsic symmetries of diffusion weighting matrix. The nonlinearity corrector maps were independent of b-value at isocenter and obtained by squared projection of the nonlinearity tensor onto DW-gradient direction, Eq.[4]. Since nonlinearity tensor is a static system characteristic (23,26) that depends only on gradient coil design, the required correctors are generated once and are independent of other specific experimental settings. Contribution from imaging cross-terms not included in b-value was confirmed to be negligible as expected for conventional (clinical) DWI pulse sequences (32) properly designed to minimize the time integral of imaging gradients that overlap with diffusion gradient waveforms (35). Residual ADC bias error due to spatial gradient nonlinearity cross-terms with anisotropic diffusion tensor, Eq.[2], was effectively reduced in DW-frame, Eq.[3]. This model assumes knowledge of gradient coil fields (23,24) and DWI-pulse sequence Eq.[A2] (32,33). In practice, leading term maps can be obtained once for a scanner system and applied for correction of b-value bias or DWI intensities in ADC measurements. For moderate tissue anisotropy (FA<0.5), this correction reduces ADC bias error over large FOV from above 15% to below experimental measurement uncertainty (<2%). Thus, this approach is well suited for body DWI oncologic applications. (5–7)
The presence of spatial and time-domain gradient cross-terms combined with tissue anisotropy complicates interpretation of measured DWI intensity ratios, Eq.[A1], (26,32). The source of non-uniformity bias in the conventional (3) ADC experiment, Eq.[2], for media of arbitrary anisotropy, is spatial dependence of all b-matrix elements (26). Thus, for an arbitrary DWI-direction, complete description of the system requires six 3D-maps for bij(r) = bji(r)-elements (18 maps for three orthogonal measurements). The effective scale (power of each bij-element) is determined by the norm of the gradient waveform and time-domain cross-terms between diffusion and imaging gradients (Eqs.[A2–A3], Fig.2). Spatial dependence of the bij(r)-map is determined by spatial dependence of the gradient nonlinearity tensor, Eq.[A10] (26), as well as DW-gradient frame orientation in respect to the gradient-coil frame, Eq.[3] (Fig.2a,d versus Fig.2b,e). Fortunately, a good approximation to the complete system description can be achieved with only three orthogonal measurements, Eqs.[3,4].
The bias error predicted by the model along SI and RL direction is qualitatively consistent with experimental measurements using a temperature-controlled isotropic phantom as depicted in Figure 3. Measured ADCs are proportionally underestimated along SI, while overestimated along RL compared to true values. Higher absolute bias is observed along SI compared to RL. The observed spatial bias depends on DW waveform (e.g., dashed versus dotted traces), while measured value for isotropic medium should be independent of diffusion gradient direction. Negligible offset of the measured curves near isocenter (Fig.3a,b) confirms small contribution of imaging cross-terms, Eqs.[A2–A3]. Qualitative agreement between our modeled and measured bias (Fig.3) strongly suggests gradient nonlinearity as the major source of the spatial ADC bias error (19). Quantitatively, our current nonlinearity model underestimates the bias scale, but this is likely due to literature values of the applied spherical harmonics coefficients (24) underestimating those of the actual clinical scanner used for phantom measurements (19). Quantitative agreement should be achieved with access to appropriate system coefficients.
As described in Theory section (and derived in Appendix), the simplified correction is possible via mathematical transformation of biased b'-matrix and tissue diffusion tensor into DW-frame (defined by orthogonal diffusion gradients). This transformation reduces contribution of spatial cross-terms, Eqs.[2,3] (Fig.2d,f) and preserves b-norm and diffusion trace (ADC). For three orthogonal measurements, this formalism is equivalent to projection of nonlinearity tensor onto DW-directions Eq.[4] that provides a single “corrected” leading term -map, Eq.[5], per measurement. Sufficient description for LAB diffusion gradients (e.g., Fig.2a,d) is obtained by including nonlinearity bias along the gradient direction, lkk. For arbitrary DWI direction away from LAB axis (e.g., OVP), the corrected -terms will include coil fields both along and orthogonal, li≠j≠k, to gradient direction, Eqs.[4] (Fig.2c). Due to different spatial dependence of corrector Ck (r)-maps for each DWI direction, Eq.[4], spatial dependence of leading -terms, Eq.[5], has to be corrected separately for individual DW-gradient directions before combining for ADC calculation, Eq.[6]. Each measurement provides only one diagonal component of the diffusion tensor, Dkk, along the corresponding DW direction used in an ADC-experiment, Eq.[A5]. These values depend on orientation of the frame defined by DW gradients, and in general case, do not represent the eigenvalues of the diffusion tensor (required for FA estimate (8,10,26)). Note that information on diffusion tensor orientation is lost by this approximation, while corrected off-diagonal elements, bi≠j, are needed to obtain FA from full DTI measurement (26).
After suggested leading-term correction according to Eqs.[4,6], residual error-distribution for ADC will depend on anisotropic properties of the media and relative orientation of gradient fields, Eqs.[3,A6,A14]. The residual error is determined by spatial dependence of spurious diffusion gradients, Eq.A9], and cross-terms with imaging gradients, which slightly perturb orientation of “effective” DW gradient frame and are neglected by our simplified correction procedure. The minimal residual error can be predicted for isotropic media, where Di≠j= 0, and off-diagonal cross-terms are effectively eliminated in Eq.[2]. This is confirmed by the results illustrated in Fig.4a, where non-uniformity bias is nearly removed for FA=0 by our correction procedure. For anisotropic case (Fig.4b), residual error exhibits clear orientation dependence and is larger for regions further from isocenter. The number of pixels with higher ADC non-uniformity error decreases approximately quadratically with the bias value (Fig.5a) reflecting general spatial nonlinearity scale of the gradient coil fields (19,24). Negative skew of the pixel histograms of ADC error before correction is independent of FA and reflects intrinsic asymmetry in the gradient coil field model used (24). Higher symmetry of residual error histograms after correction confirms that no additional spatial bias is introduced by our simplified correction procedure. The histogram statistics does not change when different b-value or model ADC are used, confirming that presented error correction efficiency estimate is independent of actual ADC or effective b0-value. Therefore, the proposed error correction procedure is adequate for arbitrary experimental conditions.
The relative amount of error corrected for all pixels within the FOV was quantified by the ratio of the histogram RMSE before and after correction (Fig.5b). Slightly higher correction efficiency observed for OVP versus LAB DWI scenario is expected due to inclusion of off-diagonal nonlinearity tensor elements into corrector Eq.[4]. This facilitates suppression of spatial cross-terms with imaging gradients. Still, major bias error reduction occurs even with LAB scenario, where corrector includes only diagonal nonlinearity terms, lkk (U=I in Eq.[4]). This is consistent with off-diagonal nonlinearity (spurious gradients) having lower effect on spatial bias. Therefore, LAB results in Fig.5b provide baseline correction efficiency if the off-diagonal nonlinearity (spurious gradients) is ignored. Single anisotropy value used by our model for all pixels within the FOV is a hypothetical scenario to illustrate the impact of anisotropy. More practical assumption is the distribution of anisotropies (37,38), with prevalence of lower anisotropies observed for non-neurologic or disease tissues (37). In the reasonable anisotropy range (FA<0.5 (37,39)), the proposed correction procedure removes > 90% of error and reduces absolute ADC non-uniformity bias to below experimental uncertainty (< 2%, Fig.3a,b) over clinically relevant FOVs.
A couple useful tips regarding efficient reduction of residual ADC error were realized by presented comprehensive gradient nonlinearity model and error analysis: (a) for highly anisotropic media, OVP gradients provide more efficient ADC correction when off-diagonal nonlinearity terms are known; (b) minimal effort correction procedure that ignores spatial dependence of off-diagonal cross-terms of nonlinearity tensor can be applied for low anisotropy tissue with LAB-gradients. In practice, the described correction can be implemented via the following three routes: (i) providing corrected b-maps (LUT, normalized by b-value) for a set of 16 DWI gradient directions, Eq.[5]; (ii) providing corrected ADC maps, Eq.[6]; and (iii) providing corrected DWI images, Eq.[7]. When it is desirable to obtain the diffusion coefficient for kth direction (Dkk) by fitting several measurements at different b-values, spatial bias correction should be applied first either to b-values or DWI intensities (Fig.1), followed by appropriate model fit of signal versus b-value (e.g, mono-exponential model versus alternative (12)).
Correction of individual DWI intensities (prior to ADC correction) is preferred since it offers greatest portability and flexibility. The corrective functions are pre-calculated once (Fig.1, dashed outline) and are stored on the MRI system for internal use. Each acquired DWI can be spatially corrected on the scanner. Since this correction is performed directly on the system, information regarding acquisition conditions and linkage between patient-based and magnet-based coordinate systems is available internally. This is analogous to geometric distortion correction currently applied on MRI scanners (25). Once the individual image intensities of each DWI are corrected as a function of spatial location, they are fully portable since existing online/offline diffusion analysis routines/models do not need any modification and can be applied directly to the spatially-corrected DWI.
To conclude, spatial dependence of b-matrix norm, described by squared projection of system nonlinearity tensor onto DWI direction, accounts for the bulk (70–90%) of ADC non-uniformity error for anisotropic medium (FA = 0.9–0.3) and >97% for isotropic medium. Residual error due to spatial and time-domain cross-terms between diffusion and imaging gradients depends on FA of the medium and the DWI-gradient direction/mode. ADC non-uniformity errors are amplified for anisotropic diffusion and gradient over-plus mode and can be corrected most efficiently. Simplified b-correction algorithm, including spatial dependence of leading diagonal b-terms rotated into diffusion gradient frame, is found to be sufficient to control conventional (i.e. three-direction) ADC measurement bias error in clinical studies (5–7). This procedure, although applicable only to ADC measurement, is mathematically robust to experimental noise since it avoids data fitting and solution of the full eigenvector/eigenvalue problem. Once calculated for specific gradient coil system and selected DWI directions, the spatial dependence of correctors are fixed, well-behaved smoothly varying functions, independent of subject or imaging sequence, which simply scale with b-value. Vendor cooperation is desirable to implement viable instrumental correction procedures in-line to control spatial ADC bias errors on clinical scanners.
Acknowledgement
We would like to acknowledge funding from the contract grant sponsor: National Institutes of Health (NIH/NCI); contract grant number: P01-CA85878, SAIC 29XS161 and U01-CA166104, as well as training support for D. Malyarenko from T32 EB005172.
Appendix
In conventional DWI MR experiment, the diffusion tensor elements, Dij, are related to measured signal intensity ratios for any image pixel, SR = So/Sb, of zero to non-zero diffusion gradient conditions via (8,10,11):
| [A1] |
where, V and Λ are matrices of eigenvectors and eigenvalues of D, respectively, I≡ I3 is a 3×3 identity matrix, and , are the elements of symmetric 3×3 b-matrix obtained by time-integration of kth-direction gradient waveform, gk(τ), according to (26,32,34) :
| [A2] |
Here γ is the gyromagnetic ratio, TE is the echo time for the spin echo DWI sequence, and gk(τ) waveform coordinates indicate active gradient coil elements X, Y and Z at time τ. This separation of system specific characteristics under the time integral of Eq.[A2] (32,34) is achievable since diffusion tensor in Eq.[A1] is independent of time. Spatial direction of applied diffusion gradients, u= gD/‖gD‖, can be described by a unit vector in gradient coil coordinates, u= (uX, uY, uZ)T, while their strength is determined by the Euclidean norm of the diffusion waveform, ‖gD‖. The general gradient waveform includes all sequence gradients with polarity reversed after TE/2 (32) to implicitly account for effect of the spin echo RF pulse (34). According to Ref.(32), coefficients of dyadic product of Eq.[A2] can be written in a 3×3 b-matrix form. When imaging gradients are included, g= gD + gIMG, each element of this matrix can be decomposed into three parts (32) that separately account for diffusion and imaging gradients, as well as their cross-products. Diffusion term (D) is proportional to the product of the desired diffusion gradient strength with their timing elements (duration and spacing) (34). The other two terms describe additional (undesired) weighting due to products of imaging gradients with themselves (IMG) and with diffusion gradients (ICT). For time-compact DWI sequences (35) with moderate imaging resolution (32), imaging cross-terms are small, such that:
| [A3] |
Here, ‖b‖ ≡ ‖b‖F, is a Frobenius (Euclidean) norm of symmetric b-matrix, invariant under rotations. When the gradient strength is independent of spatial coordinate, g(r) = g0, at isocenter r = r0 = (x0, y0, z0)T, b-matrix is uniform over the FOV and can be described by effective b-value, , for each of three kth orthogonal measurement. Using Eq.[A3] and assuming ε → 0, Eq.[A1] can be simplified for an arbitrary DWI waveform:
| [A4] |
| [A5] |
Note that, Dkk ≠ λk is not an eigenvalue of diffusion tensor, but rather a projection of the eigenvalue “vector” onto DW direction. The model error term along uk, Eq.[A3–A4], is given by:
| [A6] |
and is negligible when Eq.[A3] conditions are satisfied.
In case of linear gradients, the above simplification, Eq.[A4], allows straightforward calculation of “assumed ADC” from any three orthogonal DW measurements U = (u1, u2, u3), UUT = I:
| [A7] |
| [A8] |
In presence of nonlinearity (23,24), the strength of the gradient varies depending on location in the magnet bore and spurious gradients are produced in directions orthogonal to desired DW, leading to spatial bias of the b′(r)-matrix (26). To the first order, such variations can be described by spatially-dependent nonlinearity tensor (26), L(r):
| [A9] |
| [A10] |
Where g0-gradient waveform and b0–matrix are given at isocenter. When b0(IMG) + b0(ICT) > 0 in Eqs.[A2–A3], b′ (r) is symmetric positive definite (semi-definite for g0(IMG) → 0), and thus, possesses orthogonal eigenvectors with the largest (1st) eigenvalue close to the b’-norm, Eq.[A3]:
| [A11] |
Therefore, similar to Eq.[A3], b′ can be approximated by , and Eq.[A4–A7] formalism can be applied with ‖b′‖ replacing in Eq.[A8]. In the limit of negligible nonlinearity and imaging cross-terms: L~I, gIMG → 0 in Eqs.[A3, A10], any three orthogonal DW directions (UUT = I) satisfy Eq.[A11]: U′ ≅ U, and . In general, for arbitrary DW direction from an orthogonal set, a corrector can be devised such that :
| [A12] |
that makes Eq.[A7] universally valid as an ADC approximation. Here , Eq.[A10], where li = (l1i, l2i, l3i)T is the ith column of gradient nonlinearity tensor L(r), Eq.[A9].
An alternative corrector, independent of b0–value at isocenter, can be obtained by “projecting” Eq.[A1] onto DW direction with bk′, similar to Eqs.[A4–A5]:
| [A13] |
Using Eqs.[A6,A12], residual b-correction error due to nonlinearity and time-domain cross-terms along kth DW direction is given by: Δ
| [A14] |
References
- 1.Clark CA, Le Bihan D. Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn Reson Med. 2000;44(6):852–859. doi: 10.1002/1522-2594(200012)44:6<852::aid-mrm5>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 2.Galban CJ, Mukherji SK, Chenevert TL, Meyer CR, Hamstra DA, Bland PH, Johnson TD, Moffat BA, Rehemtulla A, Eisbruch A, Ross BD. A feasibility study of parametric response map analysis of diffusion-weighted magnetic resonance imaging scans of head and neck cancer patients for providing early detection of therapeutic efficacy. Transl Oncol. 2009;2(3):184–190. doi: 10.1593/tlo.09175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sorensen AG, Buonanno FS, Gonzalez RG, Schwamm LH, Lev MH, Huang-Hellinger FR, Reese TG, Weisskoff RM, Davis TL, Suwanwela N, Can U, Moreira JA, Copen WA, Look RB, Finklestein SP, Rosen BR, Koroshetz WJ. Hyperacute stroke: evaluation with combined multisection diffusion-weighted and hemodynamically weighted echo-planar MR imaging. Radiology. 1996;199(2):391–401. doi: 10.1148/radiology.199.2.8668784. [DOI] [PubMed] [Google Scholar]
- 4.Chenevert TL, Stegman LD, Taylor JM, Robertson PL, Greenberg HS, Rehemtulla A, Ross BD. Diffusion magnetic resonance imaging: an early surrogate marker of therapeutic efficacy in brain tumors. J Natl Cancer Inst. 2000;92(24):2029–2036. doi: 10.1093/jnci/92.24.2029. [DOI] [PubMed] [Google Scholar]
- 5.Dickinson L, Ahmed HU, Allen C, Barentsz JO, Carey B, Futterer JJ, Heijmink SW, Hoskin PJ, Kirkham A, Padhani AR, Persad R, Puech P, Punwani S, Sohaib AS, Tombal B, Villers A, van der Meulen J, Emberton M. Magnetic resonance imaging for the detection, localisation, and characterisation of prostate cancer: recommendations from a European consensus meeting. Eur Urol. 2011;59(4):477–494. doi: 10.1016/j.eururo.2010.12.009. [DOI] [PubMed] [Google Scholar]
- 6.Li SP, Padhani AR. Tumor response assessments with diffusion and perfusion MRI. J Magn Reson Imaging. 2012;35(4):745–763. doi: 10.1002/jmri.22838. [DOI] [PubMed] [Google Scholar]
- 7.Padhani AR, Liu G, Koh DM, Chenevert TL, Thoeny HC, Takahara T, Dzik-Jurasz A, Ross BD, Van Cauteren M, Collins D, Hammoud DA, Rustin GJ, Taouli B, Choyke PL. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia. 2009;11(2):102–125. doi: 10.1593/neo.81328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alexander AL, Hasan K, Kindlmann G, Parker DL, Tsuruda JS. A geometric analysis of diffusion tensor measurements of the human brain. Magn Reson Med. 2000;44(2):283–291. doi: 10.1002/1522-2594(200008)44:2<283::aid-mrm16>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 9.Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001;13(4):534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- 10.Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 11.Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161(2):401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
- 12.Riches SF, Hawtin K, Charles-Edwards EM, de Souza NM. Diffusion-weighted imaging of the prostate and rectal wall: comparison of biexponential and monoexponential modelled diffusion and associated perfusion coefficients. NMR Biomed. 2009;22(3):318–325. doi: 10.1002/nbm.1328. [DOI] [PubMed] [Google Scholar]
- 13.Delakis I, Moore EM, Leach MO, De Wilde JP. Developing a quality control protocol for diffusion imaging on a clinical MRI system. Phys Med Biol. 2004;49(8):1409–1422. doi: 10.1088/0031-9155/49/8/003. [DOI] [PubMed] [Google Scholar]
- 14.Ogura A, Hayakawa K, Miyati T, Maeda F. Imaging parameter effects in apparent diffusion coefficient determination of magnetic resonance imaging. Eur J Radiol. 2011;77(1):185–188. doi: 10.1016/j.ejrad.2009.06.031. [DOI] [PubMed] [Google Scholar]
- 15.Sasaki M, Yamada K, Watanabe Y, Matsui M, Ida M, Fujiwara S, Shibata E. Variability in absolute apparent diffusion coefficient values across different platforms may be substantial: a multivendor, multi-institutional comparison study. Radiology. 2008;249(2):624–630. doi: 10.1148/radiol.2492071681. [DOI] [PubMed] [Google Scholar]
- 16.Colagrande S, Pasquinelli F, Mazzoni LN, Belli G, Virgili G. MR-diffusion weighted imaging of healthy liver parenchyma: repeatability and reproducibility of apparent diffusion coefficient measurement. J Magn Reson Imaging. 2010;31(4):912–920. doi: 10.1002/jmri.22117. [DOI] [PubMed] [Google Scholar]
- 17.Teipel SJ, Reuter S, Stieltjes B, Acosta-Cabronero J, Ernemann U, Fellgiebel A, Filippi M, Frisoni G, Hentschel F, Jessen F, Klöppel S, Meindl T, Pouwels PJ, Hauenstein KH, Hampel H. Multicenter stability of diffusion tensor imaging measures: a European clinical and physical phantom study. Psychiatry Res. 2011;194:363–371. doi: 10.1016/j.pscychresns.2011.05.012. [DOI] [PubMed] [Google Scholar]
- 18.Chenevert TL, Galban CJ, Ivancevic MK, Rohrer SE, Londy FJ, Kwee TC, Meyer CR, Johnson TD, Rehemtulla A, Ross BD. Diffusion coefficient measurement using a temperature-controlled fluid for quality control in multicenter studies. J Magn Reson Imaging. 2011;34(4):983–987. doi: 10.1002/jmri.22363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Malyarenko D, Galban CJ, Londy FJ, Meyer CR, Johnson TD, Rehemtulla A, Ross BD, Chenevert TL. J Magn Reson Imaging. 2012. Multi-system repeatability and reproducibility of apparent diffusion coefficient measurement using an ice-water phantom. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tan ET, Marinelli L, Slavens ZW, King KF, Hardy CJ. J Magn Reson Imaging. 2012. Improved correction for gradient nonlinearity effects in diffusion-weighted imaging. in press. [DOI] [PubMed] [Google Scholar]
- 21.Bammer R, Markl M, Pelc NJ, Moseley ME. Honolulu, Hawaii, USA: 2002. May 18–24, Assessment of Spatial Gradient Field Distortions in Diffusion-Weighted Imaging; p. 1172. 2002. [DOI] [PubMed] [Google Scholar]
- 22.Robson MD. Honolulu, Hawaii, USA: 2002. May 18–24, Non-linear Gradients on Clinical MRI Systems Introduce Systematic Errors in ADC and DTI Measurements; p. 1173. 2002. [Google Scholar]
- 23.Romeo F, Hoult DI. Magnet field profiling: analysis and correcting coil design. Magn Reson Med. 1984;1(1):44–65. doi: 10.1002/mrm.1910010107. [DOI] [PubMed] [Google Scholar]
- 24.Janke A, Zhao H, Cowin GJ, Galloway GJ, Doddrell DM. Use of spherical harmonic deconvolution methods to compensate for nonlinear gradient effects on MRI images. Magn Reson Med. 2004;52(1):115–122. doi: 10.1002/mrm.20122. [DOI] [PubMed] [Google Scholar]
- 25.Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, Macfall J, Fischl B, Dale A. Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction on phantom and human data. Neuroimage. 2006;30(2):436–443. doi: 10.1016/j.neuroimage.2005.09.046. [DOI] [PubMed] [Google Scholar]
- 26.Bammer R, Markl M, Barnett A, Acar B, Alley MT, Pelc NJ, Glover GH, Moseley ME. Analysis and generalized correction of the effect of spatial gradient field distortions in diffusion-weighted imaging. Magn Reson Med. 2003;50(3):560–569. doi: 10.1002/mrm.10545. [DOI] [PubMed] [Google Scholar]
- 27.Laun FB, Schad LR, Klein J, Stieltjes B. How background noise shifts eigenvectors and increases eigenvalues in DTI. MAGMA. 2009;22(3):151–158. doi: 10.1007/s10334-008-0159-6. [DOI] [PubMed] [Google Scholar]
- 28.Ozcan A. Noise and nonlinear estimation with optimal schemes in DTI. Magn Reson Imaging. 2010;28(9):1335–1343. doi: 10.1016/j.mri.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ozcan A. Minimization of imaging gradient effects in diffusion tensor imaging. IEEE Trans Med Imaging. 2011;30(3):642–654. doi: 10.1109/TMI.2010.2090539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lemke A, Stieltjes B, Schad LR, Laun FB. Toward an optimal distribution of b values for intravoxel incoherent motion imaging. Magn Reson Imaging. 2011;29(6):766–776. doi: 10.1016/j.mri.2011.03.004. [DOI] [PubMed] [Google Scholar]
- 31.Wu YC, Alexander AL. A method for calibrating diffusion gradients in diffusion tensor imaging. J Comput Assist Tomogr. 2007;31(6):984–993. doi: 10.1097/rct.0b013e31805152fa. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gullmar D, Haueisen J, Reichenbach J. Analysis of b-Value Calculations in Diffusion Weighted and Diffusion Tensor Imaging. Concepts in Magnetic Resonance Part A. 2005;25A(1):53–66. [Google Scholar]
- 33.Wong EC, Cox RW, Song AW. Optimized isotropic diffusion weighting. Magn Reson Med. 1995;34(2):139–143. doi: 10.1002/mrm.1910340202. [DOI] [PubMed] [Google Scholar]
- 34.Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. The Journal of Chemical Physics. 1965;42:288–292. [Google Scholar]
- 35.Pipe JG. Pulse Sequences for Diffusion-weighted MRI. In: Johansen-Berg H, Behrens T, editors. Imaging brain pathways - Diffusion MRI: from quantitative measurement to in vivo neuroanatomy. Elsevier; 2009. pp. 11–35. [Google Scholar]
- 36.Holz M, Heil SR, Sacco A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys Chem Chem Phys. 2000;2:4740–4742. [Google Scholar]
- 37.Cercignani M, Inglese M, Pagani E, Comi G, Filippi M. Mean diffusivity and fractional anisotropy histograms of patients with multiple sclerosis. AJNR Am J Neuroradiol. 2001;22(5):952–958. [PMC free article] [PubMed] [Google Scholar]
- 38.Santarelli X, Garbin G, Ukmar M, Longo R. Dependence of the fractional anisotropy in cervical spine from the number of diffusion gradients, repeated acquisition and voxel size. Magn Reson Imaging. 2010;28(1):70–76. doi: 10.1016/j.mri.2009.05.046. [DOI] [PubMed] [Google Scholar]
- 39.Bourne RM, Kurniawan N, Cowin G, Sved P, Watson G. Microscopic diffusion anisotropy in formalin fixed prostate tissue: preliminary findings. Magn Reson Med. 2012;68(6):1943–1948. doi: 10.1002/mrm.24179. [DOI] [PubMed] [Google Scholar]