Detecting Identity by Descent and Estimating Genotype Error Rates in Sequence Data

Abstract

Existing methods for identity by descent (IBD) segment detection were designed for SNP array data, not sequence data. Sequence data have a much higher density of genetic variants and a different allele frequency distribution, and can have higher genotype error rates. Consequently, best practices for IBD detection in SNP array data do not necessarily carry over to sequence data. We present a method, IBDseq, for detecting IBD segments in sequence data and a method, SEQERR, for estimating genotype error rates at low-frequency variants by using detected IBD. The IBDseq method estimates probabilities of genotypes observed with error for each pair of individuals under IBD and non-IBD models. The ratio of estimated probabilities under the two models gives a LOD score for IBD. We evaluate several IBD detection methods that are fast enough for application to sequence data (IBDseq, Beagle Refined IBD, PLINK, and GERMLINE) under multiple parameter settings, and we show that IBDseq achieves high power and accuracy for IBD detection in sequence data. The SEQERR method estimates genotype error rates by comparing observed and expected rates of pairs of homozygote and heterozygote genotypes at low-frequency variants in IBD segments. We demonstrate the accuracy of SEQERR in simulated data, and we apply the method to estimate genotype error rates in sequence data from the UK10K and 1000 Genomes projects.

Introduction

Identity by descent (IBD) is the foundation for many of the important problems in genetics including determining haplotype phase, understanding familial diseases, and detecting population structure. For most of these applications, it is useful to know not just whether two alleles are identical at a locus in the genome, but whether IBD extends an appreciable distance to either side of the locus. Such segmental IBD sharing indicates that the common ancestor is relatively recent and is the focus of this study. Two individuals share a haplotype segment identical by descent when the haplotype is inherited without recombination from a recent common ancestor. In data from unrelated individuals, we are never certain that a shared haplotype is inherited without recombination from a recent common ancestor, but we can use statistical techniques to infer that this scenario is most likely given the available genotype data. Existing IBD detection methods for population samples have been developed in the context of SNP array data; here we develop statistical methodology for detecting IBD segments in sequence data.

There are fundamental differences between SNP array and sequence data that affect IBD detection. The differences in variant density and minor allele frequency (MAF) spectrum affect power to detect segments of IBD. SNP array genotyping typically interrogates 300K–2.5M variants, which are mostly common variants (MAF ≥ 0.05); whole-genome sequencing interrogates tens of millions of variants, which are mostly rare (MAF ≤ 0.005).¹ Shared rare variants provide more evidence for IBD than do shared common variants. Common variants are often shared without the presence of an appreciable underlying IBD segment, whereas rare variants by their more recent origin are more likely to be inherited from a recent common ancestor.

A further difference in IBD detection between SNP array and sequence data is that sequence data may have more genotype errors and will have mutations that have occurred since the most recent common ancestor. IBD detection methods for sequence data need to be robust to allelic differences, whether due to mutation or due to genotype error.

Several existing IBD detection methods are fast enough for application to sequence data. Beagle’s Refined IBD² looks for long shared haplotypes and uses the Beagle haplotype frequency model to calculate a LOD (log base 10 of odds) score of IBD versus non-IBD for each candidate segment. Segments with LOD score exceeding a user-specified threshold are reported. Refined IBD does not allow for genotype errors, and its accuracy depends on the accuracy of the haplotype phase estimation that is performed within the software. Although Refined IBD properly accounts for linkage disequilibrium (LD), increased marker density increases the risk of genotype errors disrupting IBD segments, and low-frequency variants reduce the accuracy of haplotype phase estimation. Beagle’s fastIBD³ is also fast enough for application to sequence data, but because it has been superseded by Refined IBD we do not consider it here. GERMLINE⁴ searches for long shared segments with length exceeding a user-specified threshold, and it allows for mismatches resulting from genotype error. PLINK’s shared segment method⁵ is a hidden Markov model method for inferring IBD status from variants that are in linkage equilibrium. It does not allow for genotype errors.

Applications for IBD segments detected in sequence data are manifold, including estimation of population structure, estimation of demographic parameters, and distinguishing between recurrent mutations and shared ancestry of mutations.⁶ Here we illustrate the use of IBD segments in sequence data to estimate the genotype error rate. Specifically our SEQERR method estimates the rate of homozygous major allele to heterozygous genotype errors for variants with low MAF. We apply this method to sequence data from the UK10K and 1000 Genomes Projects.

Material and Methods

UK10K Data

We analyzed whole-genome sequence data for 2,432 individuals from the UK10K project. The sequenced individuals are from the Avon Longitudinal Study of Parents and Children (ALSPAC) study (n = 740) and the King’s College London Department of Twin Research and Genetic Epidemiology Twins Registry (TWINSUK; n = 1,692) cohorts and were accessed from the European Genome-Phenome Archive (data set IDs EGAD00001000195 and EGAD00001000194). The data were sequenced at a median depth of 7.6 reads per sample at single-nucleotide variant (SNV) sites. We applied filters to the data to remove variants that might be enriched for sequencing artifacts. Specifically, we excluded all variants that (1) were not diallelic SNVs, (2) had an exact Hardy-Weinberg equilibrium (HWE) test p value ≤ 10⁻⁵ in either cohort separately or in the merged cohorts, (3) had a mean number of raw or high-quality reads per sample that was ≤3 or ≥13, (4) had a mean certainty ≤0.995 reported by IMPUTE2,⁷ (5) were monomorphic or singleton variants, or (6) had a p value ≤ 10⁻⁵ when testing for intercohort allele frequency differences with Fisher’s exact test. After application of these filters there were 16.9 million variants remaining on the autosomes, which equates to approximately 6 variants per kilobase. We removed 70 close relatives (one individual from each pair of individuals with more than 100 cM of long IBD segments), leaving 2,362 individuals.

1000 Genomes Data

We analyzed whole-genome sequence data from European populations from the 1000 Genomes phase 1 version 3 data. The populations analyzed were Utah residents with Northern and Western European ancestry (CEU, n = 85); British in England and Scotland (GBR, n = 89); Toscani in Italy (TSI, n = 98); and Finnish in Finland (FIN, n = 93). We removed variants that were not diallelic SNVs.

Simulated Data

The world’s population size has experienced superexponential growth since the advent of agriculture. This superexponential growth is reflected in higher numbers of rare variants in sequence data than predicted under simple exponential growth models.⁸ We fit a demographic model to match the heterozygosity, magnitude of LD, and rate of IBD observed in data from the UK. The target heterozygosity rate and mean LD were obtained from UK10K sequence data. We assessed mean LD on chromosome 20 data for pairs of variants that were separated by at most 0.1 cM and that had allele frequencies in the same MAF bin (0.04–0.06, 0.08–0.12, 0.16–0.24, or 0.4–0.5). The target rate of IBD was obtained with Illumina SNP array data from the Wellcome Trust Case Control Consortium 2 controls, which consists of 5,000 individuals genotyped on 1 million SNPs, because these data have extremely low rates of genotyping error, which makes the results comparable to those in error-free simulated data. We thinned the simulated data so that the marker density and allele frequency spectrum were similar to the SNP array data, applied Refined IBD,² and selected demographic parameters so that the real and simulated data had similar rates of detected IBD segments of size 2–2.5 cM.

Our estimated demographic model has an initial population size of 24,000 in the distant past, with an out-of-Africa reduction to 3,000 occurring 5,000 generations ago. Three hundred generations ago, at the advent of agriculture in Europe, the population begins to grow 1.4% per generation. Sixty generations ago, the growth rate increases to 6%, and ten generations ago the growth rate increases to 25%. The most recent growth rates approximate those seen in England’s census population size.² We used a mutation rate of 1.38 × 10⁻⁸, which produces a heterozgosity rate matching that in the UK10K data.

When choosing parameters for the simulation model to match the real chromosome 20 data, we used the HapMap genetic map⁹ for chromosome 20 in order to match the distribution and intensity of recombination hotspots seen in real data. Once the final demographic model was determined, we simulated data with a constant recombination rate (1 cM per 1 Mb) and used these simulated data to compare IBD detection methods. Data were simulated with the program MACS v.0.4f,¹⁰ which is a coalescent-based simulator. The MACS command line is shown in Table S1 available online. We simulated 10 data sets each with 10 Mb and 2,000 individuals. MACS outputs ancestry trees as well as genotypes. We determined shared ancestry from the ancestry trees by using the DendroPy python library.¹¹ We define “true” IBD segments between a pair of individuals as those genomic segments for which the most recent common ancestor of the pair remains constant for at least 80 kb (0.08 cM). In order to reduce computing time in detecting these segments, we interrogated trees every 5 kb rather than determining common ancestry for all ancestry trees. Thus, endpoints of the detected IBD segments may be incorrect by up to 5 kb (0.005 cM), which makes only a trivial difference to the results.

We added genotype error at a rate of 0.005 for variants with sample MAF > 0.0025 and at a rate of twice the MAF for variants with sample MAF < 0.0025. In each case where a genotype error was added, a homozygous genotype was converted to a heterozygote or a heterozygous genotype was converted to a randomly chosen homozygote (i.e., either the major or minor allele homozygote, each with probability 0.5).

Variant Filtering

Before analyzing the data (real or simulated) by any of the methods, we first eliminated all variants with only one minor allele carrier in the sample. Single-copy variants are more likely than other variants to be genotype-calling artifacts or very recent mutations, and therefore they are not particularly helpful for IBD estimation.

Some methods such as IBDseq and PLINK require LD-based thinning of the variants so that no pair of variants is strongly correlated. To identify variants to exclude for these methods, we process the variants in order along the chromosome. For each variant we compute the squared-correlation for the per-sample minor allele count between the variant and each of the 250 previous variants. If the sample squared-correlation for a pair of variants exceeds a specified threshold (r² = 0.15 or r² = 0.3 in this study), and if neither variant in the pair has been previously marked as excluded, we mark the variant with the higher MAF as excluded.

The simulated data sets contained approximately 95K variants per 10 Mb in 2,000 individuals before filtering, with approximately 18K variants removed by the single-copy filter and approximately 49K further variants removed by the LD-based thinning, leaving approximately 28K variants.

IBD LOD Score

Our IBDseq method is based on summing single-marker IBD LOD scores. We define the IBD LOD score for a variant to be the base 10 logarithm of the IBD likelihood divided by the non-IBD likelihood. Positive scores provide evidence for IBD and negative scores provide evidence against IBD. We use the variant’s MAF to compute the likelihood of the IBD model in which the two individuals share one allele IBD, and of the non-IBD model in which the two individuals do not share any allele IBD. Approximate IBD and non-IBD likelihoods under a model with independent errors in alleles are summarized in Table 1, and derivations of these likelihoods are presented in Appendix A.

Table 1.

Approximate IBD and Non-IBD Likelihoods

GT 1	GT 2	IBD Likelihood	Non-IBD Likelihood
AA	AA	$e_0{p}_A^3+2e_1{p}_A^2{p}_B+e_2{p}_A{p}_B$	$f_A^4$
AA	AB	$e_0{p}_A^2{p}_B+\left(e_1+3e_2\right)p_A{p}_B+2e_1{p}_A^3$	$2f_A^3{f}_B$
AA	BB	$\left(e_1+e_2+e_3\right)p_A{p}_B+e_2\left(p_A^3+p_B^3\right)$	$f_A^2{f}_B^2$
AB	AA	$e_0{p}_A^2{p}_B+\left(e_1+3e_2\right)p_A{p}_B+2e_1{p}_A^3$	$2f_A^3{f}_B$
AB	AB	$\left(e_0+4e_1+2e_2\right)p_A{p}_B+4e_2{p}_A^3+4e_2{p}_B^3$	$4f_A^2{f}_B^2$
AB	BB	$e_0{p}_A{p}_B^2+2e_1{p}_B^3+\left(e_1+3e_2+e_3\right)p_A{p}_B+2e_3{p}_A^3$	$2f_A{f}_B^3$
BB	AA	$\left(e_1+e_2+e_3\right)p_A{p}_B+e_2\left(p_A^3+p_B^3\right)$	$f_A^2{f}_B^2$
BB	AB	$e_0{p}_A{p}_B^2+2e_1{p}_B^3+\left(e_1+3e_2+e_3\right)p_A{p}_B+2e_3{p}_A^3$	$2f_A{f}_B^3$
BB	BB	$e_0{p}_B^3+2e_1{p}_A{p}_B^2+e_2{p}_A{p}_B+2e_3{p}_A^2{p}_B+e_4{p}_A^3$	$f_B^4$

Probabilities for a pair of genotypes having either 1 or 0 alleles shared identical by descent. Allele errors are independent and have probability $\epsilon \ge 0$, and $e_j={\epsilon }^j{\left(1-\epsilon \right)}^{4-j}$ for $0\le j\le 4$. Genotypes have major allele A, minor allele B, true allele frequencies p_A and p_B, and error-added allele frequencies f_A and f_B. We estimate f_A and f_B with the observed allele frequencies, and we estimate p_B and p_A = 1 − p_B using the relationship $p_B=\left(f_B-\epsilon \right)/\left(1-2\epsilon \right)$.

If any allele is missing, we define the pair’s IBD LOD score at the locus to be 0. We handle multiallelic variants by taking the allele with the second largest allele count as minor allele, considering all other alleles to be the major allele.

The scores in Table 1 are used at nonexcluded variants (see Variant Filtering above). However, excluded variants also contain information about IBD. To be conservative, we cannot use evidence for IBD from the excluded variants, because we have already partially incorporated the information through correlated nonexcluded variants. We can, however, use information against IBD from the excluded variants, which adds important information without increasing the false-positive IBD detection rate. In particular, discordant homozygotes provide significant evidence against IBD. Thus, the IBD LOD score at excluded variants is 0 unless the genotypes are discordant, in which case the IBD LOD score is determined by the ratio of likelihoods in Table 1.

For each pair of samples, we find and report all chromosome intervals for which the sum of the IBD LOD scores for variants in the interval is greater than a specified value and for which the sum cannot be increased by expanding the interval. We identify these maximal intervals by using a scanning algorithm that is linear in the number of markers.¹² Because we are working on the log scale, summing IBD LOD scores corresponds to multiplying likelihood ratios.

The IBDseq program also detects segments of homozygosity by descent (HBD). Detection of HBD segments is analogous to detection of IBD segments and the details are derived in Appendix A.

Analysis Allele Error Rate

In IBDseq we use an error model in which allele errors are independent and the probability ε of incorrectly calling an allele depends on the minor allele frequency. For an allele with observed minor allele frequency f_B, the allele error rate is ε = min{σ,ρf_B} where 0 ≤ σ < 1 and 0 ≤ ρ < 1. Thus the allelic error rate is σ for higher frequency variants and is proportional to the observed minor allele frequency for lower frequency variants. In this study we set ρ = 0.25 and use σ values of 0.001, 0.0025, and 0.005. We will call σ the analysis allele error rate parameter.

Comparison of IBD Detection Methods

We ran the following IBD detection methods on the simulated data: IBDseq, Refined IBD implemented in Beagle v.4 (r1106),² GERMLINE v.1.5.1,⁴ and PLINK v.1.07.⁵ The command lines that we used for these programs are shown in Table S1. We investigated a variety of parameter settings for these programs to determine which work best with sequence data. For IBDseq we used a LOD threshold of 3 and an r² threshold of 0.15 throughout, but we investigated different values of the analysis allele error rate parameter.

Because Refined IBD does not allow for genotype errors and requires highly accurate phasing, we tried several data-filtering strategies to improve its performance. Filtering out low-frequency markers improves the haplotype phase accuracy and removes some potential genotype errors. Filtering out variants in high LD (via an r² filter) removes some potential genotype errors while not losing much information, because highly correlated variants provide redundant information. We found that filtering out variants with MAF < 0.01 and thinning variants with an r² threshold of 0.8 gave good results (Figure S1). We used a LOD threshold of 2.0 and a minimum IBD length of 0.2 cM, which are less stringent than the default LOD and length thresholds.

The best setting that we found for GERMLINE had the “bits” parameter set to 128, the “h_extend” option turned on, and the “nhom” parameter set to 2 (Figures S2 and S3). Results without the h_extend option had much lower accuracy. Nonzero values of the nhom parameter allow for genotypic errors. Although GERMLINE with h_extend, nhom = 2, and MAF > 0.01 appears to have good accuracy for segments of size 0.2 cM or more (Figure S2), the accuracy for segments of size 0.2–0.8 cM is significantly less than for other methods, and because there are extremely large numbers of small segments, they tend to dominate the overall error rate. Thus, in order to make GERMLINE’s results comparable to those of the other methods, we use a length threshold (“min_m”) of 0.8 cM.

PLINK requires variants in linkage equilibrium. We therefore thinned the data with an r² threshold of 0.3. In Figure S4, we also show results for a more stringent r² threshold of 0.15. PLINK uses genome-wide estimates of relatedness as priors. Here the relatedness estimates are based on the 10 Mb segment, and we used the “all-pairs” option to make sure that all pairs had at least a small prior probability of IBD. Using relatedness estimates based on the 10 Mb segment rather than the whole genome will tend to give a high prior probability of IBD to those pairs of individuals with large IBD segments. Because these large segments are relatively easy to accurately identify, this should not overly influence the results. We used a minimum segment length of 50 kb and a minimum number of SNVs per segment of 50. We left other parameters at default values.

For each reported IBD segment in the simulated data, we determine a best-matching true IBD segment. The best-matching true IBD segment is the segment that minimizes the sum of the amount of the reported IBD segment that is not in the true IBD segment and the amount of the true IBD segment that is not in the reported IBD segment. If no true IBD segment overlaps a reported IBD segment, then the best-matching true IBD segment is undefined.

Genotype Error Rate Estimation

We use the detected IBD segments to estimate the homozygous to heterozygote genotype error rate at low-frequency variants. Consider a low-frequency variant with major allele A and minor allele B. Let p_B be the true (without genotype error) frequency of allele B, and let f_B be the error-added frequency. If f_B is small and major homozygotes are incorrectly called as heterozygotes at a rate γ, the true and error-added frequencies satisfy f_B ≈ p_B + γ/2, because almost all genotypes are homozygous for the major allele and each genotype error typically changes one of the two alleles in a genotype.

In a pair of IBD individuals, there are three independent alleles: the shared IBD allele and one other allele per individual. The pair can have one major homozygote and one heterozygote genotype (the AA/AB configuration) only if one of the nonshared alleles takes the minor allele. Without genotype error and assuming approximate HWE, the frequency of the AA/AB configuration in a pair of IBD individuals is approximately 2p_B = 2f_B. However, with error, assuming error is applied independently to each individual, the frequency of the AA/AB configuration in a pair of IBD individuals is approximately 2p_B + 2γ = 2(p_B + γ/2) + γ ≈ 2f_B + γ. Thus, without error we expect the AA/AB configuration at a rate of 2f_B, but with error we expect to see the AA/AB configuration at the higher rate of 2f_B + γ. This difference allows us to estimate the genotype error rate γ.

Note that this approach does not work without IBD, because when no alleles are IBD the number of independent alleles is the same as the number of alleles that are subject to genotype error. In the non-IBD case, the frequency of the AA/AB configuration without genotype error is approximately 4p_B ≈ 4f_B. With error, the frequency of the AA/AB configuration is approximately 4p_B + 2γ = 4(p_B + γ/2) ≈ 4f_B. Thus in the non-IBD case, the approximations for the frequency of the AA/AB configuration are the same with and without genotype error.

In Appendix B we present a more rigorous version of this argument that does not assume HWE, and we derive an estimate for the genotype error rate as a function of observed genotype and allele frequencies in IBD segments (Equation B2).

It is essential that the IBD used in estimating genotype error rates has extremely high accuracy. Because endpoints of IBD segments are difficult to determine accurately, we trim 0.5 cM from each end of each reported IBD segment before using it in the estimation. We also use only relatively long IBD segments (>2 cM) because these tend to have higher accuracy than shorter segments (see Results).

Results

IBD Detection

In simulated data, we know the true IBD status of pairs of individuals based on their shared ancestry, so we can compare this with the estimated IBD status to determine power and accuracy of the IBD detection methods. With the demographic model used in the simulation and the definition of true IBD used here (segments with a single common ancestor spanning at least 80 kb), on average approximately 15% of the genome is IBD for a random pair of haplotypes and 50% of the genome is covered by an IBD segment for a random pair of diploid individuals. The requirement of single common ancestor then becomes crucial when assessing estimated IBD. A long segment of apparent sharing may result from a mosaic of several segments from different shared ancestors, with short gaps separating some of these segments.

Figure 1 shows the results of analyses of simulated data with IBDseq for different values of the analysis allele error rate. Figures S2–S4 give analogous results for other methods when using a range of parameter settings. Figure 2 shows results for all the methods (using a single best parameter setting for each, as described in Material and Methods).

Figure 1.

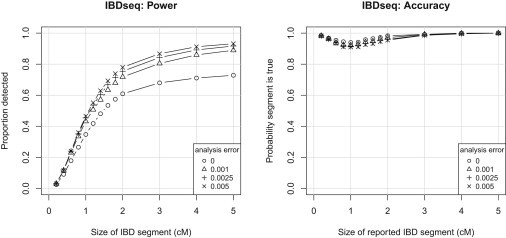
IBD Detection Power and Accuracy with IBDseq

Power (proportion detected) is the average proportion of a true IBD segment of given length that overlaps with reported IBD segments. Accuracy (probability a segment is true) is the proportion of reported segments of given length for which there is a true segment that overlaps at least half of the reported segment. Results are binned by segment size: bins extend 0.05 cM on either side of the x axis value for x axis values ≤1 cM; 0.1 cM either side for x axis values ≤2 cM; and 0.5 cM either side for x axis values >2 cM.

Figure 2.

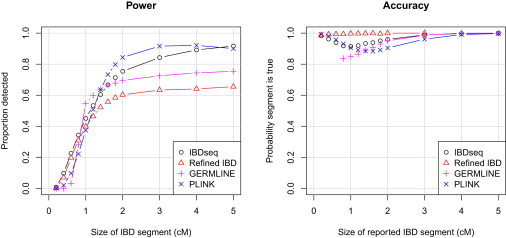
Power and Accuracy with IBDseq, Refined IBD, GERMLINE, and PLINK

See Figure 1 legend for definitions of axis labels.

One noticeable feature for all the methods except Refined IBD is that accuracy is lower for reported segments of length 1–2 cM than it is for shorter segments, which seems counterintuitive. A reported long IBD segment comprised of two neighboring short true IBD segments counts as a reporting error if neither true IBD segment overlaps more than half of the reported IBD segment. Most of the methods appear to have a tendency to make this kind of error. Very short reported segments may be less subject to this error because indicators of possible segment merging such as a homozygous discordant genotype (in a short gap between two very short segments) outweigh the small amount of evidence for IBD so that no segment is reported.

For IBDseq, power is reduced if an analysis allele error rate of 0 is used. This is unsurprising because the simulated data has allelic error added at a rate of 0.0025 for variants with MAF > 0.0025 and at a rate equal to the MAF for variants with MAF < 0.0025. Increasing the analysis allele error rate too high (e.g., to 0.005) reduces accuracy slightly. Analysis allele error rates of 0.001, 0.0025, and 0.005 give good results, indicating that IBDseq is not highly sensitive to the choice of analysis allele error rate, as long as it is greater than zero. For comparisons with other methods, we use an analysis allele error rate of 0.0025.

Because of the high rate of genotype error in the simulated data, Refined IBD has difficulty finding large parts of the largest IBD segments. Accuracy for Refined IBD is extremely high even though a relatively low LOD threshold of 2 is being used. PLINK has good accuracy and power. GERMLINE has acceptable accuracy but lower power to detect long segments than IBDseq or PLINK.

In Figure 3, we compare overall power and accuracy in a single plot. Better results are those toward the upper left for which the y value (rate of detected IBD) is high and the x value (rate of false positive IBD) is low. Thus, on these metrics, Refined IBD is giving better performance than PLINK, which in turn is giving better performance than GERMLINE. IBDseq is also giving better performance than GERMLINE. A comparison between Refined IBD and IBDseq or between PLINK and IBDseq depends on the tradeoff between accuracy and power. It is worth remembering, however, that Refined IBD, although highly accurate, has lower power than other methods for long IBD segments on these data (Figure 2), which is undesirable.

Figure 3.

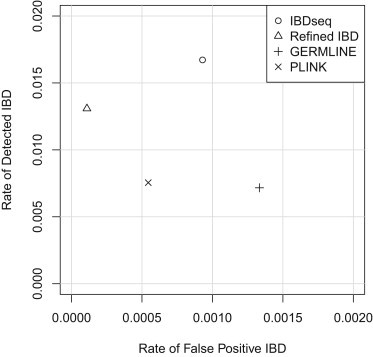
Comparing IBD Detection across Methods

The value on the y axis (rate of detected IBD) is determined by finding for each reported IBD segment the length of the overlap between the reported IBD segment and the best-matching (defined in Material and Methods) true IBD segment. If no true IBD segment overlaps the reported IBD segment, the amount of overlap is zero. Detection rate is the sum of all such overlap lengths divided by the number of pairs of individuals analyzed and by the total length of the regions analyzed. The value on the x axis (rate of false-positive IBD) is the sum of the lengths of false reported IBD segments divided by the number of pairs of individuals analyzed and by the total length of the regions analyzed. A reported segment is considered to be false if there is no true IBD segment that overlaps at least half of the reported segment.

A further consideration is how closely the reported IBD segment length matches the true underlying IBD segment length. This is important, for example, when inferring demographic parameters.¹³ In Figure 4 we compare estimated and actual IBD lengths for the methods. For each estimated segment, the estimated segment length is compared to the length of the best matching true IBD segment, with best match defined in Material and Methods. If there is no true IBD segment overlapping the estimated IBD segment, the true IBD length is 0. For short estimated segments (length < 1 cM), Refined IBD is the most accurate method, followed by IBDseq and PLINK, then GERMLINE. For these short estimated segments, GERMLINE’s lengths are biased by the hard minimum threshold of 0.8 cM on IBD segment length (GERMLINE’s -min_m parameter) because a true IBD segment with length near 0.8 cM is more likely to be detected by GERMLINE if its length is overestimated than if its length is underestimated. For larger estimated segments (>2 cM), PLINK and IBDseq are the most accurate, followed by GERMLINE. As previously noted, Refined IBD does not do well at estimating longer segment lengths in these data because it misses significant portions of larger segments as a result of the relatively high rate of genotype error in these simulated data. Refined IBD relies on estimated haplotype phase to detect IBD segments, and haplotype phase estimation errors increase as genotype errors increase.

Figure 4.

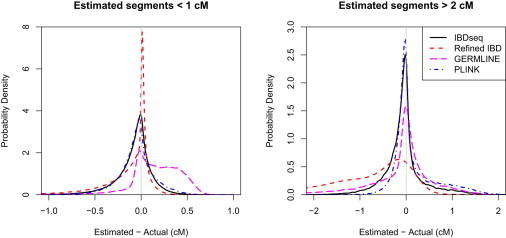
Over- and Underestimation of IBD Segment Lengths

Differences between estimated and actual segment lengths were calculated for all reported IBD segments, and probability densities of these differences were estimated with a Gaussian kernel.

We applied IBDseq to detect IBD in the autosomal UK10K data. We thinned variants with an r² threshold of 0.15, leaving 6.8 million SNVs on the autosomes. We used an analysis allele error rate of 0.001 and a LOD score threshold of 3. With IBDseq we found 390 million IBD segments totaling 224 million cM with a median length of 0.46 cM. 99% of the detected segments have lengths between 0.028 cM and 2.6 cM. The average amount of detected IBD per pair of individuals was 75.8 cM spread across 132 segments.

Genotype Error Rate Estimation

To assess the accuracy of our genotype error rate estimation method, SEQERR, we first applied it to simulated data in which the genotype error rate is known. In the simulated data, we had added error at a genotype error rate of min(2p, 0.005), where p is the observed frequency of the minor allele before adding error. Adding error changes the allele frequencies, and the error-added MAF is approximately p + min(2p, 0.005)/2 = p + min(p, 0.0025). The solid line in Figure 5 plots the genotype error rate against the sample error-added MAF. We then used SEQERR to estimate the genotype error rate in the simulated data. To do so, we used IBD segments detected with IBDseq with an analysis allele error rate of 0.0025. Only segments of size 2 cM or larger were considered. The resulting estimates are shown as points in Figure 5. The correspondence between the estimated and actual genotype error rate is very good.

Figure 5.

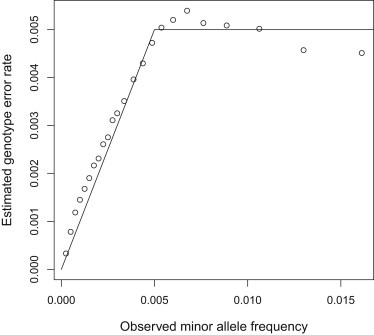
Genotype Error Estimation in Simulated Data

Estimated genotype error rates obtained from SEQERR are points; the solid line is the actual genotype error rate plotted against the observed error-added MAF. For the lowest MAFs each point is for a single minor allele count value; for higher MAFs several minor allele counts are combined to reduce noise.

We also tried other values of analysis allele error rate and minimum segment size with the simulated data. There was very little difference in the results when using a minimum segment size of 4 cM or an analysis allele error rate of 0.005.

Next, we applied our genotype error estimation to UK10K sequence data. Figure 6 shows the estimated genotype error rates for the UK10K sequence data. Error rates can also be estimated by using duplicate samples, if these are available. In the UK10K we identified 18 pairs of apparent duplicates that may be monozygotic twins. Duplicate samples and close relatives were not included in the SEQERR analysis. The number of discordant genotypes over the autosomes for each duplicate pair ranged from 8,000 to 28,000. Because genotype errors in either of the duplicate samples can cause discordance, the genotype error rate can be estimated by half the discordance rate. These values are also shown in Figure 6. The two estimates (duplicate-based and IBD-based) are very similar. In many data sets, duplicates are not available or are available only in small numbers of individuals who may not be representative of the remainder of the data set. Thus, an IBD-based method of error rate estimation provides a widely useful approach to estimating data quality.

Figure 6.

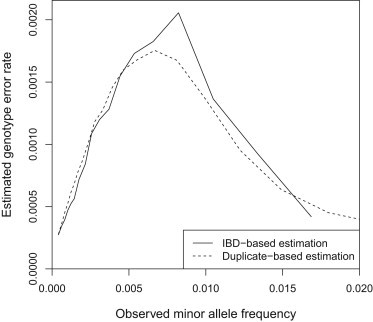
Genotype Error Rate Estimation in the UK10K Sequence Data

The solid line shows the genotype error rate estimated by SEQERR and the dashed line shows half the average genotype discordance in 18 pairs of duplicate samples.

The estimated genotype error rate reaches a maximum value of 0.2% at an observed minor allele frequency of 0.5%–1%. However, even at a very low genotype error rate, in a very low-frequency variant, a large fraction of the reported minor alleles may be errors. We can estimate the proportion of called minor alleles that are in error as half the estimated genotype error rate divided by the observed allele frequency. Figure 7 shows these ratios in the UK10K data. Although the absolute error rate is low, for variants with only two observed copies, we estimate that approximately 1/3 of the observed variants are erroneous. In these data one needs to observe at least 20 copies of the minor allele (0.4% MAF) before the estimated false reporting ratio drops below 20%, and at least 40 copies (1% MAF) before the ratio drops below 10%.

Figure 7.

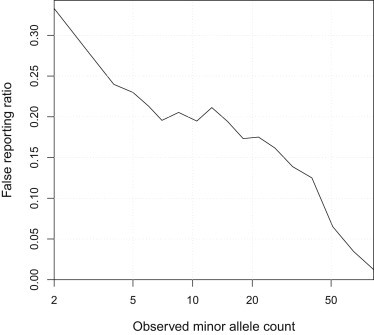
Estimated False Call Rate for Called Heterozygote Genotypes at Low-Frequency Variants in the UK10K Data

The x axis is the observed minor allele count, shown on a log scale. The y axis is the estimated genotype error rate divided by twice the observed MAF.

We note that the subset of the UK10K data analyzed in this study is from an interim release with 2,432 sequenced individuals. The complete UK10K data set will have approximately 4,000 sequenced individuals. The complete UK10K data is expected to have a lower genotype error rate than the interim data because of its larger sample size and methodological advances.

In Figure S5 we show results from analysis of groups of European populations from the 1000 Genomes phase 1 data.¹ The estimated error rates do not vary significantly as a function of MAF in these analyses. One reason for this lack of relationship may be that the MAF in the groups of populations is only moderately correlated with the minor allele count in the full 1000 Genomes data. Because the full data set was genotype-called as a unit, the full-data minor allele count is likely to be the greater driver of genotype error rate.

A requirement of SEQERR is that the samples derive from a homogeneous population, so that the allele frequencies in the whole population are appropriate for each pair of IBD individuals. The results from the 1000 Genomes European analysis give some guidance on how closely matched the populations need to be. Adding southern Europeans (TSI) to the north-western Europeans did not change the results, whereas adding the Finns (FIN) caused some inflation of the error estimates. The Finns are more divergent from the north-western Europeans (CEU and GBR) than are the southern Europeans (TSI), as shown by allele sharing and principal component analysis.¹

Computing Times

All computing times reported here are for a 2.4 GHz computer. Because IBDseq allows for parallel computing with a specified number of threads, we report times for both single- and multithreaded computation.

A single replicate of the simulated data had 2,000 individuals (1,999,000 pairs) on a 10 Mb region with 28K variants after LD-based thinning for IBDseq. Computing time for estimating IBD with IBDseq was 75 min when using 12 threads and 15 hr when using 1 thread. Computing time was 55 hr with PLINK with an r² threshold of 0.3 (56K variants analyzed). Reducing the r² threshold to 0.15 (28K variants analyzed) reduced PLINK’s computing time to 48 hr. Computing time with Refined IBD was 15 hr with only singletons removed (77K variants analyzed). With a MAF filter of 0.01, the computing time is 12 hr with or without thinning with an r² threshold of 0.8 (7K or 24K variants analyzed). In this case, a potential reduction in computing time resulting from fewer variants after thinning is balanced by the need to evaluate a larger number of candidate segments in the thinned data. Computing times for Refined IBD can be reduced by increasing the minimum IBD length parameter. Computing time with a 0.4 cM minimum IBD length was 3 hr on the thinned (7K variant) data.

Computing times for GERMLINE after phasing were only several minutes per simulated 10 Mb region. Phasing time with Beagle v.4 was 5 hr with a MAF filter of 0.01 and 12 hr with only singletons removed.

Computing time for chromosome 1 of the UK10K data was 29 hr for IBDseq with 12 computing threads. The IBDseq analysis for this chromosome included 539K variants. Computing time for chromosome 1 of the 1000 Genomes data with the CEU, GBR, TSI, and FIN populations was 52 min for IBDseq with 6 computing threads. The IBDseq analysis for this chromosome included 175K variants.

Application of SEQERR to detected IBD is fast. Error analysis of simulated data with 2,000 individuals on a 10 Mb region took 1 min. Error analysis of chromosome 1 took 42 min for the UK10K data and 2 min for the 1000 Genomes European data.

Software

The IBDseq method is implemented in the open-source IBDseq software package. The genotype error-rate estimation method is implemented in the open-source SEQERR software package. Both packages are written in Java.

Discussion

We have presented a method, IBDseq, for detecting IBD segments in sequence data, and we have evaluated IBDseq and several existing IBD detection methods via simulated sequence data. Refined IBD and IBDseq employ very different approaches to detecting IBD and have different strengths and weaknesses. Refined IBD models LD, but not genotype error, whereas IBDseq models genotype error, but not LD. Refined IBD uses estimated haplotypes, whereas IBDseq uses unphased genotypes. In our simulations, we found that IBDseq does not provide as strong control over false-positive IBD detection as does Refined IBD; however, Refined IBD has difficulty fully detecting long IBD segments (>3 cM) in sequence data because of the difficulty in correctly phasing low-frequency variants and handling genotypes with error. In contrast, IBDseq is designed to be robust to genotype error and immune to phasing error.

PLINK and GERMLINE (with the h_extend option) are also good options with appropriate thinning of variants. GERMLINE is by far the fastest method, particularly if the data are already phased, but all the methods considered here are fast enough to apply to large whole-genome sequence data such as the UK10K data with the use of a modest-sized computing cluster.

Almost all previous evaluations of IBD detection methods have used SNP array data with few low-frequency variants and low rates of genotype error. In this study, we have evaluated IBD segment detection methods by using simulated and real low-coverage sequence data with many low-frequency variants and relatively high rates of genotype error. Our comparison of IBD detection methods on sequence data expands on an earlier evaluation of fastIBD and GERMLINE on sequence data¹⁴ by evaluating additional methods, investigating multiple parameter setting for each method, and using simulated sequence data for which true IBD status is known.

We have also presented the SEQERR method, which uses IBD to estimate genotype error rates in low-frequency variants in sequence data. Allele error rates generally depend on allele frequency. Stratifying estimated allele error rates by the observed allele frequency enables one to determine how much credence to give to called low-frequency alleles. We have applied the method to estimate genotype error rates in UK10K data. This approach has advantages over other methods for estimating genotype error rates for low-frequency variants in sequence data. A common approach to estimating genotype error rates in sequence data is to compare the sequence genotypes to genotypes obtained with a SNP array, providing that the SNP array genotypes are known to have very low error rates. This can work well for higher-frequency variants, but SNP arrays tend to have relatively high error rates at low-frequency variants. Sequenced duplicate samples can also be used to estimate error rates; however, the duplicates may not be representative of the whole data set, sequencing duplicate samples is costly, and genotype errors in the duplicate samples may be correlated, which will bias error rate estimates.

Our error estimation method assumes absence of significant population structure, because the estimated genotype and allele frequencies must be applicable to each pair of IBD individuals. The method clearly works well in relatively homogeneous populations such as the UK and appears to be robust to samples with combined north-western and southern Europeans, but should not be applied to populations with significant heterogeneity. Additionally, our method may slightly underestimate actual genotype error rates. IBD detection rates will be somewhat lower in the neighborhood of variants with high error rates, so these variants will be underrepresented in the overall estimate. Also, genotype calling that uses LD is more accurate in the presence of long IBD segments, so the genotypes in the IBD individuals may be more accurate than average. However, this latter effect is not likely to be very large, because the non-IBD alleles drive the estimate, and the calling of these alleles is not likely to be greatly improved by the presence of IBD on the other haplotype.

The IBDseq method also assumes that the samples derive from a homogeneous population, because it also assumes that allele frequencies calculated from the full sample are applicable to any pair of individuals in the sample. In a structured population setting, we expect that IBDseq may give spurious short IBD segments within subpopulations. This problem can be reduced by setting a relatively large threshold on segment size, such as retaining only segments of size 1 cM or greater.

The IBDseq method for IBD detection and the SEQERR method for IBD-based genotype error rate estimation are both open source and freely available. IBDseq has multithreading capability to facilitate analysis of long chromosomes on multicore computers.

This study does not address the problem of IBD detection in whole-exome sequence data. Exome data present additional challenges because of the small portion of the genome sequenced and the gaps between sequenced regions.¹⁵ Further methods development, such as modeling of intermarker distances, may be required to obtain satisfactory IBD detection in exome data.

We anticipate that users will find a diversity of applications for IBD detection in sequence data. Such applications may include genotype error estimation, demographic inference, and reduction of the genomic search space for identifying likely causal variants in families segregating a Mendelian disease.

Appendix A: Likelihood Estimation with Allele Error

In this section we derive estimates for the likelihood of observed genotypes under Hardy-Weinberg equilibrium when each allele is observed incorrectly with probability ε ≥ 0 and errors are independent. We assume that markers are diallelic, with major allele A and minor allele B.

Relationship between True and Error-Added Minor Allele Frequencies

Let f_B be the frequency of the minor allele after adding genotype error, and let p_B be the true MAF. Because

$$f_B=\left(1-\epsilon \right)p_B+\epsilon \left(1-p_B\right)=p_B\left(1-2\epsilon \right)+\epsilon ,$$

we have

$$p_B=\frac{\left(f_B-\epsilon \right)}{\left(1-2\epsilon \right)}.$$

IBD Model

In the case where two genotypes share an allele identical by descent, we can calculate likelihoods based on the true allele frequencies p_A and p_B and the allele error rate ε ≥ 0.

In the following calculations, individuals are ordered and genotypes are unordered. We use the notation $P_O\left(·|I\right)$ to denote the probability of a pair of observed (error-added) genotypes when one allele is shared IBD between the two genotypes and the notation $P\left(·|I\right)$ to denote the corresponding probability for the true (without error) genotypes.

In the following likelihood approximations, we make use of the fact that ε is small to eliminate negligible terms, and we define

$$e_j={\epsilon }^j{\left(1-\epsilon \right)}^{4-j}$$

for 0 ≤ j ≤ 4.

$$\begin{array}{l}{P}_O\left(AA,AA|I\right)\approx e_{0}P\left(AA,AA|I\right)+e_{1}P\left(AA,AB|I\right)+e_{1}P\left(AB,AA|I\right)+e_{2}P\left(AB,AB|I\right)\\ \approx e_0{p}_A^3+e_1\left(p_A^2{p}_B+p_A^2{p}_B\right)+e_2\left(p_A^2{p}_B+p_A{p}_B^2\right)\\ =e_0{p}_A^3+2e_1{p}_A^2{p}_B+e_2{p}_A{p}_B\end{array}$$

$$\begin{array}{c}{P}_O\left(AA,AB|I\right)\approx \left(e_0+e_2\right)P\left(AA,AB|I\right)+e_{1}P\left(AB,AB|I\right)+2e_{1}P\left(AA,AA|I\right)+2e_{2}P\left(AB,AA|I\right)+2e_{2}P\left(AB,BB|I\right)+e_{2}P\left(BB,AB|I\right)\\ \approx \left(e_0+e_2\right)p_A^2{p}_B+e_1(p_A^2{p}_B+p_A{p}_B^2)+2e_1{p}_A^3+2e_2{p}_A^2{p}_B+2e_2{p}_A{p}_B^2+e_2{p}_A{p}_B^2\\ =e_0{p}_A^2{p}_B+e_1{p}_A{p}_B+2e_1{p}_A^3+3e_2\left(p_A^2{p}_B+p_A{p}_B^2\right)\\ =e_0{p}_A^2{p}_B+e_1{p}_A{p}_B+2e_1{p}_A^3+3e_2{p}_A{p}_B\\ =e_0{p}_A^2{p}_B+\left(e_1+3e_2\right)p_A{p}_B+2e_1{p}_A^3\end{array}$$

$$\begin{array}{l}{P}_O\left(AA,BB|I\right)=e_{1}P\left(AA,AB|I\right)+e_{1}P\left(AB,BB|I\right)+e_{2}P\left(AA,AA|I\right)+e_{2}P\left(BB,BB|I\right)+e_{2}P\left(AB,AB|I\right)+e_{3}P\left(AB,AA|I\right)+e_{3}P\left(BB,AB|I\right)\\ =e_1\left(p_A^2{p}_B+p_A{p}_B^2\right)+e_2{p}_A^3+e_2{p}_B^3+e_2\left(p_A^2{p}_B+p_A{p}_B^2\right)+e_3\left(p_A^2{p}_B+p_A{p}_B^2\right)\\ =\left(e_1+e_2+e_3\right)p_A{p}_B+e_2\left(p_A^3+p_B^3\right)\end{array}$$

$$\begin{array}{l}{P}_0\left(AB,AB|I\right)\approx \left(e_0+2e_2\right)P\left(AB,AB|I\right)+2e_{1}P\left(AA,AB|I\right)+2e_{1}P\left(AB,AA|I\right)+2e_{1}P\left(AB,BB|I\right)+2e_{1}P\left(BB,AB|I\right)+4e_{2}P\left(AA,AA|I\right)+4e_{2}P\left(BB,BB|I\right)\\ \approx \left(e_0+2e_2\right)\left(p_A^2{p}_B+p_A{p}_B^2\right)+2e_1{p}_A^2{p}_B+2e_1{p}_A^2{p}_B+2e_1{p}_A{p}_B^2+2e_1{p}_A{p}_B^2+4e_2{p}_A^3+4e_2{p}_B^3\\ =\left(e_0+2e_2\right)p_A{p}_B+4e_1\left(p_A^2{p}_B+p_A{p}_B^2\right)+4e_2{p}_A^3+4e_2{p}_B^3\\ =\left(e_0+4e_1+2e_2\right)p_A{p}_B+4e_2{p}_A^3+4e_2{p}_B^3\end{array}$$

$$\begin{array}{l}{P}_O\left(AB,BB|I\right)\approx \left(e_0+e_2\right)P\left(AB,BB|I\right)+2e_{1}P\left(BB,BB|I\right)+\left(e_1+e_3\right)P\left(AB,AB|I\right)+2e_{2}P\left(AA,AB|I\right)+2e_{2}P\left(BB,AB\text{|}I\right)+e_{2}P\left(AB,AA|I\right)+2e_{3}P\left(AA,AA|I\right)\\ \approx \left(e_0+e_2\right)p_A{p}_B^2+2e_1{p}_B^3+\left(e_1+e_3\right)\left(p_A^2{p}_B+p_A{p}_B^2\right)+2e_2{p}_A^2{p}_B+2e_2{p}_A{p}_B^2+e_2{p}_A^2{p}_B+2e_3{p}_A^3\\ =e_0{p}_A{p}_B^2+2e_1{p}_B^3+\left(e_1+e_3\right)p_A{p}_B+3e_2\left(p_A^2{p}_B+p_A{p}_B^2\right)+2e_3{p}_A^3\\ =e_0{p}_{\mathrm{A}}{p}_B^2+2e_1{p}_B^3+\left(e_1+3e_2+e_3\right)p_A{p}_B+2e_3{p}_A^3\end{array}$$

$$\begin{array}{l}{P}_O\left(BB,BB|I\right)=e_{0}P\left(BB,BB|I\right)+e_{1}P\left(AB,BB|I\right)+e_{1}P\left(BB,BA|I\right)+e_{2}P\left(AB,AB|I\right)+e_{3}P\left(AA,AB|I\right)+e_{3}P\left(AB,AA|I\right)+e_{4}P\left(AA,AA|I\right)\\ =e_0{p}_B^3+e_1{p}_A{p}_B^2+e_1{p}_A{p}_B^2+e_2\left(p_A^2{p}_B+p_A{p}_B^2\right)+e_3{p}_A^2{p}_B+e_3{p}_A^2{p}_B+e_4{p}_A^3\\ =e_0{p}_B^3+2e_1{p}_A{p}_B^2+e_2{p}_A{p}_B+2e_3{p}_A^2{p}_B+e_4{p}_A^3\end{array}$$

The remaining three genotype combinations have likelihoods equal to likelihoods that are approximated above.

$$P_O\left(BB,AB\text{|}I\right)=P_O\left(AB,BB\text{|}I\right)$$

$$P_O\left(AB,AA\text{|}I\right)=P_O\left(AA,AB\text{|}I\right)$$

$$P_O\left(BB,AA\text{|}I\right)=P_O\left(AA,BB\text{|}I\right)$$

Non-IBD Model

Because allele errors are independent and we assume Hardy-Weinberg equilibrium, the observed genotype frequencies can be estimated from the observed allele frequencies. In particular, if f_A and f_B are the error-added major and minor allele frequencies, then probabilities of observed genotypes AA, AB, and BB are

$$P_O\left(AA\right)\approx f_A^2$$

$$P_O\left(AB\right)\approx 2f_A{f}_B$$

$$P_O\left(BB\right)\approx f_B^2.$$

The likelihood for a model in which no alleles are identical by descent is the product of the probabilities of each genotype.

HBD Model

The approach used above can also generate probabilities for observed genotypes when the two alleles in a genotype are homozygous by descent (HBD). In the case where a genotype is homozygous by descent, denoted by H, we can calculate likelihoods based on the true allele frequencies p_A and p_B and the allele error rate ε.

$$P_O\left(AA\text{|}H\right)=P\left(AA\text{|}H\right)+{\epsilon }^{2}P\left(BB\text{|}H\right)=p_A+{\epsilon }^2{p}_B$$

$$\begin{array}{l}{P}_O\left(AB\text{|}H\right)=2\epsilon \left(1-\epsilon \right)P\left(AA\text{|}H\right)+2\epsilon \left(1-\epsilon \right)P\left(BB\text{|}H\right)\\ =2\epsilon \left(1-\epsilon \right)p_A+2\epsilon \left(1-\epsilon \right)p_B\\ =2\epsilon \left(1-\epsilon \right)\left(p_A+p_B\right)\\ =2\epsilon \left(1-\epsilon \right)\end{array}$$

$$P_O\left(BB\text{|}H\right)={\epsilon }^{2}P\left(AA\text{|}H\right)+P\left(BB\text{|}H\right)={\epsilon }^2{p}_A+p_B$$

Genotype likelihoods under the non-HBD model are identical to the genotype likelihoods under the non-IBD model presented above.

Scores based on the likelihoods above are used at nonexcluded variants. As for the IBD LOD score, excluded variants do not contribute to the HBD LOD score unless the genotypes is heterozygous, in which case the variant is scored in the same way as a nonexcluded variant.

Appendix B: Genotype Error Rate Estimation

For low-frequency variants, the majority of the true genotypes are major allele homozygotes that, if miscalled, will usually be reported as heterozygotes rather than as minor allele homozygotes. Thus, most genotype errors at low-frequency variants are expected to change major allele homozygote to heterozygote. By using detected IBD segments, we can estimate the rate of these errors for low-frequency variants. We do this by comparing in IBD regions the actual count of variants at which one of the individuals is homozygous for the major allele and the other is heterozygous to the expected counts for these genotype pairings.

Consider variants with major allele A having frequency p_A and minor allele B with frequency p_B. Let γ be the rate at which true AA genotypes are reported as AB. We assume that γ is close to zero and that p_A is close to one. The error-added major allele frequency, f_A, is typically smaller than p_A, because some AA genotypes are reported as AB, whereas there are very few true AB genotypes so the proportion of those that are reported as AA is miniscule (and the number of BB genotypes reported as AB or AA is even lower). Let p_AA denote the true frequency of the AA genotype and f_AA the error-added frequency of the AA genotype, and similarly define p_AB and f_AB for the AB genotype.

First, we derive expressions for the true genotype frequencies p_AA, p_AB as a function of the error-added frequencies f_AA, f_AB. In the derivation, we assume the probability of two errors in a genotype is sufficiently small to be negligible, and we ignore error probabilities when the true genotype is heterozygous or homozygous for the minor allele because these genotype frequencies are small when p_A ∼ 1. The relationships between the true and error-added genotype frequencies are as follows:

$$f_{AA}\approx p_{AA}\left(1-\gamma \right)$$

$$f_{AB}\approx p_{AB}+p_{AA}\gamma$$

From these relationships, we obtain approximations for the true frequencies p_AA, p_AB, and p_A in terms of the error-added frequencies f_AA, f_AB, and f_A:

$$\begin{array}{c}{p}_{AA}\approx \frac{f_{AA}}{1-\gamma }\\ \approx f_{AA}\left(1+\gamma \right)\end{array}$$

$$\begin{array}{c}{p}_{AB}\approx f_{AB}-\frac{f_{AA}\gamma }{1-\gamma }\\ \approx f_{AB}-f_{AA}\gamma \end{array}$$

$$\begin{array}{l}{p}_A=p_{AA}+\frac{p_{AB}}{2}\\ \approx f_{AA}\left(1+\gamma \right)+\frac{1}{2}\left(f_{AB}-f_{AA}\gamma \right)\\ =\left(f_{AA}+\frac{1}{2}{f}_{AB}\right)+\frac{f_{AA}}{2}\gamma \\ =f_A+\frac{f_{AA}}{2}\gamma \end{array}$$

In a pair of individuals sharing one allele IBD, we write $P\left(AB\text{|}A\right)$ for the probability that the second individual has an AB conditional on sharing the A allele IBD with the first individual. The probability that one individual has true genotype AA and the other individual has true genotype AB (where the order of individuals is not important, hence the factor of 2 below) is:

$$\begin{array}{l}{P}_{True}\left(AA,AB\right)=2P\left(AA\right)P\left(AB|A\right)=2p_{AA}\frac{P_{AB}}{2p_A}\\ \approx \frac{f_{AA}\left(1+\gamma \right)\left(f_{AB}-f_{AA}\gamma \right)}{f_A\left(1+\frac{\gamma f_{\text{AA}}}{2f_A}\right)}\\ \approx \frac{f_{AA}\left(f_{AB}-f_{AA}\gamma +f_{AB}\gamma \right)\left(1-\frac{f_{AA}}{2f_A}\gamma \right)}{f_{\text{A}}}\\ \approx \frac{f_{AA}\left(f_{AB}-f_{AA}\gamma +f_{AB}\gamma -\frac{f_{AA}{f}_{AB}}{2f_A}\gamma \right)}{f_A}\\ \approx \frac{f_{AA}{f}_{AB}+\left(f_{AA}{f}_{AB}-f_{AA}^2-\frac{f_{AA}^2{f}_{AB}}{2f_A}\right)\gamma }{f_A}\end{array}$$

Similarly, the probability that both individuals have true genotype AA is:

$$\begin{array}{l}{P}_{True}\left(AA,AA\right)=P\left(AA\right)P\left(AA\text{|}A\right)=p_{AA}\frac{p_{AA}}{p_A}\approx \frac{{\left(f_{AA}\left(1+\gamma \right)\right)}^2}{f_A\left(1+\frac{f_{AA}}{2f_A}\gamma \right)}\\ \approx \frac{f_{AA}^2\left(1+2\gamma \right)\left(1-\frac{f_{AA}}{2f_A}\gamma \right)}{f_A}\approx \frac{f_{AA}^2}{f_A}\left(1+2\gamma -\frac{f_{AA}}{2f_A}\gamma \right)\end{array}$$

Now we can calculate the probability that the observed genotypes are AA and AB (again without regard to the order of the individuals):

$$\begin{array}{l}{P}_{Obs}\left(AA,AB\right)\approx P_{True}\left(AA,AB\right)\left(1-\gamma \right)+2\gamma P_{True}\left(AA,AA\right)\\ \approx \frac{f_{AA}{f}_{AB}+\left(f_{AA}{f}_{AB}-f_{AA}^2-\frac{f_{AA}^2{f}_{AB}}{2f_A}\right)\gamma }{f_A}\left(1-\gamma \right)+2\gamma \frac{f_{AA}^2}{f_A}\left(1+2\gamma -\frac{f_{AA}}{2f_A}\gamma \right)\\ \approx \frac{f_{AA}{f}_{AB}\left(1-\gamma \right)+\left(f_{AA}{f}_{AB}-f_{AA}^2-\frac{f_{AA}^2{f}_{AB}}{2f_A}\right)\gamma }{f_A}+2\gamma \frac{f_{AA}^2}{f_A}\\ \approx \frac{f_{AA}{f}_{AB}+(f_{AA}^2-\frac{f_{AA}^2{f}_{AB}}{2f_A})\gamma }{f_A}\\ =\frac{f_{AA}{f}_{AB}}{f_A}+\frac{f_{AA}^2}{f_A}\left(1-\frac{f_{AB}}{2f_A}\right)\gamma \end{array}$$

Rearranging, we obtain:

$$\gamma \approx \frac{f_A^2{P}_{Obs}\left(AA,AB\right)-f_A{f}_{AA}{f}_{AB}}{f_{AA}^2\left(f_A-\frac{f_{AB}}{2}\right)}$$ (Equation B1)

We can use Equation B1 to estimate γ. Consider multiple variants, indexed by i, from multiple IBD pairs, indexed by j. Replace $P_{Obs}\left(AA,AB\right)$ by $I_{Obs}^{(i,j)}\left(AA,AB\right)$, an indicator of whether one individual of IBD pair j has the homozygous major and the other heterozygous genotype at variant i. Write ${\hat{f}}_{AA}^{\left(i\right)}$ for the observed frequency of the AA genotype at variant i, for example. Then

$$\hat{\gamma }=\frac{{\sum }_j{\sum }_i\left({\hat{f}}_A^{\left(i\right)2}{I}_{Obs}^{(i,j)}\left(AA,AB\right)-{\hat{f}}_A^{\left(i\right)}{\hat{f}}_{AA}^{\left(i\right)}{\hat{f}}_{AB}^{\left(i\right)}\right)}{{\sum }_j{\sum }_i{\hat{f}}_{AA}^{\left(i\right)2}\left({\hat{f}}_A^{\left(i\right)}-\frac{1}{2}{\hat{f}}_{AB}^{\left(i\right)}\right)}$$ (Equation B2)

We can include in the estimation any subset of the variants. Because error rates vary by allele frequency, we choose to use all variants with the same minor allele count (or with minor allele counts within some small range).

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://www.1000genomes.org

• IBDseq, http://faculty.washington.edu/browning/ibdseq.html

• SEQERR, http://faculty.washington.edu/browning/seqerr.html

• The European Genome-phenome Archive (EGA), https://www.ebi.ac.uk/ega

• UK10K Consortium, http://www.uk10k.org/

• WTCCC, http://www.wtccc.org.uk