A fast nonlinear regression method for estimating permeability in CT perfusion imaging

Abstract

Blood–brain barrier damage, which can be quantified by measuring vascular permeability, is a potential predictor for hemorrhagic transformation in acute ischemic stroke. Permeability is commonly estimated by applying Patlak analysis to computed tomography (CT) perfusion data, but this method lacks precision. Applying more elaborate kinetic models by means of nonlinear regression (NLR) may improve precision, but is more time consuming and therefore less appropriate in an acute stroke setting. We propose a simplified NLR method that may be faster and still precise enough for clinical use. The aim of this study is to evaluate the reliability of in total 12 variations of Patlak analysis and NLR methods, including the simplified NLR method. Confidence intervals for the permeability estimates were evaluated using simulated CT attenuation–time curves with realistic noise, and clinical data from 20 patients. Although fixating the blood volume improved Patlak analysis, the NLR methods yielded significantly more reliable estimates, but took up to 12 × longer to calculate. The simplified NLR method was ∼4 × faster than other NLR methods, while maintaining the same confidence intervals (CIs). In conclusion, the simplified NLR method is a new, reliable way to estimate permeability in stroke, fast enough for clinical application in an acute stroke setting.

Introduction

Computed tomography (CT) perfusion (CTP) imaging, or dynamic contrast enhanced CT, is frequently used for the evaluation of acute stroke.

It has previously been hypothesized that blood–brain barrier damage is a predictor for hemorrhagic transformation in acute stroke.^{1, 2, 3} With CTP imaging, blood–brain barrier damage can be quantified by measuring vascular permeability. Along with other perfusion parameters, including cerebral blood volume (CBV) and flow (CBF), vascular permeability is a tissue property that can be estimated by comparing tissue attenuation–time curves with the curve of a reference artery or arterial input function (AIF). While CBF and CBV can be measured by imaging the first-pass bolus passage, leakage of contrast agent to the extravascular space is a slower process, only discernible in a delayed phase, and therefore requiring longer scan times. In stroke imaging, permeability is most frequently estimated using linearized regression, that is, by graphical analysis of a Patlak plot.^{1, 3, 4, 5, 6} This technique transforms the data in the attenuation–time curves so that, in case of irreversible leakage, the data points lie on a straight line when the capillary tracer concentration reaches steady state. The permeability transfer constant K^trans is the slope of this line, and the relative blood volume is the intersection with the y axis. Patlak analysis is used in, e.g., Extended Brilliance Workspace 4.5 (Philips Healthcare, Best, The Netherlands), syngo Volume Perfusion-CT Neuro 2010 (Siemens Healthcare, Erlangen, Germany), and Vitrea fX 6.4 (Toshiba Medical Systems, Otawara-shi, Japan).

The Patlak method is preferred in the acute stroke setting, because it is fast, despite some inherent drawbacks. First, due to the linearized regression, only the steady-state data points, that is, the last part of the scan, can be used. The estimated values are therefore dependent on the definition of the onset of this steady state, and potentially useful information in the first part of the signal is disregarded. Second, linear least-squares regression assumes that the errors on the samples are normally distributed. For linearized data, this is not the case and therefore the result will not be an optimal least-squares fit.⁷ Third, other parameters, such as the CBV and CBF, are estimated using a different method, which usually includes Gaussian or gamma variate curve fits, or a regularized inverse filter.⁸ Because two different methods are used for estimating parameters that essentially describe the same tissue model, the results may disagree. For example, the CBV, which should measure the intravascular volume only, may be overestimated by methods that do not take into account the additional extravascular distribution volume due to increased permeability of the blood–brain barrier.^{9, 10}

As an alternative to the Patlak method, the use of a tissue perfusion model applied with nonlinear regression (NLR) uses the full length of the attenuation–time curves, does not transform the measurement errors, and allows for a simultaneous measurement of all perfusion parameters. For these reasons, NLR methods may provide a superior alternative to the use of Patlak plots in stroke imaging.^{2, 11, 12} However, NLR methods rely on iterative algorithms that are relatively time consuming. A rapid diagnosis is crucial for treatment of acute stroke; and therefore, these methods may not be practical in an acute stroke setting.

The purpose of this study was to compare the reliability and computation time of permeability estimation using various implementations of the Patlak method and NLR methods using clinical and simulated data. In addition, a novel simplified NLR method is proposed as a faster potential alternative to existing NLR methods.

Materials and methods

This section first describes a first-pass bolus model that is required for the calculation of some of the Patlak methods. Second, details are provided for the theory and technical implementation of different Patlak and NLR methods. Third, a novel method for NLR, based on the adiabatic approximation to the tissue homogeneity (TH) (AATH) model,¹³ is introduced. Table 1 summarizes all in this study included methods for estimating permeability. Finally, methods for evaluating the models' reliability of estimating K^trans in both simulated data and clinical CTP scans are presented.

Table 1. An overview of the studied methods and their free and fixed parameters, according to Equation 5.

Method	Free parameters	Vi	tm	Ktrans	Ve	tΔ
Patlak	2	✓	0	✓	∞	0
Patlak+delay	3	✓	0	✓	∞	✓a
Patlak fixed	2	✓a	0	✓	∞	0
Patlak fixed+delay	3	✓a	0	✓	∞	✓a
AATH	4	✓	✓	✓	✓	0
AATH+delay	5	✓	✓	✓	✓	✓
NLR	3	✓	✓	✓	∞	0
NLR+delay	4	✓	✓	✓	∞	✓
NLR+Ve	4	✓	✓	✓	✓	0
NLR+Ve+delay	5	✓	✓	✓	✓	✓
Simpl. NLR	3	✓	✓	✓	∞	0
Simpl. NLR+delay	4	✓	✓	✓	∞	✓

Abbreviations: AATH, adiabatic approximation to the tissue homogeneity; NLR, nonlinear regression.

t_m, 0 means that the method does not account for a transit time, V_e, ∞ assumes irreversible leakage, and t_Δ, 0 indicates a delay-sensitive method.

^aEstimated using gamma variate curve fitting.

First-Pass Bolus Fitting

Some implementations of the Patlak plot (described below) require estimates of the CBV and time-to-peak (TTP). To obtain these values, and estimates for the CBF and mean transit time (MTT), the attenuation–time curves can be analyzed using a broad range of methods. Despite that more sophisticated methods exist for estimating the CBF and MTT, this study uses gamma variate curve fitting of the first-pass bolus for obtaining the CBV and TTP, because the variability in outcome between the methods for estimating these parameters was found to be very small.⁸

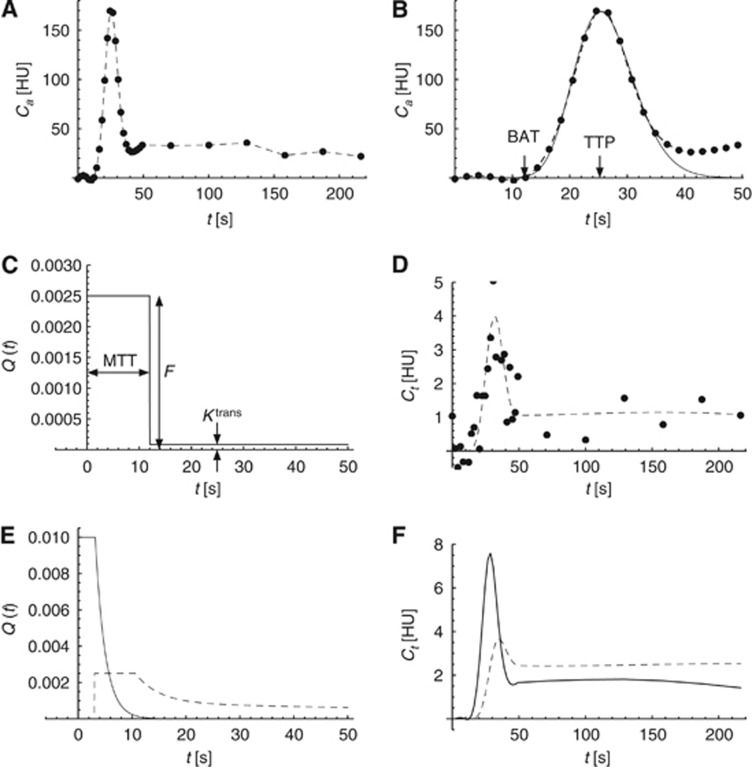
A gamma variate fit gives a robust estimate of the area under the curve (AUC) and TTP of the first-pass bolus in the attenuation–time curve.^{14, 15, 16} Subsequently, the CBV can be estimated by dividing the AUC of the tissue curve by the AUC of the AIF.¹⁰ The bolus arrival time (BAT), which is in this study used to define the start of contrast enhancement, is defined as the 0.05% quantile of the gamma variate fit (Figure 1B).

Figure 1.

An overview of the arterial input function (AIF), and simulated impulse response functions (IRFs) and tissue attenuation–time curves. (A) The full measured AIF. (B) The first 50 seconds of the AIF showing the bolus arrival time (BAT) and time-to-peak (TTP), estimated using a gamma variate fit. (C) The default AATH IRF with a mean transit time (MTT) of 12 seconds, a cerebral blood flow (CBF) of 15 mL/min per 100 g, and irreversible leakage with a K^trans of 0.5 mL/min per 100 g. (D) A simulated tissue attenuation–time curve, created by convolving the measured AIF (A) with the calculated IRF (C), and adding Gaussian noise with a standard deviation of 1 HU (dots). (E) An example of Q(t) for V_i=5 mL/100 g, t_m=5 seconds, t_Δ=0 second, and no leakage (solid line), and Q(t) for V_i=3 mL/100 g, t_m=12 seconds, t_Δ=3 seconds, and reversible leakage with K^trans=5 mL/min per 100 g, and V_e=10 mL/100 g (dashed line). (F) Simulated tissue attenuation–time curves, created by convolving the measured AIF (A) with the IRFs in (E). AATH, adiabatic approximation to the tissue homogeneity; HU, hounsfield units.

Patlak Linearized Regression

An underlying assumption of Patlak analysis is that the vascular leakage is irreversible during the acquisition time. In that case, the total tracer concentration in the tissue, C_t(t), can be described as a function of the capillary concentration C_c(t), the intravascular blood volume V_i, and a transfer constant K^trans that represents the flow from the intravascular to the extravascular space:

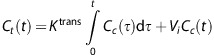If both sides of the equation are divided by C_c(t), then a parametric relationship is found that should be linear when the capillary concentration reaches a steady state:

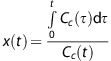Equation 1 shows that when a linear fit y(t)=ax(t)+b is applied to the Patlak plot of the delayed phase³ of the attenuation–time curves, the slope of the fit (a) and its intersection with the y axis (b) give an estimation of the transfer constant K^trans and the blood volume V_i, respectively.

The onset of the delayed phase, in which steady state is reached, is in this study empirically defined as the arterial TTP plus 3.5 × the standard deviation of the first-pass bolus, measured using a gamma variate curve fit as described above. This is a reliable method, because gamma variate fits give a robust estimate of the width and position of the first-pass bolus peak.

Patlak Analysis with a Fixed Offset

The blood volume can be read from the Patlak plot (Equation 1). Alternatively, if an estimate of V_i is available from, e.g., first-pass bolus analysis, then K^trans can be estimated more robustly, using the prior estimated CBV as a fixed offset.¹⁷

For comparison, both the ‘standard' and the ‘fixed' Patlak methods are examined (Table 1).

Patlak Analysis with Delay Correction

In CTP imaging, the arterial concentration C_a(t) rather than the capillary concentration C_c(t) is measured to solve Equation 1. In comparison with C_a(t), the average capillary tracer concentration can be affected by an arterial delay and the transit time in the tissue. Schneider et al¹⁸ suggested correcting for such a delay by incorporating the difference in TTP between the tissue curve and the AIF, d_TTP, taken from gamma variate curve fits to the first-pass bolus, into Equation 1:

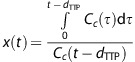In line with this, both the ‘standard' and ‘fixed' Patlak methods are also extended with a delay correction (Table 1). The gamma variate fits to the AIF and tissue curves provide a robust estimate of the TTP values if the leakage is small.

Nonlinear Regression

A Perfusion Model for Nonlinear Regression

Tissue perfusion is frequently modeled as a linear time-invariant system. Under that assumption the dynamics of the tracer concentration in the tissue can be described as the convolution of the AIF with a characteristic impulse response function (IRF). An IRF can be thought of the attenuation–time curve of a small tissue volume in response to an infinitesimal short AIF.

The NLR technique in this study uses a mathematical tissue response model to describe the IRF. The convolution of the measured AIF with a computed IRF gives an estimate of the true attenuation–time curve of the tissue volume. Non-linear regression is used to iteratively adapt any of the parameters in the mathematical model, such as the blood volume and transit time, to minimize the error between this estimate and the measured attenuation–time curve.

Sawada et al¹⁹ and Sourbron and Buckley¹² found that the detailed TH model, describing the blood flow using a complex set of differential equations,²⁰ fitted the physiology of the brain the best, because of the high density and tortuous nature of the brain capillary network. The full TH model, however, lacks a closed-form time domain solution. Lawrence and Lee¹³ noticed that, because the contrast agent concentration in the extravascular space changes slowly relative to that in the intravascular space, the IRF of the TH model can be very well approximated by a box function followed by an exponential decay. In this AATH, a box function with a width of t_t seconds (the transit time) represents the vascular phase, and an exponential decay represents the parenchymal tissue phase:

In Equation 2, U(t) is the unit step function, F is the plasma flow, and V_e is the extravascular distribution volume. Note that the intravascular distribution volume V_i (the CBV) equals t_t × F. Because this model gives estimates for t_t and F as opposed to models that only estimate V_i, this type of model is often referred to as a ‘distributed parameter' model, in contrast to ‘lumped parameter' models like the extended Tofts model.²¹

The AATH model describes the tracer concentration dynamics in a small volume containing a single capillary vessel with a uniform (plug) flow. In reality, however, brain tissue is heterogeneous and even a small volume contains capillaries with variable lengths. This heterogeneity causes a small tissue volume to have a distribution of transit times P(t_t;t_m), rather than one unique transit time t_t. t_m is known as the mean transit time, or MTT. When this distribution is taken into account, the full model that is used in this study becomes:

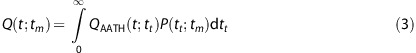In this equation, Q_AATH(t;t_t) is the IRF of the AATH model for a unique transit time t_t and P(t_t;t_m) is the probability distribution of transit times for t_m.

Bredno et al²² found, using highly detailed simulations, that an exponential decay with a delay of a × t_m is a good approximation for P(t_t;t_m) in case a=0.632. The equation for this distribution can be written as:

Solving the model assumes knowledge about the capillary concentration. In practice, due to resolution and noise limits, the AIF is measured in a large artery, often located away from the tissue of interest, so extra travel time for the contrast to arrive in the tissue needs to be accounted for. This is particularly important in the study of tissue regions that are fed through collateral routes. It has been shown that the performance of other deconvolution methods is improved by making them delay insensitive.^{23, 24} This can be performed by introducing an additional parameter for the delay, t_Δ. In the rare case that a collateral artery is chosen for the AIF, t_Δ could even be negative at the contralateral side. By substituting Equations 2 and 4 into Equation 3, and introducing t_Δ, the following solution is obtained:

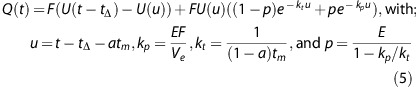The parameter E (0⩽E⩽1) in this equation is the fraction of the flow that leaks into the extravascular space, i.e., K^trans equals E × F.

The AATH model (Equation 2), and also the tracer kinetic models used by Larson et al,²⁵ are subclasses of Q(t) in which a approximates 1 and t_Δ=0. The extended Tofts model, frequently used in the analysis of dynamic contrast enhanced magnetic resonance images, reduces complexity by combining the flow and transit time into a single variable for the blood volume (a lumped parameter), requiring that t_m approximates 0 and t_Δ=0. The IRF for the standard Patlak model,⁴ i.e., assuming irreversible leakage, would require that t_m approximates 0, t_Δ=0 and V_e=∞.

Simplified Nonlinear Regression

Nonlinear regression with five unknown variables is a computational intensive task. Bottlenecks involve the calculation of exponentials, divisions, and a convolution operation in each iteration.

However, the computational complexity is highly reduced by two simplifications to Q(t). Assuming that a approximates 1 and V_e=∞, the two exponentials can be reduced to0 and 1, respectively, and Q(t) can be written as the sum of two step functions:

What is even more important, is that it is now no longer necessary to apply a convolution in each iteration. The convolution of C_a(t) (the AIF) with a shifted unit step function U(t−t_Δ) equals:

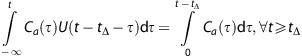The integral of C_a(t) just needs to be calculated once, and the convolution of the C_a(t) with Q_S(t) can be reduced to two interpolations into this integral, at t-t_Δ and t-t_Δ-t_t, respectively.

This simplified version of Q(t) can be used to give estimates of t_m (or MTT), F, K^trans, and t_Δ that would be found if the full model was used. These estimates are also used as initial parameters to initialize fitting the full model.

Model Variations

A total of 12 different methods were compared. Both Patlak and the NLR methods include parameters that are either free for estimation or fixed to a predefined value. The full tissue response model Q(t) (Equation 5) has five perfusion parameters, V_i, t_m, K^trans, V_e, and t_Δ. Table 1 gives an overview of all methods and parameters. The initial values for NLR were V_i=4 mL/100 g, t_m=4 seconds, K^trans=1.5 mL/min per 100 g, V_e=20 mL/100 g, and t_Δ=1 second, and the initial step sizes were2 mL/100 g, 5 seconds, 1.5 mL/min per 100 g, 25 mL/100 g, and 2 seconds, respectively. The initial parameters for the full NLR model are optimized by first applying the simplified NLR model. For all NLR methods, a generic Nelder-Mead downhill simplex method^{26, 27} with linear constraints was used for optimization.

If global optima are found, which is not guaranteed, then increasing the number of free parameters will result in a better fit (a higher R²), but as a counter-effect it may decrease the reliability of the estimated values. In other words, adding complexity to a model may not necessarily improve the results.

All methods were implemented in a similar manner in C routines that are accessible in Matlab (version 2011b, The MathWorks Inc., Natick, MA, USA) through the Matlab MEX programming interface.

Simulations were applied to gain insight in the response of the models to noise and varying perfusion parameters, and CT brain perfusion scans were analyzed to estimate the reliability of the measured permeability in clinical practice.

Simulated Data

To evaluate in a setting with controlled noise levels and perfusion parameters, tissue attenuation–time curves were simulated by convolving a measured AIF with a generated IRF, and adding Gaussian noise. An AIF (Figure 1A) was extracted from a clinical CTP brain scan as described below.

The AATH model^{20, 13} (Equation 2) was used to generate the IRFs, because the TH model is thought to match the physiology of the brain better than other published models.^{19, 12} The blood flow F was kept constant at a rate of 15 mL/min per 100 g, which is comparable to an ischemic penumbra,²⁸ and the leakage was assumed to be irreversible.

The noise level, K^trans, t_m, and delay were varied between the simulations. Four sets of simulations were made. The first is a series of Monte Carlo simulations in which the K^trans was randomized between 0 and 2 mL/min per 100 g, the t_m between 4 and 20 seconds, and the delay between 0 and 5 seconds. In all, 1,000 random simulations were made at noise levels of 0.5, 1.0, and 2.0 Hounsfield units (HU) (s.d.).

In the remaining three sets, one out of three parameters was varied while the others were fixed to 1 HU for the noise level, 0.5 mL/min per 100 g for the K^trans, 12 seconds for the t_m. The delay was fixed to 0 second. In the second set, only the standard deviation of the noise was varied between 0 and 2 HU, in the third set only the K^trans was varied between 0 and 2 mL/min per 100 g, and in the fourth set only t_m was varied between 4 and 20 seconds.

The simulated attenuation curves were analyzed using all methods listed in Table 1, while keeping track of the mean, standard error, and average approximate standard error of the estimated K^trans values.

Figures 1A, 1C, and 1D give an overview of the measured AIF, and the default IRF, and attenuation–time curve. Both the IRF and the AIF were band limited using a Bartlett kernel (triangular) with a full width at half maximum of 4 seconds. Figures 1E and 1F show how the shape of Q(t) (Equation 5) and the resulting attenuation curves change with different parameters.

Computed Tomography Brain Perfusion Scans

Data Acquisition

The CTP scans of 20 acute ischemic stroke patients that participated in the Dutch Acute Stroke Trial (NCT00880113) were included (chronological order). Dutch Acute Stroke Trial is large prospective multicenter observational cohort study, approved by the institutional medical ethics committee (METC), and in accordance with the Good Clinical Practice guidelines as provided by the International Conference on Harmonisation (ICH-GCP) and Dutch act on medical research involving human subjects (WMO).

For CTP, 40 mL of nonionic contrast agent (Iopromide, Ultravist, 300 mg/mL iodine; Bayer HealthCare Pharmaceuticals, Berlin, Germany) was injected intravenously at a rate of 6 mL/s followed by a 40-mL saline flush at a rate of 6 mL/s. The scans were acquired using a Philips Brilliance iCT scanner (Philips Healthcare) at 80 kVp and 150 mAs/rot and a field-of-view of ∼200 × 200 mm² with an axial coverage of 65 mm at most. The total acquisition time was 210 seconds, divided into 25 frames with a 2-second interval, followed by 6 frames with a 30-second interval (Figure 1A). The scans were reconstructed in a 512 × 512 matrix with filtered backprojection and a Philips UB filter.

Preprocessing

The open source registration toolbox Elastix²⁹ was used to register the original, 3D high-resolution CTP data (voxel size 0.39 × 0.39 × 0.83 mm³) to the first time frame. Next, slabs of six adjacent registered slices were averaged to obtain 8 to 13 slabs of 5 mm per volume.

Noise reduction is crucial in CTP analysis. Because of the limited radiation dose, the unfiltered scans have a very low signal-to-noise ratio, especially in the areas with low perfusion where blood–brain barrier damage is to be expected. Sophisticated noise filtering, where e.g. temporal information is used to adapt the filter kernel to its spatial neighborhood, is therefore desirable.

A temporal Gaussian filter with a standard deviation of 4 seconds, followed by a 3D bilateral filter (the time-intensity profile similarity filter, or TIPS)³⁰ with a spatial standard deviation (σ_d) of 4 mm and a profile-similarity standard deviation (σ_ζ) of 50 HU² were applied to reduce the noise with a minimum loss of resolution.

Arterial Input Function

The AIF was semiautomatically selected either in an internal carotid or in the basilar artery by drawing a circular region of interest in which the attenuation curve with the highest enhancement was chosen. To correct the AUC of the AIF for partial volume effect, a venous output function was in the same way semiautomatically selected in a great sinus perpendicular to the slices,³¹ which is in line with the clinical scan protocol. A gamma variate curve was fitted to both the AIF and venous output function to estimate their AUCs, the arterial BAT, and the steady-state concentration time (see First-Pass Bolus Fitting section).

Postprocessing

Only the voxels that were classified as penumbra (tissue at risk) were used for statistical analysis. This was performed because the signal-to-noise ratio of the attenuation–time curves in the infarct (irreversible ischemia) is low, which might hamper reliable measurements. The K^trans in the remainder of the brain (healthy tissue) should in theory be nearly zero.

To extract the penumbra and exclude vessels, tissue types in the brain were segmented based on the CT values in the first frames of the filtered scan, before the BAT. By removing voxels with a CT value of <17 HU or >55 HU (unenhanced), air, fat, and bone are excluded from the analysis, while gray and white matter remain. Within the brain tissue, the infarct and penumbra were defined based on the CBV and relative MTT that were estimated by the simplified NLR method.

To calculate the relative MTT, a symmetry plane was manually drawn to separate the hemispheres. The original MTT map is mirrored over this plane and blurred by a 3D Gaussian kernel with a standard deviation of 3 mm. The relative MTT values are found by dividing the original MTT map by the mirrored, blurred map.

Wintermark et al³² found that the CBV most accurately describes the infarct, with an optimal threshold of 2.0 mL/100 g, and that the relative MTT most accurately describes the penumbra, with an optimal threshold of 145% and the infarct excluded. A CBV threshold of 9 mL/100 g was used to exclude vessels.

A correction factor k_H=(1−H_LV)/(1−H_SV) was applied to correct the tracer concentration for the difference between the hematocrit in large vessels (AIF) and small vessels (arterioles and capillaries).¹⁰ The values used for H_LV and H_SV are 0.45 and 0.25, respectively.³³ This correction affects all perfusion parameters that scale with the plasma concentration, i.e., the CBV, CBF, K^trans, and V_e.

Statistical Analysis

Besides the K^trans estimate itself, the approximate standard error on the estimated K^trans for each method was calculated in all voxels. In all, 95% confidence intervals (CIs) were calculated by applying Student's t-distribution to these standard errors. Average CIs are more suitable for estimating the reliability than the standard deviation for two reasons. First, the standard deviation might represent a true variability instead of an error, which is what we like to measure. Second, the standard deviation might be biased due to constraints to the estimated parameter, i.e., K^trans cannot be negative, nor can it be larger than the flow.

The estimated values and CIs in the penumbra regions were averaged per patient and a Wilcoxon signed-rank test was applied to each pair of methods to test if the differences between the methods were significant (P<0.001).

Results

Simulated Data

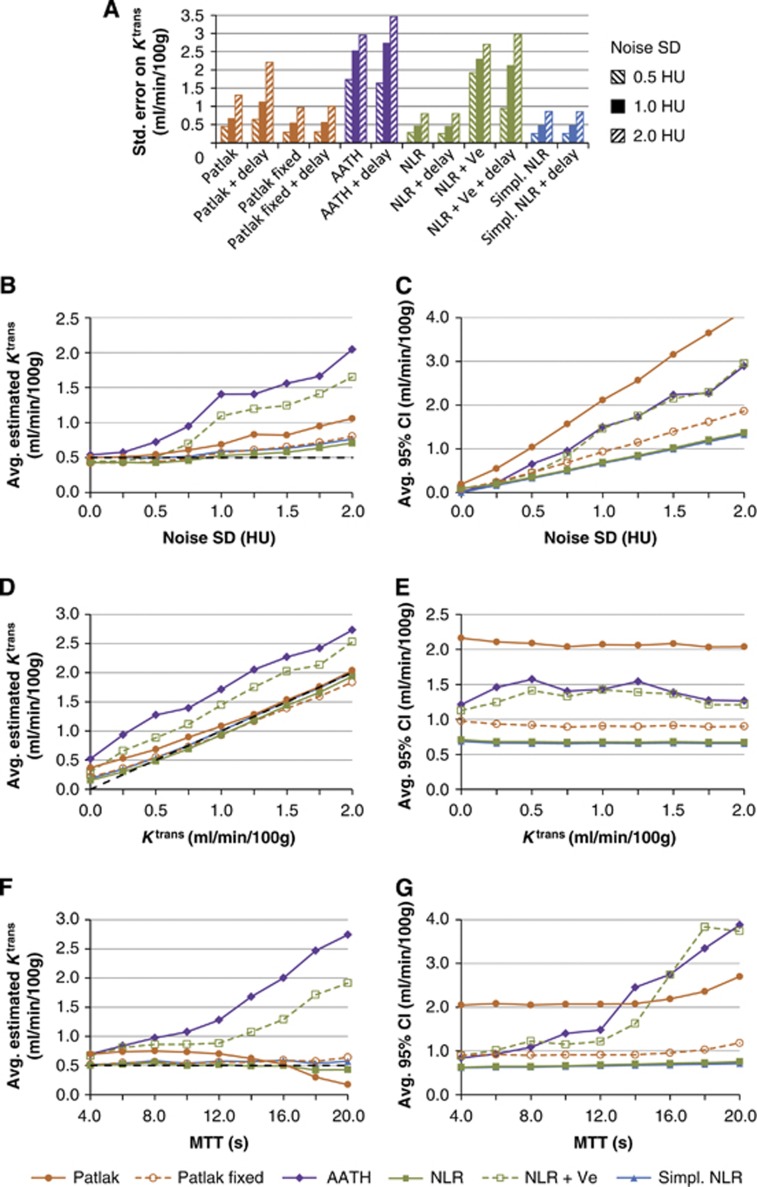
Figure 2A shows the standard error on the K^trans estimates in the Monte Carlo simulations for each method and at different noise levels. Figures 2B to 2G show graphs of the average K^trans estimates and CIs versus the varied input parameters (noise level, K^trans, and t_m). A narrower CI indicates a more reliable estimate. The results for the six delay corrected methods (Table 1) were very similar to the uncorrected methods, and for that reason the results for the delay corrected methods are not shown to make the graphs more readable. The NLR and simplified NLR methods showed very similar results, which caused these lines to overlap in all of the plots.

Figure 2.

Graph (A) shows standard errors of the K^trans estimates on Monte Carlo simulated attenuation curves with a noise s.d. of respectively 0.5, 1.0, and 2.0 HU. The other graphs show average K^trans estimates (B, D, F) and confidence intervals (CIs) (C, E, G) of the simulated data. A narrower CI suggests a more reliable estimate. The nonlinear regression (NLR) and simplified NLR methods showed very similar results, which caused these lines to overlap in all of the plots. AATH, adiabatic approximation to the tissue homogeneity; HU, hounsfield units; MTT, mean transit time.

Because the steady-state time was defined as the TTP plus 3.5 × the standard deviation of the first-pass bolus, 9 time frames were included for Patlak analysis.

The results showed that noise gives a positive bias to the average K^trans estimates (Figure 2B), affecting the standard Patlak, AATH, and NLR+V_e the most. Figure 2D shows that, at the default noise level of 1.0 HU, all methods had a positive bias for small K^trans values, while the methods that assume irreversible leakage (V_e=∞) gave unbiased estimates for larger K^trans values. The bias for the methods that assume reversible leakage (AATH and NLR+V_e) is also reflected in the high standard errors in Figure 2A. Figure 2F shows that the average K^trans is not affected by the MTT for transit times shorter than 12 seconds. For long transit times, the AATH and NLR+V_e methods overestimated the K^trans, while the standard Patlak method returned underestimated K^trans values.

In all cases with noise, the NLR methods with irreversible leakage were found to have the smallest CIs, while the standard Patlak method had the largest CI, implying that it is least reliable (Figures 2C, 2E, and 2G). All methods gave estimates of which the width of the CI scaled linearly with the noise level (Figure 2C). Figure 2E shows that the confidence of the estimation did not scale with the K^trans for the methods that assume irreversible leakage (V_e=∞). The methods that assume reversible leakage, AATH and NLR+V_e, showed an increased CI for K^trans values in the order of 1 mL/min per 100 g. For K^trans values higher than 2 mL/min per 100 g (not shown in the graph), however, the CI of these methods decreases again to reach a steady state of 0.4 mL/min per 100 g at a K^trans of 10 mL/min per 100 g, while CIs of the other methods are unaffected. In line with Figure 2F, Figure 2G shows that the average CI was not affected by the MTT for transit times shorter than 12 seconds. For long transit times, the AATH, NLR+V_e, and standard Patlak methods showed an increased CI.

Computed Tomography Brain Perfusion Scans

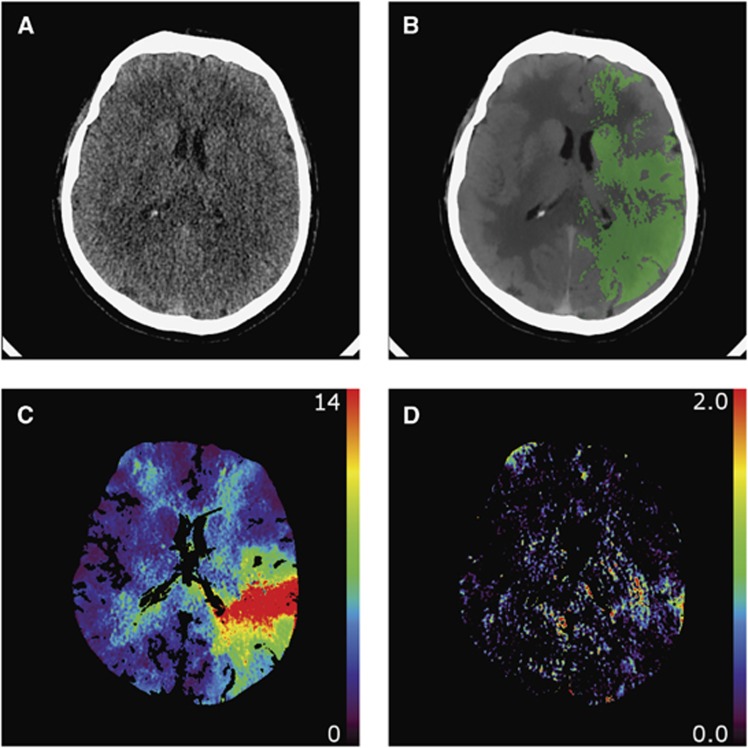
The K^trans and CI maps for K^trans were generated for 20 CTP scans (Figure 3).

Figure 3.

An example of (A) an unfiltered computed tomography (CT) perfusion (CTP) frame, (B) a filtered CTP frame with the penumbra mask as overlay, (C) a mean transit time (MTT) parameter map (seconds) measured using first-pass bolus fitting, and (D) a K^trans parameter map (mL/min per 100 g) measured with the simplified nonlinear regression (NLR) method.

There was a large variance in K^trans and CI between the patients (Table 2), but the Wilcoxon signed-rank tests (Table 3) showed that the average CIs were significantly different between most methods that assume irreversible leakage.

Table 2. The K ^trans values and 95% confidence intervals (mL/min per 100 g) in the clinical data and in the simulations (default parameters).

	Avg. Ktrans		Avg. 95% CI width
Method	Clinical data	Simulation	Clinical data	Simulation
Simpl. NLR	0.39±0.23	0.59	0.82±0.29	0.67
Simpl. NLR+delay	0.36±0.21	0.57	0.82±0.29	0.66
NLR	0.34±0.21	0.53	0.85±0.31	0.69
NLR+delay	0.33±0.19	0.53	0.85±0.32	0.67
Patlak fixed	0.43±0.33	0.57	1.42±0.49	0.93
Patlak fixed+delay	0.45±0.35	0.58	1.53±0.56	1.03
AATH	0.87±0.89	1.40	1.95±0.94	1.50
NLR+Ve+delay	0.72±0.73	0.85	1.97±1.06	1.25
AATH+delay	0.83±0.88	0.95	2.04±1.07	1.21
NLR+Ve	0.77±0.77	1.10	2.18±1.20	1.46
Patlak	0.73±0.45	0.69	2.65±1.33	2.11
Patlak+delay	0.78±0.48	0.96	2.78±1.45	2.10

Abbreviations: AATH, adiabatic approximation to the tissue homogeneity; CI, confidence interval; NLR, nonlinear regression; V_e, extravascular distribution volume.

The values are ordered to the width of the confidence interval in the clinical data. The average confidence intervals are visualized in the graph in Figure 4A.

Table 3. P values for the Wilcoxon signed-rank tests on the 95% CIs for K ^trans between the different methods.

	Patlak	Patlak+delay	Patlak fixed	Patlak fixed+delay	AATH	AATH+delay	NLR	NLR+delay	NLR+Ve	NLR+Ve+delay	Simpl. NLR
Patlak+delay	0.001
Patlak fixed	0	0
Patlak fixed+delay	0	0	0
AATH	0.056	0.035	0.015	0.052
AATH+delay	0.126	0.073	0.012	0.030	0.018
NLR	0	0	0	0	0
NLR+delay	0	0	0	0	0	0	0.823
NLR+Ve	0.232	0.145	0.009	0.017	0.005	0.153	0	0
NLR+Ve+delay	0.048	0.030	0.017	0.062	0.737	0.014	0	0	0.002
Simpl. NLR	0	0	0	0	0	0	0	0.002	0	0
Simpl. NLR+delay	0	0	0	0	0	0	0	0	0	0	0.695

Abbreviations: AATH, adiabatic approximation to the tissue homogeneity; CI, confidence interval; NLR, nonlinear regression; V_e, extravascular distribution volume.

Probabilities smaller than 0.001 are considered as significant and written as 0.

Because the steady-state time for Patlak analysis was defined as the TTP plus 3.5 × the standard deviation of the first-pass bolus, on average 9 time frames were included for Patlak analysis.

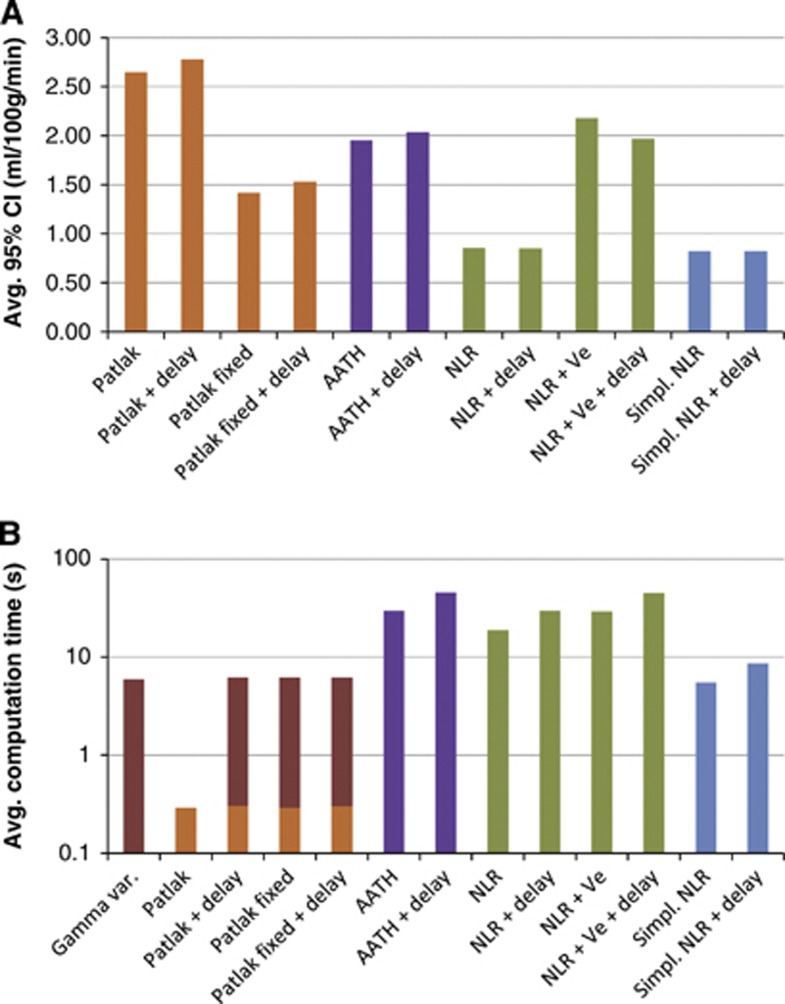
Figure 4A, and Table 2 together with Table 3 show that the K^trans values that are estimated using the NLR methods with irreversible leakage (V_e=∞) were significantly more reliable than the Patlak methods. The introduction of reversible leakage, as in the AATH method and NLR+V_e, more than doubled the width of the CI of the estimation. The difference in reliability between the full and simplified NLR methods was found to be very small.

Figure 4.

(A) The average 95% confidence interval (CI) of K^trans for of each method. More reliable estimates have narrower CIs. (B) The average computation per slice (512 × 512 pixels) for each of the methods on a low-end desktop PC. Note that the y axis is logarithmic. The Patlak methods that are extended with delay and/or fixed cerebral blood volume (CBV) require input from the gamma variate fit-based method. AATH, adiabatic approximation to the tissue homogeneity.

Figure 4A also shows that fixating the CBV significantly improved the reliability of the Patlak estimates.

The delay correction had a minor effect on the CIs. With P values higher than 0.001, the CIs of the standard Patlak, AATH, NLR, NLR+V_e, and simplified NLR methods were not significantly different from the delay corrected versions. The delay corrected CBV-fixed Patlak method performed slightly but significantly worse than its delay-sensitive version (P<0.001).

Also, the MTT distribution parameter a had a minor effect. The CI of the NLR+V_e method (a=0.632) was not significantly different from the interval of the AATH method (a=1). The CIs of the simplified NLR and simplified NLR+delay methods (a=1) were slightly but significantly smaller than respectively the NLR and NLR+delay methods (a=0.632).

Figure 4B gives an overview of the average computation time for each method. It is not surprising that the simplest method, standard Patlak, was the fastest with 0.3 second per slice (512 × 512 pixels and 31 time frames). The other Patlak methods require additional input provided by a gamma variate fit, extending the computation time to 5.9 seconds per slice. The simplified NLR methods had computation times of respectively 5 and 9 seconds per slice, where the other NLR methods required between 19 and 45 seconds.

Discussion

This study uses CIs to compare the reliability between different methods for estimating K^trans values. The ‘reliability' can be thought of as a quantity that is inversely proportional to the width of these CIs. The experiments showed that the simplified NLR method has a CI that is a bit smaller than the full NLR methods, and significantly smaller than the Patlak methods in both the simulations and clinical measurements.

‘Reliability' is a nonscientific term that should be used with care. Some ‘reliability metrics', like the Akaike information criterion,³⁴ quantify the goodness of fit of a model. For two reasons, however, this type of metric is not applicable to this study. First, the Patlak fits are applied to different (linearized) data than the nonlinear fits; and therefore, the goodness of fit between these methods may not be compared. Second, the reliability of a single parameter, K^trans, is of importance, rather than the goodness of fit of the complete model. Not all time frames have an equal contribution to the estimated K^trans, and therefore the CI, which is specific to this parameter, is more appropriate.

A wider CI means a larger standard deviation in repeated measurements. For K^trans values close to zero, the probability distribution is skewed because the estimates are constrained to positive values, and therefore the mean will have a positive bias. This phenomenon is visible in Figures 2B and 2D. The estimated CI, however, appears to be independent of the value for K^trans, which makes it a valid measure for evaluating the reliability of the methods, even if the true K^trans is close to zero. It has been shown that the estimates from the clinical data are in line with the simulations, for which reason it can be concluded that the variation in average K^trans between the methods has to be addressed to a variation in the CIs rather than a bias in estimates.

The standard Patlak method was found to be two to three times less reliable than the NLR and simplified NLR method in both the simulated and clinical cases. However, fixating the CBV to a value estimated with a more sophisticated method, which is usually available anyway, roughly doubles its reliability. This means that fixating the CBV in the Patlak plot is a simple but very effective way to enhance the reliability of the permeability estimates in general.

The standard Patlak method showed a decrease in reliability for long transit times. The performance of this method could in those cases probably be increased by determining the steady state of the tissue attenuation curve instead of the AIF, as was performed in this study. A longer MTT means that it takes more time for the capillary concentration to reach a steady state and therefore fewer samples should be included in the Patlak plot.

The addition of a delay time t_Δ as an extra parameter had a minor effect on the reliability of the K^trans. It has although been proven that delay-insensitive methods, i.e., methods that incorporate t_Δ, give better estimates for the CBV, CBF, and MTT.⁸ Therefore, and because the CIs for the NLR methods did not increase despite the introduction of an extra-free parameter, it can be concluded that t_Δ is an appropriate additional parameter for the NLR methods.

The shape of the MTT distribution, controlled by the parameter a in Equation 5, is another feature that could improve the credibility of the IRF and therefore enhance the reliability of the K^trans estimates. The methods that use a=0.632 instead of a=1 have IRFs that are thought to be more realistic,¹⁷ but none of those methods showed a significant narrower CI on the clinical data, nor did the simulations show significant differences between these methods. Although this parameter might increase the accuracy and reliability of other perfusion parameters, such as the CBF and MTT, it did not affect the estimation of K^trans.

The simulations showed that the AATH and NLR+V_e methods, both assuming reversible leakage, overestimate K^trans in case the leakage is virtually irreversible (Figure 2D). This is most likely caused by the error in the estimated extravascular distribution volume, V_e (Equations 2 and 5). In case V_e is underestimated, i.e., the model overestimated the washout from the extravascular space, then K^trans needs to be larger to compensate for the measured concentration levels. In theory, a V_e of nearly zero allows high K^trans values without noticeable leakage, because any leaked contrast is washed out instantly. The reliability of the AATH and NLR+V_e methods increases with larger K^trans values, in the order of 2 to 10 mL/min per 100 g, which can be explained by the fact that a higher permeability results in better V_e estimates. Therefore, it cannot be concluded from our study that AATH and NLR+V_e perform worse than the other NLR methods in general. Models that account for reversible leakage are more applicable in pathologies with high vascular permeability, such as tumors, and in those particular cases they will likely give more reliable estimates.

On many points, the NLR method provides a more sound theoretical basis than Patlak analysis for permeability analysis, and gamma variate fits or deconvolution^{8, 35} for perfusion analysis. First, the NLR method does not make any assumptions of the shape of the attenuation curves themselves, but rather on the process that transforms the AIF into a tissue curve. The curves do not necessarily need to have a gamma variate-like profile, nor do they have to reach a steady state. A potential second pass bolus due to recirculation does not hamper the analysis. Second, at about t_m seconds after the BAT, the permeability will start to affect the shape of the attenuation–time curve measured in the tissue, including part of the first-pass bolus. As opposed to the Patlak method, which uses only steady-state time frames, the NLR methods include all time frames. This means that no potentially useful information is wasted, and the results do not depend on the definition of the steady state. Third, because the NLR methods do not transform the attenuation curves, the (approximate) normal distribution of the measurement errors is preserved, which fulfills the requirements for proper least squares fitting. In linearized regression using a Patlak plot, this is no longer the case. Values are divided by C_c(t), which is a nonlinear operation that distorts the measurement errors. Fourth, all perfusion parameters, including permeability, are measured using a single method in which a change in one parameter affects all others. This reduces the bias in estimates that are influenced by other relevant factors that a method does not account for. For example, if the permeability is significant, then the intravascular blood volume can be biased if this is estimated by a method does not account for leakage into the extravascular volume.

A disadvantage of NLR is that it is an iterative method, and so a straightforward implementation is time consuming. This is most likely the reason why currently this technique is not much used in CTP analysis yet. The simplified NLR method, however, tackles two bottlenecks by omitting the need for convolutions and the calculation of exponentials, and is thereby at least four times faster than the full NLR methods. By further increasing the performance using, e.g., parallel computing or GPU acceleration the analysis of high-resolution volumes in a clinical setting might be feasible.

In conclusion, the CI, and thereby the reliability, of the simplified NLR method is similar to the full NLR methods, and better than the Patlak methods in both the simulations and clinical measurements. The simplified NLR analysis just takes 5 seconds per 512 × 512 slice, making it suitable for time-critical clinical use. The simplified NLR method therefore seems to be a superior alternative to Patlak analysis. Further research is required to evaluate the predictive value of the simplified NLR method for hemorrhagic transformation in acute ischemic stroke.

The techniques described in this study are potentially applicable to other purposes as well, like tumor assessment using dynamic contrast enhanced magnetic resonance imaging or positron emission tomography, even though the signal-to-noise ratio and kinetics might differ.

The authors declare no conflict of interest.