Multiple-capillary measurement of RBC speed, flux, and density with optical coherence tomography

Abstract

As capillaries exhibit heterogeneous and fluctuating dynamics even during baseline, a technique measuring red blood cell (RBC) speed and flux over many capillaries at the same time is needed. Here, we report that optical coherence tomography can capture individual RBC passage simultaneously over many capillaries located at different depths. Further, we demonstrate the ability to quantify RBC speed, flux, and linear density. This technique will provide a means to monitor microvascular flow dynamics over many capillaries at different depths at the same time.

Introduction

Interest in the brain's blood flow regulation has been evolving towards understanding the role of the spatio-temporal dynamics of capillary networks. In distinction to arterioles, capillaries have been reported to exhibit highly heterogeneous responses to neural activation, capillary by capillary,^{1, 2} and nearly stochastic distributions during baseline³ potentially masking neural activity-induced responses within single capillaries.⁴ Therefore, a technique to measure red blood cell (RBC) flow characteristics at a number of capillaries at the same time is required, so that one can study capillary responses in a statistical manner with high statistical significance. Here, this Brief Communication reports that individual RBC passage can be captured in the signal time courses of high-speed optical coherence tomography (OCT) imaging and that RBC speed and flux over many capillaries located at different depths can be simultaneously quantified from the observed RBC passages.

OCT enables 3D imaging of tissue structures with μm resolution.⁵ It needs no extrinsic contrast agents and can image at depth (up to ∼1 mm in brain tissue). Furthermore, it simultaneously resolves all voxels along the axial direction over the depth of focus thus improving the volumetric imaging speed by 1–2 orders of magnitude⁶ when compared with traditional confocal and two-photon microscopes.^{7, 8} Meanwhile, according to the Mie scattering theory suggesting that 1-μm wavelength light scattering is sensitive to scatterers of 0.1–10 μm in size (Supplementary Figure S1 of Lee et al.⁹), large backscattering (i.e., large OCT signals) will result from RBCs as well as cellular constituents and membranes. If this is true, the OCT signal at a given voxel should go up and come back down when an RBC passes through the voxel. This paper tests and demonstrates this idea, leading to measurement of the RBC speed, flux, and density over a large number of capillaries in a short period of time.

Material and methods

Animal Preparation

Sprague Dawley rats (250–300 g, n=5) were initially anesthetized with isofluorane (1.5–2.5%, v/v) and ventilated with a mixture of air and oxygen during surgical procedures. Tracheotomy and cannulation of the femoral artery and vein were done. A craniotomy was performed over the somatosensory cortex. The dura was carefully removed, and then the cranial window was covered with agarose in artificial cerebrospinal fluid and a glass cover slip. After surgery, rats were anesthetized with Alpha Chloralose (40 mg/kg intravenous bolus followed by 40–50 mg/kg/hr, intravenous). Physiological signals were continuously monitored during surgery and during the experiment.

All animal experimental procedures were reviewed and approved by the Massachusetts General Hospital Subcommittee on Research Animal Care, according to the guidelines and policies of office of laboratory animal welfare and public health service, National Institutes of Health.

Spectral-Domain Optical Coherence Tomography System

We optimized a spectral-domain OCT system (Thorlabs, Inc., Newton, NJ, USA) for rodent cerebral cortex imaging.¹⁰ The transverse resolution is 3.5 and 7 μm with × 10 and × 5 objectives, respectively. The axial resolution is matched to the transverse one for isotropic voxels by manipulating the spectrum fringe data. The imaging speed is 47,000 A-scan/s. A-scan in OCT means a single acquisition of 1D data over the depth axis (z axis), while B-scan means a single acquisition of 2D data over a cross-sectional plane (z–x plane).

Results

OCT Intensity Time Courses Capture Individual RBC Passage

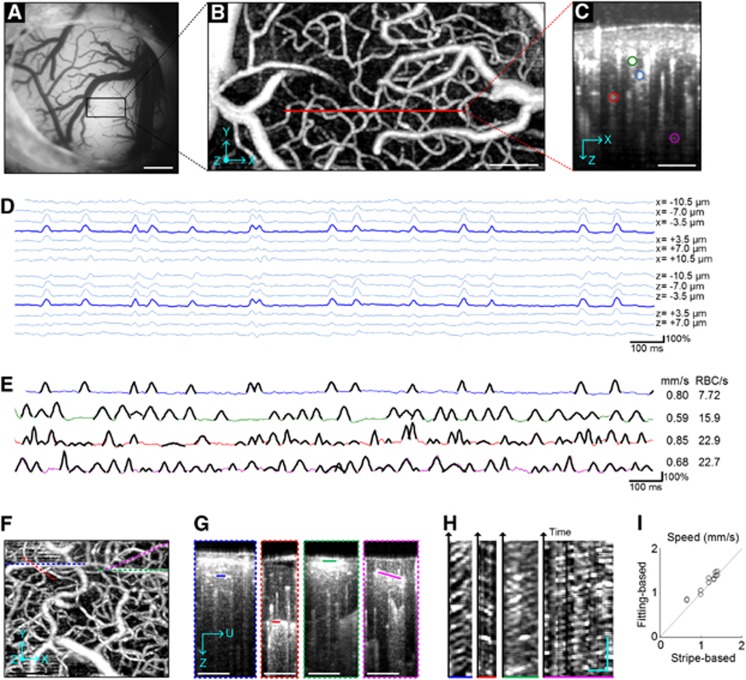
We first performed OCT angiogram imaging⁶ through the cranial window (Figures 1A and 1B). Then, on a cross-sectional (z–x) plane (red line in Figure 1B), 1,024 B-scans were consecutively repeated (time gap Δt=4 ms). This consecutive scanning produced three-dimensional data cubes of the OCT intensity, I(z,x,t). We found that RBC passages appear as peaks in the time courses of voxel intensities positioned in capillary centers, I(z_i,x_i,t). This observation was supported by the following three arguments.

Figure 1.

(A) CCD image of the cortical surface through the cranial window. As we used 570-nm wavelength for illumination, dark pixels represent absorption by hemoglobin with RBCs. (B) The en face maximum intensity projection (MIP) of the 3D OCT angiogram through the depth of 0–400 μm. The red line indicates the scan line for cross-sectional dynamic OCT imaging. Voxel numbers, 400 × 200 (x × y) with the step of 1.75 μm (Nyquist sampling frequency). Ten volumes were averaged. (C) The cross-section of the 3D angiogram. Although we could identify >10 capillaries in the cross-section, data are presented over four selected capillaries (color circles). (D) RBC passage captured in OCT intensity time courses. The lines present the time courses of relative changes in the OCT intensity at the center of the capillary indicated by the blue circle in panel C and at its laterally (top) and vertically (bottom) neighboring voxels. (E) Different fluctuations across capillaries. The lines present the time courses of relative intensity changes at the four capillaries, with colors matching to those in panel C. As shown for the first capillary (blue) in panel D, the peaks in the other capillaries were also localized over a few neighboring voxels. Gaussian fits obtained by our algorithm were overlaid (black pieces). The fitting was performed for the 4-s data, but data are presented only for the first 2 seconds for clear visualization. The estimated RBC speed (mm/s) and flux (RBC/s) are presented on the right side. (F–H) Stripe patterns in OCT imaging. We repeated B-scans over four planes aligned with capillary segments (dashed lines in panel F), resulting in 3D data I(z,u,t) spanning the capillary segments (G). Then, we extracted 2D data I(ξ,t) along the capillary segment (ξ represents an axis along the capillary segment; solid lines in panel G). Stripe patterns were observed in I(ξ,t) (H). (I) Comparison between the fitting- and stripe-based measurements of the RBC speed. Bars=500 μm (A), 100 μm (B, C, and F), 20 μm, and 100 ms (H).

First, the peaks were localized in space and time, with a spatial extent consistent with RBC size. For a capillary chosen from the cross-section of the angiogram (blue circle in Figure 1C), we plotted the first 2-s time courses of relative changes in the OCT intensity at the center of the capillary and its neighboring voxels (Figure 1D). The time course at the capillary center exhibited several peaks, spanning over 3–4 neighboring voxels (∼10 μm in size). Voxels positioned in the tissue far from the capillary center did not exhibit such significant peaks. Second, the intensity peaks did not appear from animal motion (the dominant source of noise). OCT intensity has been shown to fluctuate owing to the animal's cardiac and respiratory motion;¹⁰ however, the peaks appeared at different moments across different capillaries (Figure 1E), whereas motion artifact-oriented fluctuations are generally global in space.¹⁰ Finally, the peaks move through the capillary. As shown in Figures 1F–1H, we found stripe patterns comparable to those found in traditional two-photon line scanning results⁷ but without any fluorescence. This observation of the stripe patterns strongly supports that the peaks in the time courses represent RBC passage through capillaries.

Estimation of RBC Speed and Flux using Gaussian Fitting

We developed an algorithm to automatically detect RBC passage peaks in the time courses and fit the peaks with the Gaussian functions. The number of peaks per unit time will correspond to the RBC flux, while the mean width of the Gaussian fits will be negatively correlated with the mean RBC speed.

For each time course, the algorithm moves an 80-ms time window while fitting the data points within the window to a Gaussian function:

where t₀ is the center time point of the window, and a, b, and c are fitting coefficients. Fitting resulted in the values of a, b, and c and the coefficient of determination R² for each time point. Based on these values, we detected the RBC passage peaks by thresholding a>50% and R²>0.5. The algorithm adequately detected RBC passage peaks as shown in Figure 1E. Variations in the peak amplitude across RBCs might originate from various scattering profiles and orientations of RBCs. Note that the optimum values for a and R² may vary with the imaging system and measurement sequence.

The RBC flux was simply estimated by counting the detected peaks per unit time. The RBC speed was estimated using the mean of the fitted b values, <b>:

where w_RBC, w_voxel, and w_kernel are the full-width half-maximum of the RBC, OCT voxel, and the Gaussian kernel used in the post processing, respectively. When an RBC passes a voxel with 1 mm/s, for instance, the peak width will result from the convolution of the RBC profile with the voxel profile, leading to (w_RBC²+w_voxel²)^1/2, where all profiles were assumed to be Gaussian. As the time course was further convolved with a Gaussian kernel to suppress noise, the final width will be (w_RBC²+w_voxel²+w_kernel²)^1/2. With <b> in millisecond, we used w_RBC=6.5, w_voxel=3.5 ( × 10 objective) or 7 ( × 5 objective), and w_kernel=2(2ln2)^1/2Δt (a Gaussian kernel with σ=Δt). Generally, <b> was obtained by averaging over 100+ peaks (4-s data), excluding 10% outliers for potential error due to RBC clumping. This speed estimation requires the assumption that RBCs have an equivalently identical size (see Discussion for detail).

The precision of our estimation was tested by repeating 10 runs of OCT imaging at the same cross-section. The RBC speed and flux were reliably estimated, with relative variations across runs of 7% and 12%, respectively. Note that physiological fluctuations might have a role in these variations.

In addition, the accuracy was tested through comparison with traditional stripe pattern-based measurements. We obtained the RBC speed from the stripe pattern (Figure 1H) as in the two-photon line scanning method.⁷ We also performed the above fitting-based estimation of speed from time courses extracted from the same data. These two estimations produced results within 9% of each other (Figure 1I).

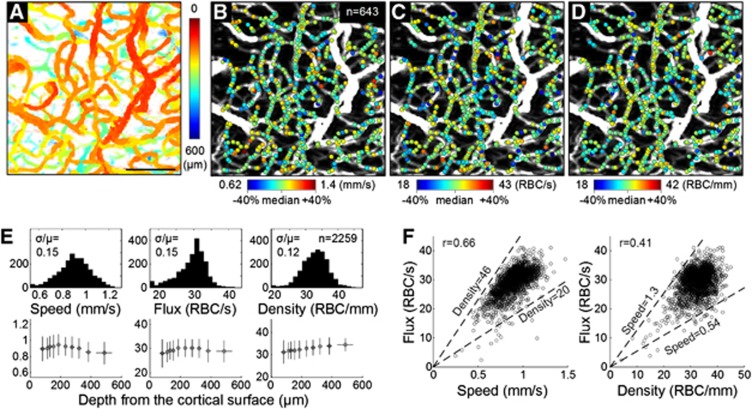
Volumetric Imaging of Capillary RBC Flux, Speed, and Density

We repeated the above cross-sectional dynamic imaging over 96 adjacent planes within the volume region of interest (total scan time=384 s). Capillaries in each plane were automatically identified, and their RBC speed and flux were estimated using the algorithm described above. In this 3D imaging, the × 5 objective was used for a larger imaging depth (Figure 2A). As a result, the RBC speed, flux, and density were estimated over a large number of positions across capillaries (n=643, Figures 2B–2D). The RBC linear density was obtained by the relation: Flux=Speed × density.

Figure 2.

(A) The en face MIP of the 3D angiogram with color indicating the depth from the cortical surface. Bar=100 μm. (B, C, D) Estimated RBC speed, flux, and density are presented as color spots on the MIP angiogram. We used relatively comparable ranges (median±40%) for all quantities. (E) Histograms (top) and depth profiles (bottom) of the RBC speed, flux, and density measured from three animals (n=2,259 measures in total). Comparable histogram ranges (median±40%) are used. In the depth profiles, data are presented as mean±s.d. (F) Correlations between the flux vs. the speed and density (n=2,259). Dashed lines indicate median±40% of the density (left) and speed (right).

This 3D imaging was repeated over three animals. Measurements of the capillary RBC flow properties were gathered over 2,259 positions in total. The ranges of the measured speed and flux overall agreed with those in the literature.^{7, 11, 12} The histograms and depth profiles of the measurements are presented in Figure 2E, although physiological interpretation of the profiles will require further study.

Discussion and conclusion

This Brief Communication demonstrates that OCT can be used to measure capillary RBC speed and flux over a large number of capillaries located at different depths at the same time. Although existing methods measure the flow properties capillary by capillary⁷ or depth by depth,³ the present method can measure them simultaneously over many capillaries located at different depths. This advantage makes it relatively easy to build spatial maps, as shown in Figures 2B–D, with a relatively short scan time. Here, we were able to estimate speed, flux, and density from ∼750 locations in 384 s. A shorter scan time will lead to less contamination arising from slow variations in the animal physiology. In addition, the present method can measure the flow properties even when a capillary is tortuous or spans through different depths. Our speed estimation does not depend, in principle, on the direction of RBC flow as it uses isotropic voxels. Finally, OCT requires no exogenous contrast agent, which makes the present technique potentially ready for in situ or clinical applications. For example, the present technique will be immediately applicable to human ophthalmology studies.

One of the disadvantages is the assumption used in the speed estimation that RBCs have equivalently similar sizes. RBCs exhibit different orientations while flowing through capillaries⁸ and thus different effective sizes in such imaging schemes as ours; however, its effect on speed estimation has been shown to be negligible (see Supplementary Figure S2 in Kamoun et al.,⁸ where the residence time line scanning method is conceptually similar to ours). We also validated that our estimation agrees with the stripe pattern-based estimation (Figure 1I). Another limitation of the present technique is practical upper limits in the measureable RBC speed and flux. For example, an RBC passing with 2 mm/s will result in a peak with a width of (w_RBC²+w_voxel²)^1/2/v=3.7 ms (in raw data with the × 10 objective), which is too sharp to be accurately characterized using our temporal sampling of Δt=4 ms. The upper limit in the measureable speed using the simple definition (w_RBC²+w_voxel²)^1/2/Δt will be 1.8 mm/s. Also, since our fitting required at least five time points, the measureable flux will be limited by 1/(5Δt)=50 RBC/s. As these upper limits are functions of Δt, they will be readily overcome with recently introduced faster OCT systems that permit sampling times of ⩽1 ms over large B-scans.¹³

The present technique will be useful for a range of cerebrophysiology studies, especially for those that benefit from simultaneous measurements over many capillaries. As an example, the technique will be used to measure flow responses during neural activation at several arterioles and capillaries at the same time, testing the hypothesis in vivo that capillaries actively regulate blood flow faster than arterioles.

The authors declare no conflict of interest.