Voxel-Wise Displacement as Independent Features in Classification of Multiple Sclerosis

Abstract

We present a method that utilizes registration displacement fields to perform accurate classification of magnetic resonance images (MRI) of the brain acquired from healthy individuals and patients diagnosed with multiple sclerosis (MS). Contrary to standard approaches, each voxel in the displacement field is treated as an independent feature that is classified individually. Results show that when used with a simple linear discriminant and majority voting, the approach is superior to using the displacement field with a single classifier, even when compared against more sophisticated classification methods such as adaptive boosting, random forests, and support vector machines. Leave-one-out cross-validation was used to evaluate this method for classifying images by disease, MS subtype (Acc: 77%–88%), and age (Acc: 96%–100%).

1. INTRODUCTION

Discriminant analysis using classifiers derived from magnetic resonance images (MRI) is an important tool in the study of neurological diseases. Several MR features have been used to classify between healthy controls and patients with disease^1–5. Our work here focuses primarily on classification using features derived from displacement fields learned by deformably registering a MR image to a template. One advantage to using these deformation based features is the ability to infer group shape differences from the classifier. For example, Golland et al.⁶ demonstrated this by analyzing the gradient of the classifier function, which described a “discriminative direction” for hippocampus shape change between populations. Similarly, Qiu et al.⁷ used a linear discriminant on surface deformations and analyzed the normal of the separating hyperplane to characterize population differences.

Related to our approach is a group of methods known as deformation-based morphometry (DBM), which finds regions with significant population differences by observing volume changes through the Jacobian of the displacement field⁸ or performing a significance test on the population means of the displacements^9,10. Our method differs from DBM in that we are focused on building a classifier between two populations, while DBM is primarily interested in localizing areas with significant differences. One advantage of our approach is that the classifiers found by our method can potentially be used to model the direction of change between two populations, such as in Golland et al.⁶

2. NEW WORK PRESENTED

While a number of works have explored using deformation based features for classification, these methods have all traditionally used only a single classifier on these features. For example, Lao et al.¹¹ performed classification using support vector machines (SVM) with volume-preserving features calculated from the Jacobian of the displacement fields. Golland et al.⁶ also used SVM, but used distance transforms to construct the feature vectors. Rueckerk et al.¹² performed principle component analysis on the control points of b-spline representations of the displacement fields. We present an approach that moves away from these single classifier frameworks. Instead, we use displacement field vectors as independent features that are classified individually on each voxel. This creates a set of weak classifiers that we then combine together to produce our final classification. Our approach follows in the spirit of multiple classifier machine learning techniques such as boosting¹³ and classifier fusion.¹⁴

3. METHODS

3.1 Voxel-wise Displacement Vectors as Independent Features

Given a subject image, S(x), and a template image, T(x), we use deformable registration to find a mapping v: ℝ³ → ℝ³, such that S(x + v(x)) ≃ T(x). This mapping is generally found by maximizing a cost function that describes the similarity between S(x + v(x)) and T(x). Popular examples of such similarity functions include mutual information, cross correlation, and sum of squared differences.¹⁵

In practice, the mapping v is represented as a displacement field that consists of a ‘pull-back’ vector located at each voxel in the template image. These vectors describe the direction and magnitude from a voxel in the template image to its corresponding location in the subject image. For a group of subjects, these displacement fields can be used to approximate the morphological difference between each subject and the template. Since the displacement vectors are all rooted in the template space, the subjects’ displacements at the same voxel can be analyzed as a group. Figure 1 shows the registration result and the three components of the displacement field for two subjects registered to the same template.

Figure 1.

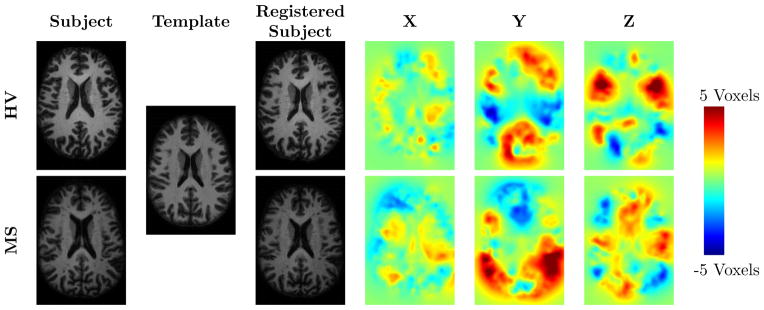
Shown are subject, template, registered subject, and the X, Y, and Z components of the displacement field images for a HV and MS subject.

Due to the regularization in the registration and the structural relationship between different subjects, we know that adjacent voxels in a displacement field are spatially dependent. However, in this method, we propose treating the vectors at each voxel as independent features. We do this by building a separate classifier at each voxel and then aggregating the collection using a simple fusion technique.

3.2 Classification Using Linear Discriminants and Majority Voting

We are given a set of N subject images, each with a classification, y ∈ {−1, 1}, and a displacement field, v, relative to the same template image. We designate the pairs, {v₁, y₁}, {v₂, y₂}, …, {v_N, y_N }, as the training set for our classification algorithm. We are interested in using this training set to build a classifier, H(v), that is able to use a displacement field to correctly estimate the classification of an unseen subject image. We propose first building a weak classifier at each voxel x:

$$h_x(·)=\underset{h(·)}{argmin}\sum _{i=1}^{N}I(y_i\ne h(v_i(x))),$$ (1)

where I is the indicator function, and h can be any standard classifier such that h: ℝ³ → {−1, 1}. For the purposes of demonstration (with the added benefits of speed and simplicity) we use Fisher’s linear discriminate¹⁶ as our voxel-wise classifier. Clearly, we do not expect the classifier at any particular voxel to be very accurate for classifying the whole image. However, several works¹⁷ have shown that a large number of weak classifiers can be combined together to perform a much more accurate classification. To perform this classifier fusion, we first compute the signed training error, α(x), at each voxel,

$$\alpha (x)=\frac{1}{N}\sum _{i=1}^{N}I(y_i=h_x(v_i(x)))-0.5.$$ (2)

These errors are then used to weight the classification from each of the weak classifiers, which are summed together to form H(v). Given a displacement field, ṽ, from an unseen subject, we estimate its classification with,

$$H(\stackrel{\sim }{v})=\text{sign}\left(\sum _x\alpha (x)h_x(\stackrel{\sim }{v}(x))\right).$$ (3)

This formulation is simply a weighted majority voting of the weak classifiers, h_x, over all the voxels in the image. Again, we choose this approach purely for brevity. More sophisticated forms of classifier fusion¹⁸ could potentially be used to improve on this method.

3.3 Preprocessing and Displacement Field Creation

All the brain images were extracted from MR head scans using SPECTRE¹⁹ to remove all non-brain voxels. For the purpose of this paper we are only interested in using local morphological differences for the classification. Hence, rotational, translational and size differences were removed by affinely registering²⁰ each image to a common space.

The displacement fields used in our classification were constructed by deformably registering each subject image to a common template. To minimize potential bias, the template was chosen to be an average brain created from all the subjects through the average template building tool provided in ANTS²⁰. The deformable registrations were performed using SyN²¹, a symmetric diffeomorphic fluid based registration, which was highly ranked in both accuracy and robustness in a comparison among publicly available registration algorithms²².

4. RESULTS AND DISCUSSION

To evaluate our approach, the template was built using 78 brain images–36 age-matched healthy volunteers (HV) as controls and 42 MS subjects (with subgroups: 29 Relapsing Remitting (RRMS); 8 Secondary Progressive (SPMS), 4 Clinically Isolated Syndrome (CIS), and 1 Primary Progressive (PPMS)). The images are MPRAGE (TR = 10 ms; TE = 6 ms; α = 8°; resolution = 0.828×0.828×1.1 mm) acquired on a Philips 3T scanner.

The displacement fields and subject classifications were used as inputs for five leave-one-out, cross-validation experiments. In each case the classification performance was compared between the proposed method and three standard machine learning tools from the Weka²³ software package – Random Forest¹⁷(“RandomForest” in Weka), Support Vector Machines²⁴ (“SMO” in Weka), and Adaptive Boosting¹³(“AdaBoostM1” in Weka). For the three standard tools, the displacement fields were reshaped into one-dimensional vectors so that they could be used directly in the classifiers. The following sections will describe the details for these experiments.

4.1 Downsampling and Parameter Tuning

While not a problem for our proposed method, the large size of the displacement fields was a major concern when used with the three standard classification tools. Each displacement field had a three dimensional vector at each of roughly eight million voxels (256 ×256 ×120). For the larger experiments, this meant the three standard tools took several hours to a full day just to train on the data. In comparison, our approach took on average 2–3 minutes to train and never exceeded more than 10 minutes. We believe this computational efficiency comes from the linear complexity of our method (with respect to the number of voxels), and overall less memory access and usage, since the majority of the computation is separable at each voxel. Although not implemented for this paper, this separability also makes our approach easily parallelizable if faster computation is necessary.

In order to run the comparison in a reasonable time, each displacement field was downsampled in each dimension before being classified by the four algorithms. This is a technique that is often performed to make the size of such displacement fields more manageable^25,26. In each experiment, the displacement field was downsampled by both a factor of two in each direction and also eight in each direction.

Several parameters for the three standard tools were manually selected to give the best average performance over all the experiments. These parameters were: for random forest – “Number of Trees”, for support vector machine – “Complexity Constant”, and for adaptive boosting - “Number of Iterations”. All other parameters were left as the default settings from Weka. We recognize that the accuracy for these methods could potentially be improved by tuning additional parameters and using more complex parameter selection approaches. However, we also note that no tuning was performed at all for our proposed approach.

4.2 Classification of Age

Two age classification experiments were performed using just the healthy volunteer data: the oldest five HV (avg. age: 55.5) vs. the youngest five HV (avg. age: 22.4), and the oldest 11 HV (avg. age: 49.9) vs. the youngest 11 HV (avg. age: 23.6). We see from Table 1 that our classifier is highly accurate for both classifications. Compared to the three standard approaches, our method was on average 10–20% more accurate. As we would expect, the accuracy dropped as the mean age between the populations became closer.

Table 1.

Experiment results on deformation fields downsampled either by a factor of two or eight in each dimension. Shown are the classification accuracy of AdaBoost (AB), Random Forest (RF), and support vector machine (SVM) compared to the proposed voxel-wise displacement classifier (VDC). For each case, the downsampling factor is indicated as a suffix to the method name.

Experiment	AB-2	AB-8	RF-2	RF-8	SVM-2	SVM-8	VDC-2	VDC-8
5 Youngest vs. 5 Oldest	0.40	0.50	0.90	0.70	0.70	0.70	1.00	1.00
11 Youngest vs. 11 Oldest	0.5	0.64	0.64	0.41	0.50	0.50	0.96	0.96
All MS vs. All Controls	0.60	0.56	0.62	0.64	0.50	0.51	0.73	0.76
SPMS vs. Controls	0.56	0.88	0.63	0.63	0.44	0.38	0.88	0.88
RRMS vs. Controls	0.48	0.54	0.52	0.48	0.41	0.41	0.77	0.79

4.3 Classification of Multiple Sclerosis

Three disease based classifications were performed using the data: the 29 RRMS patients vs. 29 age-matched HV, the eight SPMS patients vs. eight age-matched HV, and all 42 MS patients vs. all 36 HV. Table 1 shows that the proposed approach, again, had the highest accuracy in each of these classification experiments. We also observe that, for each of the experiments, the level of accuracy matched our expectation for the MS subtype being compared.

Relapsing-remitting MS (RRMS) is considered an early stage subtype of MS that is characterized by sporadic attacks. Hence, we would expect the brain morphology for the mild cases to be very similar to the healthy volunteers, and therefore more difficult to classify. In contrast, secondary-progressive MS (SPMS) is a late stage subtype that follows RRMS, and is characterized by a consistent progression of disability. For several of these patients, we could visually see significant morphological change in their brain MRI. This contributes to why the overall accuracy is fairly high for that experiment. Lastly, for the “all MS vs. all HV” experiment, we are actually grouping together four different subtypes of MS that could have entirely separate morphological characterizations. This makes such a classification task extremely difficult, and hence the low accuracy result.

4.4 Comparison Against Existing Literature

Deformation-based age classification have been reported in several work^11,27. Although different data was used, we see that the accuracy for our method is comparable, if not superior, to the 70–98% accuracy reported by these methods. We note, however, that these approaches are not direct comparison to our method. Their primarily focus was on using sophisticated feature selection to restrict the feature space for the classifier. In contrast, our method is focused on improving the classifier itself. The two are complements of each other, and it would be rather straightforward to substitute the standard classifier (i.e. SVM) in these approaches with our method in order to gain the benefits from both methods.

Several work have reported on discriminant analysis of MS and its subtypes, but (to our knowledge) only when using unconventional MR acquisitions such as magnetization transfer ratio (MTR) images¹. Since the data used were significantly different, we can only make marginal comparisons with our results. For example, we see that our accuracy is overall lower than the MTR histogram approach presented by Dehmeshki et al.¹, which achieved a classification accuracy of 86–92% for various MS subtypes. Nevertheless, our method performed surprisingly close given that we used a standard MR acquisition that lacked the features provided by these specialize scans.

5. CONCLUSION

We have presented a deformation based classifier that breaks away from the standard single classifier approach by assembling individual weak classifiers at each voxel to generate a final classification. Our approach produced high accuracy when classifying morphological differences in age and various subtypes of MS. We showed that our classifier is superior to using standard classifiers directly on the displacement fields, and that our classification accuracy is comparable to those reported when using sophisticated feature selection methods and unconventional MR modalities. In future work, we intend to utilize the classifiers learned from our method to perform shape based statistical modeling, and potentially infer the direction of change between the various MS populations.