Automatic classification of scar tissue in late gadolinium enhancement cardiac MRI for the assessment of left-atrial wall injury after radiofrequency ablation

Abstract

Radiofrequency ablation is a promising procedure for treating atrial fibrillation (AF) that relies on accurate lesion delivery in the left atrial (LA) wall for success. Late Gadolinium Enhancement MRI (LGE MRI) at three months post-ablation has proven effective for noninvasive assessment of the location and extent of scar formation, which are important factors for predicting patient outcome and planning of redo ablation procedures. We have developed an algorithm for automatic classification in LGE MRI of scar tissue in the LA wall and have evaluated accuracy and consistency compared to manual scar classifications by expert observers. Our approach clusters voxels based on normalized intensity and was chosen through a systematic comparison of the performance of multivariate clustering on many combinations of image texture. Algorithm performance was determined by overlap with ground truth, using multiple overlap measures, and the accuracy of the estimation of the total amount of scar in the LA. Ground truth was determined using the STAPLE algorithm, which produces a probabilistic estimate of the true scar classification from multiple expert manual segmentations. Evaluation of the ground truth data set was based on both inter- and intra-observer agreement, with variation among expert classifiers indicating the difficulty of scar classification for a given a dataset. Our proposed automatic scar classification algorithm performs well for both scar localization and estimation of scar volume: for ground truth datasets considered easy, variability from the ground truth was low; for those considered difficult, variability from ground truth was on par with the variability across experts.

1. INTRODUCTION

Atrial fibrillation (AF) is the most common heart arrhythmia, affecting millions of people worldwide. AF is associated with a heightened risk of stroke and an overall increase in morbidity and mortality.^1–3 Catheter-based radiofrequency ablation (RFA) therapy is a promising procedure for treating AF, with the potential to completely cure many patients. A successful RFA procedure, however, relies on accurate lesion delivery in the left atrial (LA) wall. With as many 25%–60% of patients suffering a recurrence of AF after RFA, the assessment of scar patterning and extent after RFA is important for understanding when and how procedures fail and for planning redo ablation procedures.⁴

Late gadolinium enhancement cardiac MRI (LGE MRI) at three months post-ablation has proven effective for noninvasive assessment of the location and pattern of scar formation from RFA. Current clinical methods developed at the University of Utah rely on manual segmentations of scar tissue in the LA wall to produce detailed 3D scar maps.^4–6 While effective for assessing the outcome of RFA, manual scar maps in LGE MRI can be time consuming and are prone to inconsistencies among different expert image analysts. Additionally, it is time consuming to train a new technician or researcher to be able to perform scar segmentations effectively.

A fully automatic scar segmentation algorithm promises faster and more consistent results, but has been difficult to develop due to the relatively unpredictable and inconsistent mean intensities associated with scar enhancement across LGE MRI images. Simple intensity thresholding techniques, for example, have not been demonstrated to be effective for LA scar segmentation. Automatic segmentation is further complicated by the high variability in image quality and contrast that is characteristic of cardiac LGE MRI.

To address the problem of variable image quality and scar intensity profiles in cardiac LGE MRI post-ablation images, we have evaluated a variety of image metrics for unsupervised clustering of scar tissue and compared the results in each case to a ground truth scar segmentation dataset. Ground truth was constructed from a cohort of scar maps that have been segmented by multiple experts, including practicing cardiologists specializing in cardiac imaging. Each clustering approach uses the k-means algorithm on feature vectors of voxel texture and intensity values and is compared against ground truth using metrics for overlap and overall scar volume. From this study, we identified a clustering approach based on normalized image intensity that performs on par with the expert segmenters. The proposed algorithm is simple to implement, runs in seconds on a typical image, and can be used reliably by the less experienced technicians and researchers to produce scar maps in post-ablation clinical images.

2. RELATED WORK

Current state-of-the-art studies in analyzing post-ablation scar in the left atrium rely almost exclusively on manual scar classification.^{4, 7} To date, the authors are not aware of any published fully-automatic scar segmentation for the LA. Automated scar analysis has been shown for the ventricle, particularly in clinical evaluation of myocardial infarction,⁸ but these algorithms have not been demonstrated to work in the atrium. The atrium has a much more thin and flexible wall than the ventricle, making detailed image acquisition challenging and automated analysis more difficult.

Some work has been published for automatic segmentation of the LA wall,^{9, 10} but this paper is concerned with the classification of scar within the LA wall, and not with determination of LA wall boundaries. Here the scar classification is done within manual wall segmentations, but the proposed scar segmentation approach could be used equally with little or no modification within an automatic wall segmentation.

3. METHODS

3.1 Ground truth data set

To construct our ground truth dataset for LA scar segmentation algorithm development and validation, we chose 34 patients who underwent RFA for AF at the University of Utah Hospital. This group was selected on the basis of patients who completed MRI scans at roughly three months post-ablation. Scanning was performed using a 3-T Verio MR scanner (Siemens Medical Systems, Erlangen, Germany). LGE MRI images were acquired about 15 minutes after gadolinium contrast agent injection using three-dimensional inversion-recovery-prepared, respiration-navigated, ECG-gated, gradient-echo pulse sequence with fat saturation. Typical parameters for this acquisition in post-ablation AF patients are given in McGann, et al.⁴ This work was conducted under approval by the institutional review board at the University of Utah and was compliant with the Health Insurance Portability and Accountability Act of 1996.

A ground truth LA scar map for each patient data set was created from multiple manual scar segmentations in the LGE MRI images by 5 expert segmenters at the University of Utah Hospital and the Comprehensive Arrhythmia Research and Management (CARMA) Center. The segmenters consisted of two cardiologists with specialties in medical imaging and three lab technicians with significant experience analyzing clinical cardiac LGE MRI images. To measure intra-observer variability, 8 of the 34 patient scans were randomly chosen and presented to the segmenters three separate times. All data was anonymized prior to segmentation and repeated scans were given in a random order so that segmenters could not easily tell which scans were repeated.

Each expert segmenter used a threshold tool in the Corview image processing software¹¹ to select a lower and upper threshold range of voxel values that corresponded to LA wall scarring in each scan. The threshold selected by each expert was then used to generate a scar map within a segmentation of the LA wall. For this study, all LA wall segmentations were done manually by a single expert technician using contouring tools in the Corview software. LA wall segmentations were not visible to the expert observers during scar threshold selection.

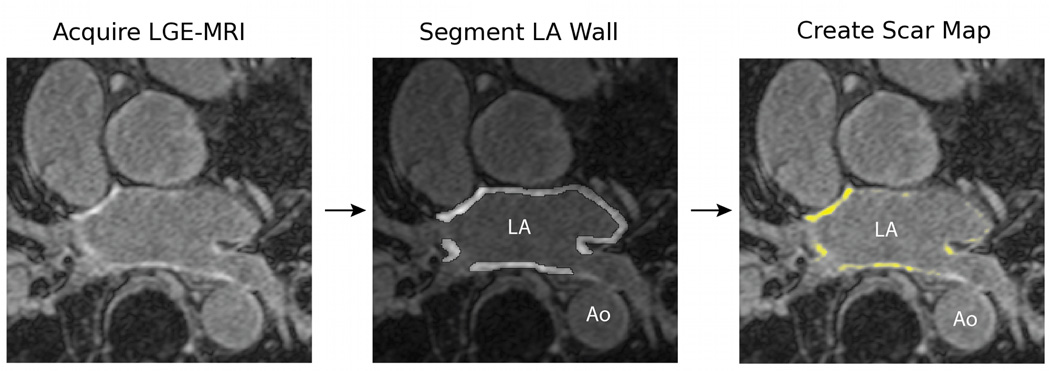
The general process of LA scar segmentation is illustrated in Figure 1. The panel at the left shows a detail of a single slice of an LGE MRI image of the heart. The panel in the middle shows one slice of a segmentation of the LA wall region. The LA wall segmentation excludes the pulmonary veins, the mitral valve, and the left-atrial appendage. The aorta (Ao) is also indicated in this image for reference. The panel at the right shows the regions within the LA wall that are classified as scar.

Figure 1.

The process of generating a scar map. An LGE MRI is acquired after an ablation procedure and the LA wall is identified and segmented manually. The voxels in the LA wall segmentation are then classified as scar or not and a scar map is generated. Current clinical methods use manual classification of scar tissue, while this paper presents an approach to automating the final classification step to generate the scar map.

We used the Simultaneous Truth and Performance Level Estimation (STAPLE) algorithm¹² to compute an estimate of true ground truth from the 5 manually generated scar maps for each patient dataset. The STAPLE algorithm produces a probabilistic segmentation from a set of expert segmentations. Pixel values in this segmentation represent the probability that a given pixel location represents scar. For this study, we thresholded each STAPLE probability map at 90% probability to create a binary ground truth segmentation.

3.2 Automatic scar classification approach

3.2.1 Scar Segmentation

LGE MRI is highly variable with respect to image quality, contrast, and mean intensity of gadolinium enhancement in the LA, so we used an experimental approach to identify an effective automatic scar segmentation algorithm. We evaluated K-means clustering^{13, 14} on 14 different texture metrics proposed by Haralick,15 in combination with both normalized voxel intensity and a Sobel edge map,¹⁶ for their ability to classify scar voxels in our ground truth datasets.

Clustering provides a mechanism for statistically separating voxels into groups that are analogous to different tissue types (scar, blood, healthy cardiac wall tissue, etc.). K-means clustering was chosen as a simple, unsupervised approach that lets us explicitly vary the number of tissue classes, but doesn’t require tuning other free parameters. In this work we assume that scar tissue corresponds to the cluster with the highest mean voxel intensity, which is a reasonable assumption when the LGE MRI image has been acquired after an appropriate gadolinium washout period. In this analysis, the number of discernible tissue types in any given LGE MRI image is also unknown, and so the number of clusters is varied in our experiments.

For each of the ground truth patient LGE MRI images, we ran K-means clustering multiple times using each image feature alone, and then in vector combinations of up to three features. Parameters were also varied in separate runs as follows: Size of the texture feature neighborhoods were varied from 3 × 3, 11 × 11, to 21 × 21, and the number of clusters (tissue classes) was varied from 3 to 10. Clustering was limited to image features derived from voxels within the LA. In all, we tested a total of 2304 combinations of features and parameters on all ground truth images. Test runs were scripted and took several days to process on a standard desktop machine using the implementation of K-means found in the OpenCV toolkit.¹⁷

For each of the K-means runs described above, we chose the cluster with the highest mean raw voxel intensity as the scar segmentation. Each segmentation result was compared to the ground truth scar map using the performance metrics for overlap of segmentations and total percentage of scar in the left atrial wall, as described further in Section 3.3. Our goal was to explore the parameter space to identify the combination of image features and parameters with the best resulting score.

3.2.2 Image features

As described above, we examined normalized voxel intensity, the Sobel filter, and the 14 texture metrics proposed by Haralick as image features. We use normalized voxel intensity (NVI) because of the assumption that, in LGE MRI, scar tissue should exhibit higher intensity values than surrounding normal tissue. Intensity is normalized to zero mean and unit standard deviation to compensate for the variability in LGE MRI mean intensity and contrast. The Sobel edge detection filter¹⁶ was used to test the usefulness of edges or boundaries in classifying scar. We also included several statistical measures from Haralick’s texture metrics including variance, Sum Average, Sum Variance, and Difference Variance to test whether statistical properties of neighborhoods might be useful in identifying scar. Texture metrics on distributions of intensity, including Uniformity (angular second moment), Inverse Difference Moment, Contrast, and Correlation were used to test whether scar exhibits any particular distribution profile. Finally, we examined information theoretic metrics such as Entropy, Difference Entropy and Sum Entropy, as well as the Information Correlation 1 and 2 textures and the Maximal correlation coefficient.

We refer the reader to Haralick’s work on texture metrics¹⁵ for specific description and computation details. We implemented all metrics in C++ using the Insight Toolkit.¹⁸

3.3 Comparison methods

To evaluate performance of the proposed automated scar segmentation algorithm, we compared results to the ground truth dataset using three different metrics. To evaluate overlap with ground truth we compute the Dice coefficient for each dataset. To better account for small overlap differences we next computed the XOR overlap. Finally, we compared the overall percentage of voxels in the LA wall that are classified as scar, which is a clinical metric used at the University of Utah.

3.3.1 Dice Coefficient

To measure overlap with ground truth, we used the standard Dice coefficient,¹⁹ which is given by

$$D(A,B)=\frac{2*\Vert A\Lambda B\Vert }{\Vert A\Vert +\Vert B\Vert },$$ (1)

where A and B are the two voxel sets for comparison.

3.3.2 XOR Overlap

For the specific case of finding overlap among scar in the LA wall, however, the standard Dice coefficient overlap is biased by the total amount of scar in the LA wall, which is highly variable among datasets. Thus, if the scan does not have a significant amount of scar, then even small differences between maps create large changes in the above ratio. To account for this bias, we also compute the following overlap measure, which we call XOR overlap:

$$O(A,B,W)=\frac{\Vert W\Vert -\Vert A\otimes B\Vert }{\Vert W\Vert },$$ (2)

where W is the set of voxels that compose the LA Wall. This overlap measure emphasizes the differences between the overlapping scar maps, and is not affected by the size of the scar map area.

To further illustrate the idea of bias in the Dice coefficient, consider two scar maps A,B we wish to compare, and two additional scar maps C,D we wish to compare, where ‖A‖ + ‖B‖ << ‖C‖ + ‖D‖ and k = ‖A Λ B‖ = ‖C Λ D‖. In the context of scar in the LA wall, we would expect that the overlap measure of these two scar map comparisons would be close if not equal, given that ‖A Λ B‖ = ‖C Λ D‖. However, D(A,B) >> D(C,D) because of the size difference of A,B and C,D. This can be misleading when scoring different automatic and manual scar maps.

Now consider the same set of scar maps A,B,C,D where ‖A‖+‖B‖ << ‖C‖+‖D‖, j = ‖A⊗B‖ = ‖C⊗D‖, and A,B,C,D ∈ W. Again, in the given context we would expect the overlap measure of these two scar map comparison to be close if not equal, and indeed $O(A,B,W)=\frac{\Vert W\Vert -j}{\Vert W\Vert }=O(C,D,W)$. Even if we relax the constraint A,B,C,D ∈ W so that A,B ∈ W and C,D ∈ Y, O(A,B,W) ≈ O(C,D, Y) so long as ‖W‖ ≈ ‖Y ‖, which, for our data, we’ve found to be a safe assumption (patients for the most part have similar LA wall volumes), in relation to the varying size of scar maps.

3.3.3 Scar Percentage

To evaluate the total extent of scarring in the LA, which is an important measure for clinical research, we computed the percentage of scar in the LA wall as

$$V(A,W)=\frac{\Vert A\Vert }{\Vert W\Vert }.$$ (3)

4. RESULTS

4.1 Top performing metrics

The top performing classification metric was found to be statistically normalized voxel intensity (NVI) in 4 clusters. Other high performing texture metric combinations included NVI with Haralicks 2nd Information Correlation Texture (2IC) in 5 clusters, NVI with Haralicks Uniformity and 2IC textures in 6 clusters, and NVI with Haralicks Maximum Probability texture in 6 clusters, which all gave similar results, but did not improve the results significantly over NVI alone.

We note that the Haralick texture metrics did not improve identification of scar regions significantly over NVI alone. Several factors may contribute to this trend. Expert segmentations and the resulting ground truth were generated mainly based on voxel intensity, via visual inspection, thus, it is likely that voxel intensity would be an especially effective identifier. It is also possible that the resolution of the images compared to the size of the LA wall (a few millimeters across) is too limited to reliably produce consistent texture signals across different images.

4.2 Automatic scar map performance

In this section we report results for the automatic scar clustering using NVI in 4 clusters, which we found to be the best performer. Overall, automatic scar segmentation compared favorably with the ground truth scar maps in both location and quantity of scar.

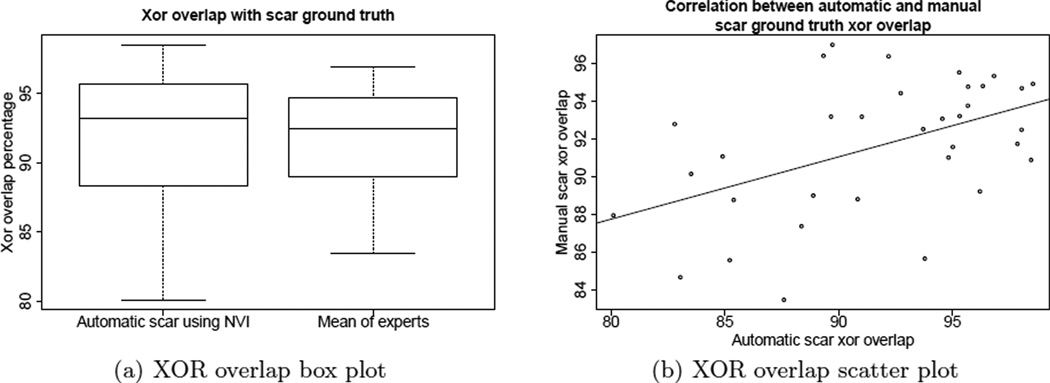
The plots in Figure 2 suggest that automatic scar classification using normalized voxel intensity (NVI) performs favorably in terms of scar localization when compared to manual expert scar classification. The box plot in Figure 2(a) indicates that automatic scar map XOR overlap varied about 2% more than manual experts, though we note that expert results are biased towards higher accuracy given that they were used to produce the ground truth data. The automatic scar map had a mean of 91.7% and a standard deviation of 5.2%, while the manual scar map XOR overlap had a mean of 91.6% with a standard deviation of 3.5%.

Figure 2.

(a) The box plots show that automatic scar difference varied about 2% more than manual experts, when using XOR overlap. (b) The scatter plot shows the performance of the automatic algorithm follows that of the manual, when measured using XOR overlap.

The scatter plot in Figure 2(b) shows the significant correlation between automatic scar XOR overlap and manual scar overlap performance, indicating that the automatic algorithm tends to perform worse on datasets that humans also find difficult to classify (Pearsons coefficient of 0.48, p=0.0035). The automatic segmentation tends to perform the best on scans with more consistent manual segmentations.

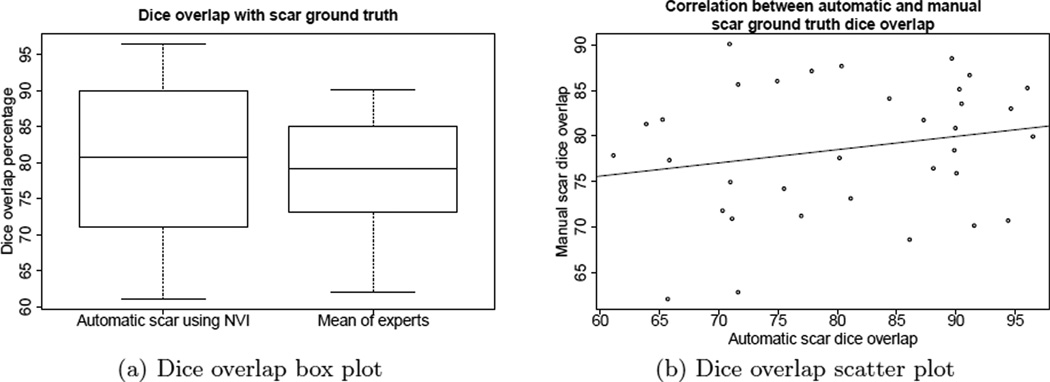
The plot in Figure 3 shows similar results but using the Dice overlap measure. As described in detail in Section 3.3, we express some concern about the bias that the Dice coefficient gives for data sets where the volume of the scar map is large, over data sets where the volume of the scar map is small. In contrast to the XOR overlap comparison, the Dice overlap measure reports overlap in one case as low as 60% for both automatic and manual scar maps. We attribute the less favorable comparison using this measure largely to that bias, as both of the other measures reported better results.

Figure 3.

(a) The box plots show that automatic scar using NVI difference varied about 3% more than manual experts, using Dice overlap. (b) The scatter plot shows no correlation between the performance of the automatic algorithm and the manual approach, when measured using Dice overlap.

The automatic algorithm, however, still performed on par with the manual scar map when measured using the Dice coefficient. The automatic scar map Dice overlap varied about 3% more than manual scar map as shown in Figure 3(a). The automatic scar map Dice overlap measures had a mean of 80.7% with a standard deviation of 10.6%, while the manual scar map Dice overlap measures had a mean of 78.6% with a standard deviation of 7.2%.

There was no correlation between automatic scar Dice overlap and the manual scar overlap performance (Pearson’s coefficient of 0.21, p=0.2263), however we present the same scatter plot for the Dice overlap data in Figure 3(b) for completeness. Again, while this measure did not show correlation, we conclude this is more a product of the measure than the algorithm, as the other two measures (one used in clinical research) do show correlation.

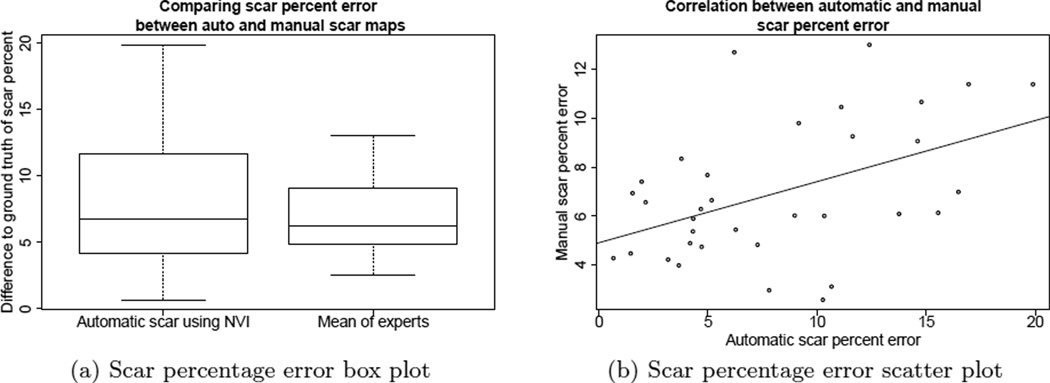
Percentage of scar in the LA wall is a clinical measure that has shown potential for interesting applications in AF research and treatment.^4–6 Figure 4 shows the difference of the automatic scar percentage and the ground truth percentage, as compared to the mean of the differences between each of the expert scar classification and ground truth. Figure 4(a) shows how the difference in the automatic scar varies 3% more than the experts. Figure 4(b) shows a significant correlation between the two (Pearsons coefficient of 0.46, p=0.0056): as the differences increase with the automatic scar, the manual differences also increase, i.e., the performance of the automatic scar classification is on par with the manual classification. The automatic scar map percentage error mean was 8.1% with a standard deviation of 5.2%, while the manual scar map percentage error mean was 6.9% with a standard deviation of 2.8%. Automatic scar percentage error varied about 2% more than manual experts.

Figure 4.

(a) The box plots show that automatic scar percentage error varied about 2% more than manual experts. (b) The scatter plot shows the performance of the automatic algorithm tracks that of the manual.

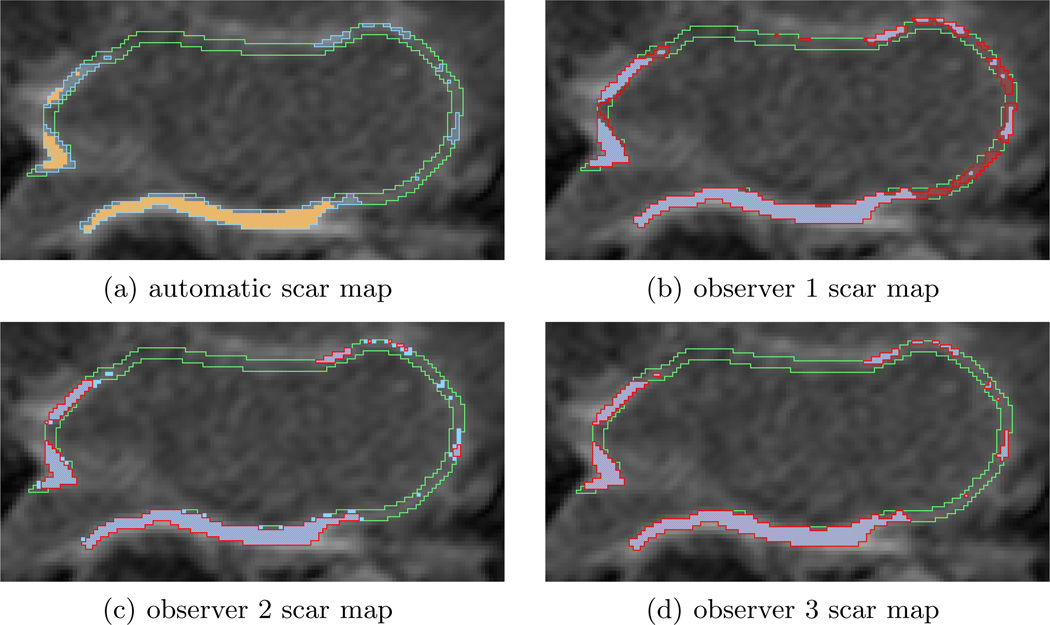
Figure 5 shows an example automatic scar map compared to several manual (expert) scar maps and ground truth. A relatively inconsistent result (only 82% XOR overlap) is displayed to better illustrate scar map overlap. Figure 5(a) shows the automatic scar map overlaid on top of the ground truth scar map. In this case the automatic scar map is smaller than the ground truth. The manual approach also performed inconsistently, as can be seen in Figures 5(b),(c),(d). This figure also illustrates some of the variability in the manual approach: Figure 5(b) is more generous in identifying scar than ground truth, while Figure 5(c) is more particular, and Figure 5(d) is actually an exact match on this slice of the scan (other slices have some mismatch for this observer).

Figure 5.

A comparison of the automatic and 3 observer scar maps to ground truth overlaid on the LGE MRI. (a) Automatic scar map (yellow solid) and ground truth (blue stripe) in the LA wall (green outline). (b) Observer 1 scar map (red stripe) and ground truth (blue solid). (c) Observer 2. (d) Observer 3.

4.3 Intra observer study findings

As described above, eight of the 34 scans were repeated 3 times to measure intra-observer variability. Our intra-observer study on the ground truth dataset showed a mean standard deviation of scar percentage among scar maps of the same image from a single expert to be 4.3% with a standard deviation of 2.7%, a maximum of 9.3% and minimum of 0.9%. We were unable to show any significant correlation between the intra-observer variability and inter-observer variability for a single scan.

By contrast, the proposed automatic scar map algorithm exhibited only minimal variability from differences in random initializations, which can be mitigated using standard approaches to k-means clustering.¹³

The variability of different observers in classifying scar for a single scan (see, for example, Figure 5) indicates that some scans are more difficult for experts to agree on, such scans can be considered ”difficult to classify”. This difficulty in classification may be related to image quality, which would explain why the automatic algorithm also performs inconsistently on those scans, as illustrated in Figures 2(b),4(b).

5. CONCLUSION

We have introduced an automatic algorithm for segmenting scar in the LA of cardiac LGE MRI that has been verified against a manual ground truth scar map data set generated by expert observers. The proposed approach clusters pixels on normalized voxel intensity and was chosen as the best combination of image features and parameters from several thousand possible combinations. The proposed algorithm improves the speed and consistency of scar classification over manual segmentation, and demonstrates accuracy that is comparable to the expert ground truth in both location and volume. Because of its ease of use, the automatic algorithm requires less training and expertise than manual segmentation, making post-RFA LGE MRI analysis more accessible to researchers and clinicians.

One attractive aspect of this algorithm is its simplicity. The algorithm is simple to implement and its parameters are easy to interpret. Some of its built-in assumptions, however, such as the equivalence of variance across classes inherent in K-means, are likely not entirely realistic for scar in the LA wall. In future work we hope to refine those assumptions and improve results further. For example, relaxing the assumption of equivalent variance, and allowing each cluster to have a different standard deviation has improved results in preliminary tests. Relaxing select other assumptions may lead to further improvements.

As described in Section 4.2, both manual and automatic approaches perform poorly on some scans - those considered difficult to classify. Most likely due to image quality, future work will explore why and possible ways of quantifying how difficult the image is to classify, as well as how to improve classification on those scans.