Abstract
Dual-laser flow cytometric resonance energy transfer (FCET) is a statistically efficient and accurate way of determining proximity relationships for molecules of cells even under living conditions. In the framework of this algorithm, absolute fluorescence resonance energy transfer (FRET) efficiency is determined by the simultaneous measurement of donor-quenching and sensitized emission. A crucial point is the determination of the scaling factor α responsible for balancing the different sensitivities of the donor and acceptor signal channels. The determination of α is not simple, requiring preparation of special samples that are generally different from a double-labeled FRET sample, or by the use of sophisticated statistical estimation (least-squares) procedures. We present an alternative, free-from-spectral-constants approach for the determination of α and the absolute FRET efficiency, by an extension of the presented framework of the FCET algorithm with an analysis of the second moments (variances and covariances) of the detected intensity distributions. A quadratic equation for α is formulated with the intensity fluctuations, which is proved sufficiently robust to give accurate α-values on a cell-by-cell basis in a wide system of conditions using the same double-labeled sample from which the FRET efficiency itself is determined. This seemingly new approach is illustrated by FRET measurements between epitopes of the MHCI receptor on the cell surface of two cell lines, FT and LS174T. The figures show that whereas the common way of α determination fails at large dye-per-protein labeling ratios of mAbs, this presented-as-new approach has sufficient ability to give accurate results. Although introduced in a flow cytometer, the new approach can also be straightforwardly used with fluorescence microscopes.
Introduction
Fluorescence resonance energy transfer (FRET) is a powerful and popular method for the determination of proximities between suitable fluorophores, called donors and acceptors, in the 1–10-nm distance range (1). In addition to its ability to perform fluorescence lifetime-based measurements, several steady-state realizations already exist—for example, for measuring simple donor quenching, acceptor sensitization, donor photobleaching, acceptor photobleaching, donor anisotropy, and acceptor anisotropy (2–6). Amongst these uses, the dual-laser flow cytometric resonance energy transfer (FCET) method (7,8) has proven itself unique—such uniqueness due not only to its high statistical power, but also to its relative simplicity, merely requiring the use of flow cytometer types that are already commercially available. (For flow cytometric applications of FRET, see Szöllősi et al. (9).)
The essence of FCET is that, in addition to the parameters proportional to the donor and acceptor concentrations, FRET efficiency is determined as a common value for both quenching efficiency and the percent-enhancement of sensitized emission after correction for the difference in signal detectabilities in the donor and acceptor channels with a scaling factor called α (7,8,10). This factor—which we call from now on “spectral α,” referring to its way of determination—is generally determined from the mean intensities of the samples labeled with donor and acceptor only in the knowledge of the amounts of the donor and acceptor dyes (which are proportional to the dye-per-protein labeling ratios of the dye-targeting ligands and the number of receptors labeled by the ligands) and from the relative absorption coefficient of the donor and acceptor measured at the donor’s excitation wavelength.
For the spectroscopic determination of α, two different epitopes on the same receptor are targeted by the donor- and acceptor-tagged ligands, and the same receptor epitope is labeled either with the donor-stained or the acceptor-stained ligand, where in both cases the 1:1 stoichiometry guaranties the required equal receptor numbers condition for the determination of the spectral α. Trouble arises when the relative numbers of the donor- and acceptor-tagged receptors are not known, e.g., in the case of engineered visible fluorescent proteins (VFPs), although sometimes a 1:1 stoichiometry can be guaranteed here (11,12). In rare cases of this kind when the donor-acceptor spatial topology is rather well described—e.g., in a Stryer-Haugland type of an experiment with rigid amino-acid polymers as donor-acceptor spacers (1,9,10), or its recently refined versions using DNA construct-based rulers, where the orientation factor (κ2) is more accurately defined (13,14)—a way out is offered by the known values of FRET efficiency estimated from the known donor-acceptor separation distances: In this inverse problem, the system of FCET equations (see Eqs. S1–S3 in the Supporting Material) is solved for α in the knowledge of FRET efficiency.
In a somewhat more complicated statistical approach restricted by the condition of constant donor-acceptor concentration ratio, least-squares estimation can also be used (10). Here FRET efficiency is estimated in two ways:
-
1.
As defined by α via the system of equations for FCET (see Eqs. S1–S3 in the Supporting Material) and
-
2.
From one extra equation when the sensitized emission intensity is expressed with the acceptor-donor absorbance ratio instead of α—and the difference of estimations is minimized.
In this communication, we develop what we believe to be a new approach for the determination of α based on a characteristic of intensity distributions, the width of the detected distributions, and the covariances between the intensity distributions. Here the width represents the standard deviation, defined as the square-root of variance (second central moment), which is an average of the squares of the deviations from the mean, i.e., the mean-squared fluctuation around the mean. Covariance is analogously defined between two different intensities: as average products, of fluctuations of two different intensities, around the respective means (15,16). We hypothesize that similarly to the distribution means, distribution variances and covariances as well as the corresponding fluctuation products convey information on the processes behind the intensity distributions. This is also corroborated by the fact that in a broad family of distributions, the distribution mean is not independent from the corresponding distribution variance (e.g., Poisson, log-normal, and Weibull distributions) (17). In the context of α determination, our hypothesis means that the difference in detection sensitivities of the donor and acceptor signals should also be manifested in differences in the widths and covariances of the donor- and acceptor-related fluorescence intensity distributions.
For an overview of the organization of the article, please see the Supporting Material.
For a Glossary of Terms, see the Appendix.
Materials and Methods
Information on cells, specificity of monoclonal antibodies, fluorescent staining of monoclonal antibodies (mAbs), and labeling of cells with fluorescent ligands is found in the Supporting Material.
Flow cytometric energy transfer measurements
FRET efficiency was determined in a combined manner from the donor quenching and the sensitized emission of acceptor (7,8) on a cell-by-cell basis. For measuring FRET applying both the Alexa-Fluor 488-546 and Alexa-Fluor 546-647 (or Cy5) donor-acceptor dye-pairs (18), we used the FACSVantage SE flow cytometer with a FACSDiVa extension (Becton-Dickinson, Franklin Lakes, NJ), equipped with triple-laser excitation, and with the lasers operating in the single-line mode at 488 nm (Coherent Enterprise Ar+-ion gas laser; Innova Technology, Coherent, Santa Clara, CA), at 532 nm (a diode-pumped solid-state laser), and at 632 nm (model No. 127 He-Ne gas laser; Spectra Physics, Santa Clara, CA).
In addition to the forward-angle light-scattering (FSC) signal, the following four signals were collected for each cell running through the laser beams with the transmitted wavelength range and the specifications of the realizing band path filters in parentheses (all filters from A. F. Analysentechnik, Tübingen, Germany): 1), the right angle (or perpendicular) side-scattered light (SSC) signal at the 488/532-nm laser line (BP 488/10, BP 532/10 filters) to separate debris and cells based on size and intracellular morphology in FSC-SSC dot-plots; 2), the donor (Alexa-Fluor 488 or 546) and 3), the acceptor (Alexa-Fluor 546 or 647) signals I1 (quenched donor intensity) and I2 (containing sensitized emission), both excited at the 488/532-nm wavelength, the maximum of the donor absorption and detected through a DM 561 LP/DM 630 LP dichroic mirror in the 515–545 nm (DF 530/30 BP filter)/570–620 nm (DF 595/50 BP filter); and 4), the 570–620 nm (DF 595/50 BP filter) >635 nm (DF 635 LP filter) wavelength ranges.
The FRET problem has three unknowns (FRET efficiency, and the donor and acceptor concentrations) for the determination of which, in addition to the aforementioned I1 and I2 signals, a third fluorescence intensity I3 is also necessary (7,8): the acceptor intensity excited at 532/632 nm, close to the maximum of the acceptor absorption, and also detected in the >561 nm (DF 561 LP filter) >635 nm (DF 635 LP filter) wavelength range. With the above I1, I2, and I3 signals, the A′, d′, d0, p, q, α and the FRET indices Q, E0, and E are calculated as described in Theoretical Results. These parameters were determined on a cell-by-cell basis in the gated cell population with a home-made software program called REFLEX (http://www.biophys.dote.hu/research.htm, http://www.freewebs.com/cytoflex.htm), specialized for processing flow cytometric histograms (19) to be displayed as frequency distribution curves (Fig. 2). A case study of the FCET calculation is presented in the Supporting Material. The frequency distribution of the α-factor shown in Fig. 2 has been computed with the software MATLAB, Ver. 7.0.1 (The MathWorks, Natick, MA).
Figure 2.
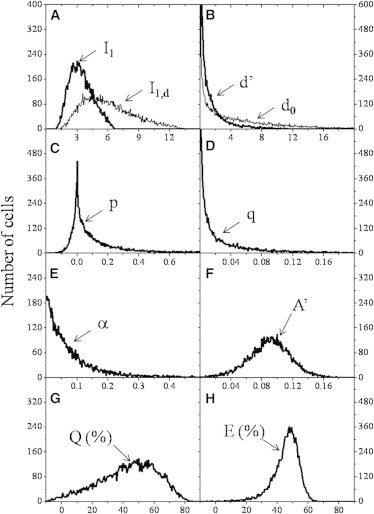
Representative histograms of covariance-based FRET determination. For the application of the quadratic equation (Eq. 9) for α, first the second moments (or variances) d’ and d0 are computed as mean values of the corresponding squared deviation (or fluctuation square) distributions (Panel B). In Panel B, d’ and d0 are distributions of the squared deviations from the respective means (or fluctuation squares) computed from the distribution of the donor intensity of the double-labeled FRET sample (I1) and the donor-only one (I1,d) of Panel A, respectively. Next, the p and q input constants for Eq. 9 are computed as averages of their respective distributions shown in Panels C, D. In Panel C, the distribution of p is that of the product of the deviations for I1 (Panel A) and A’ (Panel F) from their respective means. In Panel D, the distribution of q is that of the squared deviation of the I1·A’ product from its mean value. In Panel E shown is the distribution of α as computed by a cell-by-cell solution of Eq. 9 with the input distributions d’, p, q and with the average of the d0 distribution as an input constant. As a summary, the distributions of d’, p, q, A’, and α (Panels B-F) are determined on the double-labeled FRET sample, distributions of I1,d and d0 (Panels A, B) on the donor-only sample. Finally, histogram of donor quenching efficiency Q (Panel G) is computed from the input histogram of I1 and the average of I1,d as input constant according to Q=1-I1/I1,d. Histogram of FRET efficiency E (Panel H), taking into account both donor quenching and sensitized acceptor emission, is computed from the distribution of A’ (Panel F) and the mean of the α distribution (Panel E) as input constant according to E=A’/(α+A’). During analysis, all intensities were divided by 1000, meaning that all moments are divided by 106. The distributions (reminiscent to Weibull-type) are determined for the Alexa-Fluor 488-conjugated L368, Alexa-Fluor 546-conjugated W6/32 transfer pair labeling the β2m and heavy-chain subunits of MHCI on the surface of FT T-lymphoblast cells. The details of the computations with the mean values of the shown distributions can be found in the Supporting Material.
A case study of the FCET calculation, as well as technical details of fluorescence lifetime measurement by fluorescence lifetime imaging microscopy (FLIM), is presented in the Supporting Material.
Theoretical Results
Introducing the α-factor
The α-factor plays a crucial role in the determination of FRET efficiency in the FCET measuring scheme. Formally, according to the theory of FCET detailed in the Supporting Material, the E FRET efficiency is computed from the primarily measured A′ quantity via a kind of normalization of A′ by α as expressed by the relationship
which is analogous to Förster’s E = R60/(R6 + R60). Phenomenologically, it is a conversion or normalization factor between the donor’s and acceptor’s emission channels (meaning the acceptor signal in the acceptor channel corresponding to the signal of a single donor molecule in the donor channel). Its value is the product of the ratio of equipment sensitivities of the two channels, ηa/ηd (dictated by optical collection angles of detectors, photomultiplier sensitivities, and gains of electronic amplifiers and photomultiplier voltages) and the ratio of the quantum efficiencies, Ya/Yd of the donor and acceptor fluorophores on the labels
| (1) |
If the cell surface concentration ratio of the targeted receptors (binding sites), Ba/Bd, is known, α can be determined from the mean fluorescence intensities Ma and Md of the samples labeled with only acceptor and donor, respectively, with the molar decadic absorption coefficients of the donor and acceptor εd and εa (both in M−1 cm−1) and the dye-per-protein labeling ratios of the dye-targeting ligands Ld and La (spectroscopic α):
| (2) |
The form of Eq. 2 for α is based on the assumption that fluorescence intensity is a linear function of the dye concentration. This may not be fulfilled at large dye local concentrations, e.g., when several dye molecules are closely packed on a carrier ligand.
Determination of α with intensity correlations
The determination of α via Eq. 2 is problematic for the following reasons:
-
1.
The ratio of the labeled binding sites Bd/Ba is generally not known; it is considered an unknown parameter of the FRET problem. In our practice, α is mostly determined by using the same type of ligand conjugated with the donor and acceptor fluorophores. Alternatively, two different ligands are used, which bind to two different binding sites on the same receptor, e.g., donor-conjugated L368 and acceptor-conjugated W6/32 mAbs binding to the β2-microglobulin (β2m) and heavy-chain subunits of the major histocompatibility complex class I (MHCI) receptor, when Bd/Ba = 1. However, in important cases of genetically engineered light-emitting proteins, the ratio of the number of labeled receptor sites may be inherently not known, and Eq. 2 cannot be applied directly, in a straightforward manner (10).
-
2.
Even if the ratio of the labeled binding sites is known, the application of Eq. 2 can lead to errors in α introduced by the labeling ratio-dependence of light emission of the fluorophore-conjugated labels (mAbs) and/or the labeling-ratio dependence of binding of the ligands to their receptors. As to the light emission, by increasing labeling ratios, it decreases on average due to the larger formation probabilities of dim complexes (efficient traps of excitation energy conveyed by homo-FRET), meaning that the true number of emitters (i.e., the effective labeling ratio) is smaller than the nominal one (20–24).
The above problems with the determination of α inspired us to find more efficient and robust ways of determination of α resistant to the changes of the effective labeling ratios (effective quantum efficiency) that do not require the prior knowledge of the receptor numbers. A way forward is offered by fluctuation analysis of the measured cell-by-cell fluorescence distributions in the form of calculated variances and covariances (also called second moments) and their possible dependence on the respective mean values (fluorescence intensities and other quantities).
By computing the variance of the I1 donor signal, a quadratic equation for α can be set up that is resistant enough to experimental uncertainties for giving a meaningful α-value as its positive root in most of the cases. Starting out from Eq. S1 in the Supporting Material, the variance of I1 can be written as
| (3) |
where symbol (ξ,ψ) designates the covariance of quantity ξ with ψ (as random variables), defined as according to (25)
| (4) |
where n is the number of cells (or pixels in the case of imaging).
After replacing Id and Id × E in Eq. 3 with
| (5) |
and
| (6) |
obtainable from Eqs. S12 and S13 in the Supporting Material, and by introducing the designations
| (7) |
and
| (8) |
for the second moment of the donor intensity unperturbed by FRET (but possibly perturbed by steric interactions) and for the donor intensity perturbed by both FRET and possible steric interactions, respectively, we obtain the following quadratic equation for α:
| (9) |
with the shorthand notations
| (10) |
| (11) |
| (12) |
An alternative deduction of Eq. 9 is presented in Eq. S27 in the Supporting Material. For a summary of the correlation method, please see Fig. 1.
Figure 1.
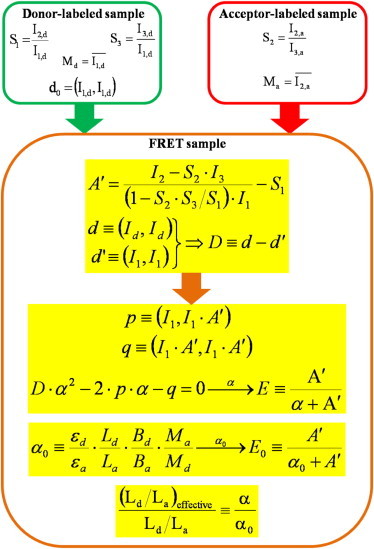
Flow-chart and summary of the main formulae for determining FRET based on intensity correlations. As the starting point, single donor-only labeled samples are analyzed for determining the S1, S3 spectral spillage factors, the Md intensity mean, and the d0 intensity variance, then single acceptor-labeled samples are analyzed for determining the S2 spectral spillage factor and the Ma intensity mean. In the knowledge of S1, S2, and S3, the FRET-related quantity A′ is determined based on the double-labeled FRET sample: A′ is a single-valued, monotonously increasing function of the transfer efficiency E for the accurate calculation of which a scaling of A′ with the scaling factor α is necessary. After scaling of A′ with α, FRET efficiency E is calculated as E = A′/(α + A′), with the meaning A′/α = (R0/R)6 (from Förster’s formula). Calculation of covariance-based α begins with determination of D, the difference between the variance of the hypothetical (immeasurable, indirectly determined) donor intensity when FRET is switched off (d), and the variance of donor intensity (measurable) when FRET is switched on (d′), both characterizing the double-labeled FRET sample. In the absence of any steric interaction between the dye-targeting labels (e.g., no competition) instead of d, the d0 variance of the donor-only sample can be used for calculation of D. In the presence of steric influence, the functional dependence of the change in the intensity variance (Q′) on the change in mean intensity (Q) characterized with the m slope and b intercept parameters (Q′ = m · Q + b) can be used for estimating d and D on the FRET sample in the knowledge of d′, A′, and α. It can be noted that whereas in the former case D does not depend on α, in the latter case it does, with the consequence that a cubic equation should be used for α, instead of a quadratic one (see below). After determining D (or expressing it as the function of α), coefficients of p and q are calculated with I1, and A′ on the double-labeled sample. In the knowledge of D, p, and q, a quadratic (or more complicated, depending on the nature of D, see also the Supporting Material) equation is solved for α. The fact that the D, p, and q coefficients are population averages of fluctuation (deviation from the mean) products implies two alternatives for solution of the equation for α: either it can be solved for α for each individual cell, i.e., on a cell-by-cell basis and histograms of α are created from which some characteristic expressing average behavior (mean, mode, median) is calculated (followed when D is independent of α); or the averages of the appropriate fluctuation product histograms (cell-by-cell distributions of D, p, q) are calculated first, then the equation is solved for an average α (followed when D depends on α). Finally, E is calculated with α and A′ on a cell-by-cell basis. The α-factor in the conventional way is determined from the relative absorption, labeling ratio, receptor number, and intensity (spectral α or α0). FRET efficiency of E0 is calculated with α0 and A′ on a cell-by-cell basis. By taking a ratio, α/α0 = (Ld/La)effective can be introduced, expressing the reduction in quantum yield or binding efficiency of the fluorescently labeled ligand as the function of the degree of labeling of ligands.
As to the meaning of the quantities D, p, and q in Eq. 9: D is the reduction of variance of the donor intensity due to FRET expressing increasing information content (or decreasing entropy) of the donor signal, q is the information (or entropy) conveyed by FRET from the donor channel toward the acceptor channel (26), and p is the covariance between transferred energy and remaining energy at the donor’s site representing possible dependence of FRET on the donor’s concentration (which could occur for nonrandom receptor distributions (27)).
More explicitly, by using Eq. S10 in the Supporting Material for A′, the p and q parameters can be expanded in zero-, first-, and second-order terms of the S1, S2, and S3 spillage factors—which are generally smaller than unity—multiplied with the covariances and variances of the basic I1, I2, and I3 intensities:
| (13) |
and
| (14) |
By replacing the spillage factors with zero, Eqs. 13 and 14 inform us that whereas p essentially reflects the covariance of the quenched donor fluorescence with the sensitized acceptor fluorescence (p = (I1, I2)), q reflects the variance of the sensitized acceptor fluorescence (q = (I2, I2)).
Applications of the variance equation for α (Eq. 9)
The case of sterically noninteracting donors and acceptors
For the application of Eq. 9, the spectral spillage factors S1, S2, and S3 are determined from the I1, I2, and I3 intensities of the single donor- and acceptor-stained samples, and the parameter A′ is calculated with the spillage factors and the intensities of the double-labeled sample. Then from A′ and I1, the covariance p and variance q terms (the second-order moments) are calculated. The most problematic factor in Eq. 9 is D: although d′ is calculated from I1 as its variance, d, the variance of Id is unknown due to a lack of a prior knowledge on the distribution of unperturbed donor intensity in the presence of the acceptor-carrying ligand. Nevertheless, some work-around can be found: With the application of an unlabeled (dim) version of the ligands used for targeting the acceptor, possible influences of the presence of the acceptor-carrying ligands can be revealed, and the variance of the detected I1 intensity can be used as an estimation of d in Eq. 10. In the absence of steric interactions, the d value can also be estimated with the variance d0 of I1 measured on the donor-only sample.
Lower and upper limits for α
A generally applicable inequality can also be stated, based on the fact that FRET reduces the value of d, i.e., d′ < d,
| (15) |
where the value of D is zero when E = 0 (d = d′), and D = d when E = 100% (d′ = 0), and because d < d0 can be generally assumed (where d0 is the variance of I1 of the donor-only sample, i.e., d0 = (I1, I1)donor only). Based on the chain of inequalities in Eq. 15, lower and upper limits for α—defined by the conditions D = d0 and D = 0, respectively—can always be computed.
Approaches when d is unknown: estimation of d from d′ and A′ based on the variation of d with the mean intensity
-
1.For the recording of Q′−Q plots, the first approach is based on the experience that the variance of the I1 signal shows a monotonic dependence on the mean of I1 intensity, which can be taken as linear with a good approximation (as judged from correlation coefficients R2 > 80%, see also Fig. 3 A). Equivalently, from this statement it also follows that if a relative change Q′ is defined with the donor-moments in the absence and presence of FRET (generally the sum of quenching induced by FRET and the effects of possible steric interactions, as a kind of FRET index), Q′ should also linearly depend on the relative change Q in intensity means. This circumstance implies that if a relationship between Q′ and Q can be stated, then the validity of this relationship in the presence of acceptor-bearing ligands could be used for the estimation of the unknown value of d. Detailing now the procedure: If Q (intensity quenching) is defined as
where I1 and Id,0 are donor intensities in the presence and absence of acceptor-bearing ligands (mAbs), and if Q′ (i.e., quenching of variance) is defined as(16)
with the corresponding donor-moments, then a linear dependence of Q′ on Q can also be expected, with a slope (i.e., amplification) m and intercept (i.e., zero-offset) b. These constants can be experimentally determined in the optical conditions of the FRET measurement (see also Eq. 27):(17)
For determining the m and b constants in Eq. 18, the donor intensity and its variance may be changed also by processes—i.e., quenching processes and steric interactions—other than FRET, inasmuch as the coefficients remain resistant to the exact type of the intensity-perturbing process in constant optical conditions. The requirement is that the biological contribution to the total variance should be the same as in the studied FRET process. Variation of donor intensity may be accomplished by changing the amount of the acceptor—e.g., via changing the labeling ratio of the acceptor-stained ligand, or the expression levels of receptors targeted by the acceptor with IFNγ, as in this study, or KI quenching (28). The advantage of formulating the dependence of d on the mean intensity via the dependence of Q′ on Q is that the latter is scale-invariant.(18) For the estimation of d via Eq. 18 with the measured values of d′ and A′, d′ is expressed first from Eq. 17 as the function of Q′, into which the value of Q′, as expressed with Q according to Eq. 18, is plugged. Finally, Q is expressed with A′ and α according to Eq. S12 in the Supporting Material, if E is replaced by Q. The result is the following expression of d as the function of A′ and α:
After plugging this estimation of d into Eq. 10, Eq. 9, originally quadratic in α, is converted into an equation now cubic in α,(19)
with coefficients(20) (21) (22) (23)
The acceptable solution of Eq. 20 (real, positive, and large enough for producing E < 1) is designated with αcubic in Table 1 and Table S1 in the Supporting Material. By inspecting Eqs. 20–24, it can be seen that the presence of a zero-offset (b ≠ 0) gives rise to the third power in Eq. 20, otherwise (with b = 0) Eq. 20 turns into a quadratic equation.(24) -
2.
Estimating intensity variation of d from a single cell-by-cell distribution of the I1 donor intensity is done by successive gating on a second parameter (see Eq. S14 in the Supporting Material).
-
3.
Estimating d by using Eq. 2, a hybrid approach, is done when the labeling ratios are small (see Eq. S23 in the Supporting Material) and linearity is guaranteed.
Figure 3.
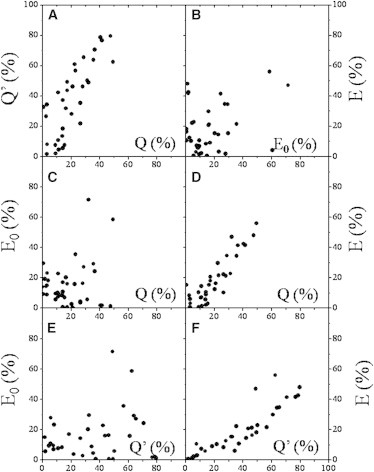
Scatter-plots of pooled data expressing the general trends in the degree of correlations between the different FRET indices. Values of different FRET indices (indicated with dots, each representing a different sample) have been put on a common scale for the L368-W6/32 and W6/32-L368 (practically noncompeting) antibody pairs stained with either the Alexa-Fluor 488/Alexa-Fluor 546 or the Alexa-Fluor 546/Alexa-Fluor 647 (or Cy5) dye-pair, for the LS174T and FT cell lines. The different FRET indices are as follows: Q′, the relative change in the variance of donor intensity when the double-labeled sample is compared to the single donor-labeled one; Q, the relative change in the mean of donor intensity when the double-labeled sample is compared to the single donor-labeled one; E0, FRET efficiency calculated by scaling A′ with the conventional α-factor (or spectral α, α0); and E, FRET efficiency calculated by scaling A′ with the covariance-based α-factor. (A) Good correlation is between Q and Q′ (r(Q, Q′) = 79.3%). (D and F) The correlations of E are good with both Q and Q′ (r(E, Q) = 88.8%, r(E, Q′) = 89.4%). (B, D, and E) However, the correlations of E0 with E, Q, and Q′ are bad (r(E0, E) = 44.9%, r(E0, Q) = 20.5%, and r(E0, Q′) = 20.2%). Seemingly, in panel B, the correlations in these cases are ruined by points whose trend line is aligned approximately parallel with the horizontal and vertical axes, implying over- and underestimation of the real FRET efficiencies, due to the large acceptor and donor labeling ratios, respectively. For panels C and E, the opposite is true. This is supported by Fig. S6 in the Supporting Material directly showing the dependence of the FRET indices on the labeling ratios. Despite the good correlations of E with Q and Q′, the individual dispersion of these quantities, and also that of E0, is substantial, due to the different types of dye-pairs and the different acceptor levels dictated by the different labeling ratios of the acceptor-targeting mAbs (La) as well as the different surface expression levels of MHCI (homo-association of MHCI has a contribution to the intramolecular FRET).
Table 1.
Conventional and the covariance-based α-factors
| FRET pairs |
Labeling ratio |
α-factors |
FRET efficiencies (%) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Donor: Alexa-Fluor 546 |
Acceptor: Alexa-Fluor 647 |
Spectral |
Covariance-based |
Quenching |
Quenching and sensitized emission |
||||||
| mAb | Epitope | mAb | Epitope | Ld | La | α0a | αb | αcubicc | Qd | E0e | Ef |
| A | |||||||||||
| L368 | β2m | W6/32 | MHCI heavy-chain | 4.7 | 1.7 | 10.07 | 0.35 | — | 28 | 2 | 30 |
| L368 | W6/32 lowg | 9.78 | 0.40 | — | 19 | 2 | 21 | ||||
| L368 lowg | W6/32 | 9.88 | 0.29 | — | 26 | 1 | 26 | ||||
| B | |||||||||||
| W6/32 | MHCI heavy-chain | L368 | β2m | 1.5 | 2.1 | 0.13 | 0.14 | — | 19 | 26 | 25 |
| W6/32 | L368 lowg | 0.12 | 0.09 | — | 16 | 18 | 22 | ||||
| W6/32 lowg | L368 | 0.13 | 0.16 | — | 23 | 27 | 24 | ||||
| C | |||||||||||
| L368 | β2m | L368 | β2m | 4.7 | 2.1 | 3.96 | 0.16 | 0.21 | 39 | 1 | 13h |
| W6/32 | MHCI heavy-chain | W6/32 | MHCI heavy-chain | 1.5 | 1.7 | 0.33 | 0.10 | 0.14 | 40 | 6 | 11h |
Deduced FRET efficiencies measured between the β2m (light-chain) and heavy-chain subunits of the MHCI receptor as well as between its heavy-chain subunits on the surface of FT T-lymphoblast cells by using Alexa-Fluor 546- and Alexa-Fluor 647-conjugated mAbs.
The conventional (or spectral) α-factors (α0) have been calculated according to Eq. 2 of the main text by using the mean intensities of the samples labeled with the donor and the acceptor as well as the labeling ratios and absorption coefficients. Because of the 1:1 stoichiometry of the two subunits of the same MHCI molecule, unity was used for the ratio of the labeled receptors (Bd/Ba). All data in this table are representative ones of three different measurements giving similar results, with relative errors <15% (mean ± SE).
Covariance-based α-factor at the donor side (α) was determined as the mean value of the corresponding cell-by-cell distribution of α obtained as the positive root of the quadratic polynomial in Eq. 9 written for the cell-by-cell distributions of the D, p, and q coefficients, examples of which are shown in Fig. 2. In calculation of the D coefficient in Eq. 9, for the noncompeting case of FRET measurement between the β2m and heavy-chain subunits, the d value of the FRET sample was approximated by the mean of d0 distribution of the corresponding single-donor labeled sample.
In the case of FRET indicating homo-association between the MHCI receptors, instead of using d0 of the single-donor labeled sample, the d′ value of the FRET sample has been corrected according to Eq. 19 and the positive root of the cubic polynomial in Eq. 20. This resulted in a meaningful FRET efficiency (αcubic) that was used in the calculation of E. Whereas the root of the quadratic polynomial of Eq. 9 has been found for each cell and the cell-by-cell distribution of α has been determined, this latter calculation have been carried out only with mean values.
Quenching efficiency (Q) is defined as the relative change in the I1 donor fluorescence due to the mAb used as acceptor. Mean values of the corresponding cell-by-cell distributions, defined as Q = 1−I1/I1,d where I1 is intensity of the double-labeled sample and I1,d is the mean intensity of the sample labeled only with the donor, are listed. In the case of competing mAbs for the measurement of MHCI homo-association, it also contains the intensity-reducing effect of mAb competition and the effect of FRET.
E0 has been calculated as the mean of the corresponding cell-by-cell distribution obtained from the A′ distribution by using E0 = A′/(α0 + A′) (see Eq. S12 in the Supporting Material) with the conventional α-factor (α0) as an input constant.
E has been calculated as the mean of the corresponding cell-by-cell distribution obtained from the A′ distribution by using E = A′/(α + A′) with the covariance-based α-factor (α) as an input constant.
Experimental Results
Comparative measurements of FRET between epitopes of MHCI at different labeling ratios of mAbs on the surface of FT T-lymphoblast cells: I. Alexa-Fluor 546-647 dye pair
Table 1 reports on FRET measurements between Alexa-Fluor 546- and Alexa-Fluor 647-conjugated mAbs bound to epitopes of MHCI. Intramolecular proximity is monitored when two different mAbs are used against the two subunits of MHCI: L368 against the light chain (β2m) and W6/32 against the heavy chain conjugated with the donor and acceptor, respectively, in the forward direction (L368→W6/32, Table 1 A), and, vice versa, in the reverse direction (W6/32→L368, Table 1 B). Approximately equal and large FRET efficiencies are expected in these cases, based on the rather well-defined distance of these subunits of ∼7.7 nm (29). In Table 1 C, the same epitope on the light or heavy chain is labeled by the donor- and acceptor-bearing mAbs of the same type (either L368 or W6/32), defining FRET pairs for measuring intermolecular proximities, i.e., homo-associations of the MHCI receptors. The quantities listed are chosen such a way as to enable comparison of α-factor and FRET indices obtained in the conventional way (spectral α or α0, and Q, E0) with those obtained with the believed-new method (covariance-based α-factors α, αcubic, and E). Examples for the cell-by-cell distributions are shown on Fig. 2.
An important feature of the intramolecular FRET systems defined by the L368 and W6/32 mAbs is that because, in these cases, there is practically no steric interaction between these ligands, the simple donor quenching (Q) values themselves can serve as a kind of internal control for the E0 and E FRET efficiencies determined with the α-factors (29,30). Whereas α0 was calculated by using the labeling ratios listed, α was determined from the quadratic equation, the coefficients of which (D = d – d′, p, q) are defined by the appropriate variances and covariances determined from the donor- and double-labeled samples. Because in the intramolecular FRET case there is only a very small competition (<10%), the d moment of the FRET sample, which indicates variance of the hypothetical donor intensity when FRET would be switched off, can be replaced by the d0 moment of the donor-only sample enabling calculation of D as d0−d′ instead of d−d′. This approximation would overestimate the real D and underestimate the real α in the case of significant competition between the donor- and acceptor-bearing ligands. The coefficient p is a covariance of I1 and I1 ⋅ A′, and q is the covariance of I1 ⋅ A′ with itself (i.e., the variance), both determined on the same double-labeled FRET sample.
Regarding the calculation of α, the case of intermolecular FRET describing homo-associations is quite different. In this case, there is an inherent steric interaction (competition) between the donor- and acceptor-stained mAbs because the same mAb is used for targeting the donor and the acceptor. One implication of the steric interaction is that the quenching value calculated as the relative decrease of donor intensity contains a contribution from the competition in addition to that of FRET; the other implication is that, in this case, the easy way of calculation by using d0−d′ instead of d−d′ in the quadratic equation for α (Eq. 9) gives only an approximation, being that the real d value is now unknown and smaller than d0 for the donor-only sample. A way forward is offered by the knowledge of the functional form of intensity dependence of the donor moment on the donor intensity. It is formulated either by a plot of relative moment change versus relative intensity change (Q′−Q plots) obtained on donor-labeled samples of different mean intensities, or in a self-contained manner, obtained on the double-labeled FRET sample itself by successive gating on an intensity parameter different from the I1 intensity, e.g., the I2, I3 or the light scatter (FSC, SSC) intensities (so-called conditional-variance versus conditional-mean plots are discussed in the Supporting Material). The advantage of the knowledge of the functional dependence of the donor moment on the mean intensity is that the unperturbed donor moment on the double-labeled FRET sample can be expressed with the FRET efficiency E, or equivalently A′ and α via Eq. S12 in the Supporting Material (Eq. 19). However, the price of estimation of the unknown d with a known functional form containing E is that the quadratic Eq. 9 turns into a cubic one (Eq. 20): hence the designation αcubic for the α-factor obtained this way.
By examining FRET efficiencies obtained in the L368→W6/32 direction for the Alexa-Fluor 546-647 dye-pair (Table 1 A), it can be seen that whereas the quenching efficiency Q and the FRET efficiency E0 calculated by using the conventional (or spectral) α0 show a considerable difference, in the one calculated with the covariance-based α, E is practically the same as the quenching efficiency. It is also clear that this large difference in E values is attributed to the large difference in α-factors, α0 being much larger than α. Importantly, because of the lack of competition, this observation implies also that the true value of the α-factor is obtained not with the conventional but with the believed-new method.
In contrast, in the reversed direction W6/32→L368 (Table 1 B), also a case of noncompeting mAbs, both FRET efficiencies E0 and E are practically coinciding with the quenching efficiency Q. In parallel with the similar E values, the α-factors obtained with the two methods are also very close to each other. The contradicting observations observed in these FRET directions can only be resolved if we assume that the cause of the large difference in α-factors observed in the L368→W632 direction is due to the large labeling ratio of the donor-bearing L368 mAb (Ld = 4.7), which largely deviates from unity, as compared to the donor-bearing W6/32 mAb (Ld = 1.5) of the reversed FRET direction, and as compared to the acceptor-bearing W6/32 and L368 mAbs in both directions, which are almost the same and stay rather small (1.7 vs. 2.1).
The evaluation of data of the L368-L368 and W6/32-W6/32 pairs (Table 1 C) is more complicated: here the FRET efficiencies E0 and E cannot be compared to the quenching efficiency Q, due to the competition. Here, again, whereas a large difference is seen between the conventional or spectral α-factors, implying a corresponding difference between the E0 and E values, seemingly the covariance-based α-factor does not deviate much, implying also similarly large E values. The indicated E-values were calculated here not from α, but from αcubic (obtained as a root of the cubic Eq. 20), which are a little larger than α, implying also correspondingly smaller E values.
Comparative measurements of FRET between epitopes of MHCI at different labeling ratios of mAbs on the surface of FT T-lymphoblast cells: II. Alexa-Fluor 488-546 dye pair
Please see the Supporting Material.
Comparative measurements of FRET between epitopes of MHCI at different labeling ratios of mAbs on the surface of LS174T cells
In addition to the FT cell line discussed above, analog experiments have been carried out on LS174T cells as a control, to demonstrate the stability of α determination with the correlation method. The influences of receptor expression levels and cluster densities as modified by IFNγ treatments have been considered (see Table S1 and additional details in the Supporting Material).
Correlating FRET indices Q, Q′, E0, and E
Because, in the case of intramolecular FRET measured between donor-labeled β2m or light-chain and acceptor labeled heavy-chain subunits of MHCI, essentially there is no competition between the mAbs, simple donor quenching can be regarded as a FRET index, a parameter monotonously changing with the real FRET efficiency. It is calculated as the decrease of donor intensity (I1) in the presence of acceptor, referenced to the mean intensity of the donor-only sample (I1,d): Q = 1 – I1/I1,d (quenching of intensity mean). Because the intensity moment of the donor is also expected to change monotonously with FRET, although with a different functional form, a FRET index can also be defined with the intensity moment d′ for the double-labeled sample, and d0 for the donor-only sample: Q′ = 1 – d′/d0 (quenching of intensity variance). Another two FRET indices are the conventional FRET efficiency E0 calculated with the conventional α0 and the intensity correlation-based FRET efficiency E calculated with the new α-value. Fig. 3 shows the plots for these FRET indices pooled for 34 different measurements as functions of each other to reveal trends in their behavior, involving the Alexa-Fluor 488-546, Alexa-Fluor 546-647, Alexa-Fluor 546-Cy5 dye-pairs, as donor-acceptor pairs attached to the light and heavy chains of the MHCI receptor on the surface of FT and LS174T cells.
As to the quenching efficiencies Q′ and Q, Fig. 3 A reports on a rather good correlation between them (79.3%, the dependence is not strictly linear), implying that the intensity moments alone may also be used for quantifying FRET after calibration. This is expected, because by starting out from the definition of Q′ and Q, it can be shown that
| (25) |
with
| (26) |
where I1 designates the donor intensity with acceptor, and I1,d without acceptor (essentially the ratio of squared coefficients of variation for I1 and I1,d, i.e., , and ). After expanding the squared term, and neglecting the term containing Q2 (this is allowed if Q2 ≪ 1), Eq. 25 reduces to
| (27) |
The same reasoning is also behind Eq. 18, when it was assumed that Q′ can be written as a linear function of Q (keeping the term second-order in Q would lead to a fourth-power term in Eq. 20 for α if μ ≠ 1). The slope and intercept values of the linear trend-line fitting data points of Fig. 3 A are 1.568 ± 0.353 and 0.025 ± 0.078 (R2 = 0.661), indicating that the assumption of the linearity is fulfilled with a good accuracy.
In contrast, essentially no correlation of E0 with these quenching efficiencies Q and Q′ is reported by Fig. 3, C and D (20.5%, 20.2%), due to the smearing effect of those mAbs having large labeling ratios. For the dependence of E, E0, Q, and Q′ on the labeling ratios Ld, La, and the Ld/La ratio, please consult Fig. S6 in the Supporting Material. However, for E, determined in a labeling ratio-free manner, good correlations are indicated with both Q (88.8%) and Q′ (89.4%) in Fig. 3, D and F. That the correlation of E is better with Q′ than with Q is supposedly because computation of each involves the donor-intensity moments. Finally, a poor correlation is seen between E and E0 (44.9%) due to inflation by those mAbs having large labeling ratios. These plots demonstrate that the intensity correlation-based α is superior to the conventional α0 for mAbs of large labeling ratio (see also Fig. S6).
Correlation plots of pooled data for FRET indices describing the L368-L368, and W6/32-W6/32 homo-associations (not shown) revealed similar trends between the correlations—namely that there is large correlation between Q and Q′ (84.5%) and correlations of E are larger than those of E0: r(E, Q) = 78.4%, r(E, Q′) = 72.9%, r(E0, E) = 26.8%, r(E0, Q) = 11.3%, and r(E0, Q′) =12.2%.
Fluorescence lifetime depends on the labeling ratios of mAbs
Data obtained by FLIM directly demonstrate that light emission by ligand-bound dyes is affected by the dye-per-protein labeling ratio (see Fig. S5 and details in the Supporting Material). Due to the interactions between dyes, the assumption of linearity between dye concentration and fluorescence intensity may not be fulfilled, and as a consequence, the form of Eq. 2 for α determination may be violated.
Discussion
Intensity correlations offer new degrees of freedom for calibrating FRET measurements
Flow cytometry is a technology inherently applicable to developing methods based on the concept of intensity fluctuations, being that the outputs of this technology are the probability distribution functions describing the different cell parameters at the level of populations. Despite this advantage offered by flow cytometry, intensity correlations that were manifested in the width of the intensity distribution curves, a scale parameter (31,32) of the distributions, have not been exploited explicitly to extend the capabilities of measurements, the majority of which concentrated on the determination of some location parameters, the mean, median, or mode.
The impetus to this work was given by a need to extend the capabilities of the FCET method, originally worked out by Trón and co-workers (7,8) to determine FRET efficiency by concentrating only on a single sample, namely on the double-labeled FRET sample. To put it another way, we were trying to reduce the number of spectroscopic-optical constants—the input parameters of FRET determination—from non-FRET samples as much as possible, to determine FRET in a self-consistent manner. However, to fulfill this requirement, finding extra parameters as yet not involved in FRET determination, like some measure of intensity correlations, is necessary. An advantage of determining a spectroscopic constant based on the intensity correlations (as a scale parameter) instead of intensity means (as a location parameter) can also be expected, namely that whereas the location parameters are off-set dependent (e.g., the subtracted background), the scale parameters are not, with the consequence of increasing accuracy of the determination of the given spectroscopic constant and ultimately the deduced FRET efficiency.
According to the scheme of the dual-laser (or dual-wavelength) FCET method (detailed in the Supporting Material), FRET efficiency is determined from intensities of the double-labeled FRET sample in the knowledge of the S1, S2, and S3 spillage factors and the scaling factor α (Eq. 2, and see Eqs. S4–S6 in the Supporting Material), all of them determined in advance from single donor- and single acceptor-labeled samples measured in the same spectroscopic (the same dyes) and optical conditions (equipment state). Among these constants, α is the candidate, the determination of which is amenable to being put on the basis of intensity correlations. This is because α is the balancing factor between the different sensitivities of donor and acceptor signal channels, so it also plays an inherent role in shaping the width of the intensity distributions. In addition to this, the role of α is the proper scaling of the A′ parameter directly determined from the primarily measured I1, I2, and I3 intensities (see Eq. S10 in the Supporting Material), which after scaling, directly determines the FRET efficiency (see Eq. S12 in the Supporting Material). The α-value also directly connects the width of the deduced FRET efficiency distribution with that of A′ via
| (28) |
(obtainable from Eq. S12 in the Supporting Material), where ΔE and ΔA′ designate the standard deviation (proportional to the distribution width) of E and A′, respectively.
The FCET method, originally elaborated upon in the field of flow cytometry, can be adapted in fluorescence microscopy (33), as is also the case with our intensity-correlation extension, based on the image pixel-cell correspondence. Especially in microscopy, combining the FCET approach with the acceptor photobleaching version of FRET determination (34) may offer promise. Because both the donor moments, with and without FRET (d′ and d), necessary for determination of α, can be measured in the same pixels, the distribution of D = d – d′ can also be determined in a pixel-by-pixel manner. This circumstance eliminates the need for estimating d with d0 the donor-only moment, or any assumption on a dependence of d on E (Eq. 19).
A similar approach could also be used in multiparameter flow cytometry, e.g., when the acceptor of the FRET sample would be bleached out with an intensive beam of light. Although in this case d′ and d would be measured sequentially (the cells first passing a probe laser beam, then a bleaching beam), the signals would be correlated. Here the D = d – d′ difference could be determined on a cell-by-cell basis, increasing accuracy compared to the case when the d donor moment without FRET is approximated with the d0 moment of the single-donor labeled sample.
The approach of applying intensity correlations for extending capabilities of FRET determination was also followed by Esposito et al. (35) in the field of FLIM. They worked out a method that is conceptually similar to ours, but totally different in details of mathematical formalism and the aimed parameter: They used the moment analysis for extending the resolution of the FRET data by determining the fraction of donors associated with acceptors (i.e., FRET fraction).
Overview of the correlation method
Please see the Supporting Material.
Comparative measurements of FRET at different labeling ratios of mAbs reveal differences in the conventional and covariance-based FRET determinations
Possible causes of the difference between the conventional and the correlation-based methods for α determination (see Fig. S6)—such as nonlinear concentration dependence of light emission and shielding of binding sites—are discussed in the Supporting Material.
Advantages of the intensity correlation-based FRET method
By comparing the defining Eqs. 2 and 9 for α, the following basic differences can be recognized:
-
1.
The correlation-based α factor (Eq. 9) does not depend on the ligand labeling ratios, implying that the error caused by the lack of knowledge of the effective labeling ratio drops out.
-
2.
Because α is computed from deviations from the means (intensity fluctuations), disturbing effects of bad zero-offsets (bad background subtractions) cancel, but not in the conventional formula (Eq. 2).
-
3.
For using the conventional formula Eq. 2, knowledge of the numbers of the labeled receptors (or at least their ratio) is necessary on the FRET sample. However, there are cases when this is unknown: e.g., when genetically engineered VFPs are expressed on the cell surface. However, the believed-new method also offers a remedy in these cases, because the need for the precise knowledge of the quantity d on the FRET sample can be replaced by a weaker condition of the need for knowing only the functional dependence of d on the mean intensity (i.e., intensity variance versus intensity mean titration plots), which can be recorded if several donor-only samples of different, but not necessarily known, receptor expression levels are available. In the linear approximation of this dependence, Eq. 9 turns into a cubic one (Eq. 20). An approximation of the required donor-intensity-variance versus intensity-mean-titration plots can also be taken up by using only the double-labeled FRET sample. The total population of the cell sample is divided into monotonously increasing subpopulations by successive gating on a second parameter (e.g., I2, I3, FSC, SSC), and the variance of I1 is plotted against the mean of I1 for these subpopulations, resulting in plots (conditional-variance versus conditional-mean plots), which can be fitted by an exponential trend line with high accuracy (R2 > 90%). Then the moment difference D can be expressed with α via this trend line and put into Eq. 9, leading to the transcendental Eq. S18 (in the Supporting Material) for α.
-
4.
Even in the lack of any knowledge on a functional form of the variation of intensity moment with intensity mean, lower and upper bounds for α can be obtained by replacing D in Eq. 9 by its maximum value Dmax = d0 (D = d – d′ < d0 − d′ = d0 when E = 100%, and d′ = 0) leading to minimal α and its minimum value Dmin = 0 (D = d – d′ = 0 when E = 0%, and d′ = d) leading to maximal α, respectively.
Conclusion
A believed-novel approach of FRET determination based on fluorescence intensity correlations has been elaborated for the first time, to our knowledge, by using flow cytometry and immunolabeling of cells. The believed-new method was demonstrated to be superior to the old one in that:
-
1.
It does not involve the knowledge of the effective labeling ratio of the used dye-conjugates for computation of the α-factor as an input parameter; rather, it allows the determination of it.
-
2.
It allows the estimation of FRET efficiency by using only the double-labeled FRET sample for estimation of α.
-
3.
Being a way of determination of α that is free from receptor density, it also allows the usage of the FCET method when receptor density is not known, e.g., in the cases of engineered VFPs. Although elaborated in flow cytometry, it can straightforwardly be adapted in fluorescence microscopy.
Acknowledgments
Thanks are due to Ms. Rita Szabó for her skillful assistance in cell culturing and sample preparations, to Dr. J. Szöllősi for his helpful comments on the manuscript, and to a Reviewer for drawing our attention to the work of Ranjit et al. (13) and Lewis et al. (14).
Financial support for this work was provided by the TÁMOP-4.2.2.A-11/1/KONV-2012-0045 project cofinanced by the European Union and the European Social Fund. The authors are indebted to Dr. T. M. Jovin for making possible FLIM measurements of the dye-conjugated mAbs in the framework of a short-term EMBO fellowship (No. ASTF No 201-06 to L.B.) to the Max Planck Institute for Biophysical Chemistry, Department of Molecular Biology, Göttingen.
Supporting Material
References
- 1.Lakowicz J.R. Principles of Fluorescence Spectroscopy. 3rd Ed. Springer; New York: 2006. Ch. 13: Energy transfer; pp. 443–472. [Google Scholar]
- 2.Jares-Erijman E.A., Jovin T.M. FRET imaging. Nat. Biotechnol. 2003;21:1387–1395. doi: 10.1038/nbt896. [DOI] [PubMed] [Google Scholar]
- 3.Clegg R.M. Ch. 1: Förster resonance energy transfer-FRET: what is it, why do it, and how it’s done. In: Gadella T.W.J., Pillai S., van der Vliet P.C., editors. Vol. 33. Elsevier; Dordrecht, The Netherlands: 2009. pp. 1–48. (FRET and FLIM Techniques. Laboratory Techniques in Biochemistry and Molecular Biology). [Google Scholar]
- 4.Bacsó Z., Bene L., Damjanovich S. A photobleaching energy transfer analysis of CD8/MHC-I and LFA-1/ICAM-1 interactions in CTL-target cell conjugates. Immunol. Lett. 1996;54:151–156. doi: 10.1016/s0165-2478(96)02665-x. [DOI] [PubMed] [Google Scholar]
- 5.Bene L., Fulwyler M.J., Damjanovich S. Detection of receptor clustering by flow cytometric fluorescence anisotropy measurements. Cytometry. 2000;40:292–306. [PubMed] [Google Scholar]
- 6.Bene L., Szöllősi J., Damjanovich S. Detection of receptor trimers on the cell surface by flow cytometric fluorescence energy homotransfer measurements. Biochim. Biophys. Acta. 2005;1744:176–198. doi: 10.1016/j.bbamcr.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 7.Trón L., Szöllősi J., Jovin T.M. Flow cytometric measurement of fluorescence resonance energy transfer on cell surfaces. Quantitative evaluation of the transfer efficiency on a cell-by-cell basis. Biophys. J. 1984;45:939–946. doi: 10.1016/S0006-3495(84)84240-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Trón L. Experimental methods to measure fluorescence resonance energy transfer. In: Damjanovich S., Szöllősi J., Trón L., Edidin M., editors. Mobility and Proximity in Biological Membranes. CRC Press; Boca Raton, FL: 1994. pp. 1–47. [Google Scholar]
- 9.Szöllősi J., Damjanovich S., Mátyus L. Application of fluorescence resonance energy transfer in the clinical laboratory: routine and research. Cytometry. 1998;34:159–179. [PubMed] [Google Scholar]
- 10.Nagy P., Bene L., Szöllósi J. Novel calibration method for flow cytometric fluorescence resonance energy transfer measurements between visible fluorescent proteins. Cytometry A. 2005;67:86–96. doi: 10.1002/cyto.a.20164. [DOI] [PubMed] [Google Scholar]
- 11.Vámosi G., Baudendistel N., Tóth K. Conformation of the c-Fos/c-Jun complex in vivo: a combined FRET and MD-modeling study. Biophys. J. 2008;94:2859–2868. doi: 10.1529/biophysj.107.120766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Szalóki N., Doan-Xuan Q.M., Bacsó Z. High throughput FRET analysis of protein-protein interactions by slide-based imaging laser scanning cytometry. Cytometry A. 2013;83:818–829. doi: 10.1002/cyto.a.22315. [DOI] [PubMed] [Google Scholar]
- 13.Ranjit S., Gurunathan K., Levitus M. Photophysics of backbone fluorescent DNA modifications: reducing uncertainties in FRET. J. Phys. Chem. B. 2009;113:7861–7866. doi: 10.1021/jp810842u. [DOI] [PubMed] [Google Scholar]
- 14.Lewis F.D., Zhang L., Zuo X. Orientation control of fluorescence resonance energy transfer using DNA as a helical scaffold. J. Am. Chem. Soc. 2005;127:10002–10003. doi: 10.1021/ja0524402. [DOI] [PubMed] [Google Scholar]
- 15.Rényi A. On measures of dependence. Acta. Math. Acad. Sci. Hungary. 1959;10:441–451. [Google Scholar]
- 16.Feller W. 3rd Ed. Vol. I. John Wiley & Sons; New York: 1968. Ch. IX: Random variables: expectations; pp. 212–237. (An Introduction to Probability Theory and its Applications). [Google Scholar]
- 17.Feller W. 2nd Ed. Vol. II. John Wiley & Sons; New York: 1970. Ch. V: Probability distributions in Rr; pp. 127–165. (An Introduction to Probability Theory and its Applications). [Google Scholar]
- 18.Horváth G., Petrás M., Szöllősi J. Selecting the right fluorophores and flow cytometer for fluorescence resonance energy transfer measurements. Cytometry A. 2005;65:148–157. doi: 10.1002/cyto.a.20142. [DOI] [PubMed] [Google Scholar]
- 19.Szentesi G., Horváth G., Mátyus L. Computer program for determining fluorescence resonance energy transfer efficiency from flow cytometric data on a cell-by-cell basis. Comput. Methods Programs Biomed. 2004;75:201–211. doi: 10.1016/j.cmpb.2004.02.004. [DOI] [PubMed] [Google Scholar]
- 20.Kerker M., van Dilla M.A., Langlois R.G. Is the central dogma of flow cytometry true: that fluorescence intensity is proportional to cellular dye content? Cytometry. 1982;3:71–78. doi: 10.1002/cyto.990030202. [DOI] [PubMed] [Google Scholar]
- 21.Hirschfeld T. Quantum efficiency independence of the time integrated emission from a fluorescent molecule. Appl. Opt. 1976;15:3135–3139. doi: 10.1364/AO.15.003135. [DOI] [PubMed] [Google Scholar]
- 22.Deka C., Lehnert B.E., Steinkamp J.A. Analysis of fluorescence lifetime and quenching of FITC-conjugated antibodies on cells by phase-sensitive flow cytometry. Cytometry. 1996;25:271–279. doi: 10.1002/(SICI)1097-0320(19961101)25:3<271::AID-CYTO8>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 23.MacDonald R.I. Characteristics of self-quenching of the fluorescence of lipid-conjugated rhodamine in membranes. J. Biol. Chem. 1990;265:13533–13539. [PubMed] [Google Scholar]
- 24.Lakowicz J.R. Principles of Fluorescence Spectroscopy. 3rd Ed. Springer; New York: 2006. Ch. 3: Fluorophores; pp. 63–94. [Google Scholar]
- 25.Kenny D.A. Correlation and Causality. 1st Ed. John Wiley & Sons; New York: 1979. Ch. 2: Covariance algebra; pp. 16–26. [Google Scholar]
- 26.Kullback S. Information Theory and Statistics. Dover; Mineola, NY: 1997. Ch. 2: Properties of information; pp. 12–31. [Google Scholar]
- 27.Wallrabe H., Elangovan M., Barroso M. Confocal FRET microscopy to measure clustering of ligand-receptor complexes in endocytic membranes. Biophys. J. 2003;85:559–571. doi: 10.1016/S0006-3495(03)74500-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hanley Q.S., Subramaniam V., Jovin T.M. Fluorescence lifetime imaging: multi-point calibration, minimum resolvable differences, and artifact suppression. Cytometry. 2001;43:248–260. doi: 10.1002/1097-0320(20010401)43:4<248::aid-cyto1057>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 29.Gáspár R., Jr., Bagossi P., Damjanovich S. Clustering of class I HLA oligomers with CD8 and TCR: three-dimensional models based on fluorescence resonance energy transfer and crystallographic data. J. Immunol. 2001;166:5078–5086. doi: 10.4049/jimmunol.166.8.5078. [DOI] [PubMed] [Google Scholar]
- 30.Damjanovich S., Bene L., Szöllősi J. Two-dimensional receptor patterns in the plasma membrane of cells. A critical evaluation of their identification, origin and information content. Biophys. Chem. 1999;82:99–108. doi: 10.1016/s0301-4622(99)00109-x. [DOI] [PubMed] [Google Scholar]
- 31.Lindley D.V. Introduction to Probability and Statistics from a Bayesian Viewpoint. Part 1: Probability. Cambridge University Press; Cambridge, UK: 1969. Ch. 2.4: Features of distributions; pp. 74–82. [Google Scholar]
- 32.Huber P.J., Ronchetti E.M. Robust Statistics. 2nd Ed. John Wiley; New York: 2009. Ch. 8: Robust covariance and correlation matrices; pp. 199–237. [Google Scholar]
- 33.Nagy P., Vámosi G., Szöllősi J. Intensity-based energy transfer measurements in digital imaging microscopy. Eur. Biophys. J. 1998;27:377–389. doi: 10.1007/s002490050145. [DOI] [PubMed] [Google Scholar]
- 34.van Munster E.B., Kremers G.J., Gadella T.W., Jr. Fluorescence resonance energy transfer (FRET) measurement by gradual acceptor photobleaching. J. Microsc. 2005;218:253–262. doi: 10.1111/j.1365-2818.2005.01483.x. [DOI] [PubMed] [Google Scholar]
- 35.Esposito A., Gerritsen H.C., Wouters F.S. Fluorescence lifetime heterogeneity resolution in the frequency domain by lifetime moments analysis. Biophys. J. 2005;89:4286–4299. doi: 10.1529/biophysj.104.053397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hori T., Uchiyama T., Uchino H. Establishment of an interleukin 2-dependent human T cell line from a patient with T cell chronic lymphocytic leukemia who is not infected with human T cell leukemia/lymphoma virus. Blood. 1987;70:1069–1072. [PubMed] [Google Scholar]
- 37.Szöllősi J., Horejsí V., Damjanovich S. Supramolecular complexes of MHC class I, MHC class II, CD20, and tetraspan molecules (CD53, CD81, and CD82) at the surface of a B cell line JY. J. Immunol. 1996;157:2939–2946. [PubMed] [Google Scholar]
- 38.Tanabe M., Sekimata M., Takiguchi M. Structural and functional analysis of monomorphic determinants recognized by monoclonal antibodies reacting with the HLA class I α3 domain. J. Immunol. 1992;148:3202–3209. [PubMed] [Google Scholar]
- 39.Szöllősi J., Damjanovich S., Brodsky F.M. Physical association between MHC class I and class II molecules detected on the cell surface by flow cytometric energy transfer. J. Immunol. 1989;143:208–213. [PubMed] [Google Scholar]
- 40.Edidin M., Wei T. Lateral diffusion of H-2 antigens on mouse fibroblasts. J. Cell Biol. 1982;95:458–462. doi: 10.1083/jcb.95.2.458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bene L., Balázs M., Damjanovich S. Lateral organization of the ICAM-1 molecule at the surface of human lymphoblasts: a possible model for its co-distribution with the IL-2 receptor, class I and class II HLA molecules. Eur. J. Immunol. 1994;24:2115–2123. doi: 10.1002/eji.1830240928. [DOI] [PubMed] [Google Scholar]
- 42.Bacsó Z., Bene L., Damjanovich S. INF-γ rearranges membrane topography of MHC-I and ICAM-1 in colon carcinoma cells. Biochem. Biophys. Res. Commun. 2002;290:635–640. doi: 10.1006/bbrc.2001.6246. [DOI] [PubMed] [Google Scholar]
- 43.Bene L., Kanyári Z., Damjanovich L. Colorectal carcinoma rearranges cell surface protein topology and density in CD4+ T cells. Biochem. Biophys. Res. Commun. 2007;361:202–207. doi: 10.1016/j.bbrc.2007.07.013. [DOI] [PubMed] [Google Scholar]
- 44.Bojarski C., Sienicki K. Ch. 1: Energy transfer and migration in fluorescent solutions. In: Rabek J.F., editor. Vol. I. CRC Press; Boca Raton, FL: 1989. pp. 1–56. (Photochemistry and Photophysics). [Google Scholar]
- 45.Murphy R.M., Slayter H., Yarmush M.L. Size and structure of antigen-antibody complexes. Electron microscopy and light scattering studies. Biophys. J. 1988;54:45–56. doi: 10.1016/S0006-3495(88)82929-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rényi A. Probability Theory. 4th Ed. Tankönyvkiadó; Budapest, Hungary: 1981. Ch. IV: Arbitrary random variables; pp. 161–238. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


