Abstract
Astrocytes are critical regulators of neural and neurovascular network communication. Potassium transport is a central mechanism behind their many functions. Astrocytes encircle synapses with their distal processes, which express two potassium pumps (Na-K and NKCC) and an inward rectifying potassium channel (Kir), whereas the vessel-adjacent endfeet express Kir and BK potassium channels. We provide a detailed model of potassium flow throughout the neurovascular unit (synaptic region, astrocytes, and arteriole) for the cortex of the young brain. Our model reproduces several phenomena observed experimentally: functional hyperemia, in which neural activity triggers astrocytic potassium release at the perivascular endfoot, inducing arteriole dilation; K+ undershoot in the synaptic space after periods of neural activity; neurally induced astrocyte hyperpolarization during Kir blockade. Our results suggest that the dynamics of the vascular response during functional hyperemia are governed by astrocytic Kir for the fast onset and astrocytic BK for maintaining dilation. The model supports the hypothesis that K+ undershoot is caused by excessive astrocytic uptake through Na-K and NKCC pumps, whereas the effect is balanced by Kir. We address parametric uncertainty using high-dimensional stochastic sensitivity analysis and identify possible model limitations.
Introduction
The conventional view of the brain has long been a large network of neurons. Other cerebral cell types and vasculature were originally considered to have supporting roles. It is now accepted that astrocytes (a specific type of glial cell) and cerebral vasculature may play a critical role in neural behavior, giving rise to the idea of a neurovascular unit (NVU). Astrocytes are believed to mediate neurovascular coupling, also called functional hyperemia, the phenomenon in which synaptic activity induces dilation in nearby microvasculature, allowing increased blood flow.
A central function of cerebral astrocytes is spatial potassium (K+) buffering, that is, transporting K+ from extracellular regions of high concentration to regions of low concentration via active uptake and release. Uptake usually occurs at the astrocyte-neural interface, where active neurons release K+, which at high extracellular levels can be excitatory to neurons; release typically occurs at the perivascular space, the extracellular region between the astrocyte endfoot and the abluminal surface of an arteriole, which dilates in response to K+. Thus, the buffering is a regulatory mechanism that both protects neurons from excessive excitation and dilates arterioles to increase blood supply to areas of increased neural activity. There may also be a functional role, as changes to extracellular K+ can increase or decrease synaptic activity. To study the neurovascular unit as an interconnected, interactional system, a quantitative mechanistic understanding of K+ spatial buffering is critical.
We recently developed a model of the neurovascular unit (1) that described a two-way signaling pathway: in one direction, astrocytes are stimulated by synaptic activity, with subsequent arteriole dilation, and in the reverse direction, vessel motion triggers astrocyte calcium response through activation of mechanosensors on the astrocyte endfoot. Although that astrocyte model included K+ movement from the synaptic to the perivascular space, the movement was a unidirectional flux and did not describe intracellular K+ dynamics.
Astrocytes express potassium inward rectifier (Kir) channels on their perisynaptic processes and perivascular endfeet (2–8), and these channels have been reported to play a major role in the potassium uptake and release involved in spatial buffering. Calcium-sensitive BK channels in the perivascular endfeet are also a critical means of potassium release (9–11). There are also active K+ uptake mechanisms in the perisynaptic processes, including a sodium-potassium (Na-K) pump and a sodium-potassium-chloride cotransport (NKCC) (12–15).
There have been some computational studies of potassium buffering in the brain, but many include only simplistic, lumped cellular models and exclude most other chemical and electrical mechanisms (16–18). Models of the astrocyte-neural interface, the tripartite synapse (19), omit the vascular component and focus primarily on detailed neural mechanisms (12,15,20), whereas we are interested in an explicit description of the astrocyte.
We present a model of the neurovascular unit in the cortex with a detailed mechanistic description of astrocytic potassium buffering. This model describes the potassium dynamics in the astrocyte intracellular space and in the extracellular spaces at the synaptic and perivascular interfaces. Astrocyte potassium uptake at the synaptic space is carried by potassium inward rectifier (Kir) channels, potassium-sodium (Na-K) exchange, and a potassium-sodium-chloride cotransporter (NKCC) on the astrocyte perisynaptic process. From here on, KirAS refers to the Kir channel on the astrocyte at the synapse-adjacent process. The perivascular endfoot expresses Kir, here referred to as KirAV, for astrocytic at the vessel-adjacent endfoot, and calcium-sensitive BK channels. Although astrocytes express other ion channels, these are not included explicitly, but are accounted for collectively by a nonspecific leak channel. This model is specific to cortical astrocytes in the developing brain, as we discuss further below.
This article is organized as follows. In the Mathematical Model section, we provide new equations developed for the model presented here. In the Results section, we compare the results of our simulation to results of several different experimental studies. In the Sensitivity Analysis section, we examine the results of global parameter sensitivity analysis of the astrocyte model. In the Discussion section, we comment on the implications of the simulations and sensitivity analysis and describe the limitations of the model and plans for future work. In the Supporting Material, we present additional sensitivity analysis results, and we describe in detail the complete set of model equations and parameter values.
Mathematical Model
A conceptual diagram of the model is shown in Fig. 1. The model equations concern the small spatial region of the developing brain cortex occupied by a single astrocyte and the synapses and arteriole segment with which it is in contact. Astrocyte-to-astrocyte signaling is left out, and the synaptic space represents the net neural synaptic activity across the entire astrocyte domain, which is assumed to be spatially uniform within the region.
Figure 1.
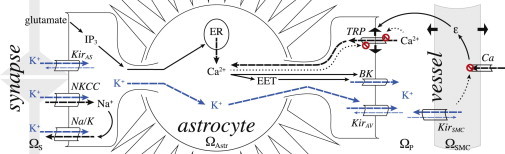
Model overview. represents the synaptic space, where active synapses release glutamate and K+, and is the astrocyte intracellular space, where K+ enters the astrocyte through the Na-K pump, NKCC, and KirAS channels. Na+ enters via NKCC and exits via the Na-K pump. Glutamate binds to metabotropic receptors on the astrocyte endfoot, effecting IP3 production inside the astrocyte wall, which leads to release of Ca2+ from internal stores, causing EET production. Ca2+ and EET open BK channels at the perivascular endfoot, releasing K+ into the perivascular space . Meanwhile, buildup of intracellular K+ in the astrocyte results in K+ efflux through the perivascular endfoot KirAV channel. is the arteriole smooth muscle cell intracellular space, where KirSMC channels are activated by the increase in extracellular K+. The resulting drop in membrane potential closes Ca2+ channels, which reduces Ca2+ influx, leading to SMC relaxation and arteriole dilation (strain, ϵ). The arteriole dilation (ϵ) stretches the membrane of the enclosing astrocyte perivascular endfoot, which activates Ca2+ influx through TRPV4 channels. The prohibition sign on the channel is meant to indicate the inhibition mechanism of the channel, as the TRPV4 channel is inhibited by intracellular and extracellular Ca2+. Note that the diagram here is not to scale. The perivascular endfoot is actually wrapped around the arteriole, but here we show them separated to make clear the ion flow at the endfoot-vessel interface. Dashed arrows indicate ion movement; solid arrows indicate causal relationships, and dotted arrows indicate inhibition. Thin dashed arrows in astrocyte Kir channels indicate the ion flux direction at baseline or, in the vessel Kir, the change in flux direction when extracellular K+ reaches over 15 mM. The potassium signaling pathway is highlighted by blue arrows. To see this figure in color, go online.
During high synaptic activity, neurons release K+ and glutamate at the synapses . K+ flows into the adjacent astrocytic process through KirAS channels, Na-K, and NKCC on the perisynaptic process. The Na-K pump exchanges three sodium (Na+) ions for two K+ ions. The NKCC is an electrically neutral import of one Na+ ion, one K+ ion, and two Cl− ions; however, the Na+ intake affects the Na-K pump activity, which is hyperpolarizing. The KirAS current is larger in magnitude than the outward Na+ current from the Na-K pump, resulting in an overall depolarization of the astrocyte membrane. The NKCC and Na-K pumps have slow dynamics, making them potentially less efficient for K+ buffering. Still, they are likely critical to the astrocyte’s role in regulating K+ in the synaptic space (see Results, below).
Cortical astrocytes in young brains express on their perisynaptic processes glutamate receptors (mGluR5) that initiate intracellular IP3 production in response to synaptic glutamate release. IP3 binds to receptors on the endoplasmic reticulum (ER), releasing calcium (Ca2+) from internal stores. This is most likely specific to astrocytes in the young brain, as Sun et al. (21) recently found that mGluR5 is expressed in cortical and hippocampal astrocytes from young (<2 weeks old) mice brains, but not in adult mouse or human brains, and, further, that glutamate-dependent astrocytic Ca2+ rises may be unlikely in the adult brain.
The mGluR5-dependent rise in intracellular Ca2+ enables production of epoxyeicosatrienoic acids (EETs). EET and Ca2+ activate BK channels in the astrocyte endfoot, releasing K+ into the perivascular space . It is unclear whether EET acts directly on the BK channels; it may act indirectly by activating TRPV4 channels (22,23). This would result in a Ca2+ influx and membrane depolarization, both of which activate BK channels. For the moment, we follow the model of Farr and David (24) which is an empirical description of the relationship between EET and BK activity, but a more mechanistic description can be added later as more data become available. K+ is also released through the endfeet KirAV channels.
The K+ buildup in the perivascular space activates arteriolar smooth muscle cell (SMC) Kir channels, referred to from here on as KirSMC . The resting SMC membrane potential is higher than the KirSMC reversal potential, so the K+ flows outward. The resulting SMC membrane voltage drop closes inward Ca2+ channels, and the intracellular Ca2+ concentration in the SMC drops. Because Ca2+ is required for myosin-actin cross-bridge attachment, the cross-bridges then detach, allowing the SMC to relax and the arteriole to expand.
As the vessel dilates, it stretches the perivascular astrocyte endfoot encircling it , opening stretch-gated Ca2+-permeable TRPV4 channels in the endfoot. TRPV4 channels are also sensitive to intra- and extracellular Ca2+ concentration (25–27). There is experimental evidence that TRPV4 channels are activated by a diverse range of chemical and physical factors, including heat (23,25,26,28), EET, and IP3 (22,27), and they are modulated by phosphorylation (23,27); for simplicity, we leave these mechanisms out for the moment. A more detailed discussion on the TRPV4 model can be found in Witthoft and Karniadakis (1). The astrocyte then experiences a depolarizing Ca2+ influx through active TRPV4, thus maintaining BK activation, which prolongs the K+ signal to the arteriole .
Below, we summarize the new, to our knowledge, ordinary differential equations we have developed and added to this model. The complete, detailed system of model equations is given in the Supporting Material.
We describe the neurovascular K+ movement between three regions in the NVU: the synaptic space, astrocytic intracellular space, and perivascular space. Potassium concentrations in these regions obey
| (1) |
in the synaptic space,
| (2) |
in the astrocyte intracellular space, and
| (3) |
in the perivascular space. The individual flux terms and parameters are all discussed in detail in Eqs. S4–S41 in the Supporting Material, but we discuss below the astrocytic flux terms that we have introduced to this model.
The flux from the NKCC is adapted from Østby et al. (15):
| (4) |
where the subscripts S and A refer to the synaptic and astrocytic spaces, respectively (for more details on the NKCC flux equation, see Eqs. S7 and S8).
The Kir fluxes at the perisynaptic process and perivascular endfoot, and , respectively, are
| (5) |
where AV and AS stand for the astrocyte vessel-adjacent endfoot and synapse-adjacent process, respectively. The ionic flux, J, is computed from the electrical current, I, as , where is the astrocyte cell capacitance, and γ is a scaling factor for relating the net movement of ion fluxes to the membrane potential (29). The conductance and reversal potential, and are
| (6) |
where is the potassium concentration (mM) in the perivascular/synaptic space, and is a proportionality constant. and are the Nernst constants for the astrocyte KirAS and KirAV channels, respectively (∼25 mV (16)).
Results
Effect of astrocyte K+ buffering on neurovascular coupling
We simulate neural activation of the astrocyte by imposing a smooth pulse of extracellular glutamate and K+ in the synaptic space to approximate neural stimulation. In this section, we consider two extracellular regions: 1), the vessel/astrocyte interface (perivascular space), where K+ buffering helps determine the dynamics of functional hyperemia, and 2), the astrocyte/neural interface, where the astrocyte modulates the extracellular environment in the synaptic space.
Astrocyte/vessel interaction
In this model, the introduction of the astrocytic Kir channels allows the astrocyte to respond to changes in extracellular and intracellular potassium concentration. To understand how KirAS and KirAV channels impact the neurovascular interaction, we compare the results of this model with a lumped version that does not include astrocytic Kir. In the lumped version, we remove the astrocyte Kir current , and instead describe the total membrane current at the synapse-adjacent side of the astrocyte, , as a lumped model for the combination of currents from the Na-K pump and KirAS and KirAV channels: (see Eqs. S4–S6), similar to the models developed by Witthoft and Karniadakis (1) and Farr and David (24). We adjust the lumped model’s leak current (see Eq. S20) so that the baseline and maximum astrocyte membrane potential match those of the detailed buffering model that includes KirAS and KirAV.
Fig. 2 shows the effect of astrocyte Kir channels on the NVU under normal conditions (black curves), and with the astrocyte KirAS and KirAV removed, that is, and are both set to 0, and using the lumped model equation above (gray curves). The system experiences a brief period of neural activity (Fig. 2 a, black and gray curves show synaptic K+; thin, red curve shows glutamate transient), triggering astrocyte membrane depolarization and intracellular K+ increase (Fig. 2 b, dashed and solid curves, respectively). The glutamate initiates IP3 production in the astrocyte (Fig. 2 c), leading to release of Ca2+ from internal stores (Fig. 2 d) and causing EET production (Fig. 2 e). The astrocytic Ca2+ and EET activate BK channels in the astrocyte endfeet (Fig. 2 f, dashed curves) where K+ is released into the perivascular space (Fig. 2 g). Meanwhile, the membrane depolarization and the increase in intracellular astrocyte K+ results in an outward K+ flux through the endfoot KirAV channels (Fig. 2 f, dash-dotted curve). In the absence of astrocyte KirAS and KirAV, astrocyte K+ release into the perivascular space is delayed, causing a delay in the vascular response (Fig. 2 h). According to the simulation results, this is because the KirAV is responsible for the immediate release of K+, whereas the BK current rises later (Fig. 2 f). This may explain why previous generations of this astrocyte model, without a description of K+ buffering or astrocyte Kir channels (24), produced a nonphysiological delay of ∼25 s in the neurovascular response.
Figure 2.
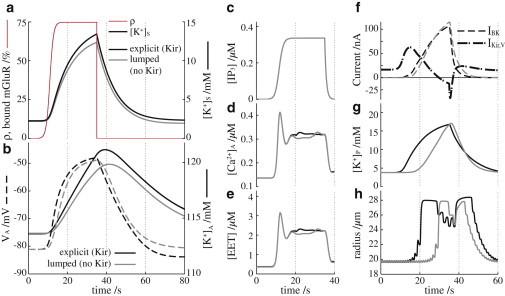
Astrocyte Kir effect on neurovascular coupling. Black curves represent the astrocyte model equations described in this article; gray curves represent the astrocyte model equations without KirAS or KirAV channels. (a) Extracellular K+ in the synaptic space. The thin red curve is the glutamate transient, represented by the ratio of bound to unbound glutamate receptors, ρ (see Eq. S2). (b) Solid lines indicate the intracellular astrocytic K+ concentration and dashed lines the astrocyte membrane potential. (c) Astrocyte intracellular IP3 concentration. (d) Astrocyte intracellular Ca2+ concentration. (e) Astrocyte intracellular EET concentration. (f) Astrocyte perivascular endfoot BK (dashed lines) and KirAV (dash-dotted lines) currents. (g) Extracellular K+ concentration in the perivascular space. (h) Arteriole radius. To see this figure in color, go online.
In the black curves, there is a short period of arteriole constriction during the neural stimulation period (Fig. 2 h): at ∼25 s, where the radius stops increasing and the vessel begins to constrict. This is a phenomenon observed by Girouard et al. (11) in which moderate increases in extracellular K+ cause vasodilation, but increases beyond ∼15 mM will cause the vessel to constrict. The results are also consistent with the simulations of Farr and David (24), who postulated that the change from dilation to constriction during sustained activity was caused by the arteriole KirSMC channels, which have a reversal potential that experiences a depolarizing shift with increasing extracellular potassium: when the extracellular K+ rises above 15 mM, the KirSMC reversal potential shifts from below to above the SMC membrane potential, reversing the direction of the current, which causes a depolarization that reopens Ca2+ channels, in turn causing constriction. This model is discussed in more detail in Farr and David (24).
Astrocyte/neuron interface: extracellular K+ undershoot
Fig. 3 shows the extracellular K+ concentration in the synaptic space over a cycle of stimulation and recovery for several different lengths of stimulus time (simulations in Fig. 3 a are compared with experimental results from Chever et al. (5), interpolated in Fig. 3 b). In the poststimulus recovery period, the extracellular K+ initially displays a fast drop to below baseline level before returning gradually to the resting-state equilibrium concentration. This undershoot is more pronounced as the length of the stimulation period increases: note that the 60 s stimulus in the top plot results in the greatest undershoot and the longest period of recovery to baseline. With decreasing length of the activation period (top to bottom), the undershoot magnitude and recovery time also decrease, a trend that has been reported from in vivo studies in the mouse hippocampus (5). The same experiments also validate the time-dependent characteristics of the undershoot: a fast drop with a slow return to baseline.
Figure 3.
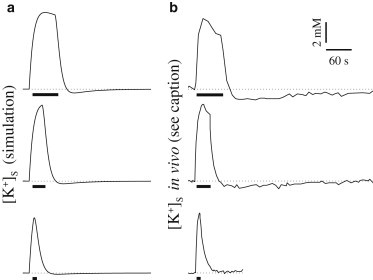
K+ undershoot in the extracellular synaptic space after stimulus is more pronounced with increasing length of the activation period. The stimulus period is indicated by thick black bars. (a) Simulation results. (b) Experimental results interpolated from Fig. 3 in Chever et al. (5).
Our model suggests that the undershoot is a result of the activities of the Na-K pump and NKCC. The astrocyte Na-K pump flux is an inward movement of K+ from the synaptic space and an outward flow of Na+ and is activated by high extracellular K+ and high intracellular Na+. Meanwhile, the NKCC flux is an inward K+ and Na+ flux that increases with decreasing concentrations of intracellular K+ and Na+. During stimulation, the rise in K+ in the synaptic space drives the Na-K exchange, and the astrocytic Na+ decreases. Although the K+ influx and Na+ outflux from the Na-K pump provide competing signals for the NKCC, the Na-K pump exchanges three Na+ ions for every two K+ ions, so the result favors an increased NKCC influx.
At the end of the stimulus, the synaptic K+ decreases toward baseline, so the decreased extracellular K+ and intracellular Na+ result in a decreased Na-K pump flux. At this time, the NKCC is required to replenish the intracellular Na+, which means that K+ uptake is continued via the cotransporter. At the same time, with rising intracellular K+ and decreasing extracellular K+, the astrocyte KirAS flux reverses, counteracting the K+ uptake through the cotransporter. Thus, there is competition at the synaptic space between K+ uptake by astrocyte NKCC and K+ release by astrocyte KirAS. When the stimulus period is sufficiently long, the Na+ has enough time to reach a low enough level that the magnitude of the NKCC flux exceeds the KirAS release, so the K+ uptake continues beyond the point at which synaptic K+ has reached baseline, resulting in an undershoot in extracellular synaptic K+. The drop below baseline continues until Na+ has risen enough for the NKCC flux to decrease, and the KirAS outflux returns the extracellular K+ back to the baseline concentration.
Kir channel blockade
Fig. 4 shows the results when the KirAS and KirAV channels in the astrocyte are blocked. We simulate the effect of the Kir channel blocker Ba2+ (30) by setting the Kir currents equal to zero (see Eq. 5 and Eq. S19). The astrocyte is activated by a transient spike of K+ in the synaptic space (Fig. 4 c). Under control conditions (black curves), the astrocyte responds with a quick rise in intracellular K+ concentration (Fig. 4 a). In the presence of Ba2+ (gray curves), the astrocyte baseline K+ is higher, and it rises more slowly to a lower peak concentration. The astrocyte membrane potential (Fig. 4 b) experiences a hyperpolarization in the presence of Ba2+ during activation and has a depolarized equilibrium value compared to the control. These results are all in good qualitative agreement with the experiments of Ballanyi et al. (30), shown here in Fig. 4, d–f, for comparison.
Figure 4.
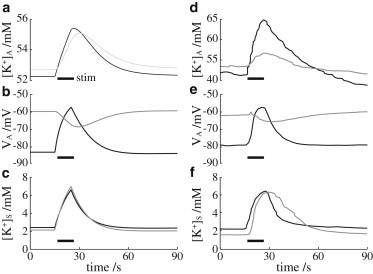
Astrocyte response to K+ channel blocker with short stimulus spike. Black curves indicate neural-induced astrocyte stimulation under control conditions; gray curves represent astrocyte stimulation in the presence of K+ channel blocker. (a) Intracellular astrocytic K+ concentration. (b) Astrocyte membrane potential. (c) Extracellular K+ concentration in the synaptic space. (d–f) Experimental results corresponding to simulation data in a–c, interpolated from Fig. 7 in Ballanyi et al. (30).
Sensitivity Analysis
Parametric uncertainty is a major limitation of this, as well as previous (1,24,31), models. The astrocyte component alone contains 55 parameters, many of which are only crude estimates because not enough experimental data are available. To address these limitations, we perform a global parameter sensitivity analysis using the ANOVA functional decomposition and stochastic collocation (32–34), in which we vary eight key parameters simultaneously. The eight parameters were identified based on preliminary sensitivity analysis used to narrow down the 55-parameter set to the subset most critical to these experiments. Sensitivity indices are computed from the ANOVA representation in (33). The sample points are Gauss-Legendre quadrature points that come from a tensor product of the one-dimensional quadrature rule computed with the code provided in (34). In the Supporting Material, we compute the system sensitivity to all 55 parameters based on an analysis in which two parameters at a time are varied simultaneously.
The results for our 8-dimensional global sensitivity analysis are shown in Fig. 5. To understand the figure in each quadrant, consider that all eight model parameters of our subset are arranged in a large ring (to make the diagram easier to see, we have only labeled the parameters we determined to be the most sensitive). The sensitivity of a single parameter is shown as a small circle, with the diameter equal to the sensitivity of that parameter. For example, in the top left quadrant, it is shown that the potassium undershoot is most sensitive to and , the maximum pump rate of the sodium-potassium exchange and the decay rate of K+ in the synaptic space, respectively. The fill color—white or black—of the circles indicates whether the sensitivity is constructive or destructive, respectively. In other words, when the value of is increased, the undershoot is increased, whereas when is increased, the undershoot effect is diminished. The gray lines show the interaction of two parameters, where the thickness of the line segment is equal to the sensitivity of the interaction pair; this means that we are measuring how much the results will be changed when two parameters are changed at once. For instance, the most critical interaction pair for the undershoot is and , the maximum flux rate of the NKCC pump. Now that we have established how to interpret the figure, we can discuss the results in more detail.
Figure 5.
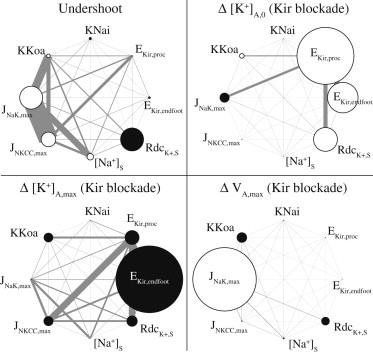
Sensitivity of K+ undershoot and effects of the Kir blockade. Diameters of small circles indicate single-parameter sensitivity; circle color indicates whether increasing parameter magnitude will increase (white) or decrease (black) the following values: the synaptic K+ undershoot (top left); the change in astrocytic K+ after Kir blockade at baseline, Δ[K+]A,0 (upper right), and in the active state, Δ[K+]A,max (lower left); the maximum astrocyte hyperpolarization, ΔVA,max, due to activation during Kir blockade (lower right). Thickness of the gray lines indicates the sensitivity of two-parameter interaction pairs.
The parameter sensitivity of the undershoot is shown in the top left quadrant of Fig. 5. We define undershoot as the amount by which the extracellular potassium in the synaptic region drops below baseline levels after a neural stimulus. The parameters and , the maximum flux rates of the Na-K and NKCC pumps, respectively, have the highest sensitivity (taking into account their individual sensitivity (white circles) and their interaction term (thick gray rectangle)). Both of these parameters have a positive impact on the undershoot: when either parameter is increased, the undershoot also increases. This is consistent with the hypothesis that the Na-K and NKCC pumps are responsible for the K+ undershoot. Note also the high sensitivity of the parameter , the decay rate of K+ in the synaptic space. This implies that the undershoot phenomenon may be a result of factors besides the astrocyte alone, for example, changes in local synaptic activity after a period of neural activation.
In the top right quadrant, we show the sensitivity of the shift in baseline astrocyte K+ concentration after a Kir channel blockade is applied, . The results demonstrate that the astrocytic KirAS on the synapse-adjacent process is more critical in setting the baseline astrocyte K+, whereas it is apparent in the lower left quadrant that the maximum astrocyte K+ level depends mainly on the endfoot KirAV.
The bottom right quadrant shows the sensitivity of the astrocyte hyperpolarization that occurs when the astrocyte is activated in the presence of a Kir blockade. Under normal conditions, the activated astrocyte would experience a depolarization due to K+ influx through the KirAS channels on the synapse-adjacent processes. The only other mechanism present on the astrocyte process in this model is the Na-K exchange, which exchanges two K+ ions into the cell for three Na+ ions leaving the cell, an overall hyperpolarizing effect (the NKCC pump is electrically neutral, as it pumps in two positive ions, one K+ and one Na+, along with one ion). Thus, it is reasonable that the maximum Na-K pump flux, , is the most sensitive parameter for the astrocyte hyperpolarization during a Kir blockade.
Discussion
Although potassium transport is accepted as a primary function of cerebral astrocytes, previous models of astrocytes omit any description of intracellular K+ dynamics even when electrical K+ currents are included (1,20,24,35). Because astrocytes express Kir channels, which are sensitive to both intra- and extracellular K+, it is necessary to model the intracellular K+ concentration, as this affects the dynamics of the astrocyte potassium release and uptake. Notably, previous generations of this model without intracellular astrocyte potassium dynamics and KirAS/KirAV (1,24) predict a nonphysiological delay (∼25 s in Farr and David (24), and 15 s in the lumped model described in the Results section) in the neurovascular response. The KirAS and KirAV included in this model accelerated the astrocytic K+ release into the perivascular space, which helped correct the delay.
Astrocyte perivascular endfeet have been observed to express both BK channels (10,11,36) and KirAV, specifically the Kir4.1 subunit (4,7,8,37), both of which may contribute to neural-induced K+ release into the perivascular space. Our results suggest that astrocyte endfoot KirAV may account for the initial response due to the faster activation rate of KirAV compared to BK, whereas the BK channels are responsible for sustaining the response, as their conductance is much higher than that of KirAV channels (9). According to our sensitivity analysis, the astrocyte KirAS and KirAV channels are essential to K+ buffering (see Supporting Material).
Part of astrocyte potassium buffering is the clearance of extracellular K+ in the synaptic region after neural activation. After extended periods of activation, the recovery to baseline K+ is preceded by a drop below baseline levels due to extra astrocyte uptake, a phenomenon observed in vivo (5). The undershoot is most likely a result of the astrocyte K+ uptake via NKCC and Na-K exchange, which temporarily exceeds K+ release through KirAS (14); in fact, the undershoot is increased in Kir knockout cases (4,5). The astrocyte also has been observed to experience a hyperpolarization during the period of extracellular K+ undershoot (38). Our results are in good agreement with these experimental findings, supporting the hypothesis that the NKCC and Na-K pumps are responsible for the undershoot, whereas the KirAS channels in the perisynaptic processes behave as a counterbalance. This is also supported by the results of our sensitivity analysis (Fig. 5, upper left).
It is well established that extracellular potassium affects neural health and behavior (38–41). Thus, astrocytic potassium buffering likely has both protective and functional implications in the neurovascular unit. Although astrocyte-controlled K+ clearance from the synaptic space could be primarily a protective mechanism to prevent potassium accumulation from reaching neurotoxic levels, it is possible that astrocytes may also regulate extracellular K+ as a means of modulating synaptic activity and overseeing neural network organization.
Rises in extracellular K+ were observed to result in heightened neural excitability due to the increase in neural potassium ion channel reversal potential (39,42). Also observed were decreases in inhibitory GABAergic synaptic transmission in the hippocampus (41,43,44). Hippocampal CA3 neurons were found to experience a hyperpolarizing shift in the Cl− reversal potential, resulting in greater inhibitory activity in the presence of low (below normal baseline) extracellular K+ (41,43). Therefore, the potassium undershoot that follows long periods of synaptic activity may behave as a balancing mechanism to reduce excitability and prevent further continued activation.
Although our model was able to produce results with a good qualitative match to several different experiments, we were unable to attain a quantitative match for all of them. In particular, our model predicts a less pronounced K+ undershoot effect than that seen in Chever et al. (5). Our sensitivity analysis offers two possible explanations: 1), because the K+ decay rate in the synaptic space turned out to be among the most sensitive parameters to the undershoot, it is possible that other local cellular activity (e.g., changes in neural behavior) may also contribute to the undershoot; or 2) the model may be limited by the fact that it is a single compartment, meaning that any changes felt at one end of the cell will be felt immediately and entirely at the other end (see the Supporting Material). This is not physiologically likely. For instance, it is probable that electrical signals will be subject to significant loss as they propagate down the long, thin astrocyte processes. In addition to the numerous studies characterizing electrical propagation along neural dendrites, some limited data suggest that similar losses occur for electrical propagation along glial cells (45). A single-compartment model assumes that there is no loss, so a membrane depolarization that occurs at the endfoot would be grossly overestimated in terms of its effect at the end of the synapse-adjacent process. In a similar way, a multicompartment model would predict a more accurate transfer of ion concentration across the cell. In fact, recent studies have demonstrated that astrocyte intracellular ion diffusion has unique characteristics in the endfeet and processes. The same studies also revealed that isolated subcellular compartments can occur within the processes and endfeet, in which highly localized ion-concentration fluctuations occur without diffusing to or from other parts of the cell (46–48).
Acknowledgments
The authors thank Jennifer Iddings (Georgia Regents University) and Christopher Moore (Brown University) for many helpful discussions. We also thank our anonymous referees for their constructive comments. Simulations were performed on the CCV high-performance computing cluster at Brown University.
This work was supported by the National Science Foundation Office of Cyber Infrastructure (0904288) and National Institutes of Health National Heart, Lung and Blood Institute (R01 HL089067-02).
Supporting Material
References
- 1.Witthoft A., Em Karniadakis G. A bidirectional model for communication in the neurovascular unit. J. Theor. Biol. 2012;311:80–93. doi: 10.1016/j.jtbi.2012.07.014. [DOI] [PubMed] [Google Scholar]
- 2.Ishii M., Fujita A., Kurachi Y. Differential expression and distribution of Kir5.1 and Kir4.1 inwardly rectifying K+ channels in retina. Am. J. Physiol. Cell Physiol. 2003;285:C260–C267. doi: 10.1152/ajpcell.00560.2002. [DOI] [PubMed] [Google Scholar]
- 3.Kofuji P., Biedermann B., Reichenbach A. Kir potassium channel subunit expression in retinal glial cells: implications for spatial potassium buffering. Glia. 2002;39:292–303. doi: 10.1002/glia.10112. [DOI] [PubMed] [Google Scholar]
- 4.Neusch C., Papadopoulos N., Hülsmann S. Lack of the Kir4.1 channel subunit abolishes K+ buffering properties of astrocytes in the ventral respiratory group: impact on extracellular K+ regulation. J. Neurophysiol. 2006;95:1843–1852. doi: 10.1152/jn.00996.2005. [DOI] [PubMed] [Google Scholar]
- 5.Chever O., Djukic B., Amzica F. Implication of Kir4.1 channel in excess potassium clearance: an in vivo study on anesthetized glial-conditional Kir4.1 knock-out mice. J. Neurosci. 2010;30:15769–15777. doi: 10.1523/JNEUROSCI.2078-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Higashimori H., Sontheimer H. Role of Kir4.1 channels in growth control of glia. Glia. 2007;55:1668–1679. doi: 10.1002/glia.20574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Butt A.M., Kalsi A. Inwardly rectifying potassium channels (Kir) in central nervous system glia: a special role for Kir4.1 in glial functions. J. Cell. Mol. Med. 2006;10:33–44. doi: 10.1111/j.1582-4934.2006.tb00289.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Higashi K., Fujita A., Kurachi Y. An inwardly rectifying K+ channel, Kir4.1, expressed in astrocytes surrounds synapses and blood vessels in brain. Am. J. Physiol. Cell Physiol. 2001;281:C922–C931. doi: 10.1152/ajpcell.2001.281.3.C922. [DOI] [PubMed] [Google Scholar]
- 9.Filosa J.A., Bonev A.D., Nelson M.T. Local potassium signaling couples neuronal activity to vasodilation in the brain. Nat. Neurosci. 2006;9:1397–1403. doi: 10.1038/nn1779. [DOI] [PubMed] [Google Scholar]
- 10.Price D.L., Ludwig J.W., Ellisman M.H. Distribution of rSlo Ca2+-activated K+ channels in rat astrocyte perivascular endfeet. Brain Res. 2002;956:183–193. doi: 10.1016/s0006-8993(02)03266-3. [DOI] [PubMed] [Google Scholar]
- 11.Girouard H., Bonev A.D., Nelson M.T. Astrocytic endfoot Ca2+ and BK channels determine both arteriolar dilation and constriction. Proc. Natl. Acad. Sci. USA. 2010;107:3811–3816. doi: 10.1073/pnas.0914722107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Øyehaug L., Østby I., Einevoll G.T. Dependence of spontaneous neuronal firing and depolarisation block on astroglial membrane transport mechanisms. J. Comput. Neurosci. 2012;32:147–165. doi: 10.1007/s10827-011-0345-9. [DOI] [PubMed] [Google Scholar]
- 13.Tas P., Massa P., Koschel K. Characterization of an Na+/K+/Cl− co-transport in primary cultures of rat astrocytes. Biochim. Biophys. Acta. 1987;903:411–416. doi: 10.1016/0005-2736(87)90047-2. [DOI] [PubMed] [Google Scholar]
- 14.Laming P.R. Potassium signalling in the brain: its role in behaviour. Neurochem. Int. 2000;36:271–290. doi: 10.1016/s0197-0186(99)00136-9. [DOI] [PubMed] [Google Scholar]
- 15.Østby I., Øyehaug L., Omholt S.W. Astrocytic mechanisms explaining neural-activity-induced shrinkage of extraneuronal space. PLOS Comput. Biol. 2009;5:e1000272. doi: 10.1371/journal.pcbi.1000272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Odette L.L., Newman E.A. Model of potassium dynamics in the central nervous system. Glia. 1988;1:198–210. doi: 10.1002/glia.440010305. [DOI] [PubMed] [Google Scholar]
- 17.Chen K.C., Nicholson C. Spatial buffering of potassium ions in brain extracellular space. Biophys. J. 2000;78:2776–2797. doi: 10.1016/S0006-3495(00)76822-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gardner-Medwin A.R. Analysis of potassium dynamics in mammalian brain tissue. J. Physiol. 1983;335:393–426. doi: 10.1113/jphysiol.1983.sp014541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Araque A., Parpura V., Haydon P.G. Tripartite synapses: glia, the unacknowledged partner. Trends Neurosci. 1999;22:208–215. doi: 10.1016/s0166-2236(98)01349-6. [DOI] [PubMed] [Google Scholar]
- 20.Postnov D.E., Koreshkov R.N., Sosnovtseva O.V. Dynamical patterns of calcium signaling in a functional model of neuron-astrocyte networks. J. Biol. Phys. 2009;35:425–445. doi: 10.1007/s10867-009-9156-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sun W., McConnell E., Nedergaard M. Glutamate-dependent neuroglial calcium signaling differs between young and adult brain. Science. 2013;339:197–200. doi: 10.1126/science.1226740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fernandes J., Lorenzo I.M., Valverde M.A. IP3 sensitizes TRPV4 channel to the mechano- and osmotransducing messenger 5′-6′-epoxyeicosatrienoic acid. J. Cell Biol. 2008;181:143–155. doi: 10.1083/jcb.200712058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nilius B., Watanabe H., Vriens J. The TRPV4 channel: structure-function relationship and promiscuous gating behaviour. Pflugers Arch. 2003;446:298–303. doi: 10.1007/s00424-003-1028-9. [DOI] [PubMed] [Google Scholar]
- 24.Farr H., David T. Models of neurovascular coupling via potassium and EET signalling. J. Theor. Biol. 2011;286:13–23. doi: 10.1016/j.jtbi.2011.07.006. [DOI] [PubMed] [Google Scholar]
- 25.Watanabe H., Vriens J., Nilius B. Modulation of TRPV4 gating by intra- and extracellular Ca2+ Cell Calcium. 2003;33:489–495. doi: 10.1016/s0143-4160(03)00064-2. [DOI] [PubMed] [Google Scholar]
- 26.Benfenati V., Amiry-Moghaddam M., Ferroni S. Expression and functional characterization of transient receptor potential vanilloid-related channel 4 (TRPV4) in rat cortical astrocytes. Neuroscience. 2007;148:876–892. doi: 10.1016/j.neuroscience.2007.06.039. [DOI] [PubMed] [Google Scholar]
- 27.Nilius B., Vriens J., Voets T. TRPV4 calcium entry channel: a paradigm for gating diversity. Am. J. Physiol. Cell Physiol. 2004;286:C195–C205. doi: 10.1152/ajpcell.00365.2003. [DOI] [PubMed] [Google Scholar]
- 28.Kung C. A possible unifying principle for mechanosensation. Nature. 2005;436:647–654. doi: 10.1038/nature03896. [DOI] [PubMed] [Google Scholar]
- 29.Koenigsberger M., Sauser R., Meister J.-J. Effects of arterial wall stress on vasomotion. Biophys. J. 2006;91:1663–1674. doi: 10.1529/biophysj.106.083311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ballanyi K., Grafe P., ten Bruggencate G. Ion activities and potassium uptake mechanisms of glial cells in guinea-pig olfactory cortex slices. J. Physiol. 1987;382:159–174. doi: 10.1113/jphysiol.1987.sp016361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bennett M.R., Farnell L., Gibson W.G. Origins of blood volume change due to glutamatergic synaptic activity at astrocytes abutting on arteriolar smooth muscle cells. J. Theor. Biol. 2008;250:172–185. doi: 10.1016/j.jtbi.2007.08.024. [DOI] [PubMed] [Google Scholar]
- 32.Smolyak S. Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Math. Dokl. 1963;4:240–243. [Google Scholar]
- 33.Sobol I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001;55:271–280. [Google Scholar]
- 34.Heiss, F., and V. Winschel. 2006. Estimation with numerical integration on sparse grids. Department of Economics Discussion paper 2006–15, University of Munich, http://econpapers.repec.org/paper/lmumuenec/916.htm.
- 35.Nadkarni S., Jung P. Dressed neurons: modeling neural-glial interactions. Phys. Biol. 2004;1:35–41. doi: 10.1088/1478-3967/1/1/004. [DOI] [PubMed] [Google Scholar]
- 36.Zhang Y., Barres B.A. Astrocyte heterogeneity: an underappreciated topic in neurobiology. Curr. Opin. Neurobiol. 2010;20:588–594. doi: 10.1016/j.conb.2010.06.005. [DOI] [PubMed] [Google Scholar]
- 37.Hibino H., Inanobe A., Kurachi Y. Inwardly rectifying potassium channels: their structure, function, and physiological roles. Physiol. Rev. 2010;90:291–366. doi: 10.1152/physrev.00021.2009. [DOI] [PubMed] [Google Scholar]
- 38.Walz W. Role of astrocytes in the clearance of excess extracellular potassium. Neurochem. Int. 2000;36:291–300. doi: 10.1016/s0197-0186(99)00137-0. [DOI] [PubMed] [Google Scholar]
- 39.Cressman J.R., Jr., Ullah G., Barreto E. The influence of sodium and potassium dynamics on excitability, seizures, and the stability of persistent states: I. Single neuron dynamics. J. Comput. Neurosci. 2009;26:159–170. doi: 10.1007/s10827-008-0132-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jensen M.S., Azouz R., Yaari Y. Variant firing patterns in rat hippocampal pyramidal cells modulated by extracellular potassium. J. Neurophysiol. 1994;71:831–839. doi: 10.1152/jn.1994.71.3.831. [DOI] [PubMed] [Google Scholar]
- 41.Thompson S.M., Gähwiler B.H. Activity-dependent disinhibition. II. Effects of extracellular potassium, furosemide, and membrane potential on ECl− in hippocampal CA3 neurons. J. Neurophysiol. 1989;61:512–523. doi: 10.1152/jn.1989.61.3.512. [DOI] [PubMed] [Google Scholar]
- 42.Balestrino M., Aitken P.G., Somjen G.G. The effects of moderate changes of extracellular K+ and Ca2+ on synaptic and neural function in the CA1 region of the hippocampal slice. Brain Res. 1986;377:229–239. doi: 10.1016/0006-8993(86)90863-2. [DOI] [PubMed] [Google Scholar]
- 43.Balena T., Acton B.A., Woodin M.A. Extracellular potassium regulates the chloride reversal potential in cultured hippocampal neurons. Brain Res. 2008;1205:12–20. doi: 10.1016/j.brainres.2008.02.038. [DOI] [PubMed] [Google Scholar]
- 44.Jensen M.S., Cherubini E., Yaari Y. Opponent effects of potassium on GABAA-mediated postsynaptic inhibition in the rat hippocampus. J. Neurophysiol. 1993;69:764–771. doi: 10.1152/jn.1993.69.3.764. [DOI] [PubMed] [Google Scholar]
- 45.Newman E.A. Distribution of potassium conductance in mammalian Müller (glial) cells: a comparative study. J. Neurosci. 1987;7:2423–2432. [PMC free article] [PubMed] [Google Scholar]
- 46.Nett W.J., Oloff S.H., McCarthy K.D. Hippocampal astrocytes in situ exhibit calcium oscillations that occur independent of neuronal activity. J. Neurophysiol. 2002;87:528–537. doi: 10.1152/jn.00268.2001. [DOI] [PubMed] [Google Scholar]
- 47.Di Castro M.A., Chuquet J., Volterra A. Local Ca2+ detection and modulation of synaptic release by astrocytes. Nat. Neurosci. 2011;14:1276–1284. doi: 10.1038/nn.2929. [DOI] [PubMed] [Google Scholar]
- 48.Nuriya M., Yasui M. Endfeet serve as diffusion-limited subcellular compartments in astrocytes. J. Neurosci. 2013;33:3692–3698. doi: 10.1523/JNEUROSCI.3050-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hamill O.P., Martinac B. Molecular basis of mechanotransduction in living cells. Physiol. Rev. 2001;81:685–740. doi: 10.1152/physrev.2001.81.2.685. [DOI] [PubMed] [Google Scholar]
- 50.Strotmann R., Schultz G., Plant T.D. Ca2+-dependent potentiation of the nonselective cation channel TRPV4 is mediated by a C-terminal calmodulin binding site. J. Biol. Chem. 2003;278:26541–26549. doi: 10.1074/jbc.M302590200. [DOI] [PubMed] [Google Scholar]
- 51.Gonzalez-Fernandez J.M., Ermentrout B. On the origin and dynamics of the vasomotion of small arteries. Math. Biosci. 1994;119:127–167. doi: 10.1016/0025-5564(94)90074-4. [DOI] [PubMed] [Google Scholar]
- 52.Haddock R.E., Hirst G.D., Hill C.E. Voltage independence of vasomotion in isolated irideal arterioles of the rat. J. Physiol. 2002;540:219–229. doi: 10.1113/jphysiol.2001.013698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hudetz A.G., Conger K.A., Kovach A.G.B. Pressure distribution in the pial arterial system of rats based on morphometric data and mathematical models. J. Cereb. Blood Flow Metab. 1987;7:342–355. doi: 10.1038/jcbfm.1987.72. [DOI] [PubMed] [Google Scholar]
- 54.Cao, R. 2011. The hemo-neural hypothesis: effects of vasodilation on astrocytes in mammalian neocortex. Ph.D. thesis. Massachusetts Institute of Technology, Cambridge, MA.
- 55.Horiuchi T., Dietrich H.H., Dacey R.G., Jr. Mechanism of extracellular K+-induced local and conducted responses in cerebral penetrating arterioles. Stroke. 2002;33:2692–2699. doi: 10.1161/01.str.0000034791.52151.6b. [DOI] [PubMed] [Google Scholar]
- 56.Ngai A.C., Winn H.R. Modulation of cerebral arteriolar diameter by intraluminal flow and pressure. Circ. Res. 1995;77:832–840. doi: 10.1161/01.res.77.4.832. [DOI] [PubMed] [Google Scholar]
- 57.Dacey R.G., Jr., Duling B.R. A study of rat intracerebral arterioles: methods, morphology, and reactivity. Am. J. Physiol. 1982;243:H598–H606. doi: 10.1152/ajpheart.1982.243.4.H598. [DOI] [PubMed] [Google Scholar]
- 58.Parthimos D., Edwards D.H., Griffith T.M. Minimal model of arterial chaos generated by coupled intracellular and membrane Ca2+ oscillators. Am. J. Physiol. 1999;277:H1119–H1144. doi: 10.1152/ajpheart.1999.277.3.H1119. [DOI] [PubMed] [Google Scholar]
- 59.Taniguchi J., Tsuruoka S., Suzuki M. TRPV4 as a flow sensor in flow-dependent K+ secretion from the cortical collecting duct. Am. J. Physiol. Renal Physiol. 2007;292:F667–F673. doi: 10.1152/ajprenal.00458.2005. [DOI] [PubMed] [Google Scholar]
- 60.Metea M.R., Kofuji P., Newman E.A. Neurovascular coupling is not mediated by potassium siphoning from glial cells. J. Neurosci. 2007;27:2468–2471. doi: 10.1523/JNEUROSCI.3204-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


