Coherent Neutron Scattering and Collective Dynamics in the Protein, GFP

Abstract

Collective dynamics are considered to be one of the major properties of soft materials, including biological macromolecules. We present coherent neutron scattering studies of the low-frequency vibrations, the so-called boson peak, in fully deuterated green fluorescent protein (GFP). Our analysis revealed unexpectedly low coherence of the atomic motions in GFP. This result implies a low amount of in-phase collective motion of the secondary structural units contributing to the boson peak vibrations and fast conformational fluctuations on the picosecond timescale. These observations are in contrast to earlier studies of polymers and glass-forming systems, and suggest that random or out-of-phase motions of the β-strands contribute greater than two-thirds of the intensity to the low-frequency vibrational spectra of GFP.

Introduction

Fundamental understanding of how dynamics and structure of proteins act together to result in complex enzymatic and other functions remains one of the major challenges in biophysics and structural biology (1). In proteins, dynamics range from vibrations of individual atoms about a bond to the collective motions of whole domains that contain hundreds or thousands of atoms moving over nanometer distances (2). These large collective motions are often connected to the rate-controlling steps in enzymatic activity (3,4). However, collective motions also occur on the much faster timescale of ∼1 ps, where low-frequency vibrations and fast conformational fluctuations are observed (5–7).

The low-frequency vibrations in proteins appear as the so-called boson peak in light and neutron scattering spectra (7–10). They are similar to the boson peak in glass-forming systems (phenomena which can be reviewed in more detail elsewhere (11–14)), bringing to mind the analogy often drawn between proteins and glassy materials (15). Recent studies suggest that the low-frequency vibrations in proteins may be connected to chemical-barrier crossing events in enzyme activity (16,17). Indeed, the lifetimes of some nonequilibrium transition states are on the order of tens of femtoseconds (18), a relevant timescale for the deformations associated with these low-frequency vibrations. In this way it is possible to consider vibrational dynamics (subpicosecond) as an attempted frequency for barrier crossing events. Similarly, one could consider these vibrational modes as an attempt frequency for the initiation of slower collective relaxations. These modes have the largest atomic mean-squared displacements due to their low frequency. However, understanding the microscopic nature of these low-frequency vibrations in proteins remains a challenge. Simulations suggest that these collective vibrations involve the entire protein, including backbone and amino-acid side chains, both hydrophilic and hydrophobic (6,19).

The study of collective dynamics can be done efficiently using coherent neutron scattering and x-ray scattering techniques. These techniques were successfully applied to analysis of the boson peak vibrations in glass-forming systems, including polymers (20–25). They revealed an acousticlike nature of the low-frequency vibrations, a hybridization of longitudinal and transverse modes (26). Moreover, coherent neutron scattering revealed strong in-phase motion of neighbor structural units in the low-frequency vibrational modes (21–24). In this work, reference to in-phase motions is made in the framework laid out by Engberg et al. (22), which explains how the pair correlations seen in the static structure factor are preserved when these paired atoms move together at a given frequency. In-phase motions have also been observed for the fast picosecond fluctuations, which are considered to be a precursor of structural relaxation in glass-forming systems (21). All these results suggest that the fast dynamics (the boson peak and fast relaxation) in glass-forming systems involves collective in-phase motions of many structural units.

To our knowledge, this type of analysis has not yet been applied to study protein dynamics. In most cases only incoherent neutron scattering has been used (10,27–29). A few studies utilizing inelastic x-ray scattering or higher energy neutron scattering on proteins have revealed some higher-frequency collective vibrational modes above the boson peak frequency (30,31). Coherent neutron scattering has also been applied to the analysis of domainlike motions in proteins on timescales of tens of nanoseconds (32–34), providing characteristic timescales and the amplitude of the domain motions and their changes upon ligand binding (33). However, this technique was not used to study the faster dynamics.

In this study we use coherent neutron scattering to analyze low-frequency collective vibrations in a fully deuterated green fluorescent protein (GFP). Our analysis reveals a surprising result: only a minor fraction of the boson peak intensity can be assigned to coherent, in-phase motion expected from acousticlike vibrations. This coherent-phase contribution is further diminished upon hydration of the protein. This result is in contrast to the earlier studies of glass-forming systems and polymers. It suggests that out-of-phase or random motions of the protein secondary structures make up the majority of the low-frequency vibrations in GFP. This is an interesting and potentially important result taking into account the relatively stable and rigid secondary structures of proteins.

Materials and Methods

Deuterated and hydrogenated GFP were overexpressed in Escherichia coli BL21 (DE3) transformed with pET28a_AvGFP (35), which results in a mutant identical to the GFPMut3 variant with the exceptions of F64L, G65T, A72S, F99S, M153T, and V163A (36). Culture conditions and purification procedures are described in Heller et al. (35) and Luo et al. (37). For fully deuterated GFP, 0.5% (w/v) D₈-glycerol was used as the carbon source. After purification, the proteins were exchanged in D₂O and lyophilized. Lyophilized fully deuterated (dGFP) and hydrogenated (hGFP) proteins were used as dry samples. We emphasize that hGFP had all exchangeable hydrogen atoms exchanged by deuterium. Hydrated samples were prepared by exposing lyophilized powder to D₂O vapor in a nitrogen atmosphere until they absorb 0.4 g of D₂O per gram of GFP. The samples were sealed in aluminum sample cans. The neutron scattering signal from hydrogenated samples exhibit predominantly incoherent scattering and the signal from the deuterated samples exhibit predominantly coherent scattering. Table 1 presents the fractional contribution from all atoms to the scattering cross-section for each sample.

Table 1.

Fraction of the scattering cross sections of dGFP samples

Sample	Protein incoherent	Protein coherent	D2O incoherent	D2O coherent	% Intensity from in-phase motion at EBP
dGFP dry	15.1%	84.9%	0.0%	0.0%	32.6 ± 3.7% at 170 K
					34.3 ± 1.2% at 295 K
dGFP D2O h = 0.4	10.8%	60.5%	6.0%	22.6%	22.6 ± 3.5% at 170 K
					9.3 ± 4.1% at 295 K

The last column gives the percentage of scattering at the boson peak resulting from in-phase coherent motions of the secondary structure.

Neutron scattering measurements were performed using the Cold Neutron Chopper Spectrometer (CNCS) at the Oak Ridge National Laboratory, the Spallation Neutron Source (38,39). A quantity of 3 meV incident neutrons was used on CNCS spectrometer for measurements up to ∼20 meV (∼0.05 ps) with instrumental resolution of ∼50 μeV (20 ps), in a Q range from 0.5 to 4 Å⁻¹. Spectra were measured on the energy gain side. All spectra were corrected using a vanadium standard and empty sample can. Data were treated using the DAVE software package from the NIST Center for Neutron Research (National Institute of Standards and Technology, Gaithersburg, MD) (40).

Results and Discussion

Elastic scattered intensity measured by CNCS provides the static structure factor, S(Q), of fully deuterated GFP samples (Fig. 1). The predominant feature in S(Q) of dGFP is the peak at 1.4 Å⁻¹ corresponding to the spacing between strands in the β-barrel (31,41). A smaller peak is also observed in all samples at Q ∼ 0.6 Å⁻¹. It corresponds to a distance of ∼10 Å, approximately the distance from the barrel to the central helix, consistent with the previous assignments of this peak to spacing between secondary structural units (31,41). This peak shifts to lower Q upon hydration (Fig. 1 a) indicating a slight expansion of the barrel to accommodate water molecules. This interpretation of the structure factor is further supported by calculations based on the crystal structure of GFP, taken from the Protein Data Bank file 1GFL (42) (Fig. 1 b). Using the program CRYSON, a part of the ATSAS suite (43), we calculated the neutron powder S(Q) for the crystal structure of the entire dGFP, and the S(Q) resulting only from the residues in the β-barrel (Fig. 1 c). The peak at Q ∼ 1.4 Å⁻¹ is clearly a result of the β-barrel contribution. The structural peak of water is also apparent in the hydrated samples at ∼1.8 Å⁻¹. Three Bragg peaks at T = 170 K indicate that some fraction of the water formed ice in this sample. The experimental S(Q) for each sample and temperature was well fit by a sum of three Gaussian peaks and a flat background (incoherent scattering) (Fig. 1 a) to be used in later fitting procedures.

Figure 1.

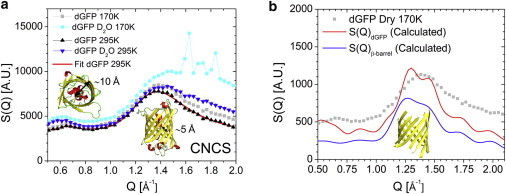
(a) Structure factor of dry dGFP and dGFP D₂O at 170 and 295 K from CNCS. The solid red line (in panel a) is an example of the structure factor fit as used in the subsequent analysis of the Q-dependence of S(Q,E). The peaks at Q > 1.6 Å⁻¹ indicate a small fraction of the hydration water has crystallized at 170 K. (b) The structure factor of dry dGFP at 170 K (symbols), superimposed with the calculated structure factor based on the deposited Protein Data Bank file, PDB:1GFL (red). (Blue line) Structure factor calculated for the atoms in the β-barrel of GFP. To see this figure in color, go online.

The experimentally measured neutron scattering spectra for deuterated and hydrogenated GFP (Fig. 2), show the boson peak at E∼2–4 meV and quasielastic scattering at lower energies. The spectra are shown for two Q values, 0.9 and 1.4, corresponding to the minimum and maximum of the static structure factor, respectively. The spectral shape appears to be rather independent of Q at these two important length scales. Moreover, the incoherently scattering spectra of hydrogenated samples are similar to the scattering spectra of deuterated GFP for both the dry and hydrated proteins (Fig. 2). The shift in peak position with temperature and hydration is the expected behavior for proteins (44). These comparisons already indicate the absence of a strong coherence in the motions contributing to the scattering spectra.

Figure 2.

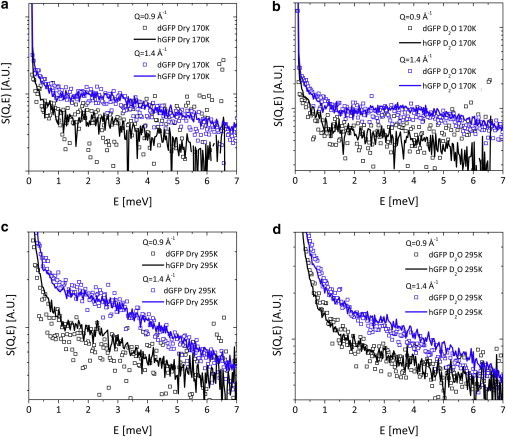
Scattering intensity of deuterated GFP (symbols) and of hydrogenated GFP (lines) measured at Q_min = 0.9 Å⁻¹ (black) and Q_max = 1.4 Å⁻¹ (blue) of the static structure factor of dGFP. The data for hydrogenated protein are scaled arbitrary to match the spectra of deuterated samples. The data for dry proteins is shown in panels (a) and (c) for T=170K and T=295K respectively; similarly data for hydrated proteins is show in panels (b) and (d) for T=170K and T=295K. Note the coherent spectra (dGFP) appear similar to the incoherent spectra (hGFP) at each Q-value. To see this figure in color, go online.

We will focus now on detailed analysis of the Q-dependence of the S(Q,E) in dGFP. According to the theoretical model of coherent scattering proposed previously (45,46), random motion of structural units in any mode at energy E will lead to the Q-dependence, S_r(Q,E) ∝ Q². We will call this kind of motion a random-phase motion. At the same time if the neighbor structural units in the mode are moving together in phase, the Q-dependence should be affected by the static structure factor: S_c(Q,E) ∝ Q²S(Q). We will call this motion an in-phase motion. This theoretical approach has been applied to analysis of coherent neutron scattering data in B₂O₃ and in deuterated polybutadiene at temperatures below and above their glass transition temperature (21–24). This analysis revealed significant contribution of in-phase motion to the boson peak. Yet, the contribution of the in-phase motion to the total scattering at energies of the boson peak, E_BP, in both materials was >50% (21–24), decreasing at energies higher than the boson peak. These results suggested the prevalence of in-phase motions of structural units in the modes contributing to the boson peak.

Our analysis of the Q-dependence of the S(Q,E) for dGFP at the energy close to the boson peak reveals only a weak increase in the region of the main peak of S(Q), ∼1.4 Å⁻¹ (Fig. 3). The difference between coherent (deuterated samples) and incoherent (hydrogenated samples) scattering is surprisingly small, especially in the hydrated case (Fig. 3). This result suggests that random or out-of-phase motions of strands in the β-barrel (the major contribution to the S(Q) peak at Q_max ∼ 1.4 Å⁻¹) are the predominant motions contributing to the modes at the boson peak in GFP. The term “out-of-phase motions” should be understood to imply all degenerate collective motions in which the local structure, as reflected in the static structure factor, are not maintained, whereas random-phase motions indicate incoherent motions of individual atoms. To quantify the random versus in-phase contributions to the total scattering in dGFP, we fit the Q-dependence of S(Q,E) at a constant energy, E, to the following equation:

$$S\left(Q,E\right)=AS\left(Q\right)Q^2+B{Q}^2+C.$$ (1)

Here, the first term represents the in-phase contribution with the amplitude A, the second term represents the random-phase motion with the amplitude B, and the third term takes into account multiple scattering and possible background contributions. In this analysis we used the fit S(Q) curve for each sample (Fig. 1 a), and constants A, B, and C were used as free fit parameters. An example of the fit is presented in Fig. 3 c. This was performed for each of the measured spectra in intervals of 1 meV from 0.5 to 9.5 meV (reported at the average position, 1 meV, 2 meV, etc.), with an additional point for the interval of 0.2–0.5 meV for quasielastic scattering. The fits reproduce well S(Q,E) both at constant energy (Fig. 3 c) and as a function of energy for both samples and both temperatures (Fig. 4).

Figure 3.

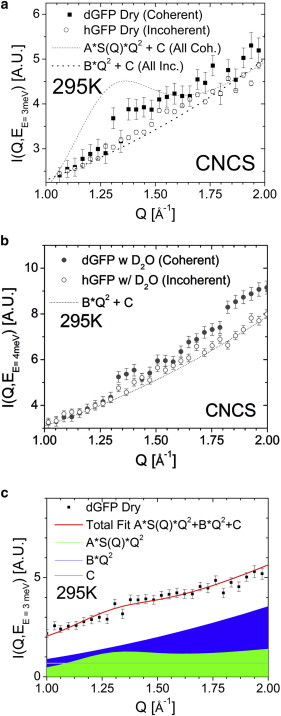
(a and b) Comparison of normalized intensity at the boson peak energy, as a function of Q for hGFP and dGFP at 295 K for the dry and hydrated states, respectively. The spectra are overlaid (dashed lines) for ∝Q², illustrating the expected spectra for random phase or out-of-phase collective motions. (Dotted line in panel a) Expected Q-dependence for a fully in-phase coherent motion, ∝S(Q)^∗Q². (c) Schematic of the fitting procedure used to decompose the random and coherent phase motions, shown here for the boson peak region of dry deuterated GFP at 295 K. To see this figure in color, go online.

Figure 4.

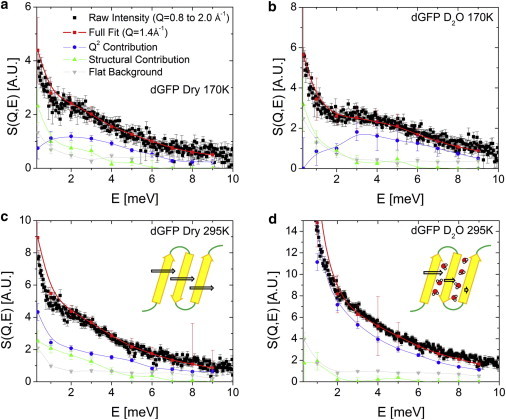
Decomposition of the random phase and coherent phase contributions for (a) dry dGFP at 170K (b) D₂O hydrated dGFP at 170K (c) dry dGFP at 295K and (d) D₂O hydrated dGFP at 295K. The coherent phase contribution is shown by green triangles, the random-phase motion by blue circles, and the contribution of multiple scattering by grey inverted triangles. The total fit is indicated by the red symbols, reproducing the data well in all conditions. Lines are only a guide to the eye.

Our analysis estimates the in-phase contribution to the modes around the boson peak at ∼35% in dry dGFP at both 170 and 295 K. The in-phase contribution decreases sharply with hydration of dGFP. Comparison to the earlier studies of glass-forming systems (20–23) shows that GFP has an unexpectedly low contribution of in-phase cooperative motions of the structural units associated with the main diffraction peak in the structure factor in the region of the boson peak. One would anticipate that randomly packed polymer chains in polybutadiene will have greater randomness of neighbor chain motions than in the well-defined secondary structures of a protein. Given that GFP has a relatively rigid β-barrel with well-defined spacing between strands (Fig. 1) and rather small atomic fluctuations (27,47). Yet the coherence of the motions of neighbor strands appears surprisingly low, weaker than in a disordered polymer (23,24).

This surprising result suggests random or out-of-phase displacements of neighbor strands in the β-barrel, despite many hydrogen bonds connecting them. While microscopic interpretation of our experimental result is clear, the reason that it differs from what is observed for glassy materials such as polybutadiene and B₂O₃ is a mystery. Simulations suggest that the modes contributing to the boson peak in proteins are highly collective, but not necessarily in-phase (19). Breathing modes are expected at frequencies near the boson peak in barrel structures (48). Despite extensive hydrogen bonding between adjacent strands in the barrel, it seems that the motions of the strands in such modes are out-of-phase or random relative to one another. We might also examine the behavior of vitreous silica, which displays a highly directional coherence in its acoustical dispersions (49–51), consistent with models predicting different localizations of acoustic excitations (52,53). It might be similar in GFP, that greater coherence of the motions will be observed along the strand. Unfortunately, the peak in S(Q) corresponding to the intrastrand distances appears at Q values >2.0 Å⁻¹, and outside of our studied Q-range.

Hydration of proteins is known to shift the boson peak to higher frequency (27,44,54). This analysis reveals that the addition of hydration water also diminishes the coherence of the motions at the boson peak (Fig. 4). Even at low temperature T = 170 K, when water translational motion is essentially frozen, the in-phase contribution in hydrated dGFP is only ∼10% of the total signal (Fig. 4 b). We speculate that hydration water decreases coherence due to forming H-bonds with the protein competing with the forces holding the secondary structural units together and complicating (or dephasing) the motions at the boson peak. At higher temperature, 295 K, we see hydration reducing the contribution of in-phase collective motions to the boson peak even more, as might be expected once the translational and rotational motions of water begin to plasticize the motions of the protein.

Conclusions

Despite many years of studies, the microscopic nature of the low-frequency vibrations that make up the boson peak remains a mystery. In this study we add to what is known about the boson peak in proteins by careful analysis of the coherent scattering of a fully deuterated protein, GFP. This analysis reveals a surprising lack of coherence in the motions of β-strands (that comprise the secondary structure of the protein) contributing to the boson peak. This is even more evident upon hydration, which not only dampens the vibrations at the boson peak, but also further diminishes the coherence of the motions in neighboring β-strands.

This result presents an unexpected difference between the dynamics of proteins and other glass-forming materials. Despite the well-defined secondary structure in proteins, the motions at the boson peak are predominantly due to random phase or out-of-phase motions of secondary structural units. This is striking when comparing to the results obtained for a synthetic polymer, where far more coherent motion is observed between adjacent chains, despite the random packing of the polymer chain. We hope that this result motivates the community to further investigate the issue of the boson peak, especially in proteins. New simulations and measurements on fully deuterated proteins will help to reveal whether these results are specific to GFP (barrels), or is a more general property of protein motions around the boson peak. In the process, we may find better understanding of the role of low-frequency vibrations in biological systems.