Abstract
Cytokinesis in bacteria is accomplished by a ring-shaped cell-division complex (the Z-ring). The primary component of the Z-ring is FtsZ, a filamentous tubulin homolog that serves as a scaffold for the recruitment of other cell-division-related proteins. FtsZ forms filaments and bundles. In the cell, it has been suggested that FtsZ filaments form the arcs of the ring and are aligned in the cell-circumferential direction. Using polarized fluorescence microscopy in live Escherichia coli cells, we measure the structural organization of FtsZ filaments in the Z-ring. The data suggest a disordered organization: a substantial portion of FtsZ filaments are aligned in the cell-axis direction. FtsZ organization in the Z-ring also appears to depend on the bacterial species. Taken together, the unique arrangement of FtsZ suggests novel unexplored mechanisms in bacterial cell division.
Introduction
FtsZ, a prokaryotic homolog of tubulin, is an essential protein in binary fission of prokaryotic cells (1). In vitro, FtsZ forms short protofilaments and long bundles (2). In vivo, along with membrane-binding FtsA and several other partners, FtsZ assembles into a ringlike structure (the Z-ring) and facilitates cytokinesis (3,4). Because cell division involves constriction of the rigid bacterial cell wall, it has been hypothesized that the Z-ring generates a mechanical force. Several force generation mechanisms have been proposed (5,6). These mechanisms are inferred from the unique biophysical properties of FtsZ (7), and from direct observations of constriction in a reconstituted FtsZ-lipid system (8). Several high-resolution structural studies of the Z-ring have appeared: in Caulobacter crescentus, cryo-electron tomography studies showed that FtsZ filaments are aligned in the circumferential direction of the cell (9). Cryo-electron microscopy of vitreous sections of Enterococcus gallinarum is also available (10). Recent super-resolution microscopy studies (11–13) seem to suggest that higher-order Z-ring structures may exist. In this article, we focus on examining the orientation of FtsZ filaments in the Escherichia coli Z-ring. In particular, although it is commonly suggested that FtsZ filaments are bundled and oriented in the circumferential direction of the cell, no direct in vivo evidence of this organization is available for E. coli. Using polarized fluorescence microscopy, we quantitatively measure the orientation of FtsZ filaments in the Z-ring. Results seem to indicate that FtsZ filaments in the Z-ring are disorganized, with a large portion of filaments oriented in the cell-axis direction in E. coli. This finding raises new questions about the division mechanism and the potential role of FtsZ.
Polarized fluorescence microscopy (PFM) is a powerful tool for analyzing dynamic organization of proteins in live cells. Excited by linearly polarized light, a fluorophore will emit fluorescence with an intensity that is proportional to the square of the cosine of the angle between the fluorophore electric dipole vector and the polarization vector (14). Thus, PFM can reveal the orientational organization of the fluorophore and any protein that is rigidly attached to the fluorophore (15,16). For example, using green fluorescent protein (GFP) attached to septin in budding yeast, PFM revealed an organizational transition in septin filaments during yeast cell division (17).
Here, we employ PFM to investigate FtsZ attached to a GFP or a yellow fluorescent protein (YFP) in live bacterial cells. We compare polarized fluorescence from live cells with purified proteins in vitro to infer organizational features of FtsZ filaments in the Z-ring. In our study, linearly polarized filters are placed in both excitation and emission light paths in a custom epifluorescence microscopy system to enhance the contrast of polarized fluorescence signal ((18); see also Materials and Methods). To quantify the degree of fluorophore alignment with a laboratory axis, we define a polarization anisotropy, P = (I|| − I=)/(I|| + I=), where I|| is the emitted fluorescence intensity when the polarizer is positioned parallel to the Y-direction of the microscope stage, and I= is the intensity when the polarizer is in the X-direction (Fig. S1 in the Supporting Material). Thus, changes in P with respect to the angle between fluorophore dipole and light polarization vector will show the direction of alignment of GFP- or YFP-tagged FtsZ in the Z-ring. P also does not depend on the absolute emission intensity (see Materials and Methods). We analyze P quantitatively, and obtain a probability distribution of FtsZ filament orientations in vitro and in vivo.
Materials and Methods
Strains and growth conditions
Strains for fluorescent detection of FtsZ in vivo all carried GFP or YFP fusions to FtsZ and were expressed as merodiploids, which replaced the native FtsZ. E. coli strains were as follows. WM3452 is XL1-Blue that contains a plasmid (pDSW209-FtsZYFP338) expressing an isopropyl-β-D-thiogalactopyranoside (IPTG)-inducible FtsZ with an enhanced YFP (EYFP) gene inserted at residue 338 of FtsZ, within the nonconserved linker domain. WM2026, used as a strain with FtsZ-GFP, expresses an IPTG-inducible chromosomal FtsZ-GFP fusion (GFP fused to the C-terminus of FtsZ) at the lambda attachment site in WM1074 (TX3772). WM3486, derived from WM2026, is a strain with a deletion of the MinCDE system. WM3498, carrying pDSW209-GFP-FtsZ in WM1074, is used as the strain with GFP fused to the N-terminus of FtsZ, whereas WM3497, carrying pDSW209 in WM1074, is used as a vector control, as it expresses GFP only. The C. crescentus strain EG444 used here contains a xylose-inducible FtsZCc-EYFP integrated at the xylX chromosomal locus.
All E. coli strains were cultured on Lysogeny broth with 50 μg/mL ampicillin. An overnight culture was diluted 1:40 into Lysogeny broth medium with 50 μg/mL ampicillin and incubated with shaking until an OD600 of 0.3–0.4 was reached; then, IPTG was added to induce FtsZ-YFP, FtsZ-GFP, GFP-FtsZ, or cytoplasmic GFP expression. Specifically, 50 μM IPTG was used for WM3452 and 100 μM for WM2026, WM3486, WM3498, and WM3497. C. crescentus strains were cultured on peptone yeast extract with 25 μg/ml kanamycin at 28°C (19). Overnight cultures were diluted 1:40 into peptone yeast extract with 25 μg/ml kanamycin and incubated with shaking until an OD600 of 0.3–0.4 was reached; then, 0.6 wt % xylose was added to induce FtsZCc-EYFP.
Microscopy configuration
In preparation for fluorescence microscopy of purified proteins, 1.5 μL of protein in buffer was dropped onto a cleaned glass slide and covered with a coverglass. For live cells, 20 μL of diluted cell culture was dropped onto a cleaned glass slide, and mixed with 20 μL 3 wt % low-melting agarose solution (20). Then, 4 μL 0.5 wt % Casamino acids solution was immediately mixed into the cell-agarose mixture (20) and a coverglass was placed on top. Microscopy was performed soon after solidification of the agarose.
The fluorescence microscope used in this study was a 3-I Marianas Live Cell Imaging Workstation (Intelligent Imaging Innovations, Denver, CO) with a 1.45 NA α-Plan-Fluor 100× oil objective (Carl Zeiss Microscopy, Thornwood, NY). Linear glass polarized filters (Edmund Optics, Barrington, NJ) were placed in both excitation and emission paths (Fig. S1), which insures that the excitation and emission polarizations were exactly parallel to each other either along the lab x axis or y axis. All the samples were illuminated by 488 nm xenon arc lamp light and the images were captured by a Cascade II 512B EMCCD camera (Roper Scientific, Sarasota, FL). For all polarized fluorescence microscopy measurements, Z-stacks were scanned with a step depth of 100 nm and captured with exposure times of 500 ms and interval times of 500 ms.
Image processing
All image analysis and processing was performed using imageJ (National Institutes of Health, Bethesda, MD) and Matlab (Mathworks, Natick, MA). In processing images of purified protein, protofilaments and bundles that were straight and lying horizontally on the coverglass were selected. Two Z-stacks of images, one for the polarizer in the x and one for that in the y direction, were recorded. These images correspond to intensity measurements I|| and I=. For each stack, 5 of 20 consecutive slices in which the protofilaments or bundles were well-focused were selected and averaged. The background noise was cut by first creating histograms of the intensity of all background pixels and then removing pixels that had intensity below a cutoff Ic. The cutoff is chosen at 1.5 SD above the most probable background intensity, which corresponds to the most likely noise intensity. All of our results are insensitive to this cutoff value. Angles between protofilaments or bundles and the lab x axis were carefully measured.
In processing images from the side view of cells, to insure all processed cells are lying horizontally, only cells that exhibited uniform fluorescence from pole to pole during Z-stack scanning were selected. Again, two stacks of images for x-axis and y-axis polarizer alignment were analyzed. For each stack, 2 of 40 consecutive slices where the top of the Z-ring is in focus were picked out and averaged. The background noise was cut in the same way as purified protein images. The angle between the Z-ring and the lab x axis was carefully measured.
In processing images from the cross-sectional view of cells, only the cells standing perpendicular to the coverglass that displayed a circular cross section were selected. For either x-axis or y-axis polarizer alignment, 5 of 40 consecutive slices where the cross section of the Z-ring was in focus were picked out and averaged. The background noise was cut in the same way as above. Then the ring was divided into 18 angular slices corresponding to angle α with respect to the lab y axis (see Fig. 4 C, inset). The intensity in each angular slice was recorded and analyzed.
Figure 4.
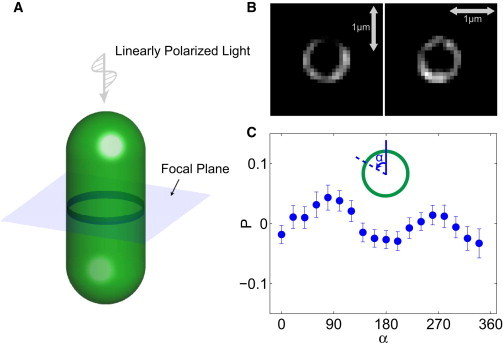
PFM of FtsZ in cross section. (A) Cells with FtsZ-YFP are made to stand vertically with respect to the microscope stage. The emitted light is collected from the Z-ring. (B) Images obtained when the polarizer is oriented in the x and y directions. Plot is based on images of 38 cells. Arrows denote scale bars of 1 μm. (C) The polarization anisotropy as a function of the angle around the ring in the xy plane. Error bars correspond to the mean ± SE. To see this figure in color, go online.
Note that the final calculated polarization parameter, P, does not depend on the absolute emission intensity. However, most microscopes show some degree of polarization anisotropy. Nevertheless, this anisotropy should not be a function of the cell orientation or filament orientation. This anisotropy can be corrected by scaling the average emission intensities, I|| and I=, so that they are equal. This also is equivalent to making by adding an overall constant to the P(α) curve. We have used this correction step to remove the microscope anisotropy.
Mathematical modeling
The experiment measures fluorescence emission intensities from FtsZ tagged with a fluorophore as a function of the angle of the incident polarized light. When interacting with the fluorophore, only the projection of excitation light in the direction of the fluorophore dipole is absorbed, and then emitted. Therefore,
| (1) |
where D is the fluorophore dipole vector (21). This is because the rotational correlation time of fluorophores such as GFP and YFP is significantly longer than their fluorescence lifetime (14,22). Thus, the emission intensity is an accurate reporter of the orientation of the fluorophore with respect to the incoming polarized light. As shown in Fig. S1, after filtering by the polarizer, the excitation light has an orientation parallel to the focal plane. Thus, neglecting phases, the incoming excitation electric vector is
| (2) |
where is the intensity of the excitation light, and p is a unit vector in the direction of the electric vector. After passage through the microscope objective, some depolarization occurs and the excitation light is no longer fully polarized in the p direction. Taking into account this depolarizing effect, the new excitation light will have components in other directions perpendicular to p. The degree of depolarization depends on the NA. The microscope objective we use has NA 1.45. This depolarization phenomenon is well studied and the relationship between Ein and Eexcitation is known (23,24). We include this depolarization effect in our data analysis for the incoming as well as the outgoing polarized light (see the Supporting Material).
For small bundles of FtsZ in vitro, at the molecular level, the fluorophore dipole is fluctuating rapidly on the timescale of the experiment. The probability distribution of the fluorophore dipole needs to be considered for quantitative analysis of the data. As shown in Fig. S1, we use two angles, and , to define D. Therefore, the average collected fluorescence intensity is
| (3) |
and similarly for . is the function that descibes the interaction between dipoles and excitation light (see the Supporting Material) The probability distribution is the orientational distribution of the dipole, which we take as
| (4) |
where the distribution functions are angular Gaussians:
| (5) |
| (6) |
Here, a and b are parameters that describe the widths of the angular distributions. and are the centers of the distributions, which represent the most probable orientation of the fluorophore. The denominators in these expressions are simply normalization factors.
When measuring polarization anistropy for a living cell, there are additional complications. We discovered that the cell envelope is a birefringent material, so the transmission of the incoming light in the cell-axis direction and the circumferential direction are slightly different. This implies that the excitation light received by the fluorophore is slightly changed after passing through the cell envelope:
| (7) |
where B is a transmission matrix that depends on the angle of the cell with respect to the incoming light, α. The transmission matrix can be obtained by measuring the polarization signal from cells expressing freely diffusing GFP (see Results). Once this transmission matrix is measured, all other aspects of the measurements are the same. Again, the emitted light is also affected by the cell envelope, and we have
| (8) |
The emitted light is then filtered by the analyzer, and the analyzed light is collected by the camera.
For fluorophores attached to FtsZ in vivo, the direction of the fluorophore dipole in the lab coordinate system, D, can be computed as
| (9) |
where u is the direction of the fluorophore dipole in the local frame with respect to the filament and R is a rotation from the local frame of the filament to the local cell frame (Fig. S3). This rotation matrix is given in the Supporting Material. Given the filament angular distribution, the total measured fluorescence intensity is then
| (10) |
where is the fluorophore angular distribution with respect to the filament. has been determined in vitro, and we use the same distribution corresponding to each construct to compute the in vivo data. Γ is the filament orientation distribution, which is the objective of our measurement. The definitions of angles are given in Fig. S3. In the fluorescence measurement, cytoplasmic FtsZ, which has an isotropic angular distribution, will contribute to the final signal. Therefore, the filament angular distribution in Eq. 10 is a sum from the cytoplasmic component and the Z-ring component: . It has been reported that 30–40% of FtsZ resides in the Z-ring (25). From our own data, we find that 40% of the labeled FtsZ is in the Z-ring. Within the cropped Z-ring image, FtsZ in the Z-ring is 70% of the total signal and the cytoplasmic FtsZ accounts for 30%. Therefore, the cytoplasmic angular distribution should be . The Z-ring FtsZ distribution, , is described by the filament angular distributions in the local cell frame as , where the individual distribution functions are similar to Eqs. 5 and 6,
| (11) |
| (12) |
and p(ψ) is similarly defined. are again the width parameters of the distribution. From the measured polarization data, we again fit parameters to obtain the average orientation, as well as the distribution widths. Tables 1 and 2 show the final best-fit parameters.
Table 1.
Best-fit parameters for angular distributions describing fluorophore orientation with respect to the FtsZ filament
| In vitro fluorophore orientation with respect to FtsZ | a | b | ||
|---|---|---|---|---|
| FtsZ-YFP | 0.87 | 0.12 | 0° | 0° |
| FtsZ-YFP bundle | 0.01 | 0.19 | 0° | 0° |
| FtsZ-GFP | 0.79 | 0.14 | 0° | 0° |
| FtsZ-GFP bundle | 1.26 | 0.25 | 0° | 0° |
| GFP-FtsZ | 1.00 | 0.17 | 0° | 0° |
| C. crescentus FtsZ-YFP | 0.92 | 0.13 | 0° | 0° |
Table 2.
Best-fit parameters for angular distributions describing FtsZ-filament orientation in the Z-ring with respect to the cell-axial and circumferential directions
| In vivo FtsZ orientation | c | d | ||
|---|---|---|---|---|
| E. coli FtsZ-YFP axial | 4.98 | 1.10 | 0° | 0° |
| E. coli FtsZ-YFP circumferential | 5.00 | 0.00 | 0° | 0° |
| E. coli FtsZ-GFP axial | 5.00 | 0.11 | 0° | 0° |
| E. coli FtsZ-GFP circumferential | 5.00 | 0.06 | 0° | 0° |
| E. coli GFP-FtsZ axial | 5.00 | 0.28 | 0° | 0° |
| E. coli GFP-FtsZ circumferential | 5.00 | 0.00 | 0° | 0° |
| C. crescentus FtsZ-YFP axial | 5.00 | 0.00 | 0° | 0° |
| C. crescentus FtsZ-YFP circumferential | 0.00 | 4.93 | 0° | 0° |
Angular distributions are given by Eqs. 11 and 12. We use two different average orientations, axial and circumferential. The fitted parameters indicate broad angular distributions and are consistent with each other. The pictorial representations of these distributions are shown in Fig. 5 and in the Supporting Material. Parameters c and d are the widths of p(β) and p(γ), respectively.
Results
Polarization anisotropy of FtsZ protofilament bundles in vitro
We first calibrated and tested PFM using FtsZ protofilaments in vitro. FtsZ can polymerize into bundles or protofilaments, mainly depending on the concentration of magnesium (2). We polymerized FtsZ tagged with GFP (at the C- or N-terminal end) or YFP (at an internal linker near the C-terminal end) into protofilaments at a concentration of 1–2 μM (26). Although most protofilaments were short (∼100 nm), a small percentage were of sufficient length (>300 nm) to resolve the filament axis in the microscope. Electron microscopy images of these longer filaments showed that they are predominately small bundles, with two or three protofilaments in each bundle (Fig. 1). We collect data from these small protofilament bundles (also referred to as small bundles), as well as large bundles with higher concentrations of magnesium.
Figure 1.
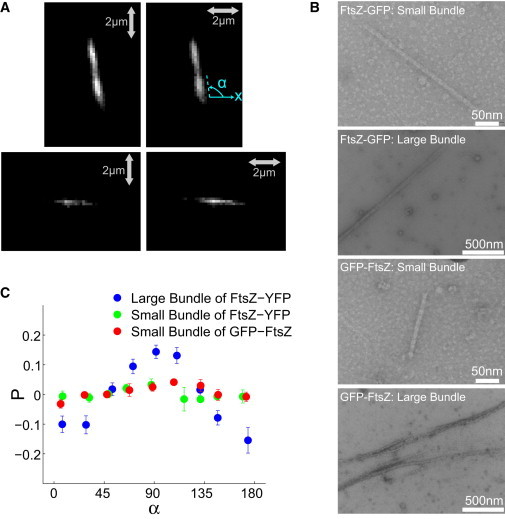
Polarized fluorescence measurement of purified FtsZ in vitro. (A and B) Polarized fluorescence images (A) and electron microscopy images (B) are shown for small and large FtsZ bundles. The electron microscopy images show parallel protofilaments of FtsZ bundled together. Fluorescence images are obtained when the linear polarizer is parallel and perpendicular to the x axis. α is the angle between the bundle and the x axis. (C) The largest polarization anisotropy, P = I|| − I−)/(I||+ I−), occurs when the angle between the bundle and the x axis is 90°. Large bundles of FtsZ show a stronger anisotropy than do small protofilament bundles. Error bars correspond to the mean ± SE. C-terminal YFP large bundles (174 samples) and small bundles (92 samples), and N-terminal GFP small bundles (64 samples), all show a similar orientational alignment (see also Fig. S2). These results indicate that the fluorophore dipole is roughly parallel to the bundle. To see this figure in color, go online.
The measured fluorescence intensities noticeably changed as we rotated the polarizer (Fig. 1 A). Fig. 1 C plots the polarization anisotropy, P, as a function of the angle between FtsZ bundles and the lab x axis. For E. coli FtsZ-YFP, FtsZ-GFP, GFP-FtsZ, and C. crescentus FtsZ-YFP, P for large and small protofilament bundles reaches a peak at 90° and a low point at 0°, although the amplitude of the peak for the small protofilament bundle is less than that of the large bundle (Fig. 1 C). This result is direct evidence that when the filament is oriented parallel to the y axis (α = 90°), I|| > I= and the polarization anisotropy reaches a maximum; when the filament is oriented parallel to the x axis (α = 0° or 180°), I= > I|| and the polarization anisotropy reaches a minimum. This is possible only if the average direction of the GFP and YFP dipole is approximately parallel to the axis of FtsZ protofilaments or bundle. From this data, we also performed a quantitative analysis and extracted angular distributions of GFP and YFP dipoles around the FtsZ filament (see below).
Orientation distribution of fluorophore dipoles in vitro
To obtain a quantitative understanding of fluorophore orientation around the FtsZ filament, it is necessary to consider an angular distribution (described by a probability density) of fluorophores around the filament axis. The mathematical details are given in Materials and Methods, and the basic idea is illustrated in Fig. S1. For a given filament in the illumination plane with spatial orientation described by angle α, we define a unit vector, D, describing the direction of the fluorophore dipole. This vector is mathematically specified by angles . Since the fluorophore fluctuates rapidly, these angles are distributed probabilistically with average orientations and SDs . We use angular Gaussian functions to describe the angular distributions. The observed fluorescence intensities are then computed by considering the projection of D in the direction of the incoming polarized light and then integrating over all possible fluorophore dipole directions. Due to the high NA of the microscope, some depolarization of the incoming and outgoing light is present. These depolarization effects are taken into account in our calculation. The formula for the dipole distribution are given in Materials and Methods.
By collecting fluorescence data from randomly oriented FtsZ filaments, we can calculate the polarization anisotropy as
| (13) |
where is the angle of the filament with respect to the lab x axis (Fig. S1). This function is experimentally measured. The signal is also a function of the dipole angular distribution with unknown parameters . Therefore, by fitting the experimental curve, we can obtain information about the orientational probability distribution of the fluorophore with respect to the filament.
Using nonlinear optimization in Matlab, we have determined the parameters for , , , and that best explain the experimental data. In Fig. S2, we see that for the in vitro FtsZ-YFP small protofilament bundles, we can only obtain a good fit to the experimental data when the average orientations are and . Thus, the most probable orientation of the fluorophore is parallel to the protofilament. However, the distributions are quite broad (relatively small a and b values), the probability of observing other fluorophore orientations is quite high. These results suggest that the fluorophore has an angular distribution roughly equal to the distribution shown in Fig. S2 around the protofilament direction.
The fitted results for FtsZ-YFP bundles show generally the same and values, but with narrower distribution widths (Fig. S2 B). This is reasonable since in a bundle, fluorophore fluctuations are presumably more constrained. PFM is able to measure this change in orientational distribution.
Results from GFP-FtsZ and FtsZ-GFP and C. crescentus FtsZ-YFP protofilament bundles are also examined using this approach. We find that and are all similar, indicating that the fluorophore generally is aligned with the filament direction. All of the fitted results are summarized in Table 1. This alignment does not appear to depend on the position of the fluorophore label, although the width of the distributions does show some variation. Since the linker between GFP and FtsZ is relatively disordered, this observed alignment is likely from nonspecific interactions between GFP and FtsZ filament, possibly from surface electrostatic charges. FtsZ-filaments themselves may also have an electric dipole, which can further align the attached fluorophore.
Polarization anisotropy of FtsZ-ring in live cells
To determine the alignment of FtsZ filaments in the Z-ring in vivo, we first imaged E. coli and C. crescentus cells expressing freely diffusing GFP or YFP in the cytoplasm to determine the possible existence of intrinsic polarization of the cell body. Many types of biological materials exhibit optical birefringence where transmitted or reflected light becomes polarized (27). In bacteria, the cell wall, the cell membrane, and other proteins may exhibit birefringence. A fully isotropic signal from freely diffusing GFP will show anisotropy after the fluorescence signal passes through a birefringent material. In this case, the measured polarization anisotropy would not be zero, but would show a dependence on the angle of the cell with respect to the polarization direction. Indeed, we found that fluorescence from E. coli cells expressing freely diffusing GFP showed polarization anisotropy (Fig. 2 A). This intrinsic birefringence was also present for free YFP in C. crescentus (Fig. 2 B). The cellular structure that is causing this apparent anisotropy is unclear. However, the data from freely diffusing GFP can be used to determine an intrinsic anisotropy factor, C, for both E. coli and C. crescentus cells. This factor accounts for the rotation of the incoming and emitted light after passing through birefringent material, such as the cell wall. The measured transmitted light field is related to the actual emitted light from free GFP by
where α is the angle of the cell with respect to the lab x axis and B is a transmission matrix that depends on α and C (see Materials and Methods and the Supporting Material). C is the transmission ratio of the emitted light in the circumferential to that in the cell-axis direction. We find that C values for E. coli and C. crescentus are 0.984 and 0.975, respectively. Thus, for isotropic freely diffusing GFP, this measured intrinsic anisotropy allows us to correct the polarization anisotropy signal for fluorophores attached to FtsZ. The correction procedure is described in the Supporting Material. We also imaged freely diffusing GFP from a cross-sectional view (along the cell axis). From this direction, the transmitted fluorescence is isotropic.
Figure 2.
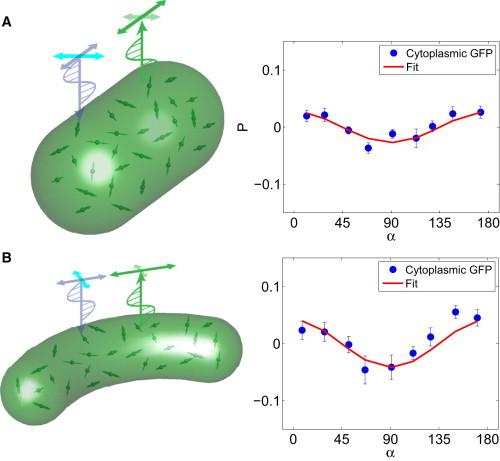
PFM of freely diffusing GFP in bacterial cells. (A) Side view of E. coli cells expressing free GFP (213 cells included). As the angle between the cell axis and the lab axis, α, changes, the images show an intrinsic polarization anisotropy. The reason for this is unclear; it is likely the result of birefringence of biomaterials such as the peptidoglycan cell wall. The results can be used to derive an anisotropy factor, C, which can be used to correct the intensity from fluorophores attached to FtsZ (see text and Supporting Material). (B) C. crescentus cells with freely diffusing YFP show a similar intrinsic anisotropy (133 cells included). To see this figure in color, go online.
To analyze polarization signal from fluorophores attached to FtsZ in the Z-ring, we imaged E. coli cells from the side as well as in cross section (Figs. 3 and 4). In the side view, a series of Z-stacks was scanned to determine variations in the fluorophore dipole orientation from the top to the middle of the Z-ring (Fig. 3 A). Images were taken from several hundred cells with random orientations on the slide. Here, we plot P as a function of the angle between the Z-ring and the lab x axis. Interestingly, FtsZ-YFP and FtsZ-GFP strains both showed significant polarization anisotropy (Fig. 3, C and D), even after correction for the intrinsic anisotropy of transmitted fluorescence. The polarization anisotropy now shows an opposite behavior compared to purified protofilament bundles: it reaches a maximum at 0° and minimum at 90°. This anisotropy is also most pronounced for light coming from the very top of the Z-ring (Fig. 3 A, slice a). These results suggest that there is a significant portion of fluorophores that are aligned in the cell-axis direction.
Figure 3.
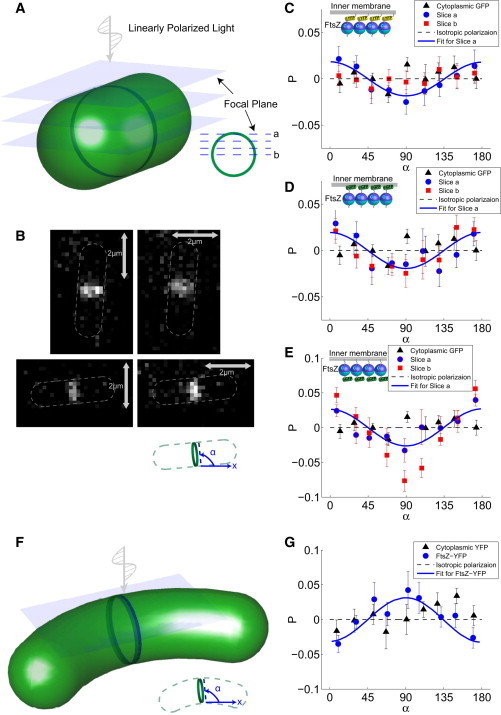
PFM of FtsZ filaments in vivo. (A) Fluorescence images are collected from a side view (with cells lying flat). To obtain 3D information, emitted fluorescence intensities are collected at different planes across the Z-ring. (B) Fluorescence images obtained at the top of the ring (plane a in A) for the polarizer in the vertical and horizontal directions. α is the angle between the Z-ring and the x axis. (C–E) Corrected polarization anisotropy as a function of α for E. coli cells with different FtsZ fluorophore labels. Here, blue and green halves of FtsZ are the C- and N-terminal ends, respectively. Measurements were made for 284 FtsZ-YFP (C), 206 FtsZ-GFP (D), and 56 GFP-FtsZ (E) cells. Error bars correspond to the mean ± SE. Fluorescence was collected at two imaging planes, a and b, which show a similar degree of anisotropy. As a negative control, corrected polarization anisotropy from cells expressing free GFP is also shown. The blue line is a quantitative fit to the data using a distribution of filament orientations, which indicates a disordered organization of FtsZ filaments. (F and G) Corrected polarization anisotropy as a function of α for C. crescentus cells expressing FtsZ-YFP, with 87 cells included. The blue line is a quantitative fit to the data, which indicate a circumferential alignment of FtsZ filaments. To see this figure in color, go online.
In E. coli, FtsZ filaments are tethered to the inner membrane through a C-terminal link between FtsZ and FtsA (28). Due to interaction with FtsA, fluorophores attached to the C-terminal domain may adopt an orientation different from the in vitro orientation. To check this, we also examined FtsZ with an N-terminal GFP in vivo. We found that just as in the in vitro purified protein situation, the N-terminal GFP-FtsZ strain in vivo shows the same polarization anisotropy as the C-terminal FtsZ-YFP and FtsZ-GFP, suggesting that the relative orientation of the fluorophore and the filament axis is not perturbed in vivo (Fig. 3 E). Thus, when the Z-ring is aligned with the x axis (α = 0°), I|| > I=; when the Z-ring is perpendicular to the x axis (α = 90°), I= > I||. These results suggest that in E. coli, FtsZ filaments are not completely oriented in the circumferential ring direction. A substantial portion of the filaments are oriented in the cell-axis direction. In fact, this conclusion does not change if we consider a fluctuating fluorophore described by orientational distributions. The measured polarization anisotropy of in vivo data is also analyzed quantitatively (see Materials and Methods).
Cell-axis alignment of FtsZ filaments can also explain polarization anisotropy measured from the cross-sectional view (Fig. 4). Fluorescently labeled FtsZ rings show polarization anisotropy as a function of the circumferential angle (Fig. 4 C). Here, P shows two maxima, at 90° and 270°. As the fluorophore fluctuates around the filament, there is a component of the fluorophore dipole in the direction of the polarized light, even when the filament is perpendicular to the plane of the cross section. However, cross-sectional data cannot unambiguously distinguish circumferential and axial alignments.
In contrast, polarization anisotropy for FtsZ-YFP in C. crescentus shows a different behavior (Fig. 3, F and G). After correcting for the intrinsic anisotropy, P reaches a maximum at 90° and a minimum at 0°. Although most articles in the literature simply assume circumferential alignment of FtsZ in bacteria, there have been studies that explicitly imaged FtsZ filaments in vivo (9,10). This study, performed using cryo-electron microscopy in C. crescentus, found that FtsZ filaments are aligned in the circumferential direction. Here, our PFM observations indicate that the fluorophores are generally aligned circumferentially. Thus, our results are consistent with the interpretation that C. crescentus FtsZ filaments are aligned in the circumferential direction, but a substantial portion of filaments in E. coli are aligned in the cell-axis direction (Fig. 5).
Figure 5.
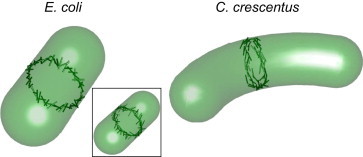
Pictorial representation of FtsZ filament organization in E. coli and C. crescentus. The angular orientation of filaments is generated from probability distributions fitted to experimental data (see the Supporting Material). The results indicate that FtsZ filaments are disorganized in E. coli but aligned circumferentially in C. crescentus. For E. coli, a Z-ring organization where regions of the ring are circumferential and toward the edge is axial could also explain our data (inset). Higher-resolution studies are needed to distinguish between these models. To see this figure in color, go online.
Orientation distribution of FtsZ filaments in live cells
To quantify the degree of FtsZ alignment in the cell, we computed and compared the expected polarization anisotropy for FtsZ aligned in the circumferential and cell-axis directions. The 3D nature of the Z-ring, fluctuations of the attached fluorophore, and variations in FtsZ filament orientations are considered. When the orientation of the fluorophores has been examined in vitro, it is possible to obtain estimates of the filament orientation in vivo. Since N- and C-terminal GFP- and YFP-tagged FtsZ all show similar polarization results both in vitro and in vivo, it is reasonable to conclude that in the live cell, the fluorophore orientation on the FtsZ protofilaments is similar to the orientation in vitro. Using the orientational distributions of fluorophores with respect to protofilaments in vitro, we can then infer the orientational distribution of FtsZ filaments in vivo by fitting the polarization data from the side view. As shown in Fig. S3, we use two spatial angles, and , to describe filament orientations in the local frame of the cell. Since there are many filaments that can potentially orient in any direction, the overall FtsZ organization can be described, as before, by the orientational distribution functions p(β) and p(γ), given explicitly in the Materials and Methods section and the Supporting Material. These distributions are again characterized by average orientations and widths.
To examine the in vivo data, we checked two preferred (average) orientations of the filament (Fig. S6), one in the axial direction (Fig. S6 B) and one in the circumferential direction (Fig. S6 C). We fixed and in those orientations and fitted widths c and d. We used the data from the very top slice to avoid any geometrical effects. The results and fitted distributions are shown in Fig. S6 for FtsZ-YFP. We see that both types of fit give similar results (Fig. S6). Both axial and circumferential filament orientations show significant angular scatter, suggesting that the filaments are disorganized. In Fig. S6, we also show the computer-generated filament organization derived from the fitted distributions. Both axial and circumferential average orientations give a similar disorganized picture, with significant portions of filaments in the axial and circumferential directions. In addition, we can also check intermediate average orientations (between axial and circumferential for and ), and the results are essentially the same as shown. If we define axially aligned filaments as those whose angles with the cell axis are <45°, we can calculate the percentage of these filaments from our orientation distributions. We find that 52% of FtsZ-YFP, 34% of FtsZ-GFP, and 42% of GFP-FtsZ are axially aligned. Therefore, quantitative analysis suggests an overall disorganized picture for FtsZ in the ring.
Similar results were obtained for C-terminal FtsZ-GFP (Fig. S7) and N-terminal GFP-FtsZ (Fig. S8). The fitted distributions are quantitatively in agreement with those obtained from the FtsZ-YFP data. The pictorial representation of filament orientations is also consistent. In contrast, data from C. crescentus FtsZ-YFP show the opposite behavior (Fig. S9). Quantitative fits reveal that the filaments are narrowly distributed in the circumferential direction; 0% of the filaments are aligned within 45° of the axial direction. These results are consistent with earlier electron microscopy findings.
Fig. 5 depicts the organization of the Z-ring as inferred from the quantitative analysis. The orientations of the filaments are directly selected from the fitted orientational distributions. Quantitative results from the fitted orientational distributions are given in Table 2. We note that our methods cannot distinguish possible spatial organization in the Z-ring. Therefore, a ring-halo type of organization is still possible (Fig. 5, inset).
Engineering FtsZ-GFP linkages
In the constructs examined so far, the fluorophore is linked to FtsZ via a flexible linker at either the C-terminal or N-terminal end. These constructs all showed similar behavior, suggesting a disordered FtsZ organization. As a positive control, we can engineer rigid linkers between FtsZ and fluorophores, so that a more accurate picture of FtsZ orientation can be obtained. The rigid linker can also potentially rotate the fluorophore dipole with respect to the filament, which would give a different polarization anisotropy signal. We attempted to do this by both truncating the linker and inserting a rigid helical section Nic96 from Saccharomyces cerevisiae. Many of these constructs were unfortunately not viable. From two that did grow and show fluorescence signal, no significant polarization anisotropy was detected (Fig. S12). If a rigid linker between FtsZ and the fluorophore could be found, then a clearer picture of FtsZ in the Z-ring could be obtained.
Dividing versus nondividing cell
To check whether FtsZ organization changes during cell division and septum formation, we examined the polarization signal for dividing versus nondividing cells. We synchronized C-terminal FtsZ-GFP E. coli cells using DL-serine hydroxamate, which stops the cell cycle by halting the new round of DNA replication. After washing out serine hydroxamate, cells resumed the cell cycle. Polarization microscopy is performed within the first cell cyle, and data are collected before and after the formation of visible septum. We find no significant difference in FtsZ organization in dividing versus nondividing cells (Fig. S10). In both of these phases, FtsZ filaments appear to be similarly disorganized before and after division. This suggests that FtsZ organization remains relatively constant throughout division. In a previous study, we measured the overall fluorescence as a function of contraction radius. It was found that the fluorescence intensity is constant during contraction, suggesting that the total number of FtsZ molecules remained relatively constant (6). These previous results, combined with the polarization results, suggest that increasing the filament density causes a disordered Z-ring contraction.
Polarization anisotropy of FtsZ in cells without MinCDE
The MinCDE system regulates the location of the Z-ring by inhibiting the assembly of FtsZ outside of the midcell region. MinC inhibits polymerization of FtsZ in vitro and has been shown to oscillate from cell pole to cell pole in vivo (26,29,30). Cells without MinCDE will form Z-rings not only in midcell but also near the cell poles. To check whether the orientation of FtsZ filaments in the Z-ring is affected by the Min system, we performed polarization microscopy for the MinCDE deletion strain WM3486 with FtsZ-GFP. The measured polarization anisotropy of FtsZ in MinCDE deletion cells is similar to that in normal cells, and the orientation distributions of FtsZ fitted by circumferential and axial alignments both show disordered organization (Fig. S13). This suggests that the MinCDE system inhibits the assembly of FtsZ, but does not significantly regulate the organization of FtsZ filaments once the Z-ring has formed. This is reasonable, since the Z-ring typically assembles in regions of low MinC concentration.
Discussion
The organization and alignment of FtsZ filaments in the Z-ring have important implications for the mechanism of bacterial cytokinesis. Using PFM to probe the spatial orientation of FtsZ in live bacterial cells, we found that the data suggest that FtsZ filaments are disordered in E. coli. This is in contrast to the primarily circumferential alignment of filaments generally assumed to exist at Z-rings. This result is also consistent with results from super-resolution measurements of Z-ring structure in E. coli (11). Interestingly, C. crescentus FtsZ filaments do exhibit such a circumferential alignment, in agreement with data from cryo-electron tomography. The reasons for the different alignment of C. crescentus FtsZ versus FtsZ of the other bacteria are not known. The difference between cell diameters in E. coli and C. crescentus may play an important role here. However, C. crescentus FtsZ has a much longer peptide linker connecting its core polymerization domain with the C-terminal tail than does FtsZ of E. coli, perhaps changing the interaction of C. crescentus FtsZ with membrane curvature. The degree of curvature of FtsZ filaments in cells is not known, but it is possible that most straight FtsZ filaments align in the cell-axis direction in E. coli to avoid having to conform to an energetically unfavorable curved circumferential direction. Unlike the axial-to-circumferential switch characteristic of septins at the yeast-bud neck during cytokinesis, E. coli FtsZ did not undergo any cell-cycle-dependent organizational changes, as FtsZ filaments were similarly disorganized before and after initiation of visible septation.
Conclusions from the measurement require that the fluorophore dipole is an accurate reporter of the FtsZ-filament direction. To minimize possible artifacts, we measured multiple fluorophores tagged at multiple locations on FtsZ, and found consistent results. We also manipulated the linker between GFP and FtsZ and searched for constructs with a different GFP dipole orientation. It is also possible that somehow the cellular environment affects how GFP fluctuates around the filament. We cannot completely rule out these effects. From the best available data, however, we tentatively conclude that FtsZ filaments are disordered in E. coli and are oriented in the circumferential direction in C. crescentus.
Our finding of disordered orientation of FtsZ filaments raises additional questions. For instance, it is possible that the Z-ring has a mixed organization of randomly oriented filaments, as illustrated in Fig. 5, and a segregated organization, with a central region of circumferential filaments with less organized orientation at the rim of this core (31,32). Since the PFM has poor spatial resolution, we cannot exclude this possibility. In addition, in E. coli cells with fluorescently tagged FtsZ, occasionally the Z-ring seems to lose coherence and develop into spiral-like structures (33,34). It is unclear how disordered FtsZ filaments can organize into a helical spiral. One possible explanation can be inferred from recent findings about MreB, another cytoskeletal bundle thought to exist as a helical spiral in prokaryotic cells (35). High-resolution imaging revealed that directed movement of MreB seems to generate the observed helices, but actual MreB filaments are short and motile in B. subtilis (36,37). A similar explanation could be valid for FtsZ.
Recently, it was shown that artificially membrane-targeted FtsZ filaments can generate a contractile force on lipid tubes (8). If this is true in vivo, then the orientation of FtsZ filaments should influence the direction of the contractile force. It is possible that the in vitro system has a larger number of filaments in the bundle, which would facilitate alignment. Alternatively, from basic physical analysis of cell-wall growth, there appears to be a geometric shape instability in bacteria that could be responsible for cell-shape changes in E. coli (38). In this mechanism, mechanical reinforcements from MreB would regulate the invagination process instead of contractile force from the Z-ring. Thus, bacterial cell division could be the result of a phenomenon rooted in the physics of growing surfaces. By recruiting cell-wall synthesis and turnover proteins, FtsZ may simply regulate the timing of cell division and not directly generate mechanical forces. Recent observations on protoplasts from B. subtilis also revealed that FtsZ is not needed during division of wall-less bacteria (39,40). Our results and others indicate that new mechanistic models for FtsZ may be needed to arrive at a consistent picture of bacterial cytokinesis.
Acknowledgments
The authors thank Lucy Shapiro, Erin Goley, Tim Mitchison, and Amy Gladfelter Labs for providing strains in this work.
This work was supported by National Institutes of Health grant 1R01GM075305.
Supporting Material
References
- 1.Cabeen M.T., Jacobs-Wagner C. Bacterial cell shape. Nat. Rev. Microbiol. 2005;3:601–610. doi: 10.1038/nrmicro1205. [DOI] [PubMed] [Google Scholar]
- 2.Chen Y., Erickson H.P. FtsZ filament dynamics at steady state: subunit exchange with and without nucleotide hydrolysis. Biochemistry. 2009;48:6664–6673. doi: 10.1021/bi8022653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bi E.F., Lutkenhaus J. FtsZ ring structure associated with division in Escherichia coli. Nature. 1991;354:161–164. doi: 10.1038/354161a0. [DOI] [PubMed] [Google Scholar]
- 4.Pichoff S., Lutkenhaus J. Unique and overlapping roles for ZipA and FtsA in septal ring assembly in Escherichia coli. EMBO J. 2002;21:685–693. doi: 10.1093/emboj/21.4.685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Osawa M., Anderson D.E., Erickson H.P. Curved FtsZ protofilaments generate bending forces on liposome membranes. EMBO J. 2009;28:3476–3484. doi: 10.1038/emboj.2009.277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lan G.H., Daniels B.R., Sun S.X. Condensation of FtsZ filaments can drive bacterial cell division. Proc. Natl. Acad. Sci. USA. 2009;106:121–126. doi: 10.1073/pnas.0807963106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stricker J., Maddox P., Erickson H.P. Rapid assembly dynamics of the Escherichia coli FtsZ-ring demonstrated by fluorescence recovery after photobleaching. Proc. Natl. Acad. Sci. USA. 2002;99:3171–3175. doi: 10.1073/pnas.052595099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Osawa M., Anderson D.E., Erickson H.P. Reconstitution of contractile FtsZ rings in liposomes. Science. 2008;320:792–794. doi: 10.1126/science.1154520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li Z., Trimble M.J., Jensen G.J. The structure of FtsZ filaments in vivo suggests a force-generating role in cell division. EMBO J. 2007;26:4694–4708. doi: 10.1038/sj.emboj.7601895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zuber B., Haenni M., Dubochet J. Granular layer in the periplasmic space of gram-positive bacteria and fine structures of Enterococcus gallinarum and Streptococcus gordonii septa revealed by cryo-electron microscopy of vitreous sections. J. Bacteriol. 2006;188:6652–6660. doi: 10.1128/JB.00391-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fu G., Huang T., Xiao J. In vivo structure of the E. coli FtsZ-ring revealed by photoactivated localization microscopy (PALM) PLoS ONE. 2010;5:e12682. doi: 10.1371/journal.pone.0012680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jennings P.C., Cox G.C., Harry E.J. Super-resolution imaging of the bacterial cytokinetic protein FtsZ. Micron. 2010;42:336–341. doi: 10.1016/j.micron.2010.09.003. [DOI] [PubMed] [Google Scholar]
- 13.Strauss M.P., Liew A.T.F., Harry E.J. 3D-SIM super resolution microscopy reveals a bead-like arrangement for FtsZ and the division machinery: implications for triggering cytokinesis. PLoS Biol. 2012;10:e1001389. doi: 10.1371/journal.pbio.1001389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lakowicz J.R. 3rd ed. Springer Science+Business Media; New York: 2006. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 15.Picart C., Discher D.E. Actin protofilament orientation at the erythrocyte membrane. Biophys. J. 1999;77:865–878. doi: 10.1016/S0006-3495(99)76938-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mattheyses A.L., Kampmann M., Simon S.M. Fluorescence anisotropy reveals order and disorder of protein domains in the nuclear pore complex. Biophys. J. 2010;99:1706–1717. doi: 10.1016/j.bpj.2010.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vrabioiu A.M., Mitchison T.J. Structural insights into yeast septin organization from polarized fluorescence microscopy. Nature. 2006;443:466–469. doi: 10.1038/nature05109. [DOI] [PubMed] [Google Scholar]
- 18.Inoué S., Shimomura O., Tran P.T. Fluorescence polarization of green fluorescence protein. Proc. Natl. Acad. Sci. USA. 2002;99:4272–4277. doi: 10.1073/pnas.062065199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johnson R.C., Ely B. Isolation of spontaneously derived mutants of Caulobacter crescentus. Genetics. 1977;86:25–32. doi: 10.1093/genetics/86.1.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sun Q., Margolin W. FtsZ dynamics during the division cycle of live Escherichia coli cells. J. Bacteriol. 1998;180:2050–2056. doi: 10.1128/jb.180.8.2050-2056.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Desper C.R., Kmura I. Mathematics of the polarized fluorescence experiment. J. Appl. Phys. 1967;88:4225–4233. [Google Scholar]
- 22.Volkmer A., Subramaniam V., Jovin T.M. One- and two-photon excited fluorescence lifetimes and anisotropy decays of green fluorescent proteins. Biophys. J. 2000;78:1589–1598. doi: 10.1016/S0006-3495(00)76711-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Richards B., Wolf E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A Math. Phys. Sci. 1959;253:358–379. [Google Scholar]
- 24.Ha T., Laurence T.A., Weiss S. Polarization spectroscopy of single fluorescent molecules. J. Phys. Chem. B. 1999;103:6839–6850. [Google Scholar]
- 25.Anderson D.E., Gueiros-Filho F.J., Erickson H.P. Assembly dynamics of FtsZ rings in Bacillus subtilis and Escherichia coli and effects of FtsZ-regulating proteins. J. Bacteriol. 2004;186:5775–5781. doi: 10.1128/JB.186.17.5775-5781.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Erickson H.P., Anderson D.E., Osawa M. FtsZ in bacterial cytokinesis: cytoskeleton and force generator all in one. Microbiol. Mol. Biol. Rev. 2010;74:504–528. doi: 10.1128/MMBR.00021-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Katoh K., Hammar K., Oldenbourg R. Birefringence imaging directly reveals architectural dynamics of filamentous actin in living growth cones. Mol. Biol. Cell. 1999;10:197–210. doi: 10.1091/mbc.10.1.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pichoff S., Lutkenhaus J. Tethering the Z ring to the membrane through a conserved membrane targeting sequence in FtsA. Mol. Microbiol. 2005;55:1722–1734. doi: 10.1111/j.1365-2958.2005.04522.x. [DOI] [PubMed] [Google Scholar]
- 29.Fischer-Friedrich E., Gov N. Modeling FtsZ ring formation in the bacterial cell-anisotropic aggregation via mutual interactions of polymer rods. Phys. Biol. 2011;8:026007. doi: 10.1088/1478-3975/8/2/026007. [DOI] [PubMed] [Google Scholar]
- 30.Tsukanov R., Reshes G., Feingold M. Timing of Z-ring localization in Escherichia coli. Phys. Biol. 2011;8:066003. doi: 10.1088/1478-3975/8/6/066003. [DOI] [PubMed] [Google Scholar]
- 31.Arumugam S., Chwastek G., Schwille P. Surface topology engineering of membranes for the mechanical investigation of the tubulin homologue FtsZ. Angew. Chem. Int. Ed. 2012;51:11858–11862. doi: 10.1002/anie.201204332. [DOI] [PubMed] [Google Scholar]
- 32.Fischer-Friedrich E., Friedrich B.M., Gov N.S. FtsZ rings and helices: physical mechanisms for the dynamic alignment of biopolymers in rod-shaped bacteria. Phys. Biol. 2012;9:016009. doi: 10.1088/1478-3975/9/1/016009. [DOI] [PubMed] [Google Scholar]
- 33.Thanedar S., Margolin W. FtsZ exhibits rapid movement and oscillation waves in helix-like patterns in Escherichia coli. Curr. Biol. 2004;14:1167–1173. doi: 10.1016/j.cub.2004.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Niu L., Yu J. Investigating intracellular dynamics of FtsZ cytoskeleton with photoactivation single-molecule tracking. Biophys. J. 2008;95:2009–2016. doi: 10.1529/biophysj.108.128751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vats P., Shih Y.L., Rothfield L. Assembly of the MreB-associated cytoskeletal ring of Escherichia coli. Mol. Microbiol. 2009;72:170–182. doi: 10.1111/j.1365-2958.2009.06632.x. [DOI] [PubMed] [Google Scholar]
- 36.Garner E.C., Bernard R., Mitchison T. Coupled, circumferential motions of the cell wall synthesis machinery and MreB filaments in B. subtilis. Science. 2011;333:222–225. doi: 10.1126/science.1203285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Domínguez-Escobar J., Chastanet A., Carballido-López R. Processive movement of MreB-associated cell wall biosynthetic complexes in bacteria. Science. 2011;333:225–228. doi: 10.1126/science.1203466. [DOI] [PubMed] [Google Scholar]
- 38.Jiang H.Y., Si F.W., Sun S.X. Mechanical control of bacterial cell shape. Biophys. J. 2011;101:327–335. doi: 10.1016/j.bpj.2011.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mercier R., Kawai Y., Errington J. Excess membrane synthesis drives a primitive mode of cell proliferation. Cell. 2013;152:997–1007. doi: 10.1016/j.cell.2013.01.043. [DOI] [PubMed] [Google Scholar]
- 40.Leaver M., Domínguez-Cuevas P., Errington J. Life without a wall or division machine in Bacillus subtilis. Nature. 2009;457:849–853. doi: 10.1038/nature07742. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


