Abstract
Time-resolved imaging, fluorescence microscopy, and hydrodynamic modeling were used to examine cell lysis and molecular delivery produced by picosecond and nanosecond pulsed laser microbeam irradiation in adherent cell cultures. Pulsed laser microbeam radiation at λ = 532 nm was delivered to confluent monolayers of PtK2 cells via a 40×, 0.8 NA microscope objective. Using laser microbeam pulse durations of 180–1100 ps and pulse energies of 0.5–10.5 μJ, we examined the resulting plasma formation and cavitation bubble dynamics that lead to laser-induced cell lysis, necrosis, and molecular delivery. The cavitation bubble dynamics are imaged at times of 0.5 ns to 50 μs after the pulsed laser microbeam irradiation, and fluorescence assays assess the resulting cell viability and molecular delivery of 3 kDa dextran molecules. Reductions in both the threshold laser microbeam pulse energy for plasma formation and the cavitation bubble energy are observed with decreasing pulse duration. These energy reductions provide for increased precision of laser-based cellular manipulation including cell lysis, cell necrosis, and molecular delivery. Hydrodynamic analysis reveals critical values for the shear-stress impulse generated by the cavitation bubble dynamics governs the location and spatial extent of cell necrosis and molecular delivery independent of pulse duration and pulse energy. Specifically, cellular exposure to a shear-stress impulse Pa s ensures cell lysis or necrosis, whereas exposures in the range of Pa s preserve cell viability while also enabling molecular delivery of 3 kDa dextran. Exposure to shear-stress impulses of Pa s leaves the cells unaffected. Hydrodynamic analysis of these data, combined with data from studies of 6 ns microbeam irradiation, demonstrates the primacy of shear-stress impulse in determining cellular outcome resulting from pulsed laser microbeam irradiation spanning a nearly two-orders-of-magnitude range of pulse energy and pulse duration. These results provide a mechanistic foundation and design strategy applicable to a broad range of laser-based cellular manipulation procedures.
Introduction
Pulsed laser microbeam irradiation is a powerful tool in cell biology and biotechnology due to its ability to deposit energy with high spatial precision. Laser microbeam irradiation was first utilized in cell and developmental biology to reveal fundamental biological processes, as demonstrated by its ability to produce gene inactivation (1), targeted cell death (2), plasma membrane disruption (3), centrosome ablation (4), and microtubule damage (5), as well as to study forces in mitotic spindle separation (6) and morphogenesis (7). During the last decade, laser microbeams have been used increasingly in biotechnology for the dissection, isolation, separation, and/or measurement of cellular or tissue constituents. Methods used in this regard include laser-tissue microdissection and pressure catapulting for the capture of single cells and microscopic tissue samples (8,9), isolation of single adherent cells by means of micropallet arrays (10,11), and targeted cell lysis and measurement of enzyme activity within single cells using laser micropipet systems (12,13). Laser microbeam irradiation has also been utilized to deliver membrane-impermeable molecules into cells through transient permeabilization, or optoporation, of the cell membrane (14–24). Efficient molecular delivery into living cells is essential in many fields, ranging from basic biological research to applied drug discovery and gene therapy (14,19,25).
Despite this broad use of pulsed laser microbeams over several decades, detailed investigations that attempt to link the characteristics of the physical processes initiated by laser microirradiation and the resulting cellular effect have been pursued only relatively recently (26–30). We have previously characterized the physical interaction and subsequent biological response of adherent cells irradiated with 6 ns, λ = 532 nm pulsed laser microbeam irradiation as a function of laser pulse energy (27,29,31). We have also demonstrated that laser-induced plasma formation is the initiating event for cellular modifications including pulsed laser microbeam cell lysis and optoporation. For nanosecond pulses, plasma formation has been observed to occur in aqueous media when the focal volume irradiance reaches 108–1010 W/mm2. The high temperature and pressure associated with the plasma causes it to expand rapidly, thereby compressing the surrounding medium and leading to shock wave emission on a nanosecond timescale and cavitation bubble formation, expansion and collapse on a microsecond timescale (32,33).
Although laser-induced plasma formation initiates a broad spectrum of cellular modifications, many studies suggest that the resulting cavitation bubble hydrodynamics determine the resulting cellular outcome (21,29,34–37). Our time-resolved imaging studies demonstrated that the cavitation bubble expansion is the primary agent for cell lysis when using 6 ns pulsed laser microbeams focused at a location 10 μm above the cell monolayer, and that the fluid shear associated with this expansion is the key physical process that determines the spatial extent of cellular injury (27,29). Postirradiation assessment of the cellular response using fluorescence assays revealed regions of 1), immediate cell lysis, 2), subsequent cell necrosis, and 3), molecular delivery via optoporation in cell monolayers cultured at a density of 1000 cells/mm2. Hydrodynamic analysis of the cavitation bubble dynamics revealed that the spatial extent of each of these regions is linked to the maximum transient shear stress, , produced by the fluid displaced by the cavitation bubble expansion. Specifically, cells exposed to values in the range 8–18 kPa were viable and successfully optoporated with 3 kDa dextran molecules (31). However, cellular exposure to maximum shear stresses either above or below this range lead to cell lysis/necrosis or continued cell viability without modification, respectively. Interestingly, we found that regardless of pulse energy, 6 ns pulse laser microbeams delivered at a 0.8 NA always resulted in the generation of permeabilized cells and lysed/necrotic cells at a fixed ratio of ∼1.3 and with a spatial precision no better than ∼70 μm.
Given this result, we seek to examine how pulsed laser microbeam irradiation parameters could be modified to alter the cavitation bubble dynamics and thereby enhance one mechanism of cellular modification (e.g., optoporation) over another (e.g., cell lysis/necrosis). Moreover, we wish to examine whether the correspondence between the maximum shear stresses generated by the cavitation bubble dynamics and resulting zones of laser injury/optoporation can be applied more generally. One approach to alter the cellular exposure to laser-generated shear stress to change the resulting cellular effect was explored by the Ohl group by varying the dimensionless stand-off distance of the cavitation bubble relative to the cell surface (21) , where s is the separation distance between the location of bubble formation and the surface on which the cells are cultured and is the maximum bubble radius. In that study, laser pulses 7 ns in duration at a wavelength of λ = 1064 nm created the most extensive zones of cell detachment for γ ∼ 0.65, whereas maximum zones of molecular delivery were achieved for γ → 0. Ohl and co-workers also attempted to correlate these findings to the shear stresses generated by the cavitation bubble dynamics. Nevertheless, the cellular damage zones were exceedingly large (∼1 mm) owing to the large energies (∼16 mJ) and low NA used to produce the optical breakdown.
Here, we examine an alternate strategy of varying the laser microbeam pulse duration to modify the hydrodynamic exposure and resultant cellular effects. This approach is valuable, since shortening the pulse duration reduces the threshold energy required for optical breakdown and alters the conversion efficiency from laser pulse energy to shock wave and cavitation bubble energies (38). Thus, adjustments in the pulse duration and pulse energy can improve the spatial precision of laser-based micromanipulation methods and provide a valuable approach to vary the ratio of necrotic/lysed cells to optoporated cells. Experimental studies have shown that the pulse energy required for plasma formation can be reduced 50-fold when the laser pulse duration is reduced from 5 ns to 50 ps (38,39). Therefore, as compared to the nanosecond pulse durations available from conventional Q-switched lasers, the use of picosecond pulses promises to provide cell lysis with greater precision and enable more subtle cellular perturbations including microsurgery and optoinjection.
Materials and Methods
Microbeam irradiation and time-resolved imaging
A frequency-doubled Nd:YAG laser (EKSPLA SL332) emitting λ = 532 nm pulses with an adjustable duration of 180–1100 ps was used for laser microbeam irradiation of confluent cell cultures. As shown in Fig. 1 a, the linearly polarized laser output was directed through a λ/2 plate followed by a polarization-sensitive beam splitter that establishes low- and high-energy beam lines. The low-energy beam line was directed through a linear polarizer to allow adjustment of the laser pulse energy, and then through a spatial filter and iris to select the central portion of the beam. The beam was then directed into the epifluorescence port of an inverted microscope (Axiovert S100, Zeiss, Thornwood, NY), and reflected upward into the rear-entrance aperture of the objective by a dichroic mirror (532rdc, Chroma Technology, Bellows Falls, VT) placed in the microscope filter cube. The laser pulse energy entering the rear-entrance aperture of the objective was measured by removing the objective from the microscope turret and allowing the unobstructed beam to illuminate an energy detector (J5-09, Coherent, Santa Clara, CA) set on the microscope stage. Pulse-to-pulse energy variation was found to be ±5%. A bright-field objective (Zeiss Achroplan 40×, 0.8 NA) was used for cell irradiation. The focal plane of the pulsed laser microbeam was positioned at a separation distance of 10 μm above the cell monolayer.
Figure 1.
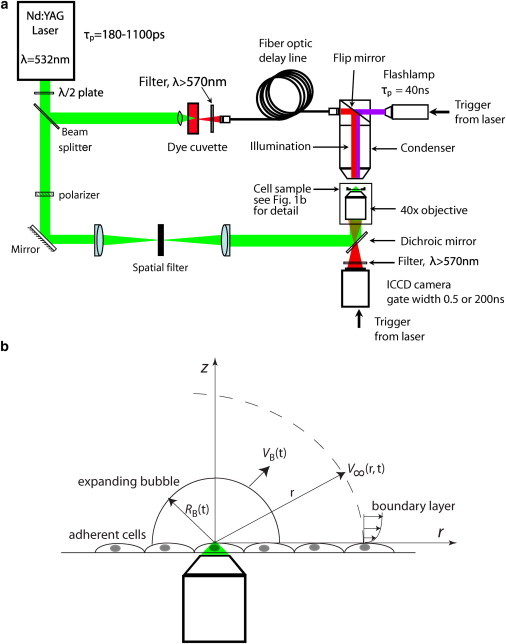
(a) Schematic of the laser-microscope setup for time-resolved imaging of pulsed laser microbeam irradiation of cell cultures. (b) Schematic of the model problem for hydrodynamic analysis. To see this figure in color, go online.
Illumination for time-resolved imaging was provided by delivering a short light pulse at the desired time delay after the arrival of the Nd:YAG laser pulse at the sample. As depicted in Fig. 1, the high-energy beam line was focused into a glass cuvette containing a fluorescent dye (LDS 698, Exciton, Dayton, OH). The delivery of the = 532 nm laser pulse resulted in fluorescence emission at nm with a full-width-at-half-maximum (FWHM) duration of 15 ns. The fluorescence emission was coupled into a 600-μm-core-diameter multimode optical fiber (UMT 600, 0.39 NA, Thorlabs, Newton, NJ), and the fiber output was directed into the microscope condenser to illuminate the sample for time-resolved imaging. Optical fibers of different length were used to provide the desired time delays between arrival of the image illumination and the pulsed laser microbeam irradiation of the sample. The maximum delay time for the fiber optic delay line was 2 μs. At longer time delays, illumination was provided by an ultrashort-duration flash lamp (Nanolite KL-L, High-Speed Photo Systems, Wedel, GERMANY) that was electronically triggered from the camera. The flash lamp emission had a broad spectral output (λ = 400–700 nm) with a FWHM duration of 40 ns.
Images were acquired using a gated intensified CCD camera (PI-MAX 512, Roper Scientific, Trenton, NJ) that was triggered by a TTL pulse from the laser Q-switch. The camera operation and image acquisition were performed using WinView32 imaging software (Princeton Instruments, Trenton, NJ). The camera gate duration was set to 0.5 ns when using the fluorescent dye cell for illumination. When using the flash lamp illumination, the gate duration was set to 200 ns due to the electronic jitter in the flash lamp triggering. Thus, for time delays <2 μs, the exposure duration was governed by the 0.5 ns camera-gate width, whereas at longer time delays, the exposure duration was governed by the 40 ns duration of the flash lamp emission. A long-pass filter (Edmund Optics LP 570, Barrington, NJ) was used to prevent scattered laser radiation from reaching the camera. This system allowed us to irradiate and image the sample at time delays of 0.5–50 μs required to capture the dynamics of the full process.
Hydrodynamic modeling of laser-induced cavitation bubble dynamics
Fig. 1 b provides a schematic for the model problem we use to analyze the hydrodynamic effects of the pulsed-laser-microbeam-generated cavitation bubbles. We utilize the Gilmore model to determine the cavitation bubble dynamics resulting from picosecond laser microbeam irradiation and compute the spatiotemporal evolution of the fluid velocity and shear stress at locations outside the cavitation bubble (40). The Gilmore equation that describes the time-resolved bubble dynamics is given by (32,40)
| (1) |
where , , and are the time-resolved bubble wall radius, velocity, and acceleration, respectively; C is the speed of sound in the liquid at the bubble wall; and H is the enthalpy difference between the fluid at the bubble wall and the fluid far away from the bubble. From the numerical solution to Eq. 1, we determine the time-resolved bubble wall velocity, , and apply conservation of mass to determine the external fluid velocity, :
| (2) |
where and .
Using Eq. 2 to define , we apply conservation of momentum to obtain for the wall shear stress, , generated by the cavitation bubble expansion (29), the expression
| (3) |
where ρ and ν are the density and kinematic viscosity of the fluid medium (29). This equation provides the temporal and spatial dependence of the cellular exposure to wall shear stress upon bubble expansion. The time-resolved shear stress can be integrated to obtain a total shear impulse, , produced by the cavitation bubble dynamics at any given radial location:
| (4) |
where is the bubble oscillation time.
Fluorescence imaging
A Quantix CCD camera (Photometrics, Roper Scientific) was used to capture the fluorescence and phase-contrast images, with 20×, 0.45 NA Phase 2 (Zeiss A Plan) and 10×, 0.3 NA Phase 1 (Zeiss Plan-NEOFLUAR) objectives. Camera operation and image acquisition were performed using V++ imaging software (Digital Optics, Auckland, NZ). The irradiation sites were imaged in both phase-contrast and epifluorescence after completion of the cell assays. A minimum of 10 sites for each pair of pulse duration and pulse energy was examined using fluorescence assays.
PtK2 cell culture
Potorous rat kidney epithelial (PtK2) cells were grown in polystyrene culture dishes with glass bottoms (P35G-0-14-C, MatTek, Ashland, MA) in advanced minimum essential medium (Invitrogen, Carlsbad, CA) supplemented with 1% fetal calf serum, L-glutamine, amphomycin, and gentamicin sulfate. The culture medium was prepared free of phenol red to ensure its transparency to λ = 532 nm radiation. Cells were cultured in a humidified incubator at 37°C and 5% CO2 level. Culture dishes with cells at 100% confluency were used in each experiment. These cells did not exhibit contact inhibition, and the surface density was measured and controlled. The results provided are for cell monolayers cultured at a surface density of 1000 cells/mm2. The cell surface density was determined by counting the number of cells in a 0.5 mm × 0.5 mm square region centered at the site of cell lysis. The site-to-site variation in cell surface density was kept below 10%.
Cell viability and molecular delivery assay
Cell viability was assessed using calcein AM (Invitrogen), a membrane-permeant dye that passes readily through the cell membrane of viable cells and is hydrolyzed by esterases to form fluorescent calcein that remains inside the cell. Dead cells were identified by propidium iodide (PI) (Invitrogen), a DNA-intercalating agent that stains the nuclei of dead cells. Cell culture dishes were incubated 30 min after laser irradiation and loaded with 2 μM calcein AM and 5 μg/mL PI by incubation for 20 min. To remove the remaining dyes, cells were washed carefully with cell culture medium before imaging.
Molecular delivery was assessed by placing cells in a 500 μM solution of fluorescein-isothiocyanate (FITC)-conjugated dextran (3 kDa molecular mass; Sigma, St. Louis, MO) before laser irradiation. After laser irradiation, the cells were incubated at 37°C, and a 5 μg/mL solution of PI was added to identify dead cells. The cells were incubated for 20 min and washed with buffer before imaging. After conducting the fluorescent assays, cells were promptly imaged for quantitative damage zone measurements 30 min after laser irradiation. This incubation time of 30 min was kept constant due to dynamic changes in size of the damage zones due to migration of the viable cells.
Results
Plasma threshold energy for varying pulse durations
Before the cell irradiation experiments, we determined the threshold pulse energy for plasma formation at specific pulse durations. This was achieved by delivering Nd:YAG laser pulses via the 40×, 0.8 NA bright-field objective into a petri dish filled with culture medium. The visual detection of plasma luminescence in a dark room was taken as evidence of plasma formation. We determined the incidence of plasma formation using 50 pulses at discrete pulse energies. This provided a data set for the probability of plasma formation, p, as a function of pulse energy, , for each pulse duration that was fit to a Gaussian error function of the form
| (5) |
where S is the sharpness of the error function and is the threshold pulse energy at which the probability of plasma formation is 50%. Fig. 2 shows the result of the experiment using pulse durations of 180, 280, 360, 540, and 1100 ps, along with data fits to the Gaussian error function. A reduction in pulse duration from 1100 to 180 ps achieves a fivefold reduction in plasma threshold pulse energy, , from 2.13 to 0.45 μJ. For each pulse duration and corresponding threshold pulse energy, we also calculated the resulting threshold irradiance, Ith, assuming the laser beam achieved a diffraction-limited diameter of 0.405 μm. Table S1 in the Supporting Material provides the values of S, , and for each pulse duration examined.
Figure 2.
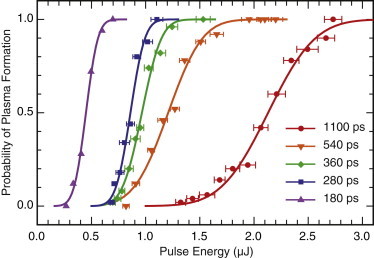
Probability of plasma formation as a function of laser pulse energy with Gaussian error function fit for pulse durations of 180, 280, 360, 540, and 1100 ps. To see this figure in color, go online.
Time-resolved imaging of laser-induced cavitation bubble dynamics
Time-resolved imaging was used to visualize the dynamics of the shock wave propagation and cavitation bubble formation, expansion, and collapse at various time points for pulse durations of 180, 540, and 1100 ps at pulse energies corresponding to 1×, 2×, 3×, and 5× the threshold energy for plasma formation, Eth. Fig. 3 provides a representative time-resolved image series depicting these dynamics at for pulse durations of 180 ps and 1100 ps. Specifically, Fig. 3, a–f, shows cavitation bubble dynamics resulting from 180 ps pulses at = 0.9 μJ and Fig. 3, g–l, shows the dynamics resulting from 1100 ps pulses at = 4.2 μJ. Fig. 3, a and g, capture the shock wave that forms as a result of the rapid plasma expansion. Pressure amplitude estimates approach 500 MPa close to the irradiation site (27). The pressure wave passage did not cause any apparent disruption within the cell monolayer.
Figure 3.
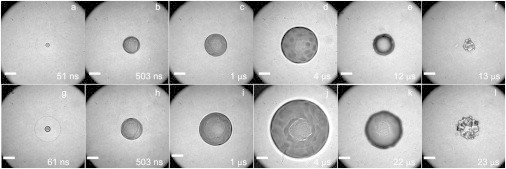
Time-resolved image series of the cell lysis process for pulse durations of 180 ps at 0.9 μJ (a–f) and 1100 ps at 4.2 μJ (g–l) pulse energies that correspond to two times the threshold for plasma formation. Scale bar, 25 μm.
The images in Fig. 3, b–d and h–j, reveal that cavitation bubble expansion is the primary agent for cell lysis and is consistent with our studies of 6 ns pulsed laser microbeam irradiation (29,31). Cellular injury is visible within the central region of the bubble and expands as the bubble continues to grow. For both pulse durations shown, we can observe the formation of a distinct zone of cellular injury/lysis within ∼500 ns. Beyond this time point, further bubble expansion does not result in additional visible cellular injury and the intact cells are clearly seen within and below the cavitation bubble (Fig. 3, d and j). An interesting feature is the transient cellular deformation produced by the bubble expansion, which is evident both outside and inside the bubble (Fig. 3, d and j). Remarkably, these cells appear to withstand this severe deformation without detachment or visible disruption. The use of shorter pulse durations and smaller pulse energies reduces the maximum size and collapse time of the cavitation bubble. The bubble collapse did not produce further cellular injury but does clear any cellular debris in the cell lysis zone.
We measured the dynamics of the cavitation bubble size from a sequence of time-resolved images for pulse durations of 180, 540, and 1100 ps for pulse energies corresponding to 1×, 2×, 3×, and 5×Eth. Data for the time-resolved bubble dynamics and comparison with the Gilmore bubble model predictions for these pulse durations at is shown in Fig. 4. A minimum of three images was used to calculate the average and standard deviation for each data point shown. The agreement between the model and the experimental measurements across all pulse durations and pulse energies are excellent.
Figure 4.
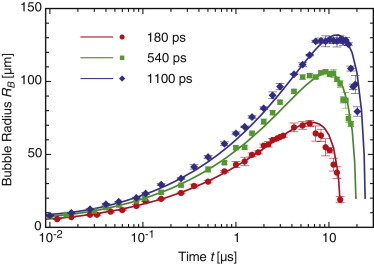
Cavitation bubble dynamics for (a) 180 ps, (b) 540 ps, and (c) 1100 ps laser microbeam pulses at pulse energies corresponding to 2×Eth with curve fits from predictions provided by the Gilmore model. To see this figure in color, go online.
Table 1 lists the values for the maximum bubble radius, , collapse time, , and hemispherical bubble energy, , for each pulse duration and pulse energy tested. This bubble energy is computed using:
| (6) |
where is the static pressure of the surrounding liquid (101,325 Pa) and is the vapor pressure of the liquid (2640 Pa at 22°C). Table 1 also provides the conversion efficiency of laser pulse energy transduction to bubble energy .
Table 1.
Experimental values of Ep, Tcol, Rmax, EB, and EB/Ep at different pulse durations
| tp (ps) | (μJ) | Measured (μs) | Measured (μm) | Fitted (μm) | (μJ) | (%) | |
|---|---|---|---|---|---|---|---|
| 180 | 1 | 0.45 | 8 | 44 ± 2 | 45 | 0.02 | 3.92 |
| 2 | 0.90 | 13 | 71 ± 2 | 72 | 0.07 | 8.24 | |
| 3 | 1.35 | 16 | 87 ± 2 | 88 | 0.14 | 10.1 | |
| 5 | 2.25 | 20 | 109 ± 2 | 110 | 0.27 | 11.9 | |
| 540 | 1 | 1.2 | 13 | 79 ± 5 | 76 | 0.10 | 8.51 |
| 2 | 2.4 | 19 | 107 ± 2 | 106 | 0.25 | 10.6 | |
| 3 | 3.6 | 23 | 129 ± 4 | 127 | 0.4 | 12.4 | |
| 5 | 6.0 | 28 | 160 ± 1 | 155 | 0.85 | 14.2 | |
| 1100 | 1 | 2.1 | 17 | 93 ± 3 | 94 | 0.17 | 7.83 |
| 2 | 4.2 | 23 | 129 ± 3 | 132 | 0.44 | 10.4 | |
| 3 | 6.3 | 27 | 151 ± 3 | 147 | 0.71 | 11.2 | |
| 5 | 10.5 | 35 | 184 ± 2 | 174 | 1.29 | 12.1 |
Results are provided for pulse energies corresponding to 1 ×, 2 ×, 3 ×, and 5 × Eth at the given pulse durations. Also provided is the Rmax fit to the Gilmore model. tp, pulse duration; Eth, threshold energy; Ep, laser pulse energy; Tcol, bubble collapse time; Rmax, maximum cavitation bubble radius; EB, bubble energy; Ep/Eth, ratio of the pulse energy to the threshold energy; EB/Ep, percentage of laser energy transduced to bubble energy.
Fluorescence assays and characterization of the zones of cellular injury
We performed viability and molecular delivery assays after laser microbeam irradiation to examine how the variation of laser parameters such as pulse duration and energy can be used to precisely control the spatial extent of cellular injury and molecular delivery. Therefore, using standard fluorescence microscopy, we measured two zones of cellular injury: 1), the radius of necrotic cells, , which specifies the maximum radius at which cell necrosis is seen and beyond which cells remain intact and viable, and 2), the maximum radius of permeabilized cells, , which specifies the spatial extent of cellulars uptake of 3 kDa FITC-conjugated dextran.
Cell cultures were irradiated with single laser pulses of 180, 540, or 1100 ps duration at energies of Ep = 1×, 2×, 3×, or 5×Eth. Viability assays confirmed that nearly all the adherent cells surrounding the irradiation site remained viable for all the conditions tested. Fig. 5 provides representative phase-contrast and epifluorescence images of cells with viability staining after pulsed laser microbeam irradiation of 180 ps and 1100 ps duration at . Very few dead cells were observed surrounding the region of cell injury and the laser irradiation site. The remaining cells that appeared intact, adherent, and viable were followed for 24 h postirradiation to confirm their continued viability and proliferation.
Figure 5.
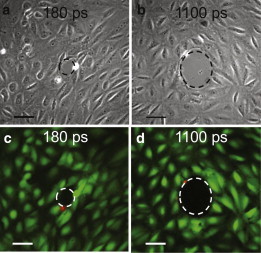
(a and b) Phase-contrast images of the irradiation site and zone of cellular damage, Rnecr. (c and d) Fluorescent images with calcein AM (green) indicating viable cells and PI stained (red) nuclei of dead cells around the periphery of the irradiation site. Cell viability after irradiation is demonstrated for pulse durations of 180 ps and 1100 ps at pulse energies corresponding to two times the threshold energy for plasma formation, i.e., 0.9 μJ for 180 ps (a and c) and 4.2 μJ for 1100 ps (b and d). Scale bar, 50 μm. To see this figure in color, go online.
Once we confirmed the viability of the vast majority of the adherent cells surrounding the irradiation site, we assessed the efficacy of laser microbeam irradiation to deliver molecules into the remaining viable cells. Cell cultures were placed in a solution of 3 kDa FITC-conjugated dextran and exposed to a single laser pulse. Fig. 6 shows representative phase-contrast and fluorescence images that demonstrate molecular uptake of dextran after pulsed laser microbeam irradiation using 180, 540, and 1100 ps pulse durations, at .
Figure 6.
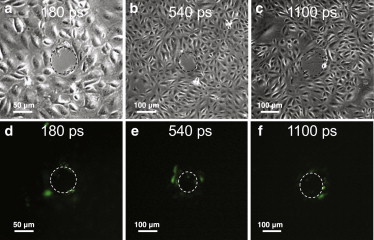
(a–c) Phase-contrast images showing the irradiation site and damage zone. (d–f) Fluorescence images showing cells loaded with FITC-dextran (green). Molecular delivery after irradiation is demonstrated using laser pulse durations of 180 ps (a and d), 540 ps (b and e), and 1100 ps (c and f) at pulse energies corresponding to 2×Eth, i.e., 0.9 μJ for 180 ps (a and d), 2.4 μJ for 540 ps (b and e), and 4.2 μJ for 1100 ps (c and f). To see this figure in color, go online.
To determine the spatial extent of cell viability and molecular delivery, and , respectively, we examined 8–10 irradiation sites for each pair of pulse duration and pulse energy. In cases where the zone of cell injury/permeabilization was slightly elliptical, the radius of a circle of equivalent area was used to determine and . Table 2 presents the radial locations that define the zones of cellular necrosis and permeabilization as a function of pulse duration and pulse energy. Again we found that for a given pulse duration, the zones of cellular injury increase with pulse energy.
Table 2.
Ep, bubble Rmax, Rnecr, and Rperm across pulse durations
| tp (ps) | Ep/Eth | Ep (μJ) | Bubble Rmax (μm) | Rnecr (μm) | Rperm (μm) |
|---|---|---|---|---|---|
| 180 | 1 | 0.45 | 44 ± 2 | 35 ± 5 | 50 ± 6 |
| 2 | 0.90 | 71 ± 2 | 46 ± 4 | 64 ± 9 | |
| 3 | 1.35 | 87 ± 2 | 51 ± 5 | 82 ± 8 | |
| 5 | 2.25 | 109 ± 2 | 69 ± 7 | 103 ± 9 | |
| 540 | 1 | 1.2 | 79 ± 5 | 43 ± 4 | 72 ± 11 |
| 2 | 2.4 | 107 ± 2 | 57 ± 5 | 109 ± 12 | |
| 3 | 3.6 | 129 ± 4 | 66 ± 5 | 135 ± 8 | |
| 5 | 6.0 | 160 ± 1 | 87 ± 7 | 159 ± 13 | |
| 1100 | 1 | 2.1 | 93 ± 3 | 51 ± 5 | 86 ± 11 |
| 2 | 4.2 | 129 ± 3 | 80 ± 6 | 137 ± 14 | |
| 3 | 6.3 | 151 ± 3 | 89 ± 6 | 143 ± 12 | |
| 5 | 10.5 | 184 ± 2 | 115 ± 8 | 175 ± 9 |
Values given are for cell cultures with a cell surface density of 1000 cells/mm2 irradiated at pulse energies corresponding to 1×, 2×, 3×, and 5×Eth. tp, pulse duration; Ep, laser pulse energy; Eth, threshold energy; Rmax, maximum cavitation bubble radius; Ep/Eth, ratio of pulse energy to threshold energy; Rnecr, radius of cell necrosis; Rperm, radius of permeabilized cells.
Analysis and Discussion
Our objectives in this study are threefold. First, we aim to establish the physical effects of laser microbeam irradiation in aqueous media as a function of pulse duration and pulse energy. Second, we seek to determine relationships between the selected laser microbeam parameters, the resulting hydrodynamics, and the subsequent cellular biological response. Third, we aim to determine how variations in laser microbeam pulse duration and energy can be used to modulate the relative extent of cell lysis and molecular delivery.
Effect of bubble-induced shear stress on cellular injury and molecular delivery
We previously established that the hydrodynamic shear stresses associated with the cavitation bubble produced by 6 ns pulsed laser microbeam irradiation focused immediately above the cell monolayer (10 μm) acts as the primary agent for cell lysis, deformation, and injury (27,29,31). Hydrodynamic analysis from these time-resolved imaging studies revealed that the maximum wall shear stress governs the location and spatial extent of cellular necrosis as well as the extent of molecular delivery, independent of laser pulse energy. We also investigated cavitation-bubble-induced optoporation and identified a well-defined range of maximum wall shear stress required to achieve molecular delivery to adherent cells (31). Specifically, we reported that laser-generated cavitation bubbles producing regions of wall shear stresses in excess of 18 ± 2 kPa result in cell lysis necrosis, whereas regions exposed to shear stress values in the range 8–18 kPa results in successful molecular delivery of 3 kDa dextran molecules (31).
To explore whether these criteria are extensible to the results of this study, we use the Gilmore model to determine the cellular exposure to hydrodynamic shear stress at the experimentally determined locations of and for all pulse durations and pulse energies tested. These results are plotted in Fig. 7 a, which reports the maximum shear stress values experienced by the cells located at and versus pulse duration. The detailed shear stress values are provided in Table S2. These results include the data from our earlier 6 ns study (31) which were reprocessed using the Gilmore model. Examination of these data reveal that the maximum shear stress necessary to achieve either cell permeabilization or cell necrosis generally decreases with increasing pulse duration. Because the duration of the cellular exposure to the bubble-generated shear stresses generally decreases with decreasing pulse duration (see Table 1), these data suggest that a time-integrated metric such as the shear stress impulse (Eq. 4) may provide a more effective criterion (41) to predict cavitation-mediated cell lysis and molecular delivery. To explore this, in Fig. 7 b, we plot the values of the shear stress impulse experienced by the cells located at and , provided by the Gilmore model, versus pulse duration; the detailed values are provided in Table S3. With the exception of the data points acquired at for the 180 ps pulse duration, we see a clear separation between the cellular exposure to shear stress impulse for cell necrosis versus molecular delivery. It is important to note that unlike the maximum shear stress criterion, the values for the shear stress impulse are remarkably uniform across pulse duration and pulse energy.
Figure 7.
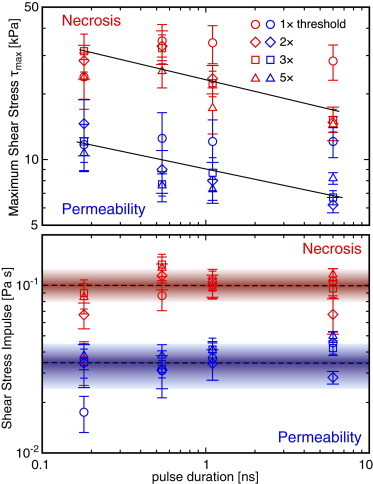
Gilmore model predictions for maximum shear stress, (upper), and shear stress impulse, J (lower), that result in cell necrosis and molecular delivery for pulse durations of 180 ps, 540 ps, 1100 ps, and 6 ns at energies corresponding to 1×, 2×, 3×, and 5×Eth. The solid lines shown in a indicate the general decrease in the maximum shear stress producing cell necrosis (red) and molecular delivery (blue) with increasing pulse duration. The colored bands in the lower chart indicate the mean ± SD of the shear-stress impulse necessary to produce cell necrosis and molecular delivery across all pulse energies and durations. To see this figure in color, go online.
This analysis suggests that independent of laser microbeam duration, energy, and resulting cavitation bubble size, the cellular exposure to shear stress impulse provides a key metric that can be used to predict cellular outcome whether it be cell necrosis, molecular delivery, or viability without molecular delivery. Specifically, if the cellular exposure to hydrodynamic shear stress impulse is Pa s, those cells are likely to become necrotic. Cells exposed to shear stress impulse in the range Pa s are likely to remain viable with successful molecular delivery. Cells exposed to shear stress impulse values Pa s remain viable and not amenable to the delivery of cell-impermeant molecules. Although the data points acquired at for the 180 ps pulse duration appear not to comply with these guidelines, one must recognize that the measured damage zones for this smallest pulse energy begin to approach the size of a single cell. As a result, there is a large variation of shear impulse across the cell surface, and using the maximum radial location for which necrosis or permeabilization occurs does not take into consideration that much of the cell body occupies smaller radial locations where the shear impulse is larger and capable of producing cellular modification. This can be seen by examining the data in Table S3, which show that for both 180 and 540 ps pulse durations at , the values of the shear stress impulse at radial locations and are significantly smaller than the remaining values in the data set, which were acquired at significantly larger energies and result in damage zones significantly larger than the dimensions of a single cell.
More broadly, shear stress impulse may serve as a valuable metric to predict the efficacy of molecular delivery in sonoporation, which employs acoustically generated cavitation bubbles for molecular delivery into suspension or adherent cells. The mechanisms of sonoporation are complex and depend on both geometrical configuration and acoustic source considerations. Although studies have examined the effects of shock-wave-mediated membrane disruption and direct membrane deformation by inertial bubbles (42–45), more recent studies have implicated the role of hydrodynamic shear stresses associated with the bubble dynamics and jetting on the efficacy of molecular delivery (34,46–51). However, hydrodynamic analysis of sonoporation is often confounded by the fact that many critical parameters are not directly controllable; these include the cavitation bubble size, the location of bubble formation relative to the cells, and the number of cavitation bubble oscillations for a given acoustic source exposure. More recent experimental and modeling efforts to examine the interaction between single cell-bubble pairs (52,53) and model the resulting hydrodynamic interaction and efficacy of molecular delivery (51,54) promise to improve our understanding. For example, the recent work of Forbes and O’Brien highlights the potential importance of shear impulse on the efficacy of sonoporation-mediated molecular delivery (51).
Use of pulse duration to control cellular injury and molecular delivery
The use of shorter pulse durations enables plasma formation at smaller pulse energies. The smaller cavitation bubbles that result produce cellular modification with greater spatial precision and specificity (see Table 2). Moreover, it is well known that changes in pulse duration affect the pathways for dissipation of the plasma energy, which includes plasma luminescence, vaporization, shock-wave energy, bubble energy, etc. (38). For this reason, we wanted to explore whether variation of laser microbeam pulse duration can be used to modulate the relative amount of cell necrosis or molecular delivery.
To accomplish this, we estimated the number of necrotic and optoinjected cells by taking the product of the cell surface density of 1000 cells/mm2 and the area of cell injury or permeabilization using the values for and (Table 2). We then divided the number of permeabilized cells by the number of necrotic cells and plotted this ratio versus the normalized pulse energy (Fig. 8). This plot shows 540 ps to be the most favorable pulse duration to maximize the ratio of permeabilized to necrotic cells across all pulse durations tested. At this pulse duration, the ratio of permeabilized to necrotic cells reaches a maximum of 3.19 for a pulse energy of 3.6 μJ. It is important to note that although in our previous study examining 6 ns laser microbeam irradiation we found a fixed ratio of permeabilized to necrotic cells of ∼1.3 (31), here we find that variation of the pulse energy and pulse duration allows for an adjustment of this ratio over the range 1–3. The detailed values used to calculate the ratio of permeabilized to necrotic cells are given in Table S4.
Figure 8.
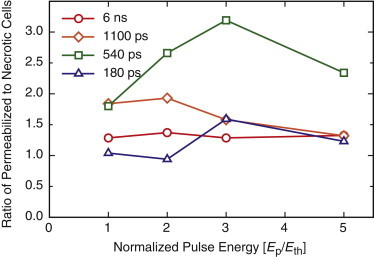
Ratio of permeabilized to necrotic cells versus normalized pulse energy for pulsed laser microbeam durations of 180 ps, 540 ps, 1100 ps, and 6 ns at energies corresponding to 1×, 2×, 3×, and 5×Eth. To see this figure in color, go online.
The finding that 540 ps duration pulses at maximizes molecular delivery while minimizing cell necrosis was unexpected. In fact, careful examination of Table S4 and Fig. 8 reveals that the use of similar pulse energies at different pulse durations (e.g., pulse energies of 5Eth, 2Eth, and Eth at 180, 540, and 1100 ps pulse durations, respectively) can provide very different results in terms of the numbers of necrotic and permeabilized cells as well as the necrotic/permeabilized cell ratios. This is not surprising, since laser pulse duration has a significant impact on the portion of the laser energy that is absorbed by the plasma and how that energy is in turn dissipated via thermal, shock wave, and cavitation processes (38). These results suggest that the pressure associated with the shock wave emission, which generally increase with decreasing pulse duration, may be a secondary contributor to cell necrosis and permeabilization (43,55,56). Specifically, for equivalent pulse energies, the higher shock wave pressure generated when using pulse durations of 180 ps, as compared to 540 ps and 1100 ps, appears to extend the region of necrosis. This is clearly seen in Table 2 when the values for are compared across pulse duration for pulse energies in the 2 μJ range. At the same time, the lower shock wave pressures generated using pulse durations of 1100 ps, as compared to 180 ps and 540 ps, may limit the range of cell permeabilization. This can also be seen in Table 2 when the values for are compared across pulse duration for pulse energies in both 2 μJ and 6 μJ ranges.
Conclusion
We have examined the effects of pulse duration and energy on the cellular response to laser microbeam pulses produced by pulsed laser microbeam irradiation at nm in PtK2 cell monolayers cultured at a density of 1000 cells/mm2. Time-resolved imaging was used to characterize the laser microbeam interactions with adherent cell cultures for pulse durations of 180–1100 ps and energies of 0.45–10.5 μJ. Examination of pulsed laser microbeam plasma formation over this range reveals a nearly fivefold reduction in the threshold pulse energy for plasma formation when the pulse duration is reduced from 1100 to 180 ps. This reduction in the pulse energy necessary to produce plasma formation greatly improves the spatial precision and specificity of the pulsed laser microbeam effects.
The cavitation bubble dynamics resulting from optical breakdown were successfully predicted using the Gilmore model, which enabled quantification of the cellular exposure to hydrodynamic shear stresses and the shear impulse. Fluorescence viability and membrane permeability assays were used to assess the cellular response and spatial extent of the resulting regions of cell necrosis and molecular delivery. Analysis of the experimental data using the Gilmore model results reveal that the spatial extent of the zones of cell necrosis and successful molecular delivery can be predicted using computed values of the shear stress impulse as opposed to the maximum wall shear stress. Specifically, cellular exposure to cavitation bubble shear stress impulse values of Pa s do not appear to affect the PtK2 cell cultures. Shear stress impulse values of Pa s preserve cell viability while also enabling molecular delivery of 3 kDa dextran molecules. Finally, shear stress impulse values of Pa s were found to result in cell necrosis. These criteria appear to be valid for pulse durations spanning 180–6000 ps and pulse energies spanning 0.45–40 μJ.
The variation of pulse duration also allows for modulation of the extent of cellular damage versus molecular delivery. The variation of pulse energy and duration employed in this study was successful in tuning this ratio over the range 1–3, with a maximum value of 3.19 achieved for the 540 ps duration laser microbeams with 3.6 μJ pulse energy. The finding that 540 ps duration pulses provide optimal conditions for cell permeabilization suggests a possible secondary role for shock wave pressure in enhancing cell necrosis at shorter pulse durations and diminishing cell permeabilization at longer pulse durations. Nevertheless, hydrodynamic models can serve as a primary mechanistic foundation for predicting cellular outcome and producing a design strategy for a broad range of laser-based manipulation procedures that will be of great value in cell biology and biotechnology. A natural target of examination for future studies is laser-microbeam-generated cavitation processes in 3D viscoelastic tissue matrices (57) and the development of models to correlate cellular response with viscoelastic stress exposure.
Acknowledgments
We thank Dr. Carole Hayakawa and Dr. Adam Gardner for computational assistance, and Helen Yoon for experimental assistance.
This work was supported by the Laser Microbeam and Medical Program, a National Institutes of Health Biomedical Technology Resource Center grant (P41-EB015890), an I3 Award from University of California Irvine, and the University of California System-wide Biotechnology Research and Education Program (UC BREP) GREAT Training grant (2006-12).
Supporting Material
References
- 1.Berns M.W., Wang Z., Venugopalan V. Gene inactivation by multiphoton-targeted photochemistry. Proc. Natl. Acad. Sci. USA. 2000;97:9504–9507. doi: 10.1073/pnas.97.17.9504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sulston J.E., White J.G. Regulation and cell autonomy during postembryonic development of Caenorhabditis elegans. Dev. Biol. 1980;78:577–597. doi: 10.1016/0012-1606(80)90353-x. [DOI] [PubMed] [Google Scholar]
- 3.McNeil P.L., Miyake K., Vogel S.S. The endomembrane requirement for cell surface repair. Proc. Natl. Acad. Sci. USA. 2003;100:4592–4597. doi: 10.1073/pnas.0736739100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Khodjakov A., Rieder C.L., Wang C.L. De novo formation of centrosomes in vertebrate cells arrested during S phase. J. Cell Biol. 2002;158:1171–1181. doi: 10.1083/jcb.200205102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Khodjakov A., Cole R.W., Rieder C.L. Centrosome-independent mitotic spindle formation in vertebrates. Curr. Biol. 2000;10:59–67. doi: 10.1016/s0960-9822(99)00276-6. [DOI] [PubMed] [Google Scholar]
- 6.Grill S.W., Gönczy P., Hyman A.A. Polarity controls forces governing asymmetric spindle positioning in the Caenorhabditis elegans embryo. Nature. 2001;409:630–633. doi: 10.1038/35054572. [DOI] [PubMed] [Google Scholar]
- 7.Hutson M.S., Tokutake Y., Edwards G.S. Forces for morphogenesis investigated with laser microsurgery and quantitative modeling. Science. 2003;300:145–149. doi: 10.1126/science.1079552. [DOI] [PubMed] [Google Scholar]
- 8.Vogel A., Lorenz K., Gebert A. Mechanisms of laser-induced dissection and transport of histologic specimens. Biophys. J. 2007;93:4481–4500. doi: 10.1529/biophysj.106.102277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vogel A., Horneffer V., Gebert A. Principles of laser microdissection and catapulting of histologic specimens and live cells. Methods Cell Biol. 2007;82:153–205. doi: 10.1016/S0091-679X(06)82005-4. [DOI] [PubMed] [Google Scholar]
- 10.Wang Y., Young G., Allbritton N.L. Collection and expansion of single cells and colonies released from a micropallet array. Anal. Chem. 2007;79:2359–2366. doi: 10.1021/ac062180m. [DOI] [PubMed] [Google Scholar]
- 11.Ma H., Mismar W., Venugopalan V. Impact of release dynamics of laser-irradiated polymer micropallets on the viability of selected adherent cells. J. R. Soc. Interface. 2012;9:1156–1167. doi: 10.1098/rsif.2011.0691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sims C.E., Meredith G.D., Allbritton N.L. Laser-micropipet combination for single-cell analysis. Anal. Chem. 1998;70:4570–4577. doi: 10.1021/ac9802269. [DOI] [PubMed] [Google Scholar]
- 13.Meredith G.D., Sims C.E., Allbritton N.L. Measurement of kinase activation in single mammalian cells. Nat. Biotechnol. 2000;18:309–312. doi: 10.1038/73760. [DOI] [PubMed] [Google Scholar]
- 14.Tao W., Wilkinson J., Berns M.W. Direct gene transfer into human cultured cells facilitated by laser micropuncture of the cell membrane. Proc. Natl. Acad. Sci. USA. 1987;84:4180–4184. doi: 10.1073/pnas.84.12.4180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Turovets I., Lewis A., Lewis S. Permeabilizing millions of cells with single pulses of an excimer laser. Biotechniques. 1993;15:1022–1024. 1026, 1028–1029. [PubMed] [Google Scholar]
- 16.Krasieva T.B., Chapman C.F., Tromberg B.J. Cell permeabilization and molecular transport by laser microirradiation. Proc. SPIE. 1998;3260:38–44. [Google Scholar]
- 17.Soughayer J.S., Krasieva T.B., Allbritton N.L. Characterization of cellular optoporation with distance. Anal. Chem. 2000;72:1342–1347. doi: 10.1021/ac990982u. [DOI] [PubMed] [Google Scholar]
- 18.Stracke F., Rieman I., König K.K. Optical nanoinjection of macromolecules into vital cells. J. Photochem. Photobiol. B. 2005;81:136–142. doi: 10.1016/j.jphotobiol.2005.07.006. [DOI] [PubMed] [Google Scholar]
- 19.Clark I.B., Hanania E.G., Koller M.R. Optoinjection for efficient targeted delivery of a broad range of compounds and macromolecules into diverse cell types. J. Biomed. Opt. 2006;11:014034. doi: 10.1117/1.2168148. [DOI] [PubMed] [Google Scholar]
- 20.Rhodes K., Clark I., Koller M.R. Cellular laserfection. Methods Cell Biol. 2007;82:309–333. doi: 10.1016/S0091-679X(06)82010-8. [DOI] [PubMed] [Google Scholar]
- 21.Dijkink R., Le Gac S., Ohl C.-D. Controlled cavitation-cell interaction: trans-membrane transport and viability studies. Phys. Med. Biol. 2008;53:375–390. doi: 10.1088/0031-9155/53/2/006. [DOI] [PubMed] [Google Scholar]
- 22.Baumgart J., Bintig W., Heisterkamp A. Quantified femtosecond laser based opto-perforation of living GFSHR-17 and MTH53 a cells. Opt. Express. 2008;16:3021–3031. doi: 10.1364/oe.16.003021. [DOI] [PubMed] [Google Scholar]
- 23.Stevenson D.J., Gunn-Moore F.J., Dholakia K. Single cell optical transfection. J. R. Soc. Interface. 2010;7:863–871. doi: 10.1098/rsif.2009.0463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baumgart J., Bintig W., Heisterkamp A. Fs-laser-induced Ca2+ concentration change during membrane perforation for cell transfection. Opt. Express. 2010;18:2219–2229. doi: 10.1364/OE.18.002219. [DOI] [PubMed] [Google Scholar]
- 25.Uchugonova A., König K., Tempea G. Targeted transfection of stem cells with sub-20 femtosecond laser pulses. Opt. Express. 2008;16:9357–9364. doi: 10.1364/oe.16.009357. [DOI] [PubMed] [Google Scholar]
- 26.Venugopalan V., Guerra A., 3rd, Vogel A. Role of laser-induced plasma formation in pulsed cellular microsurgery and micromanipulation. Phys. Rev. Lett. 2002;88:078103. doi: 10.1103/PhysRevLett.88.078103. [DOI] [PubMed] [Google Scholar]
- 27.Rau K.R., Guerra A.G., III, Venugopalan V. Investigation of laser-induced cell lysis using time-resolved imaging. Appl. Phys. Lett. 2004;84:2940–2942. [Google Scholar]
- 28.Vogel A., Noack J., Paltauf G. Mechanisms of femtosecond laser nanosurgery of cells and tissues. Appl. Phys. B. 2005;81:1015–1047. [Google Scholar]
- 29.Rau K.R., Quinto-Su P.A., Venugopalan V. Pulsed laser microbeam-induced cell lysis: time-resolved imaging and analysis of hydrodynamic effects. Biophys. J. 2006;91:317–329. doi: 10.1529/biophysj.105.079921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Quinto-Su P.A., Venugopalan V. Mechanisms of laser cellular microsurgery. Methods Cell Biol. 2007;82:113–151. doi: 10.1016/S0091-679X(06)82004-2. [DOI] [PubMed] [Google Scholar]
- 31.Hellman A.N., Rau K.R., Venugopalan V. Biophysical response to pulsed laser microbeam-induced cell lysis and molecular delivery. J. Biophotonics. 2008;1:24–35. doi: 10.1002/jbio.200710010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vogel A., Busch S., Parlitz U. Shock wave emission and cavitation bubble generation by picosecond and nanosecond optical breakdown in water. J. Acoust. Soc. Am. 1996;100:148–165. [Google Scholar]
- 33.Vogel A. Nonlinear absorption: intraocular microsurgery and laser lithotripsy. Phys. Med. Biol. 1997;42:895–912. doi: 10.1088/0031-9155/42/5/011. [DOI] [PubMed] [Google Scholar]
- 34.Ohl C.-D., Arora M., Lohse D. Sonoporation from jetting cavitation bubbles. Biophys. J. 2006;91:4285–4295. doi: 10.1529/biophysj.105.075366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hutson M.S., Ma X.Y. Plasma and cavitation dynamics during pulsed laser microsurgery in vivo. Phys. Rev. Lett. 2007;99:158104. doi: 10.1103/PhysRevLett.99.158104. [DOI] [PubMed] [Google Scholar]
- 36.Arita Y., Antkowiak M., Dholakia K. Dynamics of primary and secondary microbubbles created by laser-induced breakdown of an optically trapped nanoparticle. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:016319. doi: 10.1103/PhysRevE.85.016319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li Z.G., Liu A.Q., Ohl C.-D. Single cell membrane poration by bubble-induced microjets in a microfluidic chip. Lab Chip. 2013;13:1144–1150. doi: 10.1039/c3lc41252k. [DOI] [PubMed] [Google Scholar]
- 38.Vogel A., Noack J., Birngruber R. Energy balance of optical breakdown in water at nanosecond to femtosecond time scales. Appl. Phys. B. 1999;68:271–280. [Google Scholar]
- 39.Vogel A., Venugopalan V. Mechanisms of pulsed laser ablation of biological tissues. Chem. Rev. 2003;103:577–644. doi: 10.1021/cr010379n. [DOI] [PubMed] [Google Scholar]
- 40.Gilmore F.R. Technical Report 26–4, Hydrodynamics Laboratory, California Institute of Technology; Pasadena, CA: 1952. The growth or collapse of a spherical bubble in a viscous compressible liquid. [Google Scholar]
- 41.Tuler F.R., Butcher B.M. A criterion for the time dependence of dynamic fracture. Int. J. Fract. Mech. 1968;4:431–437. [Google Scholar]
- 42.Kodama T., Tomita Y. Cavitation bubble behavior and bubble-shock wave interaction near a gelatin surface as a study of in vivo dynamics. Appl. Phys. B. 2000;70:139–149. [Google Scholar]
- 43.Kodama T., Doukas A.G., Hamblin M.R. Shock wave-mediated molecular delivery into cells. Biochim. Biophys. Acta. 2002;1542:186–194. doi: 10.1016/s0167-4889(01)00177-x. [DOI] [PubMed] [Google Scholar]
- 44.Sundaram J., Mellein B.R., Mitragotri S. An experimental and theoretical analysis of ultrasound-induced permeabilization of cell membranes. Biophys. J. 2003;84:3087–3101. doi: 10.1016/S0006-3495(03)70034-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lokhandwalla M., Sturtevant B. Mechanical haemolysis in shock wave lithotripsy (SWL): I. Analysis of cell deformation due to SWL flow-fields. Phys. Med. Biol. 2001;46:413–437. doi: 10.1088/0031-9155/46/2/310. [DOI] [PubMed] [Google Scholar]
- 46.Marmottant P., Hilgenfeldt S. Controlled vesicle deformation and lysis by single oscillating bubbles. Nature. 2003;423:153–156. doi: 10.1038/nature01613. [DOI] [PubMed] [Google Scholar]
- 47.Wu J. Theoretical study on shear stress generated by microstreaming surrounding contrast agent attached to living cells. Ultrasound Med. Biol. 2002;28:125–129. doi: 10.1016/s0301-5629(01)00497-5. [DOI] [PubMed] [Google Scholar]
- 48.Wu J.R., Ross J.P., Chiu J.F. Reparable sonoporation generated by microstreaming. J. Acoust. Soc. Am. 2002;111:1460–1464. doi: 10.1121/1.1420389. [DOI] [PubMed] [Google Scholar]
- 49.Ohl C.-D., Wolfrum B. Detachment and sonoporation of adherent HeLa-cells by shock wave-induced cavitation. Biochim. Biophys. Acta. 2003;1624:131–138. doi: 10.1016/j.bbagen.2003.10.005. [DOI] [PubMed] [Google Scholar]
- 50.Prentice P., Prausnitz M., Campbell P. Membrane disruption by optically controlled microbubble cavitation. Nat. Phys. 2005;1:107–110. [Google Scholar]
- 51.Forbes M.M., O’Brien W.D., Jr. Development of a theoretical model describing sonoporation activity of cells exposed to ultrasound in the presence of contrast agents. J. Acoust. Soc. Am. 2012;131:2723–2729. doi: 10.1121/1.3687535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhou Y., Yang K., Deng C.X. Controlled permeation of cell membrane by single bubble acoustic cavitation. J. Control. Release. 2012;157:103–111. doi: 10.1016/j.jconrel.2011.09.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kudo N., Okada K., Yamamoto K. Sonoporation by single-shot pulsed ultrasound with microbubbles adjacent to cells. Biophys. J. 2009;96:4866–4876. doi: 10.1016/j.bpj.2009.02.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Doinikov A.A., Bouakaz A. Theoretical investigation of shear stress generated by a contrast microbubble on the cell membrane as a mechanism for sonoporation. J. Acoust. Soc. Am. 2010;128:11–19. doi: 10.1121/1.3419775. [DOI] [PubMed] [Google Scholar]
- 55.Doukas A.G., McAuliffe D.J., Flotte T.J. Physical factors involved in stress-wave-induced cell injury: the effect of stress gradient. Ultrasound Med. Biol. 1995;21:961–967. doi: 10.1016/0301-5629(95)00027-o. [DOI] [PubMed] [Google Scholar]
- 56.Koshiyama K., Kodama T., Fujikawa S. Structural change in lipid bilayers and water penetration induced by shock waves: molecular dynamics simulations. Biophys. J. 2006;91:2198–2205. doi: 10.1529/biophysj.105.077677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Cherian A.V., Rau K.R. Pulsed-laser-induced damage in rat corneas: time-resolved imaging of physical effects and acute biological response. J. Biomed. Opt. 2008;13:024009. doi: 10.1117/1.2907214. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


